下载文档原格式
一元一次方程解法知识点总结一元一次方程是数学中最基础的方程之一，也是解决实际问题的常用工具。
在解一元一次方程时，有几种常见的方法可以使用，本文将对这些解法进行总结。
1. 直接运用方程性质解法：对于形如ax + b = 0的一元一次方程，可以直接运用方程性质进行解答。
将方程中的常数项b移到等号右侧，得到ax = -b，然后将方程两边同除以系数a，即可得到x的解。
2. 倍数迭代法解法：倍数迭代法是解一元一次方程的常用方法之一。
该方法的原理是通过倍数迭代来逼近方程的解。
具体步骤如下：- 将方程中的常数项移到等号右侧，得到ax = -b。
- 初始值设为x0，可以是任意一个实数。
- 迭代公式为：xi+1 = xi - b/a。
根据公式，计算xi+1的值，并代入下一次迭代计算。
- 重复以上步骤，直到计算得到的xi+1与xi非常接近，即可得到方程的解。
3. 代入法解法：代入法是求解一元一次方程的另一种常见方法。
通过将已知的变量代入方程中，从而求解未知变量的值。
具体步骤如下：- 将方程中的已知变量用代入的方法表示出来，设为y。
- 将y代入方程中，得到一个只含有未知变量x的方程。
- 解这个只含有未知变量x的方程，求得x的解。
- 利用已知变量y和未知变量x之间的关系得到方程的解。
4. 图解法解法：对于一元一次方程，可以通过图形的方式来解答。
截取x轴和y轴的某个特定区间，将方程绘制成直线，然后通过该直线与x轴相交的点来确定方程的解。
具体步骤如下：- 将方程转化为y = ax + b的形式，其中a和b分别为方程的系数。
- 根据a的正负值和零的情况，绘制出直线的大致趋势。
- 确定直线与x轴相交的点，即为方程的解。
本文介绍了一元一次方程的四种常见解法：直接运用方程性质解法、倍数迭代法解法、代入法解法和图解法解法。
通过掌握这些解法，相信读者可以轻松解答一元一次方程的问题，并在实际应用中灵活运用。
一元一次方程的解法一元一次方程是数学中的基础知识，求解一元一次方程是我们学习数学的起点。
本文将介绍一元一次方程的解法，帮助读者理解和掌握求解一元一次方程的方法。
一元一次方程是指只含有一个未知数的一次方程，通常可以写为ax+b=0的形式，其中a、b为已知常数，x为未知数。
解一元一次方程的关键是找到方程的根，即使得方程成立的未知数的值。
解法一：等式两边同时加减法则我们可以通过对方程等式两边进行加减操作，将未知数所在的项移至方程的另一边，从而得到未知数的值。
举例说明：假设有方程3x-5=7，我们希望求解x的值。
首先，我们将方程等式两边加上5，得到3x-5+5=7+5，化简得到3x=12。
接下来，我们再将方程等式两边除以3，得到(3x)/3=12/3，化简得到x=4。
因此，方程3x-5=7的解为x=4。
解法二：移项法移项法是求解一元一次方程的另一种常见方法，通过将等式两边的项进行移位，使得方程的形式更加简化。
举例说明：假设有方程2x+4=10，我们希望求解x的值。
首先，我们将方程中的常数项4移至等式的另一边，得到2x=10-4，化简得到2x=6。
接下来，我们再将方程中的系数项2移至等式的另一边，得到x=(6/2)，化简得到x=3。
因此，方程2x+4=10的解为x=3。
解法三：代入法代入法是求解一元一次方程的一种简便方法，通常适用于方程中含有多个未知数的情况。
举例说明：假设有方程3x+y=9，2x-y=1，我们希望求解方程的解。
首先，我们可以选择其中一个方程，将其中一个未知数表示成另一个未知数的函数。
假设我们选取第二个方程2x-y=1，将y表示成x的函数，得到y=2x-1。
接下来，我们将y的表达式代入第一个方程中，得到3x+2x-1=9，化简得到5x=10。
最后，我们将方程5x=10化简，得到x=2。
将x的值代入到第二个方程2x-y=1中，得到2(2)-y=1，化简得到y=3。
因此，方程3x+y=9和2x-y=1的解为x=2，y=3。
一、知识要点梳理知识点一：一元一次方程及解的概念 1、 一元一次方程：一元一次方程的标准形式是：ax+b=0(其中x 是未知数，a,b 是已知数，且a≠0)。
要点诠释：一元一次方程须满足下列三个条件： （1） 只含有一个未知数； （2） 未知数的次数是1次； （3） 整式方程． 2、方程的解：判断一个数是否是某方程的解：将其代入方程两边，看两边是否相等． 知识点二：一元一次方程的解法1、方程的同解原理（也叫等式的基本性质）等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等。
如果，那么；(c 为一个数或一个式子)。
等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。
如果，那么；如果，那么要点诠释：分数的分子、分母同时乘以或除以同一个不为0的数，分数的值不变。
即：（其中m≠0）特别须注意：分数的基本的性质主要是用于将方程中的小数系数（特别是分母中的小数）化为整数，如方程：－=1.6，将其化为： －=1.6。
方程的右边没有变化，这要与“去分母”区别开。
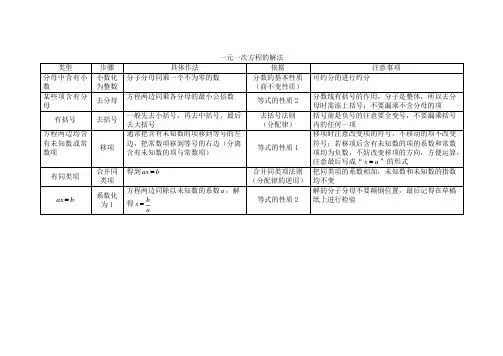
2、解一元一次方程的一般步骤：解一元一次方程的一般步骤变形步骤 具 体 方 法 变 形 根 据注 意 事 项去分母方程两边都乘以各个分母的最小公倍数等式性质21．不能漏乘不含分母的项；2．分数线起到括号作用，去掉分母后，如果分子是多项式，则要加括号去括号先去小括号，再去中括号，最后去大括号 乘法分配律、去括号法则 1．分配律应满足分配到每一项 2．注意符号，特别是去掉括号移 项 把含有未知数的项移到方程的一边，不含有未知数的项移到另一边等式性质11．移项要变号；2．一般把含有未知数的项移到方程左边，其余项移到右边合并同 类 项 把方程中的同类项分别合并，化成“b ax =”的形式（0≠a ）合并同类项法则合并同类项时，把同类项的系数相加，字母与字母的指数不变未知数的系数化成“1”方程两边同除以未知数的系数a ，得a b x = 等式性质2 分子、分母不能颠倒要点诠释：理解方程ax=b 在不同条件下解的各种情况，并能进行简单应用:①a≠0时，方程有唯一解；②a=0，b=0时，方程有无数个解；③a=0，b≠0时，方程无解。
一元一次方程所有知识点一、一元一次方程的概念。
1. 定义。
- 只含有一个未知数（元），未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程。
- 例如：2x + 3=5x - 1是一元一次方程，它只含有一个未知数x，x的次数是1，等号两边2x + 3和5x-1都是整式。
- 一般形式：ax + b = 0(a≠0)，其中a是未知数x的系数，b是常数项。
2. 方程的解。
- 使方程左右两边相等的未知数的值叫做方程的解。
- 例如：对于方程2x+3 = 7，当x = 2时，左边=2×2 + 3=4 + 3 = 7，右边=7，所以x = 2就是方程2x+3 = 7的解。
二、一元一次方程的解法。
1. 移项。
- 把方程中的某一项改变符号后，从方程的一边移到另一边，这种变形叫做移项。
- 例如：在方程2x+3 = 5x - 1中，为了求解x，我们将5x移到左边变为-5x，3移到右边变为-3，得到2x-5x=-1 - 3。
- 移项的依据是等式的基本性质1：等式两边加（或减）同一个数（或式子），结果仍相等。
2. 合并同类项。
- 将方程中含有相同字母且相同字母的指数也相同的项合并在一起。
- 例如：在2x-5x=-1 - 3中，2x-5x=-3x，-1-3 = -4，方程变为-3x=-4。
3. 系数化为1。
- 在方程ax = b(a≠0)的形式下，将方程两边同时除以a，得到x=(b)/(a)。
- 例如：对于方程-3x=-4，两边同时除以-3，得到x=(4)/(3)。
三、一元一次方程的应用。
1. 行程问题。
- 基本公式：路程=速度×时间。
- 相遇问题：两者路程之和等于总路程。
例如：甲、乙两人分别从A、B两地同时出发相向而行，甲的速度是v_1，乙的速度是v_2，经过t小时相遇，AB两地间的距离s=(v_1 + v_2)t。
- 追及问题：两者路程之差等于初始距离。
例如：甲、乙两人同向而行，甲的速度是v_1，乙的速度是v_2（v_1>v_2），开始时甲、乙相距s_0，经过t小时甲追上乙，则s_0=(v_1 - v_2)t。
元一次方程的解法(基础)知识讲解【学习目标】
1.熟悉解一元一次方程的一般步骤，理解每步变形的依据;
2.掌握一元一次方程的解法，体会解法中蕴涵的化归思想;
3.进一步熟练掌握在列方程时确定等量关系的方法
【要点梳理】
要点一、解一元一次方程的一般步骤
要点诠释:
(1 )解方程时，表中有些变形步骤可能用不到，而且也不一定要按照自上而下的顺序，有些步骤可以合并简化.
(2)去括号一般按由内向外的顺序进行，也可以根据方程的特点按由外向内的顺序进行.
(3)当方程中含有小数或分数形式的分母时，一般先利用分数的性质将分母变为整数后再
去分母，注意去分母的依据是等式的性质，而分母化整的依据是分数的性质，两者不要混淆.
要点二、解特殊的一元一次方程
1.含绝对值的一元一次方程
解此类方程关键要把绝对值化去，使之成为一般的一元一次方程，化去绝对值的依据是绝对值的意义.
要点诠释：此类问题一般先把方程化为ax b c的形式，再分类讨论：
(1)当C 0时，无解；⑵当C可化为：ax b c或且x b
2.含字母的一元一次方程
方程无解.
【典型例题】
类型一、解较简单的元一次方程0时，原方程化为：且x b 0
C.
(3)当C 0时，原方程
此类方程一般先化为最简形式(1 )当aZO 时，X »
ax = b,再分三种情况分类讨论:
当a = 0, b= 0时，x为任意有理数；(3)当a二0, bP时,
举一反三：
【变式】下列方程变形正确的是（）
A 由2x-3 二- ■x-4,得2x+x = -4-3
B 由x+3= 2-4x,得5x= 5
C 由
2 3
2X2, 得三”
由3二x-2, 得-x = -2~3
D
1 2 2x 1 10x 7 2 3 2 x 1 2 x
【思路点拨】方程中含有括号，应先去括号再移项、合并、系数化为【答案与
解析】（1）去括号得：4x 2 10x 7
移项合并得：6x 5
解得：X 5
6
（2）去括号得：3 2x 2 2x 6
移项合并得：4x 7
7
解得：X
4
【总结升华】去括号时，要注意括号前面的符号，括号前面是“是“-”，各项均变号.
举一反三：
【变式】解方程：5（x-5） +2x = -4 .
【答案】解：去括号得：5X-25+2X = -4 .移项合
并得：7x = 21.
解得：x = 3.
类型三、解含分母的一元一次方程（常数项）
ax= b（a羊0）的形式.
（3）系数化为1:即根据等式性质2:方程两边都除以未知数系数a,即得方程的解x -
a
3
1,从而解出方程.
号，不变号；括号前面
a,曲春?新乡期末)解方程筈I/'弩
【思路点拨】方程按照去分母，去括号，移项合并同类项，把X系数化为1的步骤，即可求
出解.
【答案与解析】
解：去分母得：2 (2x- 1) - 12=3 (3x+2),
去括号得：4x- 2 - 12二9x+6,
移项合并得：5x=- 20,
解得：x= - 4.
【总结升华】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1,求出解. 举一反三：
【变式】(2015?岳池县模拟)解方程：X注少-2 -上二？
2 3 4
【答案】解：去分母得：12x+30=24x - 8 - 3X+24,
移项合并得：-9x=- 14,解得：x=2\
9
类型四、解较复杂的一元一次方程
0^
.解方程：△—0^ 1
0. 7 0. 03
【思路点拨】先将方程中的小数化成整数，再去分母，这样可避免小数运算带来的失误.
10x
【答案与解析】原方程可以化成：竺3 1.
7
去分母，得：30x-7 (17-20x) = 21.
去括号、移项、合并同类项，得：170x= 140.
14
系数化成1,得：x —.
17
【总结升华】解此题的第一步是利用分数基本性质把分母、分母化整，与去分母方程两边都乘以分母的最小公倍数要区分开.
(x 1)【答案与解析】
解法1：先去小括号得:
17 20
x
分子同时扩大相同的倍数，以使
-x
1
) 2 1) 2 -X
3
Z
3 1
再去中括号得：-X
2
4’
移项，合并得：
5 一X
12
11
系数化为1,得：X —
5
解法2:两边均乘以2,去中括号得： 1 4
x 2(x 1) -(X 1) 3 去小括号，并移项合并得：
11 11 X
1
-[(x n —,解得：
6 詼
解法3:原方程可化为： 1 1)
■ 2 (x 1)]
2 (X 1)
1 1
去中括号，得丄八1）丄
11
解得X
5
【总结升华】解含有括号的一元一次方程时，一般方法是由里到外或由外到内逐层去括号, 构特点，灵活恰当地去括号，以使计算简便•例如本题的方法
左、右两边都含（X-1）,因此将方程左边括号内的一项X变为（X-1）后，把体运算.
举一反三：
3 2
s
【变式】汀2（- 1）2]
2 3 4
【答案】
解：去中括号得：（兰1）2x2
4
3
去小括号，移项合并得：°
—X 6,解得x= -8
类型五、解含绝对值的方程
—6 .解方程凶-2 = 0
【答案与解析】
解：原方程可化为：
但有时根据方程的结
3:方程（X-1）视为一个整
当x > 0时，得x=2 ,
当x〈0时，得-x=2,即，所以原
x= -2 . 方程的解是x = 2或x二-
【总结升华】此类问题一般先把方程化为ax b的形式，再根据ax的正负分类讨论，注意不要漏解.。
