工程力学第六章杆件与结构的内力计算
- 格式:pptx
- 大小:1.52 MB
- 文档页数:74


《建筑力学》课程教学大纲一、本课程的地位、作用和任务《建筑力学》是水利水电建筑工程专业的一门重要的专业基础课,在本专业中起着承上启下的作用,为后续课程打基础。
《建筑力学》的任务是:教授学生掌握物体受力分析与静力平衡问题的求解方法;杆件及结构内力与变形的分析方法;关于构件的强度、刚度与稳定性的计算及构件应力、应变的方法。
通过本课程的学习,要求学生具备对常见结构、构件进行受力分析、内力与变形计算的能力,并初步具备对结构的实验分析能力。
二、教学内容和教学要求第一章绪论1、教学内容建筑力学的研究对象、研究方法、主要内容。
2、教学要求了解建筑力学课程的性质、地位和作用,了解建筑力学各部分的内容、了解建筑力学的学习方法。
第一篇、静力学第二章刚体静力分析基础1、教学内容2—1 力与力偶1)力的概念和性质2)力对点之矩3)力偶的概念和性质2—2 约束与约束反力1)约束与约束反力的概念2)工程中常见的约束与约束反力2—3 受力分析与受力图2、教学要求(1)理解力、力对点的矩、平面力偶的概念及静力学的四个公理,合力矩定理、刚体的概念;掌握平面力偶系合成的计算。
(2)了解约束的概念及荷载的分类;了解作用在构件上荷载的计算方法;掌握常见工程中的约束类型及其约束反力的确定;第三章平面力系1、教学内容3—1 平面力系向一点的简化1)力的平移定理2)平面力系向一点的简化3)力在坐标轴上的投影主矢与主矩的计算4)平面力系向一点简化结果的进一步分析3—2 平衡方程及其应用1)平面一般力系的平衡条件和平衡方程2)平面力系的几种特殊情形3)静定与超静定问题4)物体系的平衡问题2、教学要求(1)了解力的平移定理的内容;掌握力在坐标轴上的投影的概念及计算,掌握合力的投影定理;(2)理解平面一般力系的概念;了解平面一般力系向一点简化和简化结果分析。
(3)掌握平面一般力系、平面汇交力系、平面平行力系及平面力偶系的平衡方程及其应用,重点掌握常见物体支座反力的求法。

截面法求杆件的内力教学目标:1、理解和掌握求杆件内力的方法——截面法;2、熟练运用截面法求不同杆件受到拉伸时的内力。
教学重点:截面法求杆件内力的步骤。
教学难点:如何运用截面法求内力的方法解决工程力学中求内力的实际问题。
教学方法:提出问题——实例演示——练习点拨——归纳总结教学过程:一、复习旧知1、杆件有哪几种基本变形?2、拉伸和压缩的受力特点是什么?3、拉伸和压缩的变形特点是什么?二、新课讲解思考:当杆件受到拉伸、压缩时,就会在杆件内部产生力的作用,怎样才能确定杆件的内部会产生多大的力?(引出课题)出示本节课的学习目标。
(一)、教学什么是杆件的内力?内力:杆件在外力作用下产生变形,其内部相互间的作用力称为内力。
一般情况下,内力将随外力增加而增大。
当内力增大到一定限度时,杆件就会发生破坏。
内力是与构件的强度密切相关的,拉压杆上的内力又称为轴力。
(二)、教学截面法求杆件的内力。
1、什么是截面法?截面法:将受外力作用的杆件假想地切开,用以显示内力的大小,并以平衡条件确定其合力的方法,称为截面法。
它是分析杆件内力的唯一方法。
2、实例演示:如图AB 杆受两个力,一个向左,一个向右,大小均为F 。
作用点分别为A 和B 。
①、确定要截开的次数和位置(要根据杆件的受力情况而定) ②、选取一半截面为研究对象(一般选取受力较少的一段作为研究对象)③、假设出截面上的内力(取左段内力向右设,取右段内力向左设,方向跟坐标轴方向一致,左负右正、下负上正)④、用平衡方程求出截面上的内力(求出的内力为正值为拉力,负值为压力)取左段 ∑Fx=O -F +FN =0 取右段 ∑Fx=O F -FN =0FN =F FN =F 3、总结截面法求杆件内力的步骤:(1)截:在需求内力的截面处,沿该截面假想地把构件切开。
(2)取:选取其中一部分为研究对象。
(3)代:将截去部分对研究对象的作用,以截面上的未知内力F F N来代替。
(4)平:根据研究对象的平衡条件,建立平衡方程,以确定未知内力的大小和方向。

《工程力学》课程中杆件内力的教学实践搞要:以培养学生对知识总结和系统化的良好习惯为目的,在教学实践过程中,针对杆件内力需要掌握的知识点,总结出快速计算内力和绘制内力图的方法,同时精炼出助记口诀,并取得了很好的教学效果。
关键词:工程力学杆件内力教学实践工程力学课时少,相对的课程内容多,涉及到学习新概念和新知识,这对初学者而言确实有一定难度。
而其中杆件内力是工程力学最基础的知识之一,能否准确迅速计算杆件内力或绘制内力图,对进一步分析杆件强度、刚度、稳定性有很大的影响。
但目前学生在学习中,往往感觉有难度、不容易做到准确无误地完成轴力图、剪力图和弯矩图。
针对在学习中同学们遇到一些的问题,这里介绍杆件内力需要掌握的知识点,以及总结出快速计算内力和绘制内力图的方法。
同时精炼出口诀,便于学习和记忆。
1 内力正负号轴力的正负号规定:使杆拉伸时的轴力为正,反之为负(如图1)。
即:轴力方向在截面外法线方向一致时为正。
扭矩T的正负号规定:扭矩矢量方向与截面外法线方向一致时为正;反之为负(如图2)。
简称:以外法线方向为正。
剪力Q:使截开部分杆件产生顺时针方向转动的为正,反之为负。
即:在被截开部分左面向上为正、向下为负;在被截开部分右面向下为正、向上为负。
弯矩M:使梁弯曲成上凹下凸的形状时,则弯矩为正;反之使梁弯成下凹上凸形状时,弯矩为负。
即:在被截开部分左面顺时针转动为正、逆时针方向转动为负;在被截开部分右面逆时针方向转动为正、顺时针转动为负(如图3)。
上述规律可归纳为:“左上右下,剪力为正;左顺右逆,弯矩为正”。
这里的方位“左”和“右”含义是指截面相对所取研究对象的方位。
进一步精简为:外法线方向,左上右下,左顺右逆,为正。
2 基本方法截面法是力学中研究受力构件内力的一个基本方法。
它可以概括为以下四个步骤:(1)截:在欲求内力的截面处,沿该截面假想地将杆件截分为两部分。
(2)取:取其中任何一部分为研究对象。
(3)代:用内力代替弃去部分对研究对象的作用。

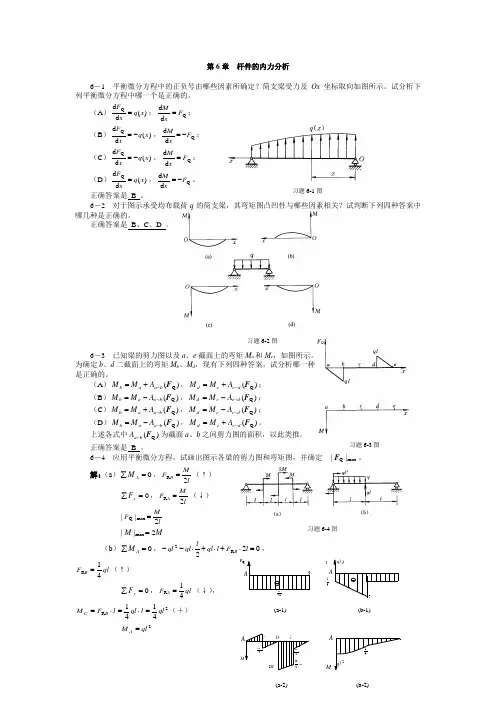
习题6-1图习题6-2图习题6-3图习题6-4图第6章 杆件的内力分析6-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A d Q F d M (B (C (D 6-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中。
6-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。
为确定b M 、M ,现有下列四种答案,试分析哪一种 (A (B (C (D 之间剪力图的面积,以此类推。
6-4 应用平衡微分方程,试画出图示各梁的剪力图和弯矩图,并确定 m axQ ||F 。
解:( (b )0=∑AM,22+⋅+⋅--F l ql l ql ql qlF B 41R =(↑)0=∑y F ,qlF A41R =(↓),2R 4141qll ql l F MB C=⋅=⋅=(+)2qlMA=51 —qlF 45||max Q =2max ||qlM =(c )0=∑y F ,qlF A =R (↑)0=∑AM ,2qlM A=0=∑DM,022=-⋅-⋅+DMl ql l ql ql223qlMD= ql F =max Q ||2max 23||qlM =(d )0=∑BM2132R =⋅-⋅⋅-⋅l ql l q l F AqlF A 45R =(↑)=∑y F ,qlF B 43R =(↑)0=∑BM,22lq M B==∑DM,23225qlMD=qlF 45||max Q =2max 3225||qlM =(e )0=∑y F ,F R C = 0 0=∑CM ,0223=+⋅+⋅-CMl ql l ql 2qlMC= 0=∑BM,221qlMB==∑y F ,qlF B=Qql F =max Q ||2max ||qlM =(f )0=∑AM,qlF B 21R =(↑) 0=∑y F ,qlF A 21R =(↓)0=∑y F ,021Q =-+-B F ql qlqlF B 21Q =0=∑DM,42221+⋅-⋅DMl l ql ql 281qlMD-=281qlME=∴qlF 21||max Q =522max 81||qlM =6-5 试作图示刚架的弯矩图,并确定max||M 。


杆件受力分析杆件的内力计算和受力平衡杆件受力分析是工程力学中一个重要的内容,能够帮助我们了解和计算杆件内力以及保证杆件的受力平衡。
本文将介绍杆件受力分析的基本概念和计算方法,并根据实际例子进行说明和分析。
一、杆件受力分析概述杆件,指的是工程结构中的长条形构件,常用于支撑和传递力量。
在实际应用中,杆件往往会受到多方向的力的作用,因此需要进行受力分析,计算出杆件内部的力,以保证其受力平衡。
在进行杆件受力分析时,我们需要明确以下几个概念:1. 受力点:指的是外力作用到杆件上的点,也是进行受力分析的起点。
2. 内力:指的是杆件内部存在的力,可以是拉力或压力。
3. 受力平衡:指的是杆件上所有受力的合力和合力矩为零的状态,保证了杆件受力的平衡。
二、杆件内力计算方法1. 自由体图法:自由体图法是杆件受力分析的基本方法,通过将杆件与外界切割开来,分析切割面上的受力情况,进而计算出杆件内力。
过程:选择合适的切割面,画出自由体图,分析受力平衡条件,解方程计算内力。
2. 杆件法:杆件法是将整个杆件视为一个整体,通过利用杆件的几何关系和受力条件进行计算。
过程:根据杆件的几何形状和受力情况,建立方程组求解。
三、杆件受力分析实例为了更好地理解和应用杆件受力分析的方法,下面以一个实际例子进行说明:假设有一根长度为L的杆件,一端固定在墙上,另一端悬挂一个质量为m的物体。
我们需要计算杆件的内力以及保证受力平衡。
首先,我们选择杆件的中点作为切割面,并画出自由体图。
根据受力平衡条件,我们可以得出以下方程:∑Fx = 0: T - F = 0 (水平方向受力平衡)∑Fy = 0: N - mg = 0 (竖直方向受力平衡)其中,T代表杆件的张力,F代表杆件所受悬挂物体的重力,N代表杆件与墙壁接触点的支撑力,g代表重力加速度。
通过解以上方程组,我们可以计算出T和N的数值,进而得到杆件内部的力。
根据实际情况,可以通过杆件截面积和材料的力学性质,计算出杆件的应力和变形情况。



第六节 杆件的强度计算由内力图可直观地判断出等直杆内力最大值所发生的截面,称为危险截面,危险截面上应力值最大的点称为危险点。
为了保证构件有足够的强度,其危险点的有关应力需满足对应的强度条件。
一、正应力与切应力强度条件轴向拉(压)杆中的任一点均处于单向应力状态。
塑性及脆性材料的极限应力u σ分别为屈服极限s σ(或2.0σ)和强度极限b σ,则材料在单向应力状态下的破坏条件为u σσ= 材料的许用拉(压)应力[]nuσσ=,则单向应力状态下的正应力强度条件为[]σσ≤ (6-24)同理可得,材料在纯剪切应力状态下的切应力强度条件[]ττ≤ (6-25)二、正应力强度计算由式(6-1)和(6-25)得,拉(压)杆的正应力强度条件为[]σσ≤=AN maxmax (6-26) 由式(6-1)和(6-25)得,梁弯曲的正应力强度条件为[]σσ≤=zW M maxmax (6-27) 应用强度条件可进行强度校核、设计截面、确定许可载荷等三方面的强度计算。
例6-7 如图6-29(a)所示托架,AB 为圆钢杆2.3=d cm ,BC 为正方形木杆a=14cm 。
杆端均用铰链连接。
在结点B 作用一载荷P=60kN 。
已知钢的许用应力[]σ=140MPa 。
木材的许用拉、压应力分别为[]t σ=8MPa ,[]5.3=c σMpa ,试求:(1)校核托架能否正常工作。
(2)为保证托架安全工作,最大许可载荷为多大;(3)如果要求载荷P=60kN 不变,应如何修改钢杆和木杆的截面尺寸。
解 (1)校核托架强度 如图6-29(b)。
图6-29由 0=∑Y ,0sin 1=-P P α解得 100c s c 1==αP P kN 由 0=∑X ,0cos 21=+-P P α 解得 80cos 12==αP P kN杆AB 、BC 的轴力分别为10011==P N kN, 8022-=-=P N kN ,即杆BC 受压、轴力负号不参与运算。
第六章 杆类构件的内力分析6.1。
(a )(b )题6.1图解:(a )应用截面法:对题的图取截面2-2以下部分为研究对象,受力图如图一所示:BM图一图二由平衡条件得:0,AM=∑6320N F ⨯-⨯=解得: N F =9KN CD 杆的变形属于拉伸变形。
应用截面法,取题所示截面1-1以右及2-2以下部分作为研究对象,其受力图如图二所示,由平衡条件有:0,OM=∑6210N F M ⨯-⨯-=(1)0,yF=∑60N S F F --=(2)将N F =9KN 代入(1)-(2)式,得: M =3 kN·m S F =3 KN AB 杆属于弯曲变形。
(b )应用截面法 ,取1-1以上部分作为研究对象,受力图如图三所示,由平衡条件有:0,Fx =∑20NF-=图三MNF =2KN0,DM=∑210M -⨯= M =2KNAB 杆属于弯曲变形 6.2题6.2图解:首先根据刚体系的平衡条件,求出AB 杆的内力。
刚体1的受力图如图一所示D2m图一图二平衡条件为:0,CM=∑104840D N F F ⨯-⨯-⨯=(1) 刚体2受力图如图二所示,平衡条件为:0,EM=∑240N D F F ⨯-⨯= (2)解以上两式有AB 杆内的轴力为:N F =5KN6.3(a )(c )题6.3图解:(a ) 如图所示,解除约束,代之以约束反力,做受力图,如图1a 所示。
利用静力平衡条件,确定约束反力的大小和方向,并标示在图1a 中,作杆左端面的外法线n ,将受力图中各力标以正负号,轴力图是平行于杆轴线的直线,轴力图线在有轴向力作用处要发生突变,突变量等于该处总用力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,轴力图如2a 所示,截面1和截面2上的轴力分别为1N F =-2KN 2N F =-8KN ,n (b 2 (面N F题6.4图解(a )如图所示,分别沿1-1,2-2截面将杆截开,受力图如1a 所示,用右手螺旋法则,并用平衡条件可分别求得:1T =16 kN·m 2T =-20 kN·m ,根据杆各段扭矩值做出扭矩图如2a 所示。