切线方位角计算
- 格式:doc
- 大小:28.00 KB
- 文档页数:1

曲线坐标计算通用公式(复化Simpson 公式)推导一、已知条件1、线元起点坐标:(),A A A x y2、线元起点切线方位角:A α3、线元起点里程:A K4、线元终点里程:B K 5、线元起点曲率半径:A ρ 6、线元终点曲率半径:B ρ二、求解问题求线元上任意点的坐标:(),C x y 。
即推导曲线坐标计算通用公式。
三、图示:如右上图(图中未示y ∆值) 四、坐标计算公式线元上任意点C 的坐标计算公式为:A x x x =+∆————① A y y y =+∆————②由上式可知,关键问题是求出x ∆、y ∆。
五、x ∆计算若AC 是直线,直接采用公式cos x l α∆=可求出x ∆(其中l 为A 、C 两点间直线距离,α为AC 直线方位角),但是,A 、C 两点间是任意曲线相连,不能直接用上述公式计算x ∆,需利用微积分原理计算。
1、曲线AB 上任意一点的曲率ρ计算采用内插法得:()B AA AB Ak k k k ρρρρ-=+--————③其中:k ——曲线AB 上任意一点的里程。
2、曲线AB 上任意一点的切线方位角α计算如右图:C 是曲线AB 上任意一点,AT 、TC 是A 、C 两点的切线,利用圆曲线求弧长公式得:()90A A k k A R π-=()90A k k Rδβπ-==其中:k ——曲线上任意点里程。
R ——曲线上任意点的曲率半径。
(通过公式③求得,1R ρ=)()()1190A A A R R k k ααπ=++-()()90A A A k k αρρπ=++-————④ 使用公式③、④时的符号规定:线元右偏:A ρ、B ρ均为“+”(即线元起终点曲率半径输正值)。
线元左偏:A ρ、B ρ均为“—”(即线元起终点曲率半径输负值)。
3、x ∆计算根据公式③、④可推知,()cos y k α=⎡⎤⎣⎦是里程间隔[],A C k k 上k 的一个连续函数,计算A 、C 两点的坐标增量x ∆,也就是求在里程段[],A C k k 内,x 坐标的改变量。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。


高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。

方位角及坐标计算公路工程各点方位角及坐标计算公式(一)各点方位角计算:1、第一直线段(K0~ZH):F=arctgΔY/ΔX注:直线方位角要考虑象限角才能定出正确线路走向 2、第一缓和曲线段(KZH~KHY):δ1=(K0-KZH)2/(2RLh)×180/π 3、圆曲线段(KHY~KYH):δ2=[2(K0-KZH)-Lh]/2R×180/π δ2=(KHY-KZH)/2R×180/π+(K0-KHY)/R×180/π无缓和曲线时:δ2=(K0-KHY)/R×180/π(即圆曲线圆心角) 4、第二缓和曲线段(KYH~KHZ):δ3=(KHZ-K0)2/(2RLh)×180/π 5、第二直线段(KHZ~KZH):F±α (左偏时F-α,右偏时F+α)注:K0――计算点的程α――曲线交点偏角Lh――缓和曲线长(注意有时第一和第二缓和曲线长不一样)(二)各点坐标计算XZH=XJD-T?CosF XHZ=XJD+T?Cos(F±α) YZH=YJD-T?SinF YHZ=YJD+T?Sin(F±α) 1、第一直线段:X=XZH+(K0-KZH)?CosF 中桩Y=YZH+(K0-KZH)?SinF X边=X中±B?Cos(F-Δ)边桩Y边=Y中±B?Sin(F-Δ)注:B――中桩至所求点的距离(左幅时为+B,右幅时为-B,当设计轴线与线路不垂直时B取斜长,即B/SinΔ)设计轴线线路方向。
BΔ 图S-12、第一缓和曲线段: XX=XZH-Y′?Sinθ+X′?Cosθ X X′ X′ 中桩′Y=YZH+Y′?Cosθ+X′?Sinθ Y ZH Y θ HZX边=X中±B?Cos(F+μδ1-Δ) HY YH 边桩Y边=Y中±B?Sin(F+μδ1-Δ)JD Y′ 注:(本公式只适用与图S-2线形)图S-2 μ――曲线左转为-1,右转为+1θ――线路方位角与Y轴所夹的锐角,见图S-2 Y′=L-L5/(40R2Lh2);X′=L3/(6RLh)-L7/(336R3Lh3);(R―圆曲线半径,L―缓和曲线上任一点至曲线起点长度)3、圆曲线段:X=XHY+2R?Sinφ?Cos(F+μ(ξ+φ))中桩Y=YHY+2R?Sinφ?Sin(F+μ(ξ+φ)) X边=X中±B?Cos(F+μδ2-Δ)边桩Y边=Y中±B?Sin(F+μδ2-Δ)注:φ=(K0-KHY)/2R×180/π;ξ=(KHY-KZH)/2R×180/π 4、第二缓和曲线段:X=XHZ-Y′?Sinθ+X′?Cosθ 中桩Y=YHZ-Y′?Cosθ-X′?Sinθ X边=X中±B?Cos(F+μδ1-Δ)边桩Y边=Y中±B?Sin(F+μδ1-Δ)注:1、本公式只适用与图S-2线形,其他线形可根据本线形公式变换2、式中符号与第一缓和曲线意义相同3、注意有时第一缓和曲线长和第二缓和曲线长不一样4、第二直线段:X=XHZ+(K0-KHZ)?Cos(F±α)中桩Y=YHZ+(K0-KHZ)?Sin(F±α) X边=X中±B?Cos(F±α-Δ)边桩Y边=Y中±B?Sin(F±α-Δ)注:F――第一直线段的方位角(三)用CASIO fx-4500P计算已知坐标点在线路上的里程和距中线距离 1、直线段(已知坐标X、Y)Pol(X-XHZ,Y-YHZ):K=V?Cos(F-W)+KHZ B=V?Sin(F-W)注: 1、在fx-4500P中计算结果存入变量储存区V和W,要显示储存区内容时按RCL V 、 W 键。
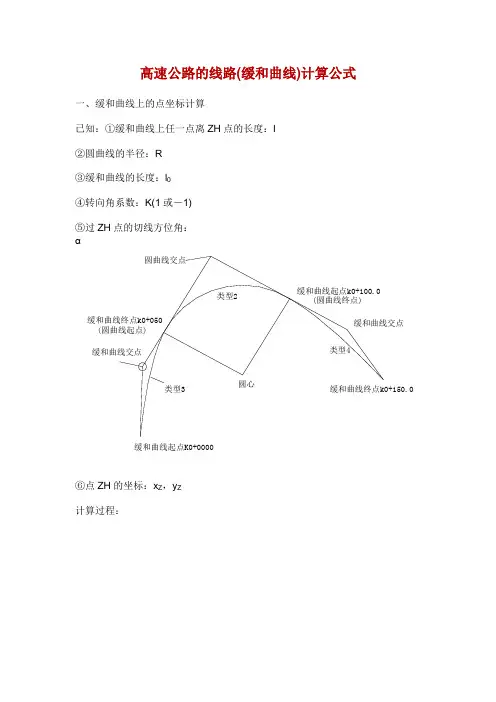
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。

在公路中线坐标计算中,我们通常采用切线支距公式来计算曲线上各点的坐标。
但当在不同的曲线上计算时就需用不同的计算公式,这为计算也带来不便。
在设有缓和曲线的圆曲线半径较小或是卵形曲线上的坐标计算时,如公式选用不当就会出现较大计算误差,即便是能对切线支距公式进行多项展开,也会增加计算的难度。
而用复化辛卜生公式不仅能解决不同曲线线型或直线上的坐标计算问题,而且用复化辛卜生公式计算完全是可逆的(即:可顺前进方向也可逆向计算),尤其在计算第二缓和曲线和卵形曲线时显得尤为方便。
用辛卜生公式计算坐标的精度可由人为或程序自行判断,其计算结果完全能保证坐标计算的精度要求。
因此,可以说复化辛卜生公式是一个计算公路中线坐标的万能公式。
下面本人就该公式在公路中线坐标计算中的具体应用进行实例解析。
一、复化辛卜生公式式中:H=(Z i-Z A)/n(公式2)(公式3)Zi —待求点桩号Z A—曲线元起点桩号Z B—曲线元终点桩号ρA—曲线元起点曲率ρB—曲线元终点曲率a i曲线上任意一点处切线方位角的计算方法有以下三种方法:1.利用公式(3)求得曲率代入公式(2)计算2.利用曲线元上已知起点和终点曲率用内插法求得曲率代入公式(2)计算3.利用切线角公式计算二、算例例:已知雅(安)攀(枝花)高速公路西昌西宁立交A匝道一卵形曲线(卵形曲线相关参数见图一,其计算略。
),相关设计数据见下表。
现用辛卜生公式来计算卵形曲线中桩坐标。
图一已知相关设计数据见下表:(一)由+271.881推算Zi=+223.715的坐标,n取2等分用公式(3)、公式(2)计算+247.798处曲线及方位角:ρ+247.798=1÷75+(1÷50-1÷75)(247.798-271.881) ÷(223.715-271.881)=0.01666666666666667a+247.798=71°24’18.5” +(0.016666667+1÷75)(247.798-271.881)×180÷π÷2=50°42’26.37”其它各点依次代入公式计算,结果见下表:切线方位角图示1将计算出的数据代入公式(1)求得+223.715中桩坐标如下:X=9880.438+(271.881-223.715)÷2÷6×(cos71°24’18.5”+4(cos61°37’52.22”+cos38°38’0.96”)+2cos50°42’26.37”+ cos25°24’35.99”)=9910.5975 (设计值:9910.603)Y=10100.904+(223.715-271.881)÷2÷6×(sin71°24’18.5”+4(sin61°37’52.22”+sin38°38’0.96”) +2sin50°42’26.37”+ sin25°24’35.99”)=10136.7945 (设计值:10136.791)(二)由+223.715推算Zi=+271.881的坐标,n取2等分用公式(3)计算+247.798处曲线及方位角:ρ+247.798=1÷50+(1÷75-1÷50)(247.798-223.715)÷(271.881-223.715)=.01666666666666667a+247.798=205°24’33.6”+ (0.016666667+1÷50)(247.798-223.715)×180÷π÷2=230°42’23.98”其它各点依次代入公式计算,结果见下表:切线方位角图示2X=9910.603+(271.881-223.715)÷2÷6×(cos205°24’33.6”+4(cos218°37’58.87”+cos241°37’49.83”)+2cos230°42’23.98”+ cos251°24’16.11”)=9880.4431 (设计值:9880.438)Y=10136.791+(271.881-223.715)÷2÷6×(sin205°24’33.6”+4(sin218°37’58.87”+sin241°37’49.83”)+2sin230°42’23.98”+ sin251°24’16.11”)=10100.9008 (设计值:10100.904)由上可知,利用复化辛卜生公式计算路线坐标时可顺向或逆向计算。

通过弧长计算出园心角,通过园心角计算出弦长,以及这段园曲线的弦切角,直线的方位角加上(左转减,右转加)这个弦切角就是弦的方位角,这样就可以求出园曲线的终点(也就是下一段曲线的直缓点)的坐标.怎样计算不完整缓和曲线起点及终点的坐标及切线方位角以上为一条匝道的曲线图及要素表。
第一缓和段长度根据公式c=R*L及C=A*A,图中A=100,R=150,可算出第一缓和段的长度为66.667米。
而HY里程减去YH里程为60.902米。
因此此段缓和曲线是在离其起点5.765米的地方与前段圆曲线相交。
图上标为YH点。
固此YH点并非第一缓和段起点。
第二缓和段也有同样的问题,DZD点亦非第二缓和段终点。
问题:怎样计算第一缓和段真正起点的坐标和第二缓和段真正终点的坐标。
及切线方位角。
本人水平有限,苦苦思索未得其解。
在此劳烦各位同仁给予小弟支援。
不胜感谢!测量路上诚与仁兄们携手同行,让我们的测量之路多一丝欣慰,少一分苦闷。
QQ26889412E-mail: yujuying@ 注:曲线要素表可能看不清楚。
但可以把图片另存为一个文件。
然打开此文件就非常清楚了。
1.计算出Y1H的坐标及方位角;2.计算出过渡段缓和曲线在Y1H点的支距dx,dy及偏角β;3.由Y1H的方位角及偏角β可反算出过渡缓和曲线虚起点的方位角。
4.由Y1H的坐标、dx,dy及方位角可反算出过渡缓和曲线起点的坐标。
(用支距到大地坐标的变换公式反算。
关于不同类型缓和曲线的判断及起点、终点曲率半径的计算方法目前在匝道或线路施工坐标计算中经常遇到缓和曲线,实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算,这就牵涉到线元的起点终点曲率半径判断的问题,一般的直线元,圆曲线元的起点终点半径判断,比较容易,可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题,缓和曲线有时候判断算对了,有时候却坐标算不对,究其原因,其实问题出于该缓和曲线是否是完整缓和曲线引起的。
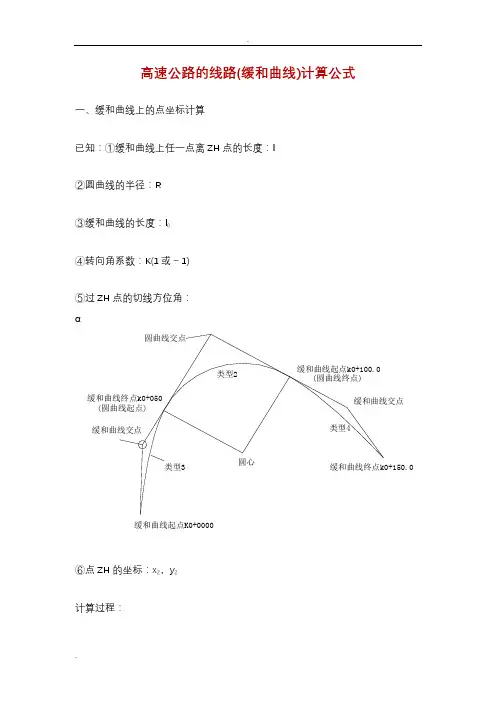
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。


非完整缓和曲线坐标计算公路、铁路主干线一般线形采用曲线基本型,而在公路匝道部分常采用线形单元组合形式,组合线形的坐标计算只能按线形单元分段计算。
通常设计文件中提供各特征点的桩号、坐标、切线方位角。
圆曲线计算较为简单,这里主要讨论非完整缓和曲线的桩点的坐标计算。
一、计算ZH(HZ)点的坐标已知数据:如图4.9.1所示,起点p的半径Rp ,桩号Lp坐标Xp、Yp,切线方位角αp,缓和曲线参数A。
式中各项计算如下:图4.9.1 非完整缓和曲线αpZ的计算:其中Δp——右偏用“-”,左偏用“+”。
ZH切线坐标方位角:其中βp——左偏用“+”,右偏用“-”(ZH换成HZ时,左偏用“-”,右偏用“+”)。
二、计算缓和曲线切线坐标系各点坐标计算出缓和曲线起点坐标后即可按式4.8.2计算各中线点坐标。
三、计算施工坐标系坐标切线坐标系转换为施工坐标系需要进行坐标平移和转轴计算,当转向角为右时按式(4.9.7)、(4.9.8)计算;当转向角为左时按式(4.9.9)、(4.9.10)计算。
(1)当转向角为右时:(2)当转向角为左时:式中 Xi ,Yi——路线统一坐标系坐标;x i ,yi——切线坐标;α——转向点之间的切线方位角。
【例4.9.1】如图4.9.2所示,起点P处半径RP =9 579.228 m,桩号lP=0+889.975,XP =19 698.065,YP=28 469.399,起点的切线方位角αP=82°34′06″,缓和曲线参数A=60。
与缓和曲线相接的圆曲线半径R=55 m,公切点的桩号lGQ=K0+824.896试计算K0+860的坐标。
图4.9.2 非完整缓和曲线【解】(1)计算ZH的桩号和XZH ,YZH:(左偏)用“+”:(2)计算αZH切线方位角:(3)计算K0+860坐标:+860点切线坐标系坐标:x=30.30 m,y=1.293 m(计算过程略)+860点施工坐标系坐标:。
高斯五点公式详细计算方法A A R K 1=,BB R K 1=, A B AB K K K -= 则p 点坐标如下: ⎥⎦⎤⎢⎣⎡+±+=∑=2212(cos i S AB i A A n i i A p V l l K lv K R l x x α ⎥⎦⎤⎢⎣⎡+±+=∑=2212(sin i S AB i A A ni i A p V l l K lv K R l y y α p 点方位角:)2(2SAB A A P l l K l K +±=αα 式中:A α=起始方位角 l =p 点到A 的距离 S l =曲线总长 P α=p 点切线方位角 280951184634425.051==R R 496832393143352.042==R R44442844444444.03=R 046910070.0151=-=V V 23076534.0142=-=V V 5.03=V 其中: A r A A K l R l l K ==π180 r S AB r B A S B A S AB l K l R R l R R l l l K )2()(902222=-=π式中:A α=起始方位角 l =p 点到A 的距离 S l =曲线总长 P α=p 点切线方位角 起点A 的曲率为A K ,终点B 的曲率为B K , R 为曲线半径。
±表示曲线元的偏向,当曲线元左偏时取负号,当曲线元右偏时取正号。
公式推导:⎥⎦⎤⎢⎣⎡+±+=∑=)2(cos 221i S AB i A A ni i A p V l l K lv K R l x x α =⎥⎦⎤⎢⎣⎡+±+∑=)2(cos 1i S AB A i A ni i A V l l K K lv R l x α =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+±+∑=)2)11(1(cos 1i S i A n i i A V l l A B A lv R l x α=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+±+∑=)2)11(1(cos 1i S i A ni i A V l l A B A lv R l x α =⎥⎦⎤⎢⎣⎡-+±+∑=)2)(1(cos 1i S i A ni i A V ABl l B A A lv R l x α 因)2)(1(i Si V ABl l B A A lv -+计算出来是弧度,所以将其转换成度 =⎥⎦⎤⎢⎣⎡-+±+∑=)2)(1(180cos 1i S i A n i i A V ABl l B A A lv R l x πα 公式中A 和B 分别为起点半径和终点半径。
公路卵形曲线任意点坐标和切线方位角的计算方法
张玲玲;张志伟
【期刊名称】《兰州交通大学学报》
【年(卷),期】2007(026)001
【摘要】针对公路卵形曲线段上任意点坐标和过该点的切线方位角的计算、测设问题,结合工程实例,将卵形曲线转化为完整缓和曲线的一部分,进而推导了简洁、实用、易懂的计算公式.此种计算公式在应用计算机编程计算方面也比较实用.
【总页数】3页(P86-88)
【作者】张玲玲;张志伟
【作者单位】兰州交通大学,土木工程学院,甘肃,兰州,730070;中铁十三局集团,第五工程有限公司,吉林,长春,130033
【正文语种】中文
【中图分类】TB22
【相关文献】
1.道路缓和曲线任意点坐标及方位角的计算方法 [J], 樊志军
2.卵形曲线要素及其上任意点坐标的严密算法 [J], 任克林
3.应用弦长与弦方位角、切线方位角推算公路曲线坐标 [J], 翁黎辉
4.非对称缓和平曲线任意点坐标及方位角计算 [J], 马志平
5.道路卵形回旋线任意点坐标及方位角计算方法 [J], 叶松林
因版权原因,仅展示原文概要,查看原文内容请购买。
曲线上点的切线方位角计算公式:
圆曲线:±1*起点到计算点的圆心角+起点的切线方位角(ZY)
完全对称缓和曲线:
第一缓和曲线:±1*ZH到计算点的缓和曲线长^2/(2*R*Ls)*(180/PI())+ZH点的切线方位角。
圆曲线:±1*(Ls/(2*R)+HY到计算点的圆弧曲线长度/R)*(180/PI())+ZH点的切线方位角。
第二缓和曲线:1*HZ到计算点的缓和曲线长^2/(2*R*Ls)*(180/PI())+HZ点的切线方位角+180。
不对称缓和曲线:
第一缓和曲线:±1*ZH到计算点的缓和曲线长^2/(2*R*Ls1)*(180/PI())+ZH点的切线方位角。
圆曲线:±1*(Ls1/(2*R)+HY到计算点的圆弧曲线长度/R)*(180/PI())+ZH点的切线方位角。
第二缓和曲线:1*HZ到计算点的缓和曲线长^2/(2*R*Ls2)*(180/PI())+HZ点的切线方位角+180。