下载文档原格式
齿轮传动效率计算公式
齿轮传动是一种常见且重要的机械传动方式，其通过齿轮的啮合实现力的传递和转速的变换。
在实际应用中，了解齿轮传动的效率对于正确设计和选择传动系统至关重要。
齿轮传动的效率是指输入功率与输出功率之间的比值，通常以百分比表示。
齿轮传动的效率计算公式如下：
效率 = （输出功率 / 输入功率）× 100%
其中，输出功率是齿轮传动转动后输出的功率，输入功率是齿轮传动输入的功率。
为了计算齿轮传动的效率，首先需要确定齿轮传动的输入功率和输出功率。
输入功率可以通过测量输入轴上的转矩和转速得到，输出功率则可以通过测量输出轴上的转矩和转速得到。
然而，齿轮传动的效率并不是一个恒定的数值，它受到多种因素的影响。
以下是一些影响齿轮传动效率的因素：
1. 摩擦损失：齿轮传动中的摩擦会导致能量损失，降低传动效率。
减少齿轮齿面的摩擦和磨损可以提高传动效率。
2. 轴向载荷：齿轮传动中的轴向载荷会增加齿轮的摩擦和变形，从而降低传动效率。
合理设计轴承和支撑结构可以减小轴向载荷，提高传动效率。
3. 齿轮啮合精度：高精度的齿轮啮合可以减小摩擦和噪声，提高传动效率。
4. 润滑状态：适当的润滑可以减小齿轮的摩擦和磨损，提高传动效率。
总之，了解齿轮传动的效率对于正确选用和设计传动系统至关重要。
通过计算齿轮传动的输入功率和输出功率，并考虑各种影响因素，可以得到准确的传动效率，从而优化机械系统的性能。
周转轮系的传动比计算周转轮系是一种用于传输运动和力的机械装置，常用于车辆和工程机械等设备中。
传动比是周转轮系中的重要参数，用于描述输入轮与输出轮的转速比和力的大小，决定了输出轮的转速和扭矩。
计算周转轮系的传动比需要确定输入轮和输出轮的直径。
假设输入轮的直径为D1，输出轮的直径为D2，其对应的转速分别为N1和N2、则周转轮系的传动比可以由下面的公式计算得到：传动比=N2/N1=D1/D2其中，传动比表示输出轮相对于输入轮的转速增益。
如果传动比大于1，输出轮的转速将大于输入轮的转速；如果传动比小于1，输出轮的转速将小于输入轮的转速；如果传动比等于1，输出轮的转速与输入轮的转速相等。
在实际应用中，周转轮系的传动比可以通过以下几种方式计算和确定。
1.机械传动计算法：根据输入轮和输出轮的直径来计算传动比。
这种方法适用于已知直径和转速的情况，但需要知道输入轮和输出轮的几何参数。
2.编码器计算法：通过安装编码器在输入轮和输出轮上，实时测量转速，然后计算传动比。
这种方法能够较准确地测量转速，但需要安装编码器和进行实时测量。
3.转速传感器计算法：通过安装转速传感器在输入轮和输出轮上，测量转速并传输给计算设备，然后计算传动比。
这种方法能够较准确地测量转速，但需要安装转速传感器和进行实时测量。
4.模拟计算法：根据输入轮和输出轮的转速曲线来进行传动比的估算。
这种方法能够通过分析转速曲线得到传动比的趋势，但需要输入轮和输出轮的转速曲线数据。
总之，传动比是周转轮系中的重要参数，能够描述输入轮和输出轮之间的转速和扭矩关系。
计算传动比需要确定输入轮和输出轮的直径，并可以通过机械传动计算法、编码器计算法、转速传感器计算法或模拟计算法来进行。
通过计算传动比可以优化周转轮系的设计和使用，满足具体设备的要求。
![毕业设计(论文)-行星轮系减速器设计[管理资料]](https://img.taocdn.com/s1/m/5371fe25b9f3f90f77c61b64.png)
第一章概述行星轮系减速器较普通齿轮减速器具有体积小、重量轻、效率高及传递功率范围大等优点，逐渐获得广泛应用。
同时它的缺点是：材料优质、结构复杂、制造精度要求较高、安装较困难些、设计计算也较一般减速器复杂。
但随着人们对行星传动技术进一步的深入地了解和掌握以及对国外行星传动技术的引进和消化吸收，从而使其传动结构和均载方式都不断完善，同时生产工艺水平也不断提高，完全可以制造出较好的行星齿轮传动减速器。
根据负载情况进行一般的齿轮强度、几何尺寸的设计计算，然后要进行传动比条件、同心条件、装配条件、相邻条件的设计计算，由于采用的是多个行星轮传动，还必须进行均载机构及浮动量的设计计算。
行星齿轮传动根据基本够件的组成情况可分为：2K—H、3K、及K—H—V三种。
若按各对齿轮的啮合方式，又可分为：NGW型、NN型、WW型、WGW型、NGWN型和N型等。
我所设计的行星齿轮是2K—H行星传动NGW型。
第二章原始数据及系统组成框图（一）有关原始数据课题: 一种自动洗衣机行星轮系减速器的设计原始数据及工作条件：使用地点：自动洗衣机减速离合器内部减速装置；传动比：p i=输入转速:n=2600r/min输入功率：P=150w行星轮个数：n=3w内齿圈齿数z=63b（二）系统组成框图洗涤：A 制动，B 放开，运动经电机、带传动、中心齿轮、行星轮、行星架、波轮脱水：A 放开，B 制动，运动经电机、带传动、内齿圈（脱水桶）、中心齿轮、行星架、波轮与脱水桶等速旋转。
自动洗衣机的工作原理：见图第三章减速器简介减速器是一种动力传达机构，利用齿轮的速度转换器，将马达的回转数减速到所要的回转数，并得到较大转矩的机构。
减速器降速同时提高输出扭矩，扭矩输出比例按电机输出乘减速比，但要注意不能超出减速器额定扭矩。
降速同时降低了负载的惯量，惯量的减少为减速比的平方。
一般的减速器有斜齿轮减速器(包括平行轴斜齿轮减速器、蜗轮减速器、锥齿轮减速器等等)、行星齿轮减速器、摆线针轮减速器、蜗轮蜗杆减速器、行星摩擦式机械无级变速机等等。
第15卷 第5期1996年 9月机械科学与技术M ECHAN ICA L SCI EN CE AN D T ECHN O LO GY V ol.15 N o.5Sep 1996 苏志霄封闭式行星轮系传动效率计算的结点功率法苏志霄 薛隆泉 崔亚辉 郗向儒 杨华成(西安理工大学 西安 710048)摘 要 利用迭加原理分析了差动轮系的功率流,提出了计算差动轮系效率的结点功率法,并将其应用于封闭式行星轮系的效率分析中,得出了具有实用价值的效率分式。
关键词 差动轮系 封闭式行星轮系 相对效率 结点功率法中图号 HT132.4引 言封闭式行星轮系的效率是由封闭体和差动轮系两部分综合影响而决定的,常见的差动轮系效率计算方法有啮合功率法[1],力矩法[1]、三平衡方程系数行列式法[2],采用上述三种方法时,一般来说需明确装置内部的主,从动构件及啮合传动路线。
由于实际轮系结构千变万化,上述三种方法应用在比较复杂的轮系中显得较为不便。
因而又常常应用M 、A 、Kpe йнec 提出的传动比法[1],但理论分析及实验结果均表明,传动比法的计算结果同实际往往存着一定的误差(有时达20%以上),这使得传动比法的应用受到了一定的限制。
本文提出了一种计算差动轮系效率的新方法结点功率法,并将其应用于封闭式行星轮系的效率计算中,得出了在各种功率流状态下封闭式行星轮系效率计算的普遍公式。
1 封闭式行星轮系的基本特征1.1 封闭式行星轮系的简化模型从封闭体和差动轮系的联接形式上来看,封闭式行星轮系分为KX 型和XK 型两大类。
KX 型的特点是封闭体和差动轮系在主动构件上联接,XK 型的特点是封闭体和差动轮系在从动构件上联接。
为便于分析计算,实际中常常采用封闭式行星轮系的简化模型。
图1和图2分别表示了KX 和XK 两类封闭式行星轮系的实际结构及其简化模型(简图中括号内的字母代表实际结构中的相应构件)。
简化模型中的K ,X 也代表其他形式的封闭式行星轮系中的封闭体和差动轮系部分。
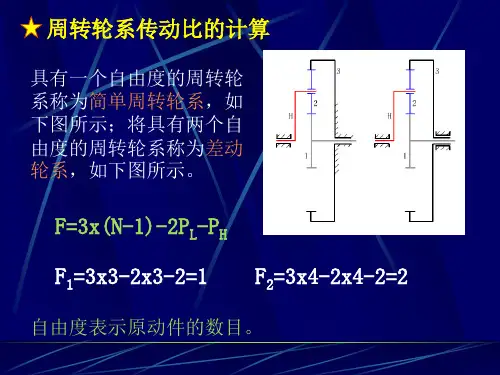
第1 章前言1.1 引言轮系传动时,有一个或几个齿轮的几何轴线位置不固定，而是绕其它齿轮的固定轴线回转,这种轮系被称作周转轮系[1]，如图1.1所示。
周转轮系是由太阳轮，行星轮和行星架组成的。
围绕着固定轴线回转的齿轮，称为太阳轮。
如图1-1中的齿轮1和齿轮3；齿轮2围绕着自己的轴线作自转的同时又与构件H通过回转副相连一起绕着固定轴线作公转就像行星一样运动故称为行星轮。
其中构件H我们称为行星架，转臂或系杆。
图1.1周转轮系根据自由度数的不同，周转轮系可分为差动轮系和行星轮系两类。
差动轮系的自由度数为2，即轮系有两个独立运动的主动件，如图1-2（a）所示；行星轮系的自由度为1，这种轮系只有一个独立运动的主动件，如图1-2(b)所示。
图1.2周转轮系此外，周转轮系还常根据其基本构件的不同来加以分类。
通常将轮系中的太阳轮以K表示，行星架以H表示，如果轮系中有两个太阳轮就称为2K-H型周转轮系，如图1-3所示：若轮系中有三个太阳轮，而行星架只是起支承行星轮的作用就称为3K 型周转轮系，如图1-4所示：轮系中只有一个太阳轮，其运动是通过等角速机构由V 轴输出就称为K-H-V行星轮系，如图1-5所示。
图1.3 2K-H型周转轮系图1.4 3K型周转轮系图1.5 K-H-V行星轮系1.2 周转轮系传动发展现状自上世纪五十年代起国内就开始对行星传动技术进行开发及应用，它的发展分为二个阶段，改革开放之前受技术水平，设计理念等因素的影响，行星传动技术处于比较低的水平，大部分行星齿轮箱仍需要从国外进口；改革开放之后随着国内科学技术的发展，国家为推进这方面技术的发展采用与研究所，高校，企业强强联合方式，在积极引进了国外先进的行星传动技术的同时对其关键的技术进行研究突破。
当前，国内行星传动技术多采用2K-H轮系传动，已发展了许多类型的系列产品，如我国应用较为普遍的通用行星齿轮减速器系列产品（JB/T6502-1993），此外还有分别用于立磨、辊压机、铝铸轧机、矿井提升机、管磨机、风电增速箱、水电增速箱及堆取料机上的行星齿轮箱等多种型式的专用系列产品[2]，如100t铸锭吊车主卷扬机行星减速器，15t转炉倾动装置差动减速器，5t电动葫芦的传动装置，50t转炉吹氧管卷扬机差动行星轮减速器。
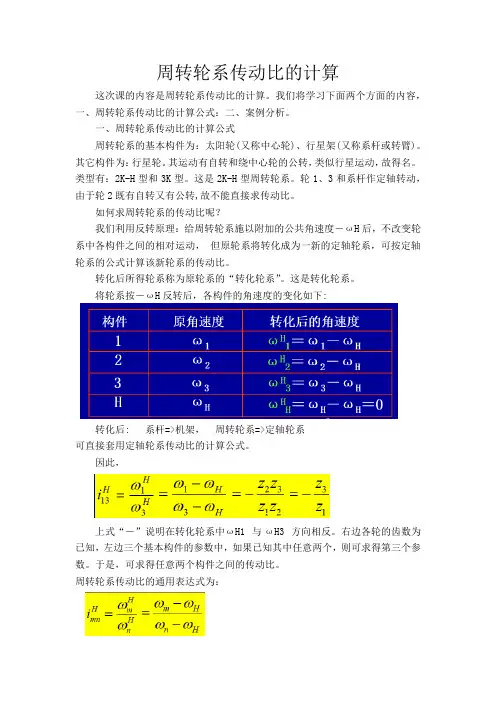
周转轮系传动比的计算这次课的内容是周转轮系传动比的计算。
我们将学习下面两个方面的内容，一、周转轮系传动比的计算公式：二、案例分析。
一、周转轮系传动比的计算公式周转轮系的基本构件为：太阳轮(又称中心轮)、行星架(又称系杆或转臂)。
其它构件为：行星轮。
其运动有自转和绕中心轮的公转，类似行星运动，故得名。
类型有：2K-H型和3K型。
这是2K-H型周转轮系。
轮1、3和系杆作定轴转动，由于轮2既有自转又有公转,故不能直接求传动比。
如何求周转轮系的传动比呢？我们利用反转原理：给周转轮系施以附加的公共角速度－ωH后，不改变轮系中各构件之间的相对运动，但原轮系将转化成为一新的定轴轮系，可按定轴轮系的公式计算该新轮系的传动比。
转化后所得轮系称为原轮系的“转化轮系”。
这是转化轮系。
将轮系按－ωH反转后，各构件的角速度的变化如下:转化后: 系杆=>机架，周转轮系=>定轴轮系可直接套用定轴轮系传动比的计算公式。
因此，上式“－”说明在转化轮系中ωH1 与ωH3 方向相反。
右边各轮的齿数为已知，左边三个基本构件的参数中，如果已知其中任意两个，则可求得第三个参数。
于是，可求得任意两个构件之间的传动比。
周转轮系传动比的通用表达式为：= f(z)应用此公式时特别注意以下几点：1.齿轮m 、n 两轮的轴线必须平行。
2.计算公式中的“±” 不能去掉，它不仅表明转化轮系中两个太阳轮m 、n 之间的转向关系，而且影响到ωm、ωn、ωH 的计算结果。
如果是行星轮系，则ωm 、ωn 中必有一个为0（不妨设ωn＝0）,则上述通式改写如下：以上公式中的ωi 可用转速ni 代替。
用转速表示有：二、案例分析例1 2K －H 轮系中， z1＝z2＝20, z3＝601)轮3固定。
求i1H 。
2)n1=1, n3=-1, 求nH 及i1H 的值。
3)n1=1, n3=1, 求nH 及i1H 的值。
∴ i1H=4 , 齿轮1和系杆转向相同。
第1 章前言1.1 引言轮系传动时,有一个或几个齿轮的几何轴线位置不固定，而是绕其它齿轮的固定轴线回转,这种轮系被称作周转轮系[1]，如图1.1所示。
周转轮系是由太阳轮，行星轮和行星架组成的。
围绕着固定轴线回转的齿轮，称为太阳轮。
如图1-1中的齿轮1和齿轮3；齿轮2围绕着自己的轴线作自转的同时又与构件H通过回转副相连一起绕着固定轴线作公转就像行星一样运动故称为行星轮。
其中构件H我们称为行星架，转臂或系杆。
图1.1周转轮系根据自由度数的不同，周转轮系可分为差动轮系和行星轮系两类。
差动轮系的自由度数为2，即轮系有两个独立运动的主动件，如图1-2（a）所示；行星轮系的自由度为1，这种轮系只有一个独立运动的主动件，如图1-2(b)所示。
图1.2周转轮系此外，周转轮系还常根据其基本构件的不同来加以分类。
通常将轮系中的太阳轮以K表示，行星架以H表示，如果轮系中有两个太阳轮就称为2K-H型周转轮系，如图1-3所示：若轮系中有三个太阳轮，而行星架只是起支承行星轮的作用就称为3K 型周转轮系，如图1-4所示：轮系中只有一个太阳轮，其运动是通过等角速机构由V 轴输出就称为K-H-V行星轮系，如图1-5所示。
图1.3 2K-H型周转轮系图1.4 3K型周转轮系图1.5 K-H-V行星轮系1.2 周转轮系传动发展现状自上世纪五十年代起国内就开始对行星传动技术进行开发及应用，它的发展分为二个阶段，改革开放之前受技术水平，设计理念等因素的影响，行星传动技术处于比较低的水平，大部分行星齿轮箱仍需要从国外进口；改革开放之后随着国内科学技术的发展，国家为推进这方面技术的发展采用与研究所，高校，企业强强联合方式，在积极引进了国外先进的行星传动技术的同时对其关键的技术进行研究突破。
当前，国内行星传动技术多采用2K-H轮系传动，已发展了许多类型的系列产品，如我国应用较为普遍的通用行星齿轮减速器系列产品（JB/T6502-1993），此外还有分别用于立磨、辊压机、铝铸轧机、矿井提升机、管磨机、风电增速箱、水电增速箱及堆取料机上的行星齿轮箱等多种型式的专用系列产品[2]，如100t铸锭吊车主卷扬机行星减速器，15t转炉倾动装置差动减速器，5t电动葫芦的传动装置，50t转炉吹氧管卷扬机差动行星轮减速器。
1.3 周转轮系传动效率研究成果近年来，国内学者一直关注着轮系传动技术的研究工作,尤其是在效率计算问题，因此当前研究的成果主要体现在以下两方面:(1)引入理想轮系的概念[3]，即轮系传动过程不考虑啮合功率损失，从而减少计算过程中繁琐数据和复杂的公式，使推导过程简单化，这样就很容易得到周转轮系的效率公式，同时根据传动效率必小于1的理论，提出不需要分析转化机构中啮合功率的流向, 便可计算效率的新方法，使效率计算变得简便和快速[4]。
（2）当考虑行星轮系啮合损失功率时，一种方法是采用啮合功率法[5]，它是一种计算轮系传动效率的近似方法,但是判断啮合功率流向一直是此法的难点,可以利用周转轮系的效率、啮合功率流动方向与有关运动参数之间的关系,得到了依据周转轮系及封闭传动链的有关传动比判断啮合功率流向的简捷方法,解决了此难点问题[6] [7]。
另一种方法是利用实际轮系与理想轮系之间的在输入输出之间的的差异来求导公式[8]。
1.4 论文研究的具体内容在当前的工业生产中，对能源需求越来越大，因此能源的利用率就显的很重要，如何提高利用率就是各国都亟待解决的问题，我国提出节能减排的方针，在本次的毕业设计是关于周转轮系传动效率公式的具体推导，课题很好应用在这方面，因为周转轮系装置应用在许多的机械设备中，例如行星差动减速器就在矿上机械，起重运输，轻工化工，小型船舶，工程机械中起着无法替代的作用，利用行星轮系提高传动比来改善其性能,因此通过推导轮系的传动效率的公式，再根据已知机械设备的相关数据可以获得效率近似值，并结合具体的工作状况，找出轮系效率损失都有哪些方面，这样可以分析出相应的解决方案来提高周转轮系的效率利用率，尽量减少在传动过程尽可能减少损失，这样可以提高经济效益，减少能源的损耗。
周转轮系分为行星轮系和差动轮系，在这两种轮系下面又有许多不同的类型，由于轮系结构的复杂性以及时间的安排，不可能将所有的轮系都一一推导出效率计算公式，因此在论文中着重对2K-H差动轮系传动效率进行具体的推导。
论文的研究内容及章节安排如下：(1) 第一章前言：本章分为三部分，第一部分引言中对周转轮系的概念，分类和应用做一个简短的介绍，对周转轮系有一个具体的认识，知道各种构件所表达的含义，然后第二部分通过对国内有关周转轮系传动效率的研究成果的了解，从中借鉴成果中所应用到的理论知识，从而形成论文的大体研究方向。
(2) 第二章基本理论：本章中对2K-H差动轮系公式推导中所应用到的基本理论进行详细的总结归纳，包括周转轮系的传动比怎样获得，转化轮系如何应用，周转轮系的受力分析以及效率计算，从中得出2K-H差动轮系传动方案并结合中心轮与转臂之间的角速度关系，得出组合方案，根据具体的计算和相关的约束条件，计算每一种组合方案验证合理性。
(3) 第三章2K-H差动轮系效率计算的推导：本章中对所有合理方案进行具体的推导，根据行列式在周转轮系中的应用的理论，得出2K-H差动轮系效率计算的公式。
(4) 第四章算例：本章针对推导出来的公式找到两个具体的算例加以验证，从而说明所求出的公式正确性。
(5) 第五章结论：本章总结出推导2K-H差动轮系所得出的具体的结论以及相关的建议。
第二章 基本理论2.1 引言本章是为推导传动效率公式所用到的基本理论作一个总结归纳，包括周转轮系传动比，受力分析及效率计算的一般公式，2K-H 差动轮系传动方案三部分。
2.2 周转轮系传动比要计算周转轮系的传动比，可以先根据定轴轮系传动比的形式来推导。
积所有主动轮齿数的连乘积所有从动轮齿数的连乘定轴轮系的传动比 （2.1）周转轮系传动比不能直接用上面求定轴轮系传动比的求法来计算，因为周转轮系有转动的行星架。
因此为得出周转轮系传动比的计算公式，可以采用行星架固定法，即转化机构法，根据理论力学相对运动的原理[9]，即“一个机构整体的绝对运动并不影响机构内部各构件之间的相对运动”。
具体方法是给整个周转轮系加上角速度 “-H w ”即这个角速度与行星架H 角速度大小相等方向相反，这时各构件之间的相对运动保持不变，而行星架的角速度变为H w - H w =0,即行星架相对不动。
于是周转轮系就转化成了定轴轮系，这样就可以用求定轴轮系传动比的公式来求周转轮系的传动比。
表2-1给整个周转轮系一个附加的角速度（-H w ）后，各构件的角速度的变化构件名称 原来角速度 在转化轮系中的角速度（即相对于行星架的角速度）行星架H H w H w - H w =H Hw =0 太阳轮a a w a w - H w =H w a行星轮b b w b w - H w =H bw 因此转化轮系传动比：H abi = H b H a w w （2.2）其中H ab i ——表示构件H 固定，a 主动，b 从动时的传动比H w a ——表示构件H 固定，主动构件a 的角速度H bw ——表示构件H 固定，从动构件b 的角速度 本次毕业设计是以周转轮系中的2K-H 型（H i <0）差动轮系为例来计算传动效率的简化公式。
如图2.1图2.1 2K-H 差动轮系结构简图由上述的关于周转轮系传动比的相关论述结合2K-H （H i <0）差动轮系结构，根据公式（2.2）可以得出2K-H 差动轮系中心轮A,B 和转臂H 之间角速度的4种关系。
HAB i =H BH A w w =0<--H B H A w w w w （2.3）1）当中心轮A,B 转向相同时，且0.>>B A w w ，代入公式（2.3）可解出H A w w >,H B w w <，整理得：0>>>B H A w w w2) 当中心轮A,B 转向相同时，且0.>>A B w w ,代入公式（2.3）可解出H B w w >,H A w w <，整理得： 0>>>A H B w w w3) 当中心轮A,B 转向相反时，且0<A w ,代入公式（2.3）可解出,,H B H A w w w w ><整理得：0,0><B A w w A H B w w w >>4) 当中心轮A,B 转向相反时, 且,0<B w 代入公式（2.3）可解出,,H A H B w w w w ><整理得：,0,0><A B w w B H A w w w >>2.3 周转轮系的受力分析及效率分析2.3.1 转矩平衡方程以2K-H 差动轮系（H i <0）为研究对象,作用于太阳轮A 上的力矩为A T ,作用于转臂H 上的阻力矩为H T ,作用于行星轮B 的力矩为B T ，根据轮系的受力平衡条件，其三个构件A,B,H 传递的扭矩必须满足(传动中的啮合损失忽略不计)：0=++H B A T T T (2.4)2.3.2 轮系的效率计算设周转轮系的输入件传递的功率01>P ,输出件传递的功率，02<P 则传动效率的一般公式为：011221212=+⇒-=P P P P ηη (2.5)现输入功率为11w T 、输出功率为12w T 、效率为12η,故应有以下功率平衡方程式:0221211=+w T w T η (2.6)同理同条件得出转化轮系传动效率的一般公式为（这里假设构件H 固定）：011221212=+⇒-=H H H H H H P P P P ηη (2.7) 0221211=+H H H w T w T βη）（ (2.8)式中:H 12η为转化机构的效率,β为反映转化机构中啮合功率流向的指数。
2.3.3 啮合功率流向差动轮系转化机构1,2两轮传递的功率H w T 21和H w T 22叫做啮合功率[10]- [13]，二者必须一正一负，当啮合功率011>H w T H w T 22<0时,轮1在转化机构中为主动件，则β=1啮合功率流由1→2;反之,当时011<H w T H w T 22>0,轮1为从动件,则β=-1啮合功率流由2→1。
2.4 周转轮系的传动方案计算2.4.1 2K-H 差动轮系传动方案在周转轮系中，太阳轮和行星轮一般作为输入和输出件，它们都围绕着同一固定轴线回转。
这样可以为划分构件的作用以及传动方案确定提供了一个重要的理论依据。
从图2.1可以看出2K-H 差动轮系有3个基本构件：中心轮A,B 和行星架H,因此按照输入件和输出件的分类方式得出6个不同的组合方式，即2K-H 差动轮系的传动方案。
