轮系及其传动比计算
- 格式:doc
- 大小:910.00 KB
- 文档页数:21






轮系传动比计算(机械基础)教案第一章:轮系传动简介1.1 轮系的定义和分类定义:轮系是由两个或多个相互啮合的齿轮组成的传动系统。
分类:定传动比轮系、变传动比轮系、混合传动比轮系。
1.2 轮系的应用和特点应用:轮系广泛应用于机械传动、汽车传动、船舶传动等领域。
特点:传动平稳、噪声小、效率高、传动比精确。
第二章:传动比的计算方法2.1 定传动比轮系的传动比计算计算公式:传动比= 驱动齿轮齿数/ 从动齿轮齿数。
2.2 变传动比轮系的传动比计算计算方法:根据变传动比轮系的传动比曲线,确定所需的传动比值。
2.3 混合传动比轮系的传动比计算计算方法:分别计算定传动比轮系和变传动比轮系的传动比,相乘或相除得到混合传动比。
第三章:轮系传动比的实验测量3.1 实验目的和原理目的:验证轮系传动比的计算结果,提高实验技能。
原理:通过测量驱动齿轮和从动齿轮的转速,计算传动比。
3.2 实验设备和步骤设备:计时器、转速计、齿轮组。
步骤:安装齿轮组,调整转速,测量并记录驱动齿轮和从动齿轮的转速,计算传动比。
3.3 实验数据的处理和分析处理:计算实验测得的传动比与理论计算值的误差。
分析:讨论误差产生的原因,改进实验方法,提高实验精度。
第四章:轮系传动比的优化设计4.1 优化设计的目的和方法目的:提高轮系传动比的性能,降低成本。
方法:选择合适的齿轮材料、齿形和齿数。
4.2 齿轮材料的选择材料:钢、铸铁、塑料、陶瓷等。
选择原则:根据工作条件和要求选择合适的齿轮材料。
4.3 齿轮齿形的设计齿形:直齿、斜齿、螺旋齿等。
设计原则:根据传动比和负载要求选择合适的齿轮齿形。
4.4 齿轮齿数的选择齿数:根据传动比和齿轮尺寸选择合适的齿数。
选择原则:齿数越多,传动比越大,但尺寸和成本也增加。
第五章:轮系传动比的实际应用案例分析5.1 汽车传动系统中的应用案例案例:分析汽车变速箱中齿轮传动比的计算和设计。
5.2 机械传动系统中的应用案例案例:分析机械设备中齿轮传动比的计算和优化设计。
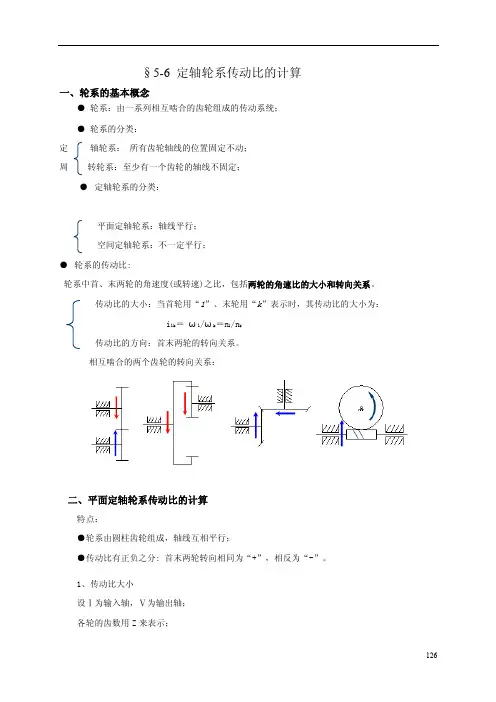
126§5-6 定轴轮系传动比的计算一、轮系的基本概念● 轮系:由一系列相互啮合的齿轮组成的传动系统; ● 轮系的分类: 定轴轮系: 所有齿轮轴线的位置固定不动; 周转轮系:至少有一个齿轮的轴线不固定; ● 定轴轮系的分类:平面定轴轮系:轴线平行; 空间定轴轮系:不一定平行;● 轮系的传动比:轮系中首、末两轮的角速度(或转速)之比,包括两轮的角速比的大小和转向关系。
传动比的大小:当首轮用“1”、末轮用“k ”表示时,其传动比的大小为: i 1k = ω1/ωk =n 1/n k 传动比的方向:首末两轮的转向关系。
相互啮合的两个齿轮的转向关系:二、平面定轴轮系传动比的计算特点:●轮系由圆柱齿轮组成,轴线互相平行;●传动比有正负之分: 首末两轮转向相同为“+”,相反为“-”。
1、传动比大小设Ⅰ为输入轴,Ⅴ为输出轴; 各轮的齿数用Z 来表示;127角速度用ω表示;首先计算各对齿轮的传动比:所以:结论: 定轴轮系的传动比等于各对齿轮传动比的连乘积,其值等于各对齿轮的从动轮齿数的乘积与主动轮齿数的乘积之比; 2、传动比方向在计算传动比时,应计入传动比的符号: 首末两轮转向相同为“+”,相反为“-”。
(1)公式法式中:m 为外啮合圆柱齿轮的对数 举例:(2)箭头标注法采用直接在图中标注箭头的方法来确定首末两轮的转向,转向相同为“+”,相反为“-”。
举例:122112z z i ==ωω32223332z i z ωωωω'''===33434443z i z ωωωω'''===455445z z i ==ωω11211)1(--==k k m k k z z z z i ωω128三、空间定轴轮系的传动比特点:●轮系中包含有空间齿轮(如锥齿轮、蜗轮蜗杆、螺旋齿轮等); ●首末两轮的轴线不一定平行。
1 传动比的大小2 传动比的方向注意:只能采用箭头标注法,不能采用(-1)m 法判断。

传动比公式是:传动比=主动轮转速除以从动轮转速的值=其分度圆直径比值的倒数。
具体含义如下:
1. 在机械传动系统中,其始端主动轮与末端从动轮的角速度或转速的比值,被称为传动比。
2. 传动比(i)=主动轮转速(n1)与从动轮转速(n2)的比值=齿轮分度圆直径的反比=从动齿轮齿数(Z2)与主动齿轮齿数(Z1)的比值。
即i=n1/n2=D2/D1 i=n1/n2=z2/z1。
3. 对于多级齿轮传动,每两轴之间的传动比按照上面的公式计算。
从第一轴到第n轴的总传动比等于各级传动比之积。
4. 传动比是机构中两转动构件角速度的比值,也称速比。
构件a和构件b的传动比为i=ωa/ωb=na/nb,式中ωa和ωb分别为构件a和b的角速度(弧度/秒);na和nb分别为构件a和b的转速(转/分)。
当式中的角速度为瞬时值时,则求得的传动比为瞬时传动比。
当式中的角速度为平均值时,则求得的传动比为平均传动比。
理论上对于大多数渐开线齿廓正确的齿轮传动,瞬时传动比是不变的;对于链传动和摩擦轮传动,瞬时传动比是变化的。
对于啮合传动,传动比可用a和b轮的齿数Za和Zb表示,i=Zb/Za;对于摩擦传动,传动比可用a和b轮的直径Da和Db表示,i=Db/Da。
希望以上信息对您有所帮助,如果您还有其他问题,欢迎告诉我。

轮系及其传动比计算1.轮系的类型和应用1.1轮系的分类根据轮系运转中各齿轮轴线的空间位置是否固定,可以将轮系分为定轴轮系和周转轮系两种基本类型。
1)定轴轮系:轮系运转时,如果各齿轮轴线的位置都不固定,则称为定轴轮系(或称为普通轮系),可分为平行定轴轮系(各轮轴线相互平行)和空间定轴轮系(各轮轴线不相互平行,含圆锥齿轮、蜗轮蜗杆等)。
2)周转轮系:轮系运转时,至少有一个齿轮轴线的位置不固定,而是绕某一固定轴线回转,则称为周转轮系,其中绕动齿轮称为行星轮,轴线不动的中心轮称为太阳轮。
按自由度数目不同可分为差动轮系和行星轮系。
1.2轮系的功用1)实现相距较远的两轴之间的传动2)实现分路传动3)实现变速变向传动4)实现大速比或大功率传动5)实现运动的合成与分解2.轮系传动比的计算轮系传动比,是指轮系运动时其输入轴与输出轴的角速度或转速之比。
它包括计算传动比的大小和确定输入轴与输出轴两者转向关系两方面内容。
2.1定轴轮系的传动比设A表示输入轴,B表示输出轴,则一般定轴轮系的传动比计算公式为:іAB=ωA/ωB=从A到B所有从动齿轮数连乘积/从A到B所有主动齿轮数连乘积平面定轴轮系和空间定轴轮系的传动比的大小均可用该式计算,但转向的确定有不同的方法。
2.1.1平面定轴轮系中的转向关系可用“+”、“-”号来表示,“+” 号表示转向相同、“-”号表示转向相反。
一对外啮合圆柱齿轮传动两轮的转向相反,其传动比前应加注“-”号;一对内啮合圆柱齿轮传动两轮的转向相同,其传动比前应加注“+”号。
设轮系中有m对外啮合齿轮,则在该式右侧的分式前应加注(-1)m。
若传动比的计算结果为正,则表示输入轴与输出轴的转向相同;若为负,则表示转向相反。
2.1.2空间定轴轮系输入轴与输出轴之间的转向关系不能用上述方法来确定,而必须在机构简图上用画箭头的方法来表示。
1)对于圆锥齿轮传动,表示方向的箭头应该同时指向啮合点即箭头对箭头,或同时背离啮合点即箭尾对箭尾。

轮系及其传动比的计算详解轮系是由一组相互连接的轮齿组成的机械系统,用于传递动力和改变转速。
根据轮齿的不同数量和排列方式,轮系可以实现不同的传动比例,从而改变输入轮的转速和输出轮的转速。
在本文中,我们将详细介绍轮系的计算方法和传动比的计算方法。
首先,我们介绍一些与轮系计算相关的基本参数和概念。
1.轮齿数(Z):每个轮齿的数量,通常用于计算轮齿的大小和分布。
2.模数(m):轮齿的大小与分布的参数,表示每个轮齿的宽度与轮齿间距的比例。
3.齿轮比(i):两个相邻轮齿的齿轮比为输出轮的齿数除以输入轮的齿数,用于表示输入轮与输出轮之间的转速比。
在轮系计算中,我们通常关注的是传动比(或齿轮比),它表示两个相邻轮齿之间的转速比。
传动比的计算方法取决于轮系的类型和轮齿的排列方式。
下面将介绍常见的轮系类型和它们的传动比计算方法。
1.平行轴齿轮传动:平行轴齿轮传动是最常见的轮系类型,用于将动力从一个轴传递到另一个轴上。
传动比的计算方法如下:- 整体齿轮比(i)=输出轮齿数(Z_out)/输入轮齿数(Z_in)- 输入轮输出转速(n_out)=输入轮输入转速(n_in)/整体齿轮比(i)2.平行轴齿轮传动(多级):平行轴齿轮传动可以通过多级配置来实现更大的传动比。
在多级传动中,每个级别的传动比相乘,以得到整体的传动比。
3.内齿轮传动:内齿轮传动是一种特殊的齿轮传动,其中至少有一个轮齿是内部轮齿。
传动比的计算方法稍有不同:- 整体齿轮比(i)=输出轮齿数(Z_out)/(输入轮齿数(Z_in)+输出轮齿数(Z_out))- 输出轮输入转速(n_in)=输入轮输出转速(n_out)×整体齿轮比(i)4.锥齿轮传动:锥齿轮传动用于连接两个轴的交叉传动,其中两个轮齿是锥形的。
传动比的计算方法如下:- 整体齿轮比(i)=输出轮齿数(Z_out)/输入轮齿数(Z_in)- 输入轮输出转速(n_out)=输入轮输入转速(n_in)/整体齿轮比(i)最后,对于复杂的传动系统,传动比的计算可以通过将每个传动单元的传动比相乘来实现,从而得到整体的传动比。

齿轮传动比计算齿轮传动是机械传动中应用广的一种传动形式。
那齿轮传动比是怎么计算的呢?一、齿轮传动比计算公式传动比=从动轮齿数/主动轮齿数=主动轮转速/从动轮转速i=z2/z1=n1/n21、对齿轮的传动比:传动比大小:i12=N1/N2 =Z2/Z1转向外啮合转向相反取“-”号内啮合转向相同取“+”号对于圆柱齿轮传动,从动轮与主动轮的转向关系可直接在传动比公式中表示即:i12=±z2/z1其中"+"号表示主从动轮转向相同,用于内啮合;"-"号表示主从动轮转向相反,用于外啮合;对于圆锥齿轮传动和蜗杆传动,由于主从动轮运动不在同一平面内,因此不能用"±"号法确定,圆锥齿轮传动、蜗杆传动和齿轮齿条传动只能用画箭头法确定。
对于齿轮齿条传动,若ω1表示齿轮1角速度,d1表示齿轮1分度圆直径,v2表示齿条的移动速度,存在以下关系:V2=d1ω1/22、行星轮系的传动比计算构件原转速相对转速中心轮1 n1 n1=n1-nH行星轮2 n2 n2=n2-nH中心轮3 n3 n3=n3-nH行星架H nH nH=nH-nH=0转化轮系为定轴轮系“-”在转化轮系中齿轮1、3转向相反。
一般公式:式中:m为齿轮G至K转之间外啮合的次数。
(1)主动轮G,从动轮K,按顺序排队主从关系。
(2)公式只用于齿轮G、K和行星架H的轴线在一条直线上的场合。
(3)nG、nK、nH三个量中需给定两个;并且需假定某一转向为正相反方向用负值代入计算。
例8—3:如图所示的行星轮系中已知电机转速n1=300r/min (顺时针转动)当z1=17,z3 =85,求当n3=0和n3=120r/min(顺时针转动)时的nH。
二、齿轮传动的特点1)效率高在常用的机械传动中,以齿轮传动效率为高,闭式传动效率为96%~99%,这对大功率传动有很大的经济意义。
2)结构紧凑比带、链传动所需的空间尺寸小。
第六章轮系及其传动比计算6.1引言轮系是指由若干个齿轮组成的一种传动装置,在机械设备中起着重要的作用。
轮系的传动比是指输入轴和输出轴的转速之比,是轮系设计的重要参数之一、本章将介绍轮系的基本概念和传动比的计算方法。
6.2轮系的基本概念轮系由多个齿轮组成,每个齿轮都有一个输入轴和一个输出轴。
输入轴的转速通过齿轮的啮合传递给下一个齿轮,最终传递到输出轴。
在一个轮系中,有一个输入轴和一个输出轴,其它齿轮都是通过啮合传递转速。
在一个轮系中,齿轮的直径与其转速成反比,即直径越大,转速越小。
齿轮之间的啮合关系可以用一个传动比来描述,传动比是输出轴的转速与输入轴的转速之比。
6.3传动比的计算方法传动比的计算方法可分为两种:直接计算法和间接计算法。
6.3.1直接计算法直接计算法是根据齿轮的齿数和直径来计算传动比。
当一组齿轮串联时,传动比等于每个齿轮的齿数比的乘积。
当一组齿轮并联时,传动比等于每个齿轮的齿数比的和。
例如,一个轮系由两个齿轮组成,第一个齿轮的齿数为20,第二个齿轮的齿数为40。
则传动比为40/20=2使用直接计算法需要知道每个齿轮的齿数,因此适用于已知齿轮参数的情况。
6.3.2间接计算法间接计算法是通过测量轮系的输入轴和输出轴的转速来计算传动比。
该方法通过使用转速计或测速仪来测量转速,然后将测得的输入轴转速和输出轴转速之比作为传动比。
例如,通过测量得到输入轴转速为1000rpm,输出轴转速为500rpm,则传动比为500/1000=0.5间接计算法适用于无法直接测量齿轮参数的情况,但需要准确测量转速。
6.4小结本章介绍了轮系的基本概念和传动比的计算方法。
轮系是由多个齿轮组成的传动装置,传动比是描述轮系传动关系的重要参数。
传动比可通过直接计算法和间接计算法来计算。
直接计算法适用于已知齿轮参数的情况,而间接计算法适用于通过测量转速来计算传动比的情况。
轮系传动比公式
轮系传动比公式指的是计算轮系传动比的数学公式。
在机械传动中,轮系传动比是指轮系中某个轮齿数量比值的大小,也是轮系输出轴转速与输入轴转速的比值。
轮系传动比公式包括简单轮系传动比公式和复杂轮系传动比公式两种类型。
简单轮系传动比公式:
1. 对于平行轴齿轮传动:i = n2 / n1
其中,i为传动比,n2为输出轮齿数,n1为输入轮齿数。
2. 对于螺旋齿轮传动:i = tanα / tanβ
其中,α为螺旋角,β为压力角。
3. 对于斜齿轮传动:i = cosα / cosβ
其中,α为斜齿轮齿面与轴线夹角,β为传动轴与齿面所成夹角。
复杂轮系传动比公式:
对于复杂轮系传动,可以通过轮系的组合、分解,逐步计算传动比。
其中,一些常用的组合轮系传动比公式包括:
1. 并联轮系传动比公式:i = i1 x i2 x… xn
其中,i1、i2、… xn分别为并联轮系中各轮系的传动比。
2. 串联轮系传动比公式:i = i1 x i2 x… xn
其中,i1、i2、… xn分别为串联轮系中各轮系的传动比。
通过以上公式的计算,可以准确地计算出轮系传动比,为机械传动的设计和优化提供理论基础。
- 1 -。
第八章 轮系及其传动比计算第四十八讲 齿轮系及其分类如图8—1所示,由一系列齿轮相互啮合而组成的传动系统简称轮系。
根据轮系中各齿轮运动形式的不同,轮系分类如下:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧==⎩⎨⎧成由几个周转轮系组合而和周转轮系混合而成或混合轮系:由定轴轮系)行星轮系()差动轮系(周转轮系(轴有公转)空间定轴轮系平面定轴轮系定轴轮系(轴线固定)轮系12F F图8—1 图8—2 图8—3 定轴轮系中所有齿轮的轴线全部固定,若所有齿轮的轴线全部在同一平面或相互平行的平面内,则称为平面定轴轮系,如图8—1所示,若所有齿轮的轴线并不全部在同一平面或相互平行的平面内,则称为空间定轴轮系;若轮系中有一个或几个齿轮轴线的位置并不固定,而是绕着其它齿轮的固定轴线回转,如图8—2,8—3所示,则这种轮系称为周转轮系,其中绕着固定轴线回转的这种齿轮称为中心轮(或太阳轮),即绕自身轴线回转又绕着其它齿轮的固定轴线回转的齿轮称为行星轮,支撑行星轮的构 图8—4件称为系杆(或转臂或行星架),在周转轮系中,一般都以中心轮或系杆作为运动的输入或输出构件,常称其为周转轮系的基本构件;周转轮系还可按其所具有的自由度数目作进一步的划分;若周转轮系的自由度为2,则称其为差动轮系如图8—2所示,为了确定这种轮系的运动,须给定两个构件以独立运动规律,若周转轮系的自由度为1,如图8—3所示,则称其为行星轮系,为了确定这种轮系的运动,只须给定轮系中一个构件以独立运动规律即可;在各种实际机械中所用的轮系,往往既包含定轴轮系部分,又包含周转轮系部分,或者由几部分周转轮系组成,这种复杂的轮系称为复合轮系如图8—4所示,该复合轮系可分为左边的周转轮系和右边的定轴轮系两部分。
第四十九讲 定轴轮系的传动比1、传动比大小的计算由前面齿轮机构的知识可知,一对齿轮:i 12 =ω1 /ω2 =z 2 /z 1对于齿轮系,设输入轴的角速度为ω1,输出轴的角速度为ωm ,按定义有:i 1m =ω1 /ωm当i 1m >1时为减速, i 1m <1时为增速。
因为轮系是由一对对齿轮相互啮合组成的,如图8—1所示,当轮系由m 对啮合齿轮组成时,有:1321432143322111--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅==m m m m m m z z z z z z z z i ωωωωωωωωωω 所有主动轮齿数连乘积所有从动轮齿数连乘积= 2、首、末轮转向的确定因为角速度是矢量,故传动比计算还有首末两轮的转向问题。
对直齿轮表示方法有两种。
1)用“+”、“-”表示适用于平面定轴轮系,由于所有齿轮轴线平行,故首末两轮转向不是相同就是相反,相同取“+”表示,相反取“-”表示,如图8—5所示,一对齿轮外啮合时两轮转向相反,用“-”表示;一对齿轮内啮合时两轮转向相同,用“+”表示。
可用此法逐一对各对啮合齿轮进行分析,直至确定首末两轮的转向关系。
设轮系中有m 对外啮合齿轮,则末轮转向为(-1)m,此时有:积所有主动轮齿数的连乘积所有从动轮齿数的连乘m m i )1(1-= 图8—5 2)画箭头如图8—6所示,箭头所指方向为齿轮上离我们最近一点的速度方向。
外啮合时:两箭头同时指向(或远离)啮合点。
头头相对或尾尾相对。
内啮合时:两箭头同向。
对于空间定轴轮系,只能用画箭头的方法来确定从动轮的转向。
(1)锥齿轮,如图8—7所示,可见一对相互啮合的锥齿轮其转向用箭头表示时箭头方向要么同时指向节点,要么同时背离节点。
(2)蜗轮蜗杆,由齿轮机构中蜗轮蜗杆一讲的知识可知,一对相互啮合的蜗轮蜗杆其转向可用左右手定则来判断,如图8—8所示。
(3)交错轴斜齿轮,用画速度多边形确定,如图8—9所示。
图8—6 图8—7图8—8 图8—9例一:已知如图8—10所示轮系中各轮齿数,求传动比i 15。
解:1.先确定各齿轮的转向,用画箭头的方法可确定首末两轮转向相反。
2. 计算传动比 '4'31543'4'32154325115Z Z Z Z Z Z Z Z Z Z Z Z Z Z i -=-==ωω其中齿轮2对传动比没有影响,但能改变从动轮的转向,称其为过轮或中介轮。
图8—10第五十讲周转轮系的传动比周转轮系的分类除按自由度以外,还可根据其基本构件的不同来加以分类,如图所示,设轮系中的太阳轮以K表示,系杆以H表示,则图8—11所示为2K —H型轮系;图8—12为3K型轮系,因其基本构件为3个中心轮,而系杆只起支撑行星轮的作用。
在实际机构中常用2K—H型轮系。
图8—11 图8—12周转轮系由回转轴线固定的基本构件太阳轮(中心轮)、行星架(系杆或转臂)和回转轴线不固定的其它构件行星轮组成。
由于有一个既有公转又有自转的行星轮,因此传动比计算时不能直接套用定轴轮系的传动比计算公式,因为定轴轮系中所有的齿轮轴线都是固定的。
为了套用定轴轮系传动比计算公式,必须想办法将行星轮的回转轴线固定,同时由不能让基本构件的回转轴线发生变化。
如图所示,我们发现在周转轮系中,基本构件的回转轴线相同,而行星轮即绕其自身轴线转动,有随系杆绕其回转轴线转动,因此,只要想办法让系杆固定,就可将行星轮的回转轴线固定,即把周转轮系变为定轴轮系,如图8—13所示。
反转原理:给周转轮系施以附加的公共转动-ω后,不改变轮系中各构件H之间的相对运动,但原轮系将转化成为一新的定轴轮系,可按定轴轮系的公式计算该新轮系的传动比。
转化后所得的定轴轮系称为原周转轮系轮系的“转化轮系”。
将整个轮系机构按-ω反转后,各构件的角速度的变化如下:H图8—13构件 原角速度 转化后的角速度1ω1 ωH 1=ω1-ωH 2ω2 ωH 2=ω2-ωH 3ω3ωH 3=ω3-ωHH ωH ωH H =ωH -ωH =0由角速度变化可知机构转化后,系杆角速度为0,既系杆变成了机架,周转轮系演变成定轴轮系,因此可直接套用定轴轮系传动比的计算公式。
132132313113Z Z Z Z Z Z i H H H H H-=-=--==ωωωωωω 上式“-”说明在转化轮系中ωH 1与ωH 3方向相反。
通用表达式:Hn H m H n H m Hmn i ωωωωωω--==所有主动轮齿数连乘积至转化轮系中由所有从动轮齿数连乘积至转化轮系中由n m n m ±=)(Z f = 特别注意:1、齿轮m 、n 的轴线必须平行。
2、计算公式中的±不能去掉,它不仅表明转化轮系中两个3、太阳轮m 、n 之间的转向关系,而且影响到ωm 、ωn 、ωH 的计算结果。
如果周转轮系是行星轮系,则ωm 、ωn 中必有一个为0(不妨设ωn =0),此时上述通式可改写如下:H m H H m H nH m Hmn i i +=--==1ωωωωω 即: )(11Z f i i H mn H m-=-= 以上公式中的ωi 可用转速n i 代替:i i i n ωππω3060)2(==用转速表示有:)(z f n n n n n n i H n H m H n H mHmn =--== 图8—14例二、如图8—14所示2K -H 轮系中,Z 1=Z 2=20,Z 3=60,轮3固定。
求:1)i 1H 。
2)n 1=1, n 3=-1,求n H 及i 1H 的值。
3)n 1=1, n 3=1,求n H 及i 1H 的值。
10)111313113+-=--=--===H H H H H H H Hi i ωωωωωωωωω解32060132132-=-=-=-=z z z z z z ∴ i 1H =4 , 齿轮1和系杆转向相同。
-311)2313113=---=--==HH H H H HHn n n n n n n n i 2/1-=H n得: i 1H = n 1 / n H =-2,两者转向相反。
311)3313113-=--=--==HH H H H HHn n n n n n n n i 1=H nn 1=1, n 3=1,得: i 1H = n 1 / n H =1,两者转向相同。
结论:1、轮1转4圈,系杆H 同向转1圈。
2、轮1逆时针转1圈,轮3顺时针转1圈,则系杆顺时针转2圈。
3、轮1轮3各逆时针转1圈,则系杆逆时针转1圈。
特别强调:1、i 13≠ i H 132、i 13≠- z 3/z 1例三:如图8—15示圆锥齿轮组成的轮系中,已知:z 1=33,z 2=12,z 2’=33,求i 3H解:判别转向:齿轮1、3方向相反11031331331-=-=+-=--=--=z z i i H H H H H H ωωωωωωω i 3H =2特别注意:转化轮系中两齿轮轴线不平行时,不能直接计算!图8—15成立否?H HH i ωωωω--=1221 不成立!ωH 2 ≠ω2-ωH事实上,因角速度ω2是一个向量,它与牵连角速度ωH 和相对角速度ωH 2之间的关系为:ω2 =ωH +ωH 2∵P 为绝对瞬心,故轮2中心速度为:V 2o =r 2ωH 2又V 2o =r 1ωH∴ωH 2=ωH r 1/ r 2=ωH t g 1=ωH c t g δ2第五十一讲 复合轮系的传动比复合轮系或者是由定轴部分与周转部分组成,或者是由几部分周转轮系组成,因此复合轮系传动比求解的思路是:先将复合轮系分解为基本轮系,分别计算各基本轮系的传动比,然后根据组合方式找出各轮系间的关系,联立求解。
根据上述方法,复合轮系分解的关键是将周转轮系分离出来。
因为所有周转轮系分离完后复合轮系要么分离完了,要么只剩下定轴轮系了。
周转轮系的分离步骤是先找回转轴线不固定的行星轮,找出后确定支撑行星轮的系杆,然后再找出与行星轮啮合的中心轮,至此,一个周转轮系就分离出来了;用上述方法一直寻找,混合轮系中可能有多个周转轮系,而一个基本周转轮系中至多只有三个中心轮。
剩余的就是定轴轮系。
例四:如图8—16示为龙门刨床工作台的变速机构,J 、K 为电磁制动器,设已知各轮的齿数,求J 、K 分别刹车时的传动比i 1B 。
解:1、刹住J 时:1-2-3为定轴轮系,B -5-4-3’为周转轮系,3-3’将两者连接。
定轴部分:i 13=ω1/ω3=-z 3/ z 1周转部分:i B3’ 5=(ω3’-ωB )/(0-ωB ) =-z 5/z 3’连接条件:ω3=ω3’ 联立解得:)1('351311z z z z i B B +-==ωω 2、刹住K 时:A-1-2-3为周转轮系,B -5-4-3’为周转轮系,5-A 将两者连接。
周转轮系1:i A 13=(ω1 -ωA ) /(0 -ωA )=-z 3/z 1 图8—16周转轮系2:i B 3’5=(ω3’-ωB )/(ω5-ωB )=-z 5/z 3’连接条件:ω5=ωA联立解得:B A BA B B i i z z z z i 51515'31311)1)(1(=⋅=++==ωωωωωω 总传动比为两个串联周转轮系的传动比的乘积。