七年级上数轴上的动点问题(最新最全版)

初一上学期动点问题练习1。

如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0)秒．（1）写出数轴上点B表示的数 ,点P表示的数用含t的代数式表示)；（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化?若变化，请说明理由；若不变，请你画出图形,并求出线段MN的长;解：(1）由题意得点B表示的数为－6；点P表示的数为8－5t;（2）设点P运动x秒时，在点C处追上点Q(如图）则AC=5，BC=3，∵AC－BC=AB∴5－3=”14”解得：=7，∴点P运动7秒时,在点C处追上点Q；(3）没有变化．分两种情况：①当点P在点A、B两点之间运动时：MN=MP+NP=AP+BP=(AP+BP)=AB="7"②当点P运动到点B的左侧时：MN=MP－NP= AP－BP=（AP－BP)=AB="7"∴综上所述,线段MN的长度不发生变化，其值为7；2。

已知数轴上有A、B、C三点,分别表示有理数—26，-10,10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．(1）用含t的代数式表示P到点A和点C的距离:PA=______，PC=______．（2）当点P运动到B点时，点Q从A出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后,请用t的代数式表示P、Q两点间的距离．解:（1）PA=t，PC=36—t；（2）当16≤t≤24时PQ=t-3（t—16）=-2t+48，当24＜t≤28时PQ=3（t-16)—t=2t—48，当28＜t≤30时PQ=72—3（t—16)-t=120-4t，当30＜t≤36时PQ=t—[72—3(t-16)]=4t-120．3。

数轴上的线段与动点问题一、与数轴上的动点问题相关的基本概念主要涉及以下几个概数轴上的动点问题离不开数轴上两点之间的距离.念：,=|a-b|1．数轴上两点间的距离，即为这两点所对应的坐标差的绝对值d右边点表示的数=也即用右边的数减去左边的数的差.即数轴上两点间的距离.—左边点表示的数÷2.中点坐标=（a+b）2.两点中点公式：线段AB因此向右运动的速点在数轴上运动时，由于数轴向右的方向为正方向，3.这样在起点的基础上加上点的度看作正速度，而向左运动的速度看作负速度.b，向左运动运动路程就可以直接得到运动后点的坐标.即一个点表示的数为a.a+bb；向右运动b个单位后所表示的数为个单位后表示的数为a—点分析数轴上点的运动要结合图形进行分析，4.数轴是数形结合的产物，. 在数轴上运动形成的路径可看作数轴上线段的和差关系数轴上的动点问题基本解题思路和方法：二、t.、表示出题目中动点运动后的坐标（一般用含有时间的式子表示）1t的式子表示）. 根据两点间的距离公式表示出题目中相关线段长度 2、（一般用含有时间 3、根据题目问题中线段的等量关系（一般是和、差关系）列绝对值方程.4、解绝对值方程并根据实际问题验算结果.注：数轴上线段的动点问题方法类似AB两点对应数为－2、4，P为数轴上一动点，对应的数为x、已知数轴上1. 、 A B－2 －1 0 1 2 3 4(1) 若P为AB线段的三等分点，求P对应的数；（2）数轴上是否存在P，使P到A点、B点距离和为10，若存在，求出x；若不存在，说明理由.（3）若点A，点B和点P（点P在原点）同时向左运动，它们的速度分别为1，2，1个长度单位/分，则第几分钟时，P为AB的中点？2 ++|abb、|=0c满足（c2、已知：-5b）是最小的正整数，且，请回答问题a、=________ b=________，c，1）请直接写出a、b、c的值．a=________（、、、、，xPc所对应的点分别为AB为一动点，其对应的数为C）（2a，点b+5|. -1|+2|xx ≤2时），请化简式子：|x+1|-|x0≤点P在0到2之间运动时（即请问个单位长度的速度向左运动，点C分别以每秒1个单位和2（3）若点A、CA，之间的距离为1个单位长度？几秒时，、、个单位长度的速度向左1A（4）点A以每秒BC开始在数轴上运动，若点个单位长度的速度向右个单位长度和5和点运动，同时，点BC分别以每秒2之A 之间的距离表示为BC，点与点BCt运动，假设秒钟过后，若点B与点的变化而改变？若变化，tAB的值是否随着时间BC间的距离表示为AB．请问：-请说明理由；若不变，请求其值．2b满足，且a，A在数轴上对应的数为a，点B在数轴上对应的数为b2.如图，若点2 B0. 1）＝ A －＋｜a2｜＋（b的长；（1）求线段AB1的根，在数轴上是否存在2x＋－x1＝C（2）点在数轴上对应的数为x，且x是方程2 2. P 对应的数；若不存在，说明理由PB＋＝PC，若存在，求出点点P，使PA点左侧运动时，点在ANPB的中点为，当PM左侧的一点，）若（3P是APA的中点为，的值不变，其中只有一个结论正确，PM的值不变；②PN－＋有两个结论：①PMPN.请判断正确结论，并求出其值3，=10cm（如图所示）=60cm，BCCB、，满足OA=20cm,AB如图，3、在射线OM上有三点A、CO 从点C出发在线段出发，沿OOM方向以1cm/s的速度匀速运动，点Q点P从点. 匀速运动，两点同时出发上向点OQ运动的速度；Q运动到的位置恰好是线段AB的三等分点，求点=2（1）当PAPB时，点、两点相距70cm3cm/s,Q运动的速度为经过多长时间P；Q2（）若点AP?OB、.的值，求EABOPABP3（）当点运动到线段上时，取和的中点F EF4。

数轴上动点问题解题技巧
WPS,a click to unlimited possibilities
汇报人：WPS
1
一、数轴上两点间的距离：右边点表示的数-左边点表示的数
已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70 （1）求出A、B两点间的距离
2
二、两点中点公式：两数和除以2
6
三动点问题
已知数轴上两点A、B对应的数分别为—1，3，点P为数轴上一动点，其对应的数为x。 ⑴若点P到点A、点B的距离相等，求点P对应的数； ⑵数轴上是否存在点P，使点P到点A、点B的距离之和为5？若存在，请求出x的值。若不存在，请说 明理由？ ⑶当点P以每分钟一个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度向左运动，点B一 每分钟20个单位长度向左运动，问它们同时出发，几分钟后P点到点A、点B的距离相等？
已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70 （2）请写出AB的中点M对应的数
3
三、用字母表示动点：数轴上的点向左移动用减法，移动几个单位长度就减去几 数轴上的点向右移动用加法，移动几个单位长度就加上几
已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70 （3)现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发, 以2个单位/秒的速度向左运动,
(3)如果A. B两点以(2)中的速度同时向数轴的负方向运动,点C从图上的位置出发也向数轴的负方向运动,
且始终保持AB=
2 3
AC.当点C运动到−6时，点A对应的数ቤተ መጻሕፍቲ ባይዱ多少?
8
7
动点折返问题
如图，在数轴上每相邻两点间的距离为一个单位长度，点A. B. C. D对应的数分别是a、b、c、d，且 d−2a=14

七年级数学上册动点问题1、如图，有一数轴原点为O，点A所对应的数是-1 12，点A沿数轴匀速平移经过原点到达点B．（1）如果OA=OB，那么点B所对应的数是什么？（2）从点A到达点B所用时间是3秒，求该点的运动速度．（3）从点A沿数轴匀速平移经过点K到达点C，所用时间是9秒，且KC=KA，分别求点K和点C所对应的数。

2、动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度．已知动点A、B的速度比是1：4．（速度单位：单位长度/秒）（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；（3）在（2）中A、B两点继续同时向数轴负方向运动时，另一动点C同时从B 点位置出发向A运动，当遇到A后，立即返回向B点运动，遇到B点后立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始到停止运动，运动的路程是多少单位长度．3、已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上一动点，其对应的数为x．（1）若点P到点A，点B的距离相等，求点P对应的数；（2）数轴上是否存在点P，使点P到点A、点B的距离之和为6？若存在，请求出x的值；若不存在，说明理由；（3）点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以6个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？①4、数轴上两个质点A、B所对应的数为-8、4，A、B两点各自以一定的速度在上运动，且A点的运动速度为2个单位/秒．（1）点A、B两点同时出发相向而行，在原点处相遇，求B点的运动速度；（2）A、B两点以（1）中的速度同时出发，向数轴正方向运动，几秒钟时两者相距6个单位长度；（3）A、B两点以（1）中的速度同时出发，向数轴负方向运动，与此同时，C 点从原点出发作同方向的运动，且在运动过程中，始终有CB：CA=1：2，若干秒钟后，C停留在-10处，求此时B点的位置？5、在数轴上，点A表示的数是-30，点B表示的数是170．（1）求A、B中点所表示的数．（2）一只电子青蛙m，从点B出发，以4个单位每秒的速度向左运动，同时另一只电子青蛙n，从A点出发以6个单位每秒的速度向右运动，假设它们在C点处相遇，求C点所表示的数．（3）两只电子青蛙在C点处相遇后，继续向原来运动的方向运动，当电子青蛙m处在A点处时，问电子青蛙n处在什么位置？（4）如果电子青蛙m从B点处出发向右运动的同时，电子青蛙n也向右运动，假设它们在D点处相遇，求D点所表示的数6、已知数轴上有A、B、C三点，分别代表—24，—10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒。

专题08难点探究专题：数轴上的动点问题压轴题六种模型全攻略【考点导航】目录【典型例题】 (1)【考点一数轴上的动点中求运动的时间问题】 (1)【考点二数轴上的动点中求定值问题】 (7)【考点三数轴上的动点中找点的位置问题】 (14)【考点四数轴上的动点中几何意义最值问题】 (18)【考点五数轴上的动点规律探究问题】 (21)【考点六数轴上的动点新定义型问题】 (24)【典型例题】【考点一数轴上的动点中求运动的时间问题】(1)数轴上点A表示的数为，点-+，在数轴上点P表示的数是104t【变式训练】1．（2023春·安徽安庆·七年级统考期末）已知如图，数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运t t>秒．动时间为()0（1）数轴上点B表示的数是___________；当点P运动到AB的中点时，它所表示的数是__________．（2）动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P，Q同时出发．求：①当点P运动多少秒时，点P追上点Q？②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？【答案】（1）−4，1；（2）①当点P运动5秒时，点P追上点Q；②当点P运动1或9秒时，点P与点Q 间的距离为8个单位长度．【分析】（1）由已知得OA＝6，则OB＝AB−OA＝4，因为点B在原点左边，从而写出数轴上点B所表示的数；动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，所以可得出点P所表示的数为6−4t，当点P运动到AB的中点时，它的运动时间t＝5÷4＝1.25秒，即可求出点P所表示的数是1；（2）①点P运动t秒时追上点Q，由于点P要多运动10个单位才能追上点Q，则4t＝10＋2t，然后解方程得到t＝5；②分两种情况：当点P运动a秒时，不超过Q，则10＋2a−4a＝8；超过Q，则10＋2a＋8＝4a；由此求解即可．【详解】解：（1）∵数轴上点A表示的数为6，∴OA＝6，则OB＝AB−OA＝4，∵点B在原点左边，∴数轴上点B所表示的数为−4；点P运动t秒的长度为4t，∵动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，∴P所表示的数为：6−4t，当点P运动到AB的中点时，它的运动时间为t＝5÷4＝1.25秒，∴它所表示的数是6−4t＝6−4×1.25＝1；故答案为：−4，1；（2）①点P运动t秒时追上点Q，根据题意得4t＝10＋2t，解得t＝5，答：当点P运动5秒时，点P追上点Q；②设当点P运动a秒时，点P与点Q间的距离为8个单位长度，当P 不超过Q ，则10＋2a −4a ＝8，解得a ＝1；当P 超过Q ，则10＋2a ＋8＝4a ，解得a ＝9；答：当点P 运动1或9秒时，点P 与点Q 间的距离为8个单位长度．【点睛】此题考查了数轴上的动点问题，根据已知得出各线段之间的关系等量关系是解题关键．2．（2023秋·湖北武汉·七年级统考期末）如图，将一条数轴在原点O 和点B 处各折一下，得到一条“折线数轴”．图中点A 表示12-，点B 表示12，点C 表示20，我们称点A 和点C 在数轴上相距32个长度单位，记为32AC L =．动点M 从点A 出发，沿着“折线数轴”的正方向运动，同时，动点N 从点C 出发，沿着“折线数轴”的负方向运动，它们在水平轴AO ，BC 上的速度都是2单位/秒，在O ，B 之间的上行速度为1单位/秒，下行速度为3单位秒．设运动的时间为t 秒．(1)当4t =秒时，M ，N 两点在数轴上相距多少个单位长度？(2)当M ，N 两点相遇时，求运动时间t 的值．(3)若“折线数轴”上定点P 与O ，B 两点相距的长度相等，且存在某一时刻t ，使得两点M ，N 与点P 相距的长度之和等于6，请直接写出t 的值为____________．【答案】(1)M ，N 两点在数轴上相距16个单位长度(2)8.5t =(3)3t =或10t =【分析】（1）先计算出AO ，BC 的长度，再计算出经过4秒，点M 和点N 运动的路程，即可求解；（2）根据相遇时，两点的路程和等于总路程，即可求解；（3）根据题意，进行分类讨论即可．【详解】（1）解：根据题意可得：()01212AO =--=，20128BC =-=，当4t =秒时，点M 的运动路程：2812t =<，点N 的运动路程：28t =，∴经过4秒，点M 在AO 上，点N 和点B 重合，∴点M 表示的数为：1284-+=-，点N 表示的数为：20812-=，∴M 、N 两点距离为：()12416--=．【考点二数轴上的动点中求定值问题】(1)点B在数轴上表示的数是，点C在数轴上表示的数是【变式训练】(1)=a___________，b=___________；(1)填空：线段AB的长度AB=______；=，点D在点A的右侧，又∵OD AC【考点三数轴上的动点中找点的位置问题】(1)操作一：折叠纸面，使表示数1的点与表示数﹣1的点重合，则此时表示数(2)操作二：折叠纸面，使表示数6的点与表示数﹣2的点重合，回答下列问题：【答案】(1)-4(2)①-5；②A、B两点表示的数分别是-3，7；③x的值为-4或8．【分析】（1）先求出中心点，再求出对应的数即可；（2）①求出中心点是表示2的点，再根据对称求出即可；②求出中心点是表示2的点，求出A、B到表示2的点的距离是5，即可求出答案；③根据点P在数轴上的位置，分类讨论，当点P在点A的左侧时，当点P在点A、B之间时，当点P在点A的右侧时，根据各种情形求解即可．【详解】（1）解：∵折叠纸面，使数字1表示的点与-1表示的点重合，可确定中心点是表示0的点，∴4表示的点与-4表示的点重合，故答案为∶-4；（2）解：①∵折叠纸面，使表示数6的点与表示数﹣2的点重合，可确定中心点是表示2的点，∴表示数9的点与表示数-5的点重合；故答案为∶-5；②∵折叠后，数轴上的A，B两点也重合，且A，B两点之间的距离为10（点A在点B的左侧），∴A、B两点距离中心点的距离为10÷2=5，∵中心点是表示2的点，∴A、B两点表示的数分别是-3，7；③当点P在点A的左侧时，∵PA+PB＝12，∴-3-x+7-x=12，解得x=-4；当点P在点A、B之间时，此时PA+PB=12不成立，故不存在点P在点A、B之间的情形；当点P在点A的右侧时，∵PA+PB＝12，∴x-(-3)+x-7=12，解得x=8，综上x的值为-4或8．【点睛】本题考查了数轴的应用，能求出折叠后的中心点的位置是解此题的关键．【变式训练】1．已知在数轴上A，B两点对应数分别为﹣2，6．（2）解：①MP=2t+2－t=t+2．当点P在点N NP=5t－6(1)直接写出线段AB的中点C对应的数；（4）①追及前相距20，设行驶的时间为t s ，由题意得，3012+90+8=20t t -，解得25t =，此时李明所在位置点F 对应的数为90825290--⨯=-；②追及后相距20，设行驶的时间为t s ，由题意得，908301220t t ---+=，解得35t =，此时李明所在位置点F 对应的数为90835370--⨯=-；答：李明所在位置点F 对应的数为290-或370-．【点睛】题目主要考查数轴上两点之间的距离及一元一次方程的应用，理解题意，进行分情况讨论分析是解题关键．【考点四数轴上的动点中几何意义最值问题】填空：因为12x x ++-的几何意义是线段PA 与PB 的长度之和，而当点点P 在线段AB 上，6PA PB +=，当点在3-和1之间时，距离之和为4，不满足题意；【变式训练】图图图图【考点五数轴上的动点规律探究问题】例题：（2022秋·北京朝阳·九年级校考阶段练习）一个动点P 从数轴上的原点O 出发开始移动，第1次向右移动1个单位长度到达点P 1，第2次向右移动2个单位长度到达点P 2，第3次向左移动3个单位长度到达点P 3，第4次向左移动4个单位长度到达点P 4，第5次向右移动5个单位长度到达点P 5…，点P 按此规律移动，则移动第158次后到达的点在数轴上表示的数为（）A ．159B ．-156C ．158D ．1【答案】A【分析】根据数轴，按题目叙述的移动方法即可得到点前五次移动后在数轴上表示的数；根据移动的规律即可得移动第158次后到达的点在数轴上表示的数．【详解】解：设向右为正，向左为负，则1P 表示的数为+1，2P 表示的数为+33P 表示的数为04P 表示的数为-45P 表示的数为+1……由以上规律可得，每移动四次相当于向左移动4个单位长度．所以当移动156次时，156=39×4相当于向左移动了39次四个单位长度．此时表示的数为()39-4156⨯=-．则第157次向右移动157个单位长度，1571P =；P=．第158次还是向右，移动了158个单位长度，所以1581+158=159P在数轴上表示的数为159．故158故选A．【点睛】本题考查了数轴上点的运动规律，正确理解题意，找出点在数轴上的运动次数与对应点所表示的数的规律是解题的关键．【变式训练】离．【详解】（1）∵A点在数轴上表示的数为﹣17，A、B两点相距54米，﹣17+54＝37或-17-54=-71答：B点在数轴上表示的数为37或-71；（2）M点到A点的距离与N点到A点的距离相等．理由如下：根据题意，得前进第一次与点A距离1米，前进第二次与点A距离2米，后退第一次与点A距离1米，后退第二次与点A距离2米，…第六次行进（即前进3次，后退3次）后，点N到A的距离为3米，点M到A的距离为3米，答：M点到A点的距离与N点到A点的距离相等．（3）∵B点在原点的左侧∴B点在点A的左侧经过10次行进后，小乌龟在点A的右侧且与点A的距离是5米，小乌龟到达的点与B点之间的距离是54+5＝59（米）；答：经过10次行进后，小乌龟到达的点与B点之间的距离是59米．【点睛】此题考查有理数的计算，正确理解点与点间的位置关系是解题的关键，（1）中注意点B可能在两侧的情况；（2）中找到乌龟爬行的规律为（3）做基础.【考点六数轴上的动点新定义型问题】例题：（2022秋·江苏·七年级期末）定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B 的距离2倍，我们就称点C是【A，B】的美好点．例如：如图1，点A表示的数为－1，点B表示的数为2.表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D 就不是【A，B】的美好点，但点D是【B，A】的美好点．(1)点E，F，G表示的数分别是－3，6.5，11，其中是【M，N】美好点的是H所表示的数是．【答案】(1)G；－4或－16(2)1.5，2.25，3，6.75，9，13.5【分析】（1）根据美好点的定义，结合图2，直观考察点E，F，G到点M，N的距离，当MP＝2PN时，PN＝3，点P对应的数为当2PM＝PN时，NP＝6，点P对应的数为2－6＝－4，因此t＝3秒；第三种情况，P为【N，M】的美好点，点P在M左侧，如图3，当PN＝2MN时，NP＝18，点P对应的数为2－18＝－16，因此t＝9秒；第四种情况，M为【P，N】的美好点，点P在M左侧，如图4，当MP＝2MN时，NP＝27，点P对应的数为2－27＝－25，因此t＝13.5秒；第五种情况，M为【N，P】的美好点，点P在M左侧，如图5，当MN＝2MP时，NP＝13.5，点P对应的数为2－13.5＝－11.5，因此t＝6.75秒；第六种情况，M为【N，P】的美好点，点P在M，N左侧，如图6，当MN＝2MP时，NP＝4.5，因此t＝2.25秒；第七种情况，N为【P，M】的美好点，点P在M左侧，当PN＝2MN时，NP＝18，因此t＝9秒，第八种情况，N为【M，P】的美好点，点P在M右侧，当MN＝2PN时，NP＝4.5，因此t＝2.25秒，综上所述，t的值为：1.5，2.25，3，6.75，9，13.5．【点睛】本题考查实数与数轴、点是【M，N】的美好点的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题．【变式训练】如图②，M ，N 为数轴上两点，点M 表示数（1）①求(),M N 的美好点表示的数为__________．②求(),N M 的美好点表示的数为_____________．（2）数轴上有一个动点P 从点M 出发，沿数轴以每秒2个单位长度的速度向右运动．设点为t 秒，当点P ，M 和N 中恰有一个点为其余两点的美好点时，求【答案】（1）①－1；②－4；（2）t的值1.5，2.25，3，6.75，9，13.5【分析】（1）根据美好点的定义，结合图2，直观考察点E，F，G到点M，N的距离，只有点G符合条件．结合图2，根据美好点的定义，在数轴上寻找到点N的距离是到点M的距离2倍的点，在点的移动过程中注意到两个点的距离的变化．（2）根据美好点的定义，P，M和N中恰有一个点为其余两点的美好点分6种情况，须区分各种情况分别确定P点的位置，进而可确定t的值．【详解】解：（1）已知点M表示数-7，点N表示数2，由题意可设N到美好点的距离为x，则(M，N)的美好点为2x+x=2-(-7)，3x=9，x=3∴①(M，N)的美好点为-7+2×3=-1；②(N，M)的美好点为-7+3=-4；（2）根据美好点的定义，P，M和N中恰有一个点为其余两点的美好点分6种情况，第一情况：当P为【M，N】的美好点，点P在M，N之间，如图1，当MP=2PN时，PN=3，点P对应的数为2-3=-1，因此t=1.5秒；第二种情况，当P为【N，M】的美好点，点P在M，N之间，如图2，当2PM=PN时，NP=6，点P对应的数为2-6=-4，因此t=3秒；第三种情况，P为【N，M】的美好点，点P在M左侧，如图3，当PN=2MN时，NP=18，点P对应的数为2-18=-16，因此t=9秒；第四种情况，M为【P，N】的美好点，点P在M左侧，如图4，当MP=2MN时，NP=27，点P对应的数为2-27=-25，因此t=13.5秒；第五种情况，M为【N，P】的美好点，点P在M左侧，如图5，当MN=2MP时，NP=13.5，点P对应的数为2-13.5=-11.5，因此t=6.75秒；第六种情况，M为【N，P】的美好点，点P在M，N左侧，如图6，当MN=2MP时，NP=4.5，因此t=2.25秒；第七种情况，N为【P，M】的美好点，点P在M左侧，当PN=2MN时，NP=18，因此t=9秒，第八种情况，N为【M，P】的美好点，点P在M右侧，当MN=2PN时，NP=4.5，因此t=2.25秒，综上所述，t的值为：1.5，2.25，3，6.75，9，13.5．【点睛】本题考查了实数与数轴、点是【M，N】的美好点的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题．。

数轴上的动点问题最新版1．如图，已知数轴上两点A 、B 对应的数分别为-1，3，点P 为数轴上一动点，其对应的数为x 。

（1）数轴上是否存在点P ，使点P 在点A 、点B 的距离之和为5？若存在，请求出x 的值，若不存在，请说明理由；（2）当点P 以每分钟1个单位长度的速度从O 点向左运动时，点A 以每分钟5个单位长度的速度向左运动，点B 以每分钟20个单位长度的速度向左运动，问它们同时出发，几分钟时点P 到点A 、点B 的距离相等？（3）如图，若点P 从B 点出发向左运动（只在线段AB 上运动），M 为AP 的中点，N 为PB 的中点，点P在运动的过程中，线段MN 的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出MN 的长。

2．如图，A 、B 、C 是数轴上的三点，O 是原点， BO=3，AB=2BO ，5AO=3CO ． （1）写出数轴上点A 、C 表示的数；图图图（2）点P 、Q 分别从A 、C 同时出发，点P 以每秒 2个单位长度的速度沿数轴向右匀速运动，点Q 以每秒6个单位长度的速度沿数轴向左匀速运 动，M 为线段AP 的中点，点N 在线段CQ 上，且 CN=CQ ．设运动的时间为t （t ＞0）秒． ①数轴上点M 、N 表示的数分别是 （用含t 的 式子表示）；②t 32为何值时，M 、N 两点到原点O 的距离相等？3．如图，数轴上有A 、B 、C 、D 四个点，分别对应数a 、b 、c 、d ，且满足a 、b 是方程的两根（），91x +=a b <与互为相反数。

2(16)c -20d -（1）求a 、b 、c 、d 的值；（2）若A 、B 两点以6个单位长度/秒的速度向右匀速运动，同时C 、D 两点以2个单位长度/秒的速度向左匀速运动，并设运动时间为t 秒。

问t 为多少时，A 、B 两点都运动在线段CD 上（不与C 、D 两个端点重合）？（3）在（2）的条件下，A 、B 、C 、D 四个点继续运动，当点B 运动到点D 的右侧时，问是否存在时间t ，使B 与C 的距离是A 与D 的距离的4倍，若存在，求时间t ，若不存在，请说明理由。

完整版)七年级上期末动点问题专题(附答案)1.已知数轴上点A对应的数为a，点B对应的数为b，且满足|2b-6|+(a+1)^2=0，定义AB的长度为|a-b|。

1) 求线段AB的长度。

解：由定义可得，AB的长度为|a-b|。

2) 设点P在数轴上的坐标为x，且满足PA-PB=2，求x的值。

解：由题意得，PA-PB=|a-x|-|b-x|=2，分成两种情况讨论：当a>b时，有a-x-b+x=2，即a-b=2，解得x=a-1.当a<b时，有b-x-a+x=2，即b-a=2，解得x=b-1.综上所述，x的取值为a-1或b-1.3) 设M、N分别为PA、PB的中点，当P移动时，指出当下列结论分别成立时，x的取值范围，并说明理由：①PM÷PN的值不变，②|PM-PN|的值不变。

解：由题意得，M、N的坐标分别为[(a+x)/2,0]和[(b+x)/2,0]，则① PM÷PN的值不变时，有|a-x|/|b-x|=|a-x0|/|b-x0|，其中x0是PM÷PN的值不变时的一个定值，化简得(a-x0)(b-x)=(b-x0)(a-x)，即ax0-bx0=ax-bx0，解得x=(ax0-bx0+bx0)/2=a/2+b/2-x0/2.② |PM-PN|的值不变时，有[(a-x)/2-(b-x)/2]^2=K，其中K 是|PM-PN|的值不变时的一个定值，化简得(x-a+b)^2=4K，解得x=(a+b±2√K)/2.综上所述，当①成立时，x的取值为a/2+b/2-x0/2；当②成立时，x的取值为(a+b±2√K)/2.2.如图1，已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上的动点，其对应的数为x。

1) PA=|x-(-1)|=|x+1|，PB=|x-3|。

2) 若PA+PB=5，则有|x+1|+|x-3|=5，分成四种情况讨论：当x≤-1时，有-(x+1)-(x-3)=5，解得x=-2.当-1<x<3时，有-(x+1)+(x-3)=5，无解。

完整版)七年级上册数学期末动点问题专题七年级上期末动点问题专题1.数轴上的动点问题已知数轴上两点A、B对应的数分别为-1和3，数轴上一动点P对应的数为x。

1) 若点P到点A和点B的距离相等，求点P对应的数。

解：由题意得，PA=PB，即 |x-(-1)|=|x-3|，解得x=1.2) 当点P以每分钟1个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度的速度向左运动，点B以每分钟20个单位长度的速度向左运动，问几分钟时点P到点A 和点B的距离相等。

解：设P点向左运动t分钟后到达距离O点x的位置，则A点和B点向左运动5t和20t个单位长度后，分别到达距离O 点-5t和3-20t的位置。

由于PA=PB，因此有：x-(-1+1t)|=|x-3-17t|解得t=2，代入得到x=-1+2t=-3.2.射线上的动点问题如图，在射线OM上有三点A、B、C，满足OA=20cm，AB=60cm，BC=10cm，点P从点O出发，沿OM方向以1cm/s的速度匀速运动，点Q从点C出发在线段CO上向点O 匀速运动（点Q运动到点O时停止运动），两点同时出发。

1) 当PA=2PB时，点Q运动到的位置恰好是线段AB的三等分点，求点Q的运动速度。

解：设Q点向左运动t秒后到达距离O点x的位置，则有：OC-x|=|OP+t|OB-2x|=2|PA-OP-t|AB-3x|=3|PA-OP-t|解得x=10，t=10，因此Q点的运动速度为3cm/s。

2) 若点Q运动速度为3cm/s，经过多长时间P、Q两点相距70cm。

解：设P点向右运动t秒后到达距离O点y的位置，则有：y|=|x+t-20|y|=|60-x-t|解得t=25，因此P、Q两点相距70cm时，P点向右运动了25秒，Q点向左运动了25秒。

3) 当点P运动到线段AB上时，分别取OP和AB的中点E、F，求OB-AP/EF的值。

解：设P点向右运动t秒后到达线段AB上的点E，则有：OE|=|20+t/2|由于AE=40，因此有AP=AE-PE=40-(20+t/2)=60-t/2.又因为OF=FB=30，因此有：OB-AP/EF=2OB/AB-AP/AF=2(20+t)-60/(2OF)=t+1.3.相向而行的动点问题甲、乙物体分别从相距70米的两处同时相向运动。

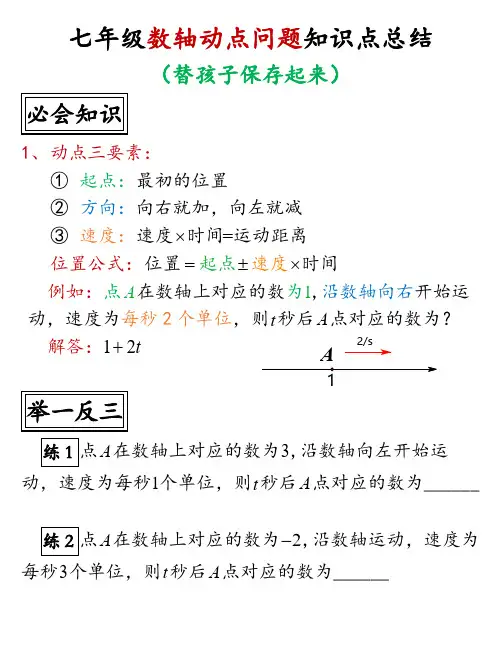
1、 动点三要素：① 起点：最初的位置② 方向：向右就加，向左就减③ 速度：=×速度时间运动距离位置公式：=±×位起点速度置时间例如：点A 在数轴上对应的数为1,沿数轴向右开始运动，速度为每秒2个单位，则t 秒后A 点对应的数为？解答：12t +练1点A 在数轴上对应的数为3,沿数轴向左开始运动，速度为每秒1个单位，则t 秒后A 点对应的数为______练2点A 在数轴上对应的数为2−,沿数轴运动，速度为每秒3个单位，则t 秒后A 点对应的数为______2、距离表示：距离右左①相对位置确定：=−②相对位置不确定：=距离右左左右=−−例1：点A在数轴上对应的数为1,点B在数轴上对应的点为3，则A、B之间的距离为多少？−=解答：312例2：点A在数轴上对应的点为1,点B在数轴上对应的点为x，则A、B之间的距离为多少？x−解答：1练1点A在数轴上对应的数为2−,点B在数轴上对应的点为4，则A、B之间的距离为_____练2点A在数轴上对应的数为a,点B在数轴上对应的点为b，则A、B之间的距离为_____3、 中点公式：已知A 在数轴上对应的数为a ，B 在数轴上对应的数为b ，则A 、B 的中点M 对应的数为2m a b +=中点公式进阶：已知A 在数轴上对应的数为a ，A 、B 的中点M 对应的数为m ，则B 在数轴上对应的数为2b a m =−例1：点A 为3,点B 为7−，则A 、B 的中点是多少？解答：()3227+−=−3、 中点公式：已知A 在数轴上对应的数为a ，B 在数轴上对应的数为b ，则A 、B 的中点M 对应的数为2m a b += 中点公式进阶：已知A 在数轴上对应的数为a ，A 、B 的中点M 对应的数为m ，则B 在数轴上对应的数为2b a m =− 练1点A 为10−,点B 为6，则A 、B 中点对应数为____ 练2点A 为10−,A 、B 中点为2，则点B 对应数为____考法1：相遇问题、相遇时，t是多少？相遇时P对应的数为多少？P Q考法2：距离问题当t为何值时，PQ之间的距离为6？考法3：定值问题若Q点运动方向改为向右，那么在运动过程中，PQ PA−是否为定值？考法4：中点问题若P Q、出发的同时，点M从原点出发，向右运动，速度为3个单位每秒，则t为何值时，P Q M、、中，任意一点是其余两点所连线段的中点？考法1：相遇问题P Q、相遇，t是多少？相遇时P对应的数为多少？分析：相遇表示同一时间到达同一位置，分别表示P、Q 位置，利用位置相等建方程即可解析：t秒后，点P位置为2t+，点Q位置为102t−P、Q相遇，则1202t t=+−解之得：83 t=248313+=，故相遇时，P点对应的数为143练习若P点运动方向改为向左，那么P Q、相遇时，t是多少？相遇时P对应的数为多少？考法2：距离问题当t为何值时，PQ之间的距离为6？分析：分别表示P、Q位置,再表示距离建方程，需注意的是P、Q相对位置不确定，故需加绝对值解析：t秒后，点P位置为2t+，点Q位置为102t−则()810223P ttQ t+=−−=−令386t−=，解之得：21433 t=或故21433t=或时，PQ之间的距离为6练习当t为何值时，PQ之间的距离为2？考法3：定值问题若Q点运动方向改为向右，那么在运动过程中，PQ PA−是否为定值？分析：分别表示PQ、P A的距离，再代入PQ PA−计算，看结果是否为定值即可，本题相对位置确定，故表示位置时，无需加绝对值解析：t秒后，点P为2t+，点Q为102t+,点A为2则()()++t t=−=+，22t10PQ t228=−=tPA+则88PQ PA t t−=+−=故PQ PA−为定值练习Q点运动方向仍为向右，BQ的中点记为M，则PM的长是否为定值？考法4：中点问题P Q 、出发同时，M 从原点出发，向右运动，速度为3个单位每秒，t 为何值时，P Q M 、、中任意一点是其余两点中点？分析：分别表示P 、Q 、M 的位置，再分三类讨论，每一类根据中点公式列方程即可解析：t 秒后，点P 为2t +，点Q 为102t −，点M 为3t①若P 为QM 中点，则310222t t t +=+−，6t = ②若Q 为PM 中点，则221230t t t +−+=，94t = ③若M 为PQ 中点，则232102t t t +=+−，127t = 练习考法4中，点P 方向改为向左，其余条件和问题均不变，则t 为何值？。

七年级动点问题大全（一）例1:如图，在数轴上A点表示数a，B点表示数b，AB表示A点和B点之间的距离，且a、b满足|a+2|+（b+3a）2=0（1）求A、B两点之间的距离；（2）若在数轴上存在一点C，且AC=2BC，求C点表示的数；（3）若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t（秒），①分别表示甲、乙两小球到原点的距离（用t表示）；①求甲、乙两小球到原点的距离相等时经历的时间．例2:如图，有一数轴原点为O，点A所对应的数是-12，点A沿数轴匀速平移经过原点到达点B．（1）如果OA=OB，那么点B所对应的数是什么？（2）从点A到达点B所用时间是3秒，求该点的运动速度．（3）在（2）的条件下，从点A沿数轴匀速平移经过点K到达点C，所用时间是9秒，且KC=KA，分别求点K和点C所对应的数。

例3动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度．已知动点A、B的速度比是1：4．（速度单位：单位长度/秒）（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；（3）在（2）中A、B两点继续同时向数轴负方向运动时，另一动点C同时从B点位置出发向A运动，当遇到A后，立即返回向B点运动，遇到B点后立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始到停止运动，运动的路程是多少单位长度．例4:已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上一动点，其对应的数为x．（1）若点P到点A，点B的距离相等，求点P对应的数；（2）数轴上是否存在点P，使点P到点A、点B的距离之和为6？若存在，请求出x的值；若不存在，说明理由；（3）点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以6个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？例5数轴上两个质点A、B所对应的数为-8、4，A、B两点各自以一定的速度在上运动，且A点的运动速度为2个单位/秒．（1）点A、B两点同时出发相向而行，在原点处相遇，求B点的运动速度；（2）A、B两点以（1）中的速度同时出发，向数轴正方向运动，几秒钟时两者相距6个单位长度；（3）A、B两点以（1）中的速度同时出发，向数轴负方向运动，与此同时，C点从原点出发作同方向的运动，且在运动过程中，始终有CB：CA=1：2，若干秒钟后，C停留在-10处，求此时B点的位置？例6:在数轴上，点A表示的数是-30，点B表示的数是170．（1）求A、B中点所表示的数．（2）一只电子青蛙m，从点B出发，以4个单位每秒的速度向左运动，同时另一只电子青蛙n，从A点出发以6个单位每秒的速度向右运动，假设它们在C点处相遇，求C点所表示的数．（3）两只电子青蛙在C点处相遇后，继续向原来运动的方向运动，当电子青蛙m处在A 点处时，问电子青蛙n处在什么位置？（4）如果电子青蛙m从B点处出发向右运动的同时，电子青蛙n也向右运动，假设它们在D点处相遇，求D点所表示的数例7、已知数轴上有A、B、C三点，分别代表- 24，- 10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒。

初一数学上册数轴动点问题一、什么是数轴动点问题数轴动点问题呢，就是在数轴这个特定的数学环境里，有一些点是可以动来动去的，然后让我们根据这些点的运动情况去解决各种各样的数学问题。

比如说，一个点从数轴上的某个位置开始，按照一定的速度向左或者向右移动，然后问我们在某个时刻这个点的位置在哪里呀，或者几个点之间的距离是多少啦之类的。

这就像一群小蚂蚁在数轴这条小路上跑来跑去，我们得搞清楚它们的位置变化情况。

二、常见的题型类型1. 求动点表示的数这种题就是给你一个动点在数轴上的初始位置，还有它运动的方向和速度，然后让你求出经过一段时间后这个动点所表示的数。

比如说，一个点在数轴上表示3，它以每秒2个单位长度的速度向右运动，经过5秒后，这个点就向右移动了2×5 = 10个单位长度，那这个点表示的数就变成了3+10 = 13啦。

2. 求两点之间的距离有时候会给你两个动点，它们分别在数轴上运动，然后问你在某个时刻这两个动点之间的距离是多少。

这就需要我们先算出这两个动点在那个时刻分别在数轴上的位置，然后用较大的数减去较小的数（如果是求绝对值距离的话就直接求两个数差的绝对值）。

就像两个人在数轴这条跑道上跑，我们要看看他们之间隔了多远。

3. 动点与线段的关系还有一种题型是关于动点和线段的关系的。

比如说，一个动点在数轴上运动，问这个动点什么时候会在线段的中点上，或者什么时候这个动点会把某条线段分成一定比例的两段。

这就比较复杂啦，我们要综合考虑线段的端点位置、动点的运动情况等很多因素呢。

三、解决数轴动点问题的小技巧1. 画数轴这可是超级重要的一步哦。

把题目中的情况在数轴上画出来，这样我们就能很直观地看到各个点的位置关系啦。

就像画画一样，把那些抽象的数字和动点变成我们能看得见的东西。

比如说，题目里说一个点在 -2的位置，另一个点在4的位置，我们就把它们在数轴上标出来，然后再根据动点的运动情况，一点一点地画出它们的新位置。

1.2.2数轴培优训练数轴上的动点问题人教版2024—2025学年七年级上册一、与数轴上的动点问题相关的基本概念数轴上的动点问题离不开数轴上两点之间的距离.主要涉及以下几个概念：1．数轴上两点间的距离，即为这两点所对应的坐标差的绝对值d =|a -b|,也即用右边的数减去左边的数的差.即数轴上两点间的距离=右边点表示的数—左边点表示的数.2．两点中点公式：线段AB 中点坐标=2a b 3．点在数轴上运动时，由于数轴向右的方向为正方向，因此向右运动的速度看作正速度，而向左运动的速度看作负速度.这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标.即一个点表示的数为a ，向左运动b 个单位后表示的数为a—b ；向右运动b 个单位后所表示的数为a+b .4．数轴是数形结合的产物，分析数轴上点的运动要结合图形进行分析，点在数轴上运动形成的路径可看作数轴上线段的和差关系.二、 数轴上的动点问题基本解题思路和方法1．表示出题目中动点运动后的坐标（一般用含有时间t 的式子表示）.2．根据两点间的距离公式表示出题目中相关线段长度（一般用含有时间t 的式子表示）.3．根据题目问题中线段的等量关系（一般是和、差关系）列绝对值方程.4．解绝对值方程并根据实际问题验算结果.注：数轴上线段的动点问题方法类似。

类型一数轴与行程问题例1.如图，在数轴上点A 、点B 表示数a 、b ，且满足|a ﹣30|+（b +6）2＝0．点O 是数轴原点．（1）点A 表示的数为 ，点B 表示的数为 ，线段AB 的长为 ．（2）若点A 与点C 之间的距离表示为AC ，点B 与点C 之间的距离表示为BC ，请在数轴上找一点C ，使AC ＝2BC ，则点C 在数轴上表示的数为 ．（3）现有动点P 、Q 都从B 点出发，点P 以每秒1个单位长度的速度向终点A 移动；当点P 移动到O 点时，点Q 才从B 点出发，并以每秒3个单位长度的速度向右移动，且当点P 到达A 点时，点Q 就停止移动，设点P 移动的时间为t 秒，问：当t 为多少时，P 、Q 两点相距4个单位长度？变式1：如图：在数轴上A点表示数a，B点表示数b，C点表示数c，且a，c 满足|a+3|+（c﹣9）2＝0，b＝1．（1）a＝，c＝；（2）若将数轴折叠，使得A点与点C重合，则点B与数表示的点重合．（3）在（1）的条件下，若点P为数轴上一动点，其对应的数为x，求当x取何值时代数式|x﹣a|﹣|x﹣c|取得最大值，并求此最大值．（4）点P从点A处以1个单位/秒的速度向左运动；同时点Q从点C处以2个单位/秒的速度也向左运动，在点Q到达点B后，以原来的速度向相反的方向运动，设运动的时间为t（秒），求第几秒时，点P、Q之间的距离是点C、Q之间距离的2倍？变式2：如图，已知A、B分别为数轴上两点，A点对应的数为—20，B点对应的数为100。

专题1数轴上的动点问题1．数轴上，点A ，B ，C ，D ，E ，F 表示的数分别是132-，2-，0，112，0.25，2.1213．请解答下列问题：(1)画出数轴，在数轴上描出A ，B ，C ，D ，E ，F 六个点，并按从小到大的顺序用“<”号连接起来；(2)若把数轴的原点取在点B 处，其余均不变，请直接写出点A ，C ，F 分别表示的数． 2．如图，一个点从数轴上的原点开始，先向左移动4cm 到达A 点，再向右移动5cm 到达B 点，然后再向右移动3cm 到达C 点，数轴上一个单位长度表示1cm ．(1)请你在数轴上标出A 、B 、C 三点的位置，并填空：A 表示的数为_______，B 表示的数为_______，C 表示的数为______．(2)把点A 到点C 的距离记为AC ，则AB =_____cm ，AC =______cm ；(3)若点A 从（1）中的位置沿数轴以每秒1cm 匀速向右运动，经过多少秒使3cm AC =？ 3．如图所示，长方形ABCD ，长为3，宽为2，如图所示放置在数轴上，点B 与1-表示的点重合，点P 是数轴上的一点，规定：ABC S ∆表示三角形ABC 的面积．(1)若点P 表示的数为3-，则PCD S是多少？ (2)若3PCD PAB S S =⨯，则点P 表示的数为多少？(3)若长方形ABCD 原来位置向左以2个单位速度移动，动点P 从20-表示的点以3个单位速度向右移动，当2PCD PAB S S =⨯，则点P 表示的数是多少？4．如图，在数轴上点A 表示的数是8，若动点P 从原点O 出发，以2个单位/秒的速度向左运动，同时另一动点Q 从点A 出发，以4个单位/秒的速度也向左运动，到达原点后立即以原来的速度返回，向右运动，设运动的时间为t （秒）．(1)当0.5t时，求点Q表示的数；=t=时，求点Q表示的数；(2)当 2.5(3)当点Q到原点O的距离为4时，求点P表示的数．5．如图，数轴上一动点A向左移动4个单位长度到达点B，再向右移动7个单位长度到达点C．(1)若点A表示的数为1，则点B，C表示的数分别为，；(2)若点A，C表示的数互为相反数，则点B表示的数为；(3)若点C距原点2个单位长度，则点A表示的数为．6．点A在数轴上所表示的数如图所示，将点A向左平移2个单位长度，得到点B的相反数，点P是数轴上一动点．(1)点B表示的数是_______；(2)若点B在数轴上移动了m个单位长度得到点C，且3AC=，求m的值；(3)若点D为AP的中点，点E为BP的中点，点P在运动过程中，线段DE的长度是否发生变化？若不发生变化，请你求出线段DE的长度；若发生变化，请你说明理由．b≥时，将点A向7．在数轴上有A，B两点，点B表示的数为b．对点A给出如下定义：当0b<时，将点A向左移动||b个单位长度，得到点P．称右移动3个单位长度，得到点P；当0点P为点A关于点B的“联动点”．如图，点A表示的数为1-．(1)在图中画出当4b=时，点A关于点B的“联动点”P；(2)点A从数轴上表示1-的位置出发，以每秒1个单位的速度向右运动．点B从数轴上表示5的位置同时出发，以相同的速度向左运动，两个点运动的时间为t秒．①点B表示的数为__________（用含t的式子表示）；①是否存在t，使得此时点A关于点B的“联动点”P佮好与原点重合？若存在，请求出t的值；若不存在，请说明理由．8．如图，点A对应的有理数为a，点B对应的有理数为b，点C对应的有理数为c，且2c=-，点C向左移动3个单位长度到达点A，向右移动5个单位长度到达点B．(1)a = ，b = ；(2)若将数轴折叠，使得点A 与点B 重合，求与点C 重合的点表示的数；(3)若点P 从点A 开始以3个单位长度/秒的速度向左运动，同时，点Q 从点B 开始以6个单位长度/秒的速度向右运动，点M 从点C 开始以4个单位长度/秒的速度向右运动，设运动时间t 秒，则72QM PM -的值是否随着t 的变化而改变？若变化，请说明理由；若不变，请求其值．9．如图，在一条不完整的数轴上一动点A 向左移动6个单位长度到达点B ，再向右移动10个单位长度到达点C ．(1)①若点A 表示的数为0，则点B 、点C 表示的数分别为：_________、_________； ①若点C 表示的数为1，则点A 、点B 表示的数分别为：_________、_________；(2)如果点A C 、表示的数互为相反数，则点B 表示的数为_________．(3)若点A 表示原点，则距离点B 三个单位长度的点表示的有理数是_________． 10．如图，在数轴上点A 表示的有理数为6-，点B 表示的有理数为6，点P 从点A 出发以每秒3个单位长度的速度在数轴上由A 向B 运动，当点P 到达点B 后立即返回，仍然以每秒3个单位长度的速度运动至点A 停止运动，设运动时间为t （单位：秒）．(1)当1t =时，点P 表示的有理数为______，当点P 与点B 重合时，t 的值为________；(2)在点P 沿数轴由点A 到点B 再回到点A 的运动过程中，求点P 与点A 的距离．（用含t 的代数式表示）11．如图，数轴上有三个点A ，B ，C ，完成下列问题．(1)A 点表示的数是__________，B 点表示的数是___________，C 点表示的数是__________．(2)将点B 向右移动5个单位长度到点D ，D 点表示的数是___________．(3)在数轴上找点E ，使点E 到B ，C 两点距离相等，E 点表示的数是___________． 12．如图，甲、乙两人（看成点）分别在数轴3-和5的位置上，沿数轴做移动游戏．每次的移动游戏规则如下：裁判先捂住一枚硬币，再让两人猜向上一面是正另一面是反，而后根据所猜结果进行移动．①若都对或都错，则甲向东移动1个单位，同时乙向西移动1个单位；①若甲对乙错，则甲向东移动4个单位，同时乙向东移动2个单位；①若甲错乙对，则甲向西移动2个单位，同时乙向西移动4个单位．(1)若第一次移动游戏，甲、乙两人都猜对了，则甲、乙两人之间的距离是_______________个单位；(2)若完成了10次移动游戏，发现甲、乙每次所猜结果均为一对一错．设乙猜对n 次，且他最终停留的位置对应的数为m ．请你用含n 的代数式表示m ；(3)经过_______________次移动游戏，甲、乙两人相遇．13．已知，如图A 、B 分别为数轴上的两点，A 点对应的数为-10，B 点对应的数为90．(1)与A 、B 两点距离相等的M 点对应的数是 ；(2)现在有一只电子蚂蚁P 从B 点出发时，以5个单位/秒的速度向左运动，同时另一只电子蚂蚁Q 恰好从A 点出发，以3个单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的C 点相遇，则C 点对应的数是 ；(3)若当电子蚂蚁P 从B 点出发时，以5个单位/秒的速度向左运动，同时另一只电子蚂蚁Q 恰好从A 点出发，以3个单位/秒的速度向右运动，经过多长的时间两只电子蚂蚁在数轴上相距24个单位长度？14．“数形结合”是重要的数学思想．如：()32--表示3与－2差的绝对值，实际上也可以理解为3与－2在数轴上所对应的两个点之间的距离．进一步地，数轴上两个点AB ，所对应的数分别用a ，b 表示，那么A ，B 两点之间的距离表示为AB a b 利用此结论，回答以下问题：(1)数轴上表示－2和5的两个点之间的距离是______； (2)若13x -=，则x =______；(3)已知数轴上两点A 、B 对应的数分别为－2，8，现在点A 、点B 分别以3个单位长度/秒和2单位长度/秒的速度同时向右运动，当点A 与点B 之间的距离为2个单位长度时，求点A所对应的数是多少？15．在数学综合实践活动课上，小亮同学借助于两根小木棒m、n研究数学问题：如图，他把两根木棒放在数轴上，木棒的端点A、B、C、D在数轴上对应的数分别为a、b、c、d，已知|a＋5|＋（b＋1）2＝0，c＝3，d＝8．(1)求m和n的长度；(2)小亮把木棒m、n同时沿x轴正方向移动，m、n的速度分别为4个单位/s和3个单位/s，设平移时间为t（s）①若在平移过程中原点O恰好是木棒m的中点，则t＝（s）；①在平移过程中，当木棒m、n重叠部分的长为2个单位长度时，求t的值．。

数轴上的动点问题目录解题知识必备..................................................................................................................................................1压轴题型讲练.. (2)类型一、点的运动时间问题 (2)类型二、单点的规律运动问题 (5)类型三、定值问题 (6)类型四、双点往返运动问题 (10)类型五、数轴的折叠问题................................................................................................................................15压轴能力测评（11题）.. (20)1.数轴：规定了原点、单位长度、正方向的直线叫做数轴。

2.数轴的三要素：原点、正方向、单位长度3.任何有理数都可以用数轴上的点表示.4.数轴上的点表示的数从左到右依次增大；原点左边的数是负数，原点右边的数是正数.5.数轴上两点间的距离如图，A 、B 表示的数为a 、b ，则A 与B 间的距离AB=|a －b|；当a ，b 的大小已知时，“大减小（右减左）”，不知大小时，“绝对值”（两数差的绝对值）.6.数轴上两点间中点表示的数如图，C 是AB 的中点，则C 表示的数x=2a b +；理由：AC=BC ，则x －a=b －x ，∴x=2a b +.7.数轴上点移动规律数轴上点向右移动则数变大（增加），向左移动数变小（减小）；当数a表示的点向右移动b个单位长度后到达点表示的数为a+b；向左移动b个单位长度后到达点表示的数为a－b.例：P从A出发，以2个单位/秒速度向右运动，t秒后达到的点表示的数为：a+2t.数轴是数形结合的产物，分析数轴上点的运动要结合图形进行分析，点在数轴上运动形成的路径可看作数轴上线段的和差关系.类型一、点的运动时间问题例1．如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P 从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t>0)秒．(1)数轴上点B表示的数是_______，点P表示的数是_______(用含t的代数式表示)；(2)动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发．求：当点P运动多少秒时，点P与点Q相遇？【答案】(1)―4；6―6t．(2)当点P运动5秒时，点P与点Q相遇．【分析】此题考查的知识点是两点间的距离及数轴，根据题意得出各线段之间的等量关系是解题关键．（1）由题意知OA=6，OB=AB―OA=10―6=4，因为B点在原点左边，从而得出数轴上点B表示的数；动点P从点A出发沿数轴向左匀速运动，根据题意则得出点P表示的数；（2）设P点运动t秒时追上点Q，根据题意列方程6t=10+4t，解得t值．【详解】（1）解：∵数轴上点A表示的数为6，∴OA=6，则OB=AB―OA=10―6=4，又∵点B在原点左边，∴数轴上点B所表示的数为―4；点P运动t秒的长度为6t，∵动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，∴P所表示的数为：6―6t．（2）设点P运动t秒时追上点Q，根据题意，得6t=10+4t，解得：t=5，答：当点P运动5秒时，点P与点Q相遇．变式1-1．已知数轴上有三个点A，B，C，点A表示的数是8，点B到点A的距离为12，点C到A点的距离为7．(1)点B表示的数为 ；(2)点C表示的数为 ；(3)若点A在点B右侧，动点R从点B以每秒2个单位长度的速度沿数轴向右匀速运动，动点P从点C以每秒1个单位长度的速度沿数轴向右匀速运动，点P，R同时出发，点R运动多少秒时追上点P？【答案】(1)20或―4(2)1或15(3)5秒或19秒【分析】（1）分点B在点A的左边和右边两种情况求解即可；（2）分点C在点A的左边和右边两种情况求解即可；（3）分点C表示1和15两种情况，然后分别求出路程差，再根据路程差列方程求解即可．【详解】（1）解：当点B在点A的左边，点B表示的数为8―12=―4；当点B在点A的右边，点B表示的数为8+12=20；综上，点B表示的数为20或―4．故答案为：20或―4．（2）解：当点C在点A的左边，点C表示的数为8―7=1；当点C在点A的右边，点C表示的数为8+7=15；综上，点C表示的数为1或15．故答案为：1或15．（3）解：设点R运动a秒时追上点P，当C表示1时，则BC的距离为1―(―4)=5，则有2a―a=5，解得：a=5；当C表示15时，则BC的距离为15―(―4)=19，则有2a―a=19，解得：a=19综上，点R运动多少秒时追上点P所需时间为5秒或19秒．答：点R运动5秒或19秒时追上点P．【点睛】本题主要考查了在数轴上表示数、数轴上的动点问题等知识点，掌握分类讨论思想是解答本题的关键．变式1-2．已知a、b为常数，且满足|a―12|+(b+20)2=0，其中a、b分别为点A、点B在数轴上表示的数，如图所示，动点E、F分别从A、B同时开始运动，点E以每秒6个单位向左运动，点F以每秒2个单位向右运动，设运动时间为t秒．(1)求a 、b 的值；(2)请用含t 的代数式表示点E 在数轴上对应的数为：______；点F 在数轴上对应的数为：______；(3)当E 、F 相遇后，点E 继续保持向左运动，点F 在原地停留4秒后向左运动且速度变为原来的5倍，在整个运动过程中，当E 、F 之间的距离为2个单位时，请求出运动时间t 的值．【答案】(1)a =12，b =―20(2)12―6t ，2t ―20(3)154,133，272，292【分析】本题主要考查了一元一次方程的应用，列代数式，（1）根据绝对值和平方式的非负性得出a 和b 的值即可；（2）根据点的运动得出代数式即可；（3）分四种不同情况进行分类讨论，根据路程=速度×时间，列方程求解即可．解题的关键是要运用分类讨论的思想．【详解】（1）解： ∵|a ―12|+(b +20)2=0，|a ―12|≥0，(b +20)2≥0，∴a ―12=0，b +20=0，∴a =12，b =―20；（2）解：由题意可知，E 点对应的数为：12―6t ，F 对应的数为―20+2t =2t ―20，故答案为：12―6t ，2t ―20；（3）解：在相遇前：t =[20―(―12)―2]÷(2+6)=154，设t ′时E 、F 相遇，即12―6t ′=2t ′―20；解得t ′=4，①当E 点在F 点左侧时，且F 点没动时，由题意可得，6(t ―4)=2，解得：t =133，②当E 点在F 点左侧时，且F 点已动时，6×(t ―4)―2×5×(t ―4―4)=2，解得：t =272，③当点E 在点F 右侧时，由题意2×5×(t ―4―4)―6×(t ―4)=2，解得：t =292，综上所述，符合条件的t 的值为：154,133，272，292．类型二、单点的规律运动问题例2．一个机器人从数轴原点出发，沿数轴正方向，以每前进3步后退2步的程序运动，设该机器人每秒钟前进或后退1步，并且每步的距离为1个单位长，x n 表示第n 秒时机器人在数轴上的位置所对应的数，给出下列结论（1）x 3=3；（2）x 5=1；（3）x 76>x 77；（4）x 103<x 104；（5）x 2018<x 2019其中，正确结论的个数是（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【分析】机器人每5秒完成一个循环，每个循环前进1步，n÷5的整数值即前进的步数，余数是1，总步数加1，是2加2，是3加3，是4加2．【详解】依题意得：机器人每5秒完成一个前进和后退，即前5秒对应的数是1，2，3，2，1；根据此规律即可推导判断：（1）和（2），显然正确；（3）中，76÷5=15……1，故x76=15+1=16，77÷5=15……2，故x77=15+2=17，16＜17，故错误；（4）中，103÷5=20……3，故x103=20+3=23，104÷5=20……4，故x104=20+2=22，23＞22，故错误；（5）中，2018÷5=403……3，故x2018=403+3=406，2019÷5=403……4，故错误．故选：B ．【点睛】本题考查的是归纳探索能力，确定循环次数和第n 次的对应数字是解题的关键．变式2-1．一动点p 从数轴上的原点出发，沿数轴的正方向以前进5个单位，后退3个单位的程序运动，已知p 每秒前进或后退1个单位．设x n 表示第n 秒点p 在数轴的位置所对应的数，如x 4=4,x 5=5,x 6=4，则x 2019为（ ）A ．504B ．505C ．506D ．507【答案】D【分析】先解出点P 每8秒完成一个循环，解出对应的数值，再根据规律推导出答案．【详解】解：依题意得，点P 每8秒完成一组前进和后退，前8个对应的数是1、2、3、4、5、4、3、2；9∼16对应的数是3、4、5、6、7、6、5、4；∵2019=8×252+3，故x 2019=252×2+3=507．故选：D ．【点睛】此题主要考查了数轴上点对应数字的规律探索，弄清题中的基本循环规律是解本题的关键．变式2-2．如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O 点出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移动到A 1，第2次移动到A 2，第3次移动到A 3，……，第n 次移动到A n ，则△O A 2A 2019的面积是（ ）A ．504B ．10092C ．20112D ．505【答案】B【分析】根据图可得移动4次完成一个循环，观察图形得出OA4n=2n ，处在数轴上的点为A4n 和A4n-1.由OA2016=1008，推出OA2019=1009，由此即可解决问题．【详解】解： 观察图形可知： OA4n=2n ，且点A4n 和点A4n-1在数轴上，又2016=504×4，∴A2016在数轴上，且OA2016=1008，∵2019=505×4-1，∴点A2019在数轴上，OA2019=1009，∴△OA2A2019的面积=12×1009×1=10092，故选：B ．【点睛】本题考查三角形的面积，数轴等知识，解题的关键是学会探究规律，利用规律解决问题，属于中考常考题型．类型三、定值问题例3．如图：在数轴上A 点表示数―3，B 点表示数1，C 点表示数9．(1)若将数轴折叠，使得A 点与C 点重合，则点B 与______表示的点重合；(2)若点A 、点B 和点C 分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动．①若t 秒钟过后，A ，B ，C 三点中恰有一点为另外两点的中点，求t 值；②当点C 在B 点右侧时，是否存在常数m ，使mBC ―2AB 的值为定值，若存在，求m 的值，若不存在，请说明理由．【答案】(1)5；(2)① t =1或4或16；②存在，m =―23．【分析】（1）求出AC 的长度和中点，然后求出中点到点B 的距离即中点到点B 的重合点的距离，即可求得点B 的重合点；（2）①分别以A、B、C为中点，列出方程求解即可；②使mBC―2AB的值为定值，列出等式中的含t项合并为0，从而求出m的值．【详解】（1）AC=9―(―3)=12，12÷2=6，∴AC的中点表示的数为：9―6=3，∵3―1=2，点B的重合点为3+2=5，故答案为：5；（2）解：①由题意可知，t秒时，点A所在的数为：―3―2t，点B所在的数为：1―t，点C所在的数为：9―4t，（1）若B为AC中点，，则1―t=(―3―2t)+(9―4t)2解得t=1；（2）若C为AB中点，，则9―4t=(―3―2t)+(1―t)2解得t=4；（3）若A为BC中点，，则―3―2t=1―t+9―4t2解得t=16；综上，当t=1或4或16时，A、B C②假设存在．∵C在B右侧，B在A右侧，∴BC=9―4t―(1―t)=8―3t，AB=1―t―(―3―2t)=t+4，∴mBC―2AB=m(8―3t)―2(t+4)=8m―8―(3m+2)t，当3m+2=0即m=―2时，3mBC―2AB=8×―8=―40，为定值，3使mBC―2AB的值为定值．故存在常数m=―23【点睛】此题考查了数轴上两点间距离，数轴上动点问题，一元一次方程的应用，解题的关键是能用两点间的距离公式列出方程．变式3-1．若点A在数轴上对应的数为a，点B在数轴上对应的数为b，我们把A、B两点之间的距离表示为AB，记AB=|a―b|，且a，b满足|a―1|+(b+2)2=0．(1)a=；b=；线段AB的长=；(2)点C在数轴上对应的数是c，且c与b互为相反数，在数轴上是否存在点P，使得PA+PB=PC?若存在，求出点P对应的数；若不存在，请说明理由；(3)在（1）、（2）的条件下，点A、B、C开始在数轴上运动，若点B以每秒1个单位长度的速度向左运动，同时点A和点C分别以每秒4个单位长度和9个单位长度的速度向右运动，t秒钟后，若点A和点C之间的距离表示为AC，点A和点B之间的距离表示为AB，那么AB―AC的值是否随着时间t的变化而变化?若变化，请说明理由；若不变，请求出AB―AC的值．【答案】(1)1，―2，3；(2)―3或―1；(3)AB―AC的值不随着时间t的变化而变化，值为2．【分析】（1）根据绝对值及平方的非负性，求出a，b的值，从而求出线段AB的长；（2）设P对应的数为y，再由PA+PB=PC，可得出点P对应的数；（3）根据A，B，C的运动情况即可确定AB，AC的变化情况，即可确定AB―AC的值．【详解】（1）∵|a―1|+(b+2)2=0，∴a―1=0，b+2=0，解得：a=1，b=―2，∴线段AB的长为：1―(―2)=3，故答案为：1，―2，3；（2）由（1）得：b=―2，∴c=2，设P对应的数为y，由图知：①P在A右侧时，不可能存在P点；②P在B左侧时，1―y―2―y=2―y，解得: y=―3，③当P在A、B中间时，3=2―y，解得: y=―1，故点P对应的数是―3或―1；（3）AB―AC的值不随着时间t的变化而变化，理由如下：t秒钟后，A点位置为：1+4t，∴B点的位置为: ―2―t，C点的位置为: 2+9t，∴AB=1+4t―(―2―t)=5t+3AC=2+9t―(1+4t)=5t+1，∴AB–AC=5t+3―(5t+1)=2，∴AB―AC的值不随着时间t的变化而变化，值为2．【点睛】此题考查了非负数的应用，数轴的应用，数轴上的距离，理解数轴上点的距离是解题的关键．变式3-2．如图，一个点从数轴上的原点开始，先向左移动4cm到达A点，再向右移动5cm到达B点，然后再向右移动3cm到达C点，数轴上一个单位长度表示1cm．(1)请你在数轴上标出A、B、C三点的位置，并填空：A表示的数为_______，B表示的数为_______，C表示的数为______．(2)把点A到点C的距离记为AC，则AB=_____cm，AC=______cm；(3)若点A从（1）中的位置沿数轴以每秒1cm匀速向右运动，经过多少秒使AC=3cm？【答案】(1)―4，1，4(2)5，8(3)5或11【分析】本题考查数轴上点的表示，数轴上两点间距离，数轴上动点问题．（1）根据题意利用观察即可得到本题答案；（2）根据题意利用两点间距离即可得到；（3）分情况讨论当点A在点C的左侧时和当点A在点C的右侧时，分别列式即可得到本题答案．【详解】（1）解：由题意得：A点对应的数为―4，B点对应的数为1，点C对应的数为4，点A，B，C在数轴上表示如图：A表示的数为―4，B表示的数为1，C表示的数为4，故答案为：―4，1，4；（2）解：∵A点对应的数为―4，B点对应的数为1，点C对应的数为4，∴AB=1―(―4)=5cm，AC=4―(―4)=8cm，故答案为：5，8；（3）解∶①当点A在点C的左侧时，设经过x秒后点A到点C的距离为3cm，由题意得：8―x=3，解得：x=5；②当点A在点C的右侧时，设经过x秒后点A到点C的距离为3cm，由题意得：x―8=3，解得：x=11，综上，经过5或11秒后点A到点C的距离为3cm．类型四、双点往返运动问题例4．如图，数轴上点A表示的数为―10，点B表示的数为20．点P从点O出发，以每秒1个单位长度的速度沿数轴正方向运动，点P出发的同时点Q从点A出发，以每秒2个单位长度的速度沿数轴正方向运动，设P、Q 两点运动的时间为t秒(t>0)．(1)点P表示的数为________，点Q表示的数为________．（用含t的代数式表示）(2)当t=3，t=12时，分别求线段PQ的长．(3)当PQ=5时，求所有符合条件的t的值．(4)若点P一直沿数轴的正方向运动，点Q运动到点B时，立即改变运动方向，以原速度沿数轴的负方向运动，到达点A时，随即停止运动，在点Q的整个运动过程中，当PQ=8时，直接写出t的值．【答案】(1)t，―10+2t；(2)当t=3时，PQ=7；当t=12时，PQ=2；(3)t=5或t=15；(4)t=2或t=58．3【分析】本题主要考查了两点间的距离，数轴，一元一次方程的应用，解题的关键是熟记两点间的距离公式，找到等量关系．（1）根据点的运动方向列代数式即可求解；（2）先根据两点间的距离公式求出PQ，再把t值代入求解；（3）根据两点间的距离公式列方程求解；（4）根据t的取值范围，分类讨论，列方程求解．【详解】（1）解：点P表示的数为t，点Q表示的数为―10+2t，故答案为：t，―10+2t；（2）PQ=|t―(―10+2t)|=|10―t|，当t=3时，PQ=|10―3|=7，当t=12时，PQ=|10―12|=2；（3）由题意得：|10―t|=5，解得：t=5或t=15；（4）当0≤t≤15时，PQ=|10―t|=8，解得：t=2或t=18（不符合题意，舍去），当15<t≤30时，PQ=|t―[20―2(t―15)]|=|t―(50―2t)|=8，或t=14（不符合题意，舍去），解得：t=583综上所述，t =2或t =583．变式4-1．如图，O 是数轴的原点，A 、B 是数轴上的两个点，A 点对应的数是―1，B 点对应的数是8，C 是线段AB 上一点，满足AC BC =54．(1)求C 点对应的数；(2)动点M 从A 点出发，以每秒2个单位长度的速度沿数轴向右匀速运动，当点M 到达C 点后停留2秒钟，然后继续按原速沿数轴向右匀速运动到B 点后停止．在点M 从A 点出发的同时，动点N 从B 点出发，以每秒1个单位长度的速度沿数轴匀速向左运动，一直运动到A 点后停止．设点N 的运动时间为t 秒．①当MN =4时，求t 的值；②在点M ，N 出发的同时，点P 从C 点出发，以每秒3个单位长度的速度沿数轴向左匀速运动，当点P 与点M 相遇后，点P 立即掉头按原速沿数轴向右匀速运动，当点P 与点N 相遇后，点P 又立即掉头按原速沿数轴向左匀速运动到A 点后停止．当PM =2PN 时，请直接写出t 的值．【答案】(1)4(2)①53或173；②t 的值为73或197或5.5【分析】（1）根据A 点，B 点对应的数，得到AB =9，根据AC 与BC 的比值，得到AC =5，BC =4，得到C 点对应的数是8―4=4；（2）①当M 、N 未相遇， M 表示的数是―1+2t ， N 表示的数是8―t ，得到8―t ―(―1+2t)=4，解得t =53；当M 、N 相遇后，M 在BC 上运动，M 表示的数是4+2t ―52―2=2t ―5， N 表示的数是8―t ，得到2t ―5―(8―t)=4，解得t =173；②当P 与M 还未第一次相遇时，P 表示的数是4―3t ，M 表示的数是―1+2t ，N 表示的数是8―t ，得到4―3t ―(―1+2t)=2[8―t ―(4―3t)]，解得t =―13，此种情况不存在；当P 与M 第一次相遇后，相遇后P 掉头按原速沿数轴向右匀速运动，在未遇到N 前，P 表示的数是(4―3×1)+3(t ―1)=3t ―2，得到3t ―2―(―1+2t)=2[8―t ―(3t ―2)]，解得t =73；当P 与N 相遇后，未与M 第二次相遇时，P 表示的数是(8―2.5)―3(t ―2.5)=13―3t ，13―3t ―4=2[8―t ―(13―3t)]，解得t =197；当P 与M 在点C 处第二次相遇后直到到达A 点前，P 表示的数是13―3t ， M表示的数是4，得到4―(13―3t)=2[8―t ―(13―3t)]，解得t =1，根据2.5<t ≤4.5，得到这种情况不存在；当P 运动到A 后，若N 为PM 的中点，此时PM =2PN ，―1+(2t ―5)=2(8―t)，解得t =5.5．本题主要考查了数轴上动点问题，熟练掌握数轴上动点表示的数，两点间的距离公式，相遇与追及问题，列代数式，列方程，分类考虑动点的位置，是解题关键．【详解】（1）∵A 点对应的数是―1，B 点对应的数是8，∴AB =8+1=9，∵AC BC =54，∴AC =5，BC =4，∴C 点对应的数是8―BC =8―4=4，答：C 点对应的数是4；（2）①∵运动t 秒时，MN =4当M 、N 未相遇，则M 在AC 上运动，M 表示的数是―1+2t ，N 在BC 上运动，N 表示的数是8―t ，∴8―t ―(―1+2t)=4，解得t =53，当M 、N 相遇后，M 在BC 上运动，M 表示的数是4+2t ―52―2=2t ―5，N 在AC 上运动，N 表示的数是8―t ，∴2t ―5―(8―t)=4，解得t =173，综上所述，t 的值为53或173；②当P 与M 还未第一次相遇时，4―3t ，M 表示的数是―1+2t ，N 表示的数是8―t ，∵PM =2PN∴4―3t ―(―1+2t)=2[8―t ―(4―3t)]，解得t =―13（舍去），此种情况不存在，由已知得，P 与M 在t =1时第一次相遇，相遇后P 掉头按原速沿数轴向右匀速运动，在未遇到N 前，P 表示的数是(4―3×1)+3(t ―1)=3t ―2，∴3t ―2―(―1+2t)=2[8―t ―(3t ―2)]，解得t =73，由已知可知，当P 与M 在表示1的点处相遇，此时N 运动到表示7的点处，再经过7―13+1=1.5秒，即t =2.5时，P 与N 相遇，此时M 正好运动到C ，P 与N 相遇后又立即掉头按原速沿数轴向左匀速运动，未与M 第二次相遇，此时P 表示的数是(8―2.5)―3(t ―2.5)=13―3t ，∴13―3t ―4=2[8―t ―(13―3t)]，解得t =197，当P 与M 在点C 处第二次相遇后直到到达A 点前，P 表示的数是13―3t ，M 在C 点处，M 表示的数是4，次情况2.5<t ≤4.5，∴4―(13―3t)=2[8―t ―(13―3t)]，解得t =1，不合，∴这种情况不存在，当P 运动到A 后，若N 为PM 的中点，此时PM =2PN ，∴―1+(2t ―5)=2(8―t)，解得t =5.5，综上所述，t 的值为73，或197，或5.5．变式4-2．已知数轴上有A 、B 、C 三个点，分别表示有理数―24、―10、10，动点P 从A 出发，以每秒1个单位长度的速度向终点C 移动，设移动时间为t 秒．若用PA ，PB ，PC 分别表示点P 与点A 、点B 、点C 的距离，试回答以下问题．(1)当点P 运动10秒时，PA =______，PB =______，PC =______；(2)当点P运动了t秒时，请用含t的代数式表示P到点A、点B、点C的距离：PA=______，PB=______，PC=______；(3)经过几秒后，点P到点A、点C的距离相等？此时点P表示的数是多少？(4)当点P运动到B点时，点Q从A点出发，以每秒3个单位长度的速度向C点运动，Q点到达C点后，再立即以同样速度返回，运动到终点A．在点Q开始运动后，P、Q两点之间的距离能否为4个单位长度？如果能，请直接写出点P表示的数；如果不能，请说明理由．【答案】(1)10，4，24；(2)t，|―14+t|，|―34+t|；(3)―7；(4)―5，―1，2.5，4.5．【分析】（1）根据题意求得t=10时，P点的位置，进而求得两点距离；（2）先表示出P点的位置表示的数，进而求得两点距离；（3）根据题意，列一元一次方程，解方程求解即可；（4）分Q点到达C点之前，和Q点到达C点之后，两种情形，根据两点距离为，建立一元一次方程解方程求解即可；此题考查了数轴上动点问题，数轴上两点距离问题，一元一次方程的应用，数形结合是解题的关键．【详解】（1）∵A、B、C三个点，分别表示有理数―24、―10、10，动点P从A出发，以每秒1个单位长度的速度向终点C移动，设移动时间为t秒，∴t=10时，P点表示的数为―24+10=―14，∴当P点运动10秒时，PA=|―14―(―24)|=10，PB=|―14―(―10)|=4，PC=|―14―10|=24，故答案为：10，4，24；（2）依题意，当P点运动了t秒时，则PA=t，点P表示的数为―24+t，∴PB=|―24+t―(―10)|=|―14+t|，PC=|―24+t―10|=|―34+t|，故答案为：t，|―14+t|，|―34+t|；（3）∵PA=PC，∴t=|―34+t|，即t=―34+t或―t=―34+t，解得：t=17，∴点P表示的数为―24+17=―7；（4）根据题意，设经过x秒后P、Q两点之间的距离为4个单位长度，P点运动到C点需要的时间为：20÷1=20（秒）①当Q点未到达C点，此时AQ =3x ，BP =x ，则Q 点表示的数为―24+3x ，点P 表示的数为―10+x ，则PQ =|―10+x ―(―24+3x)|=|14―2x|=4，即14―2x =4或14―2x =―4，解得：x =5或x =9，∴点表示的数为―5或―1；②当Q 点从C 点返回后，此时AQ =AC ―QC =|34―(3x ―34)|=|68―3x|，BP =x ，则Q 点表示的数为―24+68―3x =―3x +44，点P 表示的数为―10+x ，则PQ =|―10+x ―(―3x +44)|=|4x ―54|=4，即4x ―54=4或4x ―54=―4，解得x =292或x =252，∴点P 表示的数为4.5或2.5，综上所述，点P 表示的数为―5，―1，2.5，4.5．类型五、数轴的折叠问题例5．综合与探究数轴可以将数与形完美结合．请借助数轴，结合具体情境解答下列问题：(1)平移运动一机器人从原点O 开始，第1次向左跳1个单位，紧接着第2次向右跳2个单位，第3次向左跳3个单位，第4次向右跳4个单位，…，依此规律跳，当它跳完5次时，落在数轴上的点表示的数是 ；当它跳完2024次时，落在数轴上的点表示的数是 ．(2)翻折变换①若折叠数轴所在纸条，表示―1的点与表示3的点重合，则表示5的点与表示 的点重合．②若数轴上D 、E 两点经折叠后重合，两点之间的距离为2024（D 在E 的左侧，且折痕与①折痕相同），则D点表示，E点表示．③一条数轴上有点M、N、P，其中点M、N表示的数分别是―17、8，现以点P为折点，将数轴向右对折，若点M对应的点M′落在点N的右边，并且线段M′N的长度为3，请直接写出点P表示的数．【答案】(1)―3；1012(2)①―3；②―1011；1013；③―3【分析】本题考查图形变化的规律，熟知折叠后能重合的两个点到折点的距离相等是解题的关键．（1）根据机器人的运动方式，依次求出每次跳完落在数轴上时所表示的数，发现规律即可解决问题．（2）根据折叠后重合的点到折点的距离相等即可解决问题．【详解】（1）解：根据机器人的运动方式可知，它跳完第1次时，落在数轴上的点表示的数是：―1；它跳完第2次时，落在数轴上的点表示的数是：1；它跳完第3次时，落在数轴上的点表示的数是：―2；它跳完第4次时，落在数轴上的点表示的数是：2；它跳完第5次时，落在数轴上的点表示的数是：―3；它跳完第6次时，落在数轴上的点表示的数是：3；…，由此可见，它跳完第2n次时，落在数轴上的点表示的数是n，它跳完第(2n―1)次时，落在数轴上的点表示的数是―n；当2n―1=5，即n=3时，―n=―3，所以它跳完第5次时，落在数轴上的点表示的数是―3；当2n=2024，即n=1012时，可得它跳完第2024次时，落在数轴上的点表示的数是1012；故答案为：―3，1012．（2）①由表示―1的点与表示3的点重合可知，―1+3=1，2则折点所表示的数为1．因为5―1=1―(―3)，所以表示5的点与表示―3的点重合．故答案为：―3．②因为折痕与①的折痕相同，所以这次折叠的折点所表示的数也为1．又因为2024÷2=1012，1+1012=1013，1―1012=―1011，所以点D表示的数为―1011，点E表示的数为1013．故答案为：―1011，1013．③由折叠可知，MP=M′P，因为点M、N表示的数分别是―17、8，所以MN=8―(―17)=25．又因为点M′落在点N的右边，并且线段M′N的长度为3，所以MM′=25+3=28．因为28÷2=14，―17+14=―3，所以点P表示的数为―3．故答案为：―3．变式5-1．如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示―10，点B 表示10，点C表示17，我们称点A和点C在“折线数轴”上相距27个单位长度．动点P，Q同时出发，点P从点A出发，以2个单位长度／秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；动点Q从点C出发，以1个单位长度／秒的速度沿着“折线数轴”的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒，问：(1)动点P从点A运动至点C需要多少时间？(2)当P，Q两点相遇时，求出相遇点M所对应的数是多少？(3)当P，O两点在“折线数轴”上相距的长度与Q，B两点在“折线数轴”上相距的长度相等时，t的值为（直接写出结果）．【答案】(1)18.5秒(2)143(3)3或6或9或18【分析】本题考查了数轴上两点之间距离，一元一次方程与路程问题的应用，读懂题意，找到等量关系，列出方程是解题的关键．，分段求出每段折线上的时间再求和即可；（1）根据时间＝路程速度（2）P、Q两点相遇时，所用时间相等，根据等量关系建立一元一次方程；（3）根据P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等可以判断时间相等，根据等量关系建立一元一次方程，同时需要分情况讨论，即虽然PO=OP，但PO和OP不是同一条射线．【详解】（1）解：点P 从点 A 运动至 C 点需要的时间为：t=10÷2+10÷1+(17―10)÷2=18.5（秒）．答：点P 从点 A 运动至 C 点需要的时间是18.5 秒；（2）解：由题可知，P，Q 两点相遇在线段OB上于M 处，设OM=x，则10÷2+x÷1=7÷1+(10―x)÷2，解得：x=143．∴OM=143表示P，Q 两点相遇在线段OB上于M 处，即相遇点M 所对应的数是143．（3）解：P、O 两点在数轴上相距的长度与Q、B 两点在数轴上相距的长度相等有 4 种可能：①当动点Q 在CB上，动点P在AO上时，则：7―t=10―2t，解得：t=3；②当动点Q 在CB上，动点P在OB上时，则：7―t=(t―5)×1，解得：t=6；③当动点Q 在BO上，动点P 在OB上时，则：2(t―7)=(t―5)×1，解得：t=9；④当动点Q 在OA上，动点P 在BC上时，则：(t―7―5)×1=2(t―5―10)，解得：t=18．综上所述：t 的值为 3 或 6 或9或18．故答案为： 3 或 6 或9或18．变式5-2．七年级数学兴趣小组成员自主开展数学微项目研究，他们决定研究“折线数轴”．探索“折线数轴”：素材1 如图，将一条数轴在原点O，点B，点C处折一下，得到一条“折线数轴”．图中点A表示―9，点B表示12，点C表示24，点D表示36，我们称点A与点D在数轴上的“友好距离”为45个单位长度，并表示为AD=45．素材2 动点P从点A出发，以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动．当运动到点O与点B之间时速度变为初始速度的一半．当运动到点B与点C之间时速度变为初始速度的两倍．经过点C后立刻恢复初始速度．问题解决：探索1 ：动点P从点A运动至点B需要多少时间？探索2 ：动点P从点A出发，运动t秒至点B和点C之间时，求点P表示的数（用含t的代数式表示）；探索3 ：动点P从点A出发，运动至点D的过程中某个时刻满足PB+PC=16时，求动点P运动的时间．【答案】探索1：P从点A运动至点B的时间为16.5秒；探索2：P表示的数为4t―54；探索3：动点P运动的时间是14.5秒或20.5秒．【分析】本题考查数轴上动点计算问题及数轴上两点间距离问题，解题的关键是理解题意并掌握相关的知识．探索1：根据时间=路程÷速度，即可求解；探索2：由探索1可得P在BC段运动时间为：(t―16.5)秒，进而得到BP=4t―66，结合点B表示12，即可求解；探索3：分两种情况：①当P在BO上时，②当P在CD上时，根据线段的和差以及时间=路程÷速度，即可求解．【详解】解：探索1：∵点A表示―9，点B表示12，∴OA=9，OB=12，∵P在AO段初始速度为2个单位长度/秒，P在OB段速度为初始速度的一半，∴P在OB段速度为1个单位长度/秒，∴P从点A运动至点B的时间为：92+121=16.5（秒）；探索2：∵P的初始速度为2个单位长度/秒，P在BC段速度为初始速度的两倍，∴P在BC段速度为4个单位长度/秒，由探索1可得：P在BC段运动时间为：(t―16.5)秒，∴BP=4(t―16.5)=4t―66，∵点B表示12，∴P表示的数为：12+(4t―66)=4t―54；探索3：设t秒后PB+PC=16，①当P在BO上时，∵PB+PC=16，∴PB+(PB+BC)=16，∵BC=12，∴PB=2，∴PO=OB―BP=12―2=10，∵OA=9，∴t=92+101=4.5+10=14.5（秒）；②当P在CD上时，。

七年级动点问题大全例1 如图，在数轴上A 点表示数a ，B 点表示数b ，AB 表示A 点和B 点之间的距离，且a 、b 满足|a+2|+（b+3a ）2=0 （1）求A 、B 两点之间的距离；（2）若在数轴上存在一点C ，且AC=2BC ，求C 点表示的数；（3）若在原点O 处放一挡板，一小球甲从点A 处以1个单位/秒的速度向左运动；同时另一小球乙从点B 处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t （秒）， ①分别表示甲、乙两小球到原点的距离（用t 表示）； ②求甲、乙两小球到原点的距离相等时经历的时间．例2如图，有一数轴原点为O ，点A 所对应的数是-1 2，点A 沿数轴匀速平移经过原点到达点B ．（1）如果OA=OB ，那么点B 所对应的数是什么？（2）从点A 到达点B 所用时间是3秒，求该点的运动速度．（3）从点A 沿数轴匀速平移经过点K 到达点C ，所用时间是9秒，且KC=KA ，分别求点K 和点C 所对应的数。

例3动点A 从原点出发向数轴负方向运动，同时，动点B 也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度．已知动点A 、B 的速度比是1：4．（速度单位：单位长度/秒）（1）求出两个动点运动的速度，并在数轴上标出A 、B 两点从原点出发运动3秒时的位置；（2）若A 、B 两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；（3）在（2）中A 、B 两点继续同时向数轴负方向运动时，另一动点C 同时从B 点位置出发向A 运动，当遇到A 后，立即返回向B 点运动，遇到B 点后立即返回向A 点运动，如此往返，直到B 追上A 时，C 立即停止运动．若点C 一直以20单位长度/秒的速度匀速运动，那么点C 从开始到停止运动，运动的路程是多少单位长度．例4已知数轴上两点A 、B 对应的数分别为-1、3，点P 为数轴上一动点，其对应的数为x ．（1）若点P 到点A ，点B 的距离相等，求点P 对应的数；（2）数轴上是否存在点P ，使点P 到点A 、点B 的距离之和为6？若存在，请求出x 的值；若不存在，说明理由；（3）点A 、点B 分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P 以6个单位长度/分的速度从O 点向左运动．当遇到A 时，点P 立即以同样的速度向右运动，并不停地往返于点A 与点B 之间，求当点A 与点B 重合时，点P 所经过的总路程是多少？例5数轴上两个质点A、B所对应的数为-8、4，A、B两点各自以一定的速度在上运动，且A点的运动速度为2个单位/秒．（1）点A、B两点同时出发相向而行，在原点处相遇，求B点的运动速度；（2）A、B两点以（1）中的速度同时出发，向数轴正方向运动，几秒钟时两者相距6个单位长度；（3）A、B两点以（1）中的速度同时出发，向数轴负方向运动，与此同时，C点从原点出发作同方向的运动，且在运动过程中，始终有CB：CA=1：2，若干秒钟后，C停留在-10处，求此时B点的位置？例6在数轴上，点A表示的数是-30，点B表示的数是170．（1）求A、B中点所表示的数．（2）一只电子青蛙m，从点B出发，以4个单位每秒的速度向左运动，同时另一只电子青蛙n，从A点出发以6个单位每秒的速度向右运动，假设它们在C点处相遇，求C点所表示的数．（3）两只电子青蛙在C点处相遇后，继续向原来运动的方向运动，当电子青蛙m 处在A点处时，问电子青蛙n处在什么位置？（4）如果电子青蛙m从B点处出发向右运动的同时，电子青蛙n也向右运动，假设它们在D点处相遇，求D点所表示的数例7、已知数轴上有A、B、C三点，分别代表—24，—10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒。

-1-2-33210O B A P0123-3-2-1B A OA BCD备用图O 数轴上的动点问题最新版1．如图，已知数轴上两点A 、B 对应的数分别为-1，3，点P 为数轴上一动点，其对应的数为x 。

（1）数轴上是否存在点P ，使点P 在点A 、点B 的距离之和为5？若存在，请求出x 的值，若不存在，请说明理由；（2）当点P 以每分钟1个单位长度的速度从O 点向左运动时，点A 以每分钟5个单位长度的速度向左运动，点B 以每分钟20个单位长度的速度向左运动，问它们同时出发，几分钟时点P 到点A 、点B 的距离相等？（3）如图，若点P 从B 点出发向左运动（只在线段AB 上运动），M 为AP 的中点，N 为PB 的中点，点P 在运动的过程中，线段MN 的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出MN 的长。

2．如图，A 、B 、C 是数轴上的三点，O 是原点， BO=3，AB=2BO ，5AO=3CO ． （1）写出数轴上点A 、C 表示的数；（2）点P 、Q 分别从A 、C 同时出发，点P 以每秒 2个单位长度的速度沿数轴向右匀速运动，点Q 以每秒6个单位长度的速度沿数轴向左匀速运 动，M 为线段AP 的中点，点N 在线段CQ 上，且 CN=32CQ ．设运动的时间为t （t ＞0）秒． ①数轴上点M 、N 表示的数分别是 （用含t 的 式子表示）； ②t 为何值时，M 、N 两点到原点O 的距离相等？3．如图，数轴上有A 、B 、C 、D 四个点，分别对应数a 、b 、c 、d ，且满足a 、b 是方程91x +=的两根（a b <），2(16)c -与20d -互为相反数。

（1）求a 、b 、c 、d 的值；（2）若A 、B 两点以6个单位长度/秒的速度向右匀速运动，同时C 、D 两点以2个单位长度/秒的速度向左匀速运动，并设运动时间为t 秒。

问t 为多少时，A 、B 两点都运动在线段CD 上（不与C 、D 两个端点重合）？（3）在（2）的条件下，A 、B 、C 、D 四个点继续运动，当点B 运动到点D 的右侧时，问是否存在时间t ，使B 与C 的距离是A 与D 的距离的4倍，若存在，求时间t ，若不存在，请说明理由。