《机器人机构学》课
- 格式:doc
- 大小:178.50 KB
- 文档页数:5





机器人机构学的数学基础
机器人机构学的数学基础包括向量、矩阵、三角函数、微积分等数学知识。
首先,向量是机器人机构学中必须掌握的概念,因为机器人的运动轨迹可以表示为一系列向量。
向量的长度和方向可以描述机器人的位置和姿态,因此对于机器人的运动规划和控制非常重要。
其次,矩阵是机器人机构学中不可或缺的数学工具,因为机器人的运动学和动力学问题可以表示为矩阵方程。
例如,通过矩阵变换可以将机器人末端执行器的位姿转换为关节角度,或者将关节力矩转换为末端执行器的力和力矩。
第三,三角函数也是机器人机构学中常用的数学工具,因为机器人的运动通常涉及到角度的变化。
例如,关节角度可以用正弦和余弦函数来表示,而逆解问题中也需要使用反三角函数求解。
最后,微积分是机器人机构学中的重要数学基础,因为机器人的运动学和动力学问题往往涉及到速度、加速度和力矩等概念。
例如,求解机器人的运动学和动力学模型时需要使用微积分知识,同时在机器人控制问题中也需要使用微积分来设计控制算法。
总之,机器人机构学的数学基础包括向量、矩阵、三角函数和微积分等数学知识。
掌握这些数学知识对于理解机器人的运动规划、控制和仿真非常重要。
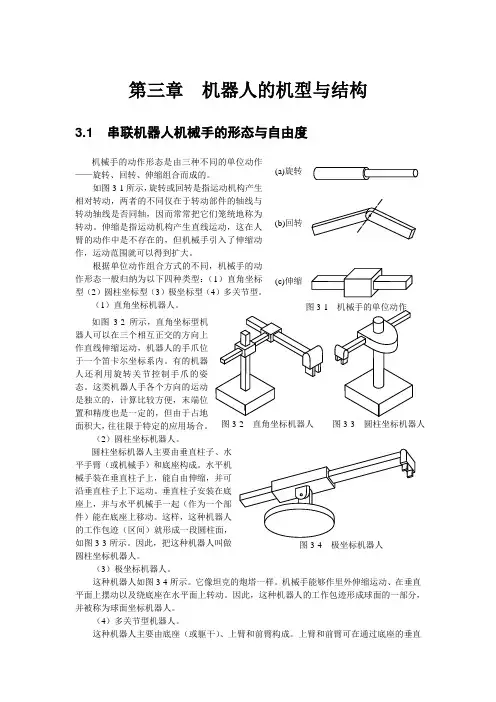
第三章 机器人的机型与结构3.1 串联机器人机械手的形态与自由度机械手的动作形态是由三种不同的单位动作——旋转、回转、伸缩组合而成的。
如图3-1所示,旋转或回转是指运动机构产生相对转动,两者的不同仅在于转动部件的轴线与转动轴线是否同轴,因而常常把它们笼统地称为转动。
伸缩是指运动机构产生直线运动,这在人臂的动作中是不存在的,但机械手引入了伸缩动作,运动范围就可以得到扩大。
根据单位动作组合方式的不同,机械手的动作形态一般归纳为以下四种类型:(1)直角坐标型(2)圆柱坐标型(3)极坐标型(4)多关节型。
(1)直角坐标机器人。
如图3-2所示,直角坐标型机器人可以在三个相互正交的方向上作直线伸缩运动,机器人的手爪位于一个笛卡尔坐标系内。
有的机器人还利用旋转关节控制手爪的姿态。
这类机器人手各个方向的运动是独立的,计算比较方便,末端位置和精度也是一定的,但由于占地面积大,往往限于特定的应用场合。
(2)圆柱坐标机器人。
圆柱坐标机器人主要由垂直柱子、水平手臂(或机械手)和底座构成。
水平机械手装在垂直柱子上,能自由伸缩,并可沿垂直柱子上下运动。
垂直柱子安装在底座上,并与水平机械手一起(作为一个部件)能在底座上移动。
这样,这种机器人的工作包迹(区间)就形成一段圆柱面,如图3-3所示。
因此,把这种机器人叫做圆柱坐标机器人。
(3)极坐标机器人。
这种机器人如图3-4所示。
它像坦克的炮塔一样。
机械手能够作里外伸缩运动、在垂直平面上摆动以及绕底座在水平面上转动。
因此,这种机器人的工作包迹形成球面的一部分,并被称为球面坐标机器人。
(4)多关节型机器人。
这种机器人主要由底座(或躯干)、上臂和前臂构成。
上臂和前臂可在通过底座的垂直(c)伸缩(a)旋转(b)回转图3-3 圆柱坐标机器人 图3-4 极坐标机器人 图3-2 直角坐标机器人平面上运动,如图3-5所示。
在前臂和上臂间,机械手有个肘关节;而在上臂和底座之间,有个肩关节。
在水平平面上的旋转运动,既可由肩关节进行,也可以绕底座旋转来实现。



机器人机构学-绪论引言机器人机构学是一门研究机器人结构和运动学的学科。
随着人工智能和自动化技术的快速发展,机器人在工业生产、医疗保健、军事应用等领域得到越来越广泛的应用。
机器人机构学的研究可以帮助我们理解机器人的结构特点和运动规律,进而设计出更加灵活、高效的机器人系统。
机器人机构的定义机器人机构是指构成机器人的各个部件之间的连接关系,包括机身、传动系统、关节、传感器等。
机器人机构的设计对机器人的性能、可靠性和适应性等方面的影响极大。
机器人机构的分类根据机器人机构的结构和运动特点,可以将其分为以下几类:1.串联机构:由一系列关节连接而成,每个关节只有一个自由度。
典型的串联机构包括人的手臂和腿等。
2.并联机构:由多个并联的关节组成,每个关节都有自由度。
并联机构具有较高的刚度和精度,常用于需要快速准确定位的任务。
3.混合机构:由串联机构和并联机构的组合构成,兼具串联机构的灵活性和并联机构的刚度。
4.柔性机构:通过柔性材料的变形实现机器人的运动。
柔性机构具有较好的适应性和承载能力,适用于狭小空间和不规则环境的工作。
机器人运动学机器人运动学研究机器人的位置、姿态和运动规律。
根据运动学理论,可以通过给定机器人关节的角度、长度和位置等参数,计算机器人末端执行器的位置和姿态。
机器人运动学分为正运动学和逆运动学两个方面:正运动学正运动学是指已知机器人关节的运动参数,推导出机器人末端执行器的位置和姿态的过程。
通过正运动学,可以确定机器人在空间中的准确位置,具有重要的实际应用价值。
逆运动学逆运动学是指已知机器人末端执行器的位置和姿态,计算机器人关节的运动参数。
逆运动学是机器人控制的核心问题之一,解决逆运动学可以实现机器人的自主控制和路径规划。
机器人机构学的应用机器人机构学的研究成果广泛应用于各个领域。
以下是机器人机构学的几个典型应用:1.工业机器人:工业机器人广泛应用于生产线上的重复性、高精度任务,如焊接、装配和搬运等。

机器人机构课程设计一、课程目标知识目标:1. 学生能够理解并描述机器人机构的基本组成、功能和原理;2. 学生能够掌握机器人机构的分类、运动特点及应用场景;3. 学生能够了解机器人机构在我国科技发展中的地位和作用。
技能目标:1. 学生能够运用所学的知识,分析并设计简单的机器人机构;2. 学生能够运用绘图软件或手工制作,展示机器人机构模型;3. 学生能够通过小组合作,完成机器人机构的搭建和调试。
情感态度价值观目标:1. 培养学生对机器人机构的兴趣,激发他们探索科技的热情;2. 培养学生动手实践、解决问题的能力,增强自信心和成就感;3. 培养学生团队协作、沟通表达的能力,提高责任感和合作意识;4. 培养学生关注我国机器人产业发展,树立科技创新的价值观。
课程性质:本课程为实践性较强的学科课程,结合理论知识与动手操作,培养学生对机器人机构的设计、搭建和创新能力。
学生特点:学生处于好奇心强、动手能力逐渐增强的年级,对新鲜事物充满兴趣,善于合作和探索。
教学要求:注重理论与实践相结合,充分调动学生的积极性,引导他们主动参与课堂活动,培养创新精神和实践能力。
将课程目标分解为具体的学习成果,以便进行有效的教学设计和评估。
二、教学内容1. 机器人机构概述- 了解机器人的定义、发展历程及分类;- 掌握机器人机构的基本组成和功能。
2. 机器人机构的类型与运动特点- 学习不同类型的机器人机构(如:移动机构、关节臂机构、并联机构等);- 分析各类机构的特点、应用场景及其运动原理。
3. 机器人机构的设计与制作- 掌握机器人机构设计的基本原则和方法;- 学习使用绘图软件(如:CAD等)进行机器人机构的设计;- 手工制作机器人机构模型,并进行搭建和调试。
4. 机器人机构的应用案例分析- 分析国内外典型机器人机构应用案例;- 了解机器人机构在工业、医疗、教育等领域的应用现状和发展趋势。
5. 我国机器人产业发展现状与展望- 了解我国机器人产业的发展历程、现状及政策支持;- 探讨机器人产业未来的发展趋势和挑战。

机器人机构学基础
1. 机器人的定义和分类:机器人是一种能够自动执行任务的机械装置,可以分为工业机器人、服务机器人、军用机器人等不同类型。
2. 机器人的机构组成:机器人的机构包括机身、臂部、腕部、手部等部分,每个部分都由一系列的关节和连杆组成。
3. 机器人的运动学:机器人的运动学主要研究机器人各关节的运动关系,以及机器人末端执行器的位置和姿态。
4. 机器人的动力学:机器人的动力学主要研究机器人各关节的驱动力和力矩,以及机器人的动态响应。
5. 机器人的控制:机器人的控制包括位置控制、速度控制、力控制等方面,常用的控制方法包括 PID 控制、模糊控制、神经网络控制等。
6. 机器人的编程:机器人的编程是指通过编程语言对机器人进行控制和操作,常用的编程语言包括 C++、Python、MATLAB 等。
7. 机器人的应用:机器人的应用非常广泛,包括工业生产、医疗保健、教育、军事等领域。
总之,机器人机构学基础是机器人领域中的一个重要分支,对于深入了解机器人的机构设计、运动学和动力学等方面具有重要意义。
《机器人机构学》课程 一.教学内容1. 机器人机构的组成,类型及特性参数。
2. 机器人机构研究的数学基础:齐次坐标,坐标变换,刚体运动的矩阵表示等。
3. 机器人机构运动学:末端执行器的描叙,D-H 变换矩阵,运动学正解,运动学逆解及其优化,微分运动,雅可比矩阵的建立等。
4. 机器人机构的工作空间分析。
5. 机器人机构轨迹规划:关节空间的轨迹规划和直角坐标空间的轨迹规划。
6. 机器人机构动力学:牛顿-欧拉方法,拉格朗日方程法。
二.参考书1. 徐卫良,钱瑞明译。
《机器人操作的数学导论》,机械工业出版社,1998三.要求1. 阅读上叙教学内容。
2. 在国内外刊物上查阅两篇与上叙内容相关的研究论文,精读后加以介绍。
3. 完成以下指定作业。
四.作业1.简叙开链机器人机构与闭链机器人机构在机构特点,运动特点及运动正逆解方面的差异。
2. 若开链机器人的雅可比矩阵J 为方阵,其行列式∣J ∣=0的机构位姿。
试分析奇异位姿的种类及对应的机构机构几何特性与运动特性。
3. 3.运动参数关系及对应的机构位置设Ta a a a ],,[321=为三维矢量,∧a是其对应的反对称矩阵,即∧a =⎢⎢⎢⎣⎡00121323a a a a a a ----⎥⎥⎥⎦⎤。
试证明=∧∧) +(I ) -(I 1-αα⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤+--+---+-++---++232221132211312322213212313123222121)(2)(2)(21)(2)(2)(21113a a a a a a a a a a a a a a a a a a a a a a a a a a a a5.空间绕两轴线旋转至给定距离:如图所示,已知是表示1ξ、2ξ交两轴位置的单位矢量,P 、q 为表示空间两点的单位矢量P 、1q 、2q 为表示空间三个点的矢量。
现将点P 先绕轴2ξ旋转,再绕轴1ξ旋转,使得P 点的最后位置q 至1q 的距离 为1ξ,至2q 点的距离为2ξ。
试求1θ和2θ及有解的条件。
7. 对于图示4种三自由度开链机器人机构,若描叙K 点线速度与关节角速度关系的雅可比矩阵的行列式值为1,试分析此时的几何运动参数关系及对应的机构位置。
五.解题 1. 解1)开链机器人的机构特点:各杆循序构成单链相邻连杆间通过转动副或移动副连接的开链机器人。
开链机器人的自由度数等于该机器人的关节数运动特点:机器人的关节空间Q 有机器人的变量的所有可能值构成,这也是机器人的位型空间,这是因为给定了关节转角也就给定了机器人所有连杆的位置。
对于转动副,关节变量用转角[)πθ2,0∈i给出,对于移动副,用轴线方向观察线位移Ri∈θ来表示,如果机器人的雅可比矩阵在某一位型降秩,则此位型为奇异位型,机器人的在这一位型的运动不确定。
运动学正解:运动学把所有的关节变量都看作是转角,当给定彝族关节转角θ∈Q ,希望确定工具坐标系相对与基础坐标系的位型。
运动学正解可用一个反映此相对关系的映射)3(:SE Q g st →来表示。
开链机器人的运动学正解映射可以通过将有各关节引起的刚体运动加以组合构成。
如果定义)(1i l l i i g θ-为相邻连杆坐标系间的变换,那么总的运动方程为:tl n l l l l sl stn n n g g g g g )()()()(121121θθθθ-⋅⋅⋅=,这是相邻连杆的坐标系的相对表示的开链操作器运动学正解的一般公式。
用各关节的运动由位于关节轴线的运动旋量产生。
将各关节加以组合,即得运动学正解映射)3(:SE Q g st →如下:)0()(2211st st g eeeg nn θξθξθξθ∧∧∧⋅⋅⋅=,此式称为机器人运动学正解的支书积公式。
iξ必须由基座开始循序编号,但是)(θst g 给出的工具坐标系的位型与转动和移动的实际循序无关。
运动学逆解:给定工具坐标系所期望的位型,找出该位型的关节转角。
也就是说,给定运动学正解映射)3(:SE Q g st →和一个期望的位型)3(SE g d ∈,通过求解下式dst g g =)(θ,获得θ∈Q 。
该问题可能有多解、唯一解或无解。
求解运动学逆解问题时,首先要将问题细分为几个子问题。
每个子问题可能无解、有一个解或多个解,这与末端执行器的给定位置有关。
如果该位型超出机器人的工作空间,那么肯定无解,且至少有一个子问题无解。
当位型空间处于工作空间内,且有多组关节转角对应与末端执行器的同一个位置映射,此时出现多解。
如果某个子问题有多解,那么整个求解过程应考虑每个解的情况。
2)闭链机器人的机构特点:它是一种在末端执行器与机器人基座之间有两个或多个分支运动链连接的机器人。
相对于开链机器人而言,闭链机器人具有刚性大和便于布置驱动装置等优点。
运动特点:对于并联机构,如果在某一位型其机构方程降秩,则在该位型机器人是运动奇异的。
在这种情况下,执行器就会失去在某个方向上瞬时运动的能力。
这一点与串联机构奇异位型的描叙。
然而在该位型,尚不能确定机构中那些关节是主动的,那些关节是被动的。
如果并联机构的关节都是主动的,则仅存在所能发生的奇异性。
如果并联机器人中仅有部分关节都是主动的,这样就会导致额外的奇异性,称之为驱动奇异性。
运动学正解:可以通过令每个分支运动链所确定的末端执行器的位置相等来描叙。
假设机器人的第一个分支运动链(包括末端执行器)有n1个关节,第二个分支运动链(包括末端执行器)有n2个关节,则运动学正解可用指数坐标表示为)()(2222212111111111θθθξθξθξθξst st st g eeg eeg n n n n ∧∧∧∧⋅⋅⋅=⋅⋅⋅=。
它建立了机器人关节转角之间的约束,正是由于这些约束的存在,从而仅须确定关节变量的子集就能控制末端执行器的位置,而其余关节转角的变量的取值必须满足上式。
由于关节变量受到上式的限制,并联机器人的关节空间就不是简单地象开链机构那样为各关节空间的笛卡儿积。
相反,它是满足上式的子集Q Q ⊂'。
'Q 维数的确定,以及并联机器人自由度的确定,需要对机构中的关节数和构件数做仔细分析。
运动学逆解:并联机器人的运动学逆解问题可以通过对联基座和末端执行器的各开链机构运动学逆解的处理来解决。
2. 解:如果操作器的雅可比矩阵在某一位型降秩,则此位型是奇异位型。
一般六自由度机器人存在奇异位型的情况有:1) 两转动轴线平行且共线,描叙奇异性在球腕结构(相当于轴线相互正交并汇交与一点的三个转动关节)很常见。
通过旋转球腕中的第二个转动关节,就可以使第一个转动关节和第三个转动关节的轴线重合,并使机器人的雅可比矩阵奇异。
2) 三个转动副,若三个转动关节轴线平行且共面。
肘机器人在其参考坐标系中即存在这种奇异性。
3) 四个转动关节轴线汇交与一点。
对于反肘式机器人,当末端关节轴线与肩关节轴线相交从而增加了一个第四轴线时,机产生上叙奇异性。
3解:先求1-) -(I ∧α=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---10010001111121323αααααα=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+---+-10010011010123223213212323a a a ααααααααα=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+++-++++-+-11101001110010123321232313232322213212323a a a a a a a a a a a a a a a a a a a =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++-+-++++-+S a Sa a a Sa a a S a a a S a S a a a Sa a a S a a a S a 233212313212232123121321111100010001 式中: 2322211a a a S +++==∧∧) +(I ) -(I 1-αα⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++-+-++++-+111111121323233212313212232123121321a a a a a a S a Sa a a S a a a S a a a S a S a a a Sa a a Sa a a S a=211a+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+---+-++---+23222113221131232221321231312322211)(2)(2)(21)(2)(2)(213a a a a a a a a a a a a a a a a a a a a a a a a a a a 4.解:满足p eeq 2211θξθξ∧∧=的点q ,q是球心分别位于1q ,2q ,r ,半径分别为21,δδ,rp -的三个球面的交点。
则有12211q p ee-∧∧θξθξ=1δ (1)22211q p ee-∧∧θξθξ=2δ(2)rp r p ee-=-∧∧2211θξθξ (3)上面三个式子中有三个未知数1θ,2θ,r 可以求的1θ,2θ。
(1)若轴线1ξ、2ξ重合于ξ,则1θ2θ,,满足θθθ=+21,则以上三式可为1q p e-∧θξ=1δ ,2q p e-∧θξ=2δ,rp r p e-=-∧θξ对于前面两式,由子问题3可分别求得⎪⎪⎭⎫⎝⎛--+-±=220arccos rq rp θθ 5解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1001ω ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1002ω, ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013ω, ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0001q ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0012l q ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=00213l l q由此产生旋量,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1000001ξ ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1000012l ξ ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=00100213l l ξ从而⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=∧1000010000cos sin 00sin cos 111111θθθθθξe⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=∧100010000c o s s in 00s in c o s 222222θθθθθξe⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--+-=∧10s in )(100)c o s 1)((0cos sin 00sin cos 321321333333θθθθθθθξl l l l e故⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡==1000001'1ξξ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==∧1000s in c o s 00)(1111211122112'211θθωωξξθξl l R v R v R R eAd ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+++-+-++-++++-+-+==∧∧001001000)cos()sin(0000)sin()cos(0000sin )cos 1(100cos )sin(000)cos()sin(cos )cos(000)sin()cos()(212121212121211211112113'32211l l l l l l l l e e Ad θθθθθθθθθθθθθθθθθθθθθθθθξξθξθξ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡++--=0)s i n ()c o s (c o s 002121212θθθθθl l 所以[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡++--==011)sin(00)cos(00cos 000sin 00cos 021212121111'3'2'1θθθθθθθξξξl l l l由已知0=sst J 得:。