固体物理第二章第二节 对称性和布拉维格子的分类
- 格式:ppt
- 大小:907.50 KB
- 文档页数:43



布拉维晶格的名词解释布拉维晶格是固体物质中最基本的结构单元之一,它描述了晶体中原子或分子的排列规律。
布拉维晶格概念源自法国物理学家布拉维尔·夏尔之名,他于 1850 年代提出了晶体的周期性结构理论。
布拉维晶格的定义是一种理想化的结构模型,用来描述晶体中原子或分子的周期性重复排列。
每个布拉维晶格单元即为晶体的最小结构单元,包含一个或多个原子或分子。
这些原子或分子的排列按照一定的对称性和周期性规律,构成了晶体的整体结构。
布拉维晶格的形状可以是各种各样的,包括立方格子、正交格子、单斜格子、正十二面体格子等。
每种晶格都具有其特定的对称性。
晶体的对称性是指晶体结构在经历特定的平移、旋转和镜面反射操作后保持不变的性质。
这些对称操作形成了晶体不同面和轴的对称元素。
布拉维晶格的特殊性在于其具有离散的倒格子。
倒格子是布拉维晶格的补充,用于描述物理量在晶体中的散射、传播和衍射等现象。
布拉维晶格和倒格子是对偶的,它们之间存在着一一对应的关系。
布拉维晶格的性质对于解释固体的电子结构、光学性质和热力学行为至关重要。
根据布拉维晶格的空间对称性,可以推导出晶体的色散关系、能带结构和声子谱等信息。
这些发现对于材料科学的发展和应用具有重要意义。
布拉维晶格的研究也涉及到了几何学和群论等数学工具的应用。
通过对布拉维晶格的几何形状和对称性的分析,可以获得晶体的对称性群和晶体系统的分类。
这些数学方法为实验与理论研究之间的桥梁,促进了晶体学领域的进展。
总而言之,布拉维晶格是对固体物质中原子或分子排列规律的抽象描述。
它不仅是晶体学的基础理论,也是材料科学和物理学研究的重要工具。
通过对布拉维晶格的研究,我们能更好地了解晶体的性质与行为,为新材料的开发和应用奠定基础。

二维布拉维格子类型-回复什么是二维布拉维格子类型?二维布拉维格子类型是指由一组正交的基矢量构成的平面,用于描述晶体的结构和性质。
布拉维格子类型的概念是基于晶体对称性的,通过将晶体复制并沿着平移矢量平移,可以填充整个平面。
这种描述方法十分有用,因为它可以简化对晶体结构的理解,并有助于预测材料的电子、磁性和光学性质。
布拉维格子类型根据平面的对称性和基矢量的选择而分类。
其中,最简单的布拉维格子类型是长方形和正交形,它们的基矢量分别是a和b。
在这两种类型中,晶格点位于基矢向量的顶点。
此外,还存在六边形、菱形和斜方形布拉维格子类型,它们的基矢量分别为a和b,但晶格点的排列方式略有不同。
接下来,我们将详细介绍每种布拉维格子类型的特点和应用:1. 长方形布拉维格子类型:长方形布拉维格子类型是最常见的一种类型。
其基矢量a和b分别垂直于平面,并且长度相等。
晶格点沿着基矢量的顶点排列,形成一个二维晶格。
这种布拉维格子类型通常用于描述金属和绝缘体的结构。
2. 正交形布拉维格子类型:正交形布拉维格子类型与长方形布拉维格子类型相似,但其基矢量a和b的长度可以不相等。
这种布拉维格子类型通常用于描述具有高度各向异性的材料,如液晶和某些晶胞轴向非晶态材料。
3. 六边形布拉维格子类型:六边形布拉维格子类型的基矢量a和b呈60度夹角。
晶格点位于基矢向量的顶点,形成一个六边形晶格。
该类型的布拉维格子用于描述石墨烯等材料,因其特殊的几何形状,六边形布拉维格子具有特殊的电子性质。
4. 菱形布拉维格子类型:菱形布拉维格子类型与六边形布拉维格子类型非常相似,其基矢向量a和b也呈60度夹角,但是晶格点位于基矢向量的中点。
这种布拉维格子类型通常用于描述铜铎氧化物等材料的结构和性质。
5. 斜方形布拉维格子类型:斜方形布拉维格子类型的基矢量a和b具有不同的长度和夹角。
这种布拉维格子类型通常用于描述薄膜材料和晶体异质结构的性质。
布拉维格子类型的研究对理解和设计晶体材料具有重要意义。
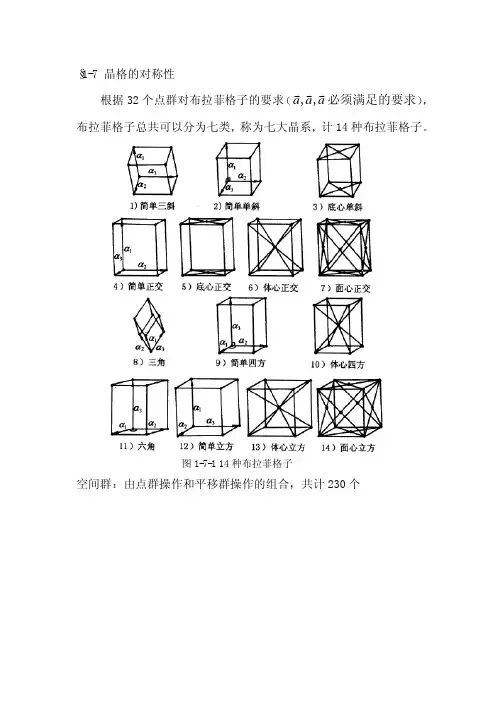
§1-7 晶格的对称性根据32个点群对布拉菲格子的要求a a a vv v ,,必须满足的要求布拉菲格子总共可以分为七类称为七大晶系计14种布拉菲格子图1-7-1 14种布拉菲格子 空间群由点群操作和平移群操作的组合共计230个1-8 晶体表面的几何结构前面关于点群和空间群的讨论都是假定晶体是无限的周期性的需求实际晶体总存在表面对于理想表面其表面同样可以引入二维布拉菲格子同体内的三维布拉菲格子一样同样可以引入基矢可以假定第三个基矢为垂直晶体表面的单位矢量倒格矢同样存在对称性表面不能简单地看成是体内同一晶面簇的平移由于环境的不同其原子排列和化学组成和体内也存在差别在离表面几个原子层1~2nm可以看成特殊相---表面相因此表面相的基矢可能和体内同一晶面簇中基矢存在差异这种现象称为表面再构固体表面宏观看起来虽然显得很平坦但实际表面层存在很多缺陷主要有化学吸附氧化和缺位间隙等即使没有杂质的理想表面由于其表面层原子受到的势环境不同于内层原子电子波函数在表面附近会发生变化因此导致表面层原子出现驰豫偏离原来三维晶格时的平衡位置1理想表面结构2Pt有序原子台阶示意图3a驰豫表面示意图b LiF001面的驰豫结构1-9非晶态材料的结构非晶态材料不具备周期性因此不具备长程有序但非晶态材料中的原子仍然保持原子排列的短程有序1近邻原子的数目和种类2近邻原子之间的距离键长3近邻原子配置的几何方位键角如下图1-10准晶态 准晶是介于非晶态和晶态物质之间的另一状态它不象晶体那样具有严格的周期性也和通常的非晶态存在区别其显著特点是原子位置仍然受到长程关联的制约而具有长程序1 从准周期性函数到Penrose 拼砌 数学上早就有准周期函数最简单的形式 x A x A x f 22112sin 2sin)(λπλπ+= 如果21λλ为一无理数则为周期等于无穷大的函数)(x f 但其又由两周期函数组合而成这就是准周期函数 从六十年代起物理学家开始研究多种类型的无公度相无公度相是指在基本晶格上附加有无公度的某种调制被调制的可以是原子的位移组分或自旋如下图周期为a 的晶格上附加了周期为λ的位移调制若a λ为有理数晶体即成为长周期的超结构若aλ为无理数那么就是无公度相这时沿这个方向的周期性不复存在在无公度相受到注意的同时数学家开始关注平面的非周期拼砌1974年R.Penrose找到能无空隙不重叠地布满平面的两种基本拼砌块该结构具有晶体学禁止的五重对称性2准晶的发现1984年Shechtman等在急冷Al-Mn合金中得到了具有五重对称轴斑点清晰的电子衍射图这和周期结构是不相容的这正是有非晶体学对称性的三维准周期性结构取名为准晶quasicrystal其和无公度相的区别在于准晶具有非晶体取向对称性非晶体取向对称性也对准周期性加以限制。


固体物理基本概念题参考解答-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN固体物理概念题1. 自由电子气体模型的三个基本近似是什么?两个基本参数是什么?自由电子近似;独立电子近似;弛豫时间近似自由电子数密度;弛豫时间2. 名词解释:K空间;k空间态密度把波矢k看做空间矢量,相应的空间称为k空间;K空间中单位体积内许可态的代表点数称为k空间态密度。
3. 自由电子模型的基态费米能和激发态费米能的物理意义是什么?费米能与哪些因素有关?物理意义:费米面上单电子态的能量称为费米能,表示电子从低到高填满能级时其最高能级的能量。
基费米能时指T=0 K时的费米能。
激发态费米能指的是T≠0 K时的费米能。
因素:费米能量与电子密度和温度有关。
4. 何为费米面金属电子气模型的费米面是何形状费米面:在K空间将占据态与未占据态分开的界面。
金属电子气模型的费米面是球形。
5. 说明为什么只有费米面附近的电子才对比热、电导和热导有贡献?对比热、电导和热导有贡献的电子是其能态能够发生变化的电子,只有费米面附近的电子才能从外界获得能量发生能态跃迁。
因为,在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上。
只有费米面附近的电子吸收声子后能跃迁到费米面附近或以外的空状态上。
对电导,考虑到泡利不相容原理的限制,只有费米面附近的电子才有可能在外电场作用下,进入较高能级,因而才会对金属电导率有贡献。
热导与电导相似。
6. 简述化学势的意义,它与费米能级满足什么样的关系。
化学势的意义是:在体积不变的条件下,系统没增加一个电子所需要的自由能。
在温度接近于0时,化学势和费米能近似相等。
7. 什么是等离子体振荡?给出金属电子气的振荡频率。
等离子体中的电子在自身惯性作用和正负电荷分离所产生的静电恢复力的作用下发生的简谐振荡称为等离子体振荡。
金属电子气的振荡频率8.名词解释:晶格,单胞,原胞,基元,布拉维格子基矢基元:在空间无限重复排列构成晶体的全同原子团晶格:将基元抽象为格点,格点的集合称为晶格晶胞:能够完整反映晶体的化学结构与晶体周期性的重复单元原胞:体积最小的晶胞布拉维格子基矢:原胞的基矢9.在三维情况下有多少种不同类型的晶格满足点对称群的要求?它们可以划分为哪7个晶系?14种布拉维格子,它们可以划分为7个晶系:三斜,单斜,正交,四方,三角,六角,立方。

布拉维格子的名词解释布拉维格子是固体中一种特殊的晶体结构,由于其独特的构造和性质,在物理学领域中被广泛研究和应用。
本文将对布拉维格子进行详细的解释和探讨。
布拉维格子的概念最早由瑞士物理学家勃拉维(Bravais)提出,他将晶体结构的排列方式进行了系统地分类和命名。
在布拉维格子中,晶体的原胞(最小重复单位)无限重复堆积而成,形成了整体具有周期性的结构。
布拉维格子的基本单位可以是点、线或面,其分类依据是基元(基本单位)的对称性。
布拉维格子的分类有14种,分别为简单立方格子、面心立方格子、体心立方格子、六方密堆积格子、多面体格子等。
这些不同类型的布拉维格子由于原胞中基元的排列不同,因而具有不同的对称性和性质。
在布拉维格子的研究中,晶格常数是一个重要的参数,它表示了格子中基元之间的距离。
晶格常数决定了布拉维格子的结构和性质,不同的晶格常数对应着不同的晶体特征。
更进一步地,布拉维格子的点阵常数是指晶体中相邻的两个基元之间距离的最小值,它是晶格常数的一个函数。
布拉维格子的性质和应用涵盖了多个领域。
在材料科学中,人们通过研究和改变布拉维格子的结构,可以获得具有特殊功能和性能的材料。
例如,面心立方格子具有良好的可塑性和导电性,因此广泛应用于金属制品的生产中。
而六方密堆积格子被广泛应用于光纤和半导体等领域,其特殊的结构使得其具有优异的机械和光学性能。
在纳米科技领域,布拉维格子也发挥着重要的作用。
纳米颗粒可以通过控制布拉维格子的大小和形状来调控其物理和化学性质。
这对于设计和制造高性能的纳米材料尤为重要,因为纳米尺度的材料往往具有与其宏观尺度不同的独特性质。
不仅如此,布拉维格子还在凝聚态物理、量子力学和电子结构等领域起到了关键作用。
通过对布拉维格子的研究,物理学家们可以深入理解材料的电子结构和输运行为,从而发现新的物理现象和规律。
总而言之,布拉维格子作为晶体结构的基本单位,其独特的结构和对称性赋予了物质一些特殊的性质。

一、填空1. 固体按其微结构的有序程度可分为_______、_______和准晶体。
2. 组成粒子在空间中周期性排列,具有长程有序的固体称为_______;组成粒子在空间中的分布完全无序或仅仅具有短程有序的固体称为_________。
3. 在晶体结构中,所有原子完全等价的晶格称为______________;而晶体结构中,存在两种或两种以上不等价的原子或离子的晶格称为____________。
4晶体结构的最大配位数是____;具有最大配位数的晶体结构包括______________晶体结构和______________晶体结构。
5. 简单立方结构原子的配位数为______;体心立方结构原子的配位数为______。
6.NaCl结构中存在_____个不等价原子,因此它是_______晶格,它是由氯离子和钠离子各自构成的______________格子套构而成的。
7. 金刚石结构中存在______个不等价原子,因此它是_________晶格,由两个_____________结构的布拉维格子沿空间对角线位移1/4的长度套构而成,晶胞中有_____个碳原子。
8. 以结晶学元胞(单胞)的基矢为坐标轴来表示的晶面指数称为________指数。
9. 满足关系的为基矢,由构成的点阵,称为_______。
10. 晶格常数为a的一维单原子链,倒格子基矢的大小为________。
11. 晶格常数为a的面心立方点阵初基元胞的体积为_______;其第一布里渊区的体积为_______。
12. 晶格常数为a的体心立方点阵初基元胞的体积为_______;其第一布里渊区的体积为_______。
13. 晶格常数为a的简立方晶格的(010)面间距为________14. 体心立方的倒点阵是________________点阵,面心立方的倒点阵是________________点阵,简单立方的倒点阵是________________。


2023年固体物理基础第三版(阎守胜著)课后题答案下载固体物理基础第三版(阎守胜著)课后答案下载第一章金属自由电子气体模型1.1 模型及基态性质1.1.1 单电子本征态和本征能量1.1.2 基态和基态的能量1.2 自由电子气体的热性质1.2.1 化学势随温度的变化1.2.2 电子比热1.3 泡利顺磁性1.4 电场中的`自由电子1.4.1 准经典模型1.4.2 电子的动力学方程1.4.3 金属的电导率1.5 光学性质1.6 霍尔效应和磁阻1.7 金属的热导率1.8 自由电子气体模型的局限性第二章晶体的结构2.1 晶格2.1.1 布拉维格子2.1.2 原胞2.1.3 配位数2.1.4 几个常见的布拉维格子2.1.5 晶向、晶面和基元的坐标2.2 对称性和布拉维格子的分类2.2.1 点群2.2.2 7个晶系2.2.3 空间群和14个布拉维格子2.2.4 单胞或惯用单胞2.2.5 二维情形2.2.6 点群对称性和晶体的物理性质 2.3 几种常见的晶体结构2.3.1 CsCl结构和立方钙钛矿结构 2.3.2 NaCl和CaF、2结构2.3.3 金刚石和闪锌矿结构2.3.4 六角密堆积结构2.3.5 实例,正交相YBa2Cu307-82.3.6 简单晶格和复式晶格2.4 倒格子2.4.1 概念的引入2.4.2 倒格子是倒易空间中的布拉维格子 2.4.3 倒格矢与晶面2.4.4 倒格子的点群对称性2.5 晶体结构的实验确定2.5.1 X射线衍射2.5.2 电子衍射和中子衍射2.5.3 扫描隧穿显微镜第三章能带论I3.1 布洛赫定理及能带3.1.1 布洛赫定理及证明3.1.2 波矢七的取值与物理意义3.1.3 能带及其图示3.2 弱周期势近似3.2.1 一维情形3.2.2 能隙和布拉格反射3.2.3 复式晶格3.3 紧束缚近似3.3.1 模型及计算3.3.2 万尼尔函数3.4 能带结构的计算3.4.1 近似方法3.4.2 n(K)的对称性3.4.3 n(K)和n的图示3.5 费米面和态密度3.5.1 高布里渊区3.5.2 费米面的构造3.5.3 态密度第四章能带论Ⅱ4.1 电子运动的半经典模型 4.1.1 模型的表述4.1.2 模型合理性的说明4.1.3 有效质量4.1.4 半经典模型的适用范围4.2 恒定电场、磁场作用下电子的运动4.2.1 恒定电场作用下的电子4.2.2 满带不导电4.2.3 近满带中的空穴4.2.4 导体、半导体和绝缘体的能带论解释 4.2.5 恒定磁场作用下电子的准经典运动 4.3 费米面的测量4.3.1 均匀磁场中的自由电子4.3.2 布洛赫电子的轨道量子化4.3.3 德哈斯一范阿尔芬效应4.3.4 回旋共振方法4.4 用光电子谱研究能带结构4.4.1 态密度分布曲线4.4.2 角分辨光电子谱测定n(K)4.5 一些金属元素的能带结构4.5.1 简单金属4.5.2 一价贵金属4.5.3 四价金属和半金属4.5.4 过渡族金属和稀土金属第五章晶格振动5.1 简谐晶体的经典运动5.1.1 简谐近似5.1.2 一维单原子链,声学支 5.1.3 一维双原子链,光学支 5.1.4 三维情形5.2 简谐晶体的量子理论5.2.1 简正坐标5.2.2 声子5.2.3 晶格比热5.2.4 声子态密度5.3 晶格振动谱的实验测定 5.3.1 中子的非弹性散射5.3.2 可见光的非弹性散射 5.4 非简谐效应5.4.1 热膨胀5.4.2 晶格热导率第六章输运现象6.1 玻尔兹曼方程6.2 电导率6.2.1 金属的直流电导率6.2.2 电子和声子的相互作用 6.2.3 电阻率随温度的变化 6.2.4 剩余电阻率6.2.5 近藤效应06.2.6 半导体的电导率6.3 热导率和热电势6.3.1 热导率6.3.2 热电势6.4 霍尔系数和磁阻第七章固体中的原子键合7.1 概述7.1.1 化学键7.1.2 晶体的分类7.1.3 晶体的结合能7.2 共价晶体7.3 离子晶体7.3.1 结合能7.3.2 离子半径7.3.3 部分离子部分共价的晶体7.4 分子晶体、金属及氢键晶体7.4.1 分子晶体7.4.2 量子晶体7.4.3 金属……第八章缺陷第九章无序第十章尺寸第十一章维度第十二章关联固体物理基础第三版(阎守胜著):基本信息阎守胜,1938生出生,1962年毕业于北京大学物理系,现任北京大学物理学院教授,博士生导师,兼任中国物理学会《物理》杂志主编,他长期从事低温物理,低温物理实验技术,高温超导电性物理和介观物理方面的实验研究,并讲授大学生的固体物理学,低温物理学和现代固体物理学等课程。