第五章-2(切比雪夫低通滤波器)

摘要随着信息和数字时代的到来，数字信号处理已成为当今一门极其重要的学科和技术领域。

在现代通信系统中，由于信号中经常混有各种复杂成分，因此很多信号的处理都是基于滤波器而进行的。

所以，数字滤波器在数字信号处理中起着举足轻重的作用。

而数字滤波器的设计都要以模拟滤波器为基础的，这是因为模拟滤波器的理论和设计方方法都已发展的相当成熟，且有典型的模拟滤波器供我们选择。

，如巴特沃思滤波器、切比雪夫滤波器等。

本次课程设计将运用MATLAB设计一个基于切比雪夫低通滤波器，并出所设计滤波器的幅度及幅度衰减特性。

关键词：模拟低通滤波切比雪夫1课题描述数字滤波器是数字信号处理的重要工具之一，它通过数值运算处理改变输入信号所含频率成分的相对比例或者滤出某些频率成分的数字器件或程序，而数字滤波器处理精度高、体积小、稳定、重量轻、灵活、不存在阻抗匹配问题，可以实现模拟滤波器无法实现的特殊功能。

故本课题使用MATLAB 信号处理箱和运用切比雪夫法设计数字低通滤波器。

2设计原理切比雪夫滤波器介绍在巴特沃兹滤波器中，幅度响应在通带和阻带内都是单调的。

因此，若滤波器的技术要求是用最大通带和阻带的逼近误差来给出的话，那么，在靠近通带低频端和阻带截止频率以上的部分都会超出技术指标。

一种比较有效的途径是使逼近误差均匀地分布于通带或阻带内，或同时在通带和阻带内都均匀分布，这样往往可以降低所要求的滤波器阶次。

通过选择一种具有等波纹特性而不是单调特性的逼近方法可以实现这一点。

切比雪夫型滤波器就具有这种性质：其频率响应的幅度既可以在通带中是等波纹的，而在阻带中是单调的（称为I 型切比雪夫滤波器），也可以在通带中是单调的，而在阻带中是等波纹的（称为II 型切比雪夫滤波器）。

I 型切比雪夫滤波器的幅度平方函数是2|)(|Ωj H C =)/(1122c N C ΩΩ+ε 式中为N 阶切比雪夫多项式，定义为)cos cos()(1x N x C N -=从定义切比雪夫多项式可以直接得出由)(x C N 和)(1x C N -求)(1x C N +的递推公式。

(完整word版)切比雪夫低通滤波器课程设计题目：院(系）：专业：学生姓名：学号：指导教师：2014 年01 月03 日切比雪夫低通滤波器摘要:利用ADS2008软件设计切比雪夫型低通滤波器，通过最终的图像，分析该滤波器的功能特性，并与其他滤波器对比分析，阐明此种滤波器的优点所在。

关键字：ADS2008软件切比雪夫低通滤波器功能特性目录摘要 (1)1滤波器概述 (3)1。

1滤波器分类 (3)1。

2根据滤波器的选频作用分类 (4)1.3根据“最佳逼近特性”标准分类 (4)1。

4理想滤波器 (5)2切比雪夫低通滤波器设计 (7)2.1新建滤波器工程 (7)2.2建立一个低通滤波器设计 (7)3 设计心得 (12)4 参考文献 (13)1、滤波器概述滤波器是一种选频装置，可以使信号中特定的频率成分通过，而极大地衰减其它频率成分。

在测试装置中，利用滤波器的这种选频作用，可以滤除干扰噪声或进行频谱分析。

广义地讲,任何一种信息传输的通道（媒质）都可视为是一种滤波器。

因为，任何装置的响应特性都是激励频率的函数，都可用频域函数描述其传输特性.因此，构成测试系统的任何一个环节，诸如机械系统、电气网络、仪器仪表甚至连接导线等等，都将在一定频率范围内，按其频域特性，对所通过的信号进行变换与处理.1.1 滤波器分类:滤波器特性可以用其频率响应来描述，按其特性的不同，可以分为低通滤波器,高通滤波器,带通滤波器和带阻滤波器等.低通滤波器有很多种，其中,最通用的就是巴特沃斯滤波器和切比雪夫滤波器。

巴特沃斯滤波器是滤波器的一种设计分类，其采用的是巴特沃斯传递函数，有高通、低通、带通、带阻等多种滤波器类型.巴特沃斯滤波器在通频带内外都有平稳的幅频特性，但有较长的过渡带，在过渡带上很容易造成失真。

切比雪夫滤波器同巴特沃斯滤波器相添加图片比，切比雪夫滤波器的过渡带很窄，但内部的幅频特性却很不稳定。

巴特沃斯响应能够最大化滤波器的通带平坦度.该响应非常平坦，非常接近DC信号，然后慢慢衰减至截止频率.巴特沃斯滤波器特别适用于低频应用，其对于维护增益的平坦性来说非常重要。

切比雪夫低通滤波器计算
切比雪夫低通滤波器是数字信号处理中常用的一种滤波器类型，用于对信号进
行滤波处理，去除高频成分。

其设计需要根据滤波器的阶数、截止频率和通带波纹等参数进行计算。

首先，切比雪夫低通滤波器的频率响应特点是在通带内具有波纹，而在截止频
率之后的阻带内频率响应快速下降，因此在设计时需要考虑通带波纹和阻带衰减的要求。

设计切比雪夫低通滤波器的步骤如下：
1. 确定滤波器的阶数：根据滤波器的设计要求，确定所需的滤波器阶数。

阶数
越高，滤波器的性能越好，但计算复杂度也越高。

2. 确定通带波纹和阻带衰减：根据设计要求确定通带波纹和阻带衰减的要求，
这些参数将直接影响滤波器的设计。

3. 计算截止频率：根据设计要求确定滤波器的截止频率，即希望滤波器在该频
率之后起作用。

4. 根据以上参数，利用切比雪夫滤波器的设计公式计算滤波器的传递函数系数。

切比雪夫低通滤波器的设计公式如下：
H(s) = 1 / [1 + ε^2 * C^2(s/s_c)^2n]
其中，H(s)为滤波器的传递函数，ε为通带波纹系数，C为滤波器的阻带衰减，n为滤波器的阶数，s为复频域变量，s_c为滤波器的截止频率。

设计切比雪夫低通滤波器的关键在于确定好滤波器的阶数、通带波纹和阻带衰减，根据设计要求利用设计公式计算滤波器的传递函数系数，从而实现滤波器的设计。

在实际的数字信号处理应用中，切比雪夫低通滤波器常用于需要较高的通带波纹和较快的阻带衰减的场合，可以根据具体的需求进行设计，滤波器的设计参数直接影响滤波器的性能和应用效果，因此设计时需谨慎考虑各个参数的取值。

.课程设计题目：院（系）：专业：学生姓名：学号：指导教师：2014 年 01 月 03 日切比雪夫低通滤波器摘要：利用ADS2008软件设计切比雪夫型低通滤波器，通过最终的图像，分析该滤波器的功能特性，并与其他滤波器对比分析，阐明此种滤波器的优点所在。

关键字：ADS2008软件切比雪夫低通滤波器功能特性目录摘要 (1)1滤波器概述 (3)1.1滤波器分类 (3)1.2根据滤波器的选频作用分类 (4)1.3根据“最佳逼近特性”标准分类 (4)1.4理想滤波器 (5)2切比雪夫低通滤波器设计 (7)2.1新建滤波器工程 (7)2.2建立一个低通滤波器设计 (7)3 设计心得 (12)4 参考文献 (13)1、滤波器概述滤波器是一种选频装置，可以使信号中特定的频率成分通过，而极大地衰减其它频率成分。

在测试装置中，利用滤波器的这种选频作用，可以滤除干扰噪声或进行频谱分析。

广义地讲，任何一种信息传输的通道（媒质）都可视为是一种滤波器。

因为，任何装置的响应特性都是激励频率的函数，都可用频域函数描述其传输特性。

因此，构成测试系统的任何一个环节，诸如机械系统、电气网络、仪器仪表甚至连接导线等等，都将在一定频率范围内，按其频域特性，对所通过的信号进行变换与处理。

1.1 滤波器分类：滤波器特性可以用其频率响应来描述，按其特性的不同，可以分为低通滤波器，高通滤波器，带通滤波器和带阻滤波器等。

低通滤波器有很多种，其中，最通用的就是巴特沃斯滤波器和切比雪夫滤波器。

巴特沃斯滤波器是滤波器的一种设计分类，其采用的是巴特沃斯传递函数，有高通、低通、带通、带阻等多种滤波器类型。

巴特沃斯滤波器在通频带内外都有平稳的幅频特性，但有较长的过渡带，在过渡带上很容易造成失真。

切比雪夫滤波器同巴特沃斯滤波器相添加图片比，切比雪夫滤波器的过渡带很窄，但内部的幅频特性却很不稳定。

巴特沃斯响应能够最大化滤波器的通带平坦度。

该响应非常平坦，非常接近DC信号，然后慢慢衰减至截止频率。

二阶切比雪夫低通滤波器结构
二阶切比雪夫低通滤波器是一种常用于信号处理和电子滤波的滤波器。

切比雪夫滤波器具有在通频带内最小化过渡带波纹的特性。

以下是二阶切比雪夫低通滤波器的结构：
切比雪夫低通滤波器的传输函数可以表示为：
其中：
•H(s) 是滤波器的传输函数。

•s是复频域变量。

•ε是过渡带波纹的最大幅度。

•Tn(s/T) 是规范化的切比雪夫多项式，具体形式取决于滤波器的阶数和类型。

切比雪夫低通滤波器的二阶结构通常由一个阻抗转换网络和一个电压跟随器组成。

以下是其基本结构：
1.阻抗转换网络：
•该网络通常由电感（L）和电容（C）组成。

•电感和电容的数值取决于滤波器的截止频率和阻带波纹的设定。

2.电压跟随器：
•电压跟随器用于提高输出阻抗，确保在通频带内滤波器的性能。

•可以使用运算放大器（Operational Amplifier）来实现电压
跟随器。

通过适当选择电感、电容和运算放大器的数值，可以调整滤波器的截止频率、过渡带波纹和阻带的性能。

切比雪夫滤波器通常用于需要在通频带内最小化幅度响应变化的应用，如通信系统和音频处理。

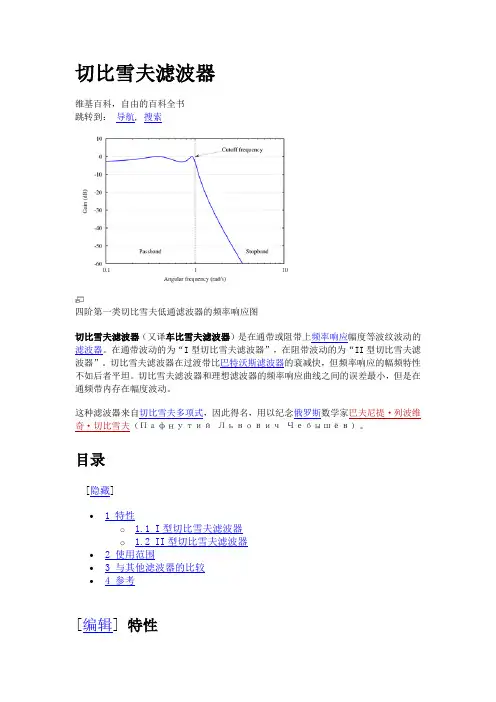
切比雪夫滤波器维基百科，自由的百科全书跳转到：导航, 搜索四阶第一类切比雪夫低通滤波器的频率响应图切比雪夫滤波器（又译车比雪夫滤波器）是在通带或阻带上频率响应幅度等波纹波动的滤波器。

在通带波动的为“I型切比雪夫滤波器”，在阻带波动的为“II型切比雪夫滤波器”。

切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快，但频率响应的幅频特性不如后者平坦。

切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小，但是在通频带内存在幅度波动。

这种滤波器来自切比雪夫多项式，因此得名，用以纪念俄罗斯数学家巴夫尼提·列波维奇·切比雪夫（ПафнутийЛьвовичЧебышёв）。

目录[隐藏]• 1 特性o 1.1 I型切比雪夫滤波器o 1.2 II型切比雪夫滤波器• 2 使用范围• 3 与其他滤波器的比较• 4 参考[编辑]特性[编辑] I型切比雪夫滤波器I型切比雪夫滤波器最为常见。

n阶第一类切比雪夫滤波器的幅度与频率的关系可用下列公式表示：其中：••而是滤波器在截止频率ω0的放大率 (注意: 常用的以幅度下降3分贝的频率点作为截止频率的定义不适用于切比雪夫滤波器!)•是n阶切比雪夫多项式：或:切比雪夫滤波器的阶数等于此滤波器的电子线路内的电抗元件数。

切比雪夫滤波器的幅度波动 = 分贝当,切比雪夫滤波器的幅度波动= 3分贝。

如果需要幅度在在阻频带边上衰减得更陡峭，可允许在复平面的jω轴上存在零点。

但结果会使通频带内振幅波动较大，而在阻频带内对信号抑制较弱。

这种滤波器叫椭圆函数滤波器或考尔滤波器。

[编辑] II型切比雪夫滤波器也称倒数切比雪夫滤波器，较不常用，因为频率截止速度不如I型快，也需要用更多的电子元件。

II型切比雪夫滤波器在通频带内没有幅度波动，只在阻频带内有幅度波动。

II型切比雪夫滤波器的转移函数为：参数ε与阻频带的衰减度γ有如下关系：分贝。

5分贝衰减度相当于ε = 0.6801; 10分贝衰减度相当于ε = 0.3333。

课程设计题目：切比雪夫低通滤波器设计院（系）：物理与电信工程学院专业：电子信息工程学生姓名：陈侃学号： 1013014056 指导教师：聂翔2014 年 01 月 03 日切比雪夫低通滤波器摘要：利用ADS2008软件设计切比雪夫型低通滤波器，通过最终的图像，分析该滤波器的功能特性，并与其他滤波器对比分析，阐明此种滤波器的优点所在。

关键字：ADS2008软件切比雪夫低通滤波器功能特性目录摘要 (1)1 滤波器概述 (3)1.1 滤波器分类 (3)1.2 根据滤波器的选频作用分类 (4)1.3 根据“最佳逼近特性”标准分类 (4)1.4 理想滤波器 (5)2 切比雪夫低通滤波器设计 (7)2.1 新建滤波器工程 (7)2.2 建立一个低通滤波器设计 (7)3 设计心得 (13)4 参考文献 (14)1、滤波器概述滤波器是一种选频装置，可以使信号中特定的频率成分通过，而极大地衰减其它频率成分。

在测试装置中，利用滤波器的这种选频作用，可以滤除干扰噪声或进行频谱分析。

广义地讲，任何一种信息传输的通道（媒质）都可视为是一种滤波器。

因为，任何装置的响应特性都是激励频率的函数，都可用频域函数描述其传输特性。

因此，构成测试系统的任何一个环节，诸如机械系统、电气网络、仪器仪表甚至连接导线等等，都将在一定频率范围内，按其频域特性，对所通过的信号进行变换与处理。

1.1 滤波器分类：滤波器特性可以用其频率响应来描述，按其特性的不同，可以分为低通滤波器，高通滤波器，带通滤波器和带阻滤波器等。

低通滤波器有很多种，其中，最通用的就是巴特沃斯滤波器和切比雪夫滤波器。

巴特沃斯滤波器是滤波器的一种设计分类，其采用的是巴特沃斯传递函数，有高通、低通、带通、带阻等多种滤波器类型。

巴特沃斯滤波器在通频带内外都有平稳的幅频特性，但有较长的过渡带，在过渡带上很容易造成失真。

切比雪夫滤波器同巴特沃斯滤波器相添加图片比，切比雪夫滤波器的过渡带很窄，但内部的幅频特性却很不稳定。

课程设计课程名称：数字信号处理题目编号： 0202题目名称：切比雪夫Ⅱ型IIR低通滤波器专业名称：电子信息工程班级：电子1204班学号： ***************：*******：***2015年09月30日课程设计任务书目录1. 数字滤波器的设计任务及要求（编号202） (2)2. 数字滤波器的设计及仿真 (3)2.1数字滤波器（编号202）的设计 (3)2.2数字滤波器（编号202）的性能分析 (6)3. 数字滤波器的实现结构对其性能影响的分析 (7)3.1数字滤波器的实现结构一（直接型）及其幅频响应 (8)3.2数字滤波器的实现结构二（级联型）及其幅频响应 (10)3.3 数字滤波器的实现结构对其性能影响的小结 (10)4. 数字滤波器的参数字长对其性能影响的分析 (11)4.1数字滤波器的实现结构一（直接型）参数字长及幅频响应特性变化 (12)4.2数字滤波器的实现结构二（级联型）参数字长及幅频响应特性变化 (14)4.3 数字滤波器的参数字长对其性能影响的小结 (16)5. 结论及体会 (16)5.1 滤波器设计、分析结论 (16)5.2 我的体会 (16)5.3 展望 (17)1.数字滤波器的设计任务及要求（0202）每位同学抽签得到一个四位数，由该四位数索引下表一确定待设计数字滤波器的类型及其设计方法， 然后用指定的设计方法完成滤波器设计。

要求：（1）滤波器设计指标：通带截止频 pc ln ()32d rad i πω=, 过渡带宽度10tz()160log drad i πω∆≤，滚降roll 60dB α=;其中， id —抽签得到那个四位数（题目编号) （2）滤波器的初始设计通过手工计算完成；（3）在计算机辅助计算基础上分析滤波器结构对其性能指标的影响（至少选择两种 以上合适的滤波器结构进行分析）；（4）在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响； （5） 以上各项要有理论分析和推导、原程序以及表示计算结果的图表； （6）课程设计结束时提交设计说明书。

切比雪夫低通滤波器设计切比雪夫低通滤波器是一种常见的数字滤波器，用于去除信号中高频成分，保留低频成分。

其特点是在通带内的波形变形较小，但对于截止频率附近的频率响应会有较大的波动。

本文将介绍切比雪夫低通滤波器的设计方法和实现步骤。

首先，我们需要确定设计的规格要求，包括截止频率、通带衰减、阻带衰减等参数。

在本文中，我们将设计一个3阶切比雪夫低通滤波器，截止频率为1kHz，通带衰减为1dB，阻带衰减为60dB。

接下来，我们可以使用切比雪夫低通滤波器的设计方程来计算滤波器的传递函数。

切比雪夫低通滤波器的传递函数可以表示为：H(s)=1/(1+εn^2*Cn^2(s/ωn))其中，ε是通带衰减，n是滤波器的阶数，Cn是阶数n的切比雪夫多项式。

ωn是规范化的截止频率，可以计算为ωn = 2πf / fs，其中f是实际的截止频率，fs是采样频率。

根据上述的设计方程，我们可以计算出滤波器的传递函数。

接下来，我们需要将传递函数转换为巴特沃斯形式，以便于实际的滤波器设计。

我们可以使用双线性变换来实现这一步骤。

双线性变换可以将连续时间域的传递函数转换为离散时间域的传递函数。

通过双线性变换，可以将连续时间域的传递函数转换为离散时间域的传递函数：H(z)=H(s)，s=(2/Ts)*(z-1)/(z+1)其中，Ts是采样周期，z是离散的复数变量。

将已经计算出的连续时间域的传递函数代入上述公式，我们可以得到离散时间域的传递函数。

现在，我们可以根据得到的离散时间域的传递函数进行滤波器的实现。

可以使用常见的数字滤波器实现方法，如直接形式、级联形式、并联等等。

最后，我们需要对实际的滤波器进行参数调整和优化。

根据设计的要求，我们可以在滤波器的传递函数中调整各个参数，以达到所需的滤波效果。

总结起来，切比雪夫低通滤波器的设计包括确定规格要求、计算传递函数、双线性变换和滤波器实现、参数调整和优化等步骤。

通过这些步骤，我们可以设计出满足要求的切比雪夫低通滤波器。

目录1 绪论 (1)1.1 课题背景 (1)1.2 课题目的 (2)2 课程设计预习与原理 (3)2.1 课程设计预习 (3)2.1.1 卷积运算的演示 (3)2.2.2 采样定理的演示 (9)2.2 课程设计原理 (11)2.2.1 频谱分析原理 (11)2.2.2 IIR设计原理 (12)2.2.3 FIR设计原理 (12)3 课程设计步骤和过程 (15)3.1 IIR设计步骤和过程 (15)3.2 FIR设计步骤和过程 (15)4 设计程序的调试和运行结果 (17)4.1 切比雪夫低通滤波器程序的调试和运行结果 (17)4.2 切比雪夫高通滤波器程序的调试和运行结果 (19)4.3 切比雪夫带通滤波器程序的调试和运行结果 (21)4.4 Kaiser低通滤波器程序的调试和运行结果 (23)4.5 Kaiser高通滤波器程序的调试和运行结果 (25)4.6 Kaiser带通滤波器程序的调试和运行结果 (27)5 总结 (29)参考文献 (32)附录 (33)附录 A (33)附录 B (45)1 绪论1.1 课题背景数字滤波器是数字信号处理的基础，用来对信号进行过滤、检测与参数估计等处理，在通信、图像、语音、雷达等许多领域都有着十分广泛的应用。

尤其在图像处理、数据压缩等方面取得了令人瞩目的进展和成就。

数字滤波器的设计有许多现成的高级语言设计程序，但他们都存在设计效率较低，不具有可视图形，不便于修改参数等缺点，而Matlab为数字滤波的研究和应用提供了一个直观、高效、便捷的利器。

他以矩阵运算为基础，把计算、可视化、程序设计融合到了一个交互式的工作环境中。

尤其是Matlab工具箱使各个领域的研究人员可以直观方便地进行科学研究与工程应用。

其中的信号处理工具箱、图像处理工具箱、小波工具箱等更是为数字滤波研究的蓬勃发展提供了可能。

MATLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

课程设计课程名称：数字信号处理题目编号： 0202题目名称：切比雪夫Ⅱ型IIR低通滤波器专业名称：电子信息工程班级：电子1204班学号： 20124470411学生姓名：刘春阳任课教师：黄国玉2015年09月30日数字信号处理课程设计课程设计任务书目录1. 数字滤波器的设计任务及要求（编号202） (2)2. 数字滤波器的设计及仿真 (3)2.1数字滤波器（编号202）的设计 (3)2.2数字滤波器（编号202）的性能分析 (6)3. 数字滤波器的实现结构对其性能影响的分析 (7)3.1数字滤波器的实现结构一（直接型）及其幅频响应 (8)3.2数字滤波器的实现结构二（级联型）及其幅频响应 (10)3.3 数字滤波器的实现结构对其性能影响的小结 (10)4. 数字滤波器的参数字长对其性能影响的分析 (11)4.1数字滤波器的实现结构一（直接型）参数字长及幅频响应特性变化 (12)4.2数字滤波器的实现结构二（级联型）参数字长及幅频响应特性变化 (14)4.3 数字滤波器的参数字长对其性能影响的小结 (16)5. 结论及体会 (16)5.1 滤波器设计、分析结论 (16)5.2 我的体会 (16)5.3 展望 (17)1.数字滤波器的设计任务及要求（0202）每位同学抽签得到一个四位数，由该四位数索引下表一确定待设计数字滤波器的类型及其设计方法， 然后用指定的设计方法完成滤波器设计。

要求：（1）滤波器设计指标：通带截止频 pc ln ()32d rad i πω=, 过渡带宽度10tz()160log drad i πω∆≤，滚降roll 60dB α=;其中， id —抽签得到那个四位数（题目编号) （2）滤波器的初始设计通过手工计算完成；（3）在计算机辅助计算基础上分析滤波器结构对其性能指标的影响（至少选择两种 以上合适的滤波器结构进行分析）；（4）在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响； （5） 以上各项要有理论分析和推导、原程序以及表示计算结果的图表； （6）课程设计结束时提交设计说明书。

一、设计一个切比雪夫Ⅱ型低通滤波器wp=0.2*pi; %通带边界频率；ws=0.4*pi; %阻带截止频率；rp=1; %通带最大衰减；rs=80; %阻带最小衰减；Fs=1000 %假设抽样脉冲1000hz[N,Wn]=cheb2ord(wp,ws,rp,rs,'s'); %Chebyshev II型滤波器参数计算（模拟域）；[Z,P,K]=cheby2(N,rs,Wn,'s'); %构造Chebyshev II型滤波器（零极点模型）；[H,W]=zp2tf(Z,P,K); %将零极点模型转化成传递函数的模型；figure(1);freqs(H,W); %在Figure1上显示滤波器的幅频响应及相频响应；[P,Q]=freqs(H,W); %返回滤波器的冲击响应的复数形式；figure(2);plot(Q*Fs/(2*pi),abs(P));grid; %在Figure2上显示幅频特性曲线；xlabel('频率/Hz');ylabel('幅值');二、设计一个高通Chebyshow型数字滤波器wp=100;ws=80;Fs=300;rp=1;rs=45; %数字滤波器的各项指标；WP=100*2*pi; %把数字滤波器的频率特征转换成模拟滤波器的频率特征；WS=300*2*pi;[N,Wn]=cheb2ord(WP,WS,rp,rs,'s'); %Chebyshev II型滤波器参数计算（模拟域）；[Z,P,K]=cheb2ap(N,rs); %创建Chebyshev滤波器原型；[A,B,C,D]=zp2ss(Z,P,K); %表达式从零极点增益形式转换成状态方程形式；[AA,BB,CC,DD]=lp2hp(A,B,C,D,Wn); %实现低通到高通滤波器类型的转换；[a,b,c,d]=bilinear(AA,BB,CC,DD,Fs); %采用双线性变换法，从模拟高通到数字高通；[P,Q]=ss2tf(a,b,c,d); %表达式从状态方程形形式转换成传输函数形式；figure(1);freqz(P,Q); %绘出频率响应；[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅值');三、设计一个带通切比雪夫数字滤波器W1=100;W2=200;rp=1;rs=30;Fs=1000; %数字滤波器的各项指标；WP=[100,200];WS=[50,250];[N,Wn]=cheb1ord(WP/(Fs/2),WS/(Fs/2),rp,rs);%Chebyshev I型滤波器参数计算（数字域）；[P,Q]=cheby1(N,rp,Wn,'bandpass');%创建Chebyshev带通滤波器；figure(1);freqz(P,Q); %显示产生滤波器的幅频及相频曲线；[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅度');。