ch18
- 格式:doc
- 大小:161.00 KB
- 文档页数:6


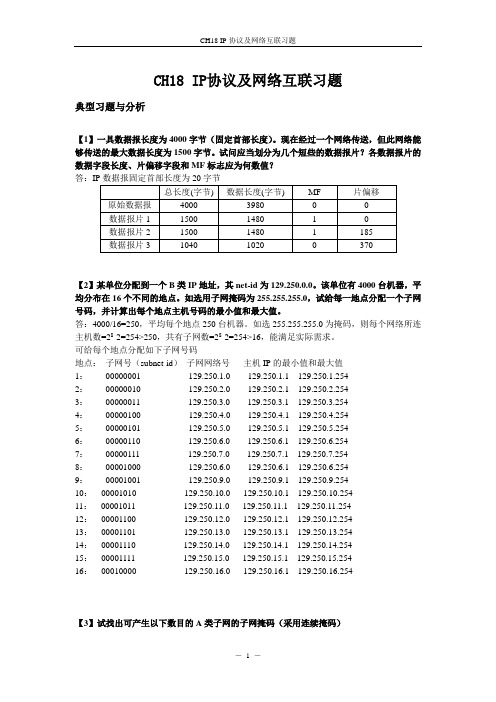
CH18 IP协议及网络互联习题典型习题与分析【1】一具数据报长度为4000字节(固定首部长度)。
现在经过一个网络传送,但此网络能够传送的最大数据长度为1500字节。
试问应当划分为几个短些的数据报片?各数据报片的数据字段长度、片偏移字段和MF标志应为何数值?答:【2】某单位分配到一个B类IP地址,其net-id为129.250.0.0。
该单位有4000台机器,平均分布在16个不同的地点。
如选用子网掩码为255.255.255.0,试给每一地点分配一个子网号码,并计算出每个地点主机号码的最小值和最大值。
答:4000/16=250,平均每个地点250台机器。
如选255.255.255.0为掩码,则每个网络所连主机数=28-2=254>250,共有子网数=28-2=254>16,能满足实际需求。
可给每个地点分配如下子网号码地点:子网号(subnet-id)子网网络号主机IP的最小值和最大值1:00000001 129.250.1.0 129.250.1.1---129.250.1.2542:00000010 129.250.2.0 129.250.2.1---129.250.2.2543:00000011 129.250.3.0 129.250.3.1---129.250.3.2544:00000100 129.250.4.0 129.250.4.1---129.250.4.2545:00000101 129.250.5.0 129.250.5.1---129.250.5.2546:00000110 129.250.6.0 129.250.6.1---129.250.6.2547:00000111 129.250.7.0 129.250.7.1---129.250.7.2548:00001000 129.250.6.0 129.250.6.1---129.250.6.2549:00001001 129.250.9.0 129.250.9.1---129.250.9.25410:00001010 129.250.10.0 129.250.10.1---129.250.10.25411:00001011 129.250.11.0 129.250.11.1---129.250.11.25412:00001100 129.250.12.0 129.250.12.1---129.250.12.25413:00001101 129.250.13.0 129.250.13.1---129.250.13.25414:00001110 129.250.14.0 129.250.14.1---129.250.14.25415:00001111 129.250.15.0 129.250.15.1---129.250.15.25416:00010000 129.250.16.0 129.250.16.1---129.250.16.254【3】试找出可产生以下数目的A类子网的子网掩码(采用连续掩码)(1)2,(2)6,(3)20,(4)62,(5)122,(6)250答:(3)20+2=22<25(加2即将不能作为子网号的全1和全0的两种,所以子网号占用5bit,所以网络号加子网号共13bit,子网掩码为前13个1后19个0,即255.246.0.0。

S F 01(数)Ch 18 隐函数定理及其应用计 6 时231Ch 18 隐函数定理及其应用 ( 6 时 )§ 1 隐函数 ( 2 时 )一. 隐函数概念:隐函数是表达函数的又一种方法.1. 隐函数及其几何意义: 以0),(=y x F 为例作介绍.2.隐函数的两个问题: ⅰ> 隐函数的存在性; ⅱ> 隐函数的解析性质.二. 隐函数存在条件的直观意义:三. 隐函数定理:Th 1 ( 隐函数存在唯一性定理 ) 若满足下列条件:ⅰ> 函数),(y x F 在以),(000y x P 为内点的某一区域D 2R ⊂上连续 ; ⅱ> ),(00y x F 0=; ( 通常称这一条件为初始条件 ) ⅲ> 在D 内存在连续的偏导数),(y x F y ; ⅳ> ),(00y x F y 0=/.则在点0P 的某邻域 (0P )⊂D 内 , 方程0),(=y x F 唯一地确定一个定义在某区间) , (00αα+-x x 内的隐函数)(x f y =, 使得⑴ )(00y x f =,∈x ) , (00αα+-x x 时()∈)( , x f x (0P )且()0)( , ≡x f x F . ⑵ 函数)(x f 在区间) , (00αα+-x x 内连续 . ( 证 )四. 隐函数可微性定理:Th 2 设函数),(y x F 满足隐函数存在唯一性定理的条件 , 又设在D 内),(y x F x 存在且连续 . 则隐函数)(x f y =在区间) , (00αα+-x x 内可导 , 且232),(),()(y x F y x F x f y x -='. ( 证 )例 1 验证方程0sin 21),(=--=y x y y x F 在点) 0 , 0 (满足隐函数存在唯一性定理的条件 , 并求隐函数的导数 . [1]P 194 E1 例2 2221x y z -=. 其中)(x f y =为由方程0333=-+axy y x 所确定的隐函数 . 求dxdz . [1]P 195 E2 ( 仿 )例3 ( 反函数存在性及其导数 ) 设函数)(x f y =在点0x 的某邻域内有连续的导函数)(x f ', 且00)(y x f =, 0)(0≠'x f . 用隐函数定理验证存在反函数 , 并求反函数的导数. [1]P 196 E4五. n 元隐函数: [1]P 194 Th3例40),,(323=-++=z y x xyzz y x F . 验证在点) 0 , 0 , 0 (存在z 是),(y x的隐函数 , 并求偏导数 . [1]P 196 E3Ex [1]P 197 1,2,3⑴—⑶,4,5.(4和5题只求一阶偏导数 )§ 2 隐函数组 ( 2 时 )一. 隐函数组:从四个未知数两个方程的方程组⎩⎨⎧=++++=++++.0 , 022********e y d x c v b u a e y d x c v b u a入手介绍隐函数组 ,一般形式为 ⎩⎨⎧==.0),,,(, 0),,,(v u y x G v u y x F *)二. 隐函数组定理:分析从上述线性方程组中解出 u 和v 的条件入手 , 对方程组*)在一定条件下拟233线性化 , 分析可解出u 和v 的条件 , 得出以下定理 .Th 1 ( 隐函数组定理 ) [1]P 199 Th 4.关于Jacobi .例1 [1]P 200 E 1.三. 反函数组和坐标变换:1. 反函数组存在定理:Th 2 (反函数组定理 ) [1]P 202 Th 52.坐标变换: 两个重要的坐标变换.例2 , 3 [1]P 203—204 E 2 , 3 .Ex [1]P 205 1,2,3,5⑵.§ 3几何应用 ( 1 时 )一. 平面曲线的切线与法线 : 设平面曲线方程为0),(=y x F . 有yx F F x f -=')(.切线方程为 ),(00y x F x +-)(0x x ),(00y x F y 0)(0=-y y , 法线方程为 ),(00y x F y --)(0x x ),(00y x F x 0)(0=-y y .例1 求Descartes 叶形线 09)(233=-+xy y x 在点) 1 , 2 (处的切线和法线 . [1]P 207 E 1.二. 空间曲线的切线与法平面 :1.曲线由参数式给出 : βαχ≤≤===t t z z t y y t x L , )( , )( , )( : .234切线的方向数与方向余弦. 切线方程为)()()(000000t z z z t y y y t x x '-='-='-χ.法平面方程为 0))(())(())((000000=-'+-'+-'z z t z y y t y x x t χ.2. 曲线由两面交线式给出 : 设曲线L 的方程为 ⎩⎨⎧==.0),,( , 0),,(z y x G z y x F 点),,(0000z y x P 在L 上. 推导切线公式. [1]P 209.切线方程为),(),(),(),(),(),(000P P P y x G F z z x z G F y y z y G F x x ∂∂-=∂∂-=∂∂-.法平面方程为0)(),(),()(),(),()(),(),(0000=-∂∂+-∂∂+-∂∂z z y x G F y y x z G F x x z y G F P P P .例2 [1]P 210 E2 .三. 曲面的切平面与法线 :设曲面∑的方程为0),,(=z y x F , 点),,(0000z y x P 在∑上. 推导切面公式. [1]P 211. 切平面方程为 0))(())(())((000000=-+-+-z z P F y y P F x x P F z y x .法定义域线方程为 )()()(000000P F z z P F y y P F x x z y x -=-=-.例3 [1]P 211 E3 .Ex [1]P 212 1—6 .§ 3条件极值 ( 1 时 )一.条件极值问题 : 先提出下例:例 要设计一个容积为V 的长方体形开口水箱 . 确定长、宽和高 , 使水箱的235表面积最小 .分别以x 、y 和z 表示水箱的长、宽和高 , 该例可表述为 : 在约束条件V xyz =之下求函数xy yz xz z y x S ++=)(2),,(的最小值 .条件极值问题的一般陈述 .二. 条件极值点的必要条件 :设在约束条件0),(=y x ϕ之下求函数=z ),(y x f 的极值 . 当满足约束条件 的点),(00y x 是函数),(y x f 的条件极值点 , 且在该点函数),(y x ϕ满足隐函数存在条件时, 由方程0),(=y x ϕ决定隐函数)(x g y =, 于是点0x 就是一元函数())( , x g x f z =的 极限点 , 有0)(='+=x g f f d xd z y x .代入 ),(),()(00000y x y x x g y x ϕϕ-=', 就有0),(),(),(),(00000000=-y x y x y x f y x f y x y x ϕϕ,( 以下x f 、y f 、x ϕ、y ϕ均表示相应偏导数在点),(00y x 的值 . ) 即 x f y ϕ—y f x ϕ0= , 亦即 (x f , y f ) (⋅y ϕ ,x ϕ-)0= .可见向量(x f , y f )与向量(y ϕ , x ϕ-)正交. 注意到向量(x ϕ , y ϕ)也与向量(y ϕ , x ϕ-)正交, 即得向量(x f , y f )与向量(x ϕ , y ϕ)线性相关, 即存在实数λ,使(x f , y f ) + λ(x ϕ , y ϕ)0=.236亦即 ⎩⎨⎧=+=+., 0y y x x f f λϕλϕ二. Lagrange 乘数法 :由上述讨论可见 , 函数=z ),(y x f 在约束条件0),(=y x ϕ之下的条件极值点应是方程组 ⎪⎩⎪⎨⎧==+=+.0),(, 0),(),(, 0),(),(y x y x y x f y x y x f y y x x ϕλϕλϕ 的解.倘引进所谓Lagrange 函数),(),(),,(y x y x f y x L λϕλ+=,( 称其中的实数λ为Lagrange 乘数 )则上述方程组即为方程组⎪⎩⎪⎨⎧===.0),,( , 0),,( , 0),,(λλλλy x L y x L y x L y x以三元函数 , 两个约束条件为例介绍Lagrange 乘数法的一般情况 .四. 用Lagrange 乘数法解应用问题举例 :例1 求容积为V 的长方体形开口水箱的最小表面积 . [1]P 216 E1例2 抛物面z y x =+22被平面1=++z y x 截成一个椭圆. 求该椭圆到坐标原点的最长和最短距离 . [1]P 217 E2例3 求函数xyz z y x f =),,(在条件)0,0,0,0( 1111>>>>=++r z y x rz y x下的极小值 . 并证明不等式 311113a b c c b a ≤⎪⎭⎫⎝⎛++- , 其中 c b a , , 为任意正常数 . [1]P 218 E3Ex [1]P 220 1⑴⑶, 2,3 .。


第十八章市场营销的新领域与新概念(一)单项选择题(在下列每小题中,选择一个最合适的答案。
)1、实施绿色营销的企业,对产品的创意、设计和生产,以及定价与促销的策划和实施,都要以_________为前提,力求减少和避免环境污染,保护和节约自然资源,维护人类社会的长远利益。
A.企业盈利B.企业经营目标C.保护生态环境D.满足股东利益2、20世纪90年代以来,一方面由于产品的同质化日益增强,另一方面是消费者的个性化、多样化日益发展,于是日渐兴起的4C观念,更新和强化了以_________为中心的营销组合。
A.沟通B.宣传C.消费者需求D.质量3、5R较4C更突出顾客的核心地位,营销的核心从交易走向_________。
A.交换B.销售C.关系D.需求4、当营销执行的结果偏离预期目标,或是执行中遇到较大阻力时,需确定问题的症结所在并寻求对策时,需运用_________。
A.营销贯彻技能B.营销诊断技能C.问题评定技能D.结果评价技能5、关系营销将建立与发展同所有利益相关者之间的关系作为企业营销的_________。
A.关键变量B.次要工作C.间接任务D.辅助工作6、_________要求建立专门的部门,用以追踪各利益相关者的态度。
A.绿色营销B.关系营销C.整合营销D.生态营销7、关系营销把一切内部和外部利益相关者都纳入研究范围,用系统的方法考察企业所有活动及其相互关系,表现积极的一方被称为_________,表现不积极的一方被称作目标公众。
A.经纪人B.信息传播者C.市场营销者D.中间商8、关系营销更为注意的是_________。
A.摇摆不定的顾客B.争取新顾客C.维系现有顾客D.以上全部答案9、_________是企业营销部门与其他职能部门之间、企业与外部环境之间联系沟通和协调行动的专门机构。
A.关系管理机构B.人事部门C.广告部门D.宣传部门10、建立营销道德最根本的还是确立并实施_________。
第十八章常用综合评价方法一、教学大纲要求(一)掌握内容综合评价的意义及一般步骤。
(二)熟悉内容评价指标的筛选及权重的估计。
(三)了解内容1.综合评分法。
2.综合指数法。
3.层次分析法。
4.Topsis法。
二、教学内容精要(一)评价与综合评价评价:通过对照某些标准来判断观测结果,并赋予这些结果以一定的意义和价值的过程称为评价(evaluation)。
综合评价:根据一个复杂系统同时受到多种因素影响的特点,在综合考察多个有关因素时,依据多个有关指标对复杂系统进行总评价的方法称为综合评价(synthetical evaluation)。
(二)综合评价的几种分类1.根据评价手段:定量评价(quantitative evaluation)、定性评价(qualitive evaluation)。
2.根据评价领域:临床评价(clinical evaluation)、卫生评价(health evaluation)和管理评价(administrative evaluation)。
临床评价包括诊断性试验和方法评价、疗效评价和预后及转归评价。
卫生评价包括环境评价、营养评价、生长发育评价和疾病防治效果评价。
管理评价包括宏观管理评价和微观管理评价。
3.根据评价方式:预评价(pre-event evaluation)、中期评价(medial evaluation)和终结评价(after-event evaluation)。
(三)综合评价的一般步骤1.根据评价目的选择恰当的评价指标(index);2.根据评价目的,确定诸评价指标在对某事物评价中的相对重要性,或各指标的权重(weight);3.合理确定各单个指标的评级等级(evaluation grade)及其界限;4.根据评价目的,数据特征,选择适当的综合评价方法,并根据已掌握的历史资料,建立综合评价模型(evaluation model);5.确定多指标综合评价的等级数量界限,在对同类事物综合评价的应用实践中,对选用的评价模型进行考察,并不断修改补充,使之具有一定的科学性、实用性与先进性,然后推广应用。
(四)评价指标的筛选筛选评价指标主要依据专业知识,即根据有关的专业理论和实践,来分析各评价指标对结果的影响,挑选那些代表性、确定性好,有一定区别能力又互相独立的指标组成评价指标体系。
系统分析法(system’s analys is method)和文献资料分析优选法是常用的评价指标筛选法。
为保证筛选指标的客观性,对于指标的初选可采用假设检验、多元回归、逐步回归和指标聚类等方法辅助筛选。
在实际工作中,往往综合使用多种方法进行指标筛选,在获得较为满意的专业解释的基础上,优先考虑那些被多种方法同时选入的指标。
(五)评价指标的权重估计用于确定指标权重的方法主要有主观定权法和客观定权法。
其中,主观定权法包括专家评分法(specialist-scored method)、成对比较法、Satty权重法;客观定权法包括模糊定权法、秩和比法、熵权法和相关系数法。
(六)几种综合评价方法1.综合评分法(synthetical scored method):建立在专家评价法基础上,根据评价目的及评价对象的特征选定必要的评价指标,逐个指标订出等级,每个等级的标准用分值表示,然后以恰当的方式确定各评价指标的权数,并选定累积总分的方案以及综合评价等级的总分值范围,以此为准则,对评级对象进行分析和评价,以决定优劣取舍的综合评价方法。
2.综合指数法(synthetical index method):利用综合指数的计算形式,定量的对某现象进行综合评价的方法。
3.层次分析法(analytic hierarchy process):用系统分析的方法,对评价对象依评价目的所确定的总评价目标进行连续性分解,得到各级(各层)评价目标,并以最下层作为衡量目标达到程度的评价指标。
然后依据这些指标计算出一综合评分指数对评价对象的总评价目标进行评价,依其大小来确定评价对象的优劣等级。
4.Topsis法:系统工程中有限方案多目标决策分析的一种常用方法。
是基于归一化后的原始数据矩阵,找出有限方案中的最优方案和最劣方案(分别用最优向量和最劣向量表示),然后分别计算诸评价对象与最优方案和最劣方案的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。
三、典型试题分析某医院1998年11项指标资料见表18-1和表18-2,试采用综合指数法计算各月综合指数。
表18-1 11项指标分类指标类型 序号 指标名称动态指标 1 出院病人数(人) 医疗质量 2 治疗有效率(%) 3 病死率(%)4 无菌手术感染数(人) 床位利用5 平均住院日(天)6 床位周转率(%)7 病床工作日(天)8 病床使用率(%)诊断水平 9 门诊住院诊断符合率(%)10 出入院诊断符合率(%) 护理服务质量11陪住率(%)表18-2 某医院1998年各月11项指标实际值月各指标实际值1 2345678910 11 1 650 90.8 3.08 3.00 20.6 1.41 28.7 92.6 99.3 100 18.0 2 560 91.1 3.04 4.00 21.6 1.24 28.7 92.7 98.6 100 17.6 3 609 91.7 1.97 4.00 20.5 1.33 27.3 97.6 98.0 99 17.0 4 587 92.7 2.39 3.00 25.6 1.25 30.0 96.9 98.3 96 17.1 5 651 88.0 4.304.00 23.31.30 28.3 94.5 97.3 97 18.0 6 601 89.72.50 10.00 19.8 1.30 29.3 94.6 97.9 96 17.0 7 584 90.0 2.91 5.00 26.3 1.30 28.0 93.2 96.9 97 18.0 8 620 90.7 2.90 2.00 22.0 1.37 28.7 92.5 97.9 96 19.0 9 626 90.2 2.244.00 22.0 1.37 29.2 94.3 98.3 98 18.0 10 604 91.9 2.965.00 20.6 1.34 27.9 93.1 99.1 99 18.5 11 653 90.5 3.37 2.00 19.5 1.44 29.4 94.8 99.5 99 21.0 12 599 90.8 3.64 5.00 23.5 1.29 28.7 95.8 89.1 99 18.8 平均值61290.7 2.944.25 22.11.33 28.7 94.4 97.59818.2[评析] 11项指标中3、4、5、11号指标为反向指标,其它均为正向指标。
由公式 (18-1)和公式(18-2)可计算出各指标的个体指数,计算结果见表18-3。
MXy =(高优指标或正指标) (18-1) XMy =(低优指标或负指标) (18-2) 如公式(18-1)和公式(18-2)所示,个体指数是某指标观测值和标准值的比值。
式中X 为某指标的观测值;M 为某指标的标准值、参考值、平均值、期望值等。
表18-3 某医院1998年各月11项指标的个体指数月 各指标的个体指数 1 2 3 4 5 6 7 8 9 10 11 1 1.06 1.00 0.96 1.42 1.07 1.06 1.00 0.98 1.02 1.02 1.01 2 0.91 1.00 0.97 1.06 1.02 0.93 1.00 0.98 1.01 1.02 1.03 3 1.00 1.01 1.49 1.06 1.08 1.00 0.95 1.03 1.00 1.01 1.07 4 0.96 1.02 1.23 1.42 0.86 0.94 1.05 1.03 1.01 0.98 1.06 5 1.06 0.97 0.68 1.06 0.95 0.98 0.99 1.00 1.00 0.99 1.01 6 0.98 0.99 1.18 0.42 1.12 0.98 1.02 1.00 1.00 0.98 1.07 7 0.95 0.99 1.01 0.85 0.84 0.98 0.98 0.99 0.99 0.99 1.01 8 1.01 1.00 1.01 2.13 1.00 1.03 1.00 0.98 1.00 0.98 0.95 9 1.02 0.99 1.31 1.06 1.00 1.03 1.02 1.00 1.01 1.00 1.01 10 11 120.99 1.07 0.981.01 1.00 1.000.99 0.87 0.810.85 1.07 1.01 0.97 0.99 1.02 1.01 0.98 2.12 1.13 1.08 1.02 1.00 1.02 1.01 0.87 0.850.94 0.97 1.001.01 0.91 1.01 0.97按同类指数相乘,异类相加的方法进行指数综合。
由公式(18 - 3)计算综合指数。
∑∏===mi nj ij y I 11(18-3)例如计算1、2月份的综合指数为:01.102.102.198.000.106.107.142.196.000.106.11+⨯+⨯⨯⨯+⨯⨯+=I 5851.5=03.102.101.198.000.193.002.106.197.000.191.02+⨯+⨯⨯⨯+⨯⨯+=I 9509.4=其余各月计算以次类推,计算结果见表18-4。
表18-4 某医院1998年各月综合指数份 1 2 3 4 5 6 7 8 9 10 11 12 指数5.5851 4.9509 5.7462 5.6642 4.6833 4.6476 4.59296.1251 5.4824 4.8934 6.0795 4.4838四、习 题(一)单项选择题:1.下列那项评价方法属于按评价手段的分类 A .定性评价 B .卫生评价 C .管理评价 D .中期评价2.使用专家评分法进行评价指标的估计时,常用哪两种指标来估计权重分配的相对合理性A .擅长系数和确定系数B .擅长系数和一致性系数C .相关系数和确定系数D .相关系数和一致性系数3.医院工作质量指标通常由三层子指标构成,以知第一层的权重为0.6370,第二层权重为0.2970,第三层权重为1.0。
由Saaty 法提供的评价指标组合权重方法可知第三层的组合权重为A .1.9340B .0.9340C .1.7636D .0.18924.以下哪一种综合评价方法是建立在专家评价法的基础上 A .综合指数法 B .层次分析法 C .综合评分法 D .Topsis 法5.在利用综合指数法评价时,综合指数能定量地反映几个指标的综合平均变动程度,表达式为:∑=my n I 11,其中A .m 为分组数B .n 为指标数C .y 为个体指标D .以上均正确(二)计算题试根据表18 - 5数据,采用Topsis 法对某市人民医院1995~1997年的医疗质量进行综合评价。