高考数学填空题限时练四

卜人入州八九几市潮王学校牌中高三选择填空限时训练四〔45分钟〕一、选择题：本大题一一共10小题，每一小题5分，一共50分。

在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的。

1、全集U ＝R ，集合}2{2x x y x A -==，}R ,2{∈==x y y B x ，那么=B A C R )(〔〕A ．{}2x x >B ．{}01x x <≤C ．{12}x x <≤D ．{}0x x <2、复数2izx i+=-为纯虚数，其中i 虚数单位，那么实数x 的值是 〔〕〔A 〕－12〔B 〕12〔C 〕2〔D 〕1 3、2≠x 或者3≠y 5≠+y x ，那么甲是乙的()A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分条件也不必要条件 4、如右图，是一程序框图，那么输出结果为〔〕〔A)94(B 〕1110〔C 〕136〔D 〕115 5、等差数列n a n 的前}{项和为m S a a a m S m m m m n 则且若,38,0,1,12211==-+>-+-等于〔〕A ．10B ．20C ．38D ．9 6、假设函数3cos(2)y x ϕ=+的图象关于点4(,0)3π中心对称，那么||ϕ的最小值为 〔〕A ．6πB ．4π C ．3π D ．2π 7、用8个数字1,1,2,2,3,3,4,4可以组成不同的四位数个数是〔〕 A ．168B.180 C.204D.4568、双曲线M ：22221x y a b -=和双曲线：22221y x a b-=，其中b ＞a ＞0，且双曲线M 与N 的交点在两坐标轴上的射影恰好是两双曲线的焦点，那么双曲线M 的离心率为〔〕A 、215+B 、215-C 、235+D 、253- 9、O 是锐角ABC ∆内一点，满足||||||OC OB OA ==，且 30=∠A OA m AC BCAB C B 2sin cos sin cos =， 那么实数=mA ．23-B ．23C ．21-D ．3〔〕10、定义域为R 的偶函数)(x f 满足对x R ∀∈，有)1()()2(f x f x f -=+，且当]3,2[∈x 时，18122)(2-+-=x x x f ，假设函数)1|(|log )(+-=x x f y a 在),0(+∞上至少有三个零点，那么a 的取值范围是〔〕A ．)22,0(B ．)33,0(C ．)55,0(D ．)66,0( 二、填空题:本大题一一共7小题,每一小题4分,一共28分。

5．
6．
7．
8．选修4－2（矩阵与变换）
解：设M= ，由题意得，Me1= λ1e1，Me2= λ1e2………………………………1分
∴ = = 8 ， ①………………3分
∴ = = 2 ， ②………………5分
联立①②解得a=6，b=2，c=4，d=4.
∴M= ……………………………………………………………………………7分
【参考答案】***试卷处理标记，请不要删除
评卷人
得分
一、填空题
1．理0，文1；
2．
评卷人
得分
二、解答题
3．
4．选修4—2：矩阵与变换
本小题主要考查二阶矩阵的变换等基础知识，考查运算求解能力．满分10分．
解：设变换T： ，则 ，即 …………………………5分
代入直线 ，得 ．
将点 代入上式，得k 4．……………………………………………………………10分
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃，匠心巨制！独家原创，欢迎下载！
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1．若行列式 ，则 ________
2．若矩阵 满足： 且 ，则这样的互不相等的矩阵共有＿＿＿＿＿＿个.
6．变换 是绕坐标原点逆时针旋转 的旋转变换，求曲线 在变换 作用下所得的曲线方程。
7．已知二阶矩阵A的属于特征值－1的一个特征向量为 ，属于特征值3的一个特征向量为 ，求矩阵A．
8．已知矩阵M有特征值λ1=8及对应的一个特征向量e1= ，并有特征值λ2=2及对应的一个特征向量e2= ，试确定矩阵M，并求出M的逆矩阵。评人得分二、解答题

高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃，匠心巨制！独家原创，欢迎下载！
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上 评卷人
得分 一、填空题
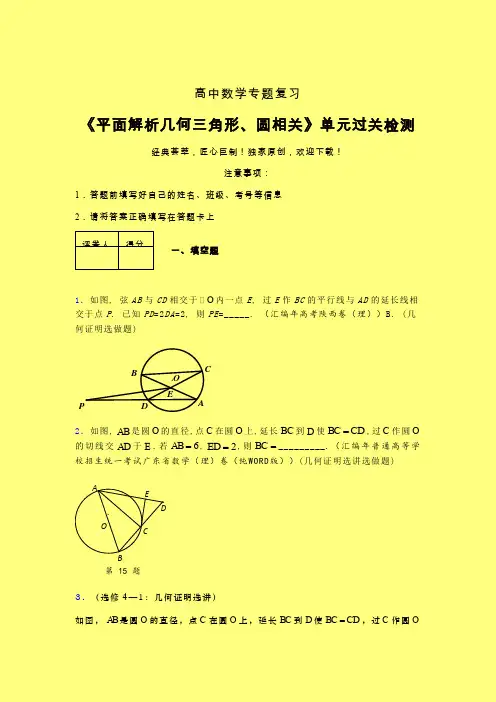
1．如图, 弦AB 与CD 相交于
O 内一点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知PD =2DA =2, 则PE =_____. （汇编年高考陕西卷（理））B. (几
何证明选做题) E
D O
P A B C
2．如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.（汇编年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））(几何证明选讲选做题)
3．（选修4—1：几何证明选讲）
如图，AB 是圆O 的直径，点C 在圆O 上，延长BC 到D 使BC CD =，过C 作圆O .
A
E D
C
B
O 第15题。

数学PA高考数学客观题训练【6套】选择、填空题专题练习（一）1．已知全集U=R ，集合)(},021|{},1|{N M C x x x N x x M U则≥-+=≥=（ ）A ．{x |x <2}B ．{x |x ≤2}C ．{x |－1<x ≤2}D ．{x |－1≤x <2}2．设,0,0<>b a 已知),(a b m ∈且0≠m ，则m1的取值范围是： ( )A ．)1,1(a b B.)1,1(b a C.)1,0()0,1(a b ⋃ D.),1()1,(+∞⋃-∞ab 3．设)(x f '是函数)(x f 的导函数,)(x f y '=的图象如图所示，则)(x f y =的图象最有可能的是4．直线052)3(057)3()1(2=-+-=-+-++yx m m y m x m 与直线垂直的充要条件是（ ）A ．2-=mB ．3=mC ．31=-=m m 或D ．23-==m m 或5．命题“042,2≤+-∈∀x x R x ”的否定为 （ ）(A) 042,2≥+-∈∀x x R x (B) 042,2>+-∈∃x x R x (C)042,2≤+-∉∀x x R x (D) 042,2>+-∉∃x x R x6. 若平面四边形ABCD 满足0AB CD +=,()0AB AD AC -⋅=,则该四边形一定是A ．直角梯形B ．矩形C ．菱形D ．正方形7．有一棱长为a 的正方体框架，其内放置一气球，是其充气且尽可能地膨胀（仍保持为球的形状），则气球表面积的最大值为 A ．2a πB ．22a πC ．32a πD ．42a π8．若22πβαπ<<<-，则βα-一定不属于的区间是 ( )A ．()ππ,- B ．⎪⎭⎫⎝⎛-2,2ππ C ．()π,0 D ． ()0,π-9．等差数列{a n } 中，a 3 =2，则该数列的前5项的和为( ) A ．10 B ．16C ． 20D ．3210．不等式10x x->成立的充分不必要条件是 A ．10x -<<或1x > B ．1x <-或01x << C ．1x >-D ．1x >二、填空题 （每题5分，满分20分，请将答案填写在题中横线上） 11. 线性回归方程ˆybx a =+必过的定点坐标是________. 12. .在如下程序框图中，已知：x xe x f =)(0，则输出的是__________.13. 如图，一个粒子在第一象限运动，在第一秒末，它从原点运 动到（0，1），接着它按如图所示的x 轴、y 轴的平行方向来 回运动，（即（0，0）→（0，1）→（1，1）→（1，0）→ （2，0）→…），且每秒移动一个单位，那么第2008秒末这 个粒子所处的位置的坐标为______。

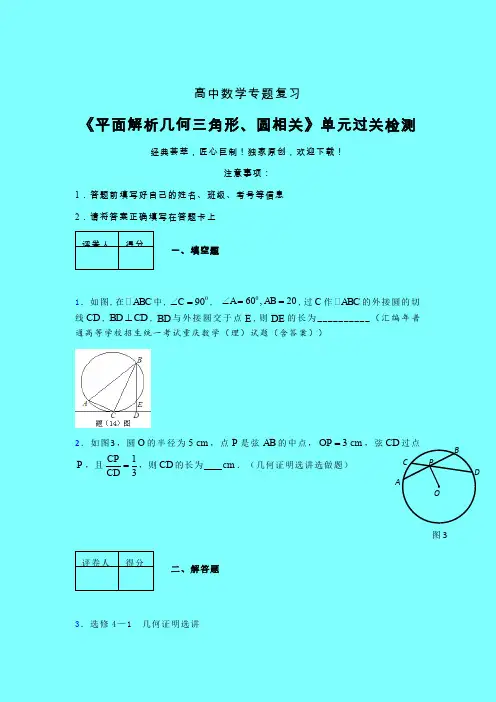
高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上 评卷人得分一、填空题1．如图,在ABC 中,090C ∠=, 060,20A AB ∠==,过C 作ABC 的外接圆的切线CD ,BD CD ⊥,BD 与外接圆交于点E ,则DE 的长为__________（汇编年普通高等学校招生统一考试重庆数学（理）试题（含答案））2．如图3，圆O 的半径为5cm ，点P 是弦AB 的中点，3OP =cm ，弦CD 过点P ，且13CP CD =，则CD 的长为 cm ．（几何证明选讲选做题）评卷人得分二、解答题3．选修4—1 几何证明选讲P OAB C D图3如图，已知⊙O 的半径为1，MN 是⊙O 的直径，过M 点作⊙O 的切线AM ，C 是AM 的中点，AN 交⊙O 于B 点，若四边形BCON 是平行四边形.求AM 的长；4．如图，圆1O 与圆2O 内切于点A ，其半径分别为1r 与212()r r r >， 圆1O 的弦AB 交圆2O 于点C （1O 不在AB 上）， 求证：:AB AC 为定值。

证明：由弦切角定理可得11212,O B r AB AO CAO B AC O C r∴== 5．过圆O 外一点A 作圆O 的两条切线AT 、AS ，切点分别为T 、S ，过点A 作圆O 的割线APN ，证明：22AT PT PSAN NT NS=．[来源:学科网ZXXK] (汇编年3月苏、锡、常、镇四市高三数学教学情况调查一) 证明：AT 是圆O 的切线，∠ATP =∠ANT ,又∠TAP =∠NAT ,∴三角形ATP 与三角形ANT ，∴AT PT AN TN =同理AS PSAN NS= 两等式相乘222,AT AS PT PSAT PT PS AT AS AN NT NSAN NT NS∙∙∙==∴=∙∙. 6．已知：如图，在△ABC 中，∠ABC ＝90°，O 是AB 上一点，以O 为圆心，OB 为半径的圆与AB 交于点E，与21-A 第图AC 切于点D ，连结DB 、DE 、OC 。

高三二轮复习选填满分“8+4+4”小题强化训练(4)一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合2{|320}A x x x =-+-≤，3{|log (2)1}B x x =+<，则A B = （）A．∅B．{1x x ≤或}2x ≥C．{}1x x <D．{}21x x -<<2.若复数312iz =-（i 为虚数单位），则复数z 在复平面上对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限3.下列函数中，最小值为4的是（）A.4y x x=+B.()4sin 0πsin y x x x=+<<C.e 4e x xy -=+ D.y =4.若函数()2f x +为偶函数，对任意的[12,2,+)x x ∈∞，且12x x ≠，都有()()()12120x x f x f x ⎡⎤--<⎣⎦，则（）A．()()212log 60log 0.2f f f ⎛⎫<< ⎪⎝⎭B．()()122log 0.20log 6f f f ⎛⎫<< ⎪⎝⎭C．()()122log 0.2log 60f f f ⎛⎫<< ⎪⎝⎭D．()()2120log 6log 0.2f f f ⎛⎫<< ⎪⎝⎭5.已知某电子产品电池充满时的电量为3000毫安时，且在待机状态下有两种不同的耗电模式可供选择．模式A ：电量呈线性衰减，每小时耗电300毫安时；模式B ：电量呈指数衰减，即：从当前时刻算起，t 小时后的电量为当前电量的12t 倍．现使该电子产品处于满电量待机状态时开启A 模式，并在m 小时后切换为B 模式，若使其在待机10小时后有超过5%的电量，则m 的取值范围是（）A．(5，6)B．(6，7)C．(7，8)D．(8，9)6.已知正项等比数列{}n a 满足2022202120202a a a =+，若215log a +是2log m a 和2log n a 的等差中项，则9n mmn+的最小值为（）A．43B．138C．85D．34217.《九章算术》中记载，堑堵是底面为直角三角形的直三棱柱，阳马指底面为矩形，一侧棱垂直于底面的四棱锥.如图，在堑堵111ABC A B C -中，AC BC ⊥，12AA =，当阳马11B ACC A -体积的最大值为43时，堑堵111ABC A B C -的外接球的体积为（）A．4π3B．82π3C．32π38.已知ln 22ln a a =，ln 33ln b b =，ln 55ln c c =，且(),,0,e ∈a b c 则（）A．c ＜a ＜bB．a ＜c ＜bC．b ＜a ＜cD．b ＜c ＜a二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求,全部选对的得5分，有选错的得0分，部分选对的得3分．9.已知()831f x x x ⎛⎫=- ⎪⎝⎭，则（）A.()f x 的展开式中的常数项是56B.()f x 的展开式中的各项系数之和为0C.()f x 的展开式中的二项式系数最大值是70D.()f x 的展开式中不含4x 的项10.已知某物体作简谐运动，位移函数为()2sin()(0,)2f t t t πϕϕ=+><，且4()23f π=-，则下列说法正确的是（）A.该简谐运动的初相为6πB.函数()f t 在区间0,2π⎛⎫⎪⎝⎭上单调递增C.若[0,]2t π∈，则(),2[]1f t ∈D.若对于任意12,0t t >，12t t ≠，都有12()()f t f t =，则12()2f t t +=11.已知正三棱锥S ABC -的底面边长为6，侧棱长为则下列说法中正确的有（）A.侧棱SA 与底面ABC 所成的角为4πB.侧面SAB 与底面ABC 所成角的正切值为C.正三棱锥S ABC -外接球的表面积为64πD.正三棱锥S ABC -内切球的半径为1-12.关于函数()sin x f x e x =+，(),x ππ∈-.下列说法正确的是（）A.()f x 在()()0,0f 处的切线方程为210x y -+=B.()f x 有两个零点C.()f x 有两个极值点D.()f x 存在唯一极小值点0x ，且()010f x -<<三、填空题：本题共4小题，每小题5分，多空题，第一空2分，第二空3分，共20分．13.已知随机变量ξ服从正态分布()2,N μσ，若函数()()1f x P x x ξ=≤≤+为偶函数，则μ=_______.14.为调查新冠疫苗的接种情况，需从5名志愿者中选取3人到3个社区进行走访调查，每个社区一人．若甲乙两人至少有一人入选，则不同的选派方法有_____________.15.数列{}n a 的各项均为正数，其前n 项和n S 满足112n n n S a a ⎛⎫=+ ⎪⎝⎭.则n a =__________.16.椭圆的光学性质，从椭圆一个焦点发出的光，经过椭圆反射后，反射光线都汇聚到椭圆的另一个焦点上.已知椭圆C ：()2221024x y b b+=<<，1F ，2F 为其左､右焦点.M 是C 上的动点，点(N ，若1MN MF +的最大值为6.动直线l 为此椭圆C 的切线，右焦点2F 关于直线l 的对称点()11,P x y ，113424S x y =+-，则：（1）椭圆C 的离心率为___________；（2）S 的取值范围为___________.高三二轮复习选填满分“8+4+4”小题强化训练(4)一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合2{|320}A x x x =-+-≤，3{|log (2)1}B x x =+<，则A B = （）A．∅B．{1x x ≤或}2x ≥C．{}1x x <D．{}21x x -<<【答案】D【解析】()()22320,32120x x x x x x -+-≤-+=--≥，解得1x ≤或2x ≥，所以{|1A x x =≤或}2x ≥.由3log y x =在()0,∞+上递增，且()33log 21log 3x +<=，所以023,21x x <+<-<<，所以{}|21B x x =-<<，所以{}21A B x x ⋂=-<<，故选：D 2.若复数312iz =-（i 为虚数单位），则复数z 在复平面上对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】由题意可知：()()3112i 2i 21i 2i 2i 2i 2i 555z --=====--++-，所以复数z 在复平面上对应的点为21,55⎛⎫- ⎪⎝⎭.位于第四象限.故选:D.3.下列函数中，最小值为4的是（）A.4y x x =+B.()4sin 0πsin y x x x=+<<C.e 4e x x y -=+D.y =【答案】C【解析】A 项，4y x x=+没有最值，故A 项错误；B 项，令sin t x =，则01t <≤，4y t t=+，由于函数在(]0,1上是减函数，所以min ()(1)5f x f ==，故B 项错误；C 项，4e 4e e 4e x x x x y -=+=+≥=，当且仅当4e e x x =，即e 2x =时，等号成立，所以函数e 4e x x y -=+的最小值为4，故C 项正确；D 项，y =≥，当且仅当==时，等号成立，所以函数y =+的最小值为，故D 项错误．故选：C．4.若函数()2f x +为偶函数，对任意的[12,2,+)x x ∈∞，且12x x ≠，都有()()()12120x x f x f x ⎡⎤--<⎣⎦，则（）A．()()212log 60log 0.2f f f ⎛⎫<< ⎪⎝⎭B．()()122log 0.20log 6f f f ⎛⎫<< ⎪⎝⎭C．()()122log 0.2log 60f f f ⎛⎫<< ⎪⎝⎭D．()()2120log 6log 0.2f f f ⎛⎫<< ⎪⎝⎭【答案】D【解析】由题意知函数()2f x +为偶函数，故函数()f x 关于直线=2x 对称，由对任意的[12,2,+)x x ∈∞，且12x x ≠，都有()()()12120x x f x f x ⎡⎤--<⎣⎦，可知函数()f x 在[2,+)x ∈∞时单调递减，而()()1220(4),log 0.52log f f f f ⎛⎫== ⎪⎝⎭，因为2252<log log 64<<，故()()2120(4)log 6log 0.2f f f f ⎛⎫=<< ⎪⎝⎭，故选：D5.已知某电子产品电池充满时的电量为3000毫安时，且在待机状态下有两种不同的耗电模式可供选择．模式A ：电量呈线性衰减，每小时耗电300毫安时；模式B ：电量呈指数衰减，即：从当前时刻算起，t 小时后的电量为当前电量的12t 倍．现使该电子产品处于满电量待机状态时开启A 模式，并在m 小时后切换为B 模式，若使其在待机10小时后有超过5%的电量，则m 的取值范围是（）A．(5，6)B．(6，7)C．(7，8)D．(8，9)【答案】D【解析】由题意可设，模式A 的函数关系为：y ＝－300t ＋3000，模式B 的函数关系为：y ＝p ⋅12t ，其中p 为初始电量，在模式A 下使用m 小时，其电量为3000－300m ，在模式B 下使用10－m 小时，则可得到(3000－300m )⋅1210－m ＞3000⋅5%，可化为2m －10(10－m )＞12，令x ＝10－m ，可得2－x ⋅x ＞12，即2x －1＜x ，可结合图形得到1＜x ＜2，即1＜10－m ＜2，解得8＜m ＜9，即m ∈(8，9)，故答案选D．6.已知正项等比数列{}n a 满足2022202120202a a a =+，若215log a +是2log m a 和2log n a 的等差中项，则9n mmn+的最小值为（）A．43B．138C．85D．3421【答案】A【解析】正项等比数列{}n a 满足2022202120202a a a =+，所以22q q =+，且0q >，解得2q =，又因为215log a +是2log m a 和2log n a 的等差中项，所以()212225log log log m n a a a +=+，得102222121log (2)log (2)m n a a +-=，即12m n +=，()9119191410101212123n m m n m n mn m n n m ⎛+⎛⎫⎛⎫=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝，当且仅当39n m ==时，等号成立.故选：A.7.《九章算术》中记载，堑堵是底面为直角三角形的直三棱柱，阳马指底面为矩形，一侧棱垂直于底面的四棱锥.如图，在堑堵111ABC A B C -中，AC BC ⊥，12AA =，当阳马11B ACC A -体积的最大值为43时，堑堵111ABC A B C -的外接球的体积为（）A．4π3B．π3C．32π3【答案】B【解析】由题意易得BC ⊥平面11ACC A ,所以()11222112113333B ACC A V BC AC AA BC AC BC AC AB -=⋅⋅=⋅≤+=,当且仅当AC BC =时等号成立,又阳马11B ACC A -体积的最大值为43,所以2AB =,所以堑堵111ABC A B C -的外接球的半径R =所以外接球的体积343V r π==,故选:B8.已知ln 22ln a a =，ln 33ln b b =，ln 55ln c c =，且(),,0,e ∈a b c 则（）A．c ＜a ＜b B．a ＜c ＜b C．b ＜a ＜c D．b ＜c ＜a【答案】A 【解析】由已知得ln 2ln 2a a =，ln 3ln 3b b=，ln ln 55c c =，令()()()ln 0e ，=∈x f x x x ，()21ln xf x x -'=，可得()f x 在()0e ，∈x 上单调递增，在()e ，+∈∞x 上单调递减，()()25lnln 5ln 23205210-=-=<f c f a ，且(),0,e ∈a c ，所以c a <，()()8lnln 2ln 390236-=-=<f a f b ，且(),0,e ∈a b ，所以a b <，所以c a b <<.故选：A.二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求,全部选对的得5分，有选错的得0分，部分选对的得3分．9.已知()831f x x x ⎛⎫=- ⎪⎝⎭，则（）A.()f x 的展开式中的常数项是56B.()f x 的展开式中的各项系数之和为0C.()f x 的展开式中的二项式系数最大值是70D.()f x 的展开式中不含4x 的项【答案】BC【解析】二项展开式通项公式为382441881()(1)rr rr r rr T C x C x x --+⎛⎫=-=- ⎪⎝⎭，2440r -=，6r =，常数项为6678(1)28T C =-=，A 错；2444r -=，=5r ，第6项是含4x 的项，D 错；令1x =得(1)0f =所有项系数和，B 正确；8n =，因此二项式系数的最大值为4870C =，C 正确．故选：BC．10.已知某物体作简谐运动，位移函数为()2sin()(0,)2f t t t πϕϕ=+><，且4()23f π=-，则下列说法正确的是（）A.该简谐运动的初相为6πB.函数()f t 在区间0,2π⎛⎫⎪⎝⎭上单调递增C.若[0,]2t π∈，则(),2[]1f t ∈D.若对于任意12,0t t >，12t t ≠，都有12()()f t f t =，则12()2f t t +=【答案】ACD【解析】因为()2sin()(0,)2f t t t πϕϕ=+><，且4()23f π=-，所以422sin 3πϕ⎛⎫-=+⎪⎝⎭，即432,32k k Z ππϕπ+=+∈，所以2,6k k Z πϕπ=+∈，因为2πϕ<，所以6π=ϕ所以()2sin 6f t t π⎛⎫=+ ⎪⎝⎭，所以对于A 选项，简谐运动的初相为6π，故正确；对于B 选项，函数()f t 在区间0,3π⎛⎫ ⎪⎝⎭上单调递增，,32ππ⎛⎫ ⎪⎝⎭上单调递减，故错误；对于C 选项，当0,2t π⎡⎤∈⎢⎥⎣⎦时，2,663t πππ⎡⎤+∈⎢⎥⎣⎦，所以sin sin sin 662t πππ⎛⎫≤+≤ ⎪⎝⎭，即1sin 126t π⎛⎫≤+≤ ⎪⎝⎭，所以(),2[]1f t ∈，故正确；对于D 选项，对于任意12,0t t >，12t t ≠，都有12()()f t f t =，则12,2t t k k Z ππ+=+∈，所以12()2f t t +=，故正确.故选：ACD11.已知正三棱锥S ABC -的底面边长为6，侧棱长为则下列说法中正确的有（）A.侧棱SA 与底面ABC 所成的角为4πB.侧面SAB 与底面ABC 所成角的正切值为C.正三棱锥S ABC -外接球的表面积为64πD.正三棱锥S ABC -1【答案】BC【解析】若,E F 分别是,BC AB 的中点，连接,AE SE ，易知AES ∠为侧棱SA 与底面ABC 所成角，由题设，SE =，AE =，SA =，则1cos2AES ∠==，∴3AES π∠=，故A 错误；若O 是底面中心，易知：SO ⊥面ABC ，连接OF 、SF ，则侧面SAB 与底面ABC 所成角为SFO ∠，又6SO =，OF =，则tan SFO ∠=B 正确.若外接球的半径为R ，则R ==，解得4R =，∴正三棱锥S ABC -外接球的表面积为2464R ππ=，故C 正确.由题设易知：S ABC V -=，若内切球的半径为r ，则()3SAB SAC SBC ABC r S S SS +++=，又SAB SAC SBC S S S ===ABC S =，则93)2r ==，故D 错误.故选：BC12.关于函数()sin x f x e x =+，(),x ππ∈-.下列说法正确的是（）A.()f x 在()()0,0f 处的切线方程为210x y -+=B.()f x 有两个零点C.()f x 有两个极值点D.()f x 存在唯一极小值点0x ，且()010f x -<<【答案】ABD【解析】()sin x f x e x =+，()00sin 01f e =+=，()cos xf x e x '=+，()00cos02f e '=+=，切线方程为()120y x -=-,即210x y -+=,故A 正确；()sin x f x e x ''=-⎡⎤⎣⎦，当0x >时，()0sin 110x x f x e x e e ''=≥-->-=⎡⎤⎣⎦，当π0x -<≤时，sin 0x ≤，0x e >,∴()sin 0x f x e x ''=>⎡⎤⎣⎦-，∴(),x ππ∈-时，()0f x ''>⎡⎤⎣⎦，∴()cos xf x e x '=+单调递增，32430422f e e --⎛⎫'-=-<-< ⎪⎝⎭ππ，2002f e -⎛⎫'-=-> ⎪⎝⎭ππ，在(),ππ-内，()cos x f x e x '=+存在唯一的零点0x ,且03,42x ππ⎛⎫∈-- ⎪⎝⎭，且在()0,x x π∈-内，()0f x '<，()f x 单调递减；()0,x x π∈，()0f x '>，()f x 单调递增，∴0x 为极值点，且为极小值点.由()000cos 0x f x e x '=+=，∴()00000sin sin cos x f x e x x x =+=-，∵03,42x ππ⎛⎫∈-- ⎪⎝⎭，∴00001sin 0,1cos 0,sin cos x x x x -<<-<<<，∴001sin cos 0x x -<-<，∴()f x 有唯一的极值点，且为极小值点0x ，且()010f x -<<，故C 错误，D 正确；又∵()()ππ0,sin 0f e f e e ππππ--=>=+=>,结合函数()f x 的单调性可知∴()f x 有两个零点，故B 正确；故选：ABD.三、填空题：本题共4小题，每小题5分，多空题，第一空2分，第二空3分，共20分．13.已知随机变量ξ服从正态分布()2,N μσ，若函数()()1f x P x x ξ=≤≤+为偶函数，则μ=_______.【答案】C【解析】因为函数()f x 为偶函数，则()()f x f x -=，即()()11P x x P x x ξξ-≤≤-+=≤≤+，所以，1122x x μ-++==.故答案为：1214.为调查新冠疫苗的接种情况，需从5名志愿者中选取3人到3个社区进行走访调查，每个社区一人．若甲乙两人至少有一人入选，则不同的选派方法有_____________.【答案】54【解析】①若甲乙两人恰有一人入选，志愿者有12236C C =种选法，再分配到3个社区，有336A =种方案，故由分步乘法计数原理知，共有6636⨯=种选派方法；②若甲乙两人都入选，志愿者有21233C C =种选法，再分配到3个社区，有336A =种方案，故由分步乘法计数原理知，共有1863=⨯种选派方法综上，由分类加法计数原理知，共有361854+=种选派方法.故答案为：54.15.数列{}n a 的各项均为正数，其前n 项和n S 满足112n n n S a a ⎛⎫=+ ⎪⎝⎭.则n a =__________.【答案】【解析】由1111112a S a a ⎛⎫==+ ⎪⎝⎭，得111a S ==.当n>1时，由112n n n S a a ⎛⎫=+ ⎪⎝⎭①1112n n n n S a a a -⎛⎫⇒+=+ ⎪⎝⎭1112n n nS a a -⎛⎫⇒=-+ ⎪⎝⎭.②①+②得11n n n S S a -+=.③又1n n n S S a --=，④③⨯④得2211n n S S --=.则{}2n S 成等差数列，2n S n =，n S =.于是，1n n n a S S -=-=当1n =时，也满足上式.综上，n a =.故答案为16.椭圆的光学性质，从椭圆一个焦点发出的光，经过椭圆反射后，反射光线都汇聚到椭圆的另一个焦点上.已知椭圆C ：()2221024x y b b+=<<，1F ，2F 为其左､右焦点.M 是C 上的动点，点(N ，若1MN MF +的最大值为6.动直线l 为此椭圆C 的切线，右焦点2F 关于直线l 的对称点()11,P x y ，113424S x y =+-，则：（1）椭圆C 的离心率为___________；（2）S 的取值范围为___________.【答案】12[]7,47【解析】根据椭圆定义得：122MF MF a +=，所以12222MN MF MN MF a NF a +=-+≤+，因为1MN MF +的最大值为6，因为2a =，所以22NF =2=，解得1c =，所以离心率为12c a =.右焦点()21,0F 关于直线的对称点()11,P x y ，设切点为A ，由椭圆的光学性质可得：P ，A ，1F 三点共线，所以111224FP F A AP F A AF a =+=+==，即点()11,P x y 的轨迹是以()1,0-为圆心，半径为4的圆，圆心()1,0-到直线34240x y +-=275=，则圆上的点到直线34240x y +-=的距离最小值277455-=，最大值2747455+=，所以点()11,P x y 到直线34240x y +-=的距离为：1134245x y +-，所以113424S x y =+-表示点()11,P x y 到直线34240x y +-=的距离的5倍，则1174734245,555S x y ⎡⎤=+-∈⨯⨯⎢⎥⎣⎦，即[]7,47S ∈.故答案为：12，[]7,47.。

，求实数 、 的值．
将上述结果代入直线 的方程得 ，
5．（本小题满分14分）
已知二阶矩阵 属于特征值－1的一个特征向量为 ，属于特征值2的一个特征向量为 ，求矩阵M及其逆矩阵 ．
6．四边形ABCD和四边形 分别是矩形和平行四边
形，其中点的坐标分别为A（－1，2），B（3，2），C（3，－2），
D（－1，－2）， （－1，0）， （3，8）， （3，4）,
高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃，匠心巨制！独家原创，欢迎下载！
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1．若 ,则 （汇编年高考上海卷（理））
2．若行列式 ，则 ________
评卷人
得分
二、解答题
（－1，－4）．求将四边形ABCD变成四边形 的变换矩阵M．
7．已知矩阵 = ，求 的特征值 ， 及对应的特征向量 ．
8．已知矩阵 ，其中 ，若点 在矩阵 的变换下得到的点
(Ⅰ)求实数 的值；
(Ⅱ)求矩阵 的特征值及特征向量.
【参考答案】***试卷处理标记，请不要删除
评卷人
得分
一、填空题
1．.
2．理0，文1；
3．选修4—2：矩阵与变换
已知矩阵 ，若矩阵 属于特征值6的一个特征向量为 ，属于特征值1的一个特征向量为 ．求矩阵 的逆矩阵．
【考点定位】本题考查的是矩阵的特征值特征向量和逆矩阵的运算，正确理解概念是本题的关键。
4．选修4-2：矩矩阵 对应的变换作用下得到直线
评卷人
得分
二、解答题
3．

小题提速练(四) “12选择＋4填空”80分练(时间：45分钟 分值：80分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知集合A ＝{x |3≤3x ≤27，x ∈N *}，B ＝{x |log 2x ＞1}，则A ∩B ＝( )A ．{1,2,3}B ．(2,3]C ．{3}D ．[2,3]C [∵3≤3x≤27，即31≤3x≤33，∴1≤x ≤3，又x ∈N *，∴A ＝{1,2,3}，∵log 2x ＞1，即log 2x ＞log 22，∴x ＞2，∴B ＝{x |x ＞2}，∴A ∩B ＝{3}，选C.] 2．已知复数z ＝15i 3＋4i，则z 的虚部为( )【导学号：07804211】A ．－95iB ．95iC ．－95D ．95D [z ＝15i 3＋4i ＝15i 3－4i 3＋4i 3－4i ＝1525(4＋3i)＝125＋95i ，故选D.]3．设D 是△ABC 所在平面内一点，AB →＝2DC →，则()A.BD →＝AC →－32AB →B ．BD →＝32AC →－AB →C.BD →＝12AC →－AB →D ．BD →＝AC →－12AB →A [BD →＝BC →＋CD →＝BC →－DC →＝AC →－AB →－12AB →＝AC →－32AB →，选A.]4．(2017·湖南三模)体育课的排球发球项目考试的规则是：每位学生最多可发球3次，一旦发球成功，则停止发球，否则一直发到3次为止．设学生一次发球成功的概率为p (p ≠0)，发球次数为X ，若X 的数学期望E (X )＞1.75，则p 的取值范围是( ) A.⎝ ⎛⎭⎪⎫0，712B ．⎝ ⎛⎭⎪⎫712，1 C.⎝ ⎛⎭⎪⎫0，12 D ．⎝ ⎛⎭⎪⎫12，1 C [根据题意，学生发球次数为1即一次发球成功的概率为p ，即P (X ＝1)＝p ，发球次数为2即二次发球成功的概率P (X ＝2)＝p (1－p )， 发球次数为3的概率P (X ＝3)＝(1－p )2， 则E (X )＝p ＋2p (1－p )＋3(1－p )2＝p 2－3p ＋3，依题意有E (X )＞1.75，则p 2－3p ＋3＞1.75， 解得，p ＞52或p ＜12，结合p 的实际意义，可得0＜p ＜12，即p ∈⎝ ⎛⎭⎪⎫0，12，故选C.]5．已知点F 1，F 2分别是双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点，过F 2且垂直于x 轴的直线与双曲线交于M ，N 两点，若MF 1→·NF 1→＞0，则该双曲线的离心率e 的取值范围是( ) A ．(2，2＋1) B ．(1，2＋1) C ．(1，3)D ．(3，＋∞)B [设F 1(－c,0)，F 2(c,0)，依题意可得c 2a 2－y 2b 2＝1，得到y ＝±b 2a ，不妨设M ⎝ ⎛⎭⎪⎫c ，b 2a ，N ⎝ ⎛⎭⎪⎫c ，－b 2a ，则MF 1→·NF 1→＝⎝⎛⎭⎪⎫－2c ，－b 2a ·⎝ ⎛⎭⎪⎫－2c ，b 2a ＝4c 2－b 4a 2＞0，得到4a 2c 2－(c 2－a 2)2＞0，即a 4＋c 4－6a 2c 2＜0，故e 4－6e 2＋1＜0，解得3－22＜e 2＜3＋22，又e ＞1，故1＜e 2＜3＋22，得1＜e ＜1＋2，故选B.]6．函数y ＝f (x )＝2sin(ωx ＋φ)⎝⎛⎭⎪⎫ω＞0，－π2＜φ＜π2的部分图象如图9所示，关于函数y ＝f (x )(x ∈R )，有下列命题：图9①y ＝f (x )的图象关于直线x ＝π6对称；②y ＝f (x )的图象可由y ＝2sin 2x 的图象向右平移π6个单位长度得到；③y ＝f (x )的图象关于点⎝ ⎛⎭⎪⎫π6，0对称； ④y ＝f (x )在⎣⎢⎡⎦⎥⎤－π12，5π12上单调递增．其中正确命题的个数是( )A ．1B ．2C ．3D ．4C [依题意可得T ＝2×⎝⎛⎭⎪⎫11π12－5π12＝π，故T ＝2πω＝π，解得ω＝2，所以f (x )＝2sin(2x＋φ)，由f (x )＝2sin(2x ＋φ)的图象经过点⎝⎛⎭⎪⎫5π12，2可得2sin ⎝ ⎛⎭⎪⎫2×512π＋φ＝2，即sin ⎝ ⎛⎭⎪⎫56π＋φ＝1，又－π2＜φ＜π2，故φ＝－π3，即f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π3，因为f ⎝ ⎛⎭⎪⎫π6＝2sin ⎝ ⎛⎭⎪⎫2×π6－π3＝0，所以①不对；y ＝2sin 2x 的图象向右平移π6个单位长度得到y ＝2sin2⎝ ⎛⎭⎪⎫x －π6＝2sin ⎝ ⎛⎭⎪⎫2x －π3的图象，②正确；因为f ⎝ ⎛⎭⎪⎫π6＝2sin ⎝ ⎛⎭⎪⎫2×π6－π3＝0，所以③正确；由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z ，取k ＝0，得－π12≤x ≤5π12，即y ＝f (x )在⎣⎢⎡⎦⎥⎤－π12，5π12上单调递增，④正确，故选C.] 7．某几何体的三视图如图10所示，则该几何体的体积为( )【导学号：07804212】图10A.17π6B ．17π3C ．5πD ．13π6A [由三视图可知，该几何体是半个圆锥，一个圆柱，一个半球的组合体， 其体积为16π＋2π＋23π＝176π.选A.]8．执行如图11所示的程序框图，输出的结果为( )图11A ．－1B ．1 C.12D ．2C [n ＝12，i ＝1进入循环，n ＝1－2＝－1，i ＝2；n ＝1－(－1)＝2，i ＝3；n ＝1－12＝12，i＝4，…，所以n 对应的数字呈现周期性的特点，周期为3，因为2 017＝3×672＋1，所以当i ＝2 017时，n ＝12，故选C.]9．若x ，y 满足⎩⎪⎨⎪⎧x ＋y －3≥0ax －y ＋3≥0y ≥0，且z ＝y －x 的最小值为－6，则a 的值为( )A ．－1B ．1C ．－12D ．12C [作出不等式组表示的可行域如图中阴影部分所示，当a ＞0时，易知z ＝y －x 无最小值，故a ＜0，目标函数所在直线过可行域内点A 时，z 有最小值，联立⎩⎪⎨⎪⎧y ＝0ax －y ＋3＝0，解得A ⎝ ⎛⎭⎪⎫－3a ，0，z min ＝0＋3a＝－6，解得a ＝－12，故选C.]10．(数学文化题)今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，问：几何日相逢？( ) A ．12日 B ．16日 C ．8日D ．9日D [由题易知良马每日所行里数构成一等差数列，其通项公式为a n ＝103＋13(n －1)＝13n ＋90，驽马每日所行里数也构成一等差数列，其通项公式为b n ＝97－12(n －1)＝－12n ＋1952，二马相逢时所走路程之和为2×1 125＝2 250，所以n a 1＋a n2＋n b 1＋b n2＝2 250，即n＋13n ＋2＋n ⎝⎛⎭⎪⎫97－12n ＋19522＝2 250，化简得n 2＋31n －360＝0，解得n ＝9或n ＝－40(舍去)，故选D.]11．设函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫A ＞0，ω＞0，|φ|＜π2与直线y ＝3的交点的横坐标构成以π为公差的等差数列，且x ＝π6是f (x )图象的一条对称轴，则下列区间中是函数f (x )的单调递减区间的是( )A.⎣⎢⎡⎦⎥⎤－π3，0 B ．⎣⎢⎡⎦⎥⎤－4π3，－5π6C.⎣⎢⎡⎦⎥⎤2π3，7π6D ．⎣⎢⎡⎦⎥⎤－5π6，－π3D [由题意得A ＝3，T ＝π，∴ω＝2.∴f (x )＝3sin(2x ＋φ)，又f ⎝ ⎛⎭⎪⎫π6＝3或f ⎝ ⎛⎭⎪⎫π6＝－3，∴2×π6＋φ＝k π＋π2，k ∈Z ，φ＝π6＋k π，k ∈Z ，又|φ|＜π2，∴φ＝π6，∴f (x )＝3sin ⎝ ⎛⎭⎪⎫2x ＋π6.令π2＋2k π≤2x ＋π6≤3π2＋2k π，k ∈Z ，得π6＋k π≤x ≤2π3＋k π，k ∈Z ，故当k ＝－1时，f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤－5π6，－π3，故选D.]12．已知直三棱柱ABC ­A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝1，∠BAC ＝60°，AA 1＝2，则该三棱柱的外接球的体积为( )A.40π3 B ．4030π27C.32030π27D ．20πB [设△A 1B 1C 1的外心为O 1，△ABC 的外心为O 2，连接O 1O 2，O 2B ，OB ，如图所示．由题意可得外接球的球心O 为O 1O 2的中点．在△ABC 中，由余弦定理可得BC 2＝AB 2＋AC 2－2AB ×AC cos∠BAC ＝32＋12－2×3×1×cos 60°＝7， 所以BC ＝7.由正弦定理可得△ABC 外接圆的直径2r ＝2O 2B ＝BC sin 60°＝273，所以r ＝73＝213. 而球心O 到截面ABC 的距离d ＝OO 2＝12AA 1＝1，设直三棱柱ABC ­A 1B 1C 1的外接球半径为R ，由球的截面性质可得R 2＝d 2＋r 2＝12＋⎝ ⎛⎭⎪⎫2132＝103，故R ＝303，所以该三棱柱的外接球的体积为V ＝4π3R 3＝4030π27.故选B.] 二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知函数f (x )＝ln x ，g (x )＝x 2＋mx (m ∈R )，若函数f (x )的图象在点(1，f (1))处的切线与函数g (x )的图象相切，则m 的值为________．[解析] 易知f (1)＝0，f ′(x )＝1x，从而得到f ′(1)＝1，函数f (x )的图象在点(1，f (1))处的切线方程为y ＝x －1.法一：(应用导数的几何意义求解)设直线y ＝x －1与g (x )＝x 2＋mx (m ∈R )的图象相切于点P (x 0，y 0)，从而可得g ′(x 0)＝1，g (x 0)＝x 0－1.又g ′(x )＝2x ＋m ，因此有⎩⎪⎨⎪⎧gx 0＝2x 0＋m ＝1x 20＋mx 0＝x 0－1，得x 2＝1，解得⎩⎪⎨⎪⎧x 0＝1m ＝－1或⎩⎪⎨⎪⎧x 0＝－1m ＝3.法二：(应用直线与二次函数的相切求解)联立⎩⎪⎨⎪⎧y ＝x －1y ＝x 2＋mx ，得x 2＋(m －1)x ＋1＝0，所以Δ＝(m －1)2－4＝0，解得m ＝－1或m ＝3. [答案] －1或314．3名医生和6名护士被分配到3所学校为学生体检，每所学校分配1名医生和2名护士，不同的分配方法共有________种.【导学号：07804213】[解析] 3所学校依次选医生、护士，不同的分配方法共有C 13C 26C 12C 24＝540种． [答案] 54015．已知直线MN 过椭圆x 22＋y 2＝1的左焦点F ，与椭圆交于M ，N 两点．直线PQ 过原点O 且与直线MN 平行，直线PQ 与椭圆交于P ，Q 两点，则|PQ |2|MN |＝________.[解析] 法一：由题意知，直线MN 的斜率不为0，设直线MN ：x ＝my －1，则直线PQ ：x ＝my .设M (x 1，y 1)，N (x 2，y 2)，P (x 3，y 3)，Q (x 4，y 4)．⎩⎪⎨⎪⎧x ＝my －1x 22＋y 2＝1⇒(m 2＋2)y 2－2my －1＝0⇒y 1＋y 2＝2m m 2＋2，y 1y 2＝－1m 2＋2. ∴|MN |＝1＋m 2|y 1－y 2|＝22·m 2＋1m 2＋2.⎩⎪⎨⎪⎧x ＝my x 22＋y 2＝1⇒(m 2＋2)y 2－2＝0⇒y 3＋y 4＝0，y 3y 4＝－2m 2＋2. ∴|PQ |＝1＋m 2|y 3－y 4|＝22m 2＋1m 2＋2.故|PQ |2|MN |＝2 2. 法二：取特殊位置，当直线MN 垂直于x 轴时，易得|MN |＝2b 2a ＝2，|PQ |＝2b ＝2，则|PQ |2|MN |＝2 2. [答案] 2 216．设函数f (x )是定义在R 上的偶函数，对任意x ∈R ，都有f (x )＝f (x ＋4)，且当x ∈[－2,0]时，f (x )＝⎝ ⎛⎭⎪⎫12－1，若在区间(－2,6]内关于x 的方程f (x )－log a (x ＋2)＝0(a ＞1)恰有3个不同的实数根，则a 的取值范围是________． [解析] 设x ∈[0,2]，则－x ∈[－2,0]，∴f (－x )＝⎝ ⎛⎭⎪⎫12－1＝2x－1，∵f (x )是定义在R 上的偶函数，∴f (x )＝f (－x )＝2x－1.∵对任意x ∈R ，都有f (x )＝f (x ＋4)， ∴当x ∈[2,4]时，(x －4)∈[－2,0]，∴f (x )＝f (x －4)＝⎝ ⎛⎭⎪⎫12－1； 当x ∈[4,6]时，(x －4)∈[0,2]， ∴f (x )＝f (x －4)＝2x －4－1.∵在区间(－2,6]内关于x 的方程f (x )－log a (x ＋2)＝0(a ＞1)恰有3个不同的实数根， ∴函数y ＝f (x )的图象与函数y ＝log a (x ＋2)的图象在区间(－2,6]内恰有3个不同的交点，作出两个函数的图象如图所示，易知⎩⎪⎨⎪⎧log a ＋＞3log a＋＜3，解得223＜a ＜2，即34＜a ＜2，因此所求a 的取值范围是(34，2)．[答案] (34，2)。

2020年高考数学120分120分(12＋4＋3＋2)保分练(四)(满分：126分 限时：90分钟)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知集合P ＝{0，m }，Q ＝{x |2x 2－7x ＋5≤0，x ∈Z}，若P ∩Q ≠∅，则m ＝( ) A ．1 B ．2 C ．1或52D ．1或2解析：选D 依题意得Q ＝{x |(2x －5)(x －1)≤0，x ∈Z}＝⎩⎨⎧⎭⎬⎫x 1≤x ≤52，x ∈Z ＝{1,2}，因为P ∩Q ≠∅，P ＝{0，m }，所以m ＝1或m ＝2.2．复数2－i 31－2i ＝( )A ．iB ．－iC ．1D ．－1解析：选A 2－i 31－2i ＝2＋i 1－2i ＝(2＋i )(1＋2i )(1－2i )(1＋2i )＝3i3＝i.3．设{a n }是公差不为零的等差数列，满足a 25＋a 26＝a 27＋a 28，则该数列的前12项和等于( )A ．－10B ．－5C ．0D ．5解析：选C 法一：设等差数列{a n }的首项为a 1，公差为d (d ≠0)，由a 25＋a 26＝a 27＋a 28，得(a 1＋4d )2＋(a 1＋5d )2＝(a 1＋6d )2＋(a 1＋7d )2，整理得2a 1＋11d ＝0，即a 1＋a 12＝0，所以S 12＝12(a 1＋a 12)2＝0.法二：由a 25＋a 26＝a 27＋a 28，得a 25－a 27＝a 28－a 26，即(a 5＋a 7)(a 5－a 7)＝(a 8＋a 6)(a 8－a 6)．因为{a n }是公差不为零的等差数列，设其公差为d (d ≠0)，则2a 6×(－2d )＝2a 7×2d ，即a 6＋a 7＝0，所以S 12＝12(a 1＋a 12)2＝6(a 6＋a 7)＝0.4．由函数g (x )＝4sin x cos x 的图象向左平移π3个单位长度得到函数f (x )的图象，则f ⎝⎛⎭⎫π8＝( )A.6＋23 B.6－23 C.6－22D.6＋22解析：选C 函数g (x )＝4sin x cos x ＝2sin 2x 的图象向左平移π3个单位得到y ＝2sin ⎝⎛⎭⎫2x ＋2π3的图象， 即f (x )＝2sin ⎝⎛⎭⎫2x ＋2π3.故f ⎝⎛⎭⎫π8＝2sin ⎝⎛⎭⎫2×π8＋2π3 ＝2sin π4＋2π3＝2⎝⎛⎭⎫sin π4cos 2π3＋cos π4sin 2π3 ＝222×⎝⎛⎭⎫－12＋22×32＝6－22. 5．已知向量a ＝(2,4)，b ＝(－1，x )，若a ⊥(a －b )，则x ＝( ) A ．2 B ．2.5 C ．5D ．5.5解析：选D 因为a ＝(2,4)，b ＝(－1，x )，所以a －b ＝(3,4－x )，因为a ⊥(a －b )，所以a ·(a －b )＝2×3＋4(4－x )＝0，解得x ＝5.5.6.如图是一个空间几何体的三视图，则该空间几何体的体积是( )A.10π3 B ．4π C ．6πD ．12π解析：选A 这个空间几何体的下半部分是一个底面半径为1，高为2的圆柱，上半部分是一个底面半径为2，高为1的圆锥，故其体积为π×12×2＋13π×22×1＝10π3.7.《周髀算经》中给出了勾股定理的绝妙证明，如图是赵爽的弦图及注文，弦图是一个以勾股形之弦为边的正方形，其面积称为弦实．图中包含四个全等的勾股形及一个小正方形，分别涂成朱(红)色及黄色，其面积分别称朱实、黄实，利用2×勾×股＋(股－勾)2＝4×朱实＋黄实＝弦实，化简得勾2＋股2＝弦2.设勾股形中勾股比为1∶3，若向弦图内随机抛掷3 000颗图钉，则落在黄色图形内的图钉数约为(3≈1.732)( )A ．134B ．268C ．402D ．536解析：选C 设大正方形的边长为2，由图中直角三角形的两直角边长之比为1∶3，可得小正方形的边长为3－1，所以小正方形与大正方形的面积比值为(3－1)24＝1－32，所以落在小正方形内的图钉数为⎝⎛⎭⎫1－32×3 000≈⎝⎛⎭⎫1－12×1.732×3 000＝402. 8．在[－4,4]上随机取一个实数m ，能使函数f (x )＝x 3＋mx 2＋3x 在R 上单调递增的概率为( )A.14B.38C.58D.34解析：选D 由题意，得f ′(x )＝3x 2＋2mx ＋3，要使函数f (x )在R 上单调递增，则3x 2＋2mx ＋3≥0在R 上恒成立，即Δ＝4m 2－36≤0，解得－3≤m ≤3，所以所求概率为3－(－3)4－(－4)＝34. 9．已知圆C 与直线y ＝x 及x －y －4＝0都相切，圆心在直线y ＝－x 上，则圆C 的方程为( )A ．(x ＋1)2＋(y －1)2＝2B ．(x ＋1)2＋(y ＋1)2＝2C ．(x －1)2＋(y －1)2＝2D ．(x －1)2＋(y ＋1)2＝2解析：选D 由题意知x －y ＝0 和x －y －4＝0之间的距离为|4|2＝22，所以r ＝ 2.又因为x ＋y ＝0与x －y ＝0，x －y －4＝0均垂直，所以由x ＋y ＝0和x －y ＝0联立得交点坐标为(0,0)，由x ＋y ＝0和x －y －4＝0联立得交点坐标为(2，－2)，所以圆心坐标为(1，－1)，圆C 的标准方程为(x －1)2＋(y ＋1)2＝2.10．函数f (x )＝1x＋ln |x |的图象大致为( )解析：选B 因为f (1)＝1，排除A 项；当x >0时，f (x )＝1x ＋ln x ，f ′(x )＝－1x 2＋1x ＝x －1x 2，所以当0<x <1时，f ′(x )<0，f (x )单调递减，当x >1时，f ′(x )>0，f (x )单调递增，排除D 项，又f (－1)＝－1，排除C 项，故选B.11．椭圆C ：x 24＋y 23＝1的左、右顶点分别为A 1，A 2，点P 在C 上且直线PA 2斜率的取值范围是[－2，－1]，那么直线PA 1斜率的取值范围是( )A.⎣⎡⎦⎤12，34B.⎣⎡⎦⎤38，34 C.⎣⎡⎦⎤12，1D.⎣⎡⎦⎤34，1解析：选B 椭圆的左顶点为A 1(－2,0)，右顶点为A 2(2，0)，设点P (x 0，y 0)，则x 204＋y 203＝1，得y 20x 20－4＝－34.又kPA 2＝y 0x 0－2，kPA 1＝y 0x 0＋2，所以kPA 2·kPA 1＝y 20x 20－4＝－34.又kPA 2∈[－2，－1]，所以kPA 1∈⎣⎡⎦⎤38，34.12．已知函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤0，x 2－2x ＋1，x >0，若关于x 的方程f 2(x )－af (x )＝0恰有5个不同的实数解，则a 的取值范围是( )A ．(0,1)B ．(0,2)C ．(1,2)D ．(0,3)解析：选A 设t ＝f (x )，则方程为t 2－at ＝0，解得t ＝0或t ＝a ，即f (x )＝0或f (x )＝a .如图所示，作出函数f (x )的图象，由函数图象，可知f (x )＝0的解有2个，故要使方程f 2(x )－af (x )＝0恰有5个不同的解，则方程f (x )＝a 的解必有3个，此时0<a <1.二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中的横线上) 13．如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率依次成等差数列，第2小组的频数为10，则抽取的学生人数为________．解析：前3个小组的频率和为1－(0.037 5＋0.012 5)×5＝0.75，所以第2小组的频率为13×0.75＝0.25， 所以抽取的学生人数为100.25＝40.答案：4014．观察下列不等式：1＋12＋13>1,1＋12＋13＋…＋17>32，1＋12＋13＋…＋115>2,1＋12＋13＋…＋131>52，…，照此规律，第6个不等式为________________．解析：观察不等式的规律知1＋12＋122－1>1＝22，1＋12＋13＋…＋123－1>32，1＋12＋13＋…＋124－1>42，1＋12＋13＋…＋125－1>52，…，由此猜测第6个不等式为1＋12＋13＋…＋1127>72.答案：1＋12＋13＋…＋1127>7215．若tan α＋1tan α＝103，α∈⎝⎛⎭⎫π4，π2，则sin ⎝⎛⎭⎫2α＋π4＋2cos π4cos 2α的值为________． 解析：因为tan α＋1tan α＝103，α∈⎝⎛⎭⎫π4，π2， 所以(tan α－3)(3tan α－1)＝0，所以tan α＝3或13.因为α∈⎝⎛⎭⎫π4，π2，所以tan α>1，所以tan α＝3， 所以sin ⎝⎛⎭⎫2α＋π4＋2cos π4cos 2α ＝22sin 2α＋22cos 2α＋2(1＋cos 2α)2 ＝22(sin 2α＋2cos 2α＋1) ＝222sin αcos αsin 2α＋cos 2α＋2cos 2α－2sin 2αsin 2α＋cos 2α＋1 ＝222tan α1＋tan 2α＋2－2tan 2α1＋tan 2α＋1 ＝0. 答案：016．设抛物线y 2＝4x 的焦点为F ，A ，B 两点在抛物线上，且A ，B ，F 三点共线，过AB 的中点M 作y 轴的垂线与抛物线在第一象限内交于点P ，若|PF |＝32，则M 点的横坐标为___．解析：由题意得F (1,0)，准线方程为x ＝－1， 设A (x 1，y 1)，B (x 2，y 2)，直线AB 方程为y ＝k (x －1)， 代入抛物线方程消去y ，得k 2x 2－(2k 2＋4)x ＋k 2＝0， 所以x 1＋x 2＝2k 2＋4k2，x 1x 2＝1.又设P (x 0，y 0)，则y 0＝12(y 1＋y 2)＝12[k (x 1－1)＋k (x 2－1)]＝2k ，所以x 0＝1k 2，所以P ⎝⎛⎭⎫1k 2，2k . 因为|PF |＝x 0＋1＝1k 2＋1＝32，解得k 2＝2，所以M点的横坐标为x1＋x22＝2k2＋4k22＝2.答案：2三、解答题(本大题共3小题，共36分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)数列{a n}的前n项和S n满足S n＝2a n－a1，且a1，a2＋1，a3成等差数列．(1)求数列{a n}的通项公式；(2)设b n＝a n＋1S n S n＋1，求数列{b n}的前n项和T n.解：(1)∵S n＝2a n－a1，∴当n≥2时，S n－1＝2a n－1－a1，∴a n＝2a n－2a n－1，即a n＝2a n－1.由a1，a2＋1，a3成等差数列，得2(a2＋1)＝a1＋a3，∴2(2a1＋1)＝a1＋4a1，解得a1＝2.∴数列{a n}是首项为2，公比为2等比数列，∴a n＝2n.(2)∵a n＋1＝2n＋1，S n＝2n＋1－2，S n＋1＝2n＋2－2.∴b n＝a n＋1S n S n＋1＝2n＋1(2n＋1－2)(2n＋2－2)＝1212n－1－12n＋1－1.∴数列{b n}的前n项和T n＝12⎝⎛⎭⎫12－1－122－1＋⎝⎛⎭⎫122－1－123－1＋…＋⎝⎛⎭⎫12n－1－12n＋1－1＝12⎝⎛⎭⎫1－12n＋1－1.18．(本小题满分12分)如图，在四棱锥S-ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1.(1)证明：SD⊥平面SAB；(2)求四棱锥S-ABCD的高．解：(1)证明：如图，取AB的中点E，连接DE，DB，则四边形BCDE为矩形，∴DE＝CB＝2，∴AD＝BD＝ 5.∵侧面SAB为等边三角形，AB＝2，∴SA＝SB＝AB＝2.又SD＝1，∴SA2＋SD2＝AD2，SB2＋SD2＝BD2，∴∠DSA ＝∠DSB ＝90°，即SD ⊥SA ，SD ⊥SB ， 又SA ∩SB ＝S ，∴SD ⊥平面SAB . (2)设四棱锥S -ABCD 的高为h ， 则h 也是三棱锥S -ABD 的高． 由(1)，知SD ⊥平面SAB .由V S -ABD ＝V D -SAB，得13S △ABD ·h ＝13S △SAB ·SD ， ∴h ＝S △SAB ·SDS △ABD.又S △ABD ＝12AB ·DE ＝12×2×2＝2，S △SAB ＝34AB 2＝34×22＝3，SD ＝1， ∴h ＝S △SAB ·SD S △ABD ＝3×12＝32.故四棱锥S -ABCD 的高为32. 19．(本小题满分12分)某校开展“翻转合作学习法”教学试验，经过一年的实践后，对“翻转班”和“对照班”的220名学生的数学学习情况进行测试，按照大于或等于120分为“成绩优秀”，120分以下为“成绩一般”统计，得到如下的2×2列联表：(1)秀与翻转合作学习法”有关；(2)为了交流学习方法，从这次测试数学成绩优秀的学生中，用分层抽样的方法抽出6名学生，再从这6名学生中抽出3名交流学习方法，求至少抽到一名“对照班”学生的概率．附：K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )，其中n ＝a ＋b ＋c ＋d .解：(1)∵K 2＝220×(20×70－40×90)60×160×110×110＝556≈9.167<10.828，∴在犯错误的概率不超过0.001的前提下，不能认为“成绩优秀与翻转合作学习法”有关．(2)设从“翻转班”中抽取x 人，从“对照班”中抽取y 人，由分层抽样的定义可知660＝x 40＝y20，解得x ＝4，y ＝2. 在这6名学生中，设“对照班”的2名学生分别为A 1，A 2，“翻转班”的4名学生分别为B 1，B 2，B 3，B 4.则所有的抽样情况如下，{A 1，A 2，B 1}，{A 1，A 2，B 2}，{A 1，A 2，B 3}，{A 1，A 2，B 4}， {A 1，B 1，B 2}，{A 1，B 1，B 3}，{A 1，B 1，B 4}，{A 1，B 2，B 3}， {A 1，B 2，B 4}，{A 1，B 3，B 4}，{A 2，B 1，B 2}，{A 2，B 1，B 3}， {A 2，B 1，B 4}，{A 2，B 2，B 3}，{A 2，B 2，B 4}，{A 2，B 3，B 4}， {B 1，B 2，B 3}，{B 1，B 2，B 4}，{B 1，B 3，B 4}，{B 2，B 3，B 4}， 共20种．其中至少有一名“对照班”学生的情况有16种．记事件A 为至少抽到一名“对照班”学生交流学习方法，则P (A )＝1620＝45.四、选做题(请在第22～23题中任选一题作答，如果多做，则按所做的第一题计分) 22．(本小题满分10分)选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝－35t ＋2，y ＝45t(t 为参数)，以原点O为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝a sin θ(a ≠0)．(1)求圆C 的直角坐标方程与直线l 的普通方程；(2)设直线l 截圆C 的弦长是半径长的3倍，求a 的值． 解：(1)圆C 的直角坐标方程为x 2＋⎝⎛⎭⎫y －a 22＝a24， 直线l 的普通方程为4x ＋3y －8＝0.(2)∵直线l 截圆C 的弦长等于圆C 的半径长的3倍，∴圆心C 到直线l 的距离d ＝⎪⎪⎪⎪3a 2－85＝12×|a |2，解得a ＝32或a ＝3211. 23．(本小题满分10分)选修4－5：不等式选讲 已知函数f (x )＝|x ＋1|＋|x －3|－m 的定义域为R. (1)求m 的取值范围；(2)若m 的最大值为n ，解关于x 的不等式：|x －3|－2x ≤2n －4.解：(1)因为函数f (x )的定义域为R ， 所以|x ＋1|＋|x －3|－m ≥0恒成立， 设函数g (x )＝|x ＋1|＋|x －3|， 则m 不大于函数g (x )的最小值， 又|x ＋1|＋|x －3|≥|(x ＋1)－(x －3)|＝4， 即g (x )的最小值为4.所以m ≤4，即m 的取值范围为(－∞，4]．(2)当m 取最大值4时，原不等式等价于|x －3|－2x ≤4，所以⎩⎪⎨⎪⎧ x ≥3，x －3－2x ≤4或⎩⎪⎨⎪⎧x ＜3，3－x －2x ≤4，解得x ≥3或－13≤x ＜3.所以原不等式的解集为⎩⎨⎧⎭⎬⎫xx ≥－13.。

高中数学专题复习《数列等差等比数列综合》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明 评卷人得分一、选择题1．已知{}n a 为等比数列.下面结论中正确的是 （ ）A ．1322a a a +≥B ．2221322a a a +≥C ．若13a a =,则12a a =D ．若31a a >,则42a a >（汇编北京文）2．已知等差数列｛n a ｝，n S 表示前n 项的和，,0,0993<>+S a a 则N S S S ,,21中最小的是（ ） A ．S 4 B ．5S C ．S 6D ．9S （汇编）3．等差数列和的前n 项和分别为S n 和T n ，对一切自然数n 都有，则等于( )B ．C ．D ．（汇编）4．数列{}n a 的通项222(cos sin )33n n n a n ππ=-，其前n 项和为n S ，则30S 为（ ）A ．470B ．490C ．495D ．510（汇编江西理）5．已知各项均为正数的等比数列{n a }，123a a a =5，789a a a =10，则456a a a =（ ） A ．52 B ．7C ．6D ．42（汇编）6．已知数列{a n }既是等差数列又是等比数列,则这个数列的前n 项和为 A.0 B.n C.na 1 D. a 1n7．设是公比为q 的等比数列，是它的前n 项和，若是等差数列，则q 的值等于（ ）A ． 1B ． 2C ． 3D ． 48．等比数列{a n }的前n 项的和为S n ,已知a 5=2S 4+3,a 6=2S 5+3,则数列的公比q 等于 A.2 B.3 C.4 D.59．如果成等比数列，那么 ( ）A ．B ．C ．D ．10．一个各项均为正数的等比数列，其任何项都等于后面两项之和，则其公比是( ） A ．52B ． 152-C ． 255D ． 512-11．设等差数列{an}的公差为d,如果它的前n 项和Sn=-n2,那么A.an=2n-1,d=-2B.an=2n-1,d=2C.an=-2n+1,d=-2D.an=-2n+1,d=212．已知a 、b 、c 的倒数成等差数列，如果a 、b 、c 互不相等，则 为A. B. C. D.第II 卷（非选择题）请点击修改第II 卷的文字说明 评卷人得分二、填空题13．若实数a,b,c 满足：数列1，a ，b ，c ，4是等比数列，则b 的值为 . 14．已知)(),(x g x f 都是定义在R 上的函数，()0,()()()()g x f x g x f x g x ''≠>,()(),x f x a g x =⋅（01a a >≠且）,(1)(1)5,(1)(1)2f f g g -+=- 在有穷数列)10,,2,1}()()({=n n g n f 中，任意取正整数k （110k ≤≤），则前k 项和不小于1615的概率是 ▲ ．15．设等差数列}{n a 的前n 项和为,n S 且满足,0,01615<>S S 则15152211,,,a S a S a S 中最大的项为 ▲ .16．等差数列{}n a 中，已知27a ≤，69a ≥，则10a 的取值范围是 ▲ ．17．已知数列{}n a 中，()12121,2,,3,n n n a a a a a n N n +--===-∈≥则2011a = ▲ ．18．在等差数列}{n a 中，若67,211234=+++=---n n n n a a a a S ，且286=n S ，则n =____19．在数列}{n a 中，3,511+==+n n a a a ，则通项公式为n a =_______20．证：lg(a ＋c)，lg(a-c)，lg(a ＋c-2b)也成等差数列． 评卷人得分三、解答题21．设等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项和为,n T 已知数列{}n b 的公比为,1),0(11==>b a q q .,452335b a T S -==（1）求数列{}n a ，{}n b 的通项公式； （2）求.13221++⋅⋅⋅++n n a a q a a q a a q （本题满分14分）22．设等差数列}{n a 的前n 项和为n S ，若),(,*q p N q p p S q S q p <∈==且，求q p S +。

必修4填空题265题一、填空题1、若α＝1 690°，角θ与α终边相同，且－360°<θ<360°，则θ＝________.2、如图所示，终边落在阴影部分(含边界)的角的集合是______________________________．3、经过10分钟，分针转了________度．4、若角α与β的终边相同，则α－β的终边落在________．5、已知一圆弧长等于其所在圆的内接正方形的周长，那么其圆心角的弧度数的绝对值为________．6、将－1 485°化为2k π＋α (0≤α<2π，k ∈Z )的形式是________．7、若扇形圆心角为216°，弧长为30π，则扇形半径为____．8、若2π<α<4π，且α与－7π6角的终边垂直，则α＝______.9、若角α的终边与角π6的终边关于直线y ＝x 对称，且α∈(－4π，4π)，则α＝________________.10、代数式：sin 2cos 3tan 4的符号是________．11、已知α终边经过点(3a －9，a ＋2)，且sin α>0，cos α≤0，则a 的取值范围为________．12、若角α的终边过点P (5，－12)，则sin α＋cos α＝______.13、在[0,2π]上满足sin x ≥12的x 的取值范围为________．14、集合A ＝[0,2π]，B ＝{α|sin α<cos α}，则A ∩B ＝________________.15、不等式tan α＋33>0的解集是______________．16、求函数f (x )＝lg(3－4sin 2x )的定义域为________．17、若角α的终边与直线y ＝3x 重合且sin α<0，又P (m ，n )是α终边上一点，且|OP |＝10，则m －n ＝________.18、已知tan θ＝2，则sin 2θ＋sin θcos θ－2cos 2θ＝________.19、已知sin αcos α＝18且π4<α<π2，则cos α－sin α＝____.20、＝ ．其中(,)2πθπ∈21、已知tan α=cos α= ．22、若sin θ＝k ＋1k －3，cos θ＝k －1k －3，且θ的终边不落在坐标轴上，则tan θ的值为________．23、已知α是第四象限角，tan α＝－512，则sin α＝________.24、sin 21°＋sin 22°＋…＋sin 288°＋sin 289°＝________.25、若sin ⎝⎛⎭⎫α＋π12＝13，则cos ⎝⎛⎭⎫α＋7π12＝________.26、已知cos(π6＋θ)＝33，则cos(5π6－θ)＝________.27、代数式sin 2(A ＋45°)＋sin 2(A －45°)的化简结果是______．28、已知tan(3π＋α)＝2，则sin (α－3π)＋cos (π－α)＋sin ⎝⎛⎭⎫π2－α－2cos ⎝⎛⎭⎫π2＋α－sin (－α)＋cos (π＋α)＝________.29、设f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)＋2，其中a 、b 、α、β为非零常数．若f (2 009)＝1，则f (2 010)＝____.30、代数式1＋2sin 290°cos 430°sin 250°＋cos 790°的化简结果是______．31、三角函数式cos (α＋π)sin 2(α＋3π)tan (α＋π)cos 3(－α－π)的化简结果是______.32、若42x ππ<< 则函数3tan 2tan y x x =的最大值为 。

2021届高考(ɡāo k ǎo)数学填空题临考押题训练〔41〕1、点在第三象限(xiàngxiàn), 那么角的终边在第 象限(xiàngxiàn)。

2、a=〔2,1〕,b =〔x,2〕,且a ＋b 与a －2b 平行(píngxíng)，那么x 等于 ．3、 集合，，假设，那么实数的取值范围是 ． 4、 设f (x )是奇函数，且当x >0时，f (x )=,那么当x <0时，f (x )=5、 函数的增区间是 ．6、 函数的图象恒过定点A 〔其坐标与a 无关〕，那么定点A 的坐标为 ．7、在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，假设，那么_ _ _．8、非负实数、同时满足,, 那么目的函数的最小值是9、〔2021年东山中学二模〕 对于数列{}，定义数列{}为数列{n a }的“差数列〞，假设，{n a }的“差数列〞的通项为，那么数列{n a }的前项和= .10、命题P ：“对∈R ，m ∈R ，使〞，假设命题P 是真命题，那么实数m 的取值范围是 .11、函数y ＝的最大值为M,最小值为m,那么的值是．12.为所在平面(píngmiàn)内一点，满足，那么(nà me)点O是ABC的心13、假设(jiǎshè)为的各位数字(shùzì)之和，如，，那么，记，，…，，，那么 . 14．表中的对数值有且只有两个是错误的：x 3 5 6 7 8 9 14lg x 3a-b+c2a-ba+c1+a-b-c2(a+c)3(1-a-c〕2(2a-b)1-a+2b请你指出这两个错误．〔答案写成如lg20≠a＋b－c的形式〕参考答案1、二2、43、．(2，3)4、1 x5、6、〔―2，―1〕7、8、 59、10、m≤111、12. 垂13、11 .14．≠3a-b+c，lg7≠2(a+c)内容总结（1）2021届高考数学填空题临考押题训练〔41〕1、点在第三象限, 那么角的终边在第象限。

创新设计（浙江专用）2017届高考数学二轮复习大题规范天天练星期六第四周综合限时练编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（创新设计（浙江专用）2017届高考数学二轮复习大题规范天天练星期六第四周综合限时练）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为创新设计（浙江专用）2017届高考数学二轮复习大题规范天天练星期六第四周综合限时练的全部内容。

星期六 (综合限时练)解答题综合练（设计意图：训练考生在规定时间内得高分，限时:80分钟） 1。

(本小题满分12分）在公比为2的等比数列｛a n }中,a 2与a 5的等差中项是93。

（1）求a 1的值;(2）若函数y ＝a 1sin 错误!(其中0〈φ〈π）的一部分图象如图所示，M （－1，a 1），N (3，－a 1）为图象上的两点，设∠MON ＝θ，其中O 为坐标原点，0〈θ<π,求cos(θ－φ）的值。

解 （1)由题可知a 2＋a 5＝18错误!，又a 5＝8a 2，故a 2＝2错误!，∴a 1＝错误!。

（2）∵点M （－1,a 1)在函数y ＝a 1sin ⎝ ⎛⎭⎪⎫π4x ＋φ的图象上，∴sin 错误!＝1，又∵0〈φ<π，∴φ＝错误!π. 连接MN ，在△MON 中，由余弦定理得 cos θ＝错误!＝错误!＝－错误!。

又∵0<θ〈π,∴θ＝错误!π,∴cos(θ－φ）＝cos 错误!＝cos 错误!cos 错误!＋sin 错误!sin 错误!＝错误!.2.(本小题满分12分）甲、乙两所学校高三年级分别有600人,500人，为了解两所学校全体高三年级学生在该地区五校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下： 甲校：分组 ［70，80)[80，90)[90，100)[100，110）频数 3 4 7 14 分组[110，120)［120,130)［130，140)[140，150]乙校：(1）计算x，y的值；(2）若规定考试成绩在［120，150］内为优秀，由以上统计数据填写下面的2×2列联表，并判断是否有90%的把握认为两所学校的数学成绩有差异；（3）若规定考试成绩在[120,150］内为优秀，现从已抽取的110人中抽取两人，要求每校抽1人,所抽的两人中有人优秀的条件下，求乙校被抽到的同学不是优秀的概率.参考公式：K2＝错误!,其中n＝a＋b＋c＋d,临界值表解（1）从甲校抽取110×错误!＝60(人)，从乙校抽取110×错误!＝50（人)，故x＝9，y＝6。

2018年（人教版）高考数学选择填空限时训练(1)1.已知P ＝{x |x 2－5x ＋4＜0}，Q ＝{}y |y ＝4－2x ，则P ∩Q 等于( ) A.[0，1) B.[0，2) C.(1，2) D.[1，2) 答案 C解析 解x 2－5x ＋4＜0，即(x －1)(x －4)＜0，得1＜x ＜4，故P ＝(1，4).Q 表示函数y ＝4－2x的值域，因为2x ＞0，所以t ＝4－2x ＜4，所以y ∈[0，2)，即Q ＝[0，2).故P ∩Q ＝(1，2).故选C.2.已知a ∈R ，i 是虚数单位.若a －i 2＋i 与3i －5i 2－i 互为共轭复数，则a 等于( )A.13B.－13 C.－3 D.3 答案 D解析 a －i 2＋i ＝(a －i )(2－i )(2＋i )(2－i )＝(2a －1)－(a ＋2)i 5＝2a －15－a ＋25i ，3i －5i2－i ＝3i －5i (2＋i )(2－i )(2＋i )＝3i －－5＋10i 5＝1＋i ，∵a －i 2＋i 与3i －5i2－i互为共轭复数， ∴2a －15＝1，－a ＋25＝－1，解得a ＝3.故选D.3.命题：∀x ∈R ，ln(e x －1)＜0的否定是( ) A.∀x ∈R ，ln(e x －1)>0 B.∀x ∈R ，ln(e x －1)≥0 C.∃x 0∈R ，ln(0e x－1)＜0 D.∃x 0∈R ，ln(0e x －1)≥0 答案 D4.(2017·四川双流中学月考)已知函数f (x )＝A sin ()ωx ＋φ⎝⎛⎭⎫A >0，ω>0，||φ＜π2的部分图象如图所示，若将f (x )图象上的所有点向右平移π12个单位长度得到函数g (x )的图象，则函数g (x )的单调递增区间为( )A.⎣⎡⎦⎤k π－π3，k π＋π6，k ∈Z B.⎣⎡⎦⎤k π＋π6，k π＋2π3，k ∈Z C.⎣⎡⎦⎤k π－π12，k π＋π12，k ∈Z D.⎣⎡⎦⎤k π－7π12，k π－π12，k ∈Z 答案 A解析 由题图可得，f (x )的振幅A ＝2， 周期T ＝4×⎝⎛⎭⎫π3－π12＝π，则ω＝2， 所以f (x )＝2sin(2x ＋φ)， 又2×π12＋φ＝π2＋2k π，|φ|＜π2，解得φ＝π3，所以f (x )＝2sin ⎝⎛⎭⎫2x ＋π3， 平移后得g (x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π12＋π3＝2sin ⎝⎛⎭⎫2x ＋π6， 令－π2＋2k π≤2x ＋π6≤π2＋2k π，k ∈Z ，解得－π3＋k π≤x ≤π6＋k π，k ∈Z ，所以g (x )的单调递增区间为⎣⎡⎦⎤－π3＋k π，π6＋k π，k ∈Z . 故选A.5.已知抛物线y 2＝4x 的准线与x 轴的交点记为A ，焦点为F ，l 是过点A 且倾斜角为π3的直线，则F 到直线l 的距离为( ) A.1 B.3 C.2 D.2 3答案 B解析 由题意，得A (－1，0)，F (1，0)，则过点A 且倾斜角为π3的直线l 的方程为y ＝3(x ＋1)，∴点F 到直线l 的距离d ＝233＋1＝ 3.故选B. 6.(2017·云南师范大学附中月考)已知三棱锥A －BCD 内接于半径为5的球O 中，AB ＝CD ＝4，则三棱锥A －BCD 的体积的最大值为( ) A.43 B.83 C.163 D.323 答案 C解析 如图，过CD 作平面ECD ，使AB ⊥平面ECD ， 交AB 于点E ，设点E 到CD 的距离为EF ，当球心在EF 上时，EF 最大，此时E ，F 分别为AB ，CD 的中点，且球心O 为EF 的中点，所以EF ＝2，所以V max ＝13×12×4×2×4＝163，故选C.7.(2017·武邑检测)已知圆M ：x 2＋y 2－2ay ＝0()a >0截直线x ＋y ＝0所得线段的长度是22，则圆M 与圆N ：(x －1)2＋()y －12＝1的位置关系是( )A.内切B.相交C.外切D.外离 答案 B 解析 化简圆M ：x 2＋(y －a )2＝a 2⇒M (0，a )，r 1＝a ⇒M到直线x ＋y ＝0的距离d ＝a 2⇒⎝⎛⎭⎫a 22＋2＝a 2⇒a ＝2⇒M (0，2)，r 1＝2，又N (1，1)，r 2＝1⇒|MN |＝2⇒|r 1－r 2|＜|MN |＜|r 1＋r 2|⇒两圆相交.8.(2017·资阳模拟)一块硬质材料的三视图如图所示，正(主)视图和俯视图都是边长为10 cm 的正方形，将该木料切削、打磨，加工成球，则能得到的最大球的半径最接近( )A.3 cmB.4 cmC.5 cmD.6 cm答案 A解析 由题意得几何体为一个三棱柱，底面是腰为10的等腰直角三角形，高为10，得到的最大球的半径为等腰直角三角形的内切圆的半径，其半径为10＋10－1022＝10－52≈2.93，最接近3 cm ，故选A.9.已知两组样本数据{x 1，x 2，…，x n }的平均数为h ，{y 1，y 2，…，y m }的平均数为k ，则把两组数据合并成一组以后，这组样本的平均数为( ) A.h ＋k 2 B.nh ＋mk m ＋n C.mh ＋nk m ＋n D.h ＋k m ＋n答案 B解析 因为样本数据{x 1，x 2，…，x n }的平均数为h ， {y 1，y 2，…，y m }的平均数为k ，所以第一组数据和为nh ，第二组数据和为mk ， 因此把两组数据合并成一组以后， 这组样本的平均数为nh ＋mkm ＋n，故选B.10.甲乙两人玩猜数字游戏，先由甲心中任想一个数字记为a ，再由乙猜甲刚才想的数字，把乙猜的数字记为b ，且a ，b ∈{0，1，2，…，9}.若|a －b |≤1，则称甲乙“心有灵犀”.现任意找两人玩这个游戏，则二人“心有灵犀”的概率为( ) A.725 B.925 C.750 D.950 答案 A解析 共有10×10＝100(种)猜字结果，其中满足|a －b |≤1的有：当a ＝0时，b ＝0，1；当a ＝1时，b ＝0，1，2；当a ＝2时，b ＝1，2，3；当a ＝3时，b ＝2，3，4；当a ＝4时，b ＝3，4，5；当a ＝5时，b ＝4，5，6；当a ＝6时，b ＝5，6，7；当a ＝7时，b ＝6，7，8；当a ＝8时，b ＝7，8，9；当a ＝9时，b ＝8，9，共28种，所以他们“心有灵犀”的概率为P ＝28100＝725，故选A.11.(2017·曲靖月考)已知函数f (x )＝x 2－kx －2在区间(1，5)上既没有最大值也没有最小值，则实数k 的取值范围是( ) A.[10，＋∞) B.(－∞，2]C.(－∞，2]∪[10，＋∞)D.(－∞，1]∪[5，＋∞) 答案 C解析 由已知可得k 2≤1或k2≥5⇒k ∈(－∞，2]∪[10，＋∞)，故选C.12.若存在m ，使得关于x 的方程x ＋a (2x ＋2m －4e x )·[ln(x ＋m )－ln x ]＝0成立，其中e 为自然对数的底数，则实数a 的取值范围是( ) A.(－∞，0)B.⎝⎛⎭⎫0，12e C.(－∞，0)∪⎣⎡⎭⎫12e ，＋∞ D.⎣⎡⎭⎫12e ，＋∞ 答案 C解析 由题意得－12a ＝⎝⎛⎭⎫1＋m x －2e ln ⎝⎛⎭⎫1＋m x ＝(t －2e)ln t ⎝⎛⎭⎫t ＝m x ＋1＞0，令f (t )＝(t －2e)ln t (t ＞0)，则f ′(t )＝ln t ＋1－2et ，(f ′(t ))′＝1t ＋2et2＞0，∴f ′(t )为增函数.当x ＞e 时，f ′(t )＞f ′(e)＝0，当0＜x ＜e 时，f ′(t )＜f ′(e)＝0， ∴f (t )≥f (e)＝－e ，∴－12a ≥－e ，解得a ＜0或a ≥12e，故选C.13.(2017·山西临汾五校联考)若tan α－1tan α＝32，α∈⎝⎛⎭⎫π4，π2，则sin ⎝⎛⎭⎫2α＋π4＝_______. 答案210解析 ∵tan α－1tan α＝32，α∈⎝⎛⎭⎫π4，π2， ∴sin αcos α－cos αsin α＝32，∴cos 2αsin 2α＝－34， ∵π4＜α＜π2， ∴π2＜2α＜π， 故cos 2α＝－35，sin 2α＝45，∴sin ⎝⎛⎭⎫2α＋π4＝sin 2α×22＋cos 2α×22＝210. 14.已知O 是边长为1的正三角形ABC 的中心，则(OA →＋OB →)·(OA →＋OC →)＝________. 答案 －16解析 如图所示，因为O 是边长为1的正三角形ABC 的中心，所以∠BAC ＝∠ABC ＝∠ACB ＝60°， ∠AOB ＝∠AOC ＝∠BOC ＝120°， OA ＝2OD ＝23×32＝33，由于AD 平分∠BAC ，∠BOC ， 所以OB →＋OC →＝2OD →＝－OA →，同理OA →＋OB →＝－OC →，OA →＋OC →＝－OB →，所以(OA →＋OB →)·(OA →＋OC →)＝(－OC →)·(－OB →)＝OC →·OB → ＝|OB →|2cos120°＝|OA →|2cos120°＝⎝⎛⎭⎫332×⎝⎛⎭⎫－12＝－16. 15.已知(x ＋a )2(x －1)3的展开式中x 4的系数为1，则a ＝________. 答案 2解析 (x ＋a )2(x －1)3的展开式中x 4的系数为1×(－3)＋2a ×1＝2a －3＝1， 所以a ＝2. 16.(2017·福建福州外国语学校模拟)在一项田径比赛中，甲、乙、丙三人的夺冠呼声最高.观众A ，B ，C 做了一项预测：A 说：“我认为冠军不会是甲，也不会是乙”.B 说：“我觉得冠军不会是甲，冠军会是丙”.C 说：“我认为冠军不会是丙，而是甲”.比赛结果出来后，发现A ，B ，C 三人中有一人的两个判断都对，一人的两个判断都错，还有一人的两个判断一对一错，根据以上情况可判断冠军是________.答案 甲解析 由题意知，B ，C 的预测截然相反，必一对一错，因为只有一个对，不论B ，C 谁对，A 必是一对一错，假设B 的预测是对的，则丙是冠军，那么A 说冠军也不会是甲，也不会是乙，即丙是冠军也对，这与题目中“一人的两个判断都对”相矛盾，即假设不成立，所以B 的预测是错误的，则C 的预测是对的，所以甲是冠军.2018年（人教版）高考数学选择填空限时训练(2)1.已知集合A ＝{x ∈R |x 2－x －2＜0}，B ＝{x ∈Z |x ＝2t ＋1，t ∈A }，则A ∩B 等于( ) A.{－1，0，1} B.{－1，0} C.{0，1} D.{0} 答案 C解析 A ＝{x ∈R |x 2－x －2＜0}＝{x |－1＜x ＜2}， 则x ＝2t ＋1∈(－1，5)，所以B ＝{0，1，2，3，4}， 所以A ∩B ＝{0，1}，故选C.2.(2017·四川联盟三诊)已知复数z 满足(2＋i)z ＝2－i(i 为虚数单位)，则z 等于( ) A.3＋4i B.3－4i C.35＋45i D.35－45i答案 D解析 由(2＋i)z ＝2－i ，得z ＝2－i 2＋i ＝(2－i )(2－i )(2＋i )(2－i )＝35－45i ，故选D.3.(2017·原创押题预测卷)给出计算12＋14＋16＋…＋12 018的值的一个程序框图(如图所示)，其中判断框内应填入的条件是( )A.i ＞1 009?B.i ＜1 009?C.i ＞2 018?D.i ＜2 018? 答案 A解析 由程序框图，得i ＝1，n ＝2，S ＝12；i ＝2，n ＝4，S ＝12＋14；i ＝3，n ＝6，S ＝12＋14＋16；…；i ＝1 009，n ＝2 018，S ＝12＋14＋16＋…＋12 018.故选A. 4.已知函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ为常数，A ＞0，ω＞0，|φ|＜π)的部分图象如图所示，则下列结论正确的是( )A.函数f (x )的最小正周期为π2B.直线x ＝－π12是函数f (x )图象的一条对称轴C.函数f (x )在区间⎣⎡⎦⎤－5π12，π6上单调递增D.将函数f (x )的图象向左平移π3个单位长度，得到函数g (x )的图象，则g (x )＝2sin 2x答案 D解析 A ＝2，T 2＝2π3－π6＝π2，即πω＝π2，即ω＝2，π2＋2π32＝7π12，当x ＝7π12时，2×7π12＋φ＝π2，解得φ＝－2π3，所以函数f (x )＝2sin ⎝⎛⎭⎫2x －2π3，函数图象向左平移π3个单位长度后得到函数y ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π3－2π3＝2sin 2x ，所以D 正确. 5.(2017·辽宁六校协作体联考)面积为332的正六边形的六个顶点都在球O 的球面上，球心O到正六边形所在平面的距离为22，记球O 的体积为V ，球O 的表面积为S ，则VS 的值为( )A.2B.1C. 3D. 2 答案 B解析 设正六边形的边长为a ， 则其面积S ＝6×34a 2＝332a 2， 由题意得332a 2＝332，所以a ＝1.由于正六边形的中心到顶点的距离为1， 所以球的半径为R ＝(22)2＋1＝3，所以V ＝4π3×27＝36π，S ＝4π×9＝36π，所以VS＝1.故选B.6.设A ，B 在圆x 2＋y 2＝1上运动，且|AB |＝3，点P 在直线3x ＋4y －12＝0上运动，则|P A →＋PB →|的最小值为( ) A.3 B.4 C.175 D.195答案 D解析 设AB 的中点为D ，由平行四边形法则可知P A →＋PB →＝2PD →， 所以当且仅当O ，D ，P 三点共线时，|P A →＋PB →|取得最小值，此时OP 垂直于直线3x ＋4y －12＝0，OP ⊥AB ， 因为圆心到直线的距离为129＋16＝125， |OD |＝1－34＝12， 所以|P A →＋PB →|取得最小值2⎝⎛⎭⎫125－12＝195.7.(2017·郑州检测)某几何体的三视图如图所示，则其体积为( )A.207B.216－9π2C.216－36πD.216－18π答案 B解析 观察三视图可知，这个几何体是挖去14个底面圆半径为3，高为6的圆锥的边长为6的正方体，所以几何体的体积是正方体的体积减去14个圆锥的体积，即几何体的体积等于63－14×13×9π×6＝216－9π2，故选B. 8.(2017·天津六校联考)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若c 2＝(a －b )2＋6，C ＝π3，则△ABC 的面积为( )A.3B.932C.332D.3 3答案 C解析 因为c 2＝(a －b )2＋6， 所以c 2＝a 2＋b 2－2ab ＋6，由C ＝π3，得c 2＝a 2＋b 2－2ab cos π3＝a 2＋b 2－ab ，因此a 2＋b 2－ab ＝a 2＋b 2－2ab ＋6，即ab ＝6， 所以△ABC 的面积为12ab sin π3＝332，故选C.9.(2017·抚顺一模)在某市记者招待会上，需要接受本市甲、乙两家电视台记者的提问，两家电视台均有记者5人，主持人需要从这10名记者中选出4名记者提问，且这4人中，既有甲电视台记者，又有乙电视台记者，且甲电视台的记者不可以连续提问，则不同的提问方式的种数为( )A.1 200B.2 400C.3 000D.3 600 答案 B解析 若4人中，有甲电视台记者1人，乙电视台记者3人，则不同的提问方式总数是C 15C 35A 44＝1 200；若4人中，有甲电视台记者2人，乙电视台记者2人，则不同的提问方式总数是C 25C 25A 22A 23＝1 200；若4人中，有甲电视台记者3人，乙电视台记者1人，则不符合主持人的规定，故所有不同提问方式的总数为1 200＋1 200＝2 400. 10.已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y －2≤0，x ＋2y －5≥0，y －2≤0，则z ＝y ＋1x ＋1的范围是( )A.⎣⎡⎦⎤13，2B.⎣⎡⎦⎤－12，12C.⎣⎡⎦⎤12，32D.⎣⎡⎦⎤32，52 答案 C解析 在平面直角坐标系中作出可行域⎩⎪⎨⎪⎧x －y －2≤0，x ＋2y －5≥0，y －2≤0.由斜率公式可知z ＝y ＋1x ＋1表示可行域内的点M (x ，y )与点P (－1，－1)连线的斜率，由图可知z max ＝2＋11＋1＝32，z min ＝1＋13＋1＝12，故选C.11.已知{a n }为等比数列， a 1>0，a 4＋a 7＝2，a 5a 6＝－8，则a 1＋a 4＋a 7＋a 10等于( ) A.－7 B.－5 C.5 D.7 答案 B解析 由等比数列的性质可得a 5a 6＝a 4a 7＝－8，又a 4＋a 7＝2，解得a 4＝－2，a 7＝4或a 7＝－2，a 4＝4，因为a 7＝a 1q 6>0，所以a 4＝－2，a 7＝4，a 7＝a 4q 3＝－2q 3＝4，所以q 3＝－2，所以a 1＝a 4q3＝1，a 10＝a 7q 3＝－8，所以a 1＋a 4＋a 7＋a 10＝－5，故选B.12.已知函数f (x )的导函数为f ′(x )，且f (1)＝12，不等式f ′(x )≤1x ＋x 的解集为(0，1]，则不等式f (x )－ln x x 2＞12的解集为( )A.(0，1)B.(0，＋∞)C.(1，＋∞)D.(0，1)∪(1，＋∞)答案 D解析 因为x ＞0，所以待求不等式可化为f (x )＞ln x ＋x 22，构造函数g (x )＝f (x )－ln x －x 22，则g ′(x )＝f ′(x )－1x －x ，因为不等式f ′(x )≤1x ＋x 的解集为(0，1]，所以在(0，1]上，g ′(x )≤0，所以函数g (x )在(0，1]上单调递减，故g (x )在(1，＋∞)上单调递增，g (x )min ＝g (1)＝f (1)－ln 1－12＝0，所以g (x )＞0的解集为(0，1)∪(1，＋∞).13.(2017·四川凉山州一诊)设向量a ＝(cos x ，－sin x )，b ＝⎝⎛⎭⎫－cos ⎝⎛⎭⎫π2－x ，cos x ，且a ＝t b ，t ≠0，则sin 2x ＝________. 答案 ±1解析 因为b ＝⎝⎛⎭⎫－cos ⎝⎛⎭⎫π2－x ，cos x ＝(－sin x ，cos x )，a ＝t b ， 所以cos x cos x －(－sin x )(－sin x )＝0， 即cos 2x －sin 2x ＝0， 所以tan 2x ＝1，tan x ＝±1， x ＝k π2＋π4(k ∈Z )，2x ＝k π＋π2(k ∈Z )，故sin 2x ＝±1.14.设P 为直线y ＝b 3a x 与双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)左支的交点，F 1是左焦点，PF 1垂直于x 轴，则双曲线的离心率e ＝________. 答案324解析 设P (－c ，y 0)，代入双曲线C ∶x 2a 2－y 2b2＝1，得y 20＝⎝⎛⎭⎫b 2a 2，由题意知y 0＜0，∴y 0＝－b 2a， 又∵P 在直线y ＝b3a x 上，代入得c ＝3b ，又∵c 2＝a 2＋b 2， ∴e ＝c a ＝324.15.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且(2a ＋2c －b )cos C ＝(a ＋c )cos B ＋b cos A ，若c ＝3，则a ＋b 的最大值为________. 答案 6解析 由正弦定理可得2sin A cos C ＋2sin C cos C －sin B cos C ＝sin A cos B ＋sin C cos B ＋sin B cos A ，即2sin A cos C ＋2sin C cos C ＝sin(B ＋C )＋sin(A ＋B )，也即2(sin A ＋sin C )cos C ＝sin A ＋sin C ，因为在△ABC 中，sin A ＋sin C ＞0， 所以2cos C ＝1，由此可得cos C ＝12，由余弦定理可得9＝a 2＋b 2－ab ，即(a ＋b )2＝9＋3ab ， 又ab ≤14(a ＋b )2，所以14(a ＋b )2≤9⇒a ＋b ≤6，故所求a ＋b 的最大值是6.16.(2017·北京东城区二模)已知函数f (x )＝⎩⎪⎨⎪⎧|x －1|，x ∈(0，2]，min{|x －1|，|x －3|}，x ∈(2，4]，min{|x －3|，|x －5|}，x ∈(4，＋∞).①若f (x )＝a 有且只有一个根，则实数a 的取值范围是________.②若关于x 的方程f (x ＋T )＝f (x )有且仅有3个不同的实根，则实数T 的取值范围是______. 答案 ①(1，＋∞) ②(－4，－2)∪(2，4)解析 ①作出函数f (x )的图象，f (x )＝a 有且只有一个根等价于y ＝f (x )的图象与y ＝a 有一个交点，故可得a ＞1，即a 的取值范围是(1，＋∞)；②方程f (x ＋T )＝f (x )有且仅有3个不同的实根等价于y ＝f (x ＋T )的图象与y ＝f (x )的图象有3个交点，而y ＝f (x ＋T )的图象是将y ＝f (x )的图象向左或向右平移|T |个单位，故可得T 的取值范围是(－4，－2)∪(2，4).2018年（人教版）高考数学选择填空限时训练(3)1.已知集合M ＝{x |x 2－x －2＜0}，N ＝⎩⎨⎧⎭⎬⎫y |y ＝－12x 2＋1，x ∈R ，则M ∩N 等于( )A.{x |－2≤x ＜1}B.{x |1＜x ＜2}C.{x |－1＜x ≤1}D.{x |1≤x ＜2}答案 C解析 M ＝{x |－1＜x ＜2}，N ＝{y |y ≤1}，则M ∩N ＝{x |－1＜x ≤1}，故选C.2.(2017·重庆模拟)已知a ＋2ii ＝b ＋i(a ，b 是实数)，其中i 是虚数单位，则ab 等于( )A.－2B.－1C.1D.3 答案 A解析 由题设可得a ＋2i ＝b i －1， 则a ＝－1，b ＝2， 故ab ＝－2，故选A.3.某校组织由5名学生参加的演讲比赛，采用抽签法决定演讲顺序，在“学生A 和B 都不是第一个出场，B 不是最后一个出场”的前提下，学生C 第一个出场的概率为( ) A.13 B.15 C.19 D.320 答案 A解析 先排B ，有A 13(非第一与最后)种方法，再排A 有A 13(非第一)种方法，其余3人自由排，共有A 13A 13A 33＝54(种)方法，这是总结果；学生C 第一个出场，先排B ，有A 13(非第一与最后)种方法，再排A 有A 13种方法，C 第一个出场，剩余2人自由排，故有A 13A 13A 22＝18(种)，故学生C 第一个出场的概率为1854＝13. 4.(2017·安阳模拟)已知函数f (x )＝A sin(2x ＋φ)－12⎝⎛⎭⎫A ＞0，0＜φ＜π2的图象在y 轴上的截距为1，且关于直线x ＝π12对称，若对于任意的x ∈⎣⎡⎦⎤0，π2，都有m 2－3m ≤f (x )，则实数m 的取值范围为( )A.⎣⎡⎦⎤1，32B.[1，2]C.⎣⎡⎦⎤32，2D.⎣⎢⎡⎦⎥⎤3－132，3＋132 答案 B解析 由已知得，sin ⎝⎛⎭⎫2×π12＋φ＝1⇒φ＝π3， f (0)＝1⇒A sin π3－12＝1⇒A ＝3，则f (x )＝3sin ⎝⎛⎭⎫2x ＋π3－12，当x ∈⎣⎡⎦⎤0，π2时，π3≤2x ＋π3≤4π3， 所以f (x )min ＝f ⎝⎛⎭⎫4π3＝－2， 则m 2－3m ≤－2⇒m 2－3m ＋2≤0， 解得1≤m ≤2，故选B.5.(2017届云南省云南师范大学附属中学月考)四面体P ABC 的四个顶点都在球O 的球面上，P A ＝8，BC ＝4，PB ＝PC ＝AB ＝AC ，且平面PBC ⊥平面ABC ，则球O 的表面积为( ) A.64π B.65π C.66π D.128π 答案 B解析 如图，D ，E 分别为BC ，P A 的中点，易知球心O 点在线段DE 上， ∵PB ＝PC ＝AB ＝AC ， 则PD ⊥BC ，AD ⊥BC ，PD ＝AD . 又∵平面PBC ⊥平面ABC ， 平面PBC ∩平面ABC ＝BC ， ∴PD ⊥平面ABC ， ∴PD ⊥AD ， ∴PD ＝AD ＝4 2. ∵点E 是P A 的中点，∴ED ⊥P A ，且ED ＝EA ＝PE ＝4.设球O 的半径为R ，OE ＝x ，则OD ＝4－x ， 在Rt △OEA 中，有R 2＝16＋x 2， 在Rt △OBD 中，有R 2＝4＋(4－x )2， 解得R 2＝654，∴S ＝4πR 2＝65π.故选B.6.(2017·唐山模拟)一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图，若输入的n ＝12，则输出的结果b 等于( )A.4B.72C.9728D.6414答案 C解析 n ＝12，a ＝6，i ＝1，b ＝4.满足i ＜3，第一次循环：i ＝2，a ＝4，b ＝72；满足i ＜3，第二次循环：i ＝3，a ＝72，b ＝9728；不满足i ＜3，退出循环.故选C.7.(2017·绵阳中学模拟)已知正项等比数列{a n }满足：a 7＝a 6＋2a 5，若存在两项a m ，a n ，使得a m a n ＝4a 1，则1m ＋16n的最小值为( )A.256B.32C.83D.215 答案 D解析 设正项等比数列{a n }的公比为q ，且q ＞0， 由a 7＝a 6＋2a 5，得q 2－q －2＝0，解得q ＝2或q ＝－1(舍去)，因为a m a n ＝16a 21， 所以(a 1q m －1)(a 1q n －1)＝16a 21， 则q m ＋n －2＝16，解得m ＋n ＝6，所以1m ＋16n ＝16×(m ＋n )×⎝⎛⎭⎫1m ＋16n ＝16⎝⎛⎭⎫17＋n m ＋16m n ≥16⎝⎛⎭⎫17＋2n m ×16m n ＝256， 因为mn 取整数，验证可得，当m ＝1，n ＝5时，取最小值为215.8.(2017·贵阳模拟)过点M ⎝⎛⎭⎫22，－22作圆x 2＋y 2＝1的切线l ，l 与x 轴的交点为抛物线E ：y 2＝2px (p ＞0)的焦点，l 与抛物线E 交于A ，B 两点，则AB 的中点到抛物线E 的准线的距离为( )A.522B.32C.722 D.4 2答案 D解析 由题意得，过点M ⎝⎛⎭⎫22，－22作圆x 2＋y 2＝1的切线l ， 可得直线l 的方程为x －y －2＝0， 此时直线l 与x 轴的交点坐标为(2，0)， 又(2，0)与抛物线的焦点重合， 即p2＝2，解得p ＝22， 即y 2＝42x ，且准线方程为x ＝－2，联立方程组⎩⎪⎨⎪⎧y 2＝42x ，x －y －2＝0，整理得x 2－62x ＋2＝0， 则x 1＋x 2＝62，则x 1＋x 22＝32，所以AB 的中点到抛物线的准线的距离为x 1＋x 22＋2＝42，故选D.9.(2017·江西省师大附中、临川一中联考)某空间几何体的三视图如图所示，则该几何体的体积为( )A.73B.8－π3C.83D.7－π3 答案 B解析 由三视图中提供的数据信息和几何特征可知该几何体是一个四棱锥去掉半圆锥的组合体，其体积V ＝13×2×2×2－13×12π×1×2＝8－π3.10.如图，茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污染，则甲的平均成绩超过乙的平均成绩的概率为( )A.12B.35C.45D.710 答案 C解析 由茎叶图可知，甲的平均成绩为x 甲＝88＋89＋90＋91＋925＝90，乙的平均成绩为x乙＝83＋83＋87＋99＋x5，因为x 甲＞x 乙，即352＋x ＜450，得到x ＜98，又由题意可知x≥90，且x 是整数，故基本事件有从90到99共10个，而满足条件的有从90到97共8个，故甲的平均成绩超过乙的平均成绩的概率为P ＝810＝45，故选C.11.(2017·江西省师大附中、临川一中联考)已知将函数f (x )＝3sin x cos x ＋cos 2x －12的图象向左平移5π12个单位长度后得到y ＝g (x )的图象，则g (x )在⎣⎡⎦⎤－π12，π3上的值域为( ) A.⎣⎡⎦⎤－12，1 B.⎣⎡⎦⎤－1，12 C.⎣⎡⎦⎤－32，12 D.⎣⎡⎦⎤－12，32 答案 B 解析 因为f (x )＝32sin 2x ＋12cos 2x ＝sin ⎝⎛⎭⎫2x ＋π6， 故g (x )＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋5π12＋π6＝sin(2x ＋π)＝－sin 2x ， 因为－π12≤x ≤π3，故－π6≤2x ≤2π3，则－12≤sin 2x ≤1，所以－1≤g (x )≤12，故选B.12.(2017届湖南衡阳期末)函数f (x )在定义域(0，＋∞)内恒满足：①f (x )＞0，②2f (x )＜xf ′(x )＜3f (x )，其中f ′(x )为f (x )的导函数，则( )A.14＜f (1)f (2)＜12B.116＜f (1)f (2)＜18C.13＜f (1)f (2)＜12D.18＜f (1)f (2)＜14 答案 D解析 令g (x )＝f (x )x 2，x ∈(0，＋∞)，则g ′(x )＝xf ′(x )－2f (x )x 3，∵∀x ∈(0，＋∞)，2f (x )＜xf ′(x )＜3f (x )恒成立， f (x )＞0，∴g ′(x )＝xf ′(x )－2f (x )x 3＞0，∴函数g (x )在x ∈(0，＋∞)上单调递增， ∴f (1)1＜f (2)4，∴f (1)f (2)＜14. 令h (x )＝f (x )x 3，x ∈(0，＋∞)，则h ′(x )＝xf ′(x )－3f (x )x 4，∵∀x ∈(0，＋∞)，2f (x )＜xf ′(x )＜3f (x )恒成立， ∴h ′(x )＝xf ′(x )－3f (x )x 4＜0，∴函数h (x )在x ∈(0，＋∞)上单调递减， ∴f (1)1＞f (2)8，∴f (1)f (2)＞18. 综上可得18＜f (1)f (2)＜14，故选D.13.在周长为10的△ABC 中，AB ＝2，则CA →·CB →的最小值是________. 答案 14解析 设CA ＝m ，CB ＝n ，则m ＋n ＝8，所以由余弦定理可得CA →·CB →＝mn cos C＝m 2＋n 2－42＝()m ＋n 2－2mn －42＝82－4－2mn 2＝30－mn ，又因为mn ≤⎝⎛⎭⎪⎫m ＋n 22＝16， 当且仅当m ＝n ＝4时，等号成立. 所以CA →·CB →≥30－16＝14.14.若ʃm 1(2x －1)d x ＝6，则二项式(1－2x )3m 的展开式中各项系数和为________.答案 －1解析 ʃm 1(2x －1)d x ＝(x 2－x )|m 1＝m 2－m ＝6，m ＝3(m ＝－2舍去)，令x ＝1，则(1－2×1)9＝－1，即为所求系数和.15.若数列{a n }满足a 1＋3a 2＋32a 3＋…＋3n －1a n ＝n 2(n ∈N *)，其前n 项和为S n ，则S n ＝____.答案 34⎝⎛⎭⎫1－13n 解析 因为a 1＋3a 2＋32a 3＋…＋3n －1a n ＝n2，所以当n ≥2时有a 1＋3a 2＋32a 3＋…＋3n －2a n －1＝n －12， 两式作差得3n －1a n ＝12，所以a n ＝12·13n －1(n ≥2，n ∈N *)，又因为当n ＝1时，a 1＝12适合此式，所以数列{}a n 的通项公式为a n ＝12·13n －1，所以S n ＝12⎝⎛⎭⎫1－13n 1－13＝34⎝⎛⎭⎫1－13n . 16.已知双曲线x 2－y 23＝1上存在两点M ，N 关于直线y ＝x ＋m 对称，且MN 的中点在抛物线y 2＝18x 上，则实数m 的值为________. 答案 0或－8解析 因为点M ，N 关于直线y ＝x ＋m 对称， 所以MN 的垂直平分线为y ＝x ＋m ， 所以直线MN 的斜率为－1. 设线段MN 的中点P (x 0，x 0＋m )， 直线MN 的方程为y ＝－x ＋b ， 则x 0＋m ＝－x 0＋b ， 所以b ＝2x 0＋m .由⎩⎪⎨⎪⎧y ＝－x ＋b ，x 2－y 23＝1，得2x 2＋2bx －b 2－3＝0， 所以x M ＋x N ＝－b ， 所以x 0＝－b 2，所以b ＝m2，所以P ⎝⎛⎭⎫－m 4，34m . 因为MN 的中点在抛物线y 2＝18x 上， 所以916m 2＝－92m ，解m ＝0或m ＝－8.2018年（人教版）高考数学选择填空限时训练(4)1.(2017·湖北部分重点中学联考)已知集合A ＝{x |x 2－2x －3＞0}，集合B ＝{x |0＜x ＜4}，则(∁R A )∩B 等于( )A.(0，3]B.[－1，0)C.[－1，3]D.(3，4) 答案 A解析 因为A ＝{x |x ＜－1或x ＞3}， 故∁R A ＝{x |－1≤x ≤3}，B ＝{x |0＜x ＜4}， 所以(∁R A )∩B ＝{x |0＜x ≤3}，故选A.2.(2017·安阳模拟)设i 为虚数单位，若复数a ＋2i1＋i 为纯虚数，则实数a 的值为( )A.－1B.1C.－2D.2 答案 C解析 由题意，得a ＋2i 1＋i ＝a ＋22＋2－a2i ，则⎩⎪⎨⎪⎧a ＋22＝0，2－a 2≠0⇒a ＝－2，故选C.3.(2017·绵阳中学实验学校模拟)将函数f (x )＝sin ⎝⎛⎭⎫3π2＋x ·(cos x －2sin x )＋sin 2x 的图象向左平移π8个单位长度后得到函数g (x )，则g (x )具有性质( ) A.在⎝⎛⎭⎫0，π4上单调递增，为奇函数 B.周期为π，图象关于⎝⎛⎭⎫π4，0对称 C.最大值为2，图象关于直线x ＝π2对称D.在⎝⎛⎭⎫－π2，0上单调递增，为偶函数 答案 A解析 函数的解析式为f (x )＝sin ⎝⎛⎭⎫3π2＋x (cos x －2sin x )＋sin 2x ＝sin 2x －cos 2x ＝2sin ⎝⎛⎭⎫2x －π4， 将其图象向左平移π8个单位长度，得到函数g (x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π8－π4＝2sin 2x 的图象， 则g (x )为奇函数，且在⎝⎛⎭⎫0，π4上单调递增，故A 正确. 4.(2017·宝鸡检测)为了得到函数y ＝sin ⎝⎛⎭⎫2x －π3的图象，只需把函数y ＝cos ⎝⎛⎭⎫2x －4π3的图象( )A.向左平移π4个单位长度B.向右平移π4个单位长度C.向左平移π2个单位长度D.向右平移π2个单位长度答案 A解析 y ＝cos ⎝⎛⎭⎫2x －4π3＝sin ⎝⎛⎭⎫2x －4π3＋π2＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4－π3， 所以函数y ＝cos ⎝⎛⎭⎫2x －4π3的图象向左平移π4个单位长度得到函数y ＝sin ⎝⎛⎭⎫2x －π3的图象，故选A.5.过点M (2，－2p )引抛物线x 2＝2py (p ＞0)的切线，切点分别为A ，B ，若|AB |＝410，则p 的值是( ) A.1或2 B.2或2 C.1 D.2答案 A解析 设切点为⎝⎛⎭⎫t ，12p t 2，因为y ′＝1p x ， 则切线斜率k ＝12p t 2＋2p t －2＝1p t ，整理可得t 2－4t －4p 2＝0，由根与系数的关系可得t 1＋t 2＝4，t 1t 2＝－4p 2， 则(t 1－t 2)2＝(t 1＋t 2)2－4t 1t 2＝16(1＋p 2). 设切点A ⎝⎛⎭⎫t 1，t 212p ，B ⎝⎛⎭⎫t 2，t 222p ， 则|AB |＝(t 1－t 2)2＋⎝ ⎛⎭⎪⎫t 21－t 222p 2＝(t 1－t 2)2⎣⎡⎦⎤1＋⎝⎛⎭⎫12p 2(t 1＋t 2)2， 即|AB |＝4(1＋p 2)⎝⎛⎭⎫1＋4p 2， 所以(1＋p 2)⎝⎛⎭⎫1＋4p 2＝10， 即p 4－5p 2＋4＝0， 解得p 2＝1或p 2＝4， 即p ＝1或p ＝2，故选A.6.(2017·云南大理检测)已知三棱锥A －BCD 的所有顶点都在球O 的球面上，AB 为球O 的直径，若该三棱锥的体积为433，BC ＝4，BD ＝3，∠CBD ＝90°，则球O 的表面积为( )A.11πB.20πC.23πD.35π 答案 C解析 设棱锥的高为h ， 因为S △BCD ＝12×BC ×BD ＝23，所以V A －BCD ＝13S △BCD ×h ＝433，所以h ＝2，因此点O 到平面BCD 的距离为1， 因为△BCD 外接圆的直径为19， 所以OB ＝1＋194＝232，所以球O 的表面积为S ＝4πr 2＝23π，故选C.7.(2017·湖北部分重点中学联考)一个几何体的三视图如图所示，则该几何体的外接球的表面积为( )A.36πB.8πC.9π2D.27π8答案 B解析 从题设中三视图所提供的图形信息与数据信息可知该几何体是棱长为2，2，2的长方体的一角所在三棱锥，其外接球与该长方体的外接球相同，其直径是该长方体的对角线l ＝22＋(2)2＋(2)2＝22，故球的半径为R ＝2，所以该外接球的表面积S ＝4π(2)2＝8π，故选B.8.已知点P 为不等式组⎩⎪⎨⎪⎧x －2y ＋1≥0，x ≤2，x ＋y －1≥0所表示的平面区域内的一点，点Q 是圆M ：(x ＋1)2＋y 2＝1上的一个动点，则|PQ |的最大值是( ) A.35＋22B.25＋33C.253D.10答案 A解析 由题意得，画出不等式组所表示的平面区域，如图中阴影部分所示，由题意知点A到圆心(－1，0)的距离最远，由⎩⎪⎨⎪⎧x －2y ＋1＝0，x ＝2，解得A ⎝⎛⎭⎫2，32，最远距离为d ＝(2＋1)2＋⎝⎛⎭⎫322＝352，所以|PQ |的最大值为352＋1＝35＋22，故选A.9.(2017·湖南师大附中月考)阅读如图所示的程序框图，若输出的数据为58，则判断框中应填入的条件为( )A.k ≤3?B.k ≤4?C.k ≤5?D.k ≤6? 答案 B解析 第一次循环，S ＝12＝1，k ＝2； 第二次循环，S ＝2×1＋22＝6，k ＝3； 第三次循环，S ＝2×6＋32＝21，k ＝4； 第四次循环，S ＝2×21＋42＝58，k ＝5， 最后输出的数据为58，所以判断框中应填入k ≤4？，故选B.10.(2017·云南大理检测)已知三个函数f (x )＝2x ＋x ，g (x )＝x －1，h (x )＝log 3x ＋x 的零点依次为a ，b ，c ，则( ) A.a ＜b ＜c B.b ＜a ＜c C.c ＜a ＜b D.a ＜c ＜b答案 D解析 由题意知f (x )，g (x )，h (x )均为各自定义域上的增函数，且有唯一零点， 因为f (－1)＝12－1＝－12＜0，f (0)＝1>0，所以－1＜a ＜0， 由g (x )＝0可得x ＝1，所以b ＝1，h ⎝⎛⎭⎫13＝－1＋13＝－23＜0，h (1)＝1>0，所以13＜c ＜1，所以a ＜c ＜b ，故选D.11.(2017·安阳模拟)已知当x ＝θ时，函数f (x )＝2sin x －cos x 取得最大值，则sin ⎝⎛⎭⎫2θ＋π4等于( )A.7210B.210C.－210D.－7210 答案 D解析 因为f (x )＝5sin(x －φ)， 所以f (x )max ＝5， 其中cos φ＝25，sin φ＝15， 当x －φ＝2k π＋π2，k ∈Z 时，函数取得最大值，即θ＝2k π＋π2＋φ，k ∈Z 时函数取得最大值.由于sin 2θ＝－sin 2φ＝－2×25×15＝－45，cos 2θ＝－cos 2φ＝－(2cos 2φ－1)＝－35，故sin ⎝⎛⎭⎫2θ＋π4＝22(sin 2θ＋cos 2θ)＝－75×22＝－7210，故选D. 12.(2017·贵州贵阳市适应性考试)已知M 是函数f (x )＝e －2|x －1|＋2sin ⎣⎡⎦⎤π⎝⎛⎭⎫x －12在x ∈[－3，5]上的所有零点之和，则M 的值为( ) A.4 B.6 C.8 D.10 答案 C解析 因为f (x )＝e －2|x －1|＋2sin ⎣⎡⎦⎤π⎝⎛⎭⎫x －12＝e －2|x －1|－2cos πx ， 所以f (x )＝f (2－x )， 因为f (1)≠0，所以函数零点有偶数个，两两关于x ＝1对称. 当x ∈[1，5]时，y ＝e －2(x －1)∈(0，1]，且单调递减； y ＝2cos πx ∈[－2，2]，且在[1，5]上有两个周期，因此当x ∈[1，5]时，y ＝e －2(x －1)与y ＝2cos πx 有4个不同的交点， 从而所有零点之和为4×2＝8，故选C. 13.(2017·宁夏银川二模)我们把满足：x n ＋1＝x n －f (x n )f ′(x n )的数列{x n }叫做牛顿数列.已知函数f (x )＝x 2－1，数列{x n }为牛顿数列，设a n ＝ln x n －1x n ＋1，已知a 1＝2，则a 3＝________.答案 8解析 由f (x )＝x 2－1，得f ′(x )＝2x ，则x n ＋1＝x n －x 2n －12x n ＝x 2n ＋12x n ，所以x n ＋1－1＝(x n －1)22x n，x n ＋1＋1＝(x n ＋1)22x n ，所以x n ＋1－1x n ＋1＋1＝(x n －1)2(x n ＋1)2，所以ln x n ＋1－1x n ＋1＋1＝ln (x n －1)2(x n ＋1)2＝2ln x n －1x n ＋1，即a n ＋1＝2a n ，所以数列{a n }是首项为2，公比为2的等比数列，则a 3＝2×22＝8.14.已知直角梯形ABCD 中，AD ∥BC ，∠ADC ＝90°，AD ＝2，BC ＝1，点P 是腰DC 上的动点，则|P A →＋3PB →|的最小值为________. 答案 5解析 方法一 以点D 为原点，分别以DA ，DC 所在直线为x ，y 轴，建立如图所示的平面直角坐标系，设DC ＝a ，DP ＝x .∴D (0，0)，A (2，0)，C (0，a )，B (1，a )，P (0，x )，P A →＝(2，－x )，PB →＝(1，a －x )，∴P A →＋3PB →＝(5，3a －4x )，|P A →＋3PB →|2＝25＋(3a －4x )2≥25， ∴|P A →＋3PB →|的最小值为5. 方法二 设DP →＝xDC →(0＜x ＜1)，∴PC →＝(1－x )DC →，P A →＝DA →－DP →＝DA →－xDC →， PB →＝PC →＋CB →＝(1－x )DC →＋12DA →，∴P A →＋3PB →＝52DA →＋(3－4x )DC →，|P A →＋3PB →|2＝254DA →2＋2×52×(3－4x )DA →·DC →＋(3－4x )2DC 2→＝25＋(3－4x )2DC →2≥25，∴|P A →＋3PB →|的最小值为5.15.点P 在双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右支上，其左、右焦点分别为F 1，F 2，直线PF 1与以坐标原点O 为圆心、a 为半径的圆相切于点A ，线段PF 1的垂直平分线恰好过点F 2，则该双曲线的渐近线的斜率为________. 答案 ±43解析 如图，A 是切点，B 是PF 1的中点，因为|OA |＝|a |，所以|BF 2|＝2a ，又|F 1F 2|＝2c ，所以|BF 1|＝2b ，|PF 1|＝4b ，又|PF 2|＝|F 1F 2|＝2c ，根据双曲线的定义，有|PF 1|－|PF 2|＝2a ，即4b －2c ＝2a ，两边平方并化简得3c 2－2ac －5a 2＝0，所以c a ＝53，因此ba＝⎝⎛⎭⎫c a 2－1＝43.16.已知数列{}a n 的前n 项和为S n ，S n ＝43()a n －1，则()4n －2＋1⎝⎛⎭⎫16a n ＋1的最小值为______. 答案 4解析 ∵S n ＝43()a n －1，∴S n －1＝43()a n －1－1()n ≥2，∴a n ＝S n －S n －1＝43()a n －a n －1，∴a n ＝4a n －1.又a 1＝S 1＝43()a 1－1，∴a 1＝4，∴{}a n 是首项为4，公比为4的等比数列， ∴a n ＝4n ， ∴()4n －2＋1⎝⎛⎭⎫16a n ＋1＝⎝⎛⎭⎫4n 16＋1⎝⎛⎭⎫164n ＋1＝2＋4n16＋164n ≥2＋2＝4，当且仅当n ＝2时取“＝”.2018年（人教版）高考数学选择填空限时训练(5)1.(2017·原创押题预测卷)已知集合A ＝{x |x 2－x －2＜0}，B ＝{y |y ＝3x ，x ≤0}，则A ∩(∁R B )等于( )A.(－1，0]B.(1，2)C.(－1，0]∪(1，2)D.(0，1] 答案 C解析 因为A ＝{x |x 2－x －2＜0}＝{x |－1＜x ＜2}，B ＝{y |y ＝3x ，x ≤0}＝{y |0＜y ≤1}，所以∁R B ＝(－∞，0]∪(1，＋∞)，所以A ∩(∁R B )＝(－1，0]∪(1，2)，故选C.2.(2017·广东七校联考)已知()a ＋i ()1－b i ＝2i(其中a ，b 均为实数，i 为虚数单位)，则||a ＋b i 等于( )A.2B.2C.1D.1或 2 答案 B解析 因为(a ＋i)(1－b i)＝a ＋b ＋(1－ab )i ＝2i ，所以⎩⎪⎨⎪⎧ a ＋b ＝0，1－ab ＝2，解得⎩⎪⎨⎪⎧ a ＝1，b ＝－1或⎩⎪⎨⎪⎧a ＝－1，b ＝1，所以|a ＋b i|＝2，故选B.3.给出如图所示的程序框图，若输入的x 的值为－5，则输出的y 值是( ) A.－2 B.－1 C.0 D.1答案 C解析 由程序框图得：若输入的x 的值为－5，⎝⎛⎭⎫12－5＝25＝32>2， 程序继续运行x ＝－3，⎝⎛⎭⎫12－3＝23＝8>2， 程序继续运行x ＝－1，⎝⎛⎭⎫12－1＝2， 不满足⎝⎛⎭⎫12x >2，∴执行y ＝log 2x 2＝log 21＝0，故选C.4.(2017·江西九江地区联考)函数f (x )＝⎩⎪⎨⎪⎧2cos πx ，－1＜x ＜0，e2x －1，x ≥0满足f ⎝⎛⎭⎫12＋f (a )＝2，则a 的所有可能值为( ) A.12 B.2 C.13 D.12或－13 答案 D解析 由已知得f ⎝⎛⎭⎫12＝1，因为f ⎝⎛⎭⎫12＋f (a )＝2， 所以f (a )＝1，所以⎩⎪⎨⎪⎧ －1＜a ＜0，2cos πa ＝1或⎩⎪⎨⎪⎧a ≥0，e 2a －1＝1，解得a ＝12或－13，故选D.5.(2017·天津南开区模拟)已知过点A (－2，m )和B (m ，4)的直线与直线2x ＋y －1＝0平行，则m 的值为( ) A.0 B.－8 C.2 D.10 答案 B解析 因为直线2x ＋y －1＝0的斜率为－2，所以过点A (－2，m )和B (m ，4)的直线的斜率k ＝－2，所以4－mm ＋2＝－2，解得m ＝－8，故选B.6.(2017届长郡中学模拟)已知f (x )＝sin(ωx ＋φ)(ω＞0，－π＜φ＜0)的最小正周期是π，将f (x )的图象向左平移π3个单位长度后所得的函数图象过点P (0，1)，则f (x )＝sin(ωx ＋φ)( )A.在区间⎣⎡⎦⎤－π6，π3上单调递减 B.在区间⎣⎡⎦⎤－π6，π3上单调递增 C.在区间⎣⎡⎦⎤－π3，π6上单调递减 D.在区间⎣⎡⎦⎤－π3，π6上单调递增 答案 B解析 由题设T ＝π＝2πω⇒ω＝2，则f (x )＝sin(2x ＋φ)，向左平移π3个单位长度后可得g (x )＝sin ⎝⎛⎭⎫2x ＋2π3＋φ，其图象经过点P (0，1)，即sin ⎝⎛⎭⎫2π3＋φ＝1， 因为－π＜φ＜0，解得φ＝－π6，所以f (x )＝sin ⎝⎛⎭⎫2x －π6， 在区间⎣⎡⎦⎤－π6，π3上，2x －π6∈⎣⎡⎦⎤－π2，π2. 函数f (x )在⎣⎡⎦⎤－π6，π3上单调递增，在区间⎣⎡⎦⎤－π3，π6上，2x －π6∈⎣⎡⎦⎤－5π6，π6， 函数f (x )在⎣⎡⎦⎤－π3，π6上不单调. 7.在等比数列{}a n 中，a 2，a 18是方程x 2＋6x ＋4＝0的两根，则a 4a 16＋a 10等于( ) A.6 B.2 C.2或6 D.－2 答案 B解析 因为a 2，a 18是方程x 2＋6x ＋4＝0的两根， 所以a 2＋a 18＝－6，a 2·a 18＝4，所以a 2＜0，a 18＜0，又数列{}a n 为等比数列， 所以a 10＜0，所以a 10＝－a 2a 18＝－2， 所以a 4a 16＋a 10＝a 210＋a 10＝2，故选B.8.已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)以及双曲线y 2a 2－x 2b 2＝1(a >0，b >0)的渐近线将第一象限三等分，则双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为( )A.2或233B.6或233C.2或 3D.3或 6答案 A解析 由题意可知，双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的渐近线的倾斜角为30°或60°，则k ＝b a ，∴k ＝3或33，则e ＝ca，∴e ＝c 2a 2＝a 2＋b 2a 2＝1＋b 2a 2＝2或233. 9.(2017·吉林普通中学调研)给出下列命题： ①函数f (x )＝sin 2x 为偶函数； ②函数f (x )＝sin 2x 的最小正周期为π； ③函数y ＝ln(x ＋1)没有零点；④函数y ＝ln(x ＋1)在区间(－1，0)上是增函数. 其中正确命题的序号是( ) A.①④ B.①③ C.②③ D.②④ 答案 D解析 由正弦函数的性质可知：f (x )＝sin 2x ，则f (－x )＝sin(－2x )＝－sin 2x ＝－f (x )， 则f (x )＝sin 2x 为奇函数，故①错误；由y ＝sin 2x 的最小正周期为T ＝2πω＝π，故②正确；令函数y ＝ln(x ＋1)＝0，即x ＝0， 函数存在零点，故③错误； 由对数函数的单调性可知：函数y ＝ln(x ＋1)在区间(－1，＋∞)上单调递增， 故函数y ＝ln(x ＋1)在区间(－1，0)上是增函数，④正确. 故选D.10.如图所示的程序框图输出的所有点都在函数( )A.y ＝x ＋1的图象上B.y ＝2x 的图象上C.y ＝2x 的图象上D.y ＝2x－1的图象上答案 D解析 由题意可知，输入x ＝1，y ＝1，由于1≤4，输出点(1，1)，进入循环，x ＝1＋1＝2，y ＝2×1＝2，由于2≤4，输出点(2，2)，进入循环，x ＝2＋1＝3，y ＝2×2＝4，由于3≤4，输出点(3，4)，进入循环，x ＝3＋1＝4，y ＝2×4＝8，由于4≤4，输出点(4，8)，进入循环，x ＝4＋1＝5>4，循环结束；故点(2，2)，点(3，4)，点(4，8)均满足在函数y ＝2x －1的图象上. 11.(2017·天津重点中学联考)已知双曲线x 2a 2－y 2b2＝1的离心率为5，圆心在x 轴的正半轴上的圆M 与双曲线的渐近线相切，且圆M 的半径为2，则以圆M 的圆心为焦点的抛物线的标准方程为( ) A.y 2＝85x B.y 2＝45x C.y 2＝25x D.y 2＝5x答案 B解析 设双曲线渐近线的方程为y ＝ba x ，圆心坐标为(x 0，0)(x 0＞0)，由双曲线的离心率a 2＋b 2a＝5，得b ＝2a ，故双曲线的渐近线方程为y ＝2x . ∵圆与渐近线相切，由点到直线的距离公式得2x 01＋22＝2，即x 0＝5，∴p2＝5，p ＝25，∴抛物线的标准方程为y 2＝45x ，故选B.12.设函数f (x )＝1－x ＋1，g (x )＝ln(ax 2－3x ＋1)，若对任意的x 1∈[0，＋∞)，都存在x 2∈R ，使得f (x 1)＝g (x 2)成立，则实数a 的最大值为( ) A.2 B.94 C.4 D.92答案 B解析 设g (x )＝ln(ax 2－3x ＋1)的值域为A ， 因为f (x )＝1－x ＋1在[0，＋∞)上的值域为(－∞，0]，所以(－∞，0]⊆A ，所以h (x )＝ax 2－3x ＋1至少要取遍(0，1]中的每一个数，又h (0)＝1，所以实数a 需要满足a ≤0或⎩⎪⎨⎪⎧a ＞0，Δ＝9－4a ≥0，解得a ≤94.所以实数a 的最大值为94，故选B.13.如图，在平行四边形ABCD 中，E 为DC 的中点，AE 与BD 交于点M ，AB ＝2，AD ＝1，且MA →·MB →＝－16，则AB →·AD →＝________.答案 34解析 MA →·MB →＝(MD →＋DA →)·23DB →＝⎝⎛⎭⎫13BD →＋DA →·23DB →＝⎝⎛⎭⎫13AD →－13AB →＋DA →·⎝⎛⎭⎫23AB →－23AD → ＝⎝⎛⎭⎫－23AD →－13AB →·⎝⎛⎭⎫23AB →－23AD →＝49AD→2－29AB →2－29AB →·AD →＝－29AB →·AD →＝－16， AB →·AD →＝34.14.下表是某工厂1—4月份用电量(单位：万度)的一组数据：由散点图可知，用电量y 与月份x 之间有较好的线性相关关系，其线性回归方程是y ^＝－0.7x ＋a ^，则a ^＝________. 答案 5.25解析 因为x ＝1＋2＋3＋44＝2.5，y ＝4.5＋4＋3＋2.54＝3.5，所以(2.5，3.5)在线性回归方程y ^＝－0.7x ＋a ^上， 即3.5＝－0.7×2.5＋a ^，a ^＝5.25.15.(2017·河北衡水中学模拟)已知{}a n 为等差数列，S n 为其前n 项和，公差为d ，若S 2 0172 017－S 1717＝100，则d 的值为________. 答案110解析 因为S nn ＝na 1＋n (n －1)2d n ＝a 1＋(n －1)2d ，所以S 2 0172 017－S 1717＝a 1＋2 017－12d －⎝ ⎛⎭⎪⎫a 1＋17－12d ＝1 000d ＝100，所以d ＝110. 16.已知函数f (x )的定义域为R ，若存在常数k ，使|f (x )|≤k2 017|x |对所有实数都成立，则称函数f (x )为“期望函数”，给出下列函数：①f (x )＝x 2；②f (x )＝x e x ；③f (x )＝x x 2－x ＋1；④f (x )＝x e x ＋1.其中函数f (x )为“期望函数”的是________.(写出所有符合条件的函数序号) 答案 ③④解析 ①假设函数f (x )＝x 2为“期望函数”，则|f (x )|＝|x 2|≤k2 017|x |，当x ≠0时，k ≥2 017|x |，因此不存在k ，因此假设错误，即函数f (x )＝x 2不是“期望函数”；②假设函数f (x )＝x e x 为“期望函数”，则|f (x )|＝|x e x |≤k2 017|x |，当x ≠0时，k ≥2 017e x ，因此不存在k ，因此假设错误；③假设函数f (x )＝x x 2－x ＋1为“期望函数”，|f (x )|＝|x |⎝⎛⎭⎫x －122＋34≤43|x |，当x ≠0时，对任意的k2 017≥43，都有|f (x )|≤k 2 017|x |成立，故正确；④假设函数f (x )＝x e x ＋1为“期望函数”，|f (x )|＝|x |e x＋1≤k2 017|x |对所有实数都成立，故正确.故答案为③④. 2018年（人教版）高考数学选择填空限时训练(6)1.(2017·长郡中学模拟)设集合A ＝⎩⎨⎧⎭⎬⎫(x ，y )⎪⎪x 24＋y 216＝1，B ＝{(x ，y )|y ＝3x }，则A ∩B 的子集的个数是( ) A.2 B.4 C.8 D.16 答案 B解析 结合图象(图略)可知函数y ＝3x 与椭圆有两个不同的交点，即集合A ∩B 中有两个元素，则其所有子集的个数是22＝4，故选B.。

高考数学客观题限时训练习题（十一套）高考数学客观题限时训练一班级 姓名 学号 记分1、已知集合{}{}|12,|35A x a x a B x x =-≤≤+=<<，则能使A B ⊇成立的实数a 的取值范围是（ ）A ．{}|34a a <≤B ．{}|34a a <<C ．{}|34a a ≤≤D ．∅ 2、等比数列{}n a 中，0n a >且21431,9a a a a =-=-，则45a a +等于（ ） A ．16 B ．27 C ．36 D ．27- 3、不等式2103x x -≤的解集为（ ）A ．{|2x x ≤≤ B ．{}|25x x -≤≤ C ．{}|25x x ≤≤ D ．{}5x x ≤ 4、曲线24y x =关于直线2x =对称的曲线方程是（ ）A ．2164y x =-B ．284y x =-C ．248y x =-D ．2416y x =-5、已知()321233y x bx b x =++++是R 上的单调增函数，则b 的范围（ ）A ．1b <-或2b >B ．1b ≤-或2b ≥C ．12b -<<D ．12b -≤≤6、直线l 是双曲线()222210,0x y a b a b-=>>的右准线，以原点为圆心且过双曲线的焦点的圆被直线l 分成弧长为21∶的两段圆弧，则该双曲线的离心率是（ ）A B C D7、空间四点A B C D 、、、，若直线,,AB CD AC BD AD BC ⊥⊥⊥同时成立，则A B C D 、、、四点的位置关系是（ ）A ．一定共面B ．一定不共面C ．不一定共面D ．这样的四点不存在8、()f x 是定义在R 上的奇函数，它的最小正周期为T ，则2T f ⎛⎫- ⎪⎝⎭的值为（ ）A ．0B ．2TC ．TD ．2T-9、已知实数x y 、满足22326x y +=，则2x y +的最大值为（ ） A ．4 BC． D10、函数222x y e -=的图象大致是（ ）选择题答案栏11、直线20x y m ++=按向量()1,2a =--平移后与圆22:240C x y x y ++-=相切，则实数m 的值为____________.12、在()()10211x x x ++-的展开式中，4x 项的系数是_______________.13、12名同学分别到三个不同的路口进行车流量的调查，若每个路口4人，则不同的分配方案共有____________14、函数()f x =是奇函数的充要条件是____________ABCD15、260100x y x x y +-≤⎧⎪+≥⎨⎪-≤⎩,z mx y =+取得最大值的最优解有无数个，则m 等于16、在下列四个命题中，①函数2cos sin y x x =+的最小值是1-。

高中数学专题复习
《矩阵与变换二阶矩阵平面逆变换等》单元过关检测
经典荟萃，匠心巨制！独家原创，欢迎下载！
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1．当πcos 12
=a 时，行列式211121a a +-的值是 ．
2．已知线性方程组的增广矩阵为024********a -⎛⎫ ⎪ ⎪ ⎪⎝⎭
，若该线性方程组无解，则
a = ． 评卷人
得分 二、解答题
3．（本小题满分12分）
二阶矩阵M 对应的变换将点(1,1)-变换成点(1,1)--，点(2,1)-变换成点(0,2)-.
（1）求矩阵M ；
（2）设直线l 在变换M 作用下得到了直线m ：24x y -=，求l 的方程．
(12,13班做)设不等式|2x －1|＜1的解集为M ．
(1)求集合M ；
(2)若a ，b ∈M ，试比较ab ＋1与a ＋b 的大小．
4．求使等式成立的矩阵M 。

卜人入州八九几市潮王学校2021届高考数学填空题临考押题训练〔45〕1. 集合A={x|x 2+x-6=0},B={x|ax+1=0},假设B ⊆A ，那么a=_________。

2(4)()(1)(4)x x f x f x x ⎧<=⎨-≥⎩,那么(5)f 的值是____________。

3．函数8ln 2)(2++-=x x x f 的单调递增区间是。

4.{}n a 是等差数列，686=+a a ,前12项的和3012=S ，那么其公差d=.5.函数f(x)=mx+6在闭区间[]3,2-上存在零点，那么实数m 的取值范围是.6．假设)127cos(,31)12sin(παπα+=+则的值是. 7.曲线在53123+-=x x y 在1=x 处的切线的方程为__________. 8．〔2021柴桥下学期期中〕函数y ＝sin x ＋cos x ，x ∈[，π]的值域是。

9.||1a =，||2b =，()a a b ⊥+，那么a 与b 夹角的度数为___10．如右图是函数32()f x x bx cx d =+++的大致图象，那么2212x x +等于11.函数πy =sin x 3在区间[]0,b 上恰好获得2个最大值,那么实数b 的取值范围是______ 12.函数+的最大值为M,最小值为m,那么m M的值是___________。

13.一个六棱柱的底面是正六边形，其侧棱垂直底面。

该六棱柱的顶点都在同一个球面上，且该六棱柱的高为3，那么这个球的体积为_________14.〔1〕在△ABC 中，“A ＜B 〞是〞sinA ＜sinB 〞的充要条件；〔2〕在同一坐标系中，函数y=sinx 的图象和函数y=x 的图象有三个公一共点； 〔3〕在△ABC 中,假设AB=2,AC=3,∠ABC=3π,那么△ABC 必为锐角三角形;(4)将函数)32sin(π+=x y 的图象向右平移3π参考答案1．0或者1/3或者-1/22，83，〔0，1〕4，15，m 2-≤或者m 3≥6,-1/37,3x+3y-13=08,[-2,3]9,12010,411,[15/2,27/2)12,2213,34π14,1,3。