二元一次方程组专题训练

二元一次方程组解法练习题精选（含答案）一．解答题（共16小题）1．求适合的x，y的值．2．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？3．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．4．二元一次方程组解法练习题精选（含答案）参考答案与试题解析1．求适合的x，y的值．考解二元一次方程组．点：分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x，求y的值，继而求出x的值．解答：解：由题意得：，由（1）×2得：3x﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x﹣4y=4（5），（5）﹣（4）得：y=﹣，把y的值代入（3）得：x=，∴．本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．点评：2．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？解二元一次方程组．考点：专计算题．题：分析：（1）将两组x，y的值代入方程得出关于k、b的二元一次方程组，再运用加减消元法求出k b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解答：解：（1）依题意得：①﹣②得：2=4k，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．3．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点此题难度较大，需同学们仔细阅读，弄清题意再解答．评：4．考解二元一次方程组．点：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．分析：解：由原方程组，得解答：，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=，∴原方程组的解为．点评：用加减法解二元一次方程组的一般步骤：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．。

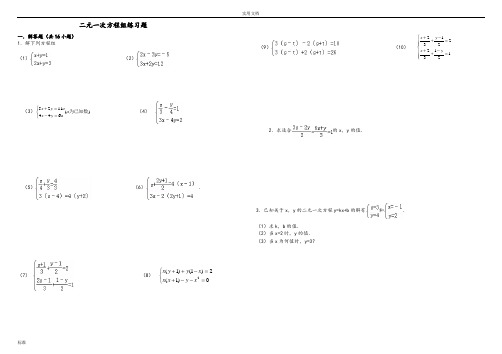
实用文档标准二元一次方程组练习题一．解答题（共16小题） 1．解下列方程组 （1）（2）（3）)(6441125为已知数a a y x ay x ⎩⎨⎧=-=+ （4）（5）（6）．（7）（8）⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x（9）（10） ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2．求适合的x ，y 的值．3．已知关于x ，y 的二元一次方程y=kx+b 的解有和．（1）求k ，b 的值．（2）当x=2时，y 的值． （3）当x 为何值时，y=3？1．解下列方程组（1）（2）；（3）；（4）（5）．（6）（7）（8）（9）（10）；2．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解.word版本二元一次方程组解法练习题精选参考答案与试题解析一．解答题（共16小题）1．求适合的x，y的值．考点：解二元一次方程组．分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x，求出y的值，继而求出x的值．解答：解：由题意得：，由（1）×2得：3x ﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x﹣4y=4（5），（5）﹣（4）得：y=﹣，把y的值代入（3）得：x=，∴．点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．2．解下列方程组（1）（2）（3）（4）．考点：解二元一次方程组．分析：（1）（2）用代入消元法或加减消元法均可；（3）（4）应先去分母、去括号化简方程组，再进一步采用适宜的方法求解．解答：解：（1）①﹣②得，﹣x=﹣2，解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．（2）①×3﹣②×2得，﹣13y=﹣39，解得，y=3，把y=3代入①得，2x﹣3×3=﹣5，解得x=2．故原方程组的解为．（3）原方程组可化为，①+②得，6x=36，x=6，①﹣②得，8y=﹣4，y=﹣．所以原方程组的解为．（4）原方程组可化为：，①×2+②得，x=，把x=代入②得，3×﹣4y=6，y=﹣．所以原方程组的解为．点评：利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．3．解方程组：考点：解二元一次方程组．word版本专题：计算题．分析：先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．解答：解：原方程组可化为，①×4﹣②×3，得7x=42，解得x=6．把x=6代入①，得y=4．所以方程组的解为．点评：；二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消元．消元的方法有代入法和加减法．4．解方程组：考点：解二元一次方程组．专题：计算题．分析：把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较简单．解答：解：（1）原方程组化为，①+②得：6x=18，∴x=3．代入①得：y=．所以原方程组的解为．点评：要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．5．解方程组：考点：解二元一次方程组．专题：计算题；换元法．分析：本题用加减消元法即可或运用换元法求解．解答：解：，①﹣②，得s+t=4，①+②，得s﹣t=6，即，解得．所以方程组的解为．点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？考点：解二元一次方程组．专题：计算题．分析：（1）将两组x ，y 的值代入方程得出关于k、b的二元一次方程组，再运用加减消元法求出k、b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解答：解：（1）依题意得：①﹣②得：2=4k，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．word 版本（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．7．解方程组：（1）；（2）．考点：解二元一次方程组．分析：根据各方程组的特点选用相应的方法：（1）先去分母再用加减法，（2）先去括号，再转化为整式方程解答．解答：解：（1）原方程组可化为，①×2﹣②得：y=﹣1，将y=﹣1代入①得：x=1．∴方程组的解为；（2）原方程可化为，即，①×2+②得：17x=51，x=3，将x=3代入x﹣4y=3中得：y=0．∴方程组的解为．点评：这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．8．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解．解答：解：原方程组可化为，①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．点评：解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减消元法解方程组．9．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．解答：解：原方程变形为：，两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得4y=11，y=．解之得．点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、消元，即可解出此类题目．word版本10．解下列方程组：（1）（2）考点：解二元一次方程组．专题：计算题．分析：此题根据观察可知：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解答：解：（1），由①，得x=4+y③，代入②，得4（4+y ）+2y=﹣1，所以y=﹣，把y=﹣代入③，得x=4﹣=．所以原方程组的解为．（2）原方程组整理为，③×2﹣④×3，得y=﹣24，把y=﹣24代入④，得x=60，所以原方程组的解为．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．11．解方程组：（1）（2）考点：解二元一次方程组．专题：计算题；换元法．分析：方程组（1）需要先化简，再根据方程组的特点选择解法；方程组（2）采用换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解答：解：（1）原方程组可化简为，解得．（2）设x+y=a，x﹣y=b，∴原方程组可化为，解得，∴∴原方程组的解为．点评：此题考查了学生的计算能力，解题时要细心．12．解二元一次方程组：（1）；（2）．考点：解二元一次方程组．word版本专题：计算题．分析：（1）运用加减消元的方法，可求出x、y的值；（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解答：解：（1）将①×2﹣②，得15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；（2）此方程组通过化简可得：，①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．13．在解方程组时，由于粗心，甲看错了方程组中的a ，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点评：此题难度较大，需同学们仔细阅读，弄清题意再解答．14．考点：解二元一次方程组．分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．解答：解：由原方程组，得，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=∴原方程组的解为．点评：用加减法解二元一次方程组的一般步骤：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；word版本2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：（1）；（2）．考点：解二元一次方程组．分析：将两个方程先化简，再选择正确的方法进行消元．解答：解：（1）化简整理为，①×3，得3x+3y=1500③，②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．（2）化简整理为，①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点评：方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方法解方程．16．解下列方程组：（1）（2）考点：解二元一次方程组．分析：观察方程组中各方程的特点，用相应的方法求解．解答：解：（1）①×2﹣②得：x=1，将x=1代入①得：2+y=4，y=2．∴原方程组的解为；（2）原方程组可化为，①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．∴原方程组的解为．点评：解此类题目要注意观察方程组中各方程的特点，采用加减法或代入法求解．word版本。

二元一次方程组练习题一．选择题1．以下方程中，是二元一次方程的是（）A ． x －5y=6zB ． 5xy+3=0 C． 1+2y=3D．x=y 22.x-2y=1x4二元一次方程 有无数多个解，以下四组解中不是该方程的解的是（）xx 1x 1 x 1A ．1BC．y1 ．yD ．1y2y3 方程 2x+y=8 的正整数解的个数是（）组A ． 4 B． 3C．2 D．14. 一轮船顺水航行的速度为 a 千米 / 小时，逆流航行的速度为b 千米 / 小时，（a ＞ b ＞ 0）．那么船在静 . 水中的速度为（）千米 / 小时．A ． a+bB．1(ab)C．1( a b)D． a-b225. 在“六 ?一”小孩节那一天，某商场推出A 、B 、C 三种特价玩具．若购置A 种 2 件、B 种 1件、 C 种 3 件，共需 23 元；若购置 A 种 1 件、 B 种 4 件、 C 种 5 件，共需 36 元．那么小明 购置 A 种 1件、B 种 2件、 C 种 3 件，共需付款（）A ．21 元B ．22 元 C．23 元D．不可以确立5． 1 有甲，乙，丙三种商品，假如购甲3 件，乙 2 件，丙 1 件共需 315 元钱，购甲 1 件，乙 2 件，丙 3 件共需 285 元钱，那么购甲，乙，丙三种商品各一件共需（）A ． 50B． 100C． 150D． 2005． 2 如图，三个天平的托盘中形状同样的物体质量相等．图（ 1）、图（ 2）所示的两个天平处于均衡状态，要使第三个天平也保持均衡，则需在它的右盘中搁置（）A ．3 个球B ．4 个球C ．5 个球D ．6 个球 二．填空题6. x 2的解，那么 k=已知是方程 x-ky=1y 37. 请你写出一个二元一次方程组，使它的解为 x 1y，这个方程组是28. 某人买了 60 分和 80 分的邮票共 20 枚，用去 13 元 2 角，设买了 60 分邮票 x 枚，买了80分邮票 y 枚，则可列方程组为x=y+5 2x-y=5 9. 已知方程组和方程组有同样的解，则 m 的值是x+y+m=0x+y+m=010. 若 a ：b ： c=2：3： 7，且 a-b+3=c-2b ，则 c 值为三．解答题6 6 1 4(x-y-1)=3(1-y)-2xy 2x y11. 解方程组（ 1）3 （2）832 + =2x =103y3x y z 4x 2y 3z 18 0（ 3） 2x 3y z 12（ 4） x 3y 2z 8 0x y z 6 x y 2z 24 0x 1x212. 已知和都是方程 y=ax+b 的解，求 a 和 b 的值．y 0y313． 1 为了防控甲型 H1N1 流感，某校踊跃进行校园环境消毒，购置了甲、乙两种消毒液共100 瓶，此中甲种 6 元 / 瓶，乙种 9 元/ 瓶．假如购置这两种消毒液共用780 元，求甲、乙两种消毒液各购置多少瓶？学校文艺部组织部分文艺踊跃分子看演出，共购得 8 张甲票， 4 张乙票， 总计用了 112 元．已知每张甲票比乙票贵 2 元，则甲票、乙票的票价分别是（）我国古代数学巨着《孙子算经》中的“鸡兔同笼”题为： “今有雉（鸡）兔同笼，上有三十五头，下有九十四足．问雉兔各几何” ．（即鸡和兔子一共有 35 只，一共有94 条腿，问鸡和兔子各有多少只？）14 某城市规定：出租车起步价同意履行的最远行程为 3 千米，超出 3 千米的部分按每千米另行收费，甲说： “我乘这种出租车走了 11 千米，付了 17 元”；乙说：“我乘这种出租车走了 23 千米，付了 35 元”．请你算一算这种出租车的起步价是多少元？以及超出 3 千米后，每千米的车资是多少元？某商铺经销一种商品，因为进价降低了 5%，销售价不变，使得收益由 m%提升到（ m+6）%，则 m的值为多少在某浓度的盐水中加入一杯水后，获得新盐水，它的浓度为20%，又在新盐水中加入与前述1一杯水的重量相等的纯盐混淆，盐水浓度变成33 % ，那么本来盐水的浓度是多少？316.甲、乙、丙三队要达成 A、 B两项工程． B 工程的工作量比 A 工程的工作量多 25%，甲、乙、丙三队独自达成 A 工程所需的时间分别是20 天、24 天、 30 天．为了共同达成这两项工程，先派甲队做 A 工程，乙、丙二队做 B 工程；经过几日后，又调丙队与甲队共同达成A 工程．问乙、丙二队合作了多少天？1-4．DBBC3.. 解：∵ 2x+y=8 ，∴y=8-2x ，∵x、 y 都是正整数，∴x=1 时， y=6；x=2 时， y=4；x=3 时， y=2．∴二元一次方程2x+y=8 的正整数解共有 3 对．应选 B．4 题的等量关系：顺水航行的速度- 静水中的速度=静水中的速度- 逆流航行的速度．5．设 A、B、C三种特价玩具单价分别为x、y、z 元，列方程组，用待定系数法求解．解答：解：设 A、B、 C 三种特价玩具单价分别为x、 y、 z 元，由题意，得{2x+y+3z=23 ， x+4y+5z=36 ，设 x+2y+3z=m（ 2x+y+3z ） +n（x+4y+5z ）比较系数，得 {2m+n=1， m+4n=2， 3m+5n=3，解得 {m=27， n=37∴x+2y+3z= （ 2/7 ）（2x+y+3z ） +（ 3/7 ）（ x+4y+5z ）=2/7 × 23+3/7 × 36=22．应选 B．评论：此题是三元不定方程组，解决这种问题，需要设待定系数，比较系数求解．5． 1 解：设购甲，乙，丙三种商品各一件需要x 元、 y 元、 z 元．依据题意，得{3x+2y+z=315x+2y+3z=285，双方程相加，得4x+4y+4z=600 ，x+y+z=150．则购甲，乙，丙三种商品各一件共需150 元．5． 2 目中的方程实质是说了然两个相等关系：设球的质量是x，小正方形的质量是y，小正三角形的质量是z．依据第一个天平获得：5x+2y=x+3z ；依据第二个天平获得：3x+3y=2y+2z ，把这两个式子构成方程组，解这个对于y， z 的方程组即可．解答：解：设球的质量是x，小正方形的质量是y，小正三角形的质量是z．依据题意获得：{5x+2y=x+3z ， 3x+3y=2y+2z ．解得： {y=x ， z=2x ，第三图中左侧是：x+2y+z=5x ，因此需在它的右盘中搁置 5 个球．应选 C．6. k=-17, 答案不独一。

二元一次方程组练习题100道（卷一）（范围：代数： 二元一次方程组）一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………（ ） 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解（ ）3、由两个二元一次方程组成方程组一定是二元一次方程组（ ）4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ，可以转化为⎩⎨⎧-=--=+27651223y x y x （ ）5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程，则a 的值为±1（ ）6、若x +y =0，且|x |=2，则y 的值为2 …………（ ）7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解，那么m 的值为m ≠-5 …………（ ）8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………（ ） 9、x +y =5且x ，y 的绝对值都小于5的整数解共有5组 …………（ ） 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解，反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………（ ）11、若|a +5|=5，a +b =1则32-的值为b a ………（）12、在方程4x -3y =7里，如果用x 的代数式表示y ，则437yx +=（ ） 二、选择：13、任何一个二元一次方程都有（ ） （A ）一个解； （B ）两个解；（C ）三个解； （D ）无数多个解；14、一个两位数，它的个位数字与十位数字之和为6，那么符合条件的两位数的个数有（ ） （A ）5个 （B ）6个 （C ）7个 （D ）8个 15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数，那么a 的取值范围是（ ）（A ）a <2； （B ）34->a ； （C ）342<<-a ； （D ）34-<a ；16、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解，那么m 的值是（ ）（A ）2； （B ）-1； （C ）1；（D ）-2；17、在下列方程中，只有一个解的是（ ） （A ）⎩⎨⎧=+=+0331y x y x（B ）⎩⎨⎧-=+=+2330y x y x（C ）⎩⎨⎧=-=+4331y x y x（D ）⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是（ ）（A ）15x -3y =6 （B ）4x -y =7 （C ）10x +2y =4 （D ）20x -4y =3 19、下列方程组中，是二元一次方程组的是（ ）（A ）⎪⎩⎪⎨⎧=+=+9114y x y x （B ）⎩⎨⎧=+=+75z y y x（C ）⎩⎨⎧=-=6231y x x（D ）⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解，则a 、b 的值等于（ ）（A ）a =-3,b =-14 （B ）a =3,b =-7 （C ）a =-1,b =9（D ）a =-3,b =14 21、若5x -6y =0，且xy ≠0，则y x yx 3545--的值等于（ ）（A ）32 （B ）23 （C ）1 （D ）-122、若x 、y 均为非负数，则方程6x =-7y 的解的情况是（ ） （A ）无解 （B ）有唯一一个解 （C ）有无数多个解 （D ）不能确定23、若|3x +y +5|+|2x -2y -2|=0，则2x 2-3xy 的值是（ ）（A ）14 （B ）-4 （C ）-12 （D ）12 24、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解，则k 与b 的值为（ ） （A ）21=k ，b =-4 （B ）21-=k ，b =4 （C ）21=k ，b =4（D ）21-=k ，b =-4 三、填空：25、在方程3x +4y =16中，当x =3时，y =________，当y =-2时，x =_______ 若x 、y 都是正整数，那么这个方程的解为___________； 26、方程2x +3y =10中，当3x -6=0时，y =_________；27、如果0.4x -0.5y =1.2，那么用含有y 的代数式表示的代数式是_____________； 28、若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解，则⎩⎨⎧==______________b a ；□x +5y =13 ①4x -□y =-2 ② 29、方程|a |+|b |=2的自然数解是_____________； 30、如果x =1，y =2满足方程141=+y ax ，那么a =____________； 31、已知方程组⎩⎨⎧-=+=+my x ay x 26432有无数多解，则a =______，m =______；32、若方程x -2y +3z =0，且当x =1时，y =2，则z =______；33、若4x +3y +5=0，则3(8y -x )-5(x +6y -2)的值等于_________；34、若x +y =a ，x -y =1同时成立，且x 、y 都是正整数，则a 的值为________； 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道，x :z =_______；y :z =________；36、已知a -3b =2a +b -15=1，则代数式a 2-4ab +b 2+3的值为__________；四、解方程组37、⎪⎪⎩⎪⎪⎨⎧=-=-1332343n m nm ； 38、)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+；39、⎪⎪⎩⎪⎪⎨⎧=++=+125432y x yx y x ； 40、⎪⎩⎪⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x ； 41、⎪⎪⎩⎪⎪⎨⎧++=++=+=+6253)23(22)32(32523233y x y x yx y x ； 42、⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x ；43、⎪⎩⎪⎨⎧=-+-=-+=-+3113y x z x z y z y x ； 44、⎪⎩⎪⎨⎧=+=+=+101216x z z y y x ；45、⎪⎩⎪⎨⎧=-+=+-=-+35351343z y x z y x z y x ； 46、⎪⎩⎪⎨⎧=+-==30325:3:7:4:z y x z x y x ；五、解答题：47、甲、乙两人在解方程组 时，甲看错了①式中的x 的系数，解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ；乙看错了方程②中的y 的系数，解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ，若两人的计算都准确无误，请写出这个方程组，并求出此方程组的解；48、使x +4y =|a |成立的x 、y 的值，满足(2x +y -1)2+|3y -x |=0，又|a |+a =0，求a 的值；49、代数式ax 2+bx +c 中，当x =1时的值是0，在x =2时的值是3，在x =3时的值是28，试求出这个代数式；50、要使下列三个方程组成的方程组有解，求常数a 的值。

二元一次方程组专题训练1.⎩⎨⎧=-=+33651643y x y x 2. ⎩⎨⎧=+=-6251023x y x y ⎩⎨⎧=-=+19542023b a b a 1、 2、 3、 ⎩⎨⎧=-=+1572532y x y x4、⎩⎨⎧=+-=18435276t s t s 5、 ⎩⎨⎧=-=+574973p q q p 6、⎩⎨⎧=-=+42634y x y x7、⎩⎨⎧-=-=+22223n m n m 8、⎩⎨⎧=--=-495336y x y x 9、10、⎩⎨⎧=-=-yx y x 23532 11、⎩⎨⎧=-=+124532n m n m12、⎩⎨⎧=+=+10232556y x y x13、⎩⎨⎧=+=+2.54.22.35.12y x y x 14、⎪⎩⎪⎨⎧=-+-=+6)(3)1(26132y x x y x15、⎪⎩⎪⎨⎧=+--=-+-04235130423512y x y x 16、⎪⎩⎪⎨⎧=--=+-4323122y x y x yx17、⎪⎩⎪⎨⎧-=-++=-+52251230223x y x y x二元一次方程组练习题一、选择题：1．下列方程中，是二元一次方程的是（ ） A ．3x －2y=4z B ．6xy+9=0 C ．1x+4y=6 D ．4x=2．下列方程组中，是二元一次方程组的是（ ）A ．228423119...23754624x y x y a b xBCD x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩3．二元一次方程5a －11b=21 （ ）A ．有且只有一解B ．有无数解C ．无解D ．有且只有两解4．方程y=1－x 与3x+2y=5的公共解是（ ）A ．3333...2422x x x x B C D y y y y ==-==-⎧⎧⎧⎧⎨⎨⎨⎨===-=-⎩⎩⎩⎩5．若│x －2│+（3y+2）2=0，则的值是（ ）A ．－1B ．－2C ．－3D ．326．方程组43235x y kx y -=⎧⎨+=⎩的解与x 与y 的值相等，则k 等于（ ）7．下列各式，属于二元一次方程的个数有（ ）①xy+2x －y=7； ②4x+1=x －y ； ③1x+y=5； ④x=y ； ⑤x 2－y 2=2⑥6x －2y ⑦x+y+z=1 ⑧y （y －1）=2y 2－y 2+x A ．1 B ．2 C ．3 D ．48．某年级学生共有246人，其中男生人数y 比女生人数x 的2倍少2人，•则下面所列的方程组中符合题意的有（ ） A ．246246216246 (22222222)x y x y x y x y B C D y x x y y x y x +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨=-=+=+=+⎩⎩⎩⎩ 二、填空题9．已知方程2x+3y －4=0，用含x 的代数式表示y 为：y=_______；用含y 的代数式表示x 为：x=________． 10．在二元一次方程－12x+3y=2中，当x=4时，y=_______；当y=－1时，x=______．11．若x 3m －3－2y n －1=5是二元一次方程，则m=_____，n=______．12．已知2,3x y =-⎧⎨=⎩是方程x －ky=1的解，那么k=_______．13．已知│x －1│+（2y+1）2=0，且2x －ky=4，则k=_____．14．二元一次方程x+y=5的正整数解有______________． 15．以57x y =⎧⎨=⎩为解的一个二元一次方程是_________． 16．已知2316x mx y y x ny =-=⎧⎧⎨⎨=--=⎩⎩是方程组的解，则m=_______，n=______．三、解答题17．当y=－3时，二元一次方程3x+5y=－3和3y －2ax=a+2（关于x ，y 的方程）•有相同的解，求a 的值．18．如果（a －2）x+（b+1）y=13是关于x ，y 的二元一次方程，则a ，b 满足什么条件？19．二元一次方程组437(1)3x y kx k y +=⎧⎨+-=⎩的解x ，y 的值相等，求k ．20．已知x，y是有理数，且（│x│－1）2+（2y+1）2=0，则x－y的值是多少？21．已知方程12x+3y=5,请你写出一个二元一次方程,使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩．22．根据题意列出方程组：（1）明明到邮局买0.8元与2元的邮票共13枚，共花去20元钱，•问明明两种邮票各买了多少枚？（2）将若干只鸡放入若干笼中，若每个笼中放4只，则有一鸡无笼可放；•若每个笼里放5只，则有一笼无鸡可放，问有多少只鸡，多少个笼？23．方程组2528x yx y+=⎧⎨-=⎩的解是否满足2x－y=8？满足2x－y=8的一对x，y的值是否是方程组2528x yx y+=⎧⎨-=⎩的解？24．（开放题）是否存在整数m ，使关于x 的方程2x+9=2－（m －2）x 在整数范围内有解，你能找到几个m 的值？你能求出相应的x 的解吗？《二元一次方程组》单元测试题一、选择题（每题3分，共30分） 1．下列方程组中，是二元一次方程组的是（ ）. （A ） 2311089x y x y ⎧+=⎨-=-⎩ （B ）426xy x y =⎧⎨+=⎩ （C ）21734x y y x-=⎧⎪⎨-=-⎪⎩（D ）24795x y x y +=⎧⎨-=⎩ 2．二元一次方程组⎩⎨⎧==+xy y x 2,102的解是( ) （A ）⎩⎨⎧==;3,4y x （B ）⎩⎨⎧==;6,3y x （C ）⎩⎨⎧==;4,2y x （D ）⎩⎨⎧==.2,4y x 3．根据图1所示的计算程序计算y 的值，若输入2=x ， 则输出的y 值是（ ）（A ）0 （B ）2- （C ）2 （D ）44．如果2315a b 与114x x y a b ++-是同类项，则x ，y 的值是( )（A ）⎩⎨⎧==31y x （B ）⎩⎨⎧==22y x （C ）⎩⎨⎧==21y x （D ）⎩⎨⎧==32y x 5．已知12x y =⎧⎨=⎩ 是方程组错误!未找到引用源。

二元一次方程组计算题100题1.解方程组：2x+9y=81，3x+y=34.2.解方程组：9x+4y=35，8x+3y=30.3.解方程组：7x+2y=52，7x+4y=62.4.解方程组：4x+6y=54，9x+2y=87.5.解方程组：2x+y=7，2x+5y=19.6.解方程组：x+2y=21，3x+5y=56.7.解方程组：5x+7y=52，5x+2y=22.8.解方程组：5x+5y=65，7x+7y=203.9.解方程组：8x+4y=56，x+4y=21.10.解方程组：5x+7y=41，5x+8y=44.11.解方程组：7x+5y=54，3x+4y=38.12.解方程组：x+8y=15，4x+y=29.13.解方程组：3x+6y=24，9x+5y=46.14.解方程组：9x+2y=62，4x+3y=36.15.解方程组：9x+4y=46，XXX。

16.解方程组：9x+7y=135，4x+y=41.17.解方程组：3x+8y=51，x+6y=27.18.解方程组：9x+3y=99，4x+7y=95.19.解方程组：9x+2y=38，3x+6y=18.20.解方程组：5x+5y=45，7x+9y=69.21.解方程组：8x+2y=28，7x+8y=62.22.解方程组：x+6y=14，3x+3y=27.23.解方程组：7x+4y=67，2x+8y=26.24.解方程组：5x+4y=52，7x+6y=74.25.解方程组：7x+y=9，4x+6y=16.26.解方程组：6x+6y=48，XXX。

27.解方程组：8x+2y=16，7x+y=11.28.解方程组：4x+9y=77，8x+6y=94.29.解方程组：6x+8y=68，7x+6y=66.30.解方程组：2x+2y=22，7x+2y=47.31.解方程组：5x+3y=8，3x+5y=8.32.解方程组：6x-7y=5，x+2y=4.33.解方程组：10x-8y=14，x+y=5.34.解方程组：4x+7y=3，x+y=0.35.解方程组：3x+y=10，7x-y=20.36.解方程组：44x+10y=27，x+y=1.37.解方程组：8x-y=0，x+y=18.38.解方程组：11x-y=12，11y-x=-12.39.解方程组：5x+6y=27，2x+3y=12.40.解方程组：2x+3y=12，7x-2y=4.41.解方程组：2x-5y=0，2x+y=2.42.解方程组：7x-3y=3，3x+2y=21.43.解方程组：7x+2y=21，6x-y=1.54.5x+6y=4805x+3y=240改写：将第一行乘以0.5，得到第二行。

专题01 二元一次方程组（五大题型）【题型1 二元一次方程的概念】【题型2 根据二元一次方程的定义求参数】【题型3 二元一次方程的解】【题型4 解二元一次方程】【题型5 二元一次方程组的概念】【题型1 二元一次方程的概念】1．（2023春•浦北县月考）下列选项中，是二元一次方程的是（ ）A．y＝x B．x+y2＝2C．x﹣y D．x+y＝z 【答案】A【解答】解：A．y＝x是二元一次方程，故此选项符合题意；B．x+y2＝2是二元二次方程，故此选项不合题意；C．x﹣y不是等式，不是方程，故此选项不合题意；D．x+y＝z是三元二次方程，故此选项不合题意．故选：A．2．（2023春•松北区期末）下列方程中，属于二元一次方程的是（ ）A．3x2+y＝8B．x﹣1＝﹣4C．x+y﹣2＝0D．x﹣y﹣z＝10【答案】C【解答】解：A．方程3x2+y＝8的最高次数是2，选项A不符合题意；B．方程x﹣1＝﹣4是一元一次方程，选项B不符合题意；C．方程x+y﹣2＝0是二元一次方程，选项C符合题意；D．方程x﹣y﹣z＝10是三元一次方程，选项D不符合题意．故选：C．3．（2023春•任丘市期末）在下列方程中，是二元一次方程的为（ ）A．2x﹣6＝y B．y﹣1＝5C．yz＝8D．【答案】A【解答】解：A．该方程是二元一次方程，故符合题意；B．该方程是一元一次方程，故不符合题意；C．该方程符合二元二次方程的定义，故不符合题意；D．该方程不是整式方程，故不符合题意．故选：A．4．（2023春•连山区月考）下列方程中，二元一次方程的个数为（ ）①xy＝1；②2x＝3y；③；④x2+y＝3；⑤．A．1个B．2个C．3个D．4个【答案】B【解答】解：∵2x＝3y，是二元一次方程；xy＝1，，x2+y＝3不是二元一次方程，∴所有方程中，只有方程①和方程⑤共2个二元一次方程，故选：B．【题型3 二元一次方程的解】11．（2023春•云阳县期末）下列哪对x ，y 的值是二元一次方程x +2y ＝6的解（ ）A ．B ．C ．D ．【答案】C【解答】解：A ．当x ＝﹣2，y ＝﹣2，得x +2y ＝﹣6，那么x ＝﹣2，y ＝﹣2不是x +2y ＝6的解，故A 不符合题意．B ．当x ＝0，y ＝2，得x +2y ＝4，那么x ＝0，y ＝2不是x +2y ＝6的解，故B 不符合题意．C ．当x ＝2，y ＝2，得x +2y ＝2+4＝6，那么x ＝2，y ＝2是x +2y ＝6的解，故C 符合题意．D ．当x ＝3，y ＝1，得x +2y ＝3+2＝5，那么x ＝3，y ＝1不是x +2y ＝6的解，故D 不符合题意．故选：C ．12．（2023春•丹徒区期末）是下面哪个二元一次方程的解（ ）A ．y ＝﹣x +2B ．x ﹣2y ＝1C ．x ＝y ﹣2D ．2x ﹣3y ＝1【答案】D【解答】解：把x ＝5代入A ，得y ＝﹣5+2＝﹣3，所以不是二元一次方程A 的解；把x ＝5代入B ，得y ＝（5﹣1）÷2＝2，所以不是二元一次方程B 的解；把x ＝5代入C ，得y ＝5+2＝7，所以不是二元一次方程C 的解；把x ＝5代入D ，得y ＝（10﹣1）÷3＝3，所以是二元一次方程D 的解．故选：D ．13．已知21x y =ìí=î是二元一次方程3kx y -=的一个解，那么k 的值是（ ）A ．1k =B ．2k =C ．1k =-D ．2k =-【答案】B【分析】本题主要考查二元一次方程的解，熟练掌握二元一次方程的解的定义是解题的关键．【详解】解：把21x y =ìí=î代入二元一次方程3kx y -=得：213k -=，解得：2k =；故选：B ．14．下列四组数值是二元一次方程26x y -=的解的是（ ）A ．26x y =ìí=îB ．42x y =ìí=îC ．24x y =ìí=-îD ．23x y =ìí=î【答案】B【分析】此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．将各项中x与y的值代入方程检验即可．【详解】解：A、把26xy=ìí=î代入方程得：左边462=-=-，右边6=，左边¹右边，不符合题意；B、把42xy=ìí=î代入方程得：左边826=-=，右边6=，左边=右边，符合题意；C、把24xy=ìí=-î代入方程得：左边448=+=，右边6=，左边¹右边，不符合题意；D、把23xy=ìí=î代入方程得：左边431=-=，右边6=，左边¹右边，不符合题意；故选：B．15．（2023•西山区校级开学）二元一次方程2x+y＝8的正整数解有（ ）A．1组B．2组C．3组D．4组【答案】C【解答】解：由2x+y＝8得：y＝8﹣2x，当x＝1时，y＝6；当x＝2时，y＝4；当x＝3时，y＝2；∴二元一次方程2x+y＝8的正整数解有3组，故选：C．16．（2023春•霸州市期末）已知关于x，y的二元一次方程●x﹣2y＝4中x的系数让墨迹盖住了，但是知道它一组解是，那么●的值是（ ）A．2B．1C．﹣3D．﹣2【答案】C【解答】解：设•＝a，由题意得：﹣2a﹣2＝4，解得：a＝﹣3，【题型4 解二元一次方程】19．（2023春•怀安县期末）已知二元一次方程3x﹣y＝6，用x表示y的式子为（ ）A．y＝3x+6B．y＝﹣3x﹣6C．y＝3x﹣6D．y＝﹣3x+6【解答】解：移项，得﹣y＝6﹣3x，系数化1，得y＝3x﹣6．故选：C．20．（2023春•天津期末）把二元一次方程2x﹣3y＝4写成用含y的式子表示x的形式，正确的是（ ）A．B．C．D．【答案】A【解答】解：2x﹣3y＝4，2x＝4+3y，x＝，故选：A．21．（2023春•浠水县校级期末）把方程3x+y﹣1＝0改写成用含x的式子表示y的形式，正确的是（ ）A．x＝B．x＝C．y＝3x﹣1D．y＝1﹣3x【答案】D【解答】解：3x+y﹣1＝0，y＝1﹣3x．故选：D．22．（2023春•梁园区期末）把方程2x+y＝3改写成用含x的代数式表示y的形式为（ ）A．y＝2x+3B．y＝2x﹣3C．y＝﹣2x+3D．y＝﹣2x﹣3【答案】C【解答】解：方程2x+y＝3，解得：y＝﹣2x+3．故选：C．23．（2022秋•朝阳区校级期末）已知方程2x+y＝6，用含x的代数式表示y，则y＝　6﹣2x　．【答案】6﹣2x．【解答】解：2x+y＝6，移项，得y＝6﹣2x．故答案为：6﹣2x．∴二元一次方程24x y +=的正整数解为21x y =ìí=î，故答案为：21x y =ìí=î．【题型5 二元一次方程组的概念】26．（2023春•攸县期中）下列方程组是二元一次方程组的是（ ）A ．B ．C ．D ．【答案】C【解答】解：A 、有3个未知数，不是二元一次方程组，故A 不符合题意；B 、有2个未知数，但是最高次数是2，不是二元一次方程组，故B 不符合题意；C 、有两个未知数，方程的次数是1次，所以是二元一次方程组，故C 符合题意；D 、有两个未知数，第二个方程不是整式方程，不是二元一次方程组，故D 不符合题意．故选：C ．27．（2023春•威海期末）下列方程组中，是二元一次方程组的是（ ）A ．B ．C ．D ．【答案】C【解答】解：A ．第一个方程是二次方程，不是二元一次方程组，故本选项不符合题意；B ．含有三个未知数，不是二元一次方程组，故本选项不符合题意；C ．是二元一次方程组，故本选项符合题意；D ．第二个方程是分式方程，不是二元一次方程组，故本选项不符合题意；故选：C ．28．（2023春•东兰县期末）下列方程组中，是二元一次方程组的是（ ）。

二元一次方程组练习题(含答案) 二元一次方程组练题一．解答题（共16小题）1.解下列方程组：1）x+2y-1=23x-2y=52）1-yx+2/3=1/22y+3=3x3）5x+2y=11a4x-4y=6a4）2x+3y=73x-2y=15）2x-3y=75x+4y=176）2x+3y=13x-2y=57）3x-4y=-12x+5y=138）x(y+1)+y(1-x)=2x(x+1)-y-x^2=09）3x+y=72x-3y=-810）x^2+xy=2y-x+2=02.求适合的x，y的值。

已知关于x，y的二元一次方程y=kx+b的解有和。

1）求k，b的值。

2）当x=2时，y的值。

3）当y=3时，x的值为多少？解答：1.1）将第二个方程变形得到y=(3x-5)/2，代入第一个方程中，得到x=3，y=-2.2）将第一个方程变形得到y=(1/2-1+xy)/x，代入第二个方程中，得到x=3，y=-1.3）将第二个方程变形得到y=x-3/2，代入第一个方程中，得到x=2，y=1.4）将第二个方程变形得到y=(3x-1)/2，代入第一个方程中，得到x=2，y=1.5）将第一个方程变形得到y=(2x-7)/3，代入第二个方程中，得到x=1，y=-1.6）将第二个方程变形得到y=(3x-5)/2，代入第一个方程中，得到x=1，y=-1.7）将第二个方程变形得到y=(3x+1)/4，代入第一个方程中，得到x=5，y=2.8）将第一个方程变形得到y=(2-x^2)/(1-x)，代入第二个方程中，得到x=1，y=1.9）将第二个方程变形得到y=(2x+8)/3，代入第一个方程中，得到x=1，y=1.10）将第一个方程变形得到y=2/x-x，代入第二个方程中，得到x=1，y=0.2.1）由于y=kx+b，所以当x=1时，y=k+b；当x=2时，y=2k+b。

又因为已知y=3时，x的值为多少，所以将y=kx+b代入得到kx+b=3，解得x=(3-b)/k。

专题11：二元一次方程组（简答题专练）一、解答题1．某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元，大樱桃售价为每千克40元，小樱桃售价为每千克16元．（1）大樱桃和小樱桃的进价分别是每千克多少元？销售完后，该水果商共赚了多少元钱？（2）该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少？（1）小樱桃的进价为每千克10元，大樱桃的进价为每千克30元，销售完后，该水果商共赚了3200元；（2）41.6元/千克．解：（1）设小樱桃的进价为每千克x 元，大樱桃的进价为每千克y 元，根据题意可得：，200200800020x y y x +=⎧⎨-=⎩解得：，1030x y =⎧⎨=⎩小樱桃的进价为每千克10元，大樱桃的进价为每千克30元，200×[（40﹣30）+（16﹣10）]=3200（元），∴销售完后，该水果商共赚了3200元；（2）设大樱桃的售价为a 元/千克，（1﹣20%）×200×16+200a﹣8000≥3200×90%，解得：a≥41.6，答：大樱桃的售价最少应为41.6元/千克．考点：1、一元一次不等式的应用；2、二元一次方程组的应用2．某人用2400元买进甲、乙两只股票在当甲股票升值15%，乙股票下跌10%时全部卖出，共获利润1350元（不含手续费、税费），试问此人买的甲、乙两只股票各是多少元？买了甲股票15000元，乙股票9000元.解：设买了甲股票x 元，乙股票y 元.依题意，得，2400015%10%1350x y x y +=⎧⎨-=⎩整理得.240003227000x y x y +=⎧⎨-=⎩解得.150009000x y =⎧⎨=⎩答：买了甲股票15000元，乙股票9000元.3．A 、B 两地相距20千米，甲、乙两人分别从A 、B 两地同时出发相向而行，2小时后在途中相遇，然后甲返回A 地，乙继续前进，当甲返回到A 地时，乙离A 地还有2千米.甲、乙两人的速度各是多少？甲的速度为5.5千米/时，乙的速度为4.5千米/时.解：设甲的速度为x 千米/时，乙的速度为y 千米/时根据题意，得，解得.2()20222x y x y +=⎧⎨-=⎩ 5.54.5x y =⎧⎨=⎩答：甲的速度为5.5千米/时，乙的速度为4.5千米/时.4．已知关于x ，y 的方程组的解满足，求k 的值.21254x y k x y k +=-⎧⎨+=+⎩5x y +=2解：21,254,x y k x y k +=-⎧⎨+=+⎩①②，得，2⨯-②①399x k =+解得.把代入①，33x k =+33x k =+得，3321k k γ++=-解得 2.y k =--5,x y += ，3325k k ∴+--=解得.2k =5．某种电器产品，每件若以原定价的8折销售，可获利120元；若以原定价的6折销售，则亏损20元，该种商品每件的进价为多少元？该商品每件的进价为440元解：设该种商品的进价为x 元/件，原定价为y 元/件.依题意，得.解得.0.81200.620y x y x -=⎧⎨-=-⎩440700x y =⎧⎨=⎩答：该商品的进价为440元6．李师傅加工1个甲种零件和1个乙种零件的时间是固定的，现知道李师傅加工3个甲种零件和5个乙种零件共需55分钟；加工4个甲种零件和9个乙种零件共需85分钟求李师傅加工2个甲种零件和4个乙种零件共需多少分钟.李师傅加工2个甲种零件和4个乙种零件共需40分钟解：设李师傅加工1个甲种零件需要x 分钟，加工1个乙种零件需要y 分钟.依题意，得，35554985x y x y +=⎧⎨+=⎩①②由，得.+①②714140x y +=所以，则.220x y +=2440x y +=答：李师傅加工2个甲种零件和4个乙种零件共需40分钟7．在解方程组时，甲正确地解，乙把c 写错得到.若两人的运算过程均1014bx ay x cy +=⎧⎨-=⎩①②42x y =⎧⎨=-⎩24x y =⎧⎨=⎩无错误，求a ，b ，c 的值..1,a =3,b =5c =解：因为甲得到的解正确，所以把甲得到的代入原方程组，得42x y =⎧⎨=-⎩，42104214b a c -=⎧⎨+=⎩③④由④，解得.5c =已知乙将c 写错得到，因为a ，b 没有写错，24x y =⎧⎨=⎩所以将这个解代入方程①，得.⑤2410b a +=解由③⑤组成的方程组，得1,a =3b =所以.1,a =3,b =5c =8．判断方程组的解法是否正确，如果不正确，请写出正确的解法.27,617.x y x y +=⎧⎨-=⎩①②解法①：由①，得.③，把③代入①，得.可以为任意实数，从而y 也为任72y x =-2(72)7x x +-=x \意实数，原方程组有无数组解.∴解法②：由①，得.③，把③代入②，得.解得.把代入③，得72y x =-67217x x --=6x =6x =. 原方程组的解为.5y =-∴65x y =⎧⎨=-⎩见解析解：解：解法都不正确，其正确的解法如下：由①，得.③72y x =-把③代入②，得.67217x x --=（）解得.把代入③，得.3x =3x =1y =原方程组的解为.∴31x y =⎧⎨=⎩9．解下列方程组：（1）；（2）.8962717x y x y -=⎧⎨+=-⎩①②1353()2(3)15x y x y x y ⎧+=⎪⎨⎪++-=⎩（1）；（2）322x y ⎧=-⎪⎨⎪=-⎩3x y =⎧⎨=⎩解：（1），得.解得，4⨯-②①3774y =-2y =-把代入①，得.解得，2y =-89(2)6x -⨯-=32x =-原方程组的解为；∴322x y ⎧=-⎪⎨⎪=-⎩（2），1353()2(3)15x y x y x y ⎧+=⎪⎨⎪++-=⎩ 53155315x y x y +=⎧∴⎨-=⎩①②，得.解得③+①②1030x =3x =把③代入①得.解得，15315y +=0y =原方程组的解是．∴30x y =⎧⎨=⎩10．阅读下列解方程组的方法，然后解答问题：解方程组时，直接消元是很繁琐的，采用下面的解法则会简单许多.141516171819x y x y +=⎧⎨+=⎩①②解：得，所以.③-②①333x y +=1x y +=，得.④14⨯③141414x y +=，得，从而得.-①④2y =1x =-所以原方程组的解是.12x y =-⎧⎨=⎩（1）请你运用上述方法解方程组，201520162017201820192020x y x y +=⎧⎨+=⎩（2）猜测关于x ，y 的方程组，的解是什么？并用方程组的解加以验证.(1)2(1)2mx m y m nx n y n ++=+⎧⎨++=+⎩()m n ≠（1）（2），验证见解析.12x y =-⎧⎨=⎩12x y =-⎧⎨=⎩解：（1），201520162017201820192020x y x y +=⎧⎨+=⎩①②，得-②①333,x y +=③1x y ∴+=，得④2015⨯③201520152015x y +=，得.把代入③，得，-①④2y =2y =21x +=解得，1x =-原方程组的解是；∴12x y =-⎧⎨=⎩（2）关于x ，y 的方程组，的解是，(1)2(1)2mx m y m nx n y n ++=+⎧⎨++=+⎩()m n ≠12x y =-⎧⎨=⎩(1)2(1)2mx m y m nx n y n ++=+⎧⎨++=+⎩①②当时，方程①左边右边，1,x =-2y =(1)2m m =-++⨯22m m =-++2m =+=方程②左边右边，(1)2n n =-++⨯222n n n =-++=+=是原方程组的解．12x y =-⎧∴⎨=⎩11．某服装点用6000购进A,B 两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价−进价)，这两种服装的进价，标价如表所示．类型价格A 型B型进价(元/件)60100标价(元/件)100160(1)求这两种服装各购进的件数；(2)如果A 种服装按标价的8折出售，B 种服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元?（1）A 种服装购进50件，B 种服装购进30件；（2）2440元解：解：（1）设A 种服装购进x 件，B 种服装购进y 件，由题意，得，60100600040603800x y x y +=⎧⎨+=⎩解得：，5030x y =⎧⎨=⎩答：A 种服装购进50件，B 种服装购进30件；（2）由题意，得：3800-50（100×0.8-60）-30（160×0.7-100）=3800-1000-360=2440（元）．答：服装店比按标价售出少收入2440元．12．若关于x 、y 的方程组和有相同的解，求a 、b 的值．451x y ax by -=⎧⎨+=-⎩393418x y ax by +=⎧⎨-=⎩11a b =⎧⎨=-⎩解：先解方程组 4539x y x y -⎧⎨+⎩＝＝解得：23x y ⎧⎨⎩＝＝将x=2、y=3代入另两个方程，得方程组：23161218a b a b +-⎧⎨-⎩＝＝解得.11a b =⎧⎨=-⎩13．已知关于的方程组的解满足，则的取值.,x y 3=1331x y a x y a ++⎧⎨+=-⎩0x y +>a a>−1解：，31331x y a x y a +=+⎧⎨+=-⎩①②①+②得：4(x+y)=2+2a ，即x+y=，12a+代入x+y>0得：>0，12a+解得：a>−1.14．某足球协会举办了一次足球联赛，记分规则是：胜一场得3分，平一场得1分，负一场得0分.当比赛进行到12轮结束（每队均需比赛12场）时，甲队得分是19分，请你通过计算分析甲队胜几场、平几场、负几场？有三种可能性，即或或4,{7,1.x y z ===5,{4,3.x y z ===6,{1,5.x y z ===解：试题分析：设甲队胜x 场、平y 场、负z 场，则有这是一个不定方程，若把x 当成已12,{319.x y z x y ++=+=知数，可以得到由题意x ≥0、平y ≥0、负z ≥0，即解得3≤x ≤6，于是x 取193,{27.y x z x =-=-0,{1930,270.x x x ≥-≥-≥12134、5、6，由此可以得到三组解.有三种可能性，即或或4,{7,1.x y z ===5,{4,3.x y z ===6,{1,5.x y z ===考点：三元一次方程组15．一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这两种货车的情况如下表所示：第一次第二次甲种货车辆数（单位：辆）25乙种货车辆数（单位：辆）36最大运货物吨数（单位：吨）15.535现租用该公司3辆甲种货车及4辆乙种货车一次刚好运完这批货，如果按每吨付运费30元计算，问货主应付运费多少元？660元．解：设甲种货车每辆运货x 吨，乙种货车每辆运货y 吨，由题意得：，2315.55635x y x y +=⎧⎨+=⎩解得，42.5x y =⎧⎨=⎩则货主应付运费为（元），()344 2.530660⨯+⨯⨯=答：货主应付运费660元．16．是否存在整数k ，使方程组的解中，x 大于1，y 不大于1，若存在，求出k 的值，若不存2+y=k 1x x y ⎧⎨-=⎩在，说明理由．存在;k 只能取3，4，5解：解:解方程组得 2+y=k 1x x y ⎧⎨-=⎩1323k x k y +⎧=⎪⎪⎨-⎪=⎪⎩∵x 大于1，y 不大于1从而得不等式组113223k k +⎧>⎪⎪⎨-⎪≤⎪⎩解之得2＜k≤5又∵k 为整数∴k 只能取3，4，5答：当k 为3，4，5时，方程组的解中，x 大于1，y 不大于1．2+y=k 1x x y ⎧⎨-=⎩17．已知是二元一次方程组的解，求2m-n 的算术平方根．21x y =⎧⎨=⎩8 -1mx ny nx my +=⎧⎨=⎩2解：∵是二元一次方程组的解,21x y =⎧⎨=⎩8 -1mx ny nx my +=⎧⎨=⎩∴，解得，2821m n n m +=⎧⎨-=⎩32m n =⎧⎨=⎩，2===即2m-n 的算术平方根为2.故2.18．温州苍南马站四季柚，声名远播，今年又是一个丰收年，某经销商为了打开销路，对1 000个四季柚进行打包优惠出售．打包方式及售价如图所示．假设用这两种打包方式恰好装完全部柚子．(1)若销售a 箱纸盒装和a 袋编织袋装四季柚的收入共950元，求a 的值；(2)当销售总收入为7 280元时：①若这批四季柚全部售完，请问纸盒装共包装了多少箱，编织袋装共包装了多少袋．②若该经销商留下b(b >0)箱纸盒装送人，其余柚子全部售出，求b 的值．(1) a ＝5；(2)①纸盒装共包装了35箱，编织袋装共包装了40袋；②b 为9.解：(1)由题意得64a ＋126a ＝950，得a ＝5.(2)①设纸盒装共包装了x 箱，编织袋装共包装了y 袋．由题意得解得∴纸盒装共包装了35箱，编织袋装共包装了40袋．②当8x ＋18y ＝1 000时，得x ＝＝125－，由题意得64＋126y ＝7 280，得y ＝40－.∵x ，y ，b 都为整数，且x≥0，y≥0，b ＞0，∴b ＝9，x ＝107，y ＝8.∴b 为9.19．在“五一”期间，小明､小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与爸爸的对话(如图)，请根据图中的信息，解答下列问题：(1)他们共去了几个成人，几个学生？(2)请你帮他们算算，用哪种方式购票更省钱？（1）他们一共去了8个成人，4个学生；（2）按团体票购票更省钱解：解：(1)设去了x 个成人，y 个学生，依题意得，，解得，1240400.5400x y x y +=⎧⎨+⨯=⎩84x y =⎧⎨=⎩答：他们一共去了8个成人，4个学生；(2)若按团体票购票，共需16×40×0.6＝384(元)，∵384＜400，∴按团体票购票更省钱．20．我校组织一批学生开展社会实践活动，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满．已知45座客车租金为每辆220元，60座客车租金为每辆300元．（1）这批学生的人数是多少？原计划租用45座客车多少辆？（2）若租用同一种客车，要使每位学生都有座位，应该怎样租用合算？（1）240人，原计划租用45座客车5辆；（2）租4辆60座客车划算．解：（1）设这批学生有x 人，原计划租用45座客车y 辆，根据题意得： ，()=4515=601x y x y +⎧⎨-⎩解得： ,=240=5x y ⎧⎨⎩答：这批学生有240人，原计划租用45座客车5辆．（2）∵要使每位学生都有座位，∴租45座客车需要5+1=6辆，租60座客车需要5-1=4辆．220×6=1320（元），300×4=1200（元），∵1320＞1200，∴若租用同一种客车，租4辆60座客车划算．21．阅读理解：解方程组时，如果设则原方程组可变形为关于、的方程组215432x y x y ⎧-=⎪⎪⎨⎪+=⎪⎩11,,a b x y ==a b ，解这个方程组得到它的解为由求的原方程组的解为，利25342a b a b -=⎧⎨+=⎩21a b =⎧⎨=-⎩112,1,x y ==-121x y ⎧=⎪⎨⎪=-⎩用上述方法解方程组：52113213x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩1312x y ⎧=⎪⎪⎨⎪=-⎪⎩解：设＝m ，＝n ，则原方程组可变形为关于m 、n 的方程组，1x 1y 52113213m n m n +=⎧⎨-=⎩①②①＋②得：8m ＝24，解得：m ＝3，将m ＝3代入①得：n ＝−2，则方程组的解为：，32m n =⎧⎨=-⎩由＝3，＝−2，1x 1y故方程组的解为：．1312x y ⎧=⎪⎪⎨⎪=-⎪⎩22．某商场计划拨款万元从厂家购进台电视机，已知厂家生产三种不同型号的电视机，出厂价分别为：950甲种每台元，乙种每台元，丙种每台元．150021002500若商场同时购进其中两种不同型号的电视机台，用去万元，请你研究一下商场的进货方案；()1509若商场销售一台甲、乙、丙电视机分别可获利元，元，元，在以上的方案中，为使获利()2150200250最多，商场应选择哪种进货方案？有种方案．方案一：甲种台，乙种台；方案二：甲种台，丙种台；购买甲种电视机()1225253515()2台，丙种电视机台获利最多．所以应选择方案二．3515解：（1）①设购进甲台，乙台，x ()50x -；()1500x 210050x 90000+-=∴ ；x 25=∴ 购进甲台，乙台．2525②设购进甲台，丙台x ()50x -；()1500x 250050x 90000+-=∴ ；x 35=购进甲台，丙台．3515③设购进乙台，丙台x ()50x -；()2100x 250050x 90000+-=∴ （舍）x 87.5=所以选择有种方案．方案一：甲种台，乙种台；22525方案二：甲种台，丙种台；3515（2）利润应为：方案一：元，25150252008750⨯+⨯=方案二：元，35150152509000⨯+⨯=∵ 元元，∴ 方案二获利多，90008750>购买甲种电视机台，丙种电视机台获利最多．所以应选择方案二．351523．一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）车型甲乙丙汽车运载量（吨/辆）5810汽车运费（元/辆）400500600（1）若全部物资都用甲、乙两种车型来运送，需运费元，问分别需甲、乙两种车型各几辆？8200（2）为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知他们的总辆数为辆，你能16通过列方程组的方法分别求出几种车型的辆数吗？（3）求出哪种方案的运费最省？最省是多少元？（1）需要甲车8辆，乙车10辆（2）有三种运送方案：①甲车型8辆，丙车型8辆；②甲车型6辆，乙车型5辆，丙车型5辆；③甲车型4辆，乙车型10辆，丙车型2辆；（3）甲车型4辆，乙车型10辆，丙车型2辆时，最少运费是7800元.解：（1）设需要甲车辆，乙车辆x y 由题意可得： 581204005008200x y x y +=⎧⎨+=⎩解得： 810x y =⎧⎨=⎩需要甲车8辆，乙车10辆∴（2）设甲车有辆，乙车有辆，丙车有辆x y z 由题意可得： 165810120x y z x y z ++=⎧⎨++=⎩消去可得：z 5240,x y +=285x y ∴=-由于是非负整数，且不大于16，得：,x y 0,5,10,15y =由是非负整数，解得z 8640,5,10852x x x y y y z z z ===⎧⎧⎧⎪⎪⎪===⎨⎨⎨⎪⎪⎪===⎩⎩⎩ 有三种运送方案：∴①甲车型8辆，丙车型8辆；②甲车型6辆，乙车型5辆，丙车型5辆；③甲车型4辆，乙车型10辆，丙车型2辆；（3）三种方案得运费分别是：①；400860088000⨯+⨯=②；4006500560057900⨯+⨯+⨯=③.40045001060027800⨯+⨯+⨯=甲车型4辆，乙车型10辆，丙车型2辆时，最少运费是7800元.∴24．为了参加2011年国际铁人三项（游泳、自行车、长跑）系列赛业余组的比赛，李明针对自行车和长跑项目进行专项训练．某次训练中，李明骑自行车的平均速度为每分钟600米，跑步的平均速度为每分钟200米，自行车路段和长跑路段共5千米，用时15分钟．求自行车路段和长跑路段的长度．自行车路段的长度为3千米，长跑路段的长度2千米．解：设自行车路段和长跑路段的长度分别是x 米、y 米则500015500200x y x y +=⎧⎪⎨+=⎪⎩解得：x=3000， y=2000答：自行车路段和长跑路段的长度分别是3000米、2000米25．在等式y ＝ax 2+bx +c 中，当x ＝﹣1时，y ＝3；当x ＝0时，y ＝1，当x ＝1时，y ＝1，求这个等式中a 、b 、c 的值．a ＝1，b ＝﹣1，c ＝1．解：由题意得，，311a b c c a b c -+=⎧⎪=⎨⎪++=⎩解得，a ＝1，b ＝﹣1，c ＝1．26．某商贸公司有、两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：A B 体积（立方米/件）质量（吨/件）型商品A 0．80．5型商品B 21（1）已知一批商品有、两种型号，体积一共是20立方米，质量一共是10．5吨，求、两种型A B A B 号商品各有几件？（2）物资公司现有可供使用的货车每辆额定载重3．5吨，容积为6立方米，其收费方式有以下两种：①按车收费：每辆车运输货物到目的地收费600元；②按吨收费：每吨货物运输到目的地收费200元．现要将（1）中商品一次或分批运输到目的地，如果两种收费方式可混合使用，商贸公司应如何选择运送、付费方式，使其所花运费最少，最少运费是多少元？（1）种型号商品有5件，种型号商品有8件；（2）先按车收费用3辆车运送18m 3，再按吨收费运A B 送1件B 型产品，运费最少为2000元解：（1））设A 、B 两种型号商品各x 件、y 件，，0.82200.510.5x y x y +=⎧⎨+=⎩解得，58x y =⎧⎨=⎩答：种型号商品有5件，种型号商品有8件；A B （2）①按车收费：（辆），10.5 3.53÷=但是车辆的容积=18<20，3辆车不够，需要4辆车，（元）；63⨯60042400⨯=②按吨收费：20010.5=2100（元）；⨯③先用车辆运送18m 3，剩余1件B 型产品，共付费3600+1200=2000（元），⨯⨯∵2400>2100>2000，∴先按车收费用3辆车运送18m 3，再按吨收费运送1件B 型产品，运费最少为2000元.27．阅读以下材料：若x +3y +5z =5，x +4y +7z =7，求x +y +z 的值．解：x +y +z =3（x +3y +5z ）﹣2（x +4y +7z ）=3×5﹣2×7=1．答：x +y +z 的值的为1．根据以上材料提供的方法解决如下问题：若2x +5y +4z =6，3x +y ﹣7z =﹣4，求x +y ﹣z 的值．x+y-z=0解：4（2x +5y +4z ）+6（3x +y ﹣7z ）=8x +20y +16z +18x +6y ﹣42z=26x +26y ﹣26z=26（x +y ﹣z ）=4×6+6×（﹣4）=24－24=0．解得：x +y ﹣z =0．【点评】本题考查了解三元一次方程组，解答本题的关键是明确题意，求出所求式子的值．28．定义运算“*”，规定，其中a ，b 为常数，且，，求的值.2*x y ax by =+1*25=2*16=2*310解：解：根据题中的新定义化简已知等式，得，解得，则.2546a b a b +=⎧⎨+=⎩12a b =⎧⎨=⎩2*34364610c =+=+=故的值为10.2*329．阅读下面资料：小明遇到这样一个问题：如图1，对面积为a 的△ABC 逐次进行以下操作：分别延长AB 、BC 、CA 至A 1、B 1、C1，使得A 1B =2AB ，B 1C =2BC ，C1A =2CA ，顺次连接A 1、B 1、C 1，得到△A 1B 1C 1，记其面积为S 1，求S 1的值.小明是这样思考和解决这个问题的：如图2，连接A 1C 、B 1A 、C 1B ，因为A 1B =2AB ，B 1C =2BC ，C 1A =2CA ，根据等高两三角形的面积比等于底之比，所以=11∆∆=A BC B CA S S =2S △ABC =2a ，由此继续推理，从而解决了这个问题.11∆∆=A BC C AB S S （1）直接写出S 1=（用含字母a 的式子表示）.请参考小明同学思考问题的方法，解决下列问题：（2）如图3，P 为△ABC 内一点，连接AP 、BP 、CP 并延长分别交边BC 、AC 、AB 于点D 、E 、F ，则把△ABC 分成六个小三角形，其中四个小三角形面积已在图上标明，求△ABC 的面积.（3）如图4，若点P 为△ABC 的边AB 上的中线CF 的中点，求S △APE 与S △BPF 的比值.（1）19a ；（2）315；（3）.23解：解：（1）连接A1C ，∵B 1C=2BC ，A 1B=2AB ，∴,,，122BCA ABC S S a == 122BCA ABC S S a == 1112A B C BCA S S = ∴，1144A B C ABC S S a == ∴，1166A B B ABC S S a == 同理可得出：，11116A AC CB C S S a== ∴S 1=6a+6a+6a+a=19a ；故19a ；（2）过点作于点，C CG BE ⊥G 设，，BPF S x ∆=APE S y ∆=；， 1·702BPC S BP CG ∆==1·352PCE S PE CG ∆==．∴1·7022135·2BPC PCE BP CG S S PE CG ∆∆===，即．∴2BP EP =2BP EP =同理，．APB APES BP S PE ∆∆=．2APB APE S S ∆∆∴=．①842x y ∴+=，， 8440APB BPD S AP x S PD∆∆+==3530APC PCD S AP y S PD ∆∆+==．②∴84354030x y ++=由①②，得，5670x y =⎧⎨=⎩．315ABC S ∆∴=（3）设，，如图所示．BPF S m ∆=APE S n ∆=依题意，得，．APF APC S S m ∆∆==BPC BPF S S m ∆∆==．PCE S m n ∆∴=-， BPC APB APEPCE S S BP S S PE ∆∆∆∆==．∴2m m nm n =-，2()m m n mn ∴-=，0m ≠ ．22m n n ∴-=．∴23n m =．∴23APE BPF S S ∆∆=30．如图，A 、B 两地有公路和铁路相连，在这条路上有一家食品厂，它到B 地的距离是到A 地的2倍，这家厂从A 地购买原料，制成食品卖到B 地．已知公路运价为1.5元/(公里•吨)，铁路运价为1元/(公里•吨)，这两次运输(第一次：A 地→食品厂，第二次：食品厂→B 地)共支出公路运费15600元，铁路运费20600元．问：(1)这家食品厂到A 地的距离是多少？(2)这家食品厂此次买进的原料每吨5000元，卖出的食品每吨10000元，此批食品销售完后工厂共获利多少元？(1)这家食品厂到A 地的距离是50公里；(2)这家食品厂此批食品销售完共获利元．解：(1)设这家食品厂到A 地的距离是x 公里，到B 地的距离是y 公里，根据题意，得： ，22030100x y x y =⎧⎨+=++⎩解得： ．50100x y =⎧⎨=⎩答：这家食品厂到A 地的距离是50公里．(2)设这家食品厂此次买进的原料m 吨，卖出食品n 吨，根据题意得： ，1.520 1.530156001(5020)1(10030)20600m m m n ⨯+⨯=⎧⎨⨯-+⨯-=⎩解得： ，220200m n =⎧⎨=⎩∴10000n ﹣5000m ﹣15600﹣20600＝．答：这家食品厂此批食品销售完共获利元．31．某汽车制造厂开发了一款新式电动汽车，计划一年生产安装240辆．由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装．生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车．(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车？(2)如果工厂招聘新工人若干名(新工人人数少于10人)和抽调的熟练工合作,刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?（1）每名熟练工每月可以安装4辆电动车，新工人每月分别安装2辆电动汽车.（2） ①调熟练工1人，新工人8人；②调熟练工2人，新工人6人；③调熟练工3人，新工人4人；④调熟练工4人，新工人2人．解：（1）设每名熟练工每月可以安装x 辆电动车，新工人每月分别安装y 辆电动汽车，根据题意得:，282314x y x y +=⎧⎨+=⎩解之得．42x y =⎧⎨=⎩答：每名熟练工每月可以安装4辆电动车，新工人每月分别安装2辆电动汽车；（2）设抽调熟练工m 人，招聘新工人n 名，由题意得：12（4m+2n ）=240，整理得，n=10-2m ，∵0＜n ＜10，∴当m=1，2，3，4时，n=8，6，4，2，即：①调熟练工1人，新工人8人；②调熟练工2人，新工人6人；③调熟练工3人，新工人4人；④调熟练工4人，新工人2人．32．阅读探索知识累计解方程组()()()()12262126a b a b ⎧-++=⎪⎨-++=⎪⎩解：设a﹣1=x ，b+2=y ，原方程组可变为2626x y x y +=⎧⎨+=⎩解方程组得：即所以此种解方程组的方法叫换元法．22x y =⎧⎨=⎩1222a b -=⎧⎨+=⎩30a b =⎧⎨=⎩（1）拓展提高运用上述方法解下列方程组：122435212535a b a b ⎧⎛⎫⎛⎫-++= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎛⎫⎛⎫⎪-++= ⎪ ⎪⎪⎝⎭⎝⎭⎩（2）能力运用已知关于x ，y 的方程组的解为，直接写出关于m 、n 的方程组111222a x b y c a x b y c +=⎧⎨+=⎩53x y =⎧⎨=⎩的解为_____________．()()()()11112253325332a m b n c a m b n c ⎧++-=⎪⎨++-=⎪⎩（1） （2）95a b =⎧⎨=-⎩23m n =-⎧⎨=⎩解：（1）拓展提高设−1=x ，+2=y ，3a 5b方程组变形得： ，24{25x y x y +=+=解得： ，即 ，21x y =⎧⎨=⎩123{215a b -=+=解得： ；9{5a b ==-（2）能力运用设 ，53){3(2)m x n y +=-=（可得 ，53)5{3(2)3m n +=-=（解得： ，2{3m n =-=故答案为2{3m n =-=33．某校规划在一块长AD 为18 m 、宽AB 为13 m 的长方形场地ABCD 上，设计分别与AD ，AB 平行的横向通道和纵向通道，其余部分铺上草皮，如图所示，若设计三条通道，一条横向，两条纵向，且它们的宽度相等，其余六块草坪相同，其中一块草坪两边之比AM ∶AN ＝8∶9，问通道的宽是多少？1解：设通道的宽是xm ，AM ＝8ym.因为AM ∶AN ＝8∶9，所以AN ＝9ym.所以解得22418,1813.x y x y +=⎧⎨+=⎩1,2.3x y =⎧⎪⎨=⎪⎩答：通道的宽是1m.故答案为1.34．水果市场将120吨水果运往各地商家，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：(假设每辆车均满载)车型甲乙丙汽车运载量(吨/辆)5810汽车运费(元/辆)400500600(1)若全部水果都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？(2)为了节约运费，市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆)，已知它们的总辆数为16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？(1) 分别需甲8辆、乙10辆；(2) 有二种运送方案：①甲车型6辆，乙车型5辆， 丙车型5辆；②甲车型4辆，乙车型10辆， 丙车型2辆详解：(1)设需甲车型x 辆，乙车型y 辆，得：，581204005008200x y x y ⎧⎨⎩＋＝＋＝解得.810x y ⎧⎨⎩＝＝答：分别需甲车型8辆，乙车型10辆.(2)设需甲车型x 辆，乙车型y 辆，丙车型z 辆，得：，165810120x y z x y z ⎧⎨⎩＋＋＝＋＋＝消去z 得5x ＋2y ＝40，，285x y -＝因x ，y 是正整数，且不大于16，得y ＝5或10，由z 是正整数，解得6451052x x y y z z ⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩＝＝＝，＝，＝＝有二种运送方案：①甲车型6辆，乙车型5辆，丙车型5辆；②甲车型4辆，乙车型10辆，丙车型2辆35．电脑中有一种游戏——蜘蛛纸牌，开始游戏前有500分的基本分，游戏规则如下：①操作一次减x 分；②每完成一列加y 分．有一次小明在玩这种“蜘蛛纸牌”游戏时，随手用表格记录了两个时段的电脑显示：第一时段第二时段完成列数25分数634898操作次数66102(1)通过列方程组，求x ，y 的值；(2)如果小明最终完成此游戏(即完成10列)，分数是1 182，问他一共操作了多少次？(1)(2)3181100x y =⎧⎨=⎩解：(1)依题意得 2666345005102898500y x y x -=-⎧⎨-=-⎩解得 1100x y =⎧⎨=⎩(2)设他一共操作了a 次，则10×100－a×1＝1 182－500，解得a ＝318.答：他一共操作了318次．。