当前位置：文档之家 › 第三章 气体内的输运过程

第三章 气体内的输运过程

  • 格式：ppt
  • 大小：2.25 MB
  • 文档页数：87

下载文档原格式

  / 87

合集下载

气体内的输运过程

气体内的输运过程

（内迁移、输运过程）
热传导：温度 T 不均匀 热的迁移； 内摩擦（粘滞）：定向速度u不均 输运过程 定向动量的迁移； 扩散：密度 不均匀 m的迁移。
热学

13
一、粘滞现象的宏观规律
1、层流 在流动过程中，相邻质点的轨迹线彼此仅稍有差别， 不同流体质点的轨迹线不相互混杂，这样的流动称 为层流。
由于分子的热运动，从而引起质量从密度大的区域 向密度小的区域迁移的现象。 d 1 2 ( z ) 密度梯度 2 dz
z z0
dM dS
表示气体的密度沿x 轴方向 的空间变化率。
在dt时间内，通过dS传递的质量
o
1
x
d dM D dSdt dz z0
热学

23
§3. 输运过程的微观解释
首先是气体分子的热运动 另一个重要原因就是分子间的碰撞。 一、粘滞现象的微观解释 气体黏性系数的导出
1 1 nmv或 v 3 3
讨论： 注意：*近平衡非平衡过程；
*气体既足够稀薄又不 太稀薄
1）、η 与n无关。 2）、 η仅仅是温度的函数。
热学

21
D 扩散系数
d dM D dSdt dz z0
' ' 表示扩散总沿减小的方向
1自扩散与互扩散 当物质中粒子数密度不均匀时，由于分子的热运动 使粒子从密度高的地方迁移到数密度低的地方的现象 称为扩散。 互扩散：发生在混合气体中，由于各成分的气体空间 分布不均匀，各成分分子均要从高密度区向低密度区 迁移的现象。 自扩散：是互扩散的一种特例
空气的平均分子量为29。
解： 已知 T 273K , p 1.0atm 1.013 105 Pa,
气体内的输运过程

气体内的输运过程


1 du f ( ) z0 dA，其中 nmv 3 dz 称为牛顿黏性定律. η的单位为泊,以P表示
1P 1N s m 0.1kg m s
2
1
1

考虑到相邻两层流体中相对速度较大的流体总是受到阻力， 即速度较大一层流体受到的黏性力的方向总与速度梯度方向相反,故在式中加上负号
1 υ 平均自由程: λ 2 z 2d n 2d 2 n
式中：d为分子的有效直径，n为分子数密度。
由 p nkT n
p kT
kT λ 2 2πd p
思考 在一封闭容器中装有1mol氦气(视作理想气体)，这 时分子无规则运动的平均自由程将决定于什么？ (A)压强p (B)体积V (C)温度T (D)平均碰撞频率 z
实验发现，流体在流速较小时将作分层平行流动， 流体质点
轨迹是有规则的光滑曲线， 不同质点轨迹线不相互混杂。 这样的流体流动称为层流。 直圆管中流体流速分布如图 流速箭头的包络面为抛物面, 其平均流速箭头的包络面为 平面
稳恒层流中的黏性 牛顿黏性定律
•流 体 作 层 流 时 ， 通过任一平行于流 速的截面两侧的相 邻两层流体上作用 有一对阻止它们相 对“滑动”的切向 作用力与反作用力。
二.热传导现象的宏观规律
当系统与外界之间或系统内部各部分之间存在温度 差时就有热量的传输. 热传递有热传导、对流与辐射 三种方式，本节将讨论热传导
1. 傅里叶定律（Fourier law of heat conduction ) •1822法国科学家傅里叶（Fourier）在热质说思想的指导下 发现了傅里叶定律。 该定律认为热流dQ/dt (单位时间内 通过的热量）与温度梯度 dT /dz 及横截面积dA成正比，
输运过程的微观解释

输运过程的微观解释

设想在气体内部有一分界平面dS,
可以得出，在dt时间内通过dS面沿z 轴输运的质量为：
dM 1 3 v ( d dz ) z d sd t
0
对照斐克定律：
d
0
则扩散系数：
D
v
dQ 1 3 nv t r 2s 2 dT dz k( dT dz ) z d sd t
0
) z d sd t
0
对照傅里叶定律：
d Q (
则导热系数（热导率）为：

1 3
nv
t r 2s 2
K
1 3
n v m cV
1 3
v cV
三、扩散现象的微观解释
一、黏滞现象的微观解释 内摩擦现象是由于分子热运动中通 过ds面交换定向动量的结果。 在层流流体中，每个分子除有热运 动动量外，还叠加上定向动量。 因为热运动动量的平均值为零，故 只需考虑流体中各层分子定向动量 设想在 z0 处，有一平面 ds 与定向动量方向平行，与z 轴垂直。如图。 1
dt 内从下方穿过 ds平面向上的平均分子数： 6
dK
1 3
nm v (
du dz
) z d sd t
0
1 3
du dz
v (
du dz
) z d sd t
0
对照前面公式：
d K (

1 3
) z d sd t
0
黏滞系数为：
v
二、热传导现象的微观解释 设想在气体内部有一分界平面dS, 可以推出，在dt时间内通过dS 面沿z轴输运的热量为：
dt
1 6
n vd td s
内从上方穿过 ds平面向下的平均分子数： n vd td s
气体动理论第3讲分子分布律和碰撞实际气体和输运过程

气体动理论第3讲分子分布律和碰撞实际气体和输运过程

n p 2.69 1025 /m3 kT
z 2d 2nv 6.58 109 s1
记住
（ ~ 66 亿次/ 秒！） 数量
v 6.46 108 m
z
级！
玻耳兹曼分布律
一、重力场中气体分子按高度分布旳规律
1、等温气压公式
H
设 高度 0 h h dh
压强 P0 P P dP
h dh P dP hP
3 . 其他分子皆静止, 某一分子以平均速率 相u
对其他分子运动 .
单位时间内平均碰撞次数 Z π d 2 u n
考虑其他分子旳运动 u 2 v
分子平均碰撞次数 Z 2π d 2 vn
分子平均碰撞次数
Z 2 πd 2 vn
p nkT
平均自由程
v
z
1 2π d 2n
kT 2π d 2 p
分布曲线趋于平坦
0 vp1 vp2
v f (v p )
f () 2
已知1：m1 ,T 1
41 3
则 2? 3?
4 : m m1, T 1 ?
5
5 : m1,T T 1 ?
O
2、平均速率
定义：气体全部分子旳速率旳算术平均值。
0 dN
N
0
f
()d
8kT m
8 RT
3、方均根速率 定义：全部分子旳速率平方旳平均值旳平方根。
旳分子数为
dN dN
m
3 / 2 m2
e 2kT
dx dy dz
2kT
m
n0
2kT
3
/
2
e
PK kT
dxdydz
dx dy dz
实际气体旳范德瓦耳斯方程
第三章-气体的迁移过程

第三章-气体的迁移过程


气体的内摩擦数系
dv dL = η ds dz
“一”号表示动量传递的方向与速度梯度方向相反。 一 号表示动量传递的方向与速度梯度方向相反。 设垂直于z轴安置两个平行板， 设垂直于z轴安置两个平行板，处于原点的一块静
止不动，上面的一块以一定速度沿y方向运动。 止不动，上面的一块以一定速度沿y方向运动。 两板间的气体流速u 两板间的气体流速u沿z方向有一陡度，即u=u(z)。 方向有一陡度， u=u(z)。 故分子携带的物理量，如为动量g=mu(z) 故分子携带的物理量，如为动量g=mu(z) 单位时间通过z=z 假象平面单位面积y方向 单位时间通过 0假象平面单位面积 方向 动量的净输运量为
mkT
π
关于内摩擦系数的讨论
λ d 气体的内摩擦系数与与n(或P)无关 气体的内摩擦系数与与n(或P)无关 n(
随气体分子密度n的增大 分子碰撞的频率增加， 的增大， ① 随气体分子密度 的增大，分子碰撞的频率增加，参与动量迁移的分子 数目增多， 数目增多， 减少，每个分子每次碰撞传递的动量亦减少， ② 但λ减少，每个分子每次碰撞传递的动量亦减少， 以上两因素共同作用的结果，使内摩擦系数保持不变。 以上两因素共同作用的结果，使内摩擦系数保持不变。
处迁移，最终使得各处密度相等，即为扩散现象， 气体质量的迁移过程。 处迁移，最终使得各处密度相等，即为扩散现象，是气体质量的迁移过程。
自扩散”发生在单一成分气体由于存在密度梯度时； “自扩散”发生在单一成分气体由于存在密度梯度时； 互扩散”发生在多成分气体由于存在密度梯度时； “互扩散”发生在多成分气体由于存在密度梯度时；
气体的能量迁移 —— 热传导现象
气体的迁移过程 ——压强较高时 λ d 压强较高时
当气体内各部分的温度不同时 热量将从高温处向低温处传递， 各部分的温度不同时， 热传导 当气体内各部分的温度不同时，热量将从高温处向低温处传递， 这种现象称为气体的热传导现象。通过热传导，最终气体各处温度趋于一致。 这种现象称为气体的热传导现象。通过热传导，最终气体各处温度趋于一致。 q---气体传递的热量，W/m2 气体传递的热量， 气体传递的热量 dT K---气体的热传导系数，W/(m K) 气体的热传导系数， 气体的热传导系数 dq = K dz dT/dz---气体内的温度梯度 气体内的温度梯度
( 基础物理学)第三章近平衡态中的输运过程

( 基础物理学)第三章近平衡态中的输运过程


理学院 物理系 陈强
2. 黏性现象的微观本质 流体内各层之间因流速不同而有宏观上的相对 运动时，产生在流层之间的定向动量迁移现象。 宏观上表现为相邻流层之间有切向摩擦力作用。
12
3. 粘滞系数
分子按方向分6组, 每组数密度n/6， z
平均速率 . 平均自由程
交换一对分子, A输运到B的定向动量: z0 A
16
理学院 物理系 陈强
第三章 近平衡态中的输运过程
1. 扩散现象的宏观规律 如图， 设各处 p, T都相同.
A S B
考虑CO: CO (x)
相同时间内通过S:
由Ａ到Ｂ的CO分子数多 由B到Ａ的CO分子数少
△Ｍ
CO N2
x0 x
S面左右两侧间
有CO质量传递
单位时间内通过S由A输运到B的CO质量:
常见的输运现象有：黏性现象、热传导 、扩散、 化学反应、生物体中的养料吸收等。 本章主要讨论三类迁移现象:即黏性现象(内摩擦)、 热传导、扩散 实际上，有些输运现象往往同时存在. 本课程仅限于：分别讨论近平衡态的黏性现象、 热传导 、扩散这三种输运过程．
9
一. 黏性现象(内摩擦)
当各层流体的流速不同，即各层流体之间有相对滑 动时，快层必然带动慢层，慢层必然阻滞快层。 层与层之间有切向摩擦力，叫内摩擦力(粘性力)。
第三章近平衡态中的输运过程菲克扩散定律由b到a的co分子数少m负号表示质量输运方向s面左右两侧间有面左右两侧间有co质量传递理学院物理系陈强18由于热运动左右两边流体不断交换分子就混合流体的某一种组分来讲由于其密度不均匀密度大的一方迁出的分子多于迁入的分子因而有净质量从密度大的地方向密度小的地方输运形成了流体由于热运动左右两边流体不断交换分子就混合流体的某一种组分来讲由于其密度不均匀密度大的一方迁出的分子多于迁入的分子因而有净质量从密度大的地方向密度小的地方输运形成了流体质量的定向迁移
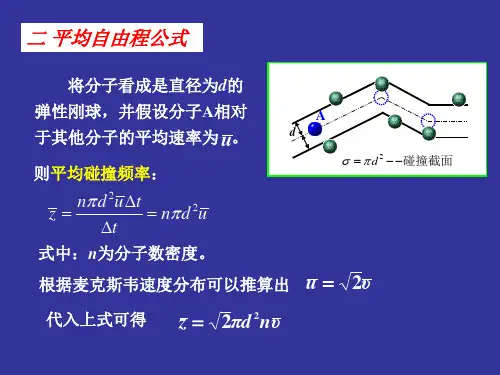
第三章 气体内的输运过程

第三章 气体内的输运过程

JP dp dt A du dz

27
男性 女性
人体全血黏度检测正常值 230 s-1：4.07～4.99(mPa·s), 11.5s-1：7.83～10.79(mPa·s)； 230s-1：3.81～4.63(mPa·s) 11.5 s-1：7.15～9.59(mPa·s)。
m
M
每个分子平均每秒与其他分子碰撞65亿次。
Z
v
6 . 5 10
9
s
1

13
前面引入的分子间碰撞的平均频率及平均自由程， 虽然均能表示分子间碰撞的主要特征，但不能反映分 子间碰撞的随机性质。
实际上，若一分子在某处刚好被碰撞过，则以后遭 受第二次碰撞的时间完全是随机的。所以它在两次碰 撞之间走过的路程也是随机的。
y
O Z
x

15
y
O
x x t N x+ dx t + dt N+dN
Z
0 0 N0
假设在 t 时刻，x 处剩下N 个分子（这N个分子的自由程在0-x之间） 经过d t 时间，分子束运动到 x + d x 处又被碰撞掉 dN 个分子。（这dN个分子的自由程在x-x+dx之间） 即自由程为x 到x + d x 的分子数为 – dN 。 因为dN 是减少了的分子数, dN ＜ 0，要加个负号。
二、菲克定律

32
一维粒子流密度 JN（单位时间内在单位 截面上扩散的粒子数）与粒子数密度梯度 dn 成正比。 dz
JN D dn dz
D为扩散系数，单位为 m2s-1 。负号表示粒子
向粒子数密度减少的方向扩散。若在与扩散方向 垂直的流体截面上 JN 处处相等,则有
热学第三章输运～1

热学第三章输运～1


f = 6πηvR
——斯托克斯公式 斯托克斯公式
R ~ 106 m,vmax ~ 104 m s1
解释云雾的形成: 2 ρgR 2 解释云雾的形成: v max = 9η 七,非牛顿流体
1,其速度梯度与互相垂直的粘性力间不呈线性 , 函数关系,如血液,泥浆,橡胶等. 函数关系,如血液,泥浆,橡胶等. 2,其粘性系数会随着时间而变的,如:油漆等 ,其粘性系数会随着时间而变的, 凝胶物质. 凝胶物质. 3,对形变具有部分弹性恢复作用,如沥青等 ,对形变具有部分弹性恢复作用, 粘弹性物质. 粘弹性物质.
y粘滞力: 粘滞力: 源自 AB = f BA二,牛顿粘性定律 1,实验表明: ,实验表明:
A
B
ds
x
z0
f BA
→u y
o
du f = η ds dz z 0
形式一
x 4-3
η
——粘度(粘性系数) 粘度(粘性系数) 粘度
单位是Pas 单位是
说明: )定律对气体和液体都是适用的. 说明: 1)定律对气体和液体都是适用的. 2)η与流体的性质及温度,压强有关 ) 与流体的性质及温度 与流体的性质及温度, 气体的黏度随温度升高而增加, 气体的黏度随温度升高而增加, 液体的黏度随温度升高而减少. 液体的黏度随温度升高而减少. 2,从效果看: ,从效果看: 设在dt 时间内,通过ds截面 截面, 轴定向输运的动量: 设在 时间内,通过 截面,沿z轴定向输运的动量:dp 若规定沿z轴正方向传递的动量 若规定沿 轴正方向传递的动量dp>0,则 轴正方向传递的动量 ,
压强均匀且温度稳定分布的一维热传导) 二,傅立叶定律 (压强均匀且温度稳定分布的一维热传导) 设等温面是x-y平面,若在稳态情况下,温度 仅是 的函数, 仅是z的函数 设等温面是 平面,若在稳态情况下,温度T仅是 的函数, 平面 且温度沿Z轴正方向逐渐加大, 处取一截面A, A,则单 且温度沿Z轴正方向逐渐加大, z=z0 处取一截面A,则单 T 位时间内通过该截面A的热量Q 位时间内通过该截面A的热量Q与温度梯度 z Z 及截面的面积A成正比: 及截面的面积A成正比: z T2 (< T ) 1 B
§4.3输运过程的微观解释

§4.3输运过程的微观解释

D = 1.0 × 10 m ⋅ s
2 −5 −1
η κ
D
00 C 38 0 C
17 . 1 × 10 − 6 N ⋅ s ⋅ m − 2 27 × 10 − 3 J ⋅ m −1 ⋅ s −1 ⋅ K −1
O 2 − 空气 1 . 78 × 10 − 5 ⋅ m 2 ⋅ s −1
在数量级上无多大差异，但其数值有一定偏差， 在数量级上无多大差异，但其数值有一定偏差，它只 能用于估计数量级。 能用于估计数量级。 这也说明， 这也说明，前面所介绍的仅是关于输运过程微观分析 的初级理论，它还存在相当大局限性。 的初级理论，它还存在相当大局限性。
平面∆ 将上面的两式相减即得从下方通过 z0 平面 ∆ A 面积 向上方净输运的总动量 1 {净动量输运 } = n v ⋅[ mu x ( z 0 − λ ) − mu x ( z 0 + λ )] ∆ A ∆ t 6
{净动量输运 } =
除以 ∆t 即得 z0 黏性力
1 nv ⋅[ mu x ( z0 − λ ) − mu x ( z0 + λ )]∆A∆t 6
∂u x u x (Z 0 + λ ) ≈ u x (Z 0 ) + ∂z ∂z λ
∂u u x (Z 0 − λ ) ≈ u x (Z 0 ) − x ∂z
λ
将它们代入
1 f = n v ⋅m[u x ( z 0 − λ ) − u x ( z 0 + λ )] ∆ A 6
方向运动， 假定单位体积中有 n / 6 个分子向 z0 方向运动， 每个分子均以平均速率运动。 每个分子均以平均速率运动。 平面上的∆ 在∆t 时间内从上方穿过 z0平面上的∆A 面积元向 下运动的平均分子数为 (1 / 6) nv∆A∆t 若再假设所有从上面（或从下面） 若再假设所有从上面（或从下面）穿越 z0平面的 分子，平均说来都分别是来自 分子，
气体内的输运过程优秀课件

气体内的输运过程优秀课件


一个分子所经过的平均距离为t，而与其它分子
碰撞的平均次数是 zt，由于每碰撞一次都将结束
一段自由程，所以
t
Zt Z
二、 平均自由程公式
将分子看成是直径为d 的 弹性刚球，并假设分子A相对
于其他分子的平均速率为 u。
则平均碰撞频率：
z n d 2u t n u
t
式中：n为分子数密度。 d2 碰 撞 截 面
实验又测出在切向面积相等时,这样的 流体中的速度梯度处处相等. 而且流体层所受到的黏性力的大小是 与流体流动的速度梯度的大小成正比的。
牛顿黏性定律
•黏性力的大小与 du / dz及切向面积S成正比 .
•比例系数以η表示，称为流体的黏度或黏性系数、黏 滞系数（coefficient of viscosity)则
2）由于气体分子无规的（平动）热运动， 在相邻流体层间交换分子对的同时，交换相 邻流体层的定向运动动量。
3）结果使流动较快的一层流体失去了定向 动量，流动较慢的一层流体获得到了定向动 量，黏性力由此而产生的.
二.热传导现象的宏观规律
当系统与外界之间或系统内部各部分之间存在温度 差时就有热量的传输. 热传递有热传导、对流与辐射 三种方式，本节将讨论热传导
三、分子按自由程的分布
• 分子在任意两次连续碰撞之间所通过的自由程不同；分子
在自由程介于任一给定长度区间 x~xdx 内的分布：
设想某个时刻一组分子共N0个，运动中与组外分子相碰， 每碰一次，组内分子减少一个。设这组分子通过路程x时还 剩下N个，在下段路程dx,又减少了dN个。
分子在长度为dx的路程上，每个分子平均碰撞 dx /
气体内的输运过程
4.1 气体分子的平均自由程
气体运输

气体运输


2.中段:PO28.0～5.3kPa (40～80mmHg)
坡度较陡。
表明：PO2降低能促进 大量氧离，血氧饱和度下 降显著。
意义:维持正常时组织 的氧供。
因正常时组织的氧供， PO2在中段范围变化。
下
中
上
下
中
上
3.下段:PO25.3～2.0kPa
(15～40mmHg)
坡度更陡。
表明：PO2稍有下降,血 氧饱和度就急剧下降。
（∵冷冻血3周后，RBC无氧代谢停止→DpG↓）
故：应注意缺氧。
④ Hb+O2的结合或解离曲线呈S形
***Pco↑
Pco↑→曲线左移→氧离难
∵①co与Hb亲和力 > o2与Hb亲和力 250 倍； ②co与Hb的结合位点与o2相同；
4. 氧利用率
氧利用率：100mml动脉血流经组织是所释放的o2占动 脉血o2含量的百分数，称氧气利用率。 公式=（---）
意义:维持活动时组织的
氧供。
因下段释放O2量为正 常时的3倍(= O2储备段)。
小结：
氧离曲线特点及其生理意义
（四）影响氧离曲线的因素
P50 ： 指 Po2 为
26.5mmHg 时 Hb 氧 饱 和 度
达到50%。P50表示氧离曲
线的正常位置。
亲和●P力5↓0（↑氧: 表离明易H）b，对需o更2的高的Po2才能使Hb氧饱和度
移
Pco2↓PH↑→氧离曲线左移
这种酸度对Hb与o2亲和力的影响，称为波尔效应
(Bohr effect)，其意义：①在肺脏促进氧合②在组织促 进氧离。
2.温度 T↑→氧离曲线右移 T↓→氧离曲线左移
∵T变化→H+的活度变化 →Hb与o2亲和力变化→Hb构 型改变→氧离曲线位移。如：

§9-6 气体内的输运过程

3
圆柱体的截面积为π 叫做分子的碰撞截面。 圆柱体的截面积为πd 2 ，叫做分子的碰撞截面。 时间内， 所走过的路程为 t 在t 时间内，A所走过的路程为 u ，相应圆柱 体的体积为 πd 2 u ，设气体分子数密度为 n，则 ， t 中心在此圆柱体内的分子总数，亦即在t 中心在此圆柱体内的分子总数，亦即在 时间内 与A 相碰的分子数为 nutπd2 。
3
12
*四、扩散(diffusion) 扩散 在混合气体系统中， 在混合气体系统中 ， 当某种气体的密度不均匀 时 ， 这种气体的分子将从密度大的地方向密度小 的地方迁移， 的地方迁移 ， 从而使整个系统的气体成分趋于均 这种现象称为扩散。 匀，这种现象称为扩散。
z
ρ2 > ρ 1 ρ2
系统中气体沿z方向的 系统中气体沿 方向的 密度逐渐增大， 即沿z 密度逐渐增大 ， 即沿 轴方向存在密度梯度 dρ/dz。 。
15
1
简化处理 :
(1) 认为气体分子是刚性球，两个分子中心之间最小距离 认为气体分子是刚性球， 的平均值称为有效直径 d，并且分子间的碰撞是完全弹性碰 ， 系统中气体分子的密度不很大， 撞；(2) 系统中气体分子的密度不很大，只要考虑两个分子 的碰撞过程就够了； 当某个分子与其它分子碰撞时， 的碰撞过程就够了；(3) 当某个分子与其它分子碰撞时，可 以认为这个分子的直径为2d， 以认为这个分子的直径为 ， 而所有与它发生碰撞的分子 都看作没有大小的质点； 都看作没有大小的质点；(4) 假定被我们跟踪的分子的热运 动的相对速率的平均值为 u ，而所有与它发生碰撞的分子 都静止不动。 都静止不动。
10
*三、热传导 物体内各部分温度不均匀时， 物体内各部分温度不均匀时 ， 将有热量由温度较 高处传递到温度较低处，这种现象叫做热传导。 高处传递到温度较低处，这种现象叫做热传导。 宏观规律 设某种气体系统的温度沿 z方向由下而上逐渐升高 ， 方向由下而上逐渐升高， 方向由下而上逐渐升高 温度T 的函数， 温度 是z 的函数，其变化 可用温度梯度dT/dz表示。 表示。 可用温度梯度 表示

气体的输运过程


2.69 1025 m3
1
2.10 107 m
2d 2n
z v 8.10 109 s 1
9
6.2 输运过程的宏观规律
当系统各部分的物理性质如流速、温度或密度 不均匀时，系统则处于非平衡态。在不受外界 干预时，系统总是要从非平衡态向平衡态过渡。 这种过渡称为输运过程。(或迁移现象).
输运过程有三种：内摩擦、热传导和扩散。它 们具有共同的宏观特性和共同的微观机构，都 是由于某些物理量不均匀，由分子热运动和碰撞 而趋向于均匀的过程。
O
A
旋转 黏度计
Q
u0
df u=u(z) dS df’
P
x
11
在流体内部z=z0处有一分界平面ds, ds上下相邻流体 层之间由于速度不同通过ds面互施大小相等方向相 反的作用力，称为内摩擦力或粘滞力。
实验表明粘滞力的大小df与该处流速梯度及ds的大
小成正比。 df du ds
dz z0
称为流体的内摩擦系数或粘滞系数；单位：帕•秒。
中碳有放射性如14C，另 O
x
一种无放射性如12C。
17
设一种组分的密度沿z轴方向减小，密度是z的
函数，其不均匀情况用密度梯度d /dz表示。
设想在z=z0处有一界面dS。实验指出，在dt内 通过dS面传递的这种组分的质量为:
dM D d dSdt
dz z0 D为扩散系数；(单位是米2/秒)
本节介绍其基本规律。
10
• 内摩擦(粘滞现象)
流体内各部分流速不同时,就 发生内摩擦现象。或叫粘滞现象。
C M B
宏观规律 设想流体被限制在两大平 行平板P、Q之间，P静止， Q以速度u0沿x方向匀速运 z 动，板间流体也被带动沿 x方向流动，但平行于板 的各层流体的流速u不同， u是z的函数。其变化情况 z0 用流速梯度du/dz表示。

热学第三章习题参考答案

热学习题答案第三章：气体分子的输运过程(内容对应参考书的第四章)1. 某一时刻，氧气中一组分子刚与其他分子碰撞过，问：经过多长时间后，其中还保留一半未与其他分子相碰。

设氧气分子都以平均速率运动，氧气温度300K ，在给定压强下，分子平均自由程为2.0cm 。

解：设这组分子个数为0N ，经过时间t （对应的路程为x ）后未碰撞的分子数为N ，根据分子按自由程的分布()dx e dx x f N dN x⋅==-λλ10 由已知：t v x =，210=N N ，则有 210===⋅--λλt v x e e N N ，即2ln v t λ= 又由πμRTv 8=，mol Kg /10323-⨯=μ，代入上式得()s RT t 532101.32ln 30031.88103214.3100.22ln 8---⨯≈⨯⨯⨯⨯⨯==πμλ。

2. （P 142。

8）在气体放电管中，电子不断与气体分子相碰，因电子的速率远远大于气体分子的平均速率，所以后者可以认为是静止不动的。

设电子的“有效直径”比起气体分子的有效直径d 来可以忽略不计。

（1）电子与气体分子的碰撞截面σ为多大？（2）证明：电子与气体分子碰撞的平均自由程为σλn e 1= 解：（1）电子与气体分子的碰撞截面22⎪⎭⎫ ⎝⎛+=d d e πσ，由于d d e <<，故 22412d d d e ππσ≈⎪⎭⎫ ⎝⎛+=（2）由于气体分子可以认为是静止不动的，则电子与气体分子间的平均相对速率就等于电子的平均速率e v 。

在时间t 内，电子走过的路程为t v e ，相应的圆柱体的体积为t v e σ，则在此圆柱体内的气体分子数为t v n e σ，即为时间t 内电子与气体分子的碰撞次数，故碰撞频率为e e v n t t v n Z σσ==电子与气体分子碰撞的平均自由程为σλn Z v e e 1==。

3. （P 143。

18）一长为2m ，截面积为410-米2的管子里贮有标准状态下的2CO 气，一半2CO 分子中的C 原子是放射性同位素C 14。

《大学基础物理学》教学课件：气体中的输运现象


dQ k dT dSdt dz
dT — 温度梯度 dz
k— 导热系数（取决于气体的 性质和状态）
z T大
dS
负号表示热量沿着温度减小
的方向传递，即dQ沿z的负方
x T 向传递。
o
小
y
3. 扩散现象
定义：在混合气体内部，当某种气体的密度不均匀时, 则这种气体分子将从密度大处移向密度小处。
dM D d dSdt
dz
d — 密度梯度
dz
D— 扩散系数
负号表示质量沿着密度减 小的方向传递
CO2 N2
输运现象的微观解释 ① 分子扩散
② 分子碰撞
总结：
dk d dSdt
dz dQ k dT dSdt
dz
dM D d dSdt
dz
— 分子的定向动量迁移 — 分子的平均能量迁移 — 分子数目迁移
2.4 气体中的输运现象
1. 粘滞现象
定义：相邻两层流体因流速不同有相对运动时，沿接触
面互施切向力（粘滞力）的现象
dk
fdt
dv dSdt
dz
z
B
vB
mvB
负号表示动量沿Z的负方向 fAB
传递，即表明动量总是朝
x 着流速减小的方向传递。
dS
A
o
f BA
vA
mvA y
2. 热传导现象
定义：如果气体内各个地方的温度不均匀时，热
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
JP dp dt A du dz

27
男性 女性
人体全血黏度检测正常值 230 s-1：4.07～4.99(mPa·s), 11.5s-1：7.83～10.79(mPa·s)； 230s-1：3.81～4.63(mPa·s) 11.5 s-1：7.15～9.59(mPa·s)。
dt 8 L

30
四、斯托克斯定律 球体在黏性流体中运动时，物体表面黏附 着一层流体，这一流体层与相邻的流体层之间 存在黏性力，在运动中需克服这一阻力。
f 6vR
五、非牛顿流体
1、速度梯度和黏性力间不呈线性关系。 2、其黏性系数会随时间而变或与流体以 前的历史过程有关。 3、对形变有部分弹性恢复作用。
N0 既然（-dN ）表示 N0 个分子中自由程为 x 到x + dx 的平均分子数，则（-dN /N0 ）是分子的自由程在 x 到 x + dx范围内的概率。这就是分子自由程的概率分布。 即分子按自由程分布的规律。

18
由分子自由程的概率分布可求平均自由程
dN N0

K exp( Kx)dx
在流动过程中，相邻质点的轨迹彼此稍 有差别，不同流体质点的轨迹不相互混杂， 这样的流动为层流。层流发生在流速较小时

22
流体作层流时，通过任一平行流速的截面两 侧的相邻两层流体上作用有一对阻止它们相对 滑动的切向作用力与反作用力，使流动快的一 层流体减速，这种力为黏性力（内摩擦力）
z
u0 A df´
m
M
每个分子平均每秒与其他分子碰撞65亿次。
Z
v
6 . 5 10
9
s
1

13
前面引入的分子间碰撞的平均频率及平均自由程， 虽然均能表示分子间碰撞的主要特征，但不能反映分 子间碰撞的随机性质。
实际上，若一分子在某处刚好被碰撞过，则以后遭 受第二次碰撞的时间完全是随机的。所以它在两次碰 撞之间走过的路程也是随机的。
上式表示单位时间内气体扩散的总质量与密 度梯度的关系

33
互扩散公式表示为：
M t D1 2 d1 dz A
D12 为“1”分子在“2”分子中作一维
互扩散时的系数。△M 为输运的“1”质量 数。 扩散系数的大小表示了扩散过程的快慢 在压强很低时的气体的扩散与常压下的扩散 完全不同.

2
§1 气体分子的平均自由程

3
无引力的弹性刚球模型
气体分子间发生碰撞，两分子间的距离较大时，它 们之间无相互作用力，分子作匀速直线运动。 当两分子质心间的距离减小到分子有效直径d 时， 便发生无穷大的斥力，以阻止分子间的接近，并使分 子运动改变方向。 因此把两个分子间的这种相互作用过程看成是两个 无引力的弹性刚球之间的碰撞。
dA
df
u=u(z)
B
u=0
x

23
对于面积为 dA 的相邻流体层来说，作 用在上一层流体的阻力 df´必等于作用于下 一层流体 df 的加速力。
牛顿黏性（viscosity）定律
在相邻两层流体中，相对速度较大的流 体总是受到阻力，即速度较大一层流体受到 的黏性力的方向总与速度梯度方向相反，故
f du dz A
34
三、气体扩散（diffusion）的微观机理 扩散是在存在同种粒子的粒子数密度空 间不均匀的情况下，由于分子热运动所产 生的宏观粒子迁移或质量迁移。 它与流体由于空间压强不均匀所产生的 流体流动不同，后者是由成团粒子整体定 向运动产生。 扩散也向相反方向进行，因为在较高密 度层的分子数较多，向较低密度层迁移的分 子数就较相反方向多。
dN Kdx N
N Kdx Ln N
0 0
x
N N 0 exp( Kx )

17
N N 0 exp( Kx )
表示从 x =0 处射出了刚被碰撞过的N0个分子，它们 行进到 x 处所残存的分子数 N 按指数衰减。 对上式之右式两边微分，得到

dN
K exp( Kx)dx
为了描述这种随机性质，必须找到它在某一个范围 内受到碰撞的概率，即分子的自由程处于这个范围内 的概率——分子按自由程的分布规律。

14
分子按自由程的分布
制备 N0 个分子所 组成的分子束，分子束 中的分子恰好在同一地 点 x = 0 处刚被碰过一 次，以后都向 x 方向 运动。分子束在行进过 程中不断受到背景气体 分子的碰撞，使分子数 逐渐减少。
2v , v 为
气体分子的平均速率。
Z 2 πd
2
vn
8 kT
p nkT ， v
（当气体较稀薄时）
m
( d )
2
Z
4p
mkT
平均碰撞频率的大小与气体的种类和所处的状态有关。分子的 大小对碰撞的频繁程度有重要作用。

10
分子的平均自由程公式

vt Zt v Z
即，分子按自由程分布的规律，亦称为自由程概率论 分布。

20
§2输运过程的宏观规律
当系统各部分的宏观物理性质如流速、 温度或密度不均匀时，系统就处于非平衡态. 在不受外界干预时，系统总要从非平衡态自 发地向平衡态过渡，这种过渡为输运过程。

21
2-1 黏性现象的宏观规律
一、层流与牛顿黏性定律
速度梯度即流速在薄层单位间距上的增量。
24
例题:旋转黏度计
M B
夹层内的空气对B 筒施
予黏性力。A 筒保持一恒定
的转速，B 筒相应地偏转一
定的角度，偏转角度的大小
A
由附在纽丝上的小镜 M 所
反射的光线测得。从偏转角
ω
的大小可计算出黏性力。

G 2R L
3
气体的黏度

25
解：
外桶的线速度 夹层流体的速度梯度

1
系统自发地进行的过程靠的是分子的热运动。 研究输运过程时，必须考虑到分子间相互作用时对 运动情况的影响。 碰撞使分子不断改变运动方向与速率大小，使分子 行进的轨迹十分曲折。 碰撞使分子间不断交换能量与动量。 系统的平衡也需借助频繁的碰撞才能达到。 本节将介绍一些描述气体分子间碰撞特征的物理量： 碰撞截面、平均碰撞频率及平均自由程。

16
又 dx 是很短的距离，则: 在 x 到 x + dx 距离内所减少的分子数 dN 与 x 处的分 子数 N 成正比。另外, dN 也与 dx 的大小成正变,更确切 说成正比。 因为dx 很小,即使不成正比,由此所产生误差仅是二阶 无穷小。 设成正比的比例系数为 K，则 dN KNdx

28
部分流体黏度参考表(21℃测得)

29
二、气体黏性微观机理 常压下气体的黏性就是由流速不同的流 体层之间的定向动量的迁移产生的。因此， 气体的黏性现象是由于气体内大量分子无规 则运动输运定向动量的结果。 三、泊肃叶定律 长为L，半径为 r 的水平直圆管中，单位 时间流过管道截面上的流体的体积 dv/dt 为 体积流量 dV r 4 p
二、菲克定律

32
一维粒子流密度 JN（单位时间内在单位 截面上扩散的粒子数）与粒子数密度梯度 dn 成正比。 dz
JN D dn dz
D为扩散系数，单位为 m2s-1 。负号表示粒子
向粒子数密度减少的方向扩散。若在与扩散方向 垂直的流体截面上 JN 处处相等,则有
M t D d dz A
分子的无引力的弹性刚球模型与理想气体微观模型相比，同样忽略了分
子间的引力，但考虑了分子斥力起作用时两个分子质心间的距离，即考虑了 分子的体积，而不象理想气体，忽略了分子本身的大小。

4
自由程 ： 分子两次相邻碰撞之间自由通过 的路程 .
5
气体分子平均自由程（mean free path） 平均自由程λ 为分子在连续两次碰撞之间所自 由走过的路程的平均值。
第三章 气体内的输运过程
前面我们对热学的学习所涉及的都是气体在平衡态 下的性质和规律，然而许多的问题都是牵扯到气体在
非平衡态下的变化过程。
非平衡态问题是至今没有完全解决的问题。理论只 能处理一部分，另一部分问题还在研究中。 最简单的非平衡态问题是：不受外界干扰时，系统 自发地从非平衡态向平衡态过渡的过程——输运过程。
K exp( Kx) xdx
0
1 K
K 1/
N N0
exp( )
x

(分子束的残存概率，即分子按自由 程分布的规律)
上式表示分子束行进到 x 处的残存的概率。 也是自由 程从 x 到无穷大范围的概率。

19
分子在 x ~ x+dx 距离内受到碰撞的概率为
P( x) dx dN N0 x exp dx 1
P 1 . 013 10 Pa
5
T 273 K


kT 2 πd p
1 . 38 10 2 π ( 3 . 5 10
23 2
2
273
5
10
) 1 . 013 10
m 6 . 9 10
8
m

12
∵空气的平均相对分子量为29 ∴
v 8 kT 8 RT 448 m s
设分子的有效直径为d ，气体单位体积内的分子数为
n，
A 分子以平均速率 u 相对于其他分子运动，其它分子都不动。

8
d d
A
碰撞截面:
2
d
d ,不 分 则 同 子 ：

1 4
(d 1 d 2 )