统计学回归分析论文
- 格式:doc
- 大小:189.50 KB
- 文档页数:11

统计学中的多元回归分析方法统计学是一门研究收集、整理和解释数据的学科,而多元回归分析是其中一种重要的方法。
本文将针对统计学中的多元回归分析方法进行详细讨论和解释。
一、引言多元回归分析是一种用于研究多个自变量与一个因变量之间关系的统计方法。
通过建立一个数学模型,它可以被用来预测或解释因变量的变化。
多元回归分析方法可以帮助我们理解不同自变量与因变量之间的影响程度和相关性。
二、多元回归模型多元回归模型可以表示为Y = β0 + β1X1 + β2X2 + ... + βnXn + ε,其中Y是因变量,X1至Xn是自变量,β0至βn是回归系数,ε是误差项。
回归系数表示了自变量对因变量的影响程度,而误差项则表示了模型无法解释的部分。
三、多元回归分析步骤1. 数据准备:收集所需自变量和因变量的数据,并进行预处理,如缺失值填充和异常值处理。
2. 模型选择:根据研究目的和数据特点选择适当的多元回归模型。
3. 参数估计:利用最小二乘法或其他估计方法估计回归系数,找到最优解。
4. 模型检验:通过统计检验和评估指标,检验模型的拟合程度和显著性。
5. 解释结果:解释回归系数的意义和影响,评估模型的可解释性。
6. 预测应用:利用得到的模型对未知数据进行预测,评估模型的预测效果。
四、多元共线性多元共线性是指自变量之间存在高度相关性的情况,会影响回归系数的估计和解释结果的准确性。
通过相关系数矩阵和方差膨胀因子等方法,可以检测和解决多元共线性问题。
五、模型评估指标在多元回归分析中,常用的模型评估指标包括决定系数(R-squared)、调整决定系数(Adjusted R-squared)、标准误差(Standard Error)、F统计量(F-statistic)等。
这些指标可以评估模型的拟合优度和显著性。
六、案例应用以房价预测为例,假设我们想通过多个自变量(如房屋面积、位置、卧室数量等)来预测房屋的价格。
通过收集相关数据并进行多元回归分析,可以建立一个房价预测模型,并根据回归系数解释不同自变量对于房价的影响程度。

生态学统计学中的回归分析方法回归分析是生态学统计学中一种重要的方法,它用于研究变量之间的关系,并预测一个变量对其他变量的影响。
通过回归分析,我们可以了解生态系统中各种因素之间的相互作用,从而更好地理解和保护自然环境。
在生态学中,回归分析可以应用于多个方面。
例如,我们可以使用回归分析来研究物种丰富度与环境因素之间的关系。
通过收集不同地理位置的样本数据,我们可以将物种丰富度作为因变量,而环境因素(如温度、湿度、土壤pH值等)作为自变量。
通过回归分析,我们可以确定哪些环境因素对物种丰富度有显著影响,从而为保护生物多样性提供科学依据。
此外,回归分析还可以用于研究生态系统中的生物量和环境因素之间的关系。
生物量是生态系统中生物体的总质量,包括植物和动物。
通过回归分析,我们可以探究生物量与环境因素(如光照、水分、土壤养分等)之间的关系。
这种研究对于了解生态系统的能量流动和物质循环具有重要意义,有助于揭示生态系统的稳定性和可持续性。
此外,回归分析还可以应用于生态学中的种群动态研究。
种群动态是指种群数量随时间的变化。
通过回归分析,我们可以了解种群数量与环境因素之间的关系,并预测未来的种群趋势。
这对于野生动物保护和资源管理具有重要意义,可以帮助我们制定科学的保护策略和可持续利用方案。
在进行回归分析时,我们需要选择适当的统计模型。
常见的回归分析模型包括线性回归、多项式回归、对数回归等。
选择合适的模型取决于研究对象的特点和数据类型。
此外,我们还需要进行模型的验证和解释。
通过检验回归模型的拟合优度和显著性,我们可以评估模型的可靠性和适用性。
同时,我们还需要解释回归模型的结果,理解变量之间的关系,并提出合理的解释和推断。
回归分析在生态学研究中发挥着重要的作用,它帮助我们揭示自然界的规律和机制。
然而,回归分析也面临一些挑战和限制。
例如,回归分析假设变量之间存在线性关系,但在生态学中,变量之间的关系往往是复杂和非线性的。
因此,我们需要进一步发展和改进回归分析方法,以应对生态学研究中的挑战。
统计学案例——相关回归分析报告《统计学》案例——相关回归分析案例⼀质量控制中的简单线性回归分析1、问题的提出某⽯油炼⼚的催化装置通过⾼温及催化剂对原料的作⽤进⾏反应,⽣成各种产品,其中液化⽓⽤途⼴泛、易于储存运输,所以,提⾼液化⽓收率,降低不凝⽓体产量,成为提⾼经济效益的关键问题。
通过因果分析图和排列图的观察,发现回流温度是影响液化⽓收率的主要原因,因此,只有确定⼆者之间的相关关系,寻找适当的回流温度,才能达到提⾼液化⽓收率的⽬的。
经认真分析仔细研究,确定了在保持原有轻油收率的前提下,液化⽓收率⽐去年同期增长1个百分点的⽬标,即达到12.24%的液化⽓收率。
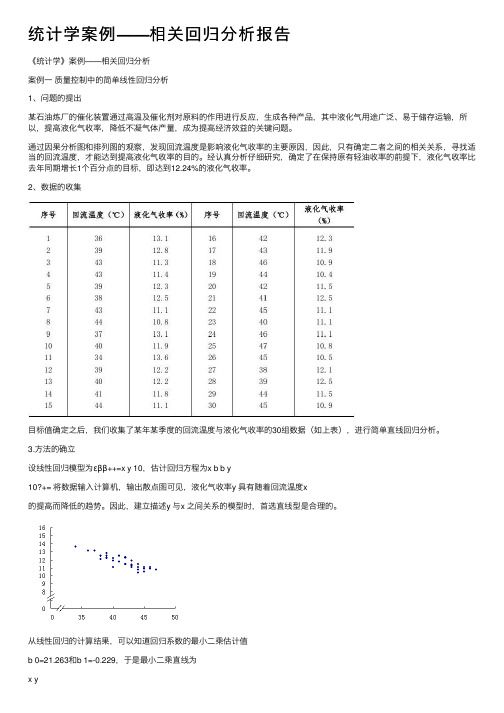
2、数据的收集⽬标值确定之后,我们收集了某年某季度的回流温度与液化⽓收率的30组数据(如上表),进⾏简单直线回归分析。
3.⽅法的确⽴设线性回归模型为εββ++=x y 10,估计回归⽅程为x b b y10?+= 将数据输⼊计算机,输出散点图可见,液化⽓收率y 具有随着回流温度x的提⾼⽽降低的趋势。
因此,建⽴描述y 与x 之间关系的模型时,⾸选直线型是合理的。
从线性回归的计算结果,可以知道回归系数的最⼩⼆乘估计值b 0=21.263和b 1=-0.229,于是最⼩⼆乘直线为x y229.0263.21?-= 这就表明,回流温度每增加1℃,估计液化⽓收率将减少0.229%。
(3)残差分析为了判别简单线性模型的假定是否有效,作出残差图,进⾏残差分析。
从图中可以看到,残差基本在-0.5—+0.5左右,说明建⽴回归模型所依赖的假定是恰当的。
误差项的估计值s=0.388。
(4)回归模型检验 a.显著性检验在90%的显著⽔平下,进⾏t 检验,拒绝域为︱t ︱=︱b 1/ s b1︱>t α/2=1.7011。
由输出数据可以找到b 1和s b1,t=b 1/ s b1=-0.229/0.022=-10.313,于是拒绝原假设,说明液化⽓收率与回流温度之间存在线性关系。

多元回归分析论文引言多元回归分析是一种利用多个自变量与因变量之间关系的统计方法。
它是统计学中重要的工具之一,在许多研究领域都有广泛的应用。
本论文将通过介绍多元回归分析的原理以及应用案例,探讨其在实践中的作用,并提出相关的方法和建议。
方法数据收集在进行多元回归分析之前,首先需要收集相关的数据。
这些数据应该包括自变量和因变量的观测值。
数十个样本的规模是多元回归分析的常见要求之一。
此外,在进行数据收集时,还需要注意数据的质量和准确性,以确保多元回归分析的可靠性。
模型设定在进行多元回归分析时,需要确定一个适当的回归模型。
回归模型是通过自变量对因变量进行预测的数学模型。
在确定回归模型时,可以使用领域知识、经验和统计指标等来指导模型设定的过程。
参数估计参数估计是多元回归分析中的关键步骤之一。
它通过最小化预测值与观测值之间的误差,来确定自变量与因变量之间的关系。
常用的参数估计方法有最小二乘法、最大似然法等。
模型诊断在进行参数估计之后,需要对模型进行诊断,以评估模型的拟合度和有效性。
常用的模型诊断方法包括检验残差的正态性、检验自变量之间的共线性等。
解释结果在完成参数估计和模型诊断之后,需要解释多元回归分析的结果。
这涉及到解释每个自变量的系数和拟合优度指标等。
通过解释结果,可以获取对因变量的预测和解释性的认识。
应用案例以某学校的学生成绩预测为例,假设因变量为学生成绩,自变量为学生的学习时间、就餐次数和睡眠时间。
收集到了100个样本的数据。
通过上述方法进行多元回归分析。
数据收集在数据收集阶段,通过学校的学生管理系统,获取了学生的学习时间、就餐次数和睡眠时间的观测值。
模型设定根据领域知识和经验,我们假设学生的学生成绩与学习时间、就餐次数和睡眠时间存在一定的关系。
因此,我们可以设定模型为:成绩= β0 + β1 * 学习时间+ β2 * 就餐次数+ β3 * 睡眠时间+ ε。
参数估计通过最小二乘法,我们可以估计回归模型的参数。

统计学在金融市场中的回归分析技术金融市场的波动性一直是投资者和分析师关注的重点。
为了更好地理解和预测金融市场的走势,统计学的回归分析技术被广泛应用。
本文将探讨统计学在金融市场中的回归分析技术,并重点介绍线性回归和多元回归两种常用的回归分析方法。
回归分析是一种通过建立数学模型来解释变量之间关系的统计学方法。
在金融市场中,回归分析可以帮助我们了解不同影响因素之间的关系,从而预测市场的未来走势。
其中,最常用的回归方法是线性回归和多元回归。
一、线性回归分析线性回归是一种基本且简单的回归方法,基于变量之间的线性关系建立模型。
在金融市场中,我们可以使用线性回归来研究一个或多个自变量对某个因变量的影响。
在线性回归分析中,首先需要确定一个因变量和一个或多个自变量。
以股票市场为例,我们可以选择股票价格作为因变量,选择与股票价格有潜在关联的自变量,如市盈率、市净率等。
然后,通过收集一定时间范围内的数据,进行回归分析,建立线性回归模型。
线性回归模型的表达式为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y代表因变量,X1、X2等代表自变量,β0、β1、β2等代表回归系数,ε代表误差项。
通过估计回归系数,我们可以得到自变量对因变量的影响程度以及整个模型的拟合程度。
二、多元回归分析多元回归是一种相对复杂的回归方法,可以考虑多个自变量对因变量的影响。
在金融市场中,多元回归可以更准确地解释市场走势,并且更全面地考虑各种因素的影响。
多元回归模型可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε与线性回归模型类似,不同之处在于多元回归考虑了多个自变量,通过估计回归系数,可以得到每个自变量对因变量的影响程度。
在金融市场中,多元回归可以通过引入更多的自变量来解释市场的波动性。
例如,我们可以将股票价格作为因变量,同时考虑市盈率、市净率、市销率等多个自变量,以获得更全面的市场分析结果。

统计学中的Logistic回归分析Logistic回归是一种常用的统计学方法,用于建立并探索自变量与二分类因变量之间的关系。
它在医学、社会科学、市场营销等领域得到广泛应用,能够帮助研究者理解和预测特定事件发生的概率。
本文将介绍Logistic回归的基本原理、应用领域以及模型评估方法。
一、Logistic回归的基本原理Logistic回归是一种广义线性回归模型,通过对数据的处理,将线性回归模型的预测结果转化为概率值。
其基本原理在于将一个线性函数与一个非线性函数进行组合,以适应因变量概率为S形曲线的特性。
该非线性函数被称为logit函数,可以将概率转化为对数几率。
Logistic回归模型的表达式如下:\[P(Y=1|X) = \frac{1}{1+e^{-(\beta_0+\beta_1X_1+...+\beta_pX_p)}}\]其中,P(Y=1|X)表示在给定自变量X的条件下,因变量为1的概率。
而\(\beta_0\)、\(\beta_1\)、...\(\beta_p\)则是待估计的参数。
二、Logistic回归的应用领域1. 医学领域Logistic回归在医学领域中具有重要的应用。
例如,研究者可以使用Logistic回归分析,探索某种疾病与一系列潜在风险因素之间的关系。
通过对患病和非患病个体的数据进行回归分析,可以估计各个风险因素对疾病患病的影响程度,进而预测某个个体患病的概率。
2. 社会科学领域在社会科学研究中,研究者常常使用Logistic回归来探索特定变量对于某种行为、态度或事件发生的影响程度。
例如,研究者可能想要了解不同性别、教育程度、收入水平对于选民投票行为的影响。
通过Logistic回归分析,可以对不同自变量对于投票行为的作用进行量化,进而预测某个选民投票候选人的概率。
3. 市场营销领域在市场营销中,Logistic回归也被广泛应用于客户分类、市场细分以及产品销量预测等方面。
通过分析客户的个人特征、购买习惯和消费行为等因素,可以建立Logistic回归模型,预测不同客户购买某一产品的概率,以便制定个性化的市场营销策略。
实用回归分析论文回归分析是一种广泛应用于研究和预测变量关系的统计方法。
它可以用来探索自变量与因变量之间的关系,并根据这些关系进行预测。
本篇论文旨在利用SPSS软件进行回归分析,并解释实验结果。
为了说明回归分析的实用性,本论文以一个假设为例进行讨论。
假设我们想研究其中一种健康饮食对人体血糖水平的影响。
我们能够搜集到500名参与者的相关数据,包括他们的饮食习惯和血糖水平。
在SPSS软件中,我们可以采用多元线性回归模型来探索自变量(饮食习惯)与因变量(血糖水平)之间的关系。
首先,我们需要将数据输入SPSS软件,并进行数据清洗和处理,确保数据的准确性和可靠性。
接下来,我们可以使用回归模型来进行实验结果的分析。
在SPSS软件中,我们可以选择"回归"选项,并指定因变量和自变量。
在这个示例中,我们将血糖水平作为因变量,饮食习惯作为自变量。
SPSS软件会给出回归模型的结果。
其中最重要的指标是相关系数和显著性水平。
相关系数用来衡量自变量与因变量之间的线性关系的强度,取值范围在-1到+1之间。
显著性水平可以告诉我们这个自变量对因变量的解释力是否显著。
通常,显著性水平小于0.05表示相关关系是显著的。
在这个案例中,回归分析的结果显示饮食习惯与血糖水平之间存在显著相关性(相关系数为0.4,显著性水平为0.01)。
这意味着饮食习惯对于解释血糖水平的变异有统计学意义。
我们可以通过这一结果来推测具体的饮食习惯与血糖水平之间的关系,进一步指导实际生活中的健康饮食选择。
此外,在SPSS软件中,我们还可以进行其他的回归分析,如逐步回归和多重回归。
这些方法可以帮助我们确定最佳的自变量组合,以及对因变量的解释力。
逐步回归可用于选择最有意义的自变量,而多重回归可以进一步探索多个自变量对因变量的解释力。
总结起来,回归分析是一种实用的统计方法,可以用来研究和预测变量之间的关系。
使用SPSS软件进行回归分析,可以对实验结果进行详细的解释和推断,从而指导实际生活中的决策和行动。
实用回归分析论文(SPSS实验结果)由于没有具体的数据或研究题目,以下仅为回归分析论文的一般模板。
1. 研究背景和目的:介绍本次研究的背景和目的。
描述相关文献对该领域的研究情况,指出知识空白和研究的必要性。
例如:本研究旨在探讨X变量与Y变量之间的关系,并研究其他可能因素对此关系的影响。
回归分析被广泛应用于社会科学、经济学和医学等领域,但在某些情况下,该方法可能被错误地应用或解读。
因此,本研究旨在提供更多有关回归分析的实用性信息,以便更好地应用于实际研究中。
2. 变量选择和数据收集:介绍所选的独立变量、因变量以及可能的干扰因素。
描述数据收集的方法和样本的特点,阐述数据的统计学特征。
例如:本研究选择了X1、X2和X3作为独立变量,Y作为因变量。
在探究X和Y之间的关系时,本研究考虑了干扰因素A和B。
数据收集采用了问卷调查的方法,样本为100位大学生。
调查数据的统计学特征如下:均值、标准差、最大值和最小值。
3. 回归模型:描述所使用的回归模型及其假设。
根据假设,说明如何进行统计分析。
例如:本研究选择了多元线性回归模型。
假设独立变量与因变量之间存在线性关系,且同时考虑了干扰因素的影响。
在此假设下,通过进行多元线性回归分析,得出具体的回归方程。
使用SPSS软件进行统计分析,通过显著性检验和模型拟合程度来验证上述假设。
4. 实验结果:解释回归分析结果,如拟合程度、系数的显著性、变量的解释等。
根据结果,提供对研究目的的回答,对假说进行证明或推翻。
例如:本研究得到的回归方程为Y = a + b1*X1 + b2*X2 + b3*X3 +c1*A + c2*B。
通过F检验,得出回归模型的显著性水平P<0.01,表明回归模型解释了数据的一定程度。
通过系数显著性检验,得出X1、X3和B对Y变量具有显著影响,而其余变量影响不显著。
对于X1、X3和B,本研究解释了其对Y变量的具体贡献,分析了研究问题的深层含义。
5. 结论和建议:总结研究结论,说明其对实践和理论的贡献,并提出未来研究的方向。
回归分析在统计学中的重要性统计学作为一门研究数据收集、分析和解释的学科,被广泛应用于各个领域。
在统计学中,回归分析是一种重要的方法,用于研究变量之间的关系。
回归分析的重要性不仅在于其应用广泛,还在于其能够提供有关变量之间关系的深入洞察。
回归分析的基本原理是通过建立数学模型,来描述自变量与因变量之间的关系。
在回归分析中,自变量是我们感兴趣的变量,而因变量是我们想要预测或解释的变量。
通过回归分析,我们可以确定自变量与因变量之间的关系的强度和方向。
首先,回归分析可以帮助我们理解变量之间的关系。
在实际问题中,我们常常需要确定某个因变量与其他自变量之间的关系。
例如,我们可能想知道体重与身高之间的关系,或者收入与教育水平之间的关系。
通过回归分析,我们可以得到一个数学模型,用来描述这些关系。
这样一来,我们就能够更好地理解变量之间的联系,并根据这些联系做出相应的决策。
其次,回归分析可以帮助我们进行预测。
在许多实际问题中,我们常常需要根据已知的自变量值来预测因变量的值。
例如,我们可能想知道某个人的身高,或者某个地区的经济增长率。
通过回归分析,我们可以利用已知的自变量值来预测因变量的值。
这样一来,我们就能够做出相应的预测,并作出相应的决策。
此外,回归分析还可以帮助我们进行因果推断。
在统计学中,因果推断是一项重要的任务。
通过回归分析,我们可以确定自变量与因变量之间的因果关系。
例如,我们可能想知道吸烟是否会导致肺癌。
通过回归分析,我们可以确定吸烟与肺癌之间的关系,并判断吸烟是否是导致肺癌的原因。
这样一来,我们就能够做出相应的干预措施,以减少吸烟导致的肺癌发病率。
此外,回归分析还可以帮助我们进行变量选择。
在实际问题中,我们常常需要从大量的自变量中选择最相关的变量。
通过回归分析,我们可以确定哪些自变量与因变量之间存在显著关系。
这样一来,我们就能够选择最相关的变量,并且可以避免不必要的变量。
这样一来,我们就能够更好地解释因变量的变异,并且可以提高模型的预测能力。
如何利用统计学方法进行金融市场回归分析金融市场回归分析是金融领域中的重要研究方法之一,通过利用统计学方法来研究金融市场中的变量之间的关系和趋势。
本文将探讨如何运用统计学方法进行金融市场回归分析。
一、回归分析简介回归分析是一种通过建立数学模型来研究自变量和因变量之间关系的方法。
在金融市场中,我们关心的是自变量(如利率、汇率、股票价格等)对因变量(如市场指数、股票收益率等)的影响程度和趋势。
二、数据收集与准备进行回归分析之前,首先需要收集所需的金融数据。
这些数据可以来自公开的金融数据库、金融机构的报告、交易所的数据等。
收集到数据后,需要对数据进行预处理,包括数据清洗、缺失值处理、异常值检测等。
三、变量选择在回归分析中,变量的选择是至关重要的。
我们需要根据研究目的和理论基础选择与研究相关的自变量和因变量。
变量的选择要基于经济理论和实际情况,避免选择不相关或多重共线性的变量。
四、模型建立在进行回归分析时,需要选择适当的回归模型。
常见的回归模型包括线性回归模型、多元回归模型、时间序列回归模型等。
选择合适的回归模型可以提高模型的拟合效果和预测准确性。
五、回归模型的评估与解释在得到回归模型后,需要对模型进行评估和解释。
评估主要包括模型的拟合优度、残差分析、假设检验等。
解释则是对模型结果进行解释和可视化展示,以便更好地理解变量之间的关系。
六、模型应用与预测通过进行回归分析,我们可以了解金融市场中各个变量之间的关系和趋势,并基于模型进行预测。
通过对市场指数、股票收益率等因变量进行预测,可以为投资者和决策者提供参考依据。
七、风险与限制回归分析在金融市场中的应用也存在一定的风险和限制。
例如,模型存在局限性,无法解释所有因素及其复杂关系。
另外,金融市场的不确定性和波动性也会对回归模型的拟合和预测造成影响。
结语统计学方法在金融市场回归分析中发挥着重要的作用。
通过合理选择变量、建立合适的模型,我们可以更好地研究金融市场的变动和趋势,提高决策的准确性和效果。
广州市简介及经济指标分析城市简介广州,南中国的中心城市,位于富饶的珠江三角洲。
广州是广东省的省会,是中国最重要的大城市之一,人口约1,OOOT,面积约7,400平方公里,其中市区面积1443平方公里。
现辖越秀、荔湾、东山、海珠4个老城区和天河、白云、黄埔、芳村、番禺、花都六个新城区,以及从化、增城两个县级市。
广州市一座有2200多年悠久历史的文化名城。
始建公元前214年,最早建城时的叫任嚣城。
公元前九世纪的周代的周夷王八年,“百越”(《史记》中称“南越”,《汉书》称“南粤”)和长江中游的楚国人已有来往,建有“楚庭”,这是广州最早的名称。
226年,孙权将交州分为交州和广州,“广州”由此得名。
古代广州曾是三朝古都。
传说有五位仙人骑着五只口衔谷穗的羊降临广州,他们把谷穗赠给了这里的人们,祝永无饥荒,言毕,仙人们乘风而去,留下在人间的五只仙羊化为石。
因此,广州便有了:“羊城”的美名。
又因北回归线从城北穿过,季如春、繁花似锦,故又有”花城”之称。
关键词:GDP;固定资产投资;全年城镇居民人均可支配收入;十二五ABSTRACTGuangzhou, south China's urban centers, located in the fertile Pearl River Delta. Guangzhou is the capital of Guangdong Province, is one of China's most important cities, a population of about 1, OOOT, an area of about 7,400 square kilometers, of which the urban area of 1443 square km. Jurisdiction over Yuexiu, Liwan, Dongshan, Haizhu four old city and the Tianhe, Baiyun, Huangpu, Fangcun, Panyu, Huadu six new city, and Conghua, Zengcheng two county-level cities.Guangzhou, a city with 2200 years of history and cultural city. Founded 214 BC, was built in the city called the office when the city clamor. The ninth century BC, the Zhou Dynasty of Zhou Yi Wang eight years, "Bai Yue" ("Historical Records", said "South Vietnam", "Han," called "Nam Yue") and the Yangtze River from the state of Chu had been out, has a "Chu court ", which is the first name of Guangzhou. 226 years, Sun Quan will pay into the state to pay state and Guangzhou, "Guangzhou" was named. The ancient dynasties, Guangzhou was the ancient capital. Legend of five fairy riding five ears of corn mouth sheep come Guangzhou, ears of corn donated them to the people here, I wish never famine, Yan Bi, immortals wind away, leaving five in the world only fairy sheep into stone.Therefore, there will be a Guangzhou: "Guangzhou" name. Because of the Tropic of Cancer passes through from the north of the city, such as the spring season, flowers are in bloom, it has "Flower City," said.Keywords: GDP; fixed asset investment; annual per capita disposable income of urban residents; second five经济现状广州市2003年生产总值(GDP)达3466.63亿元,比2002年增长15%,创8年来新高;人均生产总值4.79 万元;广州一般预算财政收入274.75亿元,同比增长15.5%;固定资产投资1157.77亿元,同比增长14.7%。
经济的迅速增长是由各个行业的迅猛发展带来的。
随着一批生产力骨干项目顺利推进,新的经济增长点正逐步形成,产业竞争力和发展后劲明显增强。
都市型农业健康发展,消费拉动作用进一步增强,外贸出口和利用外资持续增长。
以制度创新为核心的各项改革进一步深化。
重点抓好国有企业改革,一批具有较强竞争力的企业不断发展壮大。
广州开发区和南沙开发区试行行政管理“无费区”,降低了城市运行成本。
非公有制经济健康发展,全市规模以上民营工业企业完成工业总产值1157.64亿元,增长18%,私营企业达到78604户,增长18%。
外经贸发展势头强劲。
全年广州地区累计完成进出口总值达349.4亿美元,同比增长25.1%;其中出口168.9亿美元,增长22.6%。
广州市属企业进出口总值为285.68亿美元,同比增长27.87%,其中出口140.33亿美元,同比增长27.40%。
全市共批准外商直接投资项目870个,同比增长12.1%,新批合同外资40.22亿美元,同比增长27.04%;实际使用外资30.64亿美元,同比增长15.5%,其中,实际使用外商直接投资25.81亿美元,同比增长13.0%。
境外投资合同金额达1.07亿美元,同比增长37%,完成营业额1.09亿美元,同比增长19.79%,在境外劳务人员数为4080人,同比增长20.78%。
目前,世界500强跨国公司中已有115家公司进入广州,投资设立204个项目,投资总额合计58.2亿美元。
其他情况城市基础设施建设全面提速。
地铁、机场、高速公路、污水处理等重大城市基础设施建设进度加快,城市生态环境质量和管理水平明显提高。
启动“青山绿地”、“蓝天碧水”工程,全市森林覆盖率达41.4%,新增及改造城市道路绿化带45公里。
全年空气环境质量保持在国家规定优良水平的天数达86%,噪声污染持续9年下降。
四大污水处理系统的建设全面推进,全市生活垃圾全部实现无害化卫生填埋处理。
大力推进“安全放心”工程,切实加强城市管理,市场秩序和社会治安进一步好转,城乡环境面貌不断改观。
科教兴市和文化强市工作迈出新步伐。
加快区域创新体系建设,中心城市科技创新能力和国际竞争力进一步提升。
2003年,工业高新技术产品产值达1094.31,增长37.6%,占全市工业总产值的23.3%。
全社会研究和发展(R&D)经费达55亿元,占广州市生产总值的比重为1.6%。
科技进步对工业的经济增长贡献率达51.6%,提高2%。
专利申请和授权量分别增长30.5%和37.8%,发明专利申请量增长52.3%,均居全国省会城市首位。
全市人民生活质量不断改善。
全面落实促进就业和再就业的各项方针政策。
继续做好五条保障线的衔接工作,参加各项社会保险人数和社会化管理退休人员人数保持增长。
改善农民生产生活条件,全市行政村实现通水、通电、通电话、通水泥路、通有线电视。
精神文明建设和社会各项事业取得新进展。
经济指标分析一.广州市1996-2010年GDP、固定资产投资、全年城镇居民人均可支配收入年份GDP(亿元) 固定资产投资(亿元)城镇居民人均可支配收入(亿元)1996 1445.84 655.45 9910 1997 1642.83 656.58 10445 1998 1844.09 746 11256 1999 2063.37 875.16 12018 2000 2383.07 924.19 13967 2001 2684.83 964.08 14694 2002 3001.69 1001.49 15117 2003 3466.63 1157.77 15003 2004 4115.81 1321.96 16884 2005 5115.75 1445.33 18287 2006 6068.41 1696.38 19851 2007 7050.78 1863.34 22469 2008 8215.82 2104.56 25317 2009 9112.76 2659.85 27610 2010 10604.48 3263.57 30658(1)广州市1996-2010年,年份与GDP的数量关系年份GDP(亿元)x y1996 1445.841997 1642.831998 1844.091999 2063.372000 2383.072001 2684.832002 3001.692003 3466.632004 4115.812005 5115.752006 6068.412007 7050.782008 8215.822009 9112.762010 10604.48 (2)广州市1996至2010年年份与GDP的散点图如下图所示从图中可以看出广州市的GDP 大致是呈二元一次的形式快速增长的。
下面我们根据统计学的方差分析原理来分析该市的GDP 与年份的关系。
2^cxbx a y ++=表其中,y 代表GDP 的变化,x 代表年份。
经过分析可得下表表3 1996年至2010年年份与GDP 关系的回归统计SUMMARY OUTPUT 回归统计Multiple R 0.99892290304 R Square0.99784696621 Adjusted R Square0.99748812724 标准误差 148.73521453观测值15表4 2001年至2010年年份与GDP 关系的方差分析表方差分析df SSMSFSignificaneF 回归分析 2123033095.17 61516547.585 2780.7653669.9610489767E-17 残差 12 265465.96848 22122.16404 表5 1996年至2010年年份与GDP 关系的回归参数估计有关内容表Coefficients 标准误差 t StartP-value Intercept 197911769.64 9290625.549921.3023082876.6698861446E-11 X Variable 1 -198246.58512 9276.7408707-21.3702837976.4255601214E-11 X Variable 2 49.645900937 2.315710587221.438732986.1892805455E-11 Lower 95% Upper 95% 下限 95.0% 上限 95.0%177669235.52 218154303.76 177669235.52 218154303.76 -218458.86712 -178034.30312 -218458.86712 -178034.30312 44.600401006 54.691400869 44.60040100654.691400869从上表可以看出,方差分析表中F值大于两位数,可知该市的GDP与年份之间有显著的联系。