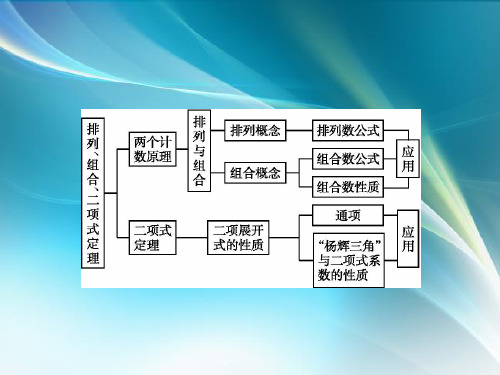
2018年秋人教B版高中数学选修2-2课件:本章整合3
- 格式:pptx
- 大小:1015.77 KB
- 文档页数:23




1.4 定积分与微积分基本定理1.4.1 曲边梯形面积与定积分1.了解曲边梯形及其面积的含义;了解求曲边梯形面积的“分割、近似代替、求和、取极限”的基本过程.(重点)2.掌握定积分的概念,会用定义求定积分.(难点)3.理解定积分的几何意义与性质.(易混点)[基础·初探]教材整理1 曲边梯形阅读教材P36,完成下列问题.由直线x=a,x=b(a≠b),y=0和曲线________所围成的图形称为曲边梯形(如图1-4-1).图1-4-1【答案】 y=f(x)教材整理2 定积分的定义阅读教材P38,完成下列问题.设函数y=f(x)定义在区间[a,b]上(如图1-4-2).用分点a=x0<x1<x2<…<x n-1<x n=b把区间[a,b]分为n个小区间,其长度依次为Δx i=x i+1-x i,i=0,1,2,…,n-1.记»为这些小区间长度的最大者,当»趋近于0时,所有的小区间长度都趋近于0.在每个小区间内任取一点¾i,作和式I n=(¾i) ”x i,当»→0时,如果和式的极限存在,我们把________________叫做____________________上的定积分,记作f(x)d x,即f(x)d x=(¾i) ”x i.其中f(x)叫做________,a叫____________,b叫________,f(x)d x叫做被积式.此时称函数f(x)在区间[a,b]上________.图1-4-2【答案】 和式I n的极限 函数f(x)在区间[a,b] 被积函数 积分下限 积分上限 可积教材整理3 定积分的性质与几何意义阅读教材P39,完成下列问题.1.定积分的性质(1)cf(x)d x=____________________________(c为常数).(2)设f(x),g(x)可积,则[f(x)±g(x)]d x=f(x)d x±________________________.【答案】 1.(1)cf(x)d x (2)g(x)d x2.定积分的几何意义从几何上看,如果在区间[a,b]上函数f(x)连续且恒有________,那么定积分f(x)d x表示由__________________所围成的曲边梯形的面积.这就是定积分f(x)d x的几何意义.【答案】 f(x)≥0 直线x=a,x=b,y=0和曲线y=f(x)1.判断(正确的打“√”,错误的打“×”)(1)f(x)d x=f(t)d t.( )(2)f(x)d x的值一定是一个正数.( )(3)(x2+2x)d x=x2d x+2x d x.( )【答案】 (1)√ (2)× (3)√2.填空(1)由y=0,y=cos x,x=0,x=围成的图形的面积用定积分的形式表示为__________.(2)f(x)d x=f(x)d x+__________.(3)2x d x__________2x d x.(填“<”“=”或“>”)【答案】 (1)cos x d x (2)f(x)d x (3)<[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1: 解惑: 疑问2: 解惑: 疑问3: 解惑: [小组合作型]求曲边梯形的面积 求由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积.【精彩点拨】 按分割、近似代替、求和、取极限四个步骤进行求解.【自主解答】 (1)分割将曲边梯形分割成n个小曲边梯形,用分点,,…,把区间[0,1]等分成n个小区间:,,…,,…,,简写作(i=1,2,…,n).每个小区间的长度为Δx=-=.过各分点作x轴的垂线,把曲边梯形分成n个小曲边梯形,它们的面积分别记作:ΔS1,ΔS2,…,ΔS i,…,ΔS n.(2)近似代替用小矩形面积近似代替小曲边梯形面积,在小区间上任取一点¾i(i=1,2,…,n),为了计算方便,取¾i为小区间的左端点,用f(¾i)的相反数-f(¾i)=-为其一边长,以小区间长度Δx=为另一边长的小矩形对应的面积近似代替第i个小曲边梯形面积,可以近似地表示为”S i≈-f(¾i) ”x=-·(i=1,2,…,n).(3)求和因为每一个小矩形的面积都可以作为相应小曲边梯形面积的近似值,所以n 个小矩形面积的和就是曲边梯形面积S的近似值,即S=S i≈-(¾i) ”x=·=-[02+12+22+…+(n-1)2]+[0+1+2+…+(n-1)]=-·n(n-1)(2n-1)+·=-=-.(4)取极限当分割无限变细,即Δx趋向于0时,n趋向于∞,此时-趋向于S.从而有S==.所以由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积为.由极限法求曲边梯形的面积的步骤第一步:分割.在区间[a,b]中等间隔地插入n-1个分点,将其等分成n个小区间[x i-1,x i](i=1,2,…,n),小区间的长度Δx i=x i-x i-1.第二步:近似代替.“以直代曲”,用矩形的面积近似代替小曲边梯形的面积,求出小曲边梯形面积的近似值.第三步:求和.将n个小矩形的面积进行求和得S n.第四步:取极限.当n→∞时,S n→S,S即为所求.[再练一题]1.求由直线x=1,x=2,y=0及曲线y=围成的图形的面积S.【解】 (1)分割在区间[1,2]上等间隔地插入n-1个点,将它等分成n个小区间:,,…,,记第i个区间为(i=1,2,…,n),其长度为Δx=-=.分别过上述n-1个分点作x轴的垂线,把曲边梯形分成n个小曲边梯形(如图),它们的面积分别记作:ΔS1,ΔS2,…,ΔS n,则小曲边梯形面积的和为S =S i,(2)近似代替记f(x)=.当n很大,即Δx很小时,在区间上,可以认为f(x)=的值变化很小,近似地等于一个常数,不妨认为它等于f.从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间上,用小矩形面积ΔS i′近似地代替ΔS i,即在局部小范围内“以直代曲”,则有ΔS i≈”S i′=f”x=·=(i=1,2,…,n).(3)求和小曲边梯形的面积和S n=S i≈S i′==++…+=n=n=.从而得到S的近似值S≈S n=.(4)取极限分别将区间[1,2]等分成8,16,20,…等份时,S n越来越趋向于S,从而有S=S n=.所以由直线x=1,x=2,y=0及曲线y=围成的图形的面积S为.利用定义求定积分【精彩点拨】 根据定积分的意义,分四步求解,即分割,近似代替,求和,取极限.【自主解答】 令f(x)=3x+2.(1)分割在区间[1,2]上等间隔地插入n-1个分点,将区间[1,2]等分成n个小区间(i =1,2,…,n),每个小区间的长度为Δx=-=.(2)近似代替、作和取¾i=(i=1,2,…,n),则S n=· ”x=·==[0+1+2+…+(n-1)]+5=×+5=-.(3)取极限(3x+2)d x=S n==.利用定义求定积分的步骤[再练一题]2.利用定积分的定义,计算(x+1)d x的值.【解】 f(x)=x+1在区间[1,2]上连续,将区间[1,2]等分成n个小区间(i =1,2,…,n),每个区间的长度为Δx=,在上取¾i=1+(i=1,2,…,n),∴f(¾i)=1+1+=2+,∴(¾i)· ”x=·==·n+[0+1+2+…+(n-1)]=2+=2+-=-,∴(1+x)d x==.定积分的几何意义(1)d x;(2)(2x+1)d x;(3)(x3+3x)d x. 【导学号:05410028】【精彩点拨】 对于本题(1)、(2)可先确定被积函数、积分区间,画出图形,然后用几何法求出图形面积,从而确定定积分的值;对于(3)可根据被积函数的奇偶性求解.【自主解答】 (1)曲线y=表示的几何图形为以原点为圆心以3为半径的上半圆,如图(1)所示.其面积为S=· À·32=À.由定积分的几何意义知d x=À.(2)曲线f(x)=2x+1为一条直线.(2x+1)d x表示直线f(x)=2x+1,x=0,x=3围成的直角梯形OABC的面积,如图(2)所示.其面积为S=(1+7)×3=12.根据定积分的几何意义知(2x+1)d x=12.(3)∵y=x3+3x在区间[-1,1]上为奇函数,图象关于原点对称,∴曲边梯形在x轴上方部分面积与x轴下方部分面积相等.由定积分的几何意义知 (x3+3x)d x=0.1.定积分的几何意义的应用(1)利用定积分的几何意义求f(x)d x的值的关键是确定由曲线y=f(x),直线x =a,x=b及y=0所围成的平面图形的形状.常见的图形有三角形、直角梯形、矩形、圆等可求面积的平面图形.(2)不规则的图形常利用分割法将图形分割成几个容易求定积分的图形求面积,要注意分割点要确定准确.2.奇、偶函数在区间[-a,a]上的定积分(1)若奇函数y=f(x)的图象在[-a,a]上连续,则=0.(2)若偶函数y=f(x)的图象在[-a,a]上连续,则=2f(x)d x.[再练一题]3.上例(1)中变为d x,如何求解?【解】 由y=,知x2+y2=9(y≥0),x∈,其图象如图所示:由定积分的几何意义,知d x等于圆心角为60°的弓形CED的面积与矩形ABCD的面积之和.S弓形=××32-×3×=,S矩形=|AB|×|BC|=2××=,∴d x=+=.[探究共研型]定积分性质的应用探究1【提示】 可先把每一段函数的定积分求出后再相加.探究2 怎样求奇(偶)函数在区间[-a,a]上的定积分?【提示】 ①若奇函数y=f(x)的图象在[-a,a]上连续,则f(x)d x=0;②若偶函数y=g(x)的图象在[-a,a]上连续,则g(x)d x=2g(x)d x. 利用定积分的性质和定义表示下列曲线围成的平面区域的面积.(1)y=0,y=,x=2;(2)y=x-2,x=y2.【精彩点拨】 由定积分的几何意义,作出图形,分割区间表示.【自主解答】 (1)曲线所围成的平面区域如图(1)所示.设此面积为S,则S=(-0)d x=d x.(1) (2)(2)曲线所围成的平面区域如图(2)所示.设面积为S,则S=A1+A2.因为A1由y=,y=-,x=1围成,A2由y=,y=x-2,x=1和x=4围成,所以A1=[-(-)]d x=2d x,A2=[-(x-2)]d x=(-x+2)d x.故S=2 d x+(-x+2)d x.利用定积分的性质求定积分的技巧灵活应用定积分的性质解题,可以把比较复杂的函数拆成几个简单函数,把积分区间分割成可以求积分的几段,进而把未知的问题转化为已知的问题,在运算方面更加简洁.应用时注意性质的推广:(1)[f1(x)±f2(x)±…±f n(x)]d x=f1(x)d x±f2(x)d x±…±f n(x)d x;(2)f(x)d x=f(x)d x+f(x)d x+…+f x d x(其中a<c1<c2<…<c n<b,n∈N+).[再练一题]4.已知x d x=,x2d x=,求下列定积分的值.(1)(2x+x2)d x;(2)(2x2-x+1)d x.【解】 (1)(2x+x2)d x=2x d x+x2d x=2×+=e2+.(2)(2x2-x+1)d x=2x2d x-x d x+1d x,因为已知x d x=,x2d x=,又由定积分的几何意义知:1d x等于直线x=0,x=e,y=0,y=1所围成的图形的面积,所以1d x=1×e=e,故(2x2-x+1)d x=2×-+e=e3-e2+e.[构建·体系]1.在“近似代替”中,函数f(x)在区间[x i,x i+1]上的近似值( )A.只能是左端点的函数值f(x i)B.只能是右端点的函数值f(x i+1)C.可以是该区间内任一点的函数值f(¾i)(¾i∈[x i,x i+1])D.以上答案均正确【解析】 作近似计算时,Δx=x i+1-x i很小,误差可忽略,所以f(x)可以是[x i,x i+1]上任一值f(¾i).【答案】 C2.图1-4-3中阴影部分的面积用定积分表示为( )图1-4-3A.2x d xB.(2x-1)d xC.(2x+1)d xD.(1-2x)d x【解析】 根据定积分的几何意义,阴影部分的面积为2x d x-1d x=(2x-1)d x.【答案】 B3.在计算由曲线y=-x2以及直线x=-1,x=1,y=0所围成的图形面积时,若将区间[-1,1]n等分,则每个小区间的长度为__________.【导学号:05410029】【解析】 每个小区间长度为=.【答案】 4.若[f(x)+g(x)]d x=3,[f(x)-g(x)]d x=1,则[2g(x)]d x=________.【解析】 [2g(x)]d x=[(f(x)+g(x))-(f(x)-g(x))]d x=[f(x)+g(x)]d x-[f(x)-g(x)]d x=3-1=2.【答案】 25.用定积分的几何意义求d x.【解】 由y=可知x2+y2=4(y≥0),其图象如图.d x等于圆心角为60°的弓形CED的面积与矩形ABCD的面积之和.S弓形=××22-×2×2sin=-.S矩形=|AB|·|BC|=2.∴d x=2+-=+.我还有这些不足:(1) (2) 我的课下提升方案:(1) (2) 。