六年级空间与图形专项训练题

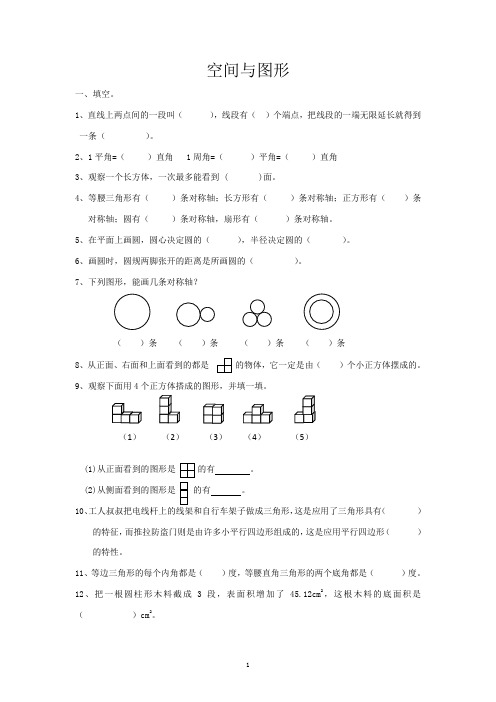
空间与图形一、填空。

1、直线上两点间的一段叫（ ），线段有（ ）个端点，把线段的一端无限延长就得到一条（ ）。

2、1平角=（ ）直角 1周角=（ ）平角=（ ）直角3、观察一个长方体，一次最多能看到 ( )面。

4、等腰三角形有（ ）条对称轴；长方形有（ ）条对称轴；正方形有（ ）条对称轴；圆有（ ）条对称轴，扇形有（ ）条对称轴。

5、在平面上画圆，圆心决定圆的（ ），半径决定圆的（ ）。

6、画圆时，圆规两脚张开的距离是所画圆的（ ）。

7、下列图形，能画几条对称轴？8、从正面、右面和上面看到的都是的物体，它一定是由（）个小正方体摆成的。

9、观察下面用4个正方体搭成的图形，并填一填。

(1)从正面看到的图形是的有 。

(2)从侧面看到的图形是的有 。

10、工人叔叔把电线杆上的线架和自行车架子做成三角形，这是应用了三角形具有（ ）的特征，而推拉防盗门则是由许多小平行四边形组成的，这是应用平行四边形（ ）的特性。

11、等边三角形的每个内角都是（ ）度，等腰直角三角形的两个底角都是（ ）度。

12、把一根圆柱形木料截成3段，表面积增加了45.12cm 2，这根木料的底面积是（ ）cm 2。

13、一个圆锥体的底面半径是6cm ，高是1dm ，体积是（ ）cm 3。

14、把一个圆柱体钢坯削成一个最大的圆锥体，要削去 1.8 cm 3，未削前圆柱的体积是（ ）cm 3。

15、一个圆柱体的侧面展开后，正好得到一个边长25.12 cm 的正方形，圆柱体的高是（ ）cm ，底面半径是（ ）cm 。

16、等底等高的圆柱和圆锥，体积的和是72 dm 3，圆柱的体积是（ ）,圆锥的体积是（ ）。

17、三角形三个角度数的比是2：4：3，最大的角是（ ）。

18、一个三角形底是3dm ，高是4dm ，它的面积是（ ）。

19、一个平行四边形的底长18cm ，高是底的12，它的面积是（ ）。

20、一个直径4cm 的半圆形，它的周长是（ ），它的面积是（ ）。

二、空间与图形专项复习第一课时（图形的认识与测量例1）基础知识达标1．填空（1）线段有（）个端点，射线有（）个端点，直线有个（）端点。

（2）两条直线相交组成4个角，如果其中一个角是90度，那么其他三个角是（）角，这两条直线叫做互相（）。

（3）6：00，时针与分针组成的角是（）角。

（4）经过两点可以画出（）条直线；两条直线相交有（）个交点。

（5）如果等腰三角形的一个底角是53°，则它的顶角是（）；直角三角形的一个钝角是48°，另一个锐角是（）。

2．判断（1）一条射线长1000米。

（）（2）大于90°的角叫钝角。

（）（3）角的两条边越长，角就越大。

（）（4）钟表的分针旋转一周，时针旋转30°。

（）（5）三角形最小的一个角是46°，这个三角形一定是锐角三角形。

（）（6）三角形中最大的角不小于60度。

（）3、选择（1）在同一平面内，画已知直线的垂线，可以画（）。

A. 1条B. 4条C. 2条D. 无数条（2）用100倍的放大镜看40°的角，这个角的度数是（）度。

A. 4B. 40C. 400D. 4000评价：（3）下面图形是用木条钉成的支架，最不容易变形的是（）。

（4）圆内最长的线段是（）。

A.直径B.半径C.其它（5）下面（）三条线段能围成一个三角形。

A. 3cm 2cm 6cmB. 3cm 3cm 3cmC. 3cm 3cm 4cmD. 4cm 5cm 9cm4、按要求作图（1）在下图中，画出表示A点到直线距离的线段，A点到已知直线的距离是（）。

（2）过A点作已知直线的平行线。

★智多星：一只猫追赶一只老鼠，老鼠沿A→B→C方向跑，猫沿A→D→C方向跑，结果在E点将老鼠抓住了。

老鼠与猫的速度比是17：20，C点与E点相距3米，四边形ABCD为平行四边形。

猫和老鼠所用的时间相等。

（1）猫比老鼠多跑了几米才追到老鼠？（2）猫和老鼠所跑的四边形的周长是多少米？DCBA第二课时（图形的认识与测量 例2）基础知识达标 1、填空（1）一个长方形的周长是42cm ，它的长与宽的比是4∶3，它的面积是（ ）cm 2。

课标实验教材六年级下册数学园地六、⑵空间与图形一、填空。

1、一条10厘米长的线段，这条线段长（）分米，是2、在括号里填上合适的单位名称。

⑴一袋牛奶245（）⑵教室的空间大约是⑶小玉的腰围约60（）⑷卫生间地面的面积约3、经过两点可以画出（）条直线；两条直线相交有（）个交点。

4、如果等腰三角形的一个底角是53°，则它的顶角是（）；直角三角形的一个钝角是48°，另一个锐角是（）。

5、看图填空。

(每格面积为1cm2)A图( )cm2B图( )cm2 C图( )cm2 D图大约是( ) cm2（5题图）（6题图）6、上图是由（）个棱长为1厘米的正方体搭成的。

将这个立体图形的表面涂上蓝色，其中只有三个面涂上蓝色的正方体有（）个，只有四个面涂上蓝色正方体有（）个。

7、在一块边长10cm的正方形硬纸板上剪下一个最大的圆，这个圆的面积是（）cm2，剩下的边角料是（）cm2。

8、一个长方形的周长是42cm，它的长与宽的比是4∶3，它的面积是（）cm2。

9、用72cm长的铁丝焊成一个正方体框架（接口处不计），这个正方体框架的棱长是（）cm，体积是（）cm3，表面积是（）cm2。

10、一个圆锥的体积是9.42立方分米，底面直径是6分米，它的高是（）分米，和它等底等高的圆柱的体积是（）立方分米。

二、判断对错。

（）1、三角形最小的一个角是30°，这个三角形一定是锐角三角形。

（）2、一条射线长20.5米。

（）3、画一个周长18.84cm的圆，圆规两脚间的距离是3cm。

（）4、两个梯形可以拼成一个平行四边形。

（）5、三角形的面积是平行四边形面积的一半。

三、选择题。

（将正确答案的序号填在括号里）1、下列图案中，对称轴条数最多的是（）。

A、B、C、D、2、下面的图形，（）是正方体的展开图。

A、B、C、D、3、下面各组线段中，能围成三角形的是（）。

A、1cm 1cm 2cmB、1cm 2.5cm 3cmC、0.8dm 1dm 2dm4、一个立体图形从正面看是，从左面看是要搭成这样的立体图形，至少要用（）个小正方体。

六年级数学空间与图形试题答案及解析1.（重庆）如图是一个梯形地平面图（单位：cm）求它的实际面积是多少平方米？【答案】它的实际距面积是64平方米【解析】分析：根据“实际距离=图上距离÷比例尺”代入数字，分别求出梯形的实际的上底、下底和高，然后根据“梯形的面积=（上底+下底）×高÷2”，代入数字，求出结论．解答：解：3÷=600（厘米），4÷=800（厘米），5÷=1000（厘米），600厘米=6米，800厘米=8米，1000厘米=10米，（6+10）×8÷2，=14×8÷2，=64（平方米）；答：它的实际距面积是64平方米．点评：考查了图上距离与实际距离的换算（比例尺的应用）；梯形的面积．此题做题的关键是根据实际距离、图上距离和比例尺”的关系，分别求出梯形的实际的上底、下底和高．2.有一个角是直角的三角形是直角三角形，有一个角是钝角的三角形是钝角三角形，有一个角是锐角的三角形是锐角三角形。

（）【答案】×【解析】略3.一个长方形长8米，宽6米，如果把它的长和宽都增加2米，它的面积增加（）。

A．4平方米B．32平方米C．16平方米D．80平方米【答案】B【解析】由题意可知，原来长方形的面积是6×8=48（平方米），现在长方形的长是8+2=10米，宽是6+2=8米，面积是10×8=80（平方米），它的面积增加了：80-48=32（平方米）。

4.在平面图上通常确定的方位是：上北下（）、左（）右（）。

【答案】南西东【解析】本题考查的是在平面图上如何确定方向。

一般来说, 在地图或平面图上，有一个统一的确定方向的标准。

通常是按上北、下南、左西、右东的规则来确定方向的。

为了标明方向，在地图和平面图上通常用箭头（板书：北）来表示方向。

这个符号叫指向标（板书：指向标），意思是说：箭头所指的方向是北面。

空间与图形专项训练基础题一、选择题1．一个正方体的棱长是20厘米，那么它的表面积是（）。

A．400平方厘米 B．1200平方厘米 C． 2400平方厘米【答案】C【解析】根据正方体的表面积＝棱长×棱长×6，代入数据：20×20×6＝2400；据此选择即可。

2．下面图形中是正方形的平面展开图的是（）。

【答案】C【解析】看图分析可知，A不能围成正方体，所以不是正方体的平面展开图，B也不能围成正方体，所以也不是正方体的平面展开图，C能围成正方体，所以C是正方体的平面展开图；据此选择即可。

3．下列说法错误的是（）。

A．正方体是长、宽、高都相等的长方体。

B．长方体与正方体都有12条棱。

C．长方体的6个面中至少有4个面是长方形。

D．长方体的6个面中最多有4个面是长方形。

【答案】D【解析】长方体的6个面一般情况下都是长方形，特殊的情况下，至少有4个面是长方形，所以D的说法是错误的；据此选择即可。

4．下列物体中，形状不是长方体的是（）A. 墨水盒B. 烟盒C. 水杯D. 电冰箱[来源【答案】C【解析】根据生活经验可知，墨水盒的形状是长方体的，烟盒的形状也是长方体的，电冰箱的形状也是长方体的，而水杯一般都不是长方体的；判断即可。

5．长方体的12条棱中，高有（）。

A．4条 B．6条 C．8条 D．12条【答案】A【解析】长方体的12条棱分成了3组，每组都有4条棱，即4个长、4个宽和4个高；据此解答即可。

6．下列现象中，（）是旋转现象。

A. 我们用手拧水龙头。

B. 写字时笔尖的移动。

C. 小朋友们荡秋千。

D. 行驶中的车轮转动。

【答案】A、C、D【解析】A是旋转现象，是以中间为中心进行旋转的；B不是旋转现象；C是旋转现象，是以秋千的绳子和支架的交点为中心进行旋转的；D是旋转现象，是以车轮的轴为中心进行旋转的；据此选择即可。

7．如下图阴影部分，可以看作是一个菱形通过（）得到的图形．A．平移 B．旋转 C．对称【答案】B【解析】看图可知，菱形ABCD以A为中心，逆时针旋转得到菱形AEFG；据此选择即可。

六年级数学空间与图形试题1.在平面图上通常确定的方位是：上北下（）、左（）右（）。

【答案】南西东【解析】本题考查的是在平面图上如何确定方向。

一般来说, 在地图或平面图上，有一个统一的确定方向的标准。

通常是按上北、下南、左西、右东的规则来确定方向的。

为了标明方向，在地图和平面图上通常用箭头（板书：北）来表示方向。

这个符号叫指向标（板书：指向标），意思是说：箭头所指的方向是北面。

2.一个长方体，如果高增加2厘米，就成了正方体，而且表面积增加56平方厘米，原来这个长方体的体积是（）立方厘米。

【答案】245【解析】本题考查正方体的形状特点及对表面积和体积的认识及计算。

根据高增加2厘米成为正方体，得出原长方体的长、宽、高的关系，进一步根据表面积的增加情况，计算出长、宽、高，进一步计算出体积，解决问题。

表面积增加的部分是高增加2厘米后周围四个面的面积和，可表示为长×2×4，计算长：56÷4÷2=7(厘米)，计算高：7－2=5(厘米)，计算体积：7×7×5=245(立方厘米)。

3.小青坐在教室的第3排第4列，用（4，3)表示，那么小明坐在教室的第5排第2列应当表示为（）。

【答案】（2，5）【解析】本题考查的是用数对表示物体的位置。

根据小青的位置可知，数对中第一个数表示小青所在的列数，第二个数表示小青所在的排数，两个数中间用逗号隔开，即（列，排）。

因为小明的位置是第5排第2列，所以小明的位置可表示为（2，5）。

4.—个长方体，如果高增加2厘米变成了正方体，而且表面积要增加56平方厘米，原来这个长方体的体积是（）立方厘米。

【答案】245【解析】本题考查的是有关长方体的侧面积、表面积和体积的有关知识。

把长方体的高增加2厘米变成了正方体，增加的表面积是长方体的侧面积，本题根据长方体的侧面积求出长方体的长和宽，再推导出长方体的高，就可以求出长方体的体积。

长方体的高增加2厘米变成了正方体，增加的表面积是长方体的侧面积，由于底面积是正方形，因此长方体的长和宽相等，长方体的长（宽）=56÷4÷2=7厘米，长方体的高=7-2=5厘米，所以长方体的体积=7×7×5=245平方厘米。

六年级数学空间与图形试题答案及解析1.你有多少种方法将任意一个三角形分成：⑴ 3个面积相等的三角形；⑵ 4个面积相等的三角形；⑶6个面积相等的三角形．【答案】（1）（2）（3）【解析】⑴如下图，D、E是BC的三等分点，F、G分别是对应线段的中点，答案不唯一：⑵如下图，答案不唯一，以下仅供参考：⑶如下图，答案不唯一，以下仅供参考：2.如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形的面积；⑵？【答案】6；1：3【解析】⑴根据蝴蝶定理，，那么；⑵根据蝴蝶定理，．=1，求：梯3.（北京）如图：梯形ABCD中，AD∥BC，AC、BD交于M，，若S△ADM形的面积．【答案】梯形的面积是16【解析】分析：根据题意知道△AMD 与△BMC 相似，由此得出△BMC 的面积，再根据，知道△ADM 与△ADB 高的比是1：4，进而求出△ABD 的面积，用△ADB 的面积乘2再减去△ADM 的面积，再计算△BMC 的面积就是梯形的面积．解答：解：因为，， 因为△ADM 和△ABM 共高，△ADM 和△CDM 共高，△CDM 和△CBM 共高， 所以S △ADM ：S △ABM ==， S △ADM ：S CDM ==， S △CDM ：S CBM ==， 因为S △ADM =1，所以S △ABM =3，S △CDM =3，S △CBM =9，所以梯形的面积为：1+3+3+9=16，答：梯形的面积是16．点评：此题考查了相似三角形的面积比等于相似比的平方的性质及底一定时，三角形的面积与高成正比的关系的灵活应用．4. （丰都县）画出周长是12厘米，面积恰好是整数平方厘米的平面图形．至少画出3个不同的图形，并在图上标出数据．【答案】【解析】分析：根据题意：可画长方形的长为4厘米宽为2厘米则周长为（4+2）×2=12厘米，面积为4×2=8平方厘米；正方形的边长为3厘米，周长则为3×4=12厘米，面积为3×3=9平方厘米；直角三角形的直角边分别为3厘米、4厘米，斜边为5厘米，这个三角形的周长为3+4+5=12厘米，面积为3×4÷2=6平方厘米，据此解答即可得到答案．解答：解：根据分析作图即可：点评：此题主要考查的是如何画指定面积和周长的图形．5. （2013•成都）将如图所示的三角形沿虚线折叠，得到如图所示的多边形，这个多边形的面积是原三角形面积的，已知图中阴影部分的面积和为6平方厘米，求原来三角形的面积．【答案】求原来三角形的面积是14平方厘米【解析】观察图可知：形成的多边形的面积比原来三角形的面积减少一个重叠部分的面积，所以重叠部分的面积就是原来三角形面积的（1﹣），阴影部分的面积和为6平方厘米所对应的是1﹣2（1﹣），用除法就可以求出原来三角形的面积．解答：解：6÷[1﹣2（1﹣）]=6÷[1﹣2×]=6÷[1﹣]=6÷=14（平方厘米）答：求原来三角形的面积是14平方厘米．点评：解决本题关键是理解“多边形的面积比原来三角形的面积减少一个重叠部分的面积”，6平方厘米所对应的是原三角形面积的减去2个重叠部分面积．6.（南山区）量出需要的数据，计算梯形的周长和面积．【答案】梯形的周长是10厘米，面积是5.1平方厘米【解析】测量出梯形的各个腰和底以及高的长度，使用梯形的周长和面积公式可直接进行计算．解答：解：由测量得知，梯形的上底是2厘米，腰是2厘米，下底是4厘米，高是1.7厘米．周长：2+2+2+4=10（厘米）；面积：（2+4）×1.7÷2，=6×1.7÷2，=5.1（平方厘米）；答：梯形的周长是10厘米，面积是5.1平方厘米．点评：准确测量梯形的上下底、腰、高的长度，正确使用梯形的周长和面积公式．7.（东莞）两个面积相等的三角形一定能拼成一个平行四边形．．（判断对错）【答案】×【解析】分析：因为只有完全一样的三角形才可以，面积相等的三角形，未必底边和高分别相等，据此举例说明即可判断．解答：解：例如：底边长为4，高为3和底边长为2，高为6的两个三角形，面积相等，但是不能拼成平行四边形．面积相等的两个三角形一定能拼成平行四边形，说法错误．故答案为：×．点评：此题应认真进行分析，通过举例进行验证，故而得出问题答案．8.（诸暨市）图中的两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积．【答案】阴影部分的面积是30平方厘米【解析】由题意得，阴影部分面积=大三角形面积﹣大三角形里空白小三角形的面积，代数计算．解答：解：大三角形面积：10×（10+6）÷2=80（平方厘米），小三角形面积：10×10÷2=50（平方厘米），阴影部分三角形面积：80﹣50=30（平方厘米）．答：阴影部分的面积是30平方厘米．点评：解决本题的关键是明确阴影部分面积=红色大三角形面积﹣红色大三角形里空白小三角形的面积．9.（2009•资中县）如图，在平行四边形中，甲的面积是46平方厘米，乙的面积是73平方厘米，则丙的面积是平方厘米．【答案】27【解析】连接EF，因为三角形ABF的面积=三角形BFE的面积（等底等高），三角形EFC的面积=三角形DFC的面积，所以丙的面积=乙的面积﹣甲的面积=73﹣46=27（平方厘米）；继而得出结论．解答：解：连接EF，因为三角形ABF面积=三角形BFE面积（等底等高），所以三角形EFC面积=三角形DFC的面积，因为丙的面积=三角形EFC的面积=三角形BEC的面积﹣三角形BEF的面积=73﹣46=27（平方厘米）；答：丙的面积是27平方厘米；故答案为：27．点评：解答此题的关键是根据三角形等底等高的性质，进行分析，把所求问题进行等量代换，进而得出结论．10.（旅顺口区）在如图中按要求操作．（1）画出梯形的高，测量高cm（精确到0.1cm）；（2）画一条线段，把梯形变成一个平行四边形和一个三角形；（3）测量∠A=．【答案】（1）2.1；（2）（3）115°【解析】（1）过梯形上底的一个顶点向下底作垂线，顶点和垂足之间的线段就是梯形形的一条高；用刻度尺即可度量出这条高的长度．（2）过三角形上底的一个顶点，作另一腰的平行线，交梯形下底于一点，即可把梯形变成一个平行四边形和一个三角形．（3）把量角器的0°刻度线与∠A的一边重合，顶点与量角器的中心重合，另一边与量角器的刻度线重合，量角器的读数就是这个角的度数．解答：解：（1）画梯形的高如下图，经测量，高是2.1cm；（2）画线如下图，线段BE把梯形ABCD分成平行四边ADEB和三角形BEC；（3）经测量，∠A=115°；故答案为： 2.1，115°．点评：本题是考查作梯形的高、线段的度量、角的度量等．注意，画图形的高时要有虚线；度量角时，注意“三重合”．11.（2013•广州）如图所示，求甲比乙的面积少多少平方厘米？【答案】甲比乙的面积少3平方厘米【解析】根据图形可知，甲加上空白梯形的面积是长6厘米，宽4厘米的长方形的面积，乙加上空白梯形的面积是一个底6厘米，高（4+5）厘米的三角形，而甲与乙的面积差即是大三角形与长方形的面积差．据此解答．解答：解：6×（4+5）÷2﹣6×4=6×9÷2﹣24=27﹣24=3（平方厘米）；答：甲比乙的面积少3平方厘米．点评：本题考查了几何问题中的等量代换，即根据两个面积同时加上或减去相同的面积，差不变．12.（2014•长沙）如图，三角形一共有个．【答案】6【解析】试题分许：因为所有的三角形都有一个公共的顶点，所以只要看斜边有几条线段就有几个三角形．解答：解：斜边上线段一共有：3+2+1=6（条），所以一共有6个三角形．故答案为：6．点评：解决本题的关键是根据三角形的边的关系将三角形的个数转化成线段的条数来解答．13.如图，长方形内有两个三角形①和②，那么①的面积（）②的面积．A．＜ B．＞ C． =【答案】C【解析】如图所示，三角形ABC和三角形DBC等底等高，则二者的面积相等，二者分别减去公共部分三角形BOC，则剩余的部分仍然相等，即三角形①和三角形②的面积相等，据此即可判断．解答：解：三角形ABC和三角形DBC等底等高，则二者的面积相等，二者分别减去公共部分三角形BOC，则剩余的部分仍然相等，即三角形①和三角形②的面积相等，故选：C．点评：解答此题的主要依据是：等底等高的三角形面积相等．14.用a表示梯形的上底，b表示下底，h表示高，S表示面积．梯形面积的计算公式是．【答案】S=（a+b）h÷2【解析】梯形的面积=（上底+下底）×高÷2，进而把对应的字母代入等式即可．解答：解：因为梯形的面积=（上底+下底）×高÷2，所以S=（a+b）h÷2．故答案为：S=（a+b）h÷2．点评：此题考查用字母表示计算公式，熟记梯形的面积计算公式，是解决此题的关键．15.下图平行四边形中（单位：厘米），长为30厘米的底边所应的高是10厘米，阴影部分面积是（）平方厘米．A．300B．150C．120D．无法确定【答案】B【解析】观察图形可知，阴影部分的面积正好等于这个平行四边形的面积的一半，据此计算即可解答问题．解答：解：30×10÷2=150（平方厘米）答：阴影部分的面积是150平方厘米．故选：B．点评：此题考查了组合图形的面积的计算方法，一般都是转化到规则图形中利用面积公式进行计算解答．16.要求如图图形的面积，请先画出相关的线段；量取某些数据（保留整厘米数），再计算出面积．【答案】三角形的面积为5平方厘米．【解析】依据过直线外一点作已知直线的垂线的方法，即可作出底上的高；再据量得底和高的值，利用三角形的面积公式即可求其面积．解答：解：如图所示，即为所要求画的三角形的底和高的长度：量得三角形的底约为5厘米，高约为2厘米，则三角形的面积为：5×2÷2=5（平方厘米）；答：三角形的面积为5平方厘米．点评：此题主要考查：过直线外一点作已知直线的垂线的方法，以及三角形面积的计算方法．17.求阴影部分面积．【答案】阴影部分的面积是12.56平方厘米【解析】如图可把阴影分为①、②两部分，图①和图③的面积相等，所以阴影部分的面积是圆面积的四分之一．据此解答．解答：解：3.14×（8÷2）2÷4=3.14×16÷4=12.56（平方厘米）答：阴影部分的面积是12.56平方厘米．点评：在求不规则图形的面积时，一般要通过转化，把图形转化为规则图形的面积来进行解答．18.在右图中，三角形DEF比三角形ABF面积小15平方厘米，求DE的长。

2024年北师大版六年级下册数学小升初分班考必刷专题：空间与图形一、单选题1．一个圆柱体和一个圆锥体的底面周长之比是1：3，它们的体积比是1：3，圆柱体和圆锥体高的比是（）。

A．3：1B．1：9C．1：1D．3：22．直角三角形ABC （如图），以直角边AB旋转360° 后得到的是（）A．底面直径是6cm，高是8cm的圆锥B．底面直径是8cm，高是6cm的圆锥C．底面半径是8cm，高是6cm的圆锥D．底面半径是6cm，高是8cm的圆锥3．把一根长3米的圆柱形木料截成3段小圆柱后，表面积比原来增加了0.6平方米，原来这根木料的体积是（）立方米。

A．0.3B．0.4C．0.45D．0.64．把一个圆柱削成一个最大的圆锥，削去部分的体积是圆锥体积的（）A．13B．23C．2倍D．6倍5．把一个棱长是6分米的实心正方体木块削成一个最大的圆柱，削去部分的体积是（）立方分米。

A．46.44B．100.48C．102.96D．169.566．一个立体图形，从上面看到的形状是，从正面看到的形状是，搭这个立体图形至少需要（）个小正方体。

A．5B．6C．7D．8二、填空题7．将一块体积是90m3的圆柱形铁块，削成一个最大的圆锥，削成的圆锥的体积是m3。

削下的铁屑还可熔铸成个这样的圆锥。

8．一个圆锥的体积是76立方厘米，底面积是19平方厘米．这个圆锥的高是厘米．9．一个圆柱与一个圆锥，圆柱的底面积是圆锥底面积的40%，圆柱的高是圆锥高的2倍，这个圆柱和圆锥的体积之比是。

10．一个圆柱的侧面积是157cm2，高是5cm，它的底面半径是cm，表面积是cm2。

11．一个周长为20厘米的大圆内有许多小圆，这些小圆的圆心都在大圆的一个直径上．则小圆的周长之和为厘米．12．一大正方体由着千个棱长为1cm的小正方体组成，在大正方体的表面涂色，其中只有一面涂色的小正方体有24个，大正方体的表面积是平方厘米。

13．用48厘米长的铁丝焊接成个最大的正方体.这个正方体的棱长厘米，体积是立方厘米14．把一个圆柱体削成一个最大的圆锥体，体积减少了120立方厘米，那么圆锥体积是立方厘米。

空间与图形专项训练基础题一、选择题1．一个长方体的长、宽、高都扩大2倍，它的体积扩大（）倍。

A、2B、6C、8【答案】C【解析】长方体的体积=长×宽×高，长、宽和高都扩大2倍，则体积就扩大了2×2×2=8倍，根据此选择即可。

2．正方体的棱长扩大2倍，它的表面积就（）。

A.扩大2倍B.扩大4倍C.扩大6倍【答案】B【解析】根据正方体的表面积计算公式，棱长扩大2倍，则表面积扩大：2×2=4倍，根据此选择即可。

3．用两个棱长是1分米的正方体小木块拼成一个长方体，拼成的长方体的表面积是（）。

A.增加了B.减少了C.没有变【答案】B【解析】把小正方体拼成一个长方体后，减少了2个小正方形的面积，因此拼成的长方体的表面积比原来减少了。

4．做一个长方体抽屉，需要（）块长方形木板。

A．4 B．5 C．6【答案】B【解析】长方体抽屉没有上面一个面，因此一共有5个面，需要5块长方形木板，根据此选择即可。

5．用一根长（）铁丝正好可以做一个长6厘米、宽5厘米、高3厘米的长方体框架。

A．28厘米 B．126平方厘米 C．56厘米 D．90立方厘米【答案】C。

【解析】长方体有4条长，4条宽和4条高，求出棱长之和，即可求出需要多少铁丝，即：（6＋5＋3）×4=56厘米，根据此选择即可。

6．我们在画长方体时一般只画出三个面，这是因为长方体（）。

A．只有三个面 B．只能看到三个面 C．最多只能看到三个面【答案】C【解析】把长方体放在桌面上，最多可以看到3个面。

根据此选择。

7．将一个正方体钢坯锻造成长方体，正方体和长方体（）。

A.体积相等，表面积不相等B.体积和表面积都不相等．C.表面积相等，体积不相等．【答案】A【解析】将一个正方体钢坯锻造成长方体，形状改变，体积不变。

8．一个正方体的棱长之和是12a厘米，它的棱长是（）厘米。

A.6aB.aC.2aD.12a【答案】B【解析】棱长之和÷12=棱长9．一个正方体的棱长是8分米，它的棱长总和是（）分米。