希望杯初赛六大必考专题系统梳理与考点总结(六)计数篇

《希望杯数学能力培训教程小学六年级【六年级数学希望杯的考点分析】》摘要：、数论部分主要考察余数问题;公约数与公倍数;3位值原理;完全平方数、完全立方数;5整除特征;6质数、合数;7奇偶性等，几何部分主要考察直线型面积;直线型周长;3水位问题，计算模块涉及到循环数分数混合运算;定义新运算;3比较分数;较多分数和、考试围分数义和性质四则运算巧算与估算;分数分率;3比和比例;计数问题规律统计图表可能性;5圆周长和面积圆柱与圆锥;6抽屉原理简单应用;7应用题(行程问题、工程问题、牛吃草问题、钟表问题等);8统筹问题值问题逻辑推理二、命题特试题容不超出现行数学教学纲不超出教学进贴近现行数学课课高课题目活而不难巧而不偏;既众化又富思考性和启发性力体现科学思维美寓科学趣味将知识、能力考察和思维能力培养结合起因跟其它杯赛试题比较起希望杯题目难易比较适般不会出现偏题怪题主要学生基础知识扎实认真备考要取得成绩并不困难希望杯主要考察学生三方面能力是计算能力这是学奥数必备基素质;二是熟记基知识这就要考生对希望杯要考察知识有清晰认识和把握;三就是要学会对知识和题方法进行归纳总结这要考生熟练掌握知识基础上具有举反三能力才能更应对题型各种变化和对知识各角考察题型主要以数论几何计算型应用题等基奥数问题主型应用题比重相对考前有计划复习和进行模拟训练很重要、数论部分主要考察余数问题;公约数与公倍数;3位值原理;完全平方数、完全立方数;5整除特征;6质数、合数;7奇偶性等希望杯数论题目整体不难考察多些基题型如(00年8届希望杯6年级试试题8)张老师带领六()班学生会种树学生恰可平分成5组已知师生每人种树样多共种树57棵则六()学生有_____人577×3由学生恰可以平分成5份则学生总数必然是5倍数而305×6+所以六()班学生共有30人二、几何部分主要考察直线型面积;直线型周长;3水位问题平面几何主要要掌握知识即等积变换模型、蝴蝶模型立体几何主要掌握圆柱圆锥体积计算以及水位问题三、计算模块涉及到循环数分数混合运算;定义新运算;3比较分数;较多分数和计算整体不难主要考察学生细心程以及计算功底对定义新运算关键就是要准新运算规律然套入给出题目即可四、应用题通下面图示我们可以清楚看到应用题是希望杯考察热也是难基上作每年压轴题出现主要包括还原问题、鸡兔笼、盈亏问题、行程问题、牛吃草、工程问题。

28.计数方法知识纵横所谓计数,通俗地说就是数数,即把我们研究的对象的个数数出来.当研究的对象比较简单,且数目也不大时,枚举法是最基本而又简单的方法,•即把对象的所有可能一一列举出来,数出总数即可.当研究的对象比较复杂,且数目较大时,计数时常常要用到如下两原理: 加法原理:做一件事,完成它可以有n 类办法,在第一类办法中有m 1种不同的方法,在第二类办法中有m 2种不同的方法…,在第n 类办法中有m n 种不同的方法,那么完成这件事共有N=m 1+m 2+…m n 种不同的方法.乘法原理:做一件事,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法……做第n 步有m n 种不同的方法,那么完成这件事共有N=m 1·m 2·…m n 种不同的方法.例题求解 【例1】如图,从甲地到乙地共有4条路可走,从乙地到丙地有3条路可走,从甲地到丙地有5条路可走,那么从甲地到丙地共有_______条. (2000年重庆市竞赛题)思路点拨 从甲地到丙地可分两类办法:直达和转乙地. 解:17 提示:共有3×4+5=17(条)路可走【例2】右图中的小方格是边长为1的正方形,则从图中一共可以数出( )个正方形.A.24B.210C.50D.90(2001年“五羊杯”邀请赛题)思路点拨 图中的正方形可以分成边长为1,边长为2,边长为3,边长为4这4种类型,分别求出每种规格的正方形个数.解:选C 提示:边长为1的正方形为4×6个,边长为2的正方形有3×5个,边长为3的正方形有2×4个,边长为4的正方形有1×3个,共有4×6+3×5+2×4+1×3=50(个)【例3】我们知道,两条直线相交,有且只有一个交点,三条直线相交,•最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n 条直线最多有多少个交点?说明理由.思路点拨 从特殊情况入手,由简到繁,深入思考,从中发现规律.解:提示:三条直线的情形:若平面上已有两条直线,再添一条直线,•则这条直线和原来平面上的两条直线各有一个交点,所以有1+2个交点,同理,4•条直线的情形为在原来三条直线的基础上添加一条直线,共多出3个交点,所以有1+2+3个交点.•一般地,n 条直线两丙乙甲B n+1B i+1B i A n+1A n两相交,其交点数为1+2+…+(n-1)= (1)2n n 个. 【例4】由0、1、2、3、4、5、6这7个数字,可以组成(1)多少个四位数,其中有多少个奇数,有多少个偶数?(2)多少个没有重复数字的四位数,其中有多少个奇数,有多少个偶数?思路点拨 要确定四位数,必须一位一位来考虑,显然计数时,需要用乘法原理,(2)问与(1)问的差别在于,增加了“没有重复”的限制.解:提示:(1)这个四位数的最高位不是0,故最高位有6种选法(即选1～6•中的任一个数字),其余各位,可以从0～6这7个数字中任选,故共有6×7×7×7=2058个四位数,在这些四位数中,奇数的个数也可用类似方法获得,有6×7×7×3=882•个,•偶数2058-882=1176个.(2)同理,没有重复数字的四位数有6×6×5×4=720个,其中奇数有3×5×5×4=300个,其中偶数有720-300=420个.【例5】两条平行直线上各有n 个点,用这n 对点按如下规则连接线段:•①同一直线上的点之间不连接,②连接的任意两条线段可以有共同的端点,但不得有其他的交点.(1)画图说明当n=1,2,3时,连接的线段最多各有多少米?(2)由(1)猜想n(n 为正整数)对点之间连接的线段最多有多少条,证明你的结论;(3)当n=2003时,所连接的线段最多有多少条? (第14•届“希望杯”邀请赛试题) 思路点拨 把直线标记为L 1,L 2,它们上面的点从左到右分别为A 1,A 2,A 3,…A n 和B 1,B 2,•B 3,…B n ,设这n 对点之间连接的直线段最多有p n 条,解题的关键是探讨p n+1与p n 的关系.解:(1)由下图①可以看出,n=1时,最多可以连接1条线段,n=2时,•最多可以连接3条线段,n=3时,最多可以连接5条线段.n=1n=2n=3图① 图②(2)猜想:对于正整数n,这n 对点之间连接的直线段最多有2n-1条.证明:将直线标记为L 1、L 2,它们上面的点从左到右排列分别为A 1,A 2,A 3,…A n 和B 1,B 2,•B 3,…,B n ,设这n 对点之间连接的直线段最多有P n 条,显然,其中必有A n B n 这一条,否则,P n 就不是最多的数.当在L 1、L 2上分别加上第n+1个点时,不妨设这两个点在A n 与B n 的右侧,•那么除了原来已经有的P n 条直线段外,还可以连接A n+1Bn,A n+1B n+1这两条线段,或连接A n B n+1,A n+1B n+1这两条线段.所以P n+1≥P n +2,另一方面,设对于n+1对点有另一种连法:考虑图②中以A n+1为端点的线段,若以A n+1为端点的线段的条数大于1,•则一定可以找到一个i ≤n,使得对于任意的j<i,A n+1B j 都不在所画的线段中,这时,B i+1,B i+2,…,B n+1只能与A n+1连接,不妨设A n+1B i+1,A n+1B i+2,…,A n+1B n+1都已连接,此时图中的线段数为P n+1,我们做如下操作:去掉A n+1B i,连接A n B i+1,得到新的连接图,而新的连接图满足要求且线段总数不变,将此操作一直进行下去,直到与A n+1连接的线段只有一条A n+1B n+1为止.最后图中,与点B n+1相关的线段只剩两条,即A n B n+1,A n+1B n+1,去掉这两条线段,则剩余P n+1-2条线段,而图形恰是n•对点的连接图,所以P n+1-2≤P n.由此我们得到P n+1=P n+2,而P1=1,P2=3,所以P n=1+2×(n-1)=2n-1.(3)当n=2003时,P2003=4005(条).学力训练一、基础夯实1.第一个口袋中装2个球,第二个口袋中装4个球,第三个口袋中装5个球,所有三个口袋中的球各不相同.(1)从口袋中任取一个球,共有______种不同的取法.(2)从三个口袋中各取一个球,有_______种不同的取法.2.如图,在四个正方形拼接成的图形中．．．,以A1、A2、A3…、A10这十个点中任意三点为顶,共能组成______个等腰直角三角形. (2003年泉州市中考题)（第2题）（第4题）3.画一条直线,可将平面分成2个部分,画2条直线,最多可将平面分成4个部分,•那么,画6条直线最多可将平面分成______个部分. (第14届“希望杯”邀请赛试题)4.一条信息可通过如图的网络线由上(A点)往下向各站点传送.例如信息到b2•点可由经a1的站点送达,也可由经a2的站点送达,共有两条途径传送,则信息由A•点到达d3的不同途径共有( ).A.3条B.4条C.6条D.12条 (2003年南宁市中考题)5.如图,图中不同的线段的条数有( ).A.52条B.63条C.141条D.154条（第5题）（第7题）6.平面内的7条直线任两条都相交,交点数最多有a个,最少有b个,则a+b等于( • ).A.42B.41C.21D.22 (2003年北京市竞赛题)7.如图,在表板上有4个开关,如果相邻的2个开关不能同时是关的,•那么所有不同的状态有( ).A.4种B.6种C.8种D.12种 (第15届江苏省竞赛题)8.如图,左右相邻两点,上下相邻两点之间距离都等于1厘米,把这些点连接起来,作为三角形的顶点,那么可以组成多少个直角三角形?9.用数字0,1,2,3,4可以组成多少个(1)四位数? (2)四位偶数?(3)没有重复数字的四位数?(4)没有重复数字的四位偶数?二、能力拓展10.5人站成一排照相,其中一人必须站在中间,有_____种站法.11.在1到300这300个自然数中,不含有数字3的自然数有_______个.12.跳格游戏:如图,人从格外只能进入第1格;在格中,每次可向前跳1格或2格,•那么人从格外跳到第6格可以有______种方法. (第15届江苏省竞赛题)（第12题）（第13题）13.如图,由18个边长相等的正方形组成的长方形ABCD中,•包含“※”在内的长方形及正方形一共有_____个. (北京市“迎春杯”竞赛题)14.如图,正方形被分成9个相同的小正方形,一共16个顶点,•以其中不在同一直线上的3个顶点为顶点,可以构成三角形,在这些三角形中,与阴影面积相等的三角形有_______个.5467 832（第14题）（第15题）（第16题）15.如图,一共能数出( )个长方形(正方形也算作长方形).A.64B.63C.60D.48 (2000年“五羊杯”竞赛题)16.如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指数轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,•右图轮子上方的箭头指着的数字为b,数对(a,b)所有可能的个数为n,其中a+b恰好偶数的不同数对的个数为m,则mn等于( ).A. 12B.16C.512D.34(2000年山东省竞赛题)17. (2002年重庆市竞赛题)如图,从A点B点(只从左向右,从上到下),共有( )种不同的走法.A.24B.20C.16D.12A18.平面上5个圆最多能把平面分成多少个部分?一般地,n•个圆最多能把平面分成多少个部分?19.5个人站成一排照相.(1)若甲、乙两人必须相邻,则有多少不同的站队方法?(2)若甲、乙两人必不相邻,则有多少不同的站队方法?三、综合创新20. (第11届“希望杯”邀请赛试题)将编号为1,2,3,4,5的5个小球放入编号为1,2,3,4,5的5个盒子中,每个盒子中只放入一个.(1)一共有多少种不同的方法?(2)若编号为1的球恰好放在1号盒子中,共有多少种不同的放法?(3)若至少有一个球放入了同号的盒子中(即对号放入)共有多少种不同的放法?答案1.2+4+5=11(种),2×4×5=40(种)2.243.22 提示:一般地n条直线最多将平面分为2+2+3+…+n=1+1+2+…+n=12(n2+2n+2)部分. 4.C5.D 提示:水平方向上的一类线段共有(6+5+4+3+2+1)×4=84(条)(只考虑线段BC上共有多少条不同的线段),同理,斜方向上的线段共有(4+3+2+1)×7=70条.6.D7.C8.将图中的每一点作为直角三角形的直角顶点时,•这样的直角三角形个数一一算出,注意图形的对称性,共有4×4+5×4+8×1=44(个)9.(1)4×5×5=500(个);(2)4×5×5×3=300(个);(3)4×4×3×2=96(个);(•4)96-2×3×3×2=60(个).10.24 提示:4×3×2×1=24(种)11.242 提示:按数的位数分类:不含3的一位数有8个,不含3的二位数有72个,•不含3的三位数有162个.12.每次跳1格,有惟一的跳法,仅有一次跳2格,其余各次跳1格,有4种跳法,有两次跳2格,其余各次跳1格,有3种跳法,共有1+4+3=8种跳法.13.3614.48 提示:图中等积三角形可分为:底长为3,高长为2的一类三角形有24个;•底长为2,高长为3一类的三角形有32个,扣除其中重复的,故有48个.15.B 提示:不包括第一行的三个小正方形时,可数出(1+2)(1+2+3+4+5)=45•个长方形;包括时,可数出3×(1+2+3)=18个长方形,共计63个.16.C17.B 提示:从A→A n点的走法数量,等于从A到A n•左边一个点的走法数量加上从A到A n上边一个点的走法数量A→B=(A→a14)+(A→a11)=10+10=20(种),•这种计数方法称为逐点标数累计法.18.提示:1个圆最多能把平面分成2个部分,2个圆最多能把平面分成4个部分;•3个圆最多能把平面分成8个部分;现在加入第4个圆,为了使分成的部分最多,第4个圆必须与前面3个圆都有两个交点,如图所示,因此得6个交点,这6个交点将第4•个圆的圆周分成6段圆弧,而每一段圆弧将原来的部分一分为二,即增加了一个部分,•于是4个圆最多将平面分成8+6=14个部分.同理,5个圆最多将平面分成14+8=22个部分,•一般地,n个圆最多分平面为:2+1×2+2×2+…+(n-1)×2=2+[1+2+…+(n-1)]=n2-n+2•个平面.19.提示:(1)把甲、乙两人看成一个整体,与剩下的3人看成4个对象,这4个对象站成一排,共有4×3×2×1×2=48种不同的站队方法(注:甲、•乙两人可以甲在乙左边或右边两种情况).(2)从5个人自由站队总数中减去甲、乙两人必须相邻的情况,剩下的就是甲、•乙两人必不相邻的情况,5个人自由站队总数是5×4×3×2×1=120种,故甲、乙两必不相邻的站队方法有120-48=72种.20.提示:(1)将第一个球先放入,有5种不同的放法;再放入第二个球,这时有4种不同的放法;依此类推,放入第三、四、五个球时，分别有3、2、1种放法，•所以总共有5×4×3×2×1=120种不同的放法.(2)将1号球放在１号盒子中，其余的4个球随意放，它们依次有4、3、2、1•种不同的放法，这样共有4×3×2×1=24种不同的放法。

小学“希望杯”历年真题专题总结——计算专题说明：涵盖了1-9届（2003-2011年）的所有计算题，并进行了专题归纳。

每题后小括号表示(届数-1/2试-第几题)例如：(5-2-3)表示第五届，第2试，第3题。

一.基本四则运算考点：去、舔括号，带符号搬家(*^__^*)要点：小心谨慎，不急不躁。

1. 计算：3×2÷2－2×6÷3÷2+3+5－3=________ 。

（1-2-1）[详解] 原式=3×（2÷2）-2×[ 6÷（2×3）]+(3-3)+5=3×1-2×1+5=3-2+5=63. 计算：234432483305+-⨯+÷ 。

（2-1-1）[详解] 234432483302344323266(23466)(43232)300400700+-⨯+÷=+-+=++-=+=4. 1＋2×3÷(4＋5)×6=__________。

(4-1-1)[详解] 原式=1+6×6÷（4+5）=1+36÷9=1+4=55. =÷++++++2008)2011201020092008200720062005(__________(6-1-1) 考点：中间数原理。

[分析] 注意到，2005+2011=2008×2，2006+2010=2008×2，2007+2009=2008×2.[详解] 原式=2008×7÷2008=76. 若B A +=2010并且2B ÷=A ，则=A __________（6-1-13）[分析]由53=B A ，可设A 为3份，B 为5份。

那么A+B=8份。

8份对应着2008 2008÷8=251，A=251×3=7537. 19199199919999199999__________++++=。

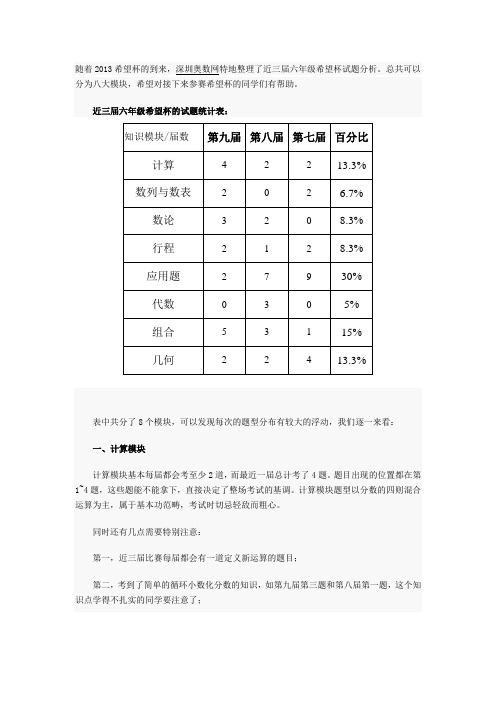
随着2013希望杯的到来，深圳奥数网特地整理了近三届六年级希望杯试题分析。

总共可以分为八大模块，希望对接下来参赛希望杯的同学们有帮助。

近三届六年级希望杯的试题统计表：表中共分了8个模块，可以发现每次的题型分布有较大的浮动，我们逐一来看：一、计算模块计算模块基本每届都会考至少2道，而最近一届总计考了4题。

题目出现的位置都在第1~4题，这些题能不能拿下，直接决定了整场考试的基调。

计算模块题型以分数的四则混合运算为主，属于基本功范畴，考试时切忌轻敌而粗心。

同时还有几点需要特别注意：第一，近三届比赛每届都会有一道定义新运算的题目；第二，考到了简单的循环小数化分数的知识，如第九届第三题和第八届第一题，这个知识点学得不扎实的同学要注意了；第三，第九届希望杯第四题涉及到了放缩法，此方法在六年级寒假班的第一讲中有提到，对放缩法不明白的同学可以参考教材。

计算模块的试题难度都不高，属于中低档题，想顺利通过第一试，计算这块一定要争取获得满分。

二、数列与数表模块这个模块不是希望杯考试的热点，近三届涉及到的知识点仅有数列找规律以及周期问题。

周期问题中需要注意商的意义，代表的是周期的组数。

数列找规律不难，但容易做错，有时间一定要验算。

另外还要特别注意的是，第九届第5题与第7届第6题考的是同一题型，都是在一个小数上点上循环点成为一个循环小数，使满足特定条件，这类问题突破口在于小数的最后一个数字上一定要标上循环点，接下去大部分同学选择分类讨论，也就转化成了一个周期问题。

实际上此题有更简洁做法，如第九届第5题，第2011位上是6，所以第2014位是9，因此周期一定是2005的因数(因为前9个数字为1~9，然后开始循环)，所以周期只能是5，另一个循环点在5上面。

三、数论模块数论模块通常是杯赛考试中的难点，但是希望杯中的数论问题考得不难，如第九届的第7、第8、第14题分别考察了数论模块中的最大公约数与最小公倍数、整除特征和分解质因数，另外第八届第16题考察的是位值原理，这些都是数论模块中需要掌握的基本知识点。

一、计算专题1．等差数列⑴通项公式：末项＝首项＋(项数－1)×公差a n ＝ a 1＋(n －1) ×d项数公式：项数＝(末项－首项)÷公差＋1n ＝(a n －a 1)÷d ＋1⑵求和公式：和＝(首项＋末项) ×项数÷2＝中间项×项数(项数为奇数的等差数列)⑶常考结论：1＋3＋5＋…＋(2n －1)＝n 21＋2＋3＋…＋n ＋…＋3＋2＋1＝n 22．常见方法与技巧⑴凑整法⑵提取公因数⑶找规律…………【例1】(2＋4＋6＋…＋2000)－(1＋3＋5＋…＋1999)＝_____ 。

【例2】2004×2003－2003×2002＋2002×2001－2001×2000＋…＋2×1＝_________。

【例3】(希望杯试题)1÷50＋2÷50＋…＋99÷50＝_______。

希望杯复赛必考知识点之计算与计数专题【例4】(希望杯试题)25×32÷14＋36÷21×25 ＝_______。

【例5】1099899899989998++++个＝ 。

【例6】55555×666667＋44445×666666－155555 ＝___________。

二、计数专题1．加乘原理加法原理：分类计数，类类独立乘法原理：分步计数，步步相关区分：可以……也可以…… 加法原理先……再……又…… 乘法原理2．几何计数数长方形3．必考方法：枚举法【例7】数一数，下边图形中有______个平行四边形。

【例8】由25个面积等于1的小正方形组成的大正方形，图中面积是6的长方形有_____个。

【例9】图中，不含“A”的正方形有____个。

【例10】利用数字1，2，3，4，5共可组成_____个数字不重复的偶数。

“希望杯”全国数学邀请赛考查内容提要加入时间：2008-9-8 9:33:52点击：25637（一）小学四年级1.整数的四则运算，运算定律，简便计算，等差数列求和。

2.基本图形，图形的拼组(分、合、移、补)，图形的变换，折叠与展开。

3.角的概念和度量，长方形、正方形的周长和面积，平行四边形、梯形的概念和周长计算。

4.整除概念，数的整除特征，带余除法，平均数。

5.小数意义和性质，分数的初步认识(不要求运算)。

6.应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。

7.几何计数(数图形)，找规律，归纳，统计，可能性。

8.数谜，分析推理能力，数位，十进制表示法。

9.生活数学(钟表，时间，人民币，位置与方向，长度、质量的单位)。

（二）小学五年级1．小数的四则运算，巧算与估算，小数近似，小数与分数的互换。

2.因数与倍数，质数与合数，奇偶性的应用，数与数位。

3.三角形、平行四边形、梯形、多边形的面积。

4.长方体和正方体的表面积、体积，三视图，图形的变换(旋转、翻转)。

5.简易方程。

6.应用题(还原问题、鸡兔同笼、盈亏问题、行程问题等)，生活数学。

7.包含与排除，分析推理能力，加法原理、乘法原理。

8.几何计数，找规律，归纳，统计，可能性。

（三）小学六年级1．分数的意义和性质，四则运算，巧算与估算。

2．百分数，百分率。

3．比和比例。

4．计数问题，找规律，统计图表，可能性。

5．圆的周长和面积，圆柱与圆锥。

6．抽屉原理的简单应用。

7．应用题(行程问题、工程问题、牛吃草问题、钟表问题等)。

8．统筹问题，最值问题，逻辑推理。

（四）初中一年级1.有理数的加、减、乘、除、乘方、正数和负数、数轴、绝对值、近似数的有效数字2.一元一次方程、二元一次方程的整数解3.直线、射线、线段、角的度量、角的比较与运算、余角、补角、对顶角；相交线、平行线4.三角形的边（角）关系、三角形的内角和5.用字母表示数、合并同类项、去括号、代数式求值、探索规律、整式的加减6.统计表、条形统计图和扇形统计图、抽样调查、数据的收集与整理7.展开与折叠、展开图8.可能还是确定、可能性、概率的基本概念、简单逻辑推理9.整式的运算（主要是整式的加减乘运算，乘法公式的正用逆用）10.数论最初步、高斯记号、应用问题11.三视图（北师大）、平面直角坐标系（人教）、坐标方法的简单应用（五）初中二年级1.平方根、立方根、实数2.整式的加减乘除、乘法公式、提取公因式法、因式分解的简单应用3.二元一次方程组4.平面直角坐标系、一次函数、反比例函数5.一元一次不等式（组）6.勾股定理7. 轴对称，中心对称8.全等三角形9.多边形及其内角和、镶嵌10.统计图的选择、抽样调查、平均数、中位数与众数11.分式加减乘除、整数指数幂、分式方程12.平移、旋转13.逻辑问题、概率问题、数论初步、应用问题14.平行四边形的性质、判别，菱形、矩形、正方形、梯形的概念、计算（六）高中一年级1.指数、对数函数（概念、性质、应用）2.集合、映射、函数（指、对、幂）3.充要条件4.等差、等比数列5.一元二次不等式和二次函数6.三角（不包含反三角函数、三角方程）7.整除、同余8.不定方程9.平面向量10.立体几何11.直线与圆12.算法初步13.逻辑问题14.实际问题（七）高中二年级1.三角2.立体几何3.解析几何4.矢量应用5.统计、概率6.不等式7.逻辑问题8.实际问题第二十二届“希望杯”全国数学邀请赛章程加入时间：2010-8-31 17:42:05点击：5488特别通告： 1.自2010年起，台湾已参加本邀请赛。

2024 IHC 6 培训题答案1. 计算：111111462011201235352010201124111111234520102011345620112012--+-++⨯⨯⨯⨯⨯⨯+-+-+-…=________。

答案：10062. 将1~9这九个数字填入到如图所示的3×3的方格后，求出其三行、三列以及一条对角线上三个数字之和，分别记为A~G 。

如果这七个数能构成一个等差数列，则其中对角线上三个数之和G=________。

答案：153. 1＋0.99－0.98－0.97＋0.96＋0.95－0.94－0.93＋…＋0.04＋0.03－0.02－0.01=________。

答案：14. 找规律：第8个图形中圆点有________个。

答案：295. 计算：3.4285714.6________∙∙∙⨯=。

答案：166. 设p ，q 是两个自然数，规定：p △q =4×q －(p ＋q )÷2。

则3△(4△6)=________。

答案：65 7. 计算：！21+！32+！43+…+99100！=（ ）。

（注：n !=1×2×3×…×(n -1)×n ） A.100!1100!- B.100!+1100! C.101!1101!- D.100!1101!- E.100!+1101!答案：A8. 计算20082008的十位上的数字是________。

答案：19. 将循环小数0.081∙∙与0.200836∙∙相乘，小数点后第2021位上的数字是________。

答案：810. 有些三位数：①它的各位数字不同且没有数字0；②这个数等于所有由它的各位数字所组成的没有重复数字的两位数的和。

那么满足以上条件的所有三位数的和是________。

答案：79211. 冬冬要把三个小球全部放入三个箱子，其中三个小球的颜色分别是红色、黄色和蓝色，而三个箱子的颜色也分别是红色、黄色和蓝色。