分数的初步认识1. 什么是分数分数是数学中的一个重要概念，它们用于表示整数之间的关系。
在分数中，一个数被表示为另外两个数的比例。
分数由一个分子和一个分母组成，用分子/分母的形式表示。
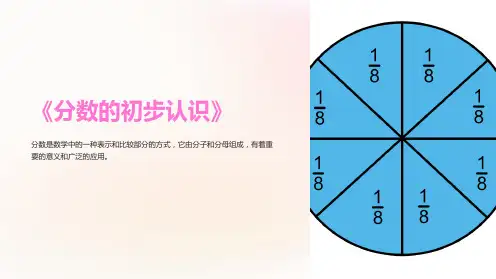
分子表示被分割的数量，分母表示分割成的份数。
例如，1/2表示将一个整体分割成两等分，取其中的一份。
2. 分数的基本性质2.1 分数的大小比较分数可以比较大小，比较分数的大小需要比较分子和分母的大小关系。
若分母相同时，分子越大，分数越大；若分子相同时，分母越小，分数越大。
2.2 分数的化简将一个分数约分到最简形式的过程称为化简。
化简分数时，需要找到分子和分母的最大公因数，然后将分子和分母同时除以最大公因数。
例如，2/4可以化简为1/2。
2.3 分数的运算分数可以进行加、减、乘、除等各种运算。
在进行运算时，需要找到分数的公共分母，然后根据运算规则进行计算。
例如，1/2 + 1/3 = 3/6 + 2/6 = 5/6。
3. 分数的表示形式3.1 假分数分子大于等于分母的分数称为假分数。
假分数可以转化为带分数。
例如，7/4可以表示为1 3/4。
3.2 带分数带分数由整数部分和真分数部分组成。
整数部分表示整体的数量，真分数部分表示整体中的一部分。
例如，1 3/4表示有一个整体和3/4的部分。
4. 分数的应用场景分数在我们的日常生活中有着广泛的应用，包括下面几个方面：4.1 长度和距离度量长度和距离时，常常会用到分数。
例如，如果一条线段被分割成4等分，我们可以表示为1/4。
4.2 百分比百分比是指一个数相对于另一个数的占比。
百分比可以用分数表示，例如50%可以表示为1/2。
4.3 比例比例是用分数表示两个数字之间的关系。
例如，1:2可以表示为1/2的比例。
4.4 概率概率是表示某件事情发生的可能性大小。
概率可以用分数表示，例如1/2表示发生的可能性为50%。
5. 总结分数是数学中的重要概念，它用于表示整数之间的关系。
我们可以通过比较分子和分母的大小来比较分数的大小；通过化简分数来使其形式更简单；通过公共分母进行分数的运算；通过假分数和带分数来更直观地表示分数。
