下载文档原格式
信号与信息处理基础习题及题解目录第1章绪论 (3)第2章连续时间信号的时域分析 (3)第3章连续时间信号的频域分析 (8)第4章连续时间信号的复频域分析 (15)第5章离散时间信号的时域分析 (19)第6章离散傅里叶变换 (22)第7章离散时间信号的复频域分析 (27)第一章1.1 结合具体实例，分析信息、消息和信号的联系与区别。
答：具体实例略。
信息、消息和信号三者既有区别又有联系，具体体现在：⑴ 信息的基本特点在于其不确定性，而通信的主要任务就是消除不确定性。
受信者在接收到信息之前，不知道发送的内容是什么，是未知的、不确定性事件。
受信者接收到信息后，可以减少或者消除不确定性。
⑵ 消息是信息的载体。
可以由消息得到信息，以映射的方式将消息与信息联系起来，如果不能建立映射关系就不能从消息中得到信息。
例如，一个不懂得中文的人看到一篇中文文章，就不能从中获取信息。
⑶ 信号是消息的具体物理体现，将消息转换为信号才能够在信道（传输信号的物理媒质，如空气、双绞线、同轴电缆、光缆等）中传输。
1.2 说明连续时间信号与模拟信号、离散时间信号与数字信号间的联系和区别。
答：按照时间函数取值的连续性与离散性可将信号划分为连续时间信号与离散时间信号，简称连续信号与离散信号。
第二章2.2 试写出题2.2图示各波形的表达式。
题2.2图解：左图：()()()[]()()()[]31312-------=t u t u t t u t u t f()()()()()33112--+---=t u t t u t t u中图：()()()()()321-----+=t u t u t u t u t f 右图：()()()()221---+=t u t u t u t f连续时间信号离散时间信号幅值连续幅值离散模拟信号幅值连续幅值离散数字信号抽样2.3 试画出时间t 在（-4，6）内以下信号的波形图。
⑴ t 2πsin ；⑵()1 2-t πsin ；⑶()t t u 21πsin -；⑷ ()t t u 2πsin ； ⑸()()1 2-t t u πsin ； ⑹()()1 21--t t u πsin 。
3.巳知长度为N=10的两个有限长序列,0 < 刀 < 45 < 90 W 刀 V 45<”<9做图表示•![(辨)、x2(n)和y(n)=X| (w)®x:(n)»循环卷积区间长度L= 10.解：石(刀)、与(”)和y〈”)=H] (rt)®x2(n)分别如题3解图(a)、(b) w (c)所示•题3解图Matlab程序代码参考(a)n=0:9;xl=[l,1,1,1,1,0,0,0,0,0];subplot(2,2,l);stem(n,xl,'fiir);xlabel('n');ylabelCxl(n)*);title(* xl(n)序列图')；(b)n=0:9;x2=[l,1,1,1,1,-1,-1,-1,-1,-1]；subplot(2,2,2);stem(n,x2,'fiir);xlabel('n');ylabel('x2(n)');title(* x2(n)序列图')；(c)Xl=fft(xl,10);X2=fft(x2,10);Y=X1.*X2;%%%或者Y=cconv(x 1 ,x2,10);%保证循环卷积区间长度L=10y=ifft(Y,10);subplot(2,2,3)；stem(n,y,'r')xlabel('n');ylabel('y(n)');title(' y(n)序列图);15.已知实序列上(")的8点DFT的前5个值为0.25, 0.125-jO. 3018. 0. 0. 125-j0.0518, 0.(1)求X(Q的其余3点的值；(2)x t(n) = Z 工(” + 5 + 8m)&.求 X1(4)=DFT[r)(n)],i(3) i2(n)=j(n)e)，,4,求x t(.k) =DFT[i J(n)]t,解：⑴因为小)是实序列，由第7题证明结果有XGO=X・(NT),即X(NT)=X-(A)，所以，X。
1.（P24,课后习题1.5（a,c,e ））试确定下列系统的（1）记忆性；（2）时不变性；（3）线性；（4）因果性；（5）稳定性。
（a ）(t)(t -2)+(1-t)y x x = （c ）()(t)sin 2(t)y t x =⎡⎤⎣⎦ （e ）()(1)()y n n x n =+解： （a ）记忆，时变，线性，非因果性，稳定性；（c ）无记忆，时变，线性，因果性，稳定性； （e ）无记忆，时变，线性，因果性，不稳定性；备注：本题中关于时变与时不变系统的判定，错误率较高，故特以（a ）为例，时变性质解答如下： 设：()0g (t )t x t =-，且有()T (t 2)+(1t)x t x x ⎡⎤=--⎣⎦，则：()()()()()0000T (t 2)+(1t)t 2+1t =(t 2)+(1t )g t g g x t x t x t x t ⎡⎤=--=--------⎣⎦又：()()()()00000(t )t 2+1t =(t 2)+1t +y t x t x t x t x t -=------- 显然：()0T (t )g t y t ⎡⎤≠-⎣⎦，故为时变系统。
又注：对于()T g t ⎡⎤⎣⎦，信号先经过系统再做时移；0(t )y t -，信号先做时移动再经过系统。
如果还不理解，做题可以这样判断：只要信号(t)x 中t 的系数不为1，则该系统必定为时变系统，如本题中(1-t)x ，t 的系数为-1，不是1，时变系统。
此外，若信号(t)x 的系数含有t ，该系统也为时变系统，如()sin 2(t)t x ⎡⎤⎣⎦，系数为()sin 2t 含有t ，为时变系统。
这是我做题自己积累的经验，大家选择性使用。
2.（P24,课后习题1.7）计算卷积并画出结果曲线-1()(1),()(1)3nx n u n h n u n ⎛⎫=--=- ⎪⎝⎭解：利用定义可知，11()()()()()1()(1)(1)31()(1)31()(1)3k kk k k kk y n x n h n x k h n k u k u n k u n k u n k ∞=-∞∞-=-∞--=-∞∞=-=*=-=----=--=+-∑∑∑∑用p 代替-1k 则，101()()()3p p y n u n p ∞+==+∑对于0n ≥，则有101111()()133213p p y n ∞+====-∑对于0n <，则有1110111113()()()()()13333213np n p n p n p y n ∞∞+-+-+=-=====-∑∑ 因此：3,02()1(),02nn y n n ⎧<⎪⎪=⎨⎪≥⎪⎩n1/61/23.（P24,课后习题1.8）设1,01(),()(/)0, t x t h t x t tα≤≤⎧==⎨⎩其余，（1）计算并画出卷积()()()y t x t h t =* （2）若d()d y tt仅含有3个不连续点，则?α=解：（a ）画出()x t 和()h t 的图形如下图所示：01α<<利用该图形，得到()()()y t x t h t =* 如图所示：因此，,0,t 1()1,1(1)0,t t y t t t otherwiseααααα≤≤⎧⎪≤≤⎪=⎨+-≤≤+⎪⎪⎩(b) 画出()x t 和()h t 的图形如下图所示：1α≥0 αh(t)1卷积后的图形如下图所示：10 1α 1+α所以,011,1t ()1,(1)0,t t y t t t otherwiseαααα≤≤⎧⎪≤≤⎪=⎨+-≤≤+⎪⎪⎩同理可以得到当1α≤-与10α-≤<时的结果，这里不再详细给出。
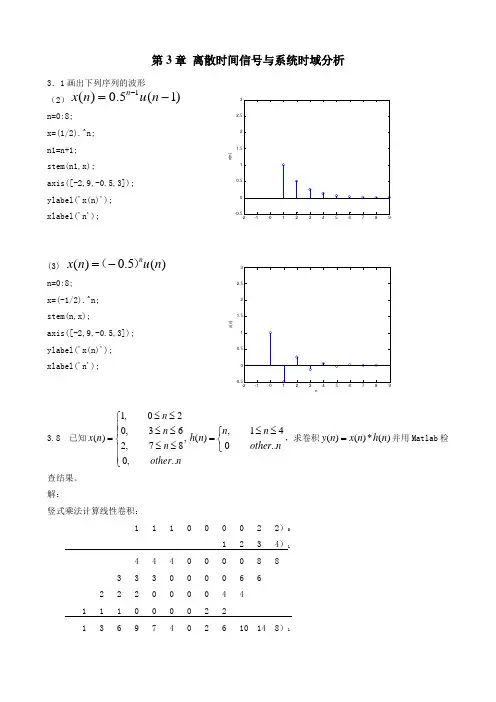
第3章 离散时间信号与系统时域分析3．1画出下列序列的波形（2）1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-（）n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩，求卷积()()*()y n x n h n =并用Matlab 检查结果。
解：竖式乘法计算线性卷积： 1 1 1 0 0 0 0 2 2）01 2 3 4）14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8）1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果：x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx （n ）=5sin(n) 解：2214337w πππ==，所以N=14 (2) 326n ππ-x （n ）=sin()-sin(n)解：22211213322212,2122612T N w T N w N ππππππ=========，所以(6) 3228n π-x （n ）=5sin()-cos(n) 解：22161116313822222()T N w T w x n ππππππ=======，为无理数，所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=，()4()nx n u n -=，(1)4y -=，(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应，并画出图形。
习题10.5试说明周期图谱估计方法。
解：周期图（periodogram ）是一种经典的功率谱密度估计方法，其主要优点是能应用快速傅里叶变换算法来进行谱估计。
当序列的长度足够长时，使用改进的周期图法，可以得到较好的功率谱估值，因而应用很广。
周期图的直接计算公式为：j j *j j 2per 11(e )(e )(e )|(e )|P X X X N Nωωωω==。
此外，功率谱密度还可以根据自相关函数估计的傅里叶变换来进行计算，称为经典谱估计的间接法，又称为BT 法，其计算公式为：j (2)j j 2per 1ˆ(e )()e |(e )|m N m P R m X Nωωω+∞−=−∞==∑，其中(2)ˆ()N R m 为自相关函数的有偏估计。
习题10.18设()x n 为一平稳随机信号，且是各态历经的，现用式()()()1||01ˆ||N m N N n r m x n x n m N m −−==+−∑ 解：估计其自相关函数，求此估计的均值和方差。
偏差的定义：ˆˆbia[()][()}()]rm E r m r m =− 式中1010101ˆ[()][()()]1 [()()]1 () ()N m N N n N m N N n N M n E r m E x n x n m N mE x n x n m N mr m N mr m −−=−−=−−==+−=+−=−=∑∑∑ 所以ˆbia[()]0rm =，即本题的自相关函数的估计是无偏估计。
由定义222ˆˆˆˆˆvar[()][()[()]][()][()]rm E r m E r m E r m E r m =−=−，其中 22ˆ[()]()E r m r m = 所以：1||22(1||)ˆˆvar[()][()()()](||)N m k N m N r m rk r k m r k m N m −−=−−−≈++−−∑。
