离散数学代数系统的基本概念
- 格式:ppt
- 大小:2.41 MB
- 文档页数:24


![离散数学ch10[2]代数系统](https://uimg.taocdn.com/373a5b1ca300a6c30c229f57.webp)




第三篇代数系统篇第3-1章代数结构本章将从引入一般代数系统出发,研究如群、环、域等这样一些代数系统,而这些代数系统中的运算所具有的性质确定了这些代数系统的数学结构。
§3-1-1 代数系统的概念在计算机科学中,常用代数系统去描述机器可计算函数,研究运算的复杂性,分析程序设计语言的语义等。
由非空集合和该集合上的一个或多个运算所组合的系统,常称为代数系统,有时简称为代数。
在研究代数系统之前,首先考察一个非空集合上运算的概念,如将有理数集合Q上的每一个数 a 的映射成它的整数部分[a];或者将Q上的每一个数a 映射成它的相反数-a,这两个映射可以称为集合Q上的一元运算;而在集合Q上,对任意两个数所进行的普通加法和乘法都是集合Q上的二元运算,也可以,x2 ,x3,看作是将Q中的每两个数映射成一个数;至于对集合Q上的任意三个数x1代数式x12+x22+x32和x1+x2+x3分别给出了Q上的两个三元运算,它们分别将Q中三个数映射成Q中的一个数。
上述这些例子有一个共同的特征,那就是其运算的结果都是在原来的集合中,我们称那些具有这种特征的运算是封闭的,简称闭运算。
相反地,没有这种特征的运算就是不封闭的。
很容易举出不封闭运算的例子,设N是自然数集,Z是整数集,普通的减法是N×N到Z的运算,但因为两个自然数相减可以不是自然数,所以减法运算不是自然数集N上的闭运算。
定义3-1-1.1设A和B都是非空集合,n是一个正整数,若Φ是A n到B的一个映射,则称Φ是A到B的一个n元运算。
当B=A时,称Φ是A上的n元运算(n-ary operation),简称A上的运算。
并称该n元运算在A上是封闭的。
例3-1-1.1(1)求一个数的倒数是非零实数集R*上的一元运算。
(2)非零实数集R*上的乘法和除法都是R*上的二元运算,而加法和减法不是。
(3)S是一非空集合,S S是S到S上的所有函数的集合,则复合运算○是S S上的二元运算。



离散数学中代数系统知识点梳理离散数学作为一门数学学科,研究的是离散化的对象和结构。
代数系统作为离散数学的一个重要分支,是对数学对象的代数性质进行研究的一种形式化工具。
在离散数学中,代数系统的概念和相关知识点是非常重要的。
一、代数系统的基本概念代数系统是指由集合和一组运算构成的数学结构。
其中,集合是代数系统中最基本的概念,可以是有限集或无限集;运算是指对集合中的元素进行操作并得到新的元素。
代数系统主要包括代数结构、代数运算和代数性质三个方面。
1. 代数结构:代数结构由集合和一组运算构成,可以包括加法、减法、乘法、除法等。
常见的代数结构有群、环、域等。
2. 代数运算:代数运算是指对集合中的元素进行操作,可以是二元运算也可以是多元运算。
常见的代数运算有加法、乘法、幂运算等。
3. 代数性质:代数系统具有一些特定的性质,如封闭性、结合律、交换律、单位元素、逆元素等。
二、代数系统的分类根据代数运算的性质,代数系统可以分为群、环、域和向量空间等不同类型。
1. 群:群是一种代数系统,具有封闭性、结合律、单位元素和逆元素等性质。
群分为有限群和无限群,可以是交换群或非交换群。
2. 环:环是一种代数系统,具有封闭性、结合律、交换律和单位元素等性质。
环分为有限环和无限环,可以是可除环或非可除环。
3. 域:域是一种代数系统,具有封闭性、结合律、交换律、单位元素、逆元素和分配律等性质。
域是一种完备的代数系统,可以进行加、减、乘、除运算。
4. 向量空间:向量空间是一种代数系统,具有封闭性、结合律、交换律、单位元素、逆元素和分配律等性质。
向量空间是一种具有线性结构的代数系统。
三、代数系统的应用代数系统作为离散数学的一个重要分支,在计算机科学、密码学、通信工程等领域有着广泛的应用。
1. 计算机科学:代数系统在计算机科学中起到重要的作用,比如在数据库设计、编译原理、算法设计等方面都有应用。
代数系统可以描述和分析计算机系统的运行和性能。
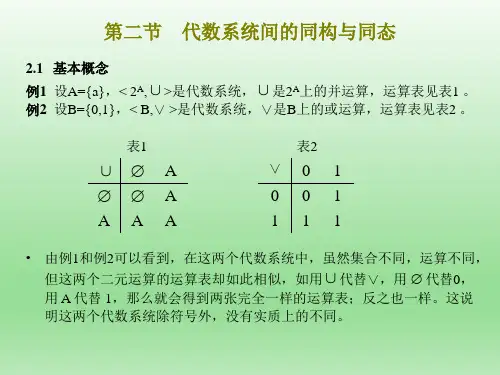
离散数学代数系统总结离散数学是数学的一个分支,主要研究离散对象和离散结构。
而代数系统是离散数学的一个重要分支,它研究的是一类具有特定性质的运算集合。
在这篇文章中,我们将从代数系统的基本概念、性质和应用几个方面对离散数学中的代数系统进行总结。
一、代数系统的基本概念代数系统是指一个非空集合A,以及在这个集合上定义的一个或多个运算。
根据运算的性质,代数系统可以分为不同的类型,包括群、环、域等。
其中,群是最基本的代数系统,它具有封闭性、结合律、单位元、逆元等性质。
环则在群的基础上增加了乘法运算,并满足了分配律。
域是环的一种扩充,它除了满足环的性质外,还具有乘法逆元。
二、代数系统的性质1. 封闭性:代数系统中的运算结果仍属于该系统,即对于任意a、b∈A,a运算b的结果仍然属于A。
2. 结合律:对于代数系统中的任意元素a、b、c,(a运算b)运算c 与a运算(b运算c)的结果相同。
3. 单位元:代数系统中存在一个元素e,对于任意元素a,a运算e与e运算a的结果均为a。
4. 逆元:代数系统中的每个元素a都存在一个逆元,使得a运算它的逆元等于单位元。
5. 交换律:对于代数系统中的任意元素a、b,a运算b与b运算a 的结果相同。
这些性质是代数系统的基本特征,不同类型的代数系统在这些性质上有所区别,比如群具有结合律和单位元,但不一定满足交换律。
三、代数系统的应用代数系统在数学及其他学科中有着广泛的应用。
以下是几个代数系统应用的例子:1. 编码理论:代数系统的运算可以用于编码和解码信息,例如循环冗余校验码(CRC)就是通过代数系统中的运算实现数据校验。
2. 密码学:代数系统中的数学运算被广泛应用于密码学中,用于加密和解密信息,保护数据的安全。
3. 图论:代数系统的概念和性质在图论中有着重要的应用,例如邻接矩阵和关联矩阵可以用于描述和分析图的结构和特性。
4. 计算机科学:代数系统在计算机科学中有着广泛的应用,例如布尔代数在逻辑电路设计和逻辑编程中的应用。