数学初中竞赛《三角形的五心》专题训练(包含答案)

有关三角形五心的经典试题三角形的外心、重心、垂心、内心及旁心，统称为三角形的五心. 一、外心.三角形外接圆的圆心，简称外心.与外心关系密切的有圆心角定理和圆周角定理. 例1．过等腰△ABC 底边BC 上一点P 引PM ∥CA 交AB 于M ；引PN ∥BA 交AC 于N .作点P 关于MN 的对称点P ′.试证：P ′点在△ABC 外接圆上. (杭州大学《中学数学竞赛习题》)分析：由已知可得MP ′=MP =MB ，NP ′=NP=NC ，故点M 是△P ′BP 的外心，点N 是△P ′PC 的外心.有∠BP ′P =21∠BMP =21∠BAC ，∠PP ′C =21∠PNC =21∠BAC . ∴∠BP ′C =∠BP ′P +∠P ′PC =∠BAC .从而，P ′点与A ，B ，C 共圆、即P ′在△ABC 外接圆上. 由于P ′P 平分∠BP ′C ，显然还有 P ′B :P ′C =BP :PC .例2．在△ABC 的边AB ，BC ，CA 上分别取点P ，Q ，S .证明以△APS ，△BQP ，△CSQ 的外心为顶点的三角形与△ABC 相似.(B ·波拉索洛夫《中学数学奥林匹克》)分析：设O 1，O 2，O 3是△APS ，△BQP ，△CSQ 的外心，作出六边形O 1PO 2QO 3S 后再由外心性质可知 ∠PO 1S =2∠A ， ∠QO 2P =2∠B ， ∠SO 3Q =2∠C .∴∠PO 1S +∠QO 2P +∠SO 3Q =360°.从而又知∠O 1PO 2+∠O 2QO 3+∠O 3SO 1=360°将△O 2QO 3绕着O 3点旋转到△KSO 3，易判断△KSO 1≌△O 2PO 1，同时可得△O 1O 2O 3≌△O 1KO 3. ∴∠O 2O 1O 3=∠KO 1O 3=21∠O 2O 1K =21(∠O 2O 1S +∠SO 1K ) =21(∠O 2O 1S +∠PO 1O 2) A B C PP M N 'A B C QK P O O O ....S 123=21∠PO 1S =∠A ； 同理有∠O 1O 2O 3=∠B .故△O 1O 2O 3∽△ABC . 二、重心三角形三条中线的交点，叫做三角形的重心.掌握重心将每 条中线都分成定比2:1及中线长度公式，便于解题.例3．AD ，BE ，CF 是△ABC 的三条中线，P 是任意一点.证明：在△PAD ，△PBE ，△PCF 中，其中一个面积等于另外两个面积的和. (第26届莫斯科数学奥林匹克)分析：设G 为△ABC 重心，直线PG 与AB，BC 相交.从A ，C ，D ，E ，F 分别 作该直线的垂线，垂足为A ′，C ′， D ′，E ′，F ′. 易证AA ′=2DD ′，CC ′=2FF ′，2EE ′=AA ′+CC ′，∴EE ′=DD ′+FF ′. 有S △PGE =S △PGD +S △PGF .两边各扩大3倍，有S △PBE =S △PAD +S △PCF .例4．如果三角形三边的平方成等差数列，那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.分析：将△ABC 简记为△，由三中线AD ，BE ，CF 围成的三角形简记为△′.G 为重心，连DE到H ，使EH =DE ，连HC ，HF ，则△′就是△HCF .(1)a 2，b 2，c 2成等差数列⇒△∽△′. 若△ABC 为正三角形，易证△∽△′. 不妨设a ≥b ≥c ，有 CF =2222221c b a -+， BE =2222221b ac -+， AD =2222221a cb -+. 将a 2+c 2=2b 2，分别代入以上三式，得 CF =a 23，BE =b 23，AD =c 23. ∴CF :BE :AD =a 23:b 23:c 23=a :b :c .故有△∽△′.(2)△∽△′⇒a 2，b 2，c 2成等差数列.AA 'F F 'GE E 'D 'C 'P C B D当△中a ≥b ≥c 时， △′中CF ≥BE ≥AD . ∵△∽△′， ∴∆∆S S '＝(aCF )2. 据“三角形的三条中线围成的新三角形面积等于原三角形面积的43”，有∆∆S S '=43.∴22aCF =43⇒3a 2=4CF 2=2a 2+b 2-c2⇒a 2+c 2=2b 2.三、垂心三角形三条高的交战，称为三角形的垂心.由三角形的垂心造成的四个等(外接)圆三角形，给我们解题提供了极大的便利.例5．设A 1A 2A 3A 4为⊙O 内接四边形，H 1，H 2，H 3，H 4依次为△A 2A 3A 4，△A 3A 4A 1，△A 4A 1A 2，△A 1A 2A 3的垂心.求证：H 1，H 2，H 3，H 4四点共圆，并确定出该圆的圆心位置.(1992，全国高中联赛) 分析：连接A 2H 1，A 1H 2，H 1H 2，记圆半径为R .由△A 2A 3A 4知13212sin H A A H A ∠=2R ⇒A 2H 1=2R cos ∠A 3A 2A 4； 由△A 1A 3A 4得A 1H 2=2R cos ∠A 3A 1A 4.但∠A 3A 2A 4=∠A 3A 1A 4，故A 2H 1=A 1H 2. 易证A 2H 1∥A 1A 2，于是，A 2H 1 A 1H 2， 故得H 1H 2 A 2A 1.设H 1A 1与H 2A 2的交点为M ，故H 1H 2与A 1A 2关于M 点成中心对称. 同理，H 2H 3与A 2A 3，H 3H 4与A 3A 4，H 4H 1与A 4A 1都关于M 点成中心对称.故四边形H 1H 2H 3H 4与四边形A 1A 2A 3A 4关于M 点成中心对称，两者是全等四边形，H 1，H 2，H 3，H 4在同一个圆上.后者的圆心设为Q ，Q 与O 也关于M 成中心对称.由O ，M 两点，Q 点就不难确定了.例6．H 为△ABC 的垂心，D ，E ，F 分别是BC ，CA ，AB 的中心.一个以H 为圆心的⊙H 交直线EF ，FD ，DE 于A 1，A 2，B 1，B 2，C 1，C 2. 求证：AA 1=AA 2=BB 1=BB 2=CC 1=CC 2.(1989，加拿大数学奥林匹克训练题) 分析：只须证明AA 1=BB 1=CC 1即可.设 BC =a ， CA =b ，AB =c ，△ABC 外接圆半径为R ，⊙H 的半径为r . 连HA 1，AH 交EF 于M . A 21A =AM 2+A 1M 2=AM 2+r 2-MH2∥=∥=.OA A A A 1234H H 12H H HM AB BA ABC CC F12111222D E=r 2+(AM 2-MH 2)， ①又AM 2-HM 2=(21AH 1)2-(AH -21AH 1)2 =AH ·AH 1-AH 2=AH 2·AB -AH 2=cos A ·bc -AH 2， ② 而ABHAH ∠sin =2R ⇒AH 2=4R 2cos 2A ,Aa sin =2R ⇒a 2=4R 2sin 2A . ∴AH 2+a 2=4R 2，AH 2=4R 2-a 2. ③ 由①、②、③有A 21A =r 2+bca cb 2222-+·bc -(4R 2-a 2)=21(a 2+b 2+c 2)-4R 2+r 2. 同理，21BB =21(a 2+b 2+c 2)-4R 2+r 2， 21CC =21(a 2+b 2+c 2)-4R 2+r 2. 故有AA 1=BB 1=CC 1.四、内心三角形内切圆的圆心，简称为内心.对于内心，要掌握张角公式，还要记住下面一个极为有用的等量关系：设I 为△ABC 的内心，射线AI 交△ABC 外接圆于A ′，则有A ′I =A ′B =A ′C .换言之，点A ′必是△IBC 之外心(内心的等量关系之逆同样有用).例7．ABCD 为圆内接凸四边形，取△DAB ，△ABC ，△BCD ， △CDA 的内心O 1， O 2，O 3， O 4.求证：O 1O 2O 3O 4为矩形.(1986，中国数学奥林匹克集训题)证明见《中等数学》1992；4例8．已知⊙O 内接△ABC ，⊙Q 切AB ，AC 于E ，F 且与⊙O 内切.试证：EF 中点P 是△ABC之内心.(B ·波拉索洛夫《中学数学奥林匹克》)分析：在第20届IMO 中，美国提供的一道题实际上是例8的一种特例，但它增加了条件AB =AC .当AB ≠AC ，怎样证明呢？A B C D O O O 234O 1如图，显然EF 中点P 、圆心Q ，BC 中点K 都在∠BAC 平分线上.易知AQ =αsin r . ∵QK ·AQ =MQ ·QN ，∴QK =AQQNMQ ⋅=αsin /)2(r rr R ⋅-=)2(sin r R -⋅α.由Rt △EPQ 知PQ =r ⋅αsin .∴PK =PQ +QK =r ⋅αsin +)2(sin r R -⋅α=R 2sin ⋅α. ∴PK =BK .α利用内心等量关系之逆定理，即知P 是△ABC 这内心. 五、旁心三角形的一条内角平分线与另两个内角的外角平分线相交于 一点，是旁切圆的圆心，称为旁心.旁心常常与内心联系在一起， 旁心还与三角形的半周长关系密切.例9．在直角三角形中，求证：r +r a +r b +r c =2p .式中r ，r a ，r b ，r c 分别表示内切圆半径及与a ，b ，c 相切的旁切圆半径，p 表示半周. (杭州大学《中学数学竞赛习题》)分析：设Rt △ABC 中，c 为斜边，先来证明一个特性：p (p -c )=(p -a )(p -b ).∵p (p -c )=21(a +b +c )·21(a +b -c ) =41[(a +b )2-c 2]=21ab ； (p -a )(p -b )=21(-a +b +c )·21(a -b +c ) =41[c 2-(a -b )2]=21ab . ∴p (p -c )=(p -a )(p -b ). ①观察图形，可得 r a =AF -AC =p -b ， r b =BG -BC =p -a ，AααMBCK NE R OQFrP Kr r r r O O O 213AOE CBabcr c =CK =p .而r =21(a +b -c ) =p -c . ∴r +r a +r b +r c=(p -c )+(p -b )+(p -a )+p =4p -(a +b +c )=2p . 由①及图形易证.例10．M 是△ABC 边AB 上的任意一点.r 1，r 2，r 分别是△AMC ，△BMC ，△ABC 内切圆的半径，q 1，q 2，q 分别是上述三角形在∠ACB 内部的旁切圆半径.证明：11q r ·22q r =qr . (IMO -12)分析：对任意△A ′B ′C ′，由正弦定理可知OD =OA ′·2'sinA =A ′B ′·'''sin 2'sinB O A B ∠·2'sin A =A ′B ′·2''sin2'sin2'sin B A B A +⋅， O ′E = A ′B ′·2''sin2'cos2'cos B A B A +. ∴2'2''B tg A tg E O OD =. 亦即有11q r ·22q r =2222Btg CNB tg CMA tgA tg ∠∠ =22B tg A tg=qr. 六、众心共圆这有两种情况：(1)同一点却是不同三角形的不同的心；(2)同一图形出现了同一三角形的几个心.例11．设在圆内接凸六边形ABCDFE 中，AB =BC ，CD =DE ，EF =FA .试证：(1)AD ，BE ，CF 三条对角线交于一点；A ...'B 'C 'O O 'ED(2)AB +BC +CD +DE +EF +FA ≥AK +BE +CF . (1991，国家教委数学试验班招生试题)分析：连接AC ，CE ，EA ，由已知可证AD ，CF ，EB 是△ACE 的三条内角平分线，I 为△ACE的内心.从而有ID =CD =DE ， IF =EF =FA ， IB =AB =BC .再由△BDF ，易证BP ，DQ ，FS 是它的三条高，I 是它的垂心，利用 不等式有：BI +DI +FI ≥2·(IP +IQ +IS ).不难证明IE =2IP ，IA =2IQ ，IC =2IS .∴BI +DI +FI ≥IA +IE +IC . ∴AB +BC +CD +DE +EF +FA=2(BI +DI +FI ) ≥(IA +IE +IC )+(BI +DI +FI )=AD +BE +CF .I 就是一点两心.例12．△ABC 的外心为O ，AB =AC ，D 是AB 中点，E 是△ACD 的重心.证明OE 丄CD . (加拿大数学奥林匹克训练题)分析：设AM 为高亦为中线，取AC 中点F ，E 必在DF 上且DE :EF =2:1.设CD 交AM 于G ，G 必为△ABC 重心. 连GE ，MF ，MF 交DC 于K .易证： DG :GK =31DC :(3121-)DC =2:1. ∴DG :GK =DE :EF ⇒GE ∥MF . ∵OD 丄AB ，MF ∥AB ，∴OD 丄MF ⇒OD 丄GE .但OG 丄DE ⇒G 又是△ODE 之垂心. 易证OE 丄CD . 例13．△ABC 中∠C =30°，O 是外心，I 是内心，边AC 上的D 点与边BC 上的E 点使得AD =BE =AB .求证：OI 丄DE ，OI =DE .(1988，中国数学奥林匹克集训题)分析：辅助线如图所示，作∠DAO 平分线交BC 于K . 易证△AID ≌△AIB ≌△EIB ，∠AID =∠AIB =∠EIB . 利用内心张角公式，有∠AIB =90°+21∠C =105°，∴∠DIE =360°-105°×3=45°. ∵∠AKB =30°+21∠DAO =30°+21(∠BAC -∠BAO ) Erdos ..I P AB CD E FQ SA B CD E F OKGO A BC DEFI K30°=30°+21(∠BAC -60°) =21∠BAC =∠BAI =∠BEI . ∴AK ∥IE .由等腰△AOD 可知DO 丄AK ，∴DO 丄IE ，即DF 是△DIE 的一条高. 同理EO 是△DIE 之垂心，OI 丄DE . 由∠DIE =∠IDO ，易知OI =DE .例14．锐角△ABC 中，O ，G ，H 分别是外心、重心、垂心.设外心到三边距离和为d 外，重心到三边距离和为d 重，垂心到三边距离和为d 垂.求证：1·d 垂+2·d 外=3·d 重. 分析：这里用三角法.设△ABC 外接圆半径为1，三个内角记为A ，B ， C . 易知d 外=OO 1+OO 2+OO 3 =cos A +co sB +cos C ，∴2d 外=2(cos A +cos B +cos C ). ① ∵AH 1=sin B ·AB =sin B ·(2sin C )=2sin B ·sin C ， 同样可得BH 2·CH 3.∴3d 重=△ABC 三条高的和=2·(sin B ·sin C +sin C ·sin A +sin A ·sin B ) ② ∴BCHBHsin =2，∴HH 1=cos C ·BH =2·cos B ·cos C . 同样可得HH 2，HH 3. ∴d 垂=HH 1+HH 2+HH 3=2(cos B ·cos C +cos C ·cos A +cos A ·cos B ) ③ 欲证结论，观察①、②、③，须证(cos B ·cos C +cos C ·cos A +cos A ·cos B )+( cos A + cos B + cos C )=sin B ·sin C +sin C ·sin A +sin A ·sin B .即可.练 习 题1.I 为△ABC 之内心，射线AI ，BI ，CI 交△ABC 外接圆于A ′， B ′，C ′.则AA ′+BB ′+CC ′＞△ABC 周长.(1982，澳大利 亚数学奥林匹克)2.△T ′的三边分别等于△T 的三条中线，且两个三角形有一组角相等.求证这两个三角形相似.(1989，捷克数学奥林匹克)3.I 为△ABC 的内心.取△IBC ，△ICA ，△IAB 的外心O 1，O 2，O 3.求证：△O 1O 2O 3与△ABC 有公共的外心.(1988，美国数学奥林匹克)4.AD 为△ABC 内角平分线.取△ABC ，△ABD ，△ADC 的外心O ，O 1，O 2.则△OO 1O 2是等腰三角B C O IA O G H O G H GO G H 123112233。

初中数学，三⾓形五⼼，必刷题集（含答案），中考⾃招拉分项快收藏！！！这么好的汇总资料不多得！
初中⼏何，三⾓形五⼼会和圆的知识点结合起来，所以难度会相对较⾼
在中考压轴题、⾃主招⽣命题中常考
所以向来是兵家必争之地！
三⾓形五⼼主要有：
①重⼼：三条中线的交点
②内⼼：三条⾓平分线交点
③外⼼：三边垂直平分线交点
④垂⼼：三条⾼交点
⑤旁⼼：旁切圆圆形
性质繁多，这⾥就不⼀⼀列举
今天给⼤家分享，《三⾓形五⼼经典题集》含答案，
让各位初中同学提前了解考题类型、知识点分布
助⼒娃娃们学的轻松，学的精通。

⽂档页数较多，如若照⽚模糊，可通过以下途径获得电⼦档：
①加关注，转发、点赞本⽂，将爱⼼传递出去。

②评论区留⾔：五⼼
希望我的分享能给您的孩⼦带来帮助！等有效果了欢迎给我反馈，分享喜悦！。

三角形的“五心”一、选择题（每题5分，共30分）1锐角ABC ∆的三边分别是c b a ,,，它的外心到三边的距离分别为p n m ,,，则p n m ::等于（ ） A ．c b a ::B ．cb a 1:1:1 C ．C B A cos ::cos :cos D ．C B a sin ::sin :sin2．如图1，D 是ABC ∆的内心，E 是ABD ∆的内心，F 是BDE ∆的内心，若BFE ∠的度数为整数，则BFE ∠至少是（ ） A ．︒111B ．︒112C ．︒113D ．︒1143．已知ABC ∆的三条高相交于点H ，若AH=BC ，则BAC ∠的度数是（ ） A ．︒45B ，︒60C ．︒30或︒150D ．︒45或︒1354．在ABC ∆中，H 是ABC ∆的垂心，O 为ABC ∆的外心，AO=AH ，则BAC ∠的度数是（ ） A ．︒60B ．︒60或︒120C ．︒45D ．︒45或︒1355．一条直线平分三角形的周长和面积，那么该直线必须通过三角形的（ ） A ．重心B ．垂心C ．外心D ．内心6．已知H 、O 分别为ABC ∆的垂心和外心，OE ⊥BC 于E ，则OEAH的值为（ ） A ．31B ．21 C ．2D ．3二．填空题(每题5分,共30分)7．如图2所示，D 是ABC ∆的边BC 上的一点，E 、F 分别是ABD ∆和ACD ∆的重心，连EF 交AD 于G ，则AG DG= ．8．设ABC ∆的重心为G ，GA=32，GB=22，GC=2，则ABC ∆的面积为 ． 9．设ABC ∆的外接圆半径为R ，内切圆半径为r ，内心为I ，延长AI 交外接圆于D ，则A I ·ID= ．10．已知Rt ABC ∆斜边上的高CH=h ，则ABC ∆，HCA ∆，HCB ∆的内切圆半径之和=++321r r r ．C图2图3图111．若z y x ,,表示锐角ABC ∆的外心O 到三边的距离，R 、r 分别表示ABC ∆外接圆和内切圆的半径，试用R 和r 表示z y x ++= .12.如图3中所示,ABC ∆的外接圆为⊙O,︒=∠60C ,N 为 中点,H为垂心,由CN 与OH 的位置关系是 ．三．解答题：(每题10分,共40分)13．已知AD 是ABC ∆的角平分线，I 是线段AD 上的一点，且,2190BAC BIC ∠+︒=∠求证：I 是ABC ∆的内心．14．如图，设O 是锐角ABC ∆的外心，BE 、DF 是两条高，M 、N 分别为BC 、EF 中点.求证:OA ∥MN ．AB15.如图,等腰ABC ∆中，P 为底边BC 上任意一点，过P 作两腰的平分线分别与AB 、AC 相交于Q 、R 两点，又P '是P 关于直线RQ 的对称点，证明：QB P '∆∽RC P '∆．16．如图，已知点P 在半径为6，圆心角为︒90的扇形OAB 的 （不含端点）上运动．PH ⊥OA ，垂足为H ，OPH∆的重心为G ．（1）当点P 在 上运动时，线段GO 、GP 、GH 中有无长度保持不变的线段？如果有，请指出并求其相应的长度；（2）设PH=x ，GP=y ，求y 关于x 的函数解析式，并写出自变量x 的取值范围；（3）如果PGH ∆是等腰三角形，试求出线段PH 的线．AB BAPG EH OAB。

数学竞赛：三角形的五心三角形的外心、重心、垂心、内心及旁心，统称为三角形的五心. 一、外心.三角形外接圆的圆心，简称外心.与外心关系密切的有圆心角定理和圆周角定理.例1．过等腰△ABC 底边BC 上一点P 引PM ∥CA 交AB 于M ；引PN ∥BA 交AC 于N .作点P 关于MN 的对称点P ′.试证：P ′点在△ABC 外接圆上. 分析：由已知可得MP ′=MP =MB ，NP ′=NP=NC ，故点M 是△P ′BP 的外心，点 N 是△P ′PC 的外心.有∠BP ′P =21∠BMP =21∠BAC ，∠PP ′C =21∠PNC =21∠BAC .∴∠BP ′C =∠BP ′P +∠P ′PC =∠BAC .从而，P ′点与A ，B ，C 共圆、即P ′在△ABC 外接圆上. 由于P ′P 平分∠BP ′C ，显然还有 P ′B :P ′C =BP :PC .例2．在△ABC 的边AB ，BC ，CA 上分别取点P ，Q ，S .证明以△APS ，△BQP ，△CSQ 的外心为顶点的三角形与△ABC 相似. 分析：设O 1，O 2，O 3是△APS ，△BQP ，△CSQ 的外心，作出六边形 O 1PO 2QO 3S 后再由外 心性质可知 ∠PO 1S =2∠A ， ∠QO 2P =2∠B ， ∠SO 3Q =2∠C .∴∠PO 1S +∠QO 2P +∠SO 3Q =360°.从而又知∠O 1PO 2+∠O 2QO 3+∠O 3SO 1=360°将△O 2QO 3绕着O 3点旋转到△KSO 3，易判断△KSO 1≌△O 2PO 1，同时可得△O 1O 2O 3≌△O 1KO 3.∴∠O 2O 1O 3=∠KO 1O 3=21∠O 2O 1K=21(∠O 2O 1S +∠SO 1K )=21(∠O 2O 1S +∠PO 1O 2)=21∠PO 1S =∠A ；同理有∠O 1O 2O 3=∠B .故△O 1O 2O 3∽△ABC . 二、重心三角形三条中线的交点，叫做三角形的重心.掌握重心将每条中线都分成定比2:1及中线长度公式，便于解题.例3．AD ，BE ，CF 是△ABC 的三条中线，P 是任意一点.证明：在△PAD ，△PBE ，△PCF 中，其中一个面积等于另外两个面积的和.分析：设G 为△ABC 重心，直线PG 与AB，BC 相交.从A ，C ，D ，E ，F 分别 作该直线的垂线，垂足为A ′，C ′， D ′，E ′，F ′. 易证AA ′=2DD ′，CC ′=2FF ′，2EE ′=AA ′+CC ′， ∴EE ′=DD ′+FF ′. 有S △PGE =S △PGD +S △PGF .两边各扩大3倍，有S △PBE =S △PAD +S △PCF .例4．如果三角形三边的平方成等差数列，那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.分析：将△ABC 简记为△，由三中线AD ，BE ，CF 围成的三角形简记为△′.G为重心，连DE 到H ，使EH =DE ，连HC ，HF ，则△′就是△HCF . (1)a 2，b 2，c 2成等差数列⇒△∽△′. 若△ABC 为正三角形，易证△∽△′. 不妨设a ≥b ≥c ，有CF =2222221c b a -+，BE =2222221b ac -+，AD =2222221a cb -+.将a 2+c 2=2b 2，分别代入以上三式，得 CF =a 23，BE =b 23，AD =c 23. ∴CF :BE :AD =a 23:b 23:c 23=a :b :c .故有△∽△′.(2)△∽△′⇒a 2，b 2，c 2成等差数列. 当△中a ≥b ≥c 时， △′中CF ≥BE ≥AD . ∵△∽△′，∴∆∆S S '＝(aCF )2.据“三角形的三条中线围成的新三角形面积等于原三角形面积的43”，有AA 'F F 'GE E 'D 'C 'P C B D∆∆S S '=43. ∴22aCF =43⇒3a 2=4CF 2=2a 2+b 2-c 2⇒a 2+c 2=2b 2.三、垂心三角形三条高的交战，称为三角形的垂心.由三角形的垂心造成的四个等(外接)圆三角形，给我们解题提供了极大的便利.例5．设A 1A 2A 3A 4为⊙O 内接四边形，H 1，H 2，H 3，H 4依次为△A 2A 3A 4，△A 3A 4A 1，△A 4A 1A 2，△A 1A 2A 3的垂心.求证：H 1，H 2，H 3，H 4四点共圆，并确定出该圆的圆心位置. 分析：连接A 2H 1，A 1H 2，H 1H 2，记圆半径为R .由△A 2A 3A 4知13212sin H A A H A ∠=2R ⇒A 2H 1=2R cos ∠A 3A 2A 4；由△A 1A 3A 4得A 1H 2=2R cos ∠A 3A 1A 4.但∠A 3A 2A 4=∠A 3A 1A 4，故A 2H 1=A 1H 2. 易证A 2H 1∥A 1A 2，于是，A 2H 1 A 1H 2， 故得H 1H 2 A 2A 1.设H 1A 1与H 2A 2的交点为M ，故H 1H 2与A 1A 2关于M 点成中心对称. 同理，H 2H 3与A 2A 3，H 3H 4与A 3A 4，H 4H 1与A 4A 1都关于M 点成中心对称.故四边形H 1H 2H 3H 4与四边形A 1A 2A 3A 4关于M 点成中心对称，两者是全等四边形，H 1，H 2，H 3，H 4在同一个圆上.后者的圆心设为Q ，Q 与O 也关于M 成中心对称.由O ，M 两点，Q 点就不难确定了.例6．H 为△ABC 的垂心，D ，E ，F 分别是BC ，CA ，AB 的中心.一个以H 为圆心的⊙H 交直线EF ，FD ，DE 于A 1，A 2，B 1，B 2，C 1，C 2. 求证：AA 1=AA 2=BB 1=BB 2=CC 1=CC 2. 分析：只须证明AA 1=BB 1=CC 1即可.设 BC =a ， CA =b ，AB =c ，△ABC 外 接圆半径为R ，⊙H 的半径为r .连HA 1，AH 交EF 于M . A 21A =AM 2+A 1M 2=AM 2+r 2-MH2=r 2+(AM 2-MH 2)， ①又AM 2-HM 2=(21AH 1)2-(AH -21AH 1)2=AH ·AH 1-AH 2=AH 2·AB -AH 2=cos A ·bc -AH 2， ②而ABHAH∠sin =2R ⇒AH 2=4R 2cos 2A ,∥=∥=H H HM AB BA ABC C C F 12111222DEAasin =2R ⇒a 2=4R 2sin 2A . ∴AH 2+a 2=4R 2，AH 2=4R 2-a 2. ③ 由①、②、③有A 21A =r 2+bca cb 2222-+·bc -(4R 2-a 2)=21(a 2+b 2+c 2)-4R 2+r 2. 同理，21BB =21(a 2+b 2+c 2)-4R 2+r 2，21CC =21(a 2+b 2+c 2)-4R 2+r 2.故有AA 1=BB 1=CC 1. 四、内心三角形内切圆的圆心，简称为内心.对于内心，要掌握张角公式，还要记住下面一个极为有用的等量关系：设I 为△ABC 的内心，射线AI 交△ABC 外接圆于A ′，则有A ′I =A ′B =A ′C .换言之，点A ′必是△IBC 之外心(内心的等量关系之逆同样有用).例7．ABCD 为圆内接凸四边形，取△DAB ，△ABC ，△BCD ， △CDA 的内心O 1， O 2，O 3， O 4.求证：O 1O 2O 3O 4为矩形.(1986，中国数学奥林匹克集训题)证明见《中等数学》1992；4例8．已知⊙O 内接△ABC ，⊙Q 切AB ，AC 于E ，F 且与⊙O 内切.试证：EF中点P 是△ABC 之内心.分析：在第20届IMO 中，美国提供的一道题实际上是例8的一种特例，但它增加了条件AB =AC .当AB ≠AC ，怎样证明呢？如图，显然EF 中点P 、圆心Q ，BC 中点K 都在∠BAC 平分线上.易知AQ =αsin r .∵QK ·AQ =MQ ·QN ，∴QK =AQQNMQ ⋅=αsin /)2(r rr R ⋅-=)2(sin r R -⋅α.由Rt △EPQ 知PQ =r ⋅αsin .∴PK =PQ +QK =r ⋅αsin +)2(sin r R -⋅α=R 2sin ⋅α. ∴PK =BK .α利用内心等量关系之逆定理，即知P 是△ABC 这内心.A B C D O O O 234O1A ααMBCKNER OQF rP五、旁心三角形的一条内角平分线与另两个内角的外角平分线相交于 一点，是旁切圆的圆心，称为旁心.旁心常常与内心联系在一起， 旁心还与三角形的半周长关系密切.例9．在直角三角形中，求证：r +r a +r b +r c =2p .式中r ，r a ，r b ，r c 分别表示内切圆半径及与a ，b ，c 相切的旁切圆半径，p 表示半周.分析：设Rt △ABC 中，c 为斜边，先来证明一个特性：p (p -c )=(p -a )(p -b ).∵p (p -c )=21(a +b +c )·21(a +b -c ) =41[(a +b )2-c 2]=21ab ； (p -a )(p -b )=21(-a +b +c )·21(a -b +c )=41[c 2-(a -b )2]=21ab .∴p (p -c )=(p -a )(p -b ). ① 观察图形，可得 r a =AF -AC =p -b ， r b =BG -BC =p -a ， r c =CK =p .而r =21(a +b -c )=p -c . ∴r +r a +r b +r c=(p -c )+(p -b )+(p -a )+p =4p -(a +b +c )=2p . 由①及图形易证.例10．M 是△ABC 边AB 上的任意一点.r 1，r 2，r 分别是△AMC ，△BMC ，△ABC 内切圆的半径，q 1，q 2，q 分别是上述三角形在∠ACB 内部的旁切圆半径.证明：11q r ·22q r =qr . (IMO -12)分析：对任意△A ′B ′C ′，由正弦定理可知OD =OA ′·2'sin A=A ′B ′·'''sin 2'sinB O A B ·2'sin A Kr r r r O O O 213A O E CB a b c A ...'B 'C 'OO 'ED=A ′B ′·2''sin2'sin 2'sinB A B A +⋅， O ′E = A ′B ′·2''sin2'cos2'cos B A B A +. ∴2'2''B tg A tg E O OD =. 亦即有11q r ·22q r =2222B tg CNB tg CMA tg A tg ∠∠ =22B tg A tg=qr. 六、众心共圆这有两种情况：(1)同一点却是不同三角形的不同的心；(2)同一图形出现了同一三角形的几个心. 例11．设在圆内接凸六边形ABCDFE 中，AB =BC ，CD =DE ，EF =FA .试证：(1)AD ，BE ，CF 三条对角线交于一点；(2)AB +BC +CD +DE +EF +FA ≥AK +BE +CF .分析：连接AC ，CE ，EA ，由已知可证AD ，CF ，EB 是△ACE 的三条内角平分线，I 为△ACE 的内心.从而有ID =CD =DE ， IF =EF =FA ， IB =AB =BC . 再由△BDF ，易证BP ，DQ ，FS 是它的三条高，I 是它的垂心，利用 不等式有： BI +DI +FI ≥2·(IP +IQ +IS ).不难证明IE =2IP ，IA =2IQ ，IC =2IS . ∴BI +DI +FI ≥IA +IE +IC .∴AB +BC +CD +DE +EF +FA =2(BI +DI +FI )≥(IA +IE +IC )+(BI +DI +FI ) =AD +BE +CF . I 就是一点两心.例12．△ABC 的外心为O ，AB =AC ，D 是AB 中点，E 是△ACD 的重心.证明OE 丄CD .分析：设AM 为高亦为中线，取AC 中点F ，E 必在DF 上且DE :EF =2:1.设CD 交AM 于G ，G 必为△ABC 重心. 连GE ，MF ，MF 交DC 于K .易证： Erdos..I P ABCD E FQSA BCD E F OKGDG :GK =31DC :(3121-)DC =2:1.∴DG :GK =DE :EF ⇒GE ∥MF . ∵OD 丄AB ，MF ∥AB ，∴OD 丄MF ⇒OD 丄GE .但OG 丄DE ⇒G 又是△ODE 之垂心. 易证OE 丄CD .例13．△ABC 中∠C =30°，O 是外心，I 是内心，边AC 上的D 点与边BC 上的E 点使得AD =BE =AB .求证：OI 丄DE ，OI =DE .分析：辅助线如图所示，作∠DAO 平分线交BC 于K . 易证△AID ≌△AIB ≌△EIB ，∠AID =∠AIB =∠EIB . 利用内心张角公式，有∠AIB =90°+21∠C =105°，∴∠DIE =360°-105°×3=45°.∵∠AKB =30°+21∠DAO=30°+21(∠BAC -∠BAO )=30°+21(∠BAC -60°)=21∠BAC =∠BAI =∠BEI .∴AK ∥IE .由等腰△AOD 可知DO 丄AK ，∴DO 丄IE ，即DF 是△DIE 的一条高. 同理EO 是△DIE 之垂心，OI 丄DE . 由∠DIE =∠IDO ，易知OI =DE .例14．锐角△ABC 中，O ，G ，H 分别是外心、重心、垂心.设外心到三边距离和为d 外，重心到三边距 离和为d 重，垂心到三边距离和为d 垂.求证：1·d 垂+2·d 外=3·d 重. 分析：这里用三角法.设△ABC 外接圆半径为1，三个内角记为A ，B ， C . 易知d 外=OO 1+OO 2+OO 3 =cos A +co sB +cos C ，∴2d 外=2(cos A +cos B +cos C ). ① ∵AH 1=sin B ·AB =sin B ·(2sin C )=2sin B ·sin C ， 同样可得BH 2·CH 3.∴3d 重=△ABC 三条高的和=2·(sin B ·sin C +sin C ·sin A +sin A ·sin B ) ②∴BCHBH∠sin =2，O A BC DEF I K30°B C O IA O G H O G H GO G H 123112233∴HH 1=cos C ·BH =2·cos B ·cos C . 同样可得HH 2，HH 3. ∴d 垂=HH 1+HH 2+HH 3=2(cos B ·cos C +cos C ·cos A +cos A ·cos B ) ③ 欲证结论，观察①、②、③，须证(cos B ·cos C +cos C ·cos A +cos A ·cos B )+( cos A + cos B + cos C )=sin B ·sin C +sin C ·sin A +sin A ·sin B .即可.练 习 题1.I 为△ABC 之内心，射线AI ，BI ，CI 交△ABC 外接圆于A ′， B ′，C ′.则AA ′+BB ′+CC ′＞△ABC 周长.2.△T ′的三边分别等于△T 的三条中线，且两个三角形有一组角相等.求证这两个三角形相似.3.I 为△ABC 的内心.取△IBC ，△ICA ，△IAB 的外心O 1，O 2，O 3.求证：△O 1O 2O 3与△ABC 有公共的外心.(4.AD 为△ABC 内角平分线.取△ABC ，△ABD ，△ADC 的外心O ，O 1，O 2.则△OO 1O 2是等腰三角形.5.△ABC 中∠C ＜90°，从AB 上M 点作CA ，CB 的垂线MP ，MQ .H 是△CPQ 的垂心.当M 是AB 上动点时，求H 的轨迹.(IMO -7)6.△ABC 的边BC =21(AB +AC )，取AB ，AC 中点M ，N ，G 为重心，I 为内心.试证：过A ，M ，N 三点的圆与直线GI 相切.7.锐角△ABC 的垂心关于三边的对称点分别是H 1，H 2，H 3.已知：H 1，H 2，H 3，求作△ABC .8.已知△ABC 的三个旁心为I 1，I 2，I 3.求证：△I 1I 2I 3是锐角三角形.9.AB ，AC 切⊙O 于B ，C ，过OA 与BC 的交点M 任作⊙O 的弦EF .求证：(1)△AEF 与△ABC 有公共的内心；(2)△AEF 与△ABC 有一个旁心重合.。

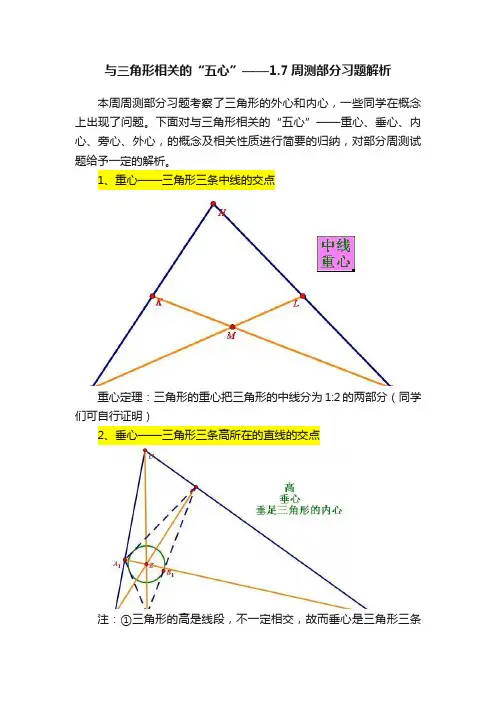
与三角形相关的“五心”——1.7周测部分习题解析本周周测部分习题考察了三角形的外心和内心，一些同学在概念上出现了问题。

下面对与三角形相关的“五心”——重心、垂心、内心、旁心、外心，的概念及相关性质进行简要的归纳，对部分周测试题给予一定的解析。

1、重心——三角形三条中线的交点重心定理：三角形的重心把三角形的中线分为1:2的两部分（同学们可自行证明）2、垂心——三角形三条高所在的直线的交点注：①三角形的高是线段，不一定相交，故而垂心是三角形三条高所在直线的交点。

锐角三角形的垂心在三角形内部，直角三角形的垂心是直角顶点，钝角三角形的垂心在三角形外部。

②上图给出了垂心的另一种定义方式，即三角形三个垂足构成的三角形内切圆的圆心，有兴趣的同学可以研究下。

3、内心——三角形内角平分线的交点（三角形内切圆的圆心）三角形的内心到三角形三边的距离相等。

4、旁心——三角形两外角平分线的交点注：①三角形的旁心有三个，到三角形三边的距离都相等；②三角形的旁心同时也在剩余的三角形内角的角平分线上；③如上图所示，与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆，旁切圆的圆心也就是三角形的旁心。

5、外心——三角形三边垂直平分线的交点（三角形外接圆的圆心）三角形的外心到三角形三个顶点的距离相等。

特别地，正三角形（等边三角形）的四心（重心、垂心、内心、外心）共点（同一个点），五心共线（与旁心在同一条直线上），我们称共点的四心为其中心。

中心的概念仅在正多边形中提起。

复习完三角形的“五心”，我们来看这周周测的两道小题。

明确了概念其实很容易求解。

7、△ABC的外心为O，∠BOC=80°，则∠BAC=（）A、40°B、100°C、40°或140°D、40°或100°分析：既然涉及到外心，就与三角形的外接圆结合起来，运用圆周角定理。

此题由于点A位置的不确定性，其实就是解决一条弦所对的圆周角的问题，度数上有两个，且为互补的关系，如图。

第 17 讲三角形的五心三角形中有很多重要的特别点，特别是三角形的“五心”，在解题时有好多应用，在本节中将分别赐予介绍．三角形的“五心”指的是三角形的外心，心里，重心，垂心和旁心．1、三角形的外心三角形的三条边的垂直均分线交于一点,这点称为三角形的外心(外接圆圆心 )．三角形的外心到三角形的三个极点距离相等．都等于三角形的外接圆半径．锐角三角形的外心在三角形内；直角三角形的外心在斜边中点；钝角三角形的外心在三角形外．2、三角形的心里三角形的三条内角均分线交于一点,这点称为三角形的心里( 内切圆圆心)．三角形的心里到三边的距离相等,都等于三角形内切圆半径．内切圆半径r 的计算：设三角形面积为S，并记1p=2(a+b+c)，则Sr =p．1特其余，在直角三角形中,有 r =2(a+b－ c)．3、三角形的重心三角形的三条中线交于一点,这点称为三角形的重心．上边的证明中，我们也获得了以下结论：三角形的重心到边的中点与到相应极点的距离之比为1∶ 2．4、三角形的垂心三角形的三条高交于一点,这点称为三角形的垂心．斜三角形的三个极点与垂心这四个点中，任何三个为极点的三角形的垂心就是第四个点．所以把这样的四个点称为一个“垂心组”．5、三角形的旁心三角形的一条内角均分线与另两个外角均分线交于一点,称为三角形的旁心(旁切圆圆心 )．每个三角形都有三个旁切圆．A类例题例 1 证明重心定理。

、 E、F 为三边中点，设BE、CF 交于 G，连结 EF，明显 EF∥1BC，由三角形 = 2 相像可得GB＝ 2GE， GC=2GF ．又设 AD、 BE 交于 G'，同理可证G'B=2G'E， G'A=2G'D，即 G、 G'都是 BE 上从 B 到 E 的三分之二处的点，故G'、 G 重合．即三条中线AD、 BE、 CF 订交于一点G．证法 2 设 BE、CF 交于 G， BG、 CG 中点为 H、 I．连 EF、FH 、HI 、 IE，∥1 ∥1由于EF= 2BC，HI = 2BC ，所以 EFHI 为平行四边形．所以 HG =GE、 IG=GF ， GB=2GE， GC=2GF ．同证法 1 可知 AG=2GD ， AD 、 BE、 CF 共点．即定理证毕．链接证明外心、心里定理是很简单的。

2020年初中数学竞赛讲义：三角形的五心一、重心 (1)二、垂心 (2)三、内心 (4)四、外心 (7)五、旁心 (9)第1 页共10 页第 1 页 共 10 页一、 重心1. （2007年全国初中数学联赛1试）设K 是ABC △内任意一点，KAB △、KBC △、KCA △的重心分别为D 、E 、F ，则:DEF ABC S S △△的值为（ ）A ．19B ．29C ．49D ．23【难度】 ★★【解析】A ， 分别延长KD 、KE 、KF ，与ABC △的三边AB 、BC 、CA 交于点M 、N 、P ，由于D 、E 、F 分别为KAB △、KBC △、KCA △的重心，易知M 、N 、P 分别为AB 、BC 、CA 的中点，所以14MNP ABC S S =△△．易证DEF △∽MNP △，且相似比为2:3， 所以22()3DEF MNP S S =△△4194ABC S =⋅△19ABC S =△．所以:DEF S △19ABC S =△．故选A ．2. （1998年全国初中数学联赛2试）已知P 为平行四边形ABCD 内一点，O 为AC与BD 的交点，M ，N 分别为PB ，PC 的中点，Q 为AN 与DM 的交点，求证： ⑴P ，Q ，O 三点在一条直线上； ⑵2PQ OQ =．【难度】 ★★★ 【解析】 证明：如图，连接PO ，设PO 与AN DM ，分别交于点Q '，Q ''．在PAC △中，∵AO OC PN NC ==，， ∴Q '为重心，2PQ OQ ''''=．这样Q Q '''=，并且Q Q '''，就是AN DM ，的交点Q ． 故P Q O ，，在一条直线上，且2PQ OQ =．3. （1992年全国初中数学联赛1试）若一等腰三角形的底边上的高等于18cm ，腰上的中线等15cm ，则这个等腰三角形的面积等于__________．N M Q PODCBAQ''Q'NMQPO DCBA。

向量三角形五心试题向量三角形的四心：（1）重心——中线的交点：重心将中线长度分成2：1；（2）垂心——高线的交点：高线与对应边垂直；（3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

1.O 是ABC ?所在平面上一点，若0=++OC OB OA ，则O 是ABC ?的（）A ．外心B ．内心C ．重心D ．垂心2.O 是ABC ?所在平面上一点，若OA OC OC OB OB OA ?=?=?，则O 为ABC ?的（）A ．外心B ．内心C ．重心D ．垂心3.O 是ABC ?所在平面上一点，且a ,b ,c 是三角形的三条边长，0=++OC c OB b OA a ，则0为ABC ?的（）A ．外心B ．内心C ．重心D ．垂心4.O 是ABC ?所在平面上一点，OCOB OA ==，则O 是ABC ?的（）A ．外心B ．内心C ．重心D ．垂心5.O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ?的（） A ．外心 B ．内心 C ．重心 D ．垂心6.（03全国理4）O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P满足)(ACAC ABAB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ?的（）A ．外心B ．内心C ．重心D ．垂心7.O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足)c o s c o s (CAC AC BAB AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ?的（）A ．外心B ．内心C ．重心D ．垂心8. 已知O 是平面上的一定点，AB C ，，是平面上不共线的三个点，动点P 满足2cos cos OB OC AB AC OP AB B AC C λ??+ ?=++，(0)λ∈+∞，，则动点P 的轨迹一定通过ABC △的（）A ．外心B ．内心C ．重心D ．垂心9. P 是ABC △所在平面上一点，若PA PC PC PB PB PA ?=?=?，则P 是ABC△的（）A ．外心B ．内心C ．重心D ．垂心10.若H 为△ABC 所在平面内一点，且222222AB HC CA HB BC HA +=+=+则点H 是△ABC 的（）A ．外心B ．内心C ．重心D ．垂心11.O 是ABC ?所在平面上一点，)|CB |CB |CA |CA (OC )|BC |BC |BA |BA (OB )ACAC |AB |AB (OA =-?=-?=-?则点O 的是ABC ?的（）A ．外心B ．内心C ．重心D ．垂心12.设△ABC 的外心为O ，若)(31OC OB OA OG ++=，则点G 为△ABC 的（） A ．外心 B ．内心 C ．重心 D ．垂心13.设△ABC 的外心为O ，若OC OB OA OH ++=，则点H 为△ABC 的（）A ．外心B ．内心C ．重心D ．垂心14. 已知O 是平面上的一定点，AB C ，，是平面上不共线的三个点，若2211,22AO AB AB AO AC AC ==；则O 为ABC 的（） A ．外心 B ．内心 C ．重心 D ．垂心练习：1．已知ABC ?三个顶点C B A 、、及平面内一点P ，满足0=++PC PB PA ，若实数λ满足：AP AC AB λ=+，则λ的值为（）A ．2B ．23C ．3D ．6 2．若ABC ?的外接圆的圆心为O ，半径为1，0=++OC OB OA ，则=?OB OA ( )A ．21 B ．0 C ．1 D ．21- 3．点O 在ABC ?内部且满足022=++OC OB OA ，则ABC ?面积与凹四边形ABOC 面积之比是（）A ．0B ．23 C ．45 D ．344．ABC ?的外接圆的圆心为O ，若OC OB OA OH ++=，则H 是ABC ?的（） A ．外心 B ．内心 C ．重心 D ．垂心 5．O 是平面上一定点，C B A 、、是平面上不共线的三个点，若222OB BC OA =+222AB OC CA +=+，则O 是ABC ?的（）A ．外心B ．内心C ．重心D ．垂心6.（06陕西）已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →| =12 ,则△ABC 为( )A ．三边均不相等的三角形B ．直角三角形C ．等腰非等边三角形D ．等边三角形7．已知ABC ?三个顶点C B A 、、，若CA BC CB AB AC AB AB ?+?+?=2，则ABC ?为（）A ．等腰三角形B ．等腰直角三角形C ．直角三角形D ．既非等腰又非直角三角形8.ABC ?的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，则实数m =9．已知a=y-x, b=2x-y, |a|=|b|=1, a ·b=0，则|x|+|y|=__________.10．设s, t 为非零实数，a, b 为单位向量，若|sa+tb|=|ta-sb|，则a 和b 的夹角为__________.11．在△ABC 中，M 是AC 中点，N 是AB 的三等分点，且NA BN 2=，BM 与CN 交于D ，若BM BD λ=，则λ=__________.12．已知OB OA ,不共线，点C 分AB 所成的比为2，OB OA OC μλ+=，则=-μλ__________.13．已知OB a OA ,==b, a ·b=|a-b|=2，当△AOB 面积最大时，a 与b 的夹角为______. 14．把函数y=2x 2-4x+5的图象按向量a 平移后得到y=2x 2的图象，c =(1, -1), 若b a ⊥，c ·b=4，则b 的坐标为__________.15．将向量a =(2, 1)绕原点按逆时针方向旋转4π得到向量b ，则b 的坐标为__________.16．在Rt △BAC 中，已知BC=a ，若长为2a 的线段PQ 以点A 为中点，试问PQ 与BC 的夹角θ取何值时CQ BP ?的值最大？并求出这个最大值。

平面几何：有关三角形五心的经典试题及证明部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑平面几何：有关三角形五心的经典试卷三角形的外心、重心、垂心、内心及旁心，统称为三角形的五心. 一、外心.三角形外接圆的圆心，简称外心.与外心关系密切的有圆心角定理和圆周角定理.例1．过等腰△ABC 底边BC 上一点P 引PM∥CA 交AB 于M ；引PN∥BA 交AC 于N.作点P 关于MN 的对称点P′.试证：P′点在△ABC 外接圆上.b5E2RGbCAP (杭州大学《中学数学竞赛习题》>分析：由已知可得MP′=MP=MB，NP′=NP=NC ，故点M 是△P′BP 的外心，点N 是△P′PC 的外心.有∠BP′P=∠BMP=∠BAC， ∠PP′C=∠PNC=∠BAC.∴∠BP′C=∠BP′P+∠P′PC=∠BAC.从而，P′点与A ，B ，C 共圆、即P′在△ABC 外接圆上. 由于P′P 平分∠BP′C，显然还有 P′B:P′C=BP:PC.例2．在△ABC 的边AB ，BC ，CA 上分别取点P ，Q ，S.证明以△APS，△BQP，△CSQ 的外心为顶点的三角形与△ABC 相似.p1EanqFDPw A BCP P MN'(B·波拉索洛夫《中学数学奥林匹克》> 分析：设O1，O2，O3是△APS，△BQP， △CSQ 的外心，作出六边形 O1PO2QO3S 后再由外 心性质可知∠PO1S=2∠A， ∠QO2P=2∠B， ∠SO3Q=2∠C.∴∠PO1S+∠QO2P+∠SO3Q=360°.从而又知∠O1PO2+∠O2QO3+∠O3SO1=360°将△O2QO3绕着O3点旋转到△KSO3，易判断△KSO1≌△O2PO1，同时可得△O1O2O3≌△O1KO3.DXDiTa9E3d ∴∠O2O1O3=∠KO1O3=∠O2O1K =(∠O2O1S+∠SO1K> =(∠O2O1S+∠PO1O2> =∠PO1S=∠A；同理有∠O1O2O3=∠B.故△O1O2O3∽△ABC. 二、重心三角形三条中线的交点，叫做三角形的重心.掌握重心将每 条中线都分成定比2:1及中线长度公式，便于解题.A BCQ K PO O O ....S123例3．AD ，BE ，CF 是△ABC 的三条中线，P 是任意一点.证明：在△PAD，△PBE，△PCF 中，其中一个面积等于另外两个面积的和.RTCrpUDGiT (第26届莫斯科数学奥林匹克> 分析：设G 为△ABC 重心，直线PG 与AB，BC 相交.从A ，C ，D ，E ，F 分别作该直线的垂线，垂足为A′，C′， D′，E′，F′.易证AA′=2DD′，CC′=2FF′，2EE′=AA′+CC′， ∴EE′=DD′+FF′.有S△PGE=S△PGD+S△PGF.两边各扩大3倍，有S△PBE=S△PAD+S△PCF.例4．如果三角形三边的平方成等差数列，那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.分析：将△ABC 简记为△，由三中线AD ，BE ，CF 围成的三角形简记为△′.G 为重心，连DE 到H ，使EH=DE ，连HC ，HF ，则△′就是△HCF.5PCzVD7HxA (1>a2，b2，c2成等差数列△∽△′.若△ABC 为正三角形，易证△∽△′. 不妨设a≥b≥c，有 CF=， BE=，A A 'F F 'GEE 'D 'C 'PCB DAD=.将a2+c2=2b2，分别代入以上三式，得CF=，BE=，AD=.∴CF:BE:AD =::=a:b:c.故有△∽△′.(2>△∽△′a2，b2，c2成等差数列.当△中a≥b≥c时，△′中CF≥BE≥AD.∵△∽△′，∴＝(>2.据“三角形的三条中线围成的新三角形面积等于原三角形面积的”，有=.∴=3a2=4CF2=2a2+b2-c2a2+c2=2b2.三、垂心三角形三条高的交战，称为三角形的垂心.由三角形的垂心造成的四个等(外接>圆三角形，给我们解题提供了极大的便利.jLBHrnAILg例5．设A1A2A3A4为⊙O内接四边形，H1，H2，H3，H4依次为△A2A3A4，△A3A4A1，△A4A1A2，△A1A2A3的垂心.求证：H1，H2，H3，H4四点共圆，并确定出该圆的圆心位置.xHAQX74J0X (1992，全国高中联赛>分析：连接A2H1，A1H2，H1H2，记圆半径 为R.由△A2A3A4知=2RA2H1=2Rcos∠A3A2A4；由△A1A3A4得 A1H2=2Rcos∠A3A1A4.但∠A3A2A4=∠A3A1A4，故A2H1=A1H2.易证A2H1∥A1A2，于是，A2H1A1H2，故得H1H2A2A1.设H1A1与H2A2的交点为M ，故H1H2与A1A2关于M 点成中心对称.同理，H2H3与A2A3，H3H4与A3A4，H4H1与A4A1都关于M点成中心对称.故四边形H1H2H3H4与四边形A1A2A3A4关于M 点成中心对称，两者是全等四边形，H1，H2，H3，H4在同一个圆上.后者的圆心设为Q ，Q 与O 也关于M 成中心对称.由O ，M 两点，Q 点就不难确定了.LDAYtRyKfE 例6．H 为△ABC 的垂心，D ，E ，F 分别是BC ，CA ，AB 的中心.一个以H 为圆心的⊙H 交直线EF ，FD ，DE 于A1，A2，B1，B2，C1，C2.Zzz6ZB2Ltk 求证：AA1=AA2=BB1=BB2=CC1=CC2. ∥=∥=.OA A A A 1234H H 12H H H MA B BA A C CF121122D E(1989，加拿大数学奥林匹克训练题>分析：只须证明AA1=BB1=CC1即可.设BC=a， CA=b，AB=c，△ABC外接圆半径为R，⊙H的半径为r.连HA1，AH交EF于M.A=AM2+A1M2=AM2+r2-MH2=r2+(AM2-MH2>，①又AM2-HM2=(AH1>2-(AH-AH1>2=AH·AH1-AH2=AH2·AB-AH2=cosA·bc-AH2，②而=2R AH2=4R2cos2A,=2R a2=4R2sin2A.∴AH2+a2=4R2，AH2=4R2-a2. ③由①、②、③有A=r2+·bc-(4R2-a2>=(a2+b2+c2>-4R2+r2.同理，=(a2+b2+c2>-4R2+r2，=(a2+b2+c2>-4R2+r2.故有AA1=BB1=CC1.四、内心三角形内切圆的圆心，简称为内心.对于内心，要掌握张角公式，还要记住下面一个极为有用的等量关系：设I 为△ABC 的内心，射线AI 交△ABC 外接圆于A′，则有A′I=A′B=A′C.换言之，点A′必是△IBC 之外心(内心的等量关系之逆同样有用>.dvzfvkwMI1例7．ABCD 为圆内接凸四边形，取△DAB，△ABC，△BCD， △CDA 的内心O1， O2，O3， O4.求证：O1O2O3O4为矩形.(1986，中国数学奥林匹克集训题> 证明见《中等数学》1992；4例8．已知⊙O 内接△ABC，⊙Q 切AB ，AC 于E ，F 且与⊙O 内切.试证：EF 中点P 是△ABC 之内心.(B·波拉索洛夫《中学数学奥林匹克》>分析：在第20届IMO 中，美国提供的一道题实际上是例8的一种特例，但它增加了条件AB=AC.当AB≠AC ，怎样证明呢？rqyn14ZNXI 如图，显然EF 中点P 、圆心Q ，BC 中点K 都在∠BAC 平分线上.易知AQ=.∵QK·AQ=MQ·QN，∴QK===.由Rt△EPQ 知PQ=. ∴PK=PQ+QK=+=.ABCDO O O 234O 1AααMBCKNE R OQF r P∴PK=BK.利用内心等量关系之逆定理，即知P 是△ABC 这内心. 五、旁心三角形的一条内角平分线与另两个内角的外角平分线相交于 一点，是旁切圆的圆心，称为旁心.旁心常常与内心联系在一起， 旁心还与三角形的半周长关系密切.例9．在直角三角形中，求证：r+ra+rb+rc=2p.式中r ，ra ，rb ，rc 分别表示内切圆半径及与a ，b ，c 相切的旁切圆半径，p 表示半周.(杭州大学《中学数学竞赛习题》>分析：设Rt△ABC 中，c 为斜边，先来证明一个特性：p(p-c>=(p-a>(p-b>.∵p(p -c>=(a+b+c>·(a+b-c> =[(a+b>2-c2]=ab ；(p-a>(p-b>=(-a+b+c>·(a-b+c> =[c2-(a-b>2]=ab.∴p(p -c>=(p-a>(p-b>. ① 观察图形，可得 ra=AF-AC=p-b ， rb=BG-BC=p-a ， rc=CK=p.Kr r r r O O O 213AOE CBabc而r=(a+b-c>=p-c.∴r+ra+rb+rc=(p-c>+(p-b>+(p-a>+p=4p-(a+b+c>=2p.由①及图形易证.例10．M是△ABC边AB上的任意一点.r1，r2，r分别是△AMC，△BMC，△ABC内切圆的半径，q1，q2，q分别是上述三角形在∠ACB内部的旁切圆半径.证明：·=.EmxvxOtOco(IMO-12>分析：对任意△A′B′C′，由正弦定理可知OD=OA′·=A′B′··=A′B′·，O ′E= A′B′·.∴.亦即有·=A...'B'C'OO'E D==.六、众心共圆这有两种情况：(1>同一点却是不同三角形的不同的心；(2>同一图形出现了同一三角形的几个心.例11．设在圆内接凸六边形ABCDFE 中，AB=BC ，CD=DE ，EF=FA.试证：(1>AD ，BE ，CF 三条对角线交于一点；SixE2yXPq5 (2>AB+BC+CD+DE+EF+FA≥AK+BE+CF. (1991，国家教委数学实验班招生试卷>分析：连接AC ，CE ，EA ，由已知可证AD ，CF ，EB 是△ACE 的三条内角平分线，I 为△ACE 的内心.从而有ID=CD=DE ，6ewMyirQFL IF=EF=FA ， IB=AB=BC.再由△BDF，易证BP ，DQ ，FS 是它的三条高，I 是它的垂心，利用 不等式有：BI+DI+FI≥2·(IP+IQ+IS>.不难证明IE=2IP ，IA=2IQ ，IC=2IS.∴BI+DI+FI≥IA+IE+IC. ∴AB+BC+CD+DE+EF+FA =2(BI+DI+FI> ≥(IA+IE+IC>+(BI+DI+FI> =AD+BE+CF. I 就是一点两心.Erdos..I PABC DEFQ S例12．△ABC 的外心为O ，AB=AC ，D 是AB 中点，E 是△ACD 的重心.证明OE 丄CD.(加拿大数学奥林匹克训练题> 分析：设AM 为高亦为中线，取AC 中点F ，E 必在DF 上且DE:EF=2:1.设 CD 交AM 于G ，G 必为△ABC 重心. 连GE ，MF ，MF 交DC 于K.易证： DG:GK=DC:(>DC=2:1.∴DG:GK=DE:EFGE∥MF.∵OD 丄AB ，MF∥AB， ∴OD 丄MFOD 丄GE.但OG 丄DEG 又是△ODE 之垂心.易证OE 丄CD.例13．△ABC 中∠C=30°，O 是外心，I 是内心，边AC 上的D 点与边BC 上的E 点使得AD=BE=AB.求证：OI 丄DE ，OI=DE.kavU42VRUs (1988，中国数学奥林匹克集训题>分析：辅助线如图所示，作∠DAO 平分线交BC 于K. 易证△AID≌△AIB≌△EIB，∠AID=∠AIB=∠EIB.利用内心张角公式，有 ∠AIB=90°+∠C=105°， ∴∠DIE=360°-105°×3=45°.AB CDE FOKG O ABCDEF I K30°∵∠AKB=30°+∠DAO=30°+(∠BAC -∠BAO> =30°+(∠BAC -60°> =∠BAC=∠BAI=∠BEI. ∴AK∥IE.由等腰△AOD 可知DO 丄AK ， ∴DO 丄IE ，即DF 是△DIE 的一条高. 同理EO 是△DIE 之垂心，OI 丄DE. 由∠DIE=∠IDO，易知OI=DE.例14．锐角△ABC 中，O ，G ，H 分别是外心、重心、垂心.设外心到三边距离和为d 外，重心到三边距 离和为d 重，垂心到三边距离和为d 垂. 求证：1·d 垂+2·d 外=3·d 重.分析：这里用三角法.设△ABC 外接圆半径为1，三个内角记为A ，B ， C. 易知d 外=OO1+OO2+OO3=cosA+cosB+cosC ，∴2d 外=2(cosA+cosB+cosC>. ① ∵AH1=sinB·AB=sinB·(2sinC>=2sinB·sinC， 同样可得BH2·CH3. ∴3d 重=△ABC 三条高的和=2·(sinB·sinC+sinC·sinA+sinA·sinB> ②BCO IAO G H O G H G O G H 123112233∴=2，∴HH1=cosC·BH=2·cosB·cosC.同样可得HH2，HH3.∴d垂=HH1+HH2+HH3=2(cosB·cosC+cosC·cosA+cosA·cosB>③欲证结论，观察①、②、③，须证(cosB·cosC+cosC·cosA+cosA·cosB>+( cosA+ cosB+ cosC>=sinB·sinC+sinC·sinA+sinA·sinB.即可.y6v3ALoS89练习题1.I为△ABC之内心，射线AI，BI，CI交△ABC外接圆于A′，B′，C′.则AA′+BB′+CC′＞△ABC周长.(1982，澳大利亚数学奥林匹克>2.△T′的三边分别等于△T的三条中线，且两个三角形有一组角相等.求证这两个三角形相似.(1989，捷克数学奥林匹克>M2ub6vSTnP3.I为△ABC的内心.取△IBC，△ICA，△IAB的外心O1，O2，O3.求证：△O1O2O3与△ABC有公共的外心.(1988，美国数学奥林匹克>0YujCfmUCw4.AD为△ABC内角平分线.取△ABC，△ABD，△ADC的外心O，O1，O2.则△OO1O2是等腰三角形.eUts8ZQVRd5.△ABC中∠C＜90°，从AB上M点作CA，CB的垂线MP，MQ.H是△CPQ的垂心.当M是AB上动点时，求H的轨迹.(IMO-7>sQsAEJkW5T6.△ABC的边BC=(AB+AC>，取AB，AC中点M，N，G为重心，I为内心.试证：过A，M，N三点的圆与直线GI相切.(第27届莫斯科数学奥林匹克>GMsIasNXkA7.锐角△ABC的垂心关于三边的对称点分别是H1，H2，H3.已知：H1，H2，H3，求作△ABC.(第7届莫斯科数学奥林匹克>TIrRGchYzg8.已知△ABC的三个旁心为I1，I2，I3.求证：△I1I2I3是锐角三角形.9.AB，AC切⊙O于B，C，过OA与BC的交点M任作⊙O的弦EF.求证：(1>△AEF与△ABC有公共的内心；(2>△AEF与△ABC有一个旁心重合.7EqZcWLZNX申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

三角形的五心一、重心 (1)二、垂心 (2)三、内心 (4)四、外心 (7)五、旁心 (9)1. （2007年全国初中数学联赛1试）设K 是ABC △内任意一点，KAB △、KBC △、KCA △的重心分别为D 、E 、F ，则:DEF ABC S S △△的值为（ ）A ．19B ．29C ．49D ．23【难度】 ★★【解析】A ， 分别延长KD 、KE 、KF ，与ABC △的三边AB 、BC 、CA 交于点M 、N 、P ，由于D 、E 、F 分别为KAB △、KBC △、KCA △的重心，易知M 、N 、P 分别为AB 、BC 、CA 的中点，所以14MNP ABC S S =△△．易证DEF △∽MNP △，且相似比为2:3，所以22()3DEF MNP S S =△△4194ABC S =⋅△19ABC S =△．所以:DEF S △19ABC S =△．故选A ．2. （1998年全国初中数学联赛2试）已知P 为平行四边形ABCD 内一点，O 为AC与BD 的交点，M ，N 分别为PB ，PC 的中点，Q 为AN 与DM 的交点，求证： ⑴P ，Q ，O 三点在一条直线上； ⑵2PQ OQ =．【难度】 ★★★ 【解析】 证明：如图，连接PO ，设PO 与AN DM ，分别交于点Q '，Q ''．在PAC △中，∵AO OC PN NC ==，， ∴Q '为重心，2PQ OQ ''''=．这样Q Q '''=，并且Q Q '''，就是AN DM ，的交点Q ． 故P Q O ，，在一条直线上，且2PQ OQ =．3. （1992年全国初中数学联赛1试）若一等腰三角形的底边上的高等于18cm ，腰上的中线等15cm ，则这个等腰三角形的面积等于__________．N M Q PODCBAQ''Q'NMQPO DCBA【解析】 2144cm如图，在ABC △中，设AB AC =，AD BC ⊥，AM MC =，则18cm AD =，15cm BM =．又设AD 与BM 相交于G ，则是ABC △的重心．∴16cm 3GD AD ==，210cm 3BG BM ==，∴8cm BD =∴21144cm 2ABC S BC AD =⋅=△．二、 垂心4. （1993年全国初中数学联赛2试）设H 是等腰三角形ABC 垂心，在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小，这时乘积ABC HBC S S ⋅△△的值变小、变大，还是不变？证明你的结论．【难度】 ★★ 【解析】 解法一：不妨设角A 是锐角，连接AH 并延长交BC 于D 点，延长BH ，CH 分别交AC 于E ，交AB 于F ，如图∵BH D AH E ∠=∠，∴H BD H AE ∠=∠． 因为Rt Rt BDH ADC △≌△，∴AC DCBD HD=． GDMCBAHCBA图 2F D E ABCH又12BD DC BC ==，∴214AD HD BD CD BC ⋅=⋅=． ∴4111:2216ABC HBC S S BC AD BC HD BC ⎛⎫⎛⎫=⋅⨯⋅= ⎪ ⎪⎝⎭⎝⎭△△．当90A ∠︒≥时，同理可证上式也成立，由于BC 是不变的，所以当A 点至BC 的距离变小时，乘积ABC HBC S S ⋅△△保持不变．解法二：作图如解法一，再延长AD 至G ，使DG DH =，并分别连接BG ，GC ．由HBD GBD △≌△，CBG CBH CAG ∠=∠=∠， 因而，A ，B ，G ，C 四点共圆，由相交弦定理，得214AD HD AD DG BD DC BC ⋅=⋅=⋅=．因此，41112216ABC HBC S S AD BC HD BC BC ⎛⎫⎛⎫⋅=⋅⋅= ⎪⎪⎝⎭⎝⎭△△由于BC 是不变的，所以当点A 至BC 的距离变小时，乘积ABC HBC S S ⋅△△保持不变．5. （2007年全国初中数学联赛1试）已知锐角ABC △的顶点A 到垂心H 的距离等于它的外接圆的半径，则∠A 的度数是（） A ．30 B ．45 C ．60 D ．75【难度】 ★★【解析】C ， 锐角ABC △的垂心在三角形内部，如图，设ABC △的外心为O ，D 为BC 的中点，BO 的延长线交⊙O 于点E ，连CE 、AE ，则CE //AH ，AE //CH ，则2OB AH CE OD ===，所以30OBD ∠=︒，60BOD ∠=︒，所以60A BOD ∠=∠=︒．答案为C ．G H F E D CBA图 3AECBDOH三、 内心6. （1992年全国初中数学联赛1试）在ABC △中，90C ∠=︒，A ∠和B ∠的平分线相交于P 点，又PE AB ⊥于E 点，若2BC =，3AC =，则AE AB ⋅=_________． 【难度】 ★★【解析】3， 如图，作PD AC ⊥于D ，PF BC ⊥于F ，则：()11()51322CD CF AC BC AB ==+-=-，()11312AD AC CD =-=+，()11312BF BC CF =-=-，∴3AE EB AD BF ⋅=⋅=7. （1995年全国初中数学联赛2试）已知90ACE CDE ∠=∠=︒，点B 在CE 上，CA CB CD ==，经A ，C ，D 三点的圆交AB 于F （如图），求证F 为CDE△的内心．【难度】 ★★★ 【解析】 首先指出，本题有IM0295-(1989年)的背景，该题是：在直角ABC △中，斜边BC 上的高，过ABD △的内心与ACD △的内心的直线分别交边AB 和AC 于K 和L ，ABC △和AKL △的面积分别记为S 和T ．求证2S T ≥． 在这个题目的证明中，要用到AK AL AD ==．2004年的初中联赛题相当于反过来，先给出AK AL AD ==(斜边上的高)，再求证KL 通过ABD ADC ，△△的内心（如下图）．PEFDC BAGFED B CA证法1：如图，连DF ，则由已知，有1452CDF CAB CDE ∠=∠=︒=∠，故DF 为CDE ∠的平分线．连BD CF ，，由CD CB =，知145452FBD CBD CDB FDB ∠=∠-︒=∠-︒=∠，得FB FD =，即F 到B D ，和距离相等，F 在线段BD 的垂直平分线上，从而也在等腰三角形CBD 的顶角平分线上，CF 是ECD ∠的平分线．由于F 是CDE △上两条角平分线的交点，因而就是CDE △的内心． 证法2：同证法1，得出459045CDF FDE ∠=︒=︒-︒=∠之后，由于ABC FDE ∠=∠，故有B E D F ，，，四点共圆．连EF ， 在证得FBD FDB ∠=∠之后，立即有FED FBD FDB FEB ∠=∠=∠=∠， 即EF 是CED ∠的平分线．本来，点E 的信息很少，证EF 为角平分线应该是比较难的，但四点共圆把许多已知信息集中并转移到E 上来了，因而证法2并不比证法1复杂． 由以上证明可知，F 是DCB △的外心．1452CDF CAB CDE ∠=∠=︒=∠，知DF 是CDE ∠的平分线，故F 为CDE △的内心．证法3：如图，只证CF 为DCE ∠的平分线．LKDCBAFED B CA图 5G G 图 6ACB D EF由1451AGC ADC CAD CAB ∠=∠=∠=∠+∠=︒+∠， 得12∠=∠．从而DCF GCF ∠=∠，得CF 为DCE ∠的平分线．证法4：首先DF 是CDE ∠的平分线，故CDE △的外心I 在直线DF 上． 现以CA 为y 轴、CB 为x 轴建立坐标系，并记CA CB CD d ===， 则直线AB 是一次函数y x d =-+①的图像（如图）．若记内心I 的坐标为11()x y ，，则11x y CH IH CH HB CB d +=+=+==满足①，即I 在直线AB 上，但I 在DF 上，故I 是AB 与DF 的交点．由交点的惟一性知I 就是F ，从而证得F 为Rt CDE △的内心．不可延长ED 交O ⊙于P ，利用CP 为直径来证．8. （1996年全国初中数学联赛1试）如果一个三角形的面积和周长都被一直线所平分，那么该直线必通过这个三角形的（ ） A ．内心 B ．外心 C ．重心 D ．垂心 【难度】 ★★ 【解析】A ， 我们首先要了解各种三角形的面积的算法，正弦公式，底乘高公式以及利用三角形内切圆半径来计算三角形的面积公式．如果内切圆的半径为r ，三角形的周长为l ，则三角形的面积为：12S r l =⨯⨯． 如图：上面一部分的面积为()12r AD AE ⨯⨯+，下面一部分的面积为()12r BD CE BC ⨯⨯++,由于直线m 分三角形周长为两半，即BD CE BC AD AE ++=+， 所以上下两部分的面积相等，因此直线m 过内心．故选A ．图 7y 1x 1IH E DC B Axym IED CBA四、 外心9. （1993年全国初中数学联赛1试）锐角三角形ABC 的三边是a ，b ，c ，它的外心到三边的距离分别为m ，n ，p ，那么::m n p 等于（ ）A ．111::a b cB ．::a b cC ．cos :cos :cos A B CD ．sin :sin :sin A B C【难度】 ★★【解析】C ， 如图，设O 是ABC △的外心， OA OB OC R ===，1cos cos 2m BOC A R =∠=， ∴cos m R A =． 同理cos n R B =，cos p R C =．∴::cos :cos :cos m n p A B C =．10. （2006年全国初中数学联赛2试）如图，在平行四边形ABCD 中，A ∠的平分线分别与BC 及DC 的延长线交于E 、F ，点O 、1O 分别为CEF △、ABE △的外心．⑴求证：O 、E 、1O 三点共线；⑵求证：若70ABC ∠=︒，求OBD ∠的度数．【难度】 ★★★【解析】 ⑴如图，连结OE 、OF 、1O A 、1O E ．因为四边形ABCD 为平行四边形，所以ABE ECF ∠=∠．Cnmp O B AA BCDEFO O 1又因为点O 、1O 分别为CEF △、ABE △的外心，所以OE OF =，11O A O E =，122EOF ECF ABE AO E ∠=∠=∠=∠． 于是有1OEF O EA △∽△．故1OEF AEO ∠=∠，所以O 、E 、1O 三点共线．⑵连接OD 、OC ．因为四边形ABCD 为平行四边形，所以，CEF DAE BAF CFE ∠=∠=∠=∠． 故CE CF =．又因为点O 为CEF △的外心，所以OE OF OC ==． 则OCE OCF △≌△，有OEC OFC OCF ∠=∠=∠．故OEB OCD ∠=∠．又BAE EAD AEB ∠=∠=∠，则EB AB DC ==． 因此OCD OEB △≌△．所以，ODC OBE ∠=∠，OD OB =，ODC OBC ∠=∠，OBD ODB ∠=∠，OBD OBC CBD ∠=∠+∠ODC BDA =∠+∠ADC BDO =∠-∠ABC OBD =∠-∠．故1352OBD ABC ∠=∠=︒．11. （2013年全国初中数学联赛2试）在ABC △中，AB AC >，O 、I 分别是ABC △的外心和内心，且满足2AB AC OI -=．求证：⑴ OI BC ∥；⑵ 2AOC AOB AOI S S S -=△△△．【难度】 ★★★★ 【解析】 ⑴ 作OM BC ⊥于M ，IN BC ⊥于N ．设BC a =，AC b =，AB c =．易求得12CM a =，1()2CN a b c =+-，所以1()2MN CM CN c b OI =-=-=．O 1O FEDCBA N M IO CB A又MN 恰好是两条平等线OM ，IN 之间的垂线段，所以OI 也是两条平等线OM ，IN 之间的垂线段，所以OI MN ∥，所以OI BC ∥．⑵ 由⑴知OMNI 是矩形，连接BI ，CI ，设OM IN r ==（即为ABC △的内切圆半径，则()()AOC AOB AOI COI AIC AIB AOI BOI S S S S S S S S -=++---△△△△△△△△ 2AOI BOI COI AIC AIBS S S S S =+++-△△△△△111122222AOI S OI r OI r AC r AB r =+⋅⋅+⋅⋅+⋅⋅-⋅⋅△112222AOI AOI S r OI b c S ⎛⎫=+⋅+-= ⎪⎝⎭△△．五、 旁心。