凃逍羽 用光学多道分析器研究氢原子光谱

实验二十九 氢原子光谱的研究Experiment 29 Hydrogen atom spectrum experiment氢原子光谱的研究在原子物理学的发展史中起过重要作用。

由于它是最简单、最典型、规律性最明显的一种光谱，因此最早为人们所注意，研究的也最为透彻。

实验方面进行了精细结构的探测，数据越来越精确。

理论方面则相当完满地解释了这些谱线的成因，发展了电子与电磁场相互作用的理论（量子电动力学）。

因此，本实验的操作过程对学生能力的培养无疑有较大的意义。

实验目的Experimental purpose1．测量氢光谱巴尔末线系在可见光区域的几条谱线的波长、验证巴尔末规律的正确性。

2．验算里德堡常数。

3．熟悉棱镜摄谱仪、光谱投影仪、阿贝比长仪的使用方法，并了解棱镜摄谱仪的工作原理。

实验原理Experimental principle1885年巴尔末根据实验数据发现了氢原子光谱在可见光区域内的各条谱线波长遵循下述规律4220-=n n λλ (1) 式中λ0为恒量。

当n =3，4，5，6，…时，则对应谱线分别称为H α、H β、H γ、H δ、…谱线。

继巴尔末之后，里德堡又把（1）式改写为⎪⎭⎫ ⎝⎛-=221211n R H λ (2) 式中n =3，4，5，6，…，R H =（10967758.1±0.8）m -1，称为里德堡常数。

通常取R H =1.097×107m -1即可。

氢原子光谱线中遵循上述两式规律的许多谱线组成氢光谱的巴尔末线系。

对于巴尔末线系来说，谱线的间隔和强度由长波向短波方向，以一种十分规则的方式递减，间隔越来越小。

强度越来越弱。

在巴尔末和里德堡经验公式的基础上，玻尔建立起原子模型理论，该理论能较好地解释气体放电时的发光现象。

玻尔理论认为：原子由原子核及核外电子组成，核外电子围绕原子核运动，它们可以有许多分立的运动轨道（见图1所示）。

电子在不同的轨道上运动时具有不同的能量，能量值是不连续的，是量子化的，只能取由量子数决定的各个分立的能量值。

近代物理实验实验报告实验课题：使用光学多道测量光谱与光谱分析班级：物理学061姓名：任军培学号：06180130指导老师：方允樟2008年11月21日一、摘要：本实验通过使用光学多道测量光谱了解和学会使用光学多道分析仪，并学会了通过光学多道分析仪分析氢、氮、氦、氖等光谱。

测量了氢光谱的巴尔末系中Hα、Hβ，Hγ，Hδ四种谱线的波长和里德伯常数。

二、关键词：光学多道分析器里德伯常数光谱三、引言：常用的光谱涉及的波段从X射线，紫外线，可见光，红外线，微波到射频波段。

所以光谱技术是研究物质微观结构的重要手段，它被广泛地应用于医学，生物，化学，地质考古，冶金等许多场所。

光谱实验的数据为了解原子、分子和晶体等精细结构提供了重要依据。

而光学多通道分析器是用平面光栅衍射的方法获得多级衍射光的仪器，用它可对给定波长范围的单色光进行光谱分析，与单缝，双缝衍射相比，平面光栅衍射具有衍射本领大，衍射光线亮，分辨率高等特点。

因而在特征谱线分析中有着广泛的应用。

本实验通过测量各种气体灯光的原子在可见光波段的发射光谱使大家了解光谱与微观结构（能级）间的联系和学习光谱测量的基本方法。

四、正文：1、实验原理衍射包括单缝衍射，双缝衍射和光栅衍射。

它们都可用来测量光波的波长，但由于单缝衍射，双缝衍射在各级衍射的分辨率与亮度存在矛盾，而光栅正好解决了两者间的矛盾，所以实验中大多采用平面光栅来做实验。

光栅一般分两类，一类是透射式(见图1)，另一类是反射式(见图2)。

透射式光栅是在一块平面透明的玻璃板上刻上平行，等间距又等宽的直痕，刻痕部分不透光，两刻痕间能透光，相当于狭缝。

相邻刻痕间的距离d称为光栅常数。

反射式光栅是在镀有金属层的表面上刻划斜的平行等间距刻痕，斜面能反射光。

本实验用反射式平面光栅。

图1平面透射光栅图2平面反射光栅利用现代电子技术和计算机技术接收和处理某一波长范围内光谱信息的光学多通道分析与检测系统的基本框图如图3所示。

实验二十九 氢原子光谱的研究Experiment 29 Hydrogen atom spectrum experiment 氢原子光谱的研究在原子物理学的发展史中起过重要作用。

由于它是最简单、最典型、规律性最明显的一种光谱，因此最早为人们所注意，研究的也最为透彻。

实验方面进行了精细结构的探测，数据越来越精确。

理论方面则相当完满地解释了这些谱线的成因，发展了电子与电磁场相互作用的理论（量子电动力学）。

因此，本实验的操作过程对学生能力的培养无疑有较大的意义。

实验目的Experimental purpose 1．测量氢光谱巴尔末线系在可见光区域的几条谱线的波长、验证巴尔末规律的正确性。

2．验算里德堡常数。

3．熟悉棱镜摄谱仪、光谱投影仪、阿贝比长仪的使用方法，并了解棱镜摄谱仪的工作原理。

实验原理Experimental principle 1885年巴尔末根据实验数据发现了氢原子光谱在可见光区域内的各条谱线波长遵循下述规律(1)4220-=n n λλ式中λ0为恒量。

当n =3，4，5，6，…时，则对应谱线分别称为H α、H β、H γ、H δ、…谱线。

继巴尔末之后，里德堡又把（1）式改写为(2)⎪⎭⎫ ⎝⎛-=221211n R H λ式中n =3，4，5，6，…，R H =（10967758.1±0.8）m -1，称为里德堡常数。

通常取R H =1.097×107m -1即可。

氢原子光谱线中遵循上述两式规律的许多谱线组成氢光谱的巴尔末线系。

对于巴尔末线系来说，谱线的间隔和强度由长波向短波方向，以一种十分规则的方式递减，间隔越来越小。

强度越来越弱。

在巴尔末和里德堡经验公式的基础上，玻尔建立起原子模型理论，该理论能较好地解释气体放电时的发光现象。

玻尔理论认为：原子由原子核及核外电子组成，核外电子围绕原子核运动，它们可以有许多分立的运动轨道（见图1所示）。

电子在不同的轨道上运动时具有不同的能量，能量值是不连续的，是量子化的，只能取由量子数决定的各个分立的能量值。

用光学多道分析器(OMA)研究氢原子光谱
马厂
【期刊名称】《读写算（教研版）》
【年(卷),期】2012(000)015
【摘要】使用光学多道分析器(OMA)测定了氢原子巴尔末系中Hα、Hβ、Hγ、Hδ谱线的波长，并利用所测的波长通过Origin 拟合计算出氢原子的精确的里德伯常量。

【总页数】1页(P262-262)
【作者】马厂
【作者单位】湖北理工学院,湖北黄石435000
【正文语种】中文
【中图分类】G307
【相关文献】
1.改善光源光谱特性提高光学多道分析器用于吸收光谱测量的信噪比
2.光学多道分析仪（OMA）时间分辨光谱分析
3.教学型CCD光学多道分析器及其在光谱实验中的应用
4.光学多道分析仪（OMA）与条纹相机互连测量皮秒时间分辨光谱
D光学多道分析器及其在光谱数据采集中的应用
因版权原因，仅展示原文概要，查看原文内容请购买。

111实验5-10 氢原子光谱的观察与测定每一种原子都有其特定的线状光谱。

光谱分析是鉴别物质成分及物质含量的有效手段。

氢原子的光谱最为简单，且具有明显的规律。

测定氢原子可见光谱线的波长对认识原子的分离能级、以及光谱规律有重要作用。

本实验用读谱仪测量氢原子可见光谱的波长，并通过巴耳末公式推算出氢原子的里德伯常数。

【实验目的】1．观察氢原子的可见光谱。

2．了解读谱仪的结构，掌握读谱仪的调节与使用方法。

3．通过测量氢原子可见光谱线的波长，验证巴耳末公式。

4．测定氢原子的里德伯常数。

5．理解曲线拟合法的意义。

【实验器材】WPL-2型读谱仪、氢灯、氦氖灯、会聚透镜。

【实验原理】 一、氢原子光谱线公式 氢原子光谱的实验公式为⎪⎭⎫ ⎝⎛-=22111n kR H λ （5-10-1） 式中的H R 叫做里德伯常数，其实验值为1013.0306.10967758-±=m R H ）（实。

氢原子光谱系如表5-10-1。

玻尔认为，氢原子之所以发光，是因为氢原子中的电子可以处在不同的能态（能级）上，当电子从高能级向低能级跃迁时，就发出光线。

玻尔推出了氢原子光谱的理论公式⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=22223204111181n kR n k c h me H 理ελ（5-10-2） 里德伯常数的理论值为.H R m -=110973731534理。

本实验测定在可见光谱内巴耳末系的氢红线（对应32==n k 、）的波长。

二、曲线拟合法在式（5-10-1）和式（5-10-2）中，不同的k 对应不同的线系，不同的n 对应同一线系中不同的谱线。

注意到谱线位置的测量值是相对的，所以必须用已知波长的谱线作为基准。

在本实验中的基准是氦氖灯的谱线。

实验方法是先分别通过目镜观察氦氖谱线和氢谱，然后112 用读数显微镜测出氢红谱线（波长为H λ）及其两侧近邻的（已知波长分别为1λ和2λ）氦氖谱线的位置1y 、H y 和2y 。

光学多道与氢氘同位素光谱
首先，光学多道谱仪是一种用于测量光谱的仪器。

它通过将光分散成不同波长的组成部分，并将其定量地记录下来，从而提供了有关光的能量分布和波长特性的信息。

光学多道谱仪通常由光源、入射系统、分光系统、检测器和数据处理系统等组成。

它可以用于研究物质的吸收、发射、散射等光学性质，从而揭示物质的结构和特性。

氢和氘是两种同位素，它们的原子核中分别含有一个质子和一个中子，或一个质子和两个中子。

由于氢和氘的核结构不同，它们的光谱特性也有所不同。

氢氘同位素光谱研究主要关注氢和氘在光谱中的吸收、发射、散射等现象，以及它们与其他物质相互作用的过程。

在研究氢氘同位素光谱时，可以使用光学多道谱仪来记录氢和氘的光谱信息。

通过测量氢氘光谱的特征峰的位置、强度和形状等参数，可以获得有关氢氘同位素的结构、能级和相互作用等信息。

这对于理解原子和分子的性质、反应机制以及物质的动力学过程具有重要意义。

此外，研究氢氘同位素光谱还可以应用于其他领域。

例如，在
天文学中，通过观测氢氘同位素的光谱可以研究星系、星际介质和
宇宙的演化过程。

在化学和生物化学中，氢氘同位素标记技术被广
泛应用于研究分子结构、代谢途径和药物代谢动力学等方面。

总结起来，光学多道与氢氘同位素光谱是一个涉及到光学和原
子物理的研究领域。

通过使用光学多道谱仪来记录氢氘光谱的信息，可以获得有关氢氘同位素的结构、能级和相互作用等重要信息。

这
对于理解物质的性质、反应机制以及宇宙的演化过程具有重要意义。

光学多道与氢氘同位素光谱作者：北师南乡子 实验日期： 2013年9月 指导教师：王海燕 【摘要】本实验先利用CCD 光学多道系统，通过对已知波长的氦、氖光谱进行定标测量氢光谱巴耳末系的谱线，然后用单色仪测量氢氘同位素光谱，得到氢氘光谱的波长值；利用这些测得值计算出了氢、氘的里德伯常量分别为R H =109685.07cm -1和R D =109715.98cm -1，同时通过计算得出了质子与电子质量之比为/p e m m =1783.18，与理论值1836.15相比误差为2.88%。

关键词：光学多道 、CCD 、氢氘光谱、光电倍增管一、 引言光谱学在原子分子物理、天文物理、等离子体物理、激光物理和材料物理等物理学科中有重要作用。

纵观整个光谱学史，氢光谱的实验和理论研究都占有特别重要的地位。

在1885年，瑞士物理学家巴耳末就发现了巴耳末公式，即可见光区氢光谱谱线波长的规律。

1892年美国物理学家尤雷等发现氢的同位素氘（D ）的光谱。

氢原子和氘原子的核外都只有一个电子，故光谱极为相似，但由于原子核质量的不同波长也有所差别，这种差别就称为“同位素位移”。

本实验利用光学多道分析仪，从巴尔末公式出发研究氢氘光谱，了解其谱线特点， 并学习光学多道仪的使用方法及基本的光谱学技术。

二、 实验原理在原子体系中，原子的能量状态是量子化的。

用1E 和2E 表示不同能级的能量，ε表示跃迁发出光子的能量，h 表示波尔兹曼常量，ν表示光子的频率，对于原子从低能级到高能级的跃迁我们有：21h E E εν==-，其中21E E hν-=（1） 由于原子能级的分立，频率ν也为分立值，在分光仪上表现为一条条分立的“线性光谱”，这些频率由巴耳末公式确定：H 原子：2212111H H R n n λ⎛⎫=- ⎪⎝⎭ （2） 其中1n 和2n 为轨道量子数，H R 为氢原子的里德伯常数。

当1n =2，2n =3，4，5……时，公式（2）对应氢原子巴耳末系。

光学多道与氢、氘同位素光谱【摘要】本实验利用光学多道分析仪，以氦（He ）、氖（Ne ）为标准谱，研究了氢（H ）光谱的波长规律，并用光电倍增管对氢、氘谱线进行了分析，测出氢、氘在巴莫尔线系的谱线波长，并求出氢、氘的里德伯常数及电子质子质量比，最后根据实验数据，以波数为单位画出氢、氘的能级图。

【关键词】光学多道 光栅多色仪 氢、氘同位素光谱 电子质子质量比【引言】光谱是不同强度的电磁辐射按照波长的有序排列。

光谱学在物理学科中占有极为重要的地位，在计量学、化学、生物学、医学、地质学等诸多方向也有着广泛的应用。

主要用于材料结构的参数测定、物理性质的诊断以及物质中元素的定性和定量分析。

在光谱学史乃至近代物理学史上，氢光谱的实验和理论研究都占有特别重要的地位。

1885年，瑞士物理学家巴耳末发现了可见光区的氢（H ）光谱谱线波长规律，即巴耳末公式。

这些谱线构成了一个谱线系，即巴耳末系，并用⋯γβαH H H ，，代表巴耳末系的第一条、第二条、第三条……谱线。

1892年，美国物理学家尤雷等发现了氢（H ）的同位素氘（D ）的光谱。

D 的巴耳末系前几条线则用⋯γβαD D D ，，表示。

由于H 原子和D 原子的核外都只有一个电子，故光谱极为相似，但由于它们的原子核质量不同，因而对应的谱线的波长都稍有差别，这种差别被称为“同位素位移”。

本实验利用光学多道分析仪研究H 的同位素光谱，了解H 、D 原子谱线的特点，用实验结果计算出H 、D 的里德伯常量及质子电子的质量比，并得到H 、D 的能级谱线图。

【实验原理】在量子化的原子体系里，原子能量状态为一系列的分立值，每一个能量状态都称为原子的一个能级，原子的最低能级称为原子的基态，高于基态的称为激发态。

处于高能级的原子总是会自发的跃迁到低能级，并且发射光子，设光子能量为ε，频率为ν，高能级为E 2，低能级为E 1，则有：h E E E E h 1212,-=-==ννε （1） 由于原子的能级是分立的，所以原子由高能级向低能级跃迁时会发射一些特定频率的光，这些光在分光仪上表现为一条条分立的光谱线，称为“线状光谱”或“原子光谱”。

用光学多道分析器研究氢原子光谱俞维民（物理科学与技术学院物理学基地班学号：2008301020001）摘要：使用光学多道分析器测定氢原子巴尔末系中HαHβHγHδ波长，并利用所测的波长拟合计算出氢原子的里德伯常量。

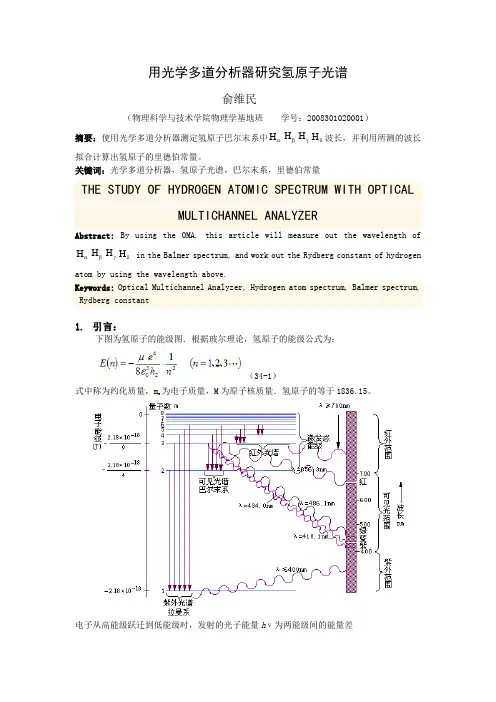
关键词：光学多道分析器，氢原子光谱，巴尔末系，里德伯常量THE STUDY OF HYDROGEN ATOMIC SPECTRUM WITH OPTICALMULTICHANNEL ANALYZERAbstract:By using the OMA, this article will measure out the wavelength ofHαHβHγHδin the Balmer spectrum, and work out the Rydberg constant of hydrogenatom by using the wavelength above.Keywords: Optical Multichannel Analyzer, Hydrogen atom spectrum, Balmer spectrum, Rydberg constant1.引言：下图为氢原子的能级图．根据玻尔理论，氢原子的能级公式为：（34-1）式中称为约化质量，m e为电子质量，M为原子核质量．氢原子的等于1836.15。

电子从高能级跃迁到低能级时，发射的光子能量hν为两能级间的能量差如以波数表示，则上式为式中R H 称为氢原子的里德伯常数，单位是m -1，T(n)称为光谱项，它与能级E(n)是对应的．从R H 可得氢原子各能级的能量式中-1584.1356710, 2.9979210-1h=eV s m s c ⨯⋅=⨯⋅从能级图可知，从3≥m 至2n =的跃迁．光子波长位于可见光区．其光谱符合规律这就是1885年巴耳末发现并总结的经验规律，称为巴耳末系．2. 实验原理：由于H α线波长为656.28nm ，H δ波长为410.17nm ，波长间隔246nm 超过CCD 一帧159nm 范围，无法在同屏中观察到，故需分两次观察测量。

近代物理实验报告[光学多道与氢、氘同位素光谱]学号：[201311141925]学生姓名：[张静]指导教师：[王海燕]实验时间：[2015年9月25日]摘要：本实验利用光学多道分析仪，以氦（He ）、氖（Ne ）为标准谱进行定标测量了氢光谱，并在此基础上用光电倍增管对氢、氘谱线进行分析，测出氢、氘在巴耳末线系的谱线波长，求出了氢、氘的里德伯常量分别为R H =109657.218cm -1，R D =109625.62cm -1，根据实验数据，画出了氢的巴耳末系跃迁能级图，最后通过计算得出电子与质子质量之比为m e /m p =0.000549,与理论值0.000545的相对误差为0.734%。

关键词：光学多道仪、CCD 光电探测器、光电倍增管、光栅多色仪、氢氘光谱一、引言光谱学是一门主要涉及物理学及化学的重要交叉学科，通过光谱来研究电磁波与物质之间的相互作用。

光谱是一类借助光栅、棱镜、傅里叶变换等分光手段将一束电磁辐射的某项性质解析成此辐射的各个组成波长对此性质的贡献的图表。

从19世纪中叶起实验光谱学一直是光谱学研究的重要课题之一。

氢原子光谱中最强的一条谱线是1853年由瑞典物理学家A.J.埃斯特朗探测出来的（光波波长的单位即以他的姓氏命名，1埃等于10-8厘米）。

此后的20年中，在星体的光谱中观测到了更多的氢原子谱线。

1885年，从事天文测量的瑞士科学家J.J.巴耳末找到一个经验公式来说明已知的氢原子谱线的位置。

此后便把这一组线称为巴耳末系。

1889年，瑞典光谱学家J.R.里德伯发现了许多元素的线状光谱系，其中最为明显的为碱金属原子的光谱系，它们都能满足巴尔末公式。

其中R 的值对于所有元素的线系都几乎相同，称为里德伯常数。

1892年，尤雷（H.C.Urey ）等发现氢(H)同位素——氘(D)的光谱。

氢氘原子核外都只有一个电子，光谱极为相似，但由于原子核质量不同，故其对应谱线波长稍有差别，即存在“同位素位移”。

实验三氢原子光谱的研究实验三氢原子光谱的研究引言氢原子的结构最简单，它的线光谱明显地具有规律，早就为人们所注意。

各种原子光谱的规律性的研究正式首先在氢原子上得到突破的，氢原子又是一种典型的最适合于进行理论与实验比较的原子。

本世纪上半世纪中对氢原子光谱的种种研究在量子论的发展中多次起过重要作用。

1913年玻尔建立了半经典的氢原子理论，成功地解释了包括巴耳末线系在内的氢光谱的规律。

事实上氢的每一谱线都不是一条单独的线，换言之，都具有精细结构，不过用普通的光谱仪器难以分析，因而被当作单独一条而已。

这一事实意味氢原子的每一能级都具有精细结构。

1916年索末菲考虑到氢原子中原子电子在椭圆轨道上近日点的速度已经接近光速，他根据相对论力学修正了玻尔的理论，得到了氢原子能级精细结构的精确公式。

但这仍是一个半经典理论的结果。

1925年薛定谔建立了波动力学（即量子力学中的薛定谔方程），重新解释了玻尔理论所得到的氢原子能级。

不久海森伯和约丹（1926年）根据相对论性薛定谔方程推得一个比索末菲所得的在理论基础上更加坚实的结果；将这结果与托马斯(1926)推得的电子自旋轨道相互作用的结果合并起来，也得到了精确的氢原子能级精细结构公式。

尽管如此，根据该公式所得巴耳末系第一条的（理论）精细结构与不断发展着的精密测量中所得实验结果相比，仍有约百分之几的微小差异。

1947年蓝姆和李瑟福用射频波谱学方法，进一步肯定了氢原子第二能级中轨道角动量为零的一个能级确实比上述精确公式所预言的高出1057MHz（乘以谱郎克常数即得相应的能量值），这就是有名的蓝姆移动。

直到1949年，利用量子电动力学理论将电子与电磁场的相互作用考虑在内，这一事实才得到了解释，成为量子电动力学的一项重要实验根据。

实验目的1、学习摄谱、识谱和谱线测量等光谱研究的基本技术。

2、通过测量氢光谱可见谱线的波长，验证巴耳末公式的正确性，从而对玻尔理论的实验基础有具体了解。

实验四 OMA 研究氢氘原子光谱光谱线系的规律与原子结构有内在的联系，因此，原子光谱是研究原子结构的一种重要方法。

1885年巴尔末总结了人们对氢光谱的测量结果，发现了氢光谱的规律，提出了著名的巴尔末公式，氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础。

1932年尤里根据里德伯常数随原子核质量不同而变化的规律，对重氢赖曼线系进行摄谱分析，发现氢的同位素——氘的存在。

通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一，成为检验原理论可靠性的标准和测量其它基本物理常数的依据。

一、实验目的1． 熟悉光栅光谱仪的性能与用法。

2． 用光栅光谱仪测量氢（氘）原子光谱巴尔末线系的波长，求里德伯常数。

二、实验仪器光学多通道分析仪、原子定标灯（氮灯、氖灯、汞灯）、氢氘灯。

三、实验原理原子光谱是线光谱，光谱排列的规律不同，反映出原子结构的不同，研究原子结构的基本方法之一是进行光谱分析。

氢（氘）原子光谱是最简单、最典型的原子光谱。

瑞士物理学家巴尔末根据实验结果给出氢原子光谱在可见光区域的经验公式为：422:-=n n B Hλ （1）式中H λ为氢原子谱线在真空中的波长，nm B 56.364=， 5,4,3=n 上式分别给出αH 、βH 、γH 、δH 各谱线波长，（1）式是瑞士物理学家巴耳末根据实验结果首先总结出来的。

故称为巴耳末公式。

若用波数λν1~=表示谱线，则（1）式可改写为： ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=222222121121441~n R n B n n B H ν （2） 式中H R 为里德伯常数。

根据波尔理论，可得出氢和类氢原子的里德伯常数为：()()Mm 1R M m 1m c h 4z e 2ch 4z e 2R 32044320442z +=+⋅==∞πεππεμπ （3） 其中：M 为原子核质量，m 为电子质量，e 为电子电荷，C 为光速，h 为普朗克常数，0ε为真空介电常数，z 为原子序数。

用光学多道分析器研究氢原子光谱摘要：光谱是光的频率和强度的分布关系图，是研究物质微观结构的一个重要途径。

在本实验中，使用光学多道分析器来测量氢原子的巴耳末系的,,,H H H H αβγδ的波长，并利用所测波长计算里德伯常量。

关键词：氢原子光谱、汞灯定标、光学多道分析器、巴耳末系、里德伯常量实验目的：1：测定氢原子巴耳末系发射光谱的波长的氢的里德伯常量。

2：了解氢原子能级与光谱的关系，画出氢原子的能级图。

3：了解光学多道分析器的原理和使用方法。

实验原理：根据玻尔理论，氢原子的能级公式为()()432021,1,2,,=81/1836.15e e e em e E n n m M h n m M Mm μμε=-=+ 其中称为约化质量，为电子质量，为原子核质量，氢原子的为。

电子从高能级跃迁到低能级时，发射的光子能量h ν为两能级间的能量差()()(),h E m E n m n ν=->，如以波数1/σλ=表示，则上式为()()()()2211H E m E n T n T m R hc n m σ-⎛⎫==-=- ⎪⎝⎭，式中H R 为氢原子里德伯常量，()T n 称为光谱项，它与能级()E n 是对应的，从H R 可得氢原子各能级的能量()21H E n R ch n=- ，式中1584.1356710eV s, 2.9979210/h c m s -=⨯⋅=⨯。

从3m ≥至2n =的跃迁，光子的波长位于可见光区，其光谱符合规律()2211,3,4,5,2H R m m σ⎛⎫=-=⎪⎝⎭，这是巴耳末发现并总结的经验规律，称为巴耳末系，氢原子的莱曼系位于紫外，其他线系均位于红外。

实验仪器：光学多道分析器是利用现代电子技术接收和处理某一波长范围内光谱信息的光学多通道检测系统。

多色仪及光源部分的光路见图1，图1光源S 经透镜L 成像于多色仪的入射狭缝S 1,，入射光经平面反射镜M 1转向90 ，经球面镜M 2反射后成为了平行光射向光栅G ，衍射光经球面镜M 3和平面镜M 4成像于观察屏P 。

光学多道与氢氘光谱学摘要：本实验利用光学多道分析仪，使用已知波长的氦光谱进行定标测量了氢光谱，并在此基础上测量氢氘同位素光谱，获得了氢氘光谱的波长值；利用这些测得值计算出了氢氘的里德伯常量分别为1109673.12H R cm -=和1109702.66D R cm -=，得到了氢氘光谱的各光谱项；除此之外，还通过计算得出了电子与质子质量之比为0.000539e p m m =，与理论值0.000545符合得很好。

关键词：光学多道仪、CCD 光电探测器、光电倍增管、氢氘光谱1． 引言光谱学在物理学各分支学科中都占有重要地位，而且在生物学、考古学等诸多方面有着广泛的应用。

而在光谱学史上，氢光谱的实验和理论研究都占有特别重要的地位。

1885年，巴耳末（J.J.Balmer ）发现了可见光区氢光谱线波长的规律。

1892年，尤雷（H.C.Urey ）等发现氢(H)同位素——氘(D)的光谱。

氢氘原子核外都只有一个电子，光谱极为相似，但由于原子核质量不同，故其对应谱线波长稍有差别，即存在“同位素位移”。

本实验利用光学多道分析仪，从巴尔末公式出发研究氢氘光谱，了解其谱线特点， 并学习光学多道仪的使用方法及基本的光谱学技术。

2． 实验原理在原子体系中，原子的能量状态是量子化的，每一个能量状态称原子的一个能级。

能量最低的状态称为原子的基态，高于基态的其余各能级称为原子的激发态。

处于高能级的原子，总是会自发跃迁到低能级，并发射出光子。

设光子能量为ε，频率为υ，高能级为2E ，低能为 1E ，则2121,E E h E E hευυ-==-=（1） 而由于原子能级的分立，所以当原子由高能级向低能级跃迁时，会发出一些特定频率的光，这些光在分光仪上表现为一条条分立的“线性光谱”。

这些频率由巴耳末公式确定。

对H 原子有：2212111H H R n n λ⎛⎫=- ⎪⎝⎭ （2）式中H R 是H 原子的里德伯常量。

当122,3,4,5n n ==时，光谱大部分位于可见光区，对应线系为巴尔末系，即22111,3,4,52H H R n n λ⎛⎫=-= ⎪⎝⎭（3）与H 类似，D 的巴耳末系的公式为： 22111,3,4,5...2D D R n n λ⎛⎫=-= ⎪⎝⎭ （4） 式中D R 为D 原子的里德伯常量。

用光学多道分析器研究氢原子光谱俞维民（物理科学与技术学院物理学基地班学号：2008301020001）摘要：使用光学多道分析器测定氢原子巴尔末系中HαHβHγHδ波长，并利用所测的波长拟合计算出氢原子的里德伯常量。

关键词：光学多道分析器，氢原子光谱，巴尔末系，里德伯常量THE STUDY OF HYDROGEN ATOMIC SPECTRUM WITH OPTICALMULTICHANNEL ANALYZERAbstract:By using the OMA, this article will measure out the wavelength ofHαHβHγHδin the Balmer spectrum, and work out the Rydberg constant of hydrogenatom by using the wavelength above.Keywords: Optical Multichannel Analyzer, Hydrogen atom spectrum, Balmer spectrum, Rydberg constant1.引言：下图为氢原子的能级图．根据玻尔理论，氢原子的能级公式为：（34-1）式中称为约化质量，m e为电子质量，M为原子核质量．氢原子的等于1836.15。

电子从高能级跃迁到低能级时，发射的光子能量hν为两能级间的能量差如以波数表示，则上式为式中R H 称为氢原子的里德伯常数，单位是m -1，T(n)称为光谱项，它与能级E(n)是对应的．从R H 可得氢原子各能级的能量式中-1584.1356710, 2.9979210-1h=eV s m s c ⨯⋅=⨯⋅从能级图可知，从3≥m 至2n =的跃迁．光子波长位于可见光区．其光谱符合规律这就是1885年巴耳末发现并总结的经验规律，称为巴耳末系．2. 实验原理：由于H α线波长为656.28nm ，H δ波长为410.17nm ，波长间隔246nm 超过CCD 一帧159nm 范围，无法在同屏中观察到，故需分两次观察测量。