全等三角形的判定ASA-AAS专题练习题

《三角形全等ASA 和AAS 》专题班级 姓名宝剑锋从磨砺出,梅花香自苦寒来【温馨提示】证明的书写步骤：一、填空题1．（1）全等三角形判定方法3——“角边角”（即______）指的是________________________________________________________________________；（2）全等三角形判定方法4——“角角边” （即______）指的是________________________________________________________________________．2．已知：如图，PM ＝PN ，∠M ＝∠N ．求证：AM ＝BN ．分析：∵PM ＝PN ，∴ 要证AM ＝BN ，只要证P A ＝______，只要证______≌______．证明：在△______与△______中，⎪⎩⎪⎨⎧∠=∠=∠=∠),______(______),______(______),______(______ ∴ △______≌△______ （ ）．∴P A ＝______ （ ）．∵PM ＝PN （ ），∴PM －______＝PN －______，即AM ＝______．3．已知：如图，AC BD ．求证：OA ＝OB ，OC ＝OD ．分析：要证OA ＝OB ，OC ＝OD ，只要证______≌______．证明：∵ AC ∥BD ，∴ ∠C ＝______．在△______与△______中，⎪⎩⎪⎨⎧==∠∠=∠),______(______),______(),______(C AOC ∴______≌______ （ ）．∴ OA ＝OB ，OC ＝OD （ ）．二、选择题4．能确定△ABC ≌△DEF 的条件是 （ ）A ．AB ＝DE ，BC ＝EF ，∠A ＝∠E B ．AB ＝DE ，BC ＝EF ，∠C ＝∠EC ．∠A ＝∠E ，AB ＝EF ，∠B ＝∠D D ．∠A ＝∠D ，AB ＝DE ，∠B ＝∠E5．如图，已知△ABC 的六个元素，则下面甲、乙、丙三个三角形中，和△ABC全等的图形是 （ ）A ．甲和乙B ．乙和丙C ．只有乙D ．只有丙6．AD 是△ABC 的角平分线，作DE ⊥AB 于E ，DF ⊥AC 于F ，下列结论错误的是（ ）A ．DE ＝DFB ．AE ＝AFC ．BD ＝C D ．∠ADE ＝∠ADF三、解答题7．阅读下题及一位同学的解答过程：如图，AB 和CD 相交于点O ，且OA ＝OB ，∠A ＝∠C ．那么△AOD 与△COB 全等吗？若全等，试写出证明过程；若不全等，请说明理由．答：△AOD ≌△COB ．证明：在△AOD 和△COB 中，⎪⎩⎪⎨⎧∠=∠=∠=∠),(),(),(对顶角相等已知已知COB AOD OB OA C A∴ △AOD ≌△COB （ASA ）．问：这位同学的回答及证明过程正确吗？为什么？综合、应用、诊断8．已知：如图，AB ⊥AE ，AD ⊥AC ，∠E ＝∠B ，DE ＝CB ．求证：AD ＝AC ．9．已知：如图，在△MPN中，H是高MQ和NR的交点，且MQ＝NQ．求证：HN＝PM.10．已知：AM是ΔABC的一条中线，BE⊥AM的延长线于E，CF⊥AM于F，BC＝10，BE＝4．求BM、CF的长．拓展、探究、思考11．填空题（1）已知：如图，AB＝AC，BD⊥AC于D，CE⊥AB于E.欲证明BD＝CE，需证明Δ______≌△______，理由为______．（2）已知：如图，AE＝DF，∠A＝∠D，欲证ΔACE≌ΔDBF，需要添加条件______,证明全等的理由是______；或添加条件______，证明全等的理由是______；也可以添加条件______，证明全等的理由是______．12．如图，已知ΔABC≌ΔA'B'C'，AD、A'D'分别是ΔABC和ΔA'B'C'的角平分线．（1）请证明AD＝A'D'；（2）把上述结论用文字叙述出来；（3）你还能得出其他类似的结论吗？13．如图，在△ABC中，∠ACB＝90°，AC＝BC，直线l经过顶点C，过A、B两点分别作l的垂线AE、BF，E、F为垂足．（1）当直线l不与底边AB相交时，求证：EF＝AE＋BF．（2）如图，将直线l绕点C顺时针旋转，使l与底边AB交于点D，请你探究直线l在如下位置时，EF、AE、BF之间的关系．①AD＞BD；②AD＝BD；③AD＜BD．。

第十二章全等三角形12.2.3 三角形全等的判定(三)ASA、AAS1．如图，已知△ABC三条边、三个角，则甲、乙两个三角形中和△ABC全等的是( ) A．甲B．乙C．甲和乙都是D．都不是2．如图，∠ABC＝∠DCB，BD，CA分别是∠ABC，∠DCB的平分线．求证：AB＝DC.3．如图，BD⊥AC于点D，CE⊥AB于点E，AD＝AE.求证：BE＝CD.4．如图，在△ABC中，∠B＝∠C，D为BC的中点，过点D分别向AB，AC作垂线段，则能够说明△BDE≌△CDF的理由是( )A．SSS B．SASB．C．ASA D．AAS5．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，CE＝BF，∠A ＝∠D.求证：AB＝CD.6．如图，∠B＝∠DEF，AB＝DE，要说明△ABC≌△DEF.(1)若以“SAS”为依据，还需添加的条件为；(2)若以“ASA”为依据，还需添加的条件为；(3)若以“AAS”为依据，还需添加的条件为．7．如图，AE∥DF，AE＝DF，则添加下列条件还不能确定△EAC≌△FDB( ) A．AB＝CD B．CE∥BF C．CE＝BF D．∠E＝∠F第7题图第8题图第9题图第10题图8．如图，已知D是△ABC的边AB上一点，DF交AC于点E，DE＝EF，FC∥AB，若BD ＝2，CF＝5，则AB的长为( )A．2 B．5C．7 D．39．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC(不添加其他字母及辅助线)，你添加的条件是．10．如图，要测量河两岸相对的两点A，B的距离，在AB的垂线BF上取两点C，D，使BC＝CD，过点D作BF的垂线DE，与AC的延长线交于点E，则∠ABC＝∠CDE＝90°，BC＝DC，∠1＝，△ABC≌．若测得DE的长为25米，则河宽AB的长为．11．如图，已知点A，F，E，C在同一直线上，AB∥CD，∠ABE＝∠CDF，AF＝CE.(1)从图中任找两组全等三角形；(2)从(1)中任选一组进行证明．12．已知△ABN和△ACM位置如图所示，AB＝AC，AD＝AE，∠1＝∠2.求证：(1)BD＝CE；(2)∠M＝∠N.13．如图1，在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥MN 于点M，BN⊥MN于点N.(1)求证：MN＝AM＋BN；(2)如图2，若过点C作直线MN与线段AB相交，AM⊥MN于点M，BN⊥MN于点N(AM＞BN)，(1)中的结论是否仍然成立？说明理由．参考答案1．B2．证明：∵∠ABC ＝∠DCB ，BD ，CA 分别是∠ABC ，∠DCB 的平分线，∴∠DBC ＝∠ACB.在△ABC 和△DCB 中，⎩⎪⎨⎪⎧∠ABC ＝∠DCB ，BC ＝CB ，∠ACB ＝∠DBC ，∴△ABC ≌△DCB(ASA )．∴AB ＝DC.3．证明：∵BD ⊥AC 于点D ，CE ⊥AB 于点E ，∴∠ADB ＝∠AEC ＝90°.在△ABD 和△ACE 中，⎩⎪⎨⎪⎧∠ADB ＝∠AEC ，AD ＝AE ，∠A ＝∠A ，∴△ABD ≌△ACE(ASA )．∴AB ＝AC.又∵AD ＝AE ，∴AB －AE ＝AC －AD ，即BE ＝CD.4．D5．证明：∵AB ∥CD ，∴∠B ＝∠C.∵CE ＝BF ，∴CE ＋EF ＝BF ＋EF ，即CF ＝BE.在△ABE 和△DCF 中，⎩⎪⎨⎪⎧∠A ＝∠D ，∠B ＝∠C ，BE ＝CF ，∴△ABE ≌△DCF(AAS )，∴AB ＝CD.6． (1) BC ＝EF 或BE ＝CF ；(2) ∠A ＝∠D ；(3) ∠ACB ＝∠F ．7．C8．C9．AC ＝BC ．10．25米．11．解：(1)△ABE ≌△CDF ，△AFD ≌△CEB.(2)选△ABE ≌△CDF ，证明：∵AB ∥CD ，∴∠BAE ＝∠DCF.∵AF ＝CE ，∴AF ＋EF ＝CE ＋EF ，即AE ＝CF.在△ABE 和△CDF 中，⎩⎪⎨⎪⎧∠BAE ＝∠DCF ，∠ABE ＝∠CDF ，AE ＝CF ，∴△ABE ≌△CDF(AAS )．12．证明：(1)在△ABD 和△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠1＝∠2，AD ＝AE ，∴△ABD ≌△ACE(SAS )．∴BD ＝CE.(2)∵∠1＝∠2，∴∠1＋∠DAE ＝∠2＋∠DAE ，即∠BAN ＝∠CAM.由(1)，得△ABD ≌△ACE ，∴∠B ＝∠C. 在△ACM 和△ABN 中，⎩⎪⎨⎪⎧∠C ＝∠B ，AC ＝AB ，∠CAM ＝∠BAN ，∴△ACM ≌△ABN(ASA )．∴∠M ＝∠N.13．解：(1)证明：∵∠ACB ＝90°，∴∠ACM ＋∠BCN ＝90°.又∵AM ⊥MN ，BN ⊥MN ，∴∠AMC ＝∠CNB ＝90°.∴∠BCN ＋∠CBN ＝90°.∴∠ACM ＝∠CBN. 在△ACM 和△CBN 中，⎩⎪⎨⎪⎧∠ACM ＝∠CBN ，∠AMC ＝∠CNB ，AC ＝CB ，∴△ACM ≌△CBN(AAS )．∴MC ＝NB ，MA ＝NC.∵MN ＝MC ＋CN ，∴MN ＝AM ＋BN.(2)(1)中的结论不成立，结论为MN ＝AM －BN. 理由如下：同(1)中证明可得△ACM ≌△CBN ，∴CM＝BN，AM＝CN.∵MN＝CN－CM，∴MN＝AM－BN.。

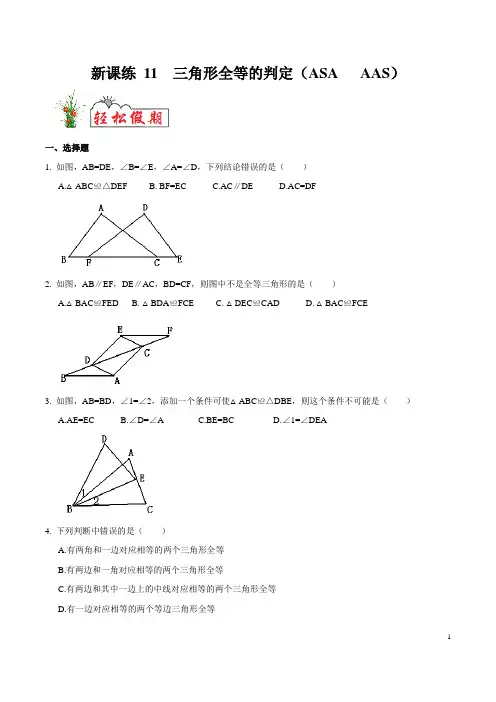
新课练11 三角形全等的判定（ASA AAS）一、选择题1. 如图，AB=DE，∠B=∠E，∠A=∠D，下列结论错误的是（）A.△ABC≌△DEFB. BF=ECC.AC∥DED.AC=DF2. 如图，AB∥EF，DE∥AC，BD=CF，则图中不是全等三角形的是（）A.△BAC≌FEDB. △BDA≌FCEC. △DEC≌CADD. △BAC≌FCE3. 如图，AB=BD，∠1=∠2，添加一个条件可使△ABC≌△DBE，则这个条件不可能是（）A.AE=ECB.∠D=∠AC.BE=BCD.∠1=∠DEA4. 下列判断中错误的是（）A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5. △ABC 和△'''A B C 中， 条件 ①AB =''A B ， ②BC =''B C ， ③ AC=''A C ， ④ ∠A = ∠'A ， ⑤ ∠B = ∠'B ， ⑥ ∠C = ∠'C ， 则下列各组条件中， 不能保证△ABC ≌△'''A B C 的是( ) A.①②③B. ①②⑤C. ①③⑤D. ②⑤⑥6．如图，点A 在DE 上，AC=CE ，∠1=∠2=∠3，则DE 的长等于（ ）A ．DCB ．BCC ．ABD ．AE ＋AC二、填空题7. 已知：如图，AE=DF ，∠A=∠D ，欲证ΔACE ≌ΔDBF ，需要添加条件______，证明全等的理由是______；或添加条件______，证明全等的理由是______；也可以添加条件______，证明全等的理由是______．8. 如图，点D 在AB 上，点E 在AC 上，且∠B=∠C ，在条件①AB=AC ，②AD=AE ，③BE=CD ，④∠AEB=∠ADC 中，不能使△ABE ≌△ACD 的是_______.（填序号）9. 已知，如图，AB ∥CD ，AF ∥DE ，AF=DE ，且BE=2，BC=10，则EF=________.10. 如图，AB ∥CD ，AD ∥BC ，OE=OF ，图中全等三角形共有______对.11．如图，直线l 过正方形ABCD 的顶点B ，点A 、C 到直线l 的距离分别是1和2，则EF 的长是___________．.12. 在△ABC 和△DEF 中（1）AB=DE ；（2）BC=EF ；（3）AC=DF ；（4）∠A=∠D ；（5）∠B=∠E ；（6）∠C=∠F 从这六个条件中选取三个条件可判定△ABC 与△DEF 全等的方法共有____种. 三、解答题13．已知：如图，在梯形ABCD 中，AD ∥BC ，E 是AB 的中点，CE 的延长线与DA 的延长线相交于点F ． （1）求证：△BCE ≌△AFE ；（2）连接AC 、FB ，则AC 与FB 的数量关系是，位置关系是 ．FE BCA D14. 已知：如图，ABC △中，45ABC ∠=°，CD AB ⊥于D ，BE AC ⊥于E ，BE 与CD 相交于点F ．求证：BF AC =.参考答案及解析新课练11 三角形全等的判定（ASA AAS）一、选择题1. 如图，AB=DE，∠B=∠E，∠A=∠D，下列结论错误的是（）A．△ABC≌△DEF B．BF=ECC．AC∥DE D．AC=DF【答案】C；2. 如图，AB∥EF，DE∥AC，BD=CF，则图中不是全等三角形的是（）A．△BAC≌FED B．△BDA≌FCEC．△DEC≌CAD D．△BAC≌FCE【答案】D；3. 如图，AB=BD，∠1=∠2，添加一个条件可使△ABC≌△DBE，则这个条件不可能是（）A．AE=EC B．∠D=∠A C．BE=BC D．∠1=∠DEA【答案】A ；【解析】D 选项可证得∠D=∠A ，从而用ASA 证全等. 4. 下列判断中错误的是（ ）A ．有两角和一边对应相等的两个三角形全等B ．有两边和一角对应相等的两个三角形全等C ．有两边和其中一边上的中线对应相等的两个三角形全等D ．有一边对应相等的两个等边三角形全等 【答案】B ；【解析】C 选项和D 选项都可以由SSS 定理证全等.5. △ABC 和△'''A B C 中， 条件 ①AB =''A B ， ②BC =''B C ， ③ AC=''A C ， ④ ∠A = ∠'A ， ⑤ ∠B = ∠'B ， ⑥ ∠C = ∠'C ， 则下列各组条件中， 不能保证△ABC ≌△'''A B C 的是( ) A ．①②③ B ． ①②⑤C ． ①③⑤D ． ②⑤⑥【答案】C ；【解析】C 选项是两边及一边的对角对应相等，不能保证全等.6．如图，点A 在DE 上，AC=CE ，∠1=∠2=∠3，则DE 的长等于（ ）A ．DCB ．BCC ．ABD ．AE ＋AC【答案】C ；【解析】可证∠BAC=∠E ，∠BCA=∠DCE ，所以△ABC ≌△EDC ，DE=AB ． 二、填空题7. 已知：如图，AE=DF ，∠A=∠D ，欲证ΔACE ≌ΔDBF ，需要添加条件______，证明全等的理由是______；或添加条件______，证明全等的理由是______；也可以添加条件______，证明全等的理由是______．【答案】∠2=∠1，AAS；AC=DB，SAS；∠E=∠F，ASA．8. 如图，点D在AB上，点E在AC上，且∠B=∠C，在条件①AB=AC，②AD=AE，③BE=CD，④∠AEB=∠ADC中，不能使△ABE≌△ACD的是_______.（填序号）【答案】④【解析】三个角对应相等不能判定三角形全等.9. 已知，如图，AB∥CD，AF∥DE，AF=DE，且BE=2，BC=10，则EF=________.【答案】6；【解析】△ABF≌△CDE，BE=CF=2，EF=10－2－2=6.10. 如图，AB∥CD，AD∥BC，OE=OF，图中全等三角形共有______对.【答案】6；【解析】△ABO≌△CDO，△AFO≌△CEO，△DFO≌△BEO，△AOD≌△COB，△ABD≌△CDB，△ABC≌△CDA．11．如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是1和2，则EF的长是___________．【答案】3；【解析】由AAS 证△ABF ≌△CBE ，EF=FB ＋BE=CE ＋AF=2＋1=3.12. 在△ABC 和△DEF 中（1）AB=DE ；（2）BC=EF ；（3）AC=DF ；（4）∠A=∠D ；（5）∠B=∠E ；（6）∠C=∠F 从这六个条件中选取三个条件可判定△ABC 与△DEF 全等的方法共有____种. 【答案】13；【解析】ASA 类型3种，AAS 类型6种，SAS 类型3种，SSS 类型一种，共13种 三、解答题13．已知：如图，在梯形ABCD 中，AD ∥BC ，E 是AB 的中点，CE 的延长线与DA 的延长线相交于点F ． （1）求证：△BCE ≌△AFE ；（2）连接AC 、FB ，则AC 与FB 的数量关系是 ，位置关系是 ．【解析】（1）证明：∵AD ∥BC ， ∴∠1 =∠F ． ∵点E 是AB 的中点， ∴BE=AE.在△BCE 和△AFE 中，1F32BE AE ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BCE ≌△AFE （AAS ）. （2）相等， 平行.14. 已知：如图，ABC △中，45ABC ∠=°，CD AB ⊥于D ，BE AC ⊥于E ，BE 与CD 相交于点F ．求证：BF AC =.【解析】证明： ∵ CD AB ⊥∴ 90BDC CDA ∠=∠=︒ ∵ 45ABC ∠=︒∴ 45DCB ABC ∠=∠=︒ ∴ DB DC = ∵ BE AC ⊥ ∴ 90AEB ∠=︒ ∴ 90A ABE ∠+∠=︒ ∵ 90CDA ∠=︒ ∴ 90A ACD ∠+∠=︒ ∴ ABE ACD ∠=∠ 在BDF ∆和CDA ∆中BDC CDA DB DCABE ACD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆ （ASA ） ∴BF AC =。

12.2 全等三角形判定二（ASA ，AAS ）全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA”）.注意：如图，如果∠A ＝∠'A ，AB ＝''A B ，∠B ＝∠'B ，则△ABC ≌△'''A B C .题型1：用ASA 判定三角形全等1.已知：如图，E ，F 在AC 上，AD ∥CB 且AD ＝CB ，∠D＝∠B．求证：AE ＝CF ．【答案与解析】证明：∵AD ∥CB∴∠A ＝∠C在△ADF 与△CBE 中A C AD CBD B Ð=Ðìï=íïÐ=Ðî∴△ADF ≌△CBE （ASA ）∴AF ＝CE ，AF ＋EF ＝CE ＋EF故得：AE ＝CF【总结】利用全等三角形证明线段(角)相等的一般方法和步骤如下：(1)找到以待证角(线段)为内角(边)的【变式1-1】如图，已知AB=AC，∠B=∠C，求证：△ABE≌△ACD．【答案】证明：在△ABE和△ACD中，∵∠A=∠AAB=AC∠B=∠C，∴△ABE≌△ACD（ASA）．【解析】【分析】利用ASA证明△ABE和△ACD全等即可．【变式1-2】如图，AB=AE，∠1=∠2，∠B=∠AED．求证：△ABC≌△AED．【答案】证明：∵∠1=∠2，∴∠1+∠EAC=∠2+∠EAC,∴∠BAC=∠EAD,在△ABC与△AED中，∠BAC=∠EADAB=AE∠B=∠AED∴△ABC≌△AED(ASA)【解析】【分析】由∠1=∠2，证明∠BAC=∠EAD,再结合：AB=AE，∠B=∠AED，利用角边角公理可得结论．全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）题型2：用AAS 判定三角形全等2.已知：如图，AB ⊥AE ，AD ⊥AC ，∠E ＝∠B ，DE ＝CB ．求证：AD ＝AC ．【思路点拨】要证AC ＝AD ，就是证含有这两个线段的三角形△BAC ≌△EAD.【答案与解析】证明：∵AB ⊥AE ，AD ⊥AC ，∴∠CAD ＝∠BAE ＝90°∴∠CAD ＋∠DAB ＝∠BAE ＋∠DAB ，即∠BAC ＝∠EAD在△BAC 和△EAD 中BAC EAD B ECB=DE Ð=ÐìïÐ=Ðíïî∴△BAC ≌△EAD （AAS ）∴AC ＝AD【总结】我们要善于把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．【变式2-1】如图，在△ABC 和△CDE 中，点B 、D 、C 在同一直线上，已知∠ACB=∠E ，AC=CE ，AB ∥DE ，求证：△ABC ≌△CDE ．【答案】证明：∵AB ∥DE ，∴∠B =∠EDC ，在△ABC 和△CDE 中，∠B =∠EDC ∠ACB =∠E AC =CE，∴△ABC≌△CDE (AAS )．【解析】【分析】利用“AAS”证明△ABC≌△CDE 即可。

①AB＝DE，②∠ACB＝∠F，③∠A＝∠D，④AC＝DF．选出两个作为条件，推出 ．并予以证明．（写出一种即可）
已知：，．
求证： ．
证明：
22.如图，在△AEC和△DFB中，∠E=∠F，点A，B，C，D在同一直线上，有 如下三个关系式：①AE∥DF，②AB=CD，③CE=BF。
（1）请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题（用序号写出命题书写形式：“如果 ， ，那么 ”）；
C.△DCG≌△ECFD.△ADB≌△CEA
8.如图，在△ABC中，AB=AC，∠ABC．∠ACB的平分线BD，CE相交于O点，且
BD 交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：
①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；
⑤△ACE≌△BCE；上述结论一定正确的是（ ）
C.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC
6.如图，已知 中， ， 是 高 和 的交点， ，则线段 的长度为（）.
A． B．4C． D．
7.如图，点B、C、E在同 一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（ ）
A.△ACE≌△BCDB.△BGC≌△AFC
12.如图，AD=BC，AC=BD，则图中全等三角形有对.
13.如图，已知AB∥CF, E为DF的中点.若AB=9 cm,CF=5 cm,则BD的长度
为cm.
14. 如图，∠A =∠D，OA=OD,∠DOC=50°，则∠DBC=度.
15．如图， ，请你添加一个条件：，使 （只添一个即可）．
16.如图，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B，C作过点A的直线的垂线BD，C E，垂足分别为点D,E.若BD=2，CE=3，则AE=，AD=.

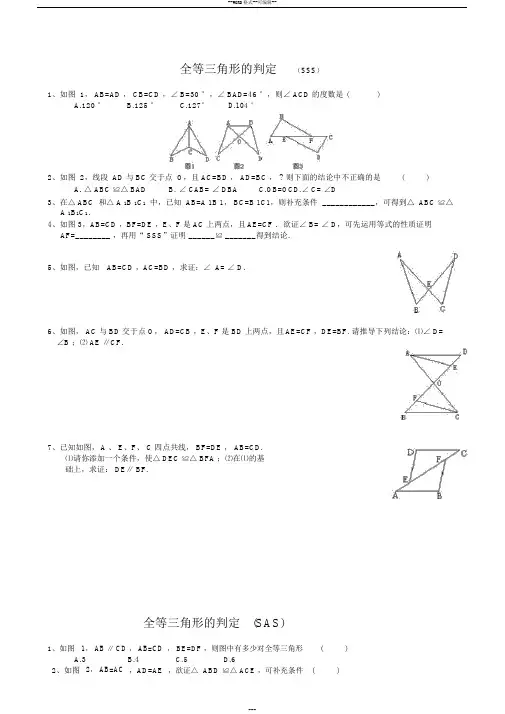
全等三角形的判定（SSS）1、如图 1， AB=AD ， CB=CD ，∠ B=30 °，∠ BAD=46 °，则∠ ACD 的度数是 ()A.120 °B.125 °C.127°D.104 °2、如图 2，线段 AD 与 BC 交于点 O，且 AC=BD ， AD=BC ， ? 则下面的结论中不正确的是()A. △ ABC ≌△ BADB. ∠ CAB= ∠ DBAC.OB=OCD.∠ C= ∠D3、在△ ABC 和△ A 1B 1C1中，已知 AB=A 1B 1， BC=B 1C1，则补充条件 ____________，可得到△ ABC ≌△A 1B1C1．4、如图 3，AB=CD ，BF=DE ，E、F 是 AC 上两点，且AE=CF ．欲证∠ B= ∠ D，可先运用等式的性质证明AF=________ ，再用“ SSS”证明 ______≌ _______得到结论．5、如图，已知AB=CD ，AC=BD ，求证：∠ A= ∠ D．6、如图， AC 与 BD 交于点 O， AD=CB ，E、F 是 BD 上两点，且AE=CF ，DE=BF. 请推导下列结论：⑴∠ D=∠B ；⑵ AE ∥CF．7、已知如图，A 、 E、F、 C 四点共线， BF=DE ， AB=CD.⑴请你添加一个条件，使△ DEC ≌△ BFA ；⑵在⑴的基础上，求证： DE∥ BF.全等三角形的判定(SAS)1、如图1， AB ∥ CD ， AB=CD， BE=DF ，则图中有多少对全等三角形()A.3B.4C.5D.62、如图2， AB=AC，AD=AE，欲证△ABD≌△ ACE ，可补充条件()A. ∠ 1= ∠23、如图 3， AD=BCA.AB ∥ CDB.∠ B= ∠ C，要得到△ ABDB.AD ∥ BCC.∠ D= ∠ ED. ∠BAE= ∠CAD 和△CDB 全等，可以添加的条件是 ( C.∠A=∠ C D. ∠ABC= ∠ CDA)4、如图 4， AB 与 CD 交于点 O， OA=OC ， OD=OB ，∠ AOD=________ ， ? 根据 _________可得到△ AOD≌△ COB，从而可以得到AD=_________ ．5、如图 5，已知△ ABC 中， AB=AC ， AD 平分∠ BAC ，请补充完整过程说明△∵ AD 平分∠ BAC ，∴∠ ________=∠ _________(角平分线的定义).在△ ABD 和△ ACD 中，∵ ____________________________ ，∴△ ABD≌△ ACD（ABD）≌△ ACD的理由．6、如图 6，已知 AB=AD ， AC=AE ，∠ 1= ∠ 2，求证∠ ADE= ∠ B.7、如图，已知AB=AD ，若 AC 平分∠ BAD ，问 AC 是否平分∠ BCD ？为什么？BA CD8、如图，在△ABC 和△ DEF 中， B 、 E、 F、 C，在同一直线上，下面有 4 个条件，请你在其中选 3 个作为题设，余下的一个作为结论，写一个真命题，并加以证明.①AB=DE ；② AC=DF ；③∠ ABC= ∠ DEF ；④ BE=CF.9、如图⑴， AB ⊥ BD ， DE⊥ BD ，点 C 是 BD 上一点，且BC=DE ， CD=AB ．⑴试判断AC 与 CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线 BD 向左平移，使△CDE 的顶点 C 与 B 重合，此时第⑴问中的位置关系还成立吗？(注意字母的变化)AC与BE全等三角形（三） AAS和 ASA【知识要点】1．角边角定理（ ASA）：有两角及其夹边对应相等的两个三角形全等.2 ．角角边定理（ AAS）：有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例 1．如图， AB∥ CD， AE=CF，求证： AB=CDD FC O例 2．如图，已知： AD=AE，ACD ABE ，求证：BD=CE.AE BAD E例 3．如图，已知：CD . BAC ABD ，求证：OC=OD.B CD COA B例 4．如图已知： AB=CD，AD=BC，O是 BD中点，过 O点的直线分别交DA和 BC的延长线于E，F. 求证： AE=CF.FDCOAB例 5．如图，已知123 ，AB=AD.求证：BC=DE.EA2E1OB D 3C例6．如图，已知四边形 ABCD中， AB=DC，AD=BC，点 F 在 AD 上，点 E 在 BC上， AF=CE， EF 的对角线 BD 交于 O，请问 O点有何特征？A F DOB EC【经典练习】1. △ ABC和△A B C中，A A' , BC B C ，C C 则△ABC与△ A B C.2．如图，点 C，F 在 BE上，12, BC EF ,请补充一个条件，使△ABC≌DFE,补充的条件是.A DB 12EC F3．在△ ABC和△A B C中，下列条件能判断△ABC和△A B C全等的个数有（）① A AB B ， BC B C② AA ， B B ， AC A C③ A AB B ， AC B C④ AA ， B B ， AB A CA ． 1 个 B. 2 个 C. 3 个 D. 4 个4．如图，已知 MB=ND，MBA NDC ，下列条件不能判定是△ABM≌△CDN的是（）A．M NB. AB=CD M NC． AM=CND. AM∥ CN5．如图 2 所示，∠E=∠ F=90°，∠ B=∠ C， AE=AF，给出下列结论：①∠ 1=∠2② BE=CF③△ ACN≌△ ABM④ CD=DN A C B D 其中正确的结论是_________ _________ 。

全等三角形判定练习(ASA、AAS、HL) 判定定理3、有两角及其夹边对应相等的两个三角形全等(ASA)在△ABC和△DFE中∠A=∠D （已知）AB=DE（已知）∠B=∠E（已知）∴△ABC≌△DEF（ASA）判定定理4、有两角及一角的对边对应相等的两个三角形全等(AAS)在△ABC和△DFE中∠A=∠D ,∠C=∠FAB=DE∴△ABC≌△DFE(AAS)判定定理5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL) 在Rt△ABC和Rt△A′B′C′中AB=AB (直角边)BC = B′C′（斜边）∴Rt△ABC≌Rt△A′B′C′（HL）1 如图，∠E=∠B，∠1=∠2，EC=BC，求证：DE=AB。

2 已知：如图点C是AB的中点，CD∥BE，且∠D=∠E.求证：. CD=BE3 如图，DC=BC，∠B＝∠D=90°，求证：AB＝AD.ACB ED4 如图，AC⊥OB，BD⊥OA，AC与BD交于E点(1)如果OC=OD，求证：∠A=∠B。

(2)如果∠A=∠B ,OC=OD，求证：AC=BD。

(3)如果AO=BO,OC=OD，求证：∠A=∠B。

OBACDE5 如图.已知AC∥DF，且BE=CF、（1）请你只添加一个条件，使△ABC≌△DEF，你添加的条件是；．．（2）添加条件后，证明△ABC≌△DEF.6 如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．请从下列三个条件中选择一个合适．．．．的条件．．．，添加到已知条件中，使AB∥ED成立，并给出证明．供选择的三个条件（请从其中选择一个）：①AB=ED；②BC=EF；③∠ACB=∠DFE．7 如图，∠A=∠D，AB=CD，则△≌△，请证明8如图，O为AC中点，AB∥CD，证明AB=CDDOC BAAB EFC9 在ABC △中，D 是AB 上一点，DF 交AC 于点E ，DE FE =，AE CE =，AB 与CF 有什么位置关系？证明你的结论10 已知：如图∠B=∠E=90°AC=DF FB=EC ，证明：AB=DEAD BCFE11如图，已知AB=AC，AD=AE，BE与CD相交于O，证明：（1）ΔABE≌ΔACD（2）ΔDOB≌ΔEOC （3）ΔDBC≌ΔECB12 正方形ABCD 中, F 分别是AB 和AD 上的点，已知CE ⊥BF ，垂足为M ，证明BE=AFDMFEA。

全等三角形的判定办法SAS 专题练习之邯郸勺丸创作1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可弥补条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是（ ）A ．AB=A′B′,AC=A′C′,∠C=∠C′B. AB=A′B′, ∠A=∠A′,BC=B′C′C. AC=A′C′, ∠A=∠A′,BC=B′CD. AC=A′C′, ∠C=∠C′,BC=B′C3.如图,AB 与CD 交于点O,OA=OC,OD=OB,∠AOD=,按照_________可得到△AOD≌△COB,从而可以得到AD=_________．4.如图,已知BD=CD,要按照“SAS”判定△ABD≌△ACD,则还需添加的条件是.5.如图,AD=BC,要按照“SAS”判定△ABD≌△BAC,则还需添加的条件是6.如图,已知△ABC 中,AB=AC,AD 平分∠BAC,请弥补完整过程说明△ABD≌△ACD 的理由． 解：∵AD 平分∠BAC,∴∠________=∠_________(角平分线的定义).在△ABD 和△ACD 中,∵∴△ABD≌△ACD（ ）7.如图,AC 与BD 相交于点O,已知OA=OC,OB=OD, 第3题第4题第6题第5题求证:△AOB≌△COD证明：在△AOB和△COD中∵∴△AOB≌△COD( )第7题8.已知：如图,AB=CB,∠1=∠2 △ABD 和△CBD 全等吗？9.已知：如图,AB=AC,AD=AE ,∠1 =∠2 .试说明：△ABD ≌△ACE .10.已知：如图,△ABC中, AD⊥BC 于D,AD=BD, DC=DE,∠C=50°.求∠ EBD的度数.全等三角形的判定办法AAS、ASA专题练习1. 已知：如图, FB=CE , AB∥ED ,AC∥FD.F、C在直线BE上．求证：AB=DE , AC=DF．2.已知：如图, AB⊥BC于B , EF⊥AC于G ,DF⊥BC于D , BC=DF．求证：AC=EF.3. 已知：如图AC⊥CD于C , BD⊥CD于D , M是AB的中点 , 连结CM并延长交BD于点F.求证：AC=BF．4. 已知：如图 , E、D、B、F在同一条直线上 ,AD∥CB , ∠BAD=∠BCD , DE=BF．求证：AE∥CF.5.如图在△ABC和△DBC中, ∠1=∠2 , ∠3=∠4 ,P是BC上任意一点．求证：PA=PD.6.已知：如图, AE=BF , AD∥BC , AD=BC.AB、CD 交于O点．求证：OE=OF7.已知：如图AC∥BD , AE和BE辨别平分∠CAB∠DBA ,CD过点E．求证AB＝AC＋BD时间：二O二一年七月二十九日。

全等三角形的判定（SSS）之南宫帮珍创作1、如图1, AB=AD, CB=CD, ∠B=30°, ∠BAD=46°, 则∠ACD的度数是( )°°°°2、如图2, 线段AD与BC交于点O, 且AC=BD, AD=BC, •则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中, 已知AB=A1B1, BC=B1C1, 则弥补条件____________, 可获得△ABC≌△A1B1C1．4、如图3, AB=CD, BF=DE, E、F是AC上两点, 且AE=CF．欲证∠B=∠D, 可先运用等式的性质证明AF=________, 再用“SSS”证明______≌_______获得结论．5、如图, 已知AB=CD, AC=BD, 求证：∠A=∠D．6、如图, AC与BD交于点O, AD=CB, E、F是BD上两点, 且AE=CF, DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．7、已知如图, A、E、F、C四点共线, BF=DE, AB=CD.⑴请你添加一个条件, 使△DEC≌△BFA；⑵在⑴的基础上, 求证：DE∥BF.全等三角形的判定(SAS)1、如图1, AB∥CD, AB=CD, BE=DF, 则图中有几多对全等三角形( )2、如图2, AB=AC, AD=AE, 欲证△ABD≌△ACE, 可弥补条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、如图3, AD=BC, 要获得△ABD和△CDB全等, 可以添加的条件是( )∥∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4, AB与CD交于点O, OA=OC, OD=OB, ∠AOD=________,•根据_________可获得△AOD≌△COB,从而可以获得AD=_________．DC BA5、如图5, 已知△ABC 中, AB=AC, AD 平分∠BAC, 请弥补完整过程说明△ABD ≌△ACD 的理由．∵AD 平分∠BAC, ∴∠________=∠_________(角平分线的界说).在△ABD 和△ACD 中,∵____________________________, ∴△ABD ≌△ACD （ ）6、如图6, 已知AB=AD, AC=AE, ∠1=∠2, 求证∠ADE=∠B.7、如图, 已知AB=AD, 若AC 平分∠BAD, 问AC 是否平分∠BCD ？为什么？8、如图, 在△ABC 和△DEF 中, B 、E 、F 、C, 在同一直线上, 下面有4个条件, 请你在其中选3个作为题设, 余下的一个作为结论, 写一个真命题, 并加以证明.①AB=DE ；②AC=DF ；③∠ABC=∠DEF ；④BE=CF.9、如图⑴, AB ⊥BD, DE ⊥BD, 点C 是BD 上一点, 且BC=DE, CD=AB ．⑴试判断AC 与CE 的位置关系, 并说明理由．⑵如图⑵, 若把△CDE 沿直线BD 向左平移, 使△CDE 的极点C 与B 重合, 此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变动)全等三角形（三）AAS 和ASA 【知识要点】1．角边角定理（ASA ）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS ）：有两角和其中一角的对边对应相等的两个三角形全等. 【典范例题】例1．如图, AB ∥CD, AE=CF, 求证：AB=CD例2．如图, 已知：AD=AE, ABE ACD ∠=∠, 求证：BD=CE.例3．如图, 已知：ABD BAC D C ∠=∠∠=∠., 求证：OC=OD.例4．如图已知：AB=CD, AD=BC, O 是BD 中点, 过O别交DA 和BC 的延长线于E, F.求证：AE=CF.例5．如图, 已知321∠=∠=∠, AB=AD.求证：例6．如图, 已知四边形ABCD 中点E 在BC 上, AF=CE, EF 的对角线BD交于征？【经典练习】1.△ABC 和△C B A '''中, C B C B A A ''='∠=∠,', ∠C B A '''.2．如图, 点C, F 在BE 上, ,,21EF BC =∠=∠请弥补一个条件, 使△ABC ≌DFE,弥补的条件是.3．在△ABC 和△C B A '''中, C B A '''全等的个数有（ ）①A A '∠=∠B B '∠=∠, C B BC ''=②A A '∠=∠, B B '∠=∠, C A C A ''='③A A '∠=∠B B '∠=∠, C B AC ''=④A A '∠=∠,B B '∠=∠,C A B A ''='A ． 1个B. 2个C. 3个D. 4个4．如图, 已知MB=ND, NDC MBA ∠=∠, 下列条件不能判定是△ABM ≌△CDN 的是（ ）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN5．如图2所示, ∠E =∠F =90°, ∠B =∠C , AE =AF , 给出下列结论：C①∠1=∠2 ②BE=CF ③△ACN≌△ABM ④CD=DN其中正确的结论是__________________.(注：将你认为正确的结论填上)图2 图36．如图3所示, 在△ABC和△DCB中, AB=DC, 要使△ABO≌DCO, 请你弥补条件________________(只填写一个你认为合适的条件). 7. 如图, 已知∠A=∠C, AF=CE, DE∥BF, 求证：△ABF≌△CDE. 8．如图, CD⊥AB, BE⊥AC, 垂足分别为D、E, BE交CD于F, 且AD=DF, 求证：AC= BF.9.如图, AB, CD相交于点O, 且AO=BO, 试添加一个条件, 使△AOC≌△BOD, 并说明添加的条件是正确的.（很多于两种方法）10．如图, 已知：BE=CD, ∠B=∠C, 求证：∠1=∠2.11.如图, 在Rt△ABC中, AB=AC, ∠BAC=90º, 多点AAN, BD⊥AN于D,CE⊥AN于E, 你能说说DE=BD-CE的理由吗？直角三角形全等HL【知识要点】斜边直角边公理：有斜边和直角边对应相等的两个直角三角形全等.【典范例题】例1 如图, B、E、F、C在同一直线上, AE⊥BC, DF⊥BC, AB=DC, BE=CF, 试判断AB与CD的位置关系. A例2 已知 如图, AB ⊥BD, CD ⊥BD, AB=DC, 求证：AD ∥BC.例 3 公路上A 、B为两村落（视为两个点）, DA ⊥AB 于点A, CB DA=16km, BC=10km, 现要在公路AB 上建一个土特产收购站CD两村落到E 站的距离相等, 那么E 站应建在距A 理？例4 如图, AD 是△ABC 的高, E 为AC 上一点, BE 交AD 于F, 具有BF=AC, FD=CD, 试探究BE 与AC 的位置关系.例 5 如图, A 、E 、F 、B 四点共线, AC ⊥CE AC=BD, 求证：△ACF ≌△BDE. 【经典练习】1．在Rt △ABC 和Rt △DEF 中, ∠ACB=∠DFE=90那么Rt △ABC 与Rt △DEF（填全等或不全等）2．如图, 点C 在∠DAB 的内部, CD ⊥AD 于D, CB ⊥AB 于B, CD=CB 那么Rt △ADC ≌Rt △ABC 的理由是（ ）A ．SSS B. ASA C. SAS D. HL3．如图, CE ⊥AB, DF ⊥AB, 垂足分别为E 、F, AC ∥DB, 且AC=BD, 那么Rt △AEC ≌Rt △BFC 的理由是（ ）.A ．SSSB. AASC. SASD. HL 4．下列说法正确的个数有（ ）.②有两边对应相等的两个直角三角形全等；③有两边和一角对应相等的两个直角三角形全等；BBC BC④有两角和一边对应相等的两个直角三角形全等. A ．1个B. 2个C. 3个D. 4个5．过等腰△ABC 的极点A 作底面的垂线, 就获得两个全等三角形, 其理由是.6．如图, △ABC 中, ∠C=︒90, AM 平分∠CAB, CM=20cm, 那么M 到AB 的距离是（ ）cm.7．在△ABC 和△C B A '''中, 如果AB=B A '', ∠B=∠B ', AC=C A '', 那么这两个三角形（ ）.A ．全等B. 纷歧定全等 C. 不全等D. 面积相等, 但不全等 8．如图, ∠B=∠D=︒90, 要证明△ABC 与△ADC 全等, 还需要弥补的条件是.9．如图, 在△ABC 中, ∠ACB=︒90, AC=BC, 直线MN 经过点C, 且AD ⊥MN 于D, BE ⊥MN 于E,求证：DE=AD+BE.10．如图, 已知AC ⊥BC, AD ⊥BD, AD=BC, CE ⊥AB, DF ⊥AB,垂足分别为E 、F, 那么, CE=DF 吗？谈谈你的理由! 11．如图, 已知AB=AC, AB ⊥BD, AC ⊥CD, AD, BC 相交于点E, 求证：（1）CE=BE ；（2）CB ⊥AD.提高题型： 1.如图, △ABC 中, D 是BC 上一点, DE⊥AB, DF⊥AC, E、F 分别为垂足, 且AE=AF, 试说明：DE=DF, AD 平分∠BAC.2.如图, 在ABC 中, D 是BC 的中点, DE⊥AB, DF⊥AC, 垂足分别是E 、F, 且DE=DF, 试说明AB=AC.3.如图, AB=CD, DF ⊥AC 于F, BE ⊥AC 于E, DF=BE, 求证：AF=CE.4.如图, △ABC 中, ∠C=90°, AB=2AC, M 是AB 的中点, 点N 在BC 上, MN ⊥AB.求证:AN 平分∠BAC.创作时间：二零二一年六月三十日┐ AB M CAC DBA DB ENC A B C DE F AE DBCAD C BFEM。

14．(2016·福州)如图，∠1＝∠2，∠3＝∠4.求证：AC＝AD.
解 ： ∵∠3 ＝ ∠4 ， ∴ ∠ ABC ＝ ∠ABD. 在 △ABC 和 △ABD 中 ， ∠1＝∠2， ∴△ABC≌△ABD(ASA)，∴AC＝AD AB＝AB， ∠ABC＝∠ABD，
15．(习题变式)如图，点A，F，E，C在同一直线上，AB∥CD，∠ABE＝
1．如图，要测量池塘两岸相对的两点A，B的距离，可以在AB的垂线BF上 取两点C，D，使BC＝CD，再画出BF的垂线DE，使E与A，C在一条直线上， 这时测得DE的长就是AB的长，它的理论依据是( C A．SSS B．SAS C．ASA D．AAA )
2．如图，在四边形ABCD中，AB∥CD，若用“ASA”证明 ∠ACB＝∠CAD(或AD∥BC) △ABC≌△CDA，需添加条件_____________________________ ．
)
A．4个 B．3个
C．2个 D．1个
11．如图，在△ABC中，∠BAC＝90°，AB＝AC，分别过B，C两点作过 A的直线的垂线BD，CE，D，E为垂足，若BD＝4，CE＝3，则DE的长为 ____ 7 ．

12．如图，有一块边长为4的正方形塑料模板ABCD，将一块足够大的直角 三角板的直角顶点放在A点，两条直角边分别与CD交于点F，与CB的延长线 交于点E，则四边形 AECF的面积是______ 16 ．
八年级上册人教版数学
第十二章 全等三角形
12．2 三角形全等的判定
第3课时 用“ASA”或“AAS”证三角形全等
相等 夹边 1．_______ ASA 分别_________的两个三角形全等，可简写成 角边角 和它们的________ “____________”或“__________”． 练习1：如图，BD平分∠ABC和∠ADC，则△ABD≌△CBD，依据是 ( A ) A．ASA C．SAS

CBA全等三角形的判定（SSS）不要写在上面，答案写在纸上1、如图1，已知AB=CD，AC=BD，求证：∠A=∠D．图1 图2 图3 图42、如图2，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．3、已知如图3，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.4、如图4，AB=AC，BD=CD，求证：∠1=∠2．全等三角形的判定(SAS)4、如图4，AB与CD交于点O，OA=OC，OD=OB，求证AD=CB．图7 图8 图95、如图5，已知△ABC中，AB=AC，AD平分∠BAC，求证△ABD≌△ACD6、如图6，已知AB=AD，AC=AE，∠1=∠2，求证∠ADE=∠B.7、如图7，已知AB=AD，若AC平分∠BAD，求证AC平分∠BCD8、如图8，在△ABC和△DEF中，B、E、F、C，在同一直线上，①AB=DE；③∠ABC=∠DEF；④BE=CF. 证明AC=DF9、如图9，AB⊥BD，DE⊥BD，点C是BD上一点，且BC=DE，CD=AB．⑴如图1证明AC与CE垂直⑵如图2，若把△CDE沿直线BD向左平移，使△CDE的顶点C与B重合，此时第⑴问中AC与BE的位置关系还成立吗？(注意字母的变化)【典型题】1．如图1，AB∥图5图2 图32．如图2，已知：AD=AE，ABEACD∠=∠，求证：BD=CE.3．如图3，已知：ABDBACDC∠=∠∠=∠.，求证：OC=OD. 图64．如图4已知：AB=CD，AD=BC，O是BD中点，过O点的直线分别交DA和BC的延长线于E，F.求证：AE=CF.5．如图5，已知321∠=∠=∠，AB=AD.求证：BC=DE.6．如图6，已知四边形ABCD中，AB=DC，AD=BC，点F在AD上，点E在BC上，AF=CE，EF的对角线BD交于O，求证：OF=OE 7. 如图7，已知∠A=∠C，AF=CE，DE∥BF，求证：△ABF≌△CDE.8．如图8，CD⊥AB，BE⊥AC，垂足分别为D、E，BE交CD于F，且AD=DF，求证：AC= BF。

2020—2021八年级上学期专项冲刺卷（人教版）专项12.4 三角形全等的判定（AAS）与（ASA）姓名：___________考号：___________分数：___________（考试时间：100分钟满分：120分）一、选择题（本大题共12小题，每小题3分，共36分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．如图，聪聪书上的三角形被墨迹污染了一部分，他根据所学知识很快就画了一个与书本上完全一样的三角形，那么聪聪画图的依据是（）A．SSS B．SAS C．ASA D．以上全不对【答案】C【分析】根据图形，三角形有两角和它们的夹边是完整的，所以可以根据“角边角”画出．【详解】根据题意，三角形的两角和它们的夹边是完整的，所以可以利用“角边角”定理作出完全一样的三角形．故选C．【点睛】本题考查了三角形全等的判定的实际运用，熟练掌握判定定理并灵活运用是解题的关键．2．如图所示，亮亮课本上的一个三角形被墨迹污染了一部分，很快他就根据所学知识画一出一个与这个三角形全等的图形，那么这两个三角形全等的依据是（）A．SSS B．SAS C．AAS D．ASA【答案】D【分析】根据全等三角形的判定方法解答即可．【详解】解：画一个三角形A ′B ′C ′，使∠A ′=∠A ，A ′B ′=AB ，∠B ′=∠B ，符合全等三角形的判定定理ASA ，故选：D ．【点睛】本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键．3．如图四个三角形中，能构成全等三角形的是（ ）A ．①②B ．②③C ．①③D ．③④【答案】C【分析】 先根据三角形内角和定理得到一个内角的度数，再根据ASA 可证2个三角形全等，依此即可求解．【详解】解：①中未知角的度数为：180°﹣70°﹣50°＝60°；②中未知角的度数为180°﹣70°﹣60°＝50°； ③中未知角的度数为180°﹣70°﹣60°＝50°；④中未知角的度数为180°﹣60°﹣50°＝70°； 又三角形中边长为25所相邻的角分别为：①70°、50°；②60°、50°；③70°、50°；④60°、50°；根据ASA 可证2个三角形全等是③和①、②和④；故选：C【点睛】本题考查三角形全等，利用ASA 定理进行证明去，重点在寻找对应角和对应边相等；4．如图，已知BAD CAD ∠=∠，则下列条件中用AAS 使ABD ACD △≌△的是（ ）A ．BC ∠=∠B ．BDA CDA ∠=∠C ．AB AC =D ．BD CD =【答案】A【分析】 利用全等三角形判定定理ASA ，SAS ，AAS 对各个选项逐一分析即可得出答案.【详解】A ：∠BAD =∠CAD ，AD 为公共边，若∠B =∠C ，则△ABD ≌△ACD (AAS)，此选项符合； B ：∠BAD =∠CAD ，AD 为公共边，若∠BDA =∠CDA ，则△ABD ≌△ACD (ASA )；此选项不符 合；C ：∠BAD =∠CAD ，AD 为公共边，若AB= AC ，则△ABD ≌△ACD (SAS)，此选项不符合； D ：∠BAD =∠CAD ，AD 为公共边，若BD=CD ，不能判定△ABD ≌△ACD ，此选项不符合； 故选: D.【点睛】此题主要考查学生对全等三角形判定定理的理解和掌握，此题难度不大，属于基础题.5．如图，某同学把一块三角形的玻璃打碎成3块，现要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是______，这么做的依据是______．（ ）A ．带①去，SASB ．带②去，SASC ．带③去，ASAD ．①②③都带去，SSS【答案】C【分析】 根据全等三角形的判定定理，结合实际分析即可．【详解】第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA 来配一块一样的玻璃．应带③去．故选：C ．【点睛】全等三角形判定的实际应用．6．如图，在MPN △中，H 是高MQ 和NR 的交点，且MQ =NQ ，已知PQ ＝5，NQ ＝9，则MH 的长为（ ）A ．3B ．4C ．5D ．6【答案】B【分析】 先证明MQP NQH △≌△，再由全等三角形的性质可得PQ =QH =5，根据MQ =NQ =9，即可得到答案．【详解】解：∵MQ ⊥PN ，NR ⊥PM ，∴∠NQH ＝∠NRP ＝∠HRM ＝90︒，∵∠RHM ＝∠QHN ，∴∠PMH ＝∠HNQ ，在MQP △和NQH 中，90PMQ QNH MQ NQMQP NQH ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴MQP NQH △≌△（ASA ），∴PQ ＝QH ＝5，∵NQ ＝MQ ＝9，∴MH ＝MQ ﹣HQ ＝9﹣5＝4，【点睛】本题考查全等三角形的判定和性质，解题的关键是推理证明三角形的全等三角形，找到边与边的关系解决问题．7．如图，已知AB CD =，12∠=∠，和3AO =，则OC =（ ）A ．3B ．4C ．5D ．6【答案】A【分析】 由“AAS ”可证△AOB ≌△COD ，可得AO =CO =3，即可求OC 的长．【详解】解：∵AB =CD ，∠1=∠2，∠AOB =∠COD ，∴△AOB ≌△COD （AAS ），∴AO =CO =3，故选：A ．【点睛】本题考查了全等三角形的判定和性质，证明△AOB ≌△COD 是本题的关键．8．如图，点D ，E 分别在线段AB ，AC 上，且BD CE =，BE 与CD 交于点O ，则从下列三个条件①B C ∠=∠，②BDO CEO ∠=∠，③OD OE =中选一个能使OB OC =成立的是（ ）A ．①B ．①或②C ．②或③D ．①或②或③【答案】B根据全等三角形的判定和性质定理即可得到结论．【详解】解：选①或②，理由：∵∠BOD=∠COE ，∠B=∠C ，BD=CE ，∴△BOD ≌△COE （AAS ），∴OB=OC ；∵∠BOD=∠COE ，∠BDO=∠CEO ，BD=CE ，∴△BOD ≌△COE （AAS ），∴OB=OC ；故选：B ．【点睛】本题考查了全等三角形的判定和性质，熟练掌握全等三角形的性质和判定是解题的关键． 9．如图，D 是AB 上一点．DF 交AC 于点,,//E DE FE FC AB =，若1,3BD CF ==，则AB 的长是（ ）A ．6B ．72C ．3D ．4【答案】D【分析】 根据平行线的性质，得出A FCE ∠=∠，ADE F ∠=∠，根据全等三角形的判定，得出ADE CFE ∆≅∆，根据全等三角形的性质，得出AD CF =，即可求线段AB 的长．【详解】∵//CF AB ，∴A FCE ∠=∠，ADE F ∠=∠，在ADE ∆和FCE ∆中A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()ADE CFE AAS ∆≅∆，∴3AD CF ==，∴314AB AD BD =+=+=，故选D ．【点睛】本题考查了全等三角形的性质和判定，平行线的性质的应用，能判定ADE FCE ∆≅∆是解此题的关键．10．如图，90ACB ∠=︒，AC=BC ．AD CE ⊥，BE CE ⊥，垂足分别是点D 、E ．若AD=6，BE=2，则DE 的长是（ ）A ．2B ．3C ．4D ．5【答案】C【分析】 由一线三直角∠ADC=∠CEB=90º推得∠ACD=∠CBE ，再加上AC=BC ，易证△ACD ≌△CBE （AAS ）便可求出ED=EC-CD 即可．【详解】∵90ACB ∠=︒，∴∠ACD+∠ECB=90º，∵AD CE ⊥，BE CE ⊥，∴∠ADC=∠CEB=90º，∴∠ECB+∠CBE=90º，∴∠ACD=∠CBE ，在△ACD 和△CBE 中，∵∠ADC=∠CEB=90º，∠ACD=∠CBE ，AC=BC ，∴AD=CE=6，CD=BE=2，∴ED=EC-CD=6-2=4．故选择：C．【点睛】本题考查全等三角形中的线段差问题，关键掌握三角形全等的证明方法，会用差线段来解决问题．11．如图，△ABC的面积为1cm2，AP垂直∠B的平分线BP于P，则△PBC的面积为（）A．0.4 cm2B．0.5 cm2C．13cm2D．0.6 cm2【答案】B【分析】延长AP交BC于T．利用全等三角形的性质证明AP＝PT即可解决问题．【详解】解：如图，延长AP交BC于T．∵BP⊥AT，∴∠BPA＝∠BPT＝90°，∵BP＝BP，∠PBA＝∠PBT，∴PA ＝PT ，∴S △BPA ＝S △BPT ，S △CAP ＝S △CPT ，∴S △PBC ＝12S △ABC ＝12=0.5， 故选：B ．【点睛】本题考查全等三角形的判定和性质，三角形的面积，等高模型等知识，解题的关键是学会添加常用辅助线吗，构造全等三角形解决问题．12．如图，在△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别是D 、E ，AD 、CE 交于点H ，已知EH ＝EB ＝3，AE ＝5，则CH 的长是（ ）A ．1B ．2C ．35D ．53【答案】B 【分析】 由AD 垂直于BC ，CE 垂直于AB ，利用垂直的定义得到一对角为直角，再由一对对顶角相等，利用三角形的内角和定理得到一对角相等，再由一对直角相等，以及一对边相等，利用AAS 得到三角形AEH 与三角形EBC 全等，由全等三角形的对应边相等得到AE EC =，由EC EH -，即AE EH -即可求出HC 的长．【详解】解：AD BC ⊥，CE AB ⊥，90ADB AEH ∴∠=∠=︒，AHE CHD ∠=∠，BAD BCE ∴∠=∠，在HEA ∆和BEC ∆中，BAD BCE AEH BEC EH EB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()HEA BEC AAS ∴∆≅∆，5AE EC ∴==，则532CH EC EH AE EH =-=-=-=．故选：B ．【点睛】此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．二、 填空题（本大题共6小题，每小题3分，共18分）13．如图，在△ABC 中，AD 是BC 边上的高，BE 是AC 边上的高，且AD 、BE 的交于点F ，若BF ＝AC ，CD =6，BD ＝8，则线段AF 的长度为___．【答案】2【分析】首先证明△BDF ≌△ADC ，再根据全等三角形的性质可得FD =CD ，AD =BD ，根据AD =8，DF =6，即可算出AF 的长．【详解】解：∵AD 是BC 边上的高，BE 是AC 边上的高，∴∠ADC =∠FDB =90°，∠AEB =90°，∴∠1+∠C =90°，∠1+∠2=90°，∴∠2=∠C ，∵∠2=∠3，∴∠3=∠C ，在△ADC 和△BDF 中，3C FDB CDA BF AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BDF ≌△ADC （AAS ），∴FD =CD ，AD =BD ，∵CD =6，BD =8，∴AD =8，DF =6，∴AF =8-6=2，故答案为：2．【点睛】本题考查的是全等三角形的判定及性质，熟练掌握性质定理是解题的关键．14．如图，要测量池塘两岸相对的两点A ，B 的距离，可以在池塘外取AB 的垂线BF 上的两点C ，D ，使BC CD =，再画出BF 的垂线DE ，使E 与A ，C 在一条直线上．若想知道两点A ，B 的距离，只需要测量出线段__________即可．【答案】D E【分析】由垂线的定义可得出∠B =∠EDC =90°，结合BC =DC ，∠ACB =∠ECD ，即可证出△ABC ≌△EDC （ASA ），利用全等三角形的性质可得出AB =ED ．【详解】解：∵AB ⊥BF ，DE ⊥BF ，∴∠B =∠EDC =90°．在△ABC 和△EDC 中，B EDC BC DC ACB ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABC ≌△EDC （ASA ），∴AB =ED ．故想知道两点A ，B 的距离，只需要测量出线段DE 即可．故答案为：DE ．【点睛】本题考查了全等三角形的应用，利用全等三角形的判定定理ASA 证出△ABC ≌△EDC 是解题的关键．15．如图，已知224m ABC S =△，AD 平分BAC ∠，且AD BD ⊥于点D ，则ADC S =△________2m ．【答案】12【分析】如图，延长BD 交AC 于点E ，根据已知证得ADB ADE ≌，则得BD DE =，由三角形的面积公式得ABD AED S S =△△，BCD ECD SS =，即可证明12ADC ABC S S =，从而可以解答本题．【详解】解：如图，延长BD 交AC 于点E ，∵AD 平分BAC ∠，AD BD ⊥，∴BAD EAD ∠=∠，90ADB ADE ∠=∠=︒．∵AD AD ＝，∴()ADB ADE ASA ≌．∴BD DE =．∴ABD AED S S =△△，BCD ECD S S =． ∴12ABD BCD AED ECD ABC S S S S S =++=△△△△△． 即12ADC ABC S S =．∵224m ABC S =△，∴212m ADC S =△．故答案为：12．【点睛】本题主要考查全等三角形的判定与性质，明确题意，利用三角形全等证明12ADC ABC SS =是解答此题的关键．16．如图，BE ⊥AE ，CF ⊥AE ，垂足分别为E 、F ，D 是EF 的中点，CF ＝AF ．若BE ＝4，DE ＝2，则△ACD 的面积为_______．【答案】12【分析】由BE ⊥AE ，CF ⊥AE ，得∠BED =∠CFD ，再由D 是EF 的中点，得ED =FD ，根据角边角公里可得出△BED 与△CFD 全等，进而可得CF =EB =4，然后可得CF =4，再计算出AD 的长，利用三角形面积公式可得答案．【详解】解：∵BE ⊥AE ，CF ⊥AE ，∴∠BED =∠CFD ，∵D 是EF 的中点，∴ED =FD ，CFD DEB DF DECDF BDE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△BED ≌△CFD （ASA ）．∴CF =EB =4，∵AF =CF ，∴AF =4，∵D 是EF 的中点，∴DF =DE =2，∴AD =6，∴△ACD 的面积：11641222AD CF ⋅=⨯⨯=． 故答案为：12.【点睛】本题考查了全等三角形的判定和性质，判定一般三角形全等有SSS 、SAS 、ASA 、AAS ，判定两个直角三角形全等还有HL ．17．如图，B 、C 、E 共线，AB BE ⊥，DE BE ⊥，AC DC ⊥，AC DC =，5cm BE =，则AB DE +=______．【答案】5cm【分析】根据三垂直模型，可证得ABC CED △≌△，从而得到AB DE BC CE BE +=+=计算即可．【详解】由题意：∠ACD=90°，∠B=∠E=90°，∴∠ACB 与∠ECD 互余，∠A 与∠ACB 互余，∴∠A=∠ECD ，B E A ECD AC DC ⎧⎪⎨⎪=∠=∠∠=⎩∠∴△ABC ≌△CED （AAS ）∴AB=CE ，BC=DE ，∴AB+DE=BC+CE=BE=5cm ，故答案为：5cm ．【点睛】本题考查全等三角形的判定与性质，熟练根据题意证明全等三角形，并运用全等三角形的性质是解题关键．18．如图，90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥，垂足分别为,D E ，若9,6AD DE ==，则BE 的长为________________________．【答案】3【分析】由AD ⊥CE ，BE ⊥CE ，可以得到∠BEC=∠CDA=90°，再根据∠ACB=90°，可以得到∠BCE=∠CAD ，从而求得△CEB ≌△ADC ，然后利用全等三角形的性质可以求得BE 的长．【详解】解：∵∠ACB=90°，BE ⊥CE ，AD ⊥CE ，∴∠BCE+∠DCA=90°，∠BEC=∠CDA=90°，∴∠ACD+∠CAD=90°，∴∠BCE=∠CAD ，在△CEB和△ADC中，BCE CADBEC CDA AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CEB≌△ADC（AAS）；∴BE=CD，CE=AD=9．∵DC=CE-DE，DE=6，∴DC=9-6=3，∴BE=3．故答案为：3【点睛】本题考查全等三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．三、解答题（本大题共6小题，共66分，解答应写出文字说明、演算步骤或推理过程）19．如图，点E在△ABC的边AC上，且∠ABE＝∠C，AF平分∠BAE交BE于F，FD∥BC交AC 于点D．（1）求证：△ABF≌△ADF；（2）若BE＝7，AB＝8，AE＝5，求△EFD的周长．【答案】（1）见详解；（2）10【分析】（1）由“AAS”可证△DAF≌△BAF；（2）由全等三角形的性质得AD=AB＝8，BF=DF，结合BE＝7，AB＝8，AE＝5，即可求解．【详解】（1）证明：∵FD∥BC，∴∠ADF＝∠C，∵∠ABE＝∠C，∴∠ADF ＝∠ABF ，∵AF 平分∠BAE ，∴∠DAF ＝∠BAF ，又∵AF ＝AF ，∴△ABF ≌△ADF （AAS ）；（2）∵△ABF ≌△ADF ，∴AD =AB ＝8，BF =DF ，∵AE ＝5，∴DE =8-5=3，∴EF +DF = EF +BF =BE =7，∴△EFD 的周长= EF +DF +DE =7+3=10．【点睛】本题主要考查全等三角形的判定和性质，角平分线的定义，熟练掌握“AAS ”证三角形全等，是解题的关键．20．如图，在ABC 中，AC BC =，点D 在AB 边上，点E 在BC 边上，连接CD ，DE ．已知ACD BDE ∠=∠，CD DE =．（1）猜想AC 与BD 的数量关系，并证明你的猜想；（2）若3AD =，5BD =，求CE 的长．【答案】（1）AC BD =，证明见解析；（2）2【分析】（1）根据“AAS ”证ADC BED △≌△可得；（2）由（1）ADC BED △≌△，根据全等三角形性质可得；【详解】（1）解：AC BD =，理由如下：在ABC 中，AC BC =A B ∴∠=∠∴在ADC 和BED 中A B ACD BED CD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC BED AAS ∴△≌△AC BD ∴=（2）由（1）知ADC BED △≌△5AC BD ∴==，3BE AD ==5BC AC ∴==2CE BC BE ∴=-=【点睛】考核知识点：全等三角形的判定和性质．理解全等三角形的判定和性质是关键．21．如图123,,5AB AD AE ∠=∠=∠==，求AC 的长度．【答案】5【分析】根据三角形内角和得到∠D =∠B ，再根据等量代换得到∠DAE =∠BAC ，利用ASA 证明△ADE ≌△ABC ，得到AE =AC 即可．【详解】解：如图，∵∠1=∠3，∠AFD =∠BFE ，∴∠D =∠B ，∵∠1=∠2，∴∠1+∠BAE =∠2+∠BAE ，即∠DAE =∠BAC ，又∵AD =AB ，∴△ADE ≌△ABC （ASA ），∴AE =AC =5．【点睛】本题考查了全等三角形的判定和性质，解题的关键是根据已知条件找到三角形全等的条件． 22．如图，点B ，F ，C ，E 在直线l 上（F ，C 之间不能直接测量），点A ，D 在l 异侧，测得AB DE =，//AB DE ，A D ∠=∠．（1）求证：ABC DEF △≌△；（2）若10BE =，3BF =，求FC 的长度．【答案】（1）见解析；（2）4【分析】（1）先证明∠ABC =∠DEF ，再根据ASA 即可证明．（2）根据全等三角形的性质即可解答．【详解】解：（1）证明：∵AB ∥DE ，∴∠ABC =∠DEF ，在△ABC 与△DEF 中，ABC DEF AB DEA D ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△DEF ；（2）∵△ABC ≌△DEF ，∴BC =EF ，∴BF +FC =EC +FC ，∴BF =EC ，∵BE =10，BF =3，∴FC =10-3-3=4．【点睛】本题考查全等三角形的判定和性质、平行线的判定等知识，解题的关键是正确寻找全等三角形的条件，记住平行线的判定方法，属于基础题，中考常考题型．23．如图，在△ABC 中，∠BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为D ，E ．（1）求证：△ABD ≌△ACE ；（2）若BD ＝2cm ，CE ＝4cm ，DE ＝ cm ．【答案】（1）见解析；（2）6【分析】（1）根据BD ⊥直线m ，CE ⊥直线m 得∠BDA ＝∠CEA ＝90°，而∠BAC ＝90°，根据等角的余角相等得∠CAE ＝∠ABD ，然后根据“AAS”可判断△ADB ≌△CEA ；（2）根据全等三角形的性质得出AE ＝BD ，AD ＝CE ，于是DE ＝AE+AD ＝BD+CE ．【详解】证明：（1）∵BD ⊥直线m ，CE ⊥直线m ，∴∠BDA ＝∠CEA ＝90°，∵∠BAC ＝90°，∴∠BAD+∠CAE ＝90°，∵∠BAD+∠ABD ＝90°，∴∠CAE ＝∠ABD ，∵在△ABD 和△ACE 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （AAS ），（2）∵△ABD ≌△ACE ，∴AE ＝BD ，AD ＝CE ，∴DE ＝AE+AD ＝BD+CE ，∵BD ＝2cm ，CE ＝4cm ，∴DE ＝6cm ；故答案为：6．【点睛】本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；得出∠CAE=∠ABD 是解题的关键．24．如图，在△ABC 和△DEF 中，B ，E ，C ，F 在同一条直线上，AB // DE ，AB = DE ，∠A = ∠D ． （1）求证：ABC DEF ≌；（2）若BF = 11，EC = 5，求BE 的长．【答案】（1）见解析；（2）BE =3．【分析】（1）根据平行线的性质由AB ∥DE 得到∠ABC ＝∠DEF ，然后根据“ASA”可判断△ABC ≌△DEF ；（2）根据三角形全等的性质可得BC ＝EF ，由此可求出BE ＝CF ，则利用线段的和差关系求出BE ．【详解】（1）证明：∵AB ∥DE ，∴∠ABC ＝∠DEF ，在△ABC 和△DEF 中A D AB DEABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF （ASA ）；（2）解：∵△ABC ≌△DEF ，∴BC ＝EF ，∴BC －EC ＝EF －EC ，即BE ＝CF ，∵BF ＝11，EC ＝5，∴BF －EC ＝6．∴BE ＋CF ＝6．∴BE ＝3．【点睛】本题考查了全等三角形的判定与性质，掌握全等三角形的判定与性质是解答此题的关键．。

全等三角形的判定（SSS）1、如图 1， AB=AD ， CB=CD ，∠ B=30 °，∠ BAD=46 °，则∠ ACD 的度数是 ()A.120 °B.125 °C.127°D.104 °2、如图 2，线段 AD 与 BC 交于点 O，且 AC=BD ， AD=BC ， ? 则下面的结论中不正确的是()A. △ ABC ≌△ BADB. ∠ CAB= ∠ DBAC.OB=OCD.∠ C= ∠D3、在△ ABC 和△ A 1B 1C1中，已知 AB=A 1B 1， BC=B 1C1，则补充条件 ____________，可得到△ ABC ≌△A 1B1C1．4、如图 3，AB=CD ，BF=DE ，E、F 是 AC 上两点，且AE=CF ．欲证∠ B= ∠ D，可先运用等式的性质证明AF=________ ，再用“ SSS”证明 ______≌ _______得到结论．5、如图，已知AB=CD ，AC=BD ，求证：∠ A= ∠ D．6、如图， AC 与 BD 交于点 O， AD=CB ，E、F 是 BD 上两点，且AE=CF ，DE=BF. 请推导下列结论：⑴∠ D=∠B ；⑵ AE ∥CF．7、已知如图，A 、 E、F、 C 四点共线， BF=DE ， AB=CD.⑴请你添加一个条件，使△ DEC ≌△ BFA ；⑵在⑴的基础上，求证： DE∥ BF.全等三角形的判定(SAS)1、如图1， AB ∥ CD ， AB=CD， BE=DF ，则图中有多少对全等三角形()A.3B.4C.5D.62、如图2， AB=AC，AD=AE，欲证△ABD≌△ ACE ，可补充条件()A. ∠ 1= ∠23、如图 3， AD=BCA.AB ∥ CDB.∠ B= ∠ C，要得到△ ABDB.AD ∥ BCC.∠ D= ∠ ED. ∠BAE= ∠CAD 和△CDB 全等，可以添加的条件是 ( C.∠A=∠ C D. ∠ABC= ∠ CDA)4、如图 4， AB 与 CD 交于点 O， OA=OC ， OD=OB ，∠ AOD=________ ， ? 根据 _________可得到△ AOD≌△ COB，从而可以得到AD=_________ ．5、如图 5，已知△ ABC 中， AB=AC ， AD 平分∠ BAC ，请补充完整过程说明△∵ AD 平分∠ BAC ，∴∠ ________=∠ _________(角平分线的定义).在△ ABD 和△ ACD 中，∵ ____________________________ ，∴△ ABD≌△ ACD（ABD）≌△ ACD的理由．6、如图 6，已知 AB=AD ， AC=AE ，∠ 1= ∠ 2，求证∠ ADE= ∠ B.7、如图，已知AB=AD ，若 AC 平分∠ BAD ，问 AC 是否平分∠ BCD ？为什么？BA CD8、如图，在△ABC 和△ DEF 中， B 、 E、 F、 C，在同一直线上，下面有 4 个条件，请你在其中选 3 个作为题设，余下的一个作为结论，写一个真命题，并加以证明.①AB=DE ；② AC=DF ；③∠ ABC= ∠ DEF ；④ BE=CF.9、如图⑴， AB ⊥ BD ， DE⊥ BD ，点 C 是 BD 上一点，且BC=DE ， CD=AB ．⑴试判断AC 与 CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线 BD 向左平移，使△CDE 的顶点 C 与 B 重合，此时第⑴问中的位置关系还成立吗？(注意字母的变化)AC与BE全等三角形（三） AAS和 ASA【知识要点】1．角边角定理（ ASA）：有两角及其夹边对应相等的两个三角形全等.2 ．角角边定理（ AAS）：有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例 1．如图， AB∥ CD， AE=CF，求证： AB=CDD FC O例 2．如图，已知： AD=AE，ACD ABE ，求证：BD=CE.AE BAD E例 3．如图，已知：CD . BAC ABD ，求证：OC=OD.B CD COA B例 4．如图已知： AB=CD，AD=BC，O是 BD中点，过 O点的直线分别交DA和 BC的延长线于E，F. 求证： AE=CF.FDCOAB例 5．如图，已知123 ，AB=AD.求证：BC=DE.EA2E1OB D 3C例6．如图，已知四边形 ABCD中， AB=DC，AD=BC，点 F 在 AD 上，点 E 在 BC上， AF=CE， EF 的对角线 BD 交于 O，请问 O点有何特征？A F DOB EC【经典练习】1. △ ABC和△A B C中，A A' , BC B C ，C C 则△ABC与△ A B C.2．如图，点 C，F 在 BE上，12, BC EF ,请补充一个条件，使△ABC≌DFE,补充的条件是.A DB 12EC F3．在△ ABC和△A B C中，下列条件能判断△ABC和△A B C全等的个数有（）① A AB B ， BC B C② AA ， B B ， AC A C③ A AB B ， AC B C④ AA ， B B ， AB A CA ． 1 个 B. 2 个 C. 3 个 D. 4 个4．如图，已知 MB=ND，MBA NDC ，下列条件不能判定是△ABM≌△CDN的是（）A．M NB. AB=CD M NC． AM=CND. AM∥ CN5．如图 2 所示，∠E=∠ F=90°，∠ B=∠ C， AE=AF，给出下列结论：①∠ 1=∠2② BE=CF③△ ACN≌△ ABM④ CD=DN A C B D 其中正确的结论是_________ _________ 。

全等三角形的判定方法SAS专题练习1. 如图，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B. ∠B=∠CC. ∠D =∠ED. ∠BAE=∠CAD2. 能判定△ABC≌△A′B′C′的条件是（）A．AB=A′B′，AC=A′C′，∠C =∠C′第1 题B. AB=A′B′，∠A=∠A′，BC=B′C′C. AC=A′C′，∠A=∠A′，BC=B′C第3 题D. AC=A′C′，∠C=∠C′，BC=B′C3. 如图，AB与CD交于点O，OA=O，C OD=O，B∠AOD=，根据_________可得到△AOD≌△COB，从而可以得到AD=_________．4. 如图，已知BD=C，D要根据“SAS”判定△ABD≌△ACD，第4 题需添加的条件是。

则还5. 如图，AD=BC，要根据“SAS”判定△ABD≌△BAC，需添加的条件是则还6. 如图，已知△ABC中，AB=AC，AD平分∠BAC，明△ABD≌△ACD的理由．程说请补充完整过解：∵AD平分∠BAC，第5 题∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中，∵第6 题∴△ABD≌△ACD（）7. 如图，AC与BD相交于点O，已知OA=O，C OB=O，D:△AOB≌△COD求证证明：在△AOB和△COD中∵第7 题∴△AOB≌△COD( )8. 已知：如图，AB=CB，∠1=∠2 △ABD和△CBD全等吗？9. 已知：如图，AB=AC，AD=AE，∠1 = ∠2 。

试说明：△ABD≌△ACE。

10. 已知：如图，△ABC中，AD⊥BC 于D，AD=BD，DC=DE，∠C=50°。

求∠EBD的度数。

习全等三角形的判定方法AAS、ASA专题练1. 已知：如图, FB=CE , AB∥ED , AC∥FD.F、C 在直线B E 上．：AB=DE , AC=DF ．求证2.已知：如图, AB⊥BC 于B , EF⊥AC 于G , DF⊥BC 于D , BC=DF．：AC=EF .求证3. 已知：如图A C⊥CD 于 C , B D⊥CD 于D , M 是AB 的中点, 连结CM 并延长交BD 于点F。

全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，已知AB=CD，AC=BD，求证：∠A=∠D．6、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．7、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定(SAS)1、如图1，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形( )A.3B.4C.5D.6CBA 2、如图2，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．5、如图5，已知△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由． ∵AD 平分∠BAC ， ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中，∵____________________________， ∴△ABD ≌△ACD （ ） 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形（三）AAS 和ASA【知识要点】1．角边角定理（ASA ）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS ）：有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD. 例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA 和BC 的延长线于E ，F.求证：AE=CF.例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？ABD C O12 3AFDOBE C【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（ ） ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''=' A ． 1个 B. 2个 C. 3个 D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（ ）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。