电解质溶液活度系数的计算方法

电解质溶液活度计算理论进展【摘要】：由于溶液大多数不是理想溶液，需要用活度来代替浓度。

活度系数又是描述活度与浓度的差异程度，因此活度系数的计算对于反应过程相当的重要。

近几年，随着活度系数理论模型的不断发展，活度系数的计算方法也在不断的提高、创新。

本文在回顾电解质溶液热力学经典理论的基础上，对活度系数计算做了综述。

【关键词】：活度系数活度模型热力学模型活度计算Electrolyte solution activity in recent years, progressin computational theoryAbstract：Solution is not ideal because most of the solution need to replace the concentration of activity. Activity coefficient is described differences in degree of activity and concentration, so the calculation of activity coefficients for the reaction process was very important. In recent years, with the activity coefficient of the continuous development of theoretical models, the calculation of activity coefficients are also constantly improving and innovation. In this paper, recalling the classical theory of thermodynamics of electrolyte solution, based on calculations made on the activity coefficient is reviewed.Keywords: Activity coefficient, Activity Model, Thermodynamic model, Activity calculation1、活度与活度系数绝大多数的反应都有溶液（固溶体、冶金熔体及水溶液）参加，而这些溶液经常都不是理想溶液，在进行定量的热力学计算和分析，溶液中各组分的浓度必须代以活度。

实验7 电解质溶液活度系数的测定一、实验目的1. 掌握用电动势法测定电解质溶液平均离子活度系数的基本原理和方法。

2. 通过实验加深对活度、活度系数、平均活度、平均活度系数等概念的理解。

学会应用外推法处理实验数据。

3. 进一步掌握电位差计的原理及其使用方法。

二、基本原理活度系数是用于表示真实溶液与理想溶液中任一组分浓度的偏差而引入的一个校正因子，它与活度a、质量摩尔浓度m之间的关系为：(7.1)在理想溶液中各电解质的活度系数为1，在稀溶液中活度系数近似为1。

对于电解质溶液，由于溶液是电中性的，所以单个离子的活度和活度系数是不可测量、无法得到的。

通过实验只能测量离子的平均活度系数，它与平均活度、平均质量摩尔浓度之间的关系为：(7.2)平均活度和平均活度系数测量方法主要有：气液相色谱法、动力学法、稀溶液依数性法、电动势法等。

本实验采用电动势法测定ZnCl2溶液的平均活度系数。

其原理如下：用ZnCl2 溶液构成如下单液化学电池：该电池反应为：其电动势为：(7.3)(7.4)根据：(7.5)(7.6)(7.7)得：(7.8)式中：，称为电池的标准电动势。

可见，当电解质的浓度m为已知值时，在一定温度下，只要测得E 值，再由标准电极电势表的数据求得，即可求得。

值还可以根据实验结果用外推法得到，其具体方法如下：将代入式（7.8），可得：(7.9)将德拜-休克尔公式：和离子强度的定义：代入到式（7.9），可得：(7.10)可见，可由图外推至时得到。

因而，只要由实验测出用不同浓度的ZnCl2 溶液构成前述单液化学电池的相应电动势E值，作图，得到一条曲线，再将此曲线外推至m=0，纵坐标上所得的截距即为。

三、仪器及试剂仪器：恒温装置一套，UJ-25 型电位差计，检流计，标准电池，直流稳压电源，电池装置，100 ml容量瓶6只，5 ml和10 ml移液管各1支，250 ml和400 ml 烧杯各1 只，Ag/AgCl电极，细砂纸。

llAdnaemit由图可知K’=-0.5539将各不同浓度的m时所测得的相应E值代入lg =1/0.1183 (K’- E – 0.1183lgm)γ可计算出各种不同浓度下的平均离子活度系数。

γlg1 =1/0.1183 (K’- E1 – 0.1183lgm)γ=1/0.1183 {-0.5539 + 0.2644 – 0.1183lg0.005} = -0.14611 =0.7143γlg2 =1/0.1183 (K’- E2 – 0.1183lgm)γ=1/0.1183 {-0.5539 + 0.2831 – 0.1183lg0.01} =-0.28912 =0.5139γlg3 =1/0.1183 (K’- E3 – 0.1183lgm)γ=1/0.1183 {-0.5539 + 0.2976 – 0.1183lg0.02} =-0.46763 =0.3407γlg4 =1/0.1183 (K’- E4 – 0.1183lgm)γ=1/0.1183 {-0.5539 + 0.3180 – 0.1183lg0.05} =-0.69314 = 0.2027γlg5 =1/0.1183(K’- E5 – 0.1183lgm)γ=1/0.1183{-0.5539 + 0.3328 – 0.1183lg0.1} =-0.86905= 0.1352γ5、根据公式及之关系，算出各0/(/)B B B a b b γ=22HCL a a ()H Cl a a m γ+-±±±===溶液中HCl 相应的活度。

由公式可计算出Bγ B1 = (1m 1)2 = (0.7143 * 0.005)2 = 1.276 * 10-5γγB 2 = (2m 2)2 = (0.5139 * 0.01)2 = 2.641 * 10-5γγB3 = (3m 3)2 = (0.3407 * 0.02)2 = 4.644 * 10-5γγB4 = (4m 4)2 = (0.2027 * 0.05)2 = 1.027 * 10-4γγB5 = (5m 5)2 = (0.1352 * 0.1)2 = 1.828 * 10-4γγ思考讨论1、试述电动势法测定平均离子活度系数的基本原理。

离子强度与活度系数的关系电解质溶液中实际发挥作用的浓度成为有效浓度，即为活度（activity）。

活度系数是指活度与浓度的比例系数。

在电解质溶液中由于离子之间的相互作用，使电解质的总浓度不能代表其有效浓度，需要引进一个经验校正系数γ（活度系数），以表示实际溶液与理想溶液的偏差。

一、相关计算由拉乌尔定律及亨利定律排序活度溶液就是由两种或两种以上的物质（称作组分）共同组成的均一相。

如果异种质点（原子、分子或离子）间的作用力和同种质点间的作用力相同。

则此溶液称为理想溶液，而服从拉乌尔定律，也即溶液中组分i的蒸气压pi与其以摩尔分数表示的浓度ni成正比，比例常数是纯组分i的蒸气压。

在真实溶液绝大部分的浓度范围内，组分i既不顺从拉乌尔定律，又不顺从亨利定律。

对组分i的活度可以按拉乌尔定律排序，获得ar，其活度系数用γi则表示，浓度用ni则表示；也可以按亨利定律排序，获得ah，其活度系数根据冶金工作者的惯例用fi则表示，浓度用xi（即为百分数）则表示。

由于活度有不同标准态，所以计算出的标准溶解自由焓随所用活度标准态的不同而有不同值。

但无论用哪种活度标准态，对已定条件下的冶金反应，算出的自由焓变量δg将永有同一值。

二、活度应用领域在人工制备放射源时，如果反应堆中的中子注量率或加速器中带电粒子束流强度是恒定的，则制备的人工放射性核素的产生率p是恒定的，而放射性核素同时又在衰变，因此它的数目变化率为dn（t）/dt=p-λn（t）。

对热中子场的情况，产生率为可以抒发为p=ntδoφ，式中nt为样品中被用作制取放射源的靶核总数，而且指出在紫外光过程中维持恒定；δo为靶核的热中子横截面；φ为热中子的注量率为。

这一情况相当于两代连续衰变时母核有恒定的衰变率jo。

根据长期平衡，人工放射性核素的衰变率（或活度）最终将达到jo，而不可能超过jo，其活度有一饱和值jo。

§7.4 强电解质的活度和活度系数1．溶液中离子的活度和活度系数由于阴阳离子间存在较强的静电吸引，与非电解质溶液相比，电解质溶液更容易偏离理想溶液的行为。

从理论上应如何描述电解质溶液的行为呢？原则上讲，以活度代替浓度将化学势表示为ln B B B RT a μμ=+同样适用于电解质溶液，但由于电解质的电离，使得其情况比非电解质溶液更复杂。

在电解质稀溶液中，强电解质完全电离成阴阳离子，它们的化学势可分别表示为： ln RT a μμ+++=+； ln RT a μμ---=+其中阳离子活度α+=γ+m +/m ，阴离子活度α-=γ-m -/m ，γ+、γ-和m +、m -分别是阳离子和阴离子的活度系数和质量物质的量浓度。

由于强电解质溶液由阴阳离子共同组成，其溶液总的化学势应该是各离子化学势的加和。

对任一强电解质M A v v +-：M A M A z z v v v v +-+-+-−−→+有： ()ln ln v vv v v v RT a a RT aμμμμμμ+-++--++--+-=+=++=+ (7.12)比较可知v v μμμ++--=+v v a a a +-+-=⋅ (7.13)由于单一离子的溶液不存在，故无法测定单一离子的活度及活度系数，实验测量的只能是阴阳离子共同的对外表现，为此需引入离子的平均活度a ±、平均活度系数γ±和平均质量物质的量浓度m ±，令ν++ν-＝ν，根据式(7.13)定义定义a ±为defv vv a a a +-±+-===⋅ (7.14)令a ± = γ± m ±/m ，将其代入(7.14)式可得()()v v v v v vm m m γγγ+-+-±±+-+-⋅=⋅⋅⋅ 所以v v vγγγ+-±+-=⋅ (7.15)v v v m m m +-±+-=⋅ (7.16)可见，离子平均活度、平均活度系数和平均质量物质的量浓度都是几何平均值。

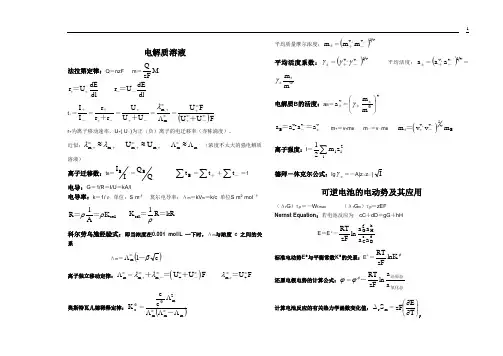
电解质溶液法拉第定律：Q ＝nzF m ＝M zFQ dE r U dl ++＝ dE r U dl－－＝t ＋＝－＋I I ＝－＋＋r r r +＝－＋U U U ++＝∞∞+Λm,m λ＝()FU U F U ∞∞+∞+－＋ r +为离子移动速率，U +( U －)为正（负）离子的电迁移率（亦称淌度）。

近似：+∞+≈,m ,m λλ +∞+≈,m ,m U U m m Λ≈Λ∞（浓度不太大的强电解质溶液）离子迁移数：t B ＝II B＝QQ B∑Bt＝∑＋t＋∑－t＝1电导：G ＝1/R ＝I/U ＝kA/l电导率：k ＝1/ρ 单位：S·m -1 莫尔电导率：Λm ＝kV m ＝k/c 单位S·m 2·mol －1cell l R K A ρρ＝＝ cell 1K R kR ρ＝＝科尔劳乌施经验式：即当浓度在0.001 mol/L 一下时，Λm 与浓度 c 之间的关系Λm ＝()c 1mβ－∞Λ离子独立移动定律：∞Λm ＝()m,m,+U U F λλ∞∞∞∞+－－＋＝＋ m U F λ∞∞+，+＝奥斯特瓦儿德稀释定律：Φc K ＝()mm m 2m c c ΛΛΛΛ∞∞Φ－平均质量摩尔浓度：±m ＝()1v v m m－－＋+平均活度系数：±γ＝()v1vv－－＋γγ+ 平均活度：±a ＝()v1v v a a－－＋+＝m m γ±±Φ电解质B 的活度：a B ＝va ±＝vm m ⎪⎭⎫ ⎝⎛Φ±±γ+v v vB +a a a a±－－＝＝ m +＝v +m B m －＝v －m B()1v v vB m v vm +±+－－＝离子强度：I ＝∑i2i i z m 21德拜－休克尔公式：lg ±γ＝－A|z ＋z -－|I可逆电池的电动势及其应用（Δr G ）T,p ＝－W f,max （Δr G m ）T,p ＝zEF Nernst Equation ：若电池反应为 cC ＋dD ＝gG ＋hH E ＝Eφ－dDc C hH g G a a a a ln zF RT标准电动势E φ与平衡常数K φ的关系：E φ＝φlnK zFRT还原电极电势的计算公式：ϕ＝氧化态还原态－a a lnzF RT φϕ计算电池反应的有关热力学函数变化值：m r S ∆＝pT E zF ⎪⎭⎫⎝⎛∂∂m r H ∆＝－zEF ＋p T E zFT ⎪⎭⎫ ⎝⎛∂∂ Q R ＝T m r S ∆＝pT E zFT ⎪⎭⎫⎝⎛∂∂zF ⎪⎪⎭⎫ ⎝⎛∆⎪⎪⎭⎫⎝⎛21m r 1122T 1T 1H T E T E －＝－ zF ⎰⎪⎭⎫ ⎝⎛T2E2T E 11T E d ＝dT T H 21T T 2mr ⎰∆ 电极书面表示所采用的规则：负极写在左方，进行氧化反应（是阳极），正极写在右方，进行还原反应（是阴极） 电动势测定的应用：(1) 求热力学函数变量Δr G m 、Δr G m Φ、m r H ∆、m r S ∆及电池的可逆热效应Q R 等。

活度计算公式
活度系数计算公式: V=P(B)/kC(B)。

电解质溶液中实际发挥作用的浓度成为有效浓度，即为活度。

活度系数是指活度与浓度的比例系数。

在电解质溶液中由于离子之间的相互作用，使电解质的总浓度不能代表其有效浓度，需要引进一个经验校正系数y (活度系数)，以表示实际溶液与理想溶液的偏差。

电解质的活度系数通常可由测定电动势、溶解度和凝固点等求得。

活度系数的大小受温度水的介电常数、离子的浓度和价数等影响。

为使理想溶液(或极稀溶液)的热力学公式适用于真实溶液，用来代替浓度的一种物理量。

活度系数应用于冶金过程，使得治金反应能定量地进行热力学计算和分析，在阐明多种反应能否选择地进行，在控制调整产物能否达到最大产率，在控制治炼操作如何在最优化条件下进行等等方面，已经起了并将继续起到应有的作用。

物理化学实验报告姓名：吴菲 分数：实验日期：2013.11.11 温度：19℃ 大气压：102.23KpaNaCl 在H2O 中活度系数测定一.实验目的1.了解电导法测定电解质溶液活度系数的原理。

2.了解电导率仪的基本原理并熟悉使用方法。

二．实验原理由Dehye-Hiicker 公式lgf ±= —A ·|Z +·Z -|I1+Ba o I(1) 和Osager-Falkenhangen 公式 λ=λ0 - (B 1·λ0+B 2)I1+Ba o I(2)可以推出公式lgf ±=A ·|Z +·Z -|B 1 λ0+B 2 (λ-λ0) (3)令a= A ·|Z +·Z -|B 1 λ0+B 2(λ-λ0) 则：lgf ±=a ·(λ-λ0) (4)其中：A=1.8246×106(εT )3/2 ;B 1 = 2.801×106|Z +·Z -|·q(εT )3/2·(1+I)B 2=41.25(|Z +|+|Z -|)η(εT)1/2ε—溶剂的介电常数; η—溶剂的粘度; T —热力学温度;λ—电解质无限稀释摩尔电导率; I —溶液的离子强度。

q=|Z+·Z-||Z+|+|Z-|·L++L-|Z-|·L++|Z-|L-;L+0 , L-0是正、负离子的无限稀释摩尔电导率，Z+,Z_是正负离子的电荷数。

对于实用的活度系数(电解质正、负离子的平均活度系数)γ±，则有f±=γ±(1+0.001vmM)所以lgγ±=lg f±-lg (1+0.001vmM )即lgγ±= a(λ-λ0)- lg (1+0.001vmM )(5)其中:M—溶剂的摩尔质量(g/mol) ;v一为一个电解质分子中所含正、负离子数目的总和，即v=v++v-m—为电解质溶液的质量摩尔浓度( mol/kg )。

最近20年内电解质溶液活度计算理论进展班级：2009级化学工程与工艺1班 姓名：吴明川 学号：200910901090 摘 要: 近年来,电解质溶液理论的研究日益活跃，本文介绍了最近20年内电解质溶液活度计算的方法和进展。

人们根据活度计算的基础理论原理，建立起不同的理论模型来计算电解质的活度系数。

本文整理了部分比较常见的理论模型，简单介绍了近些年来电解质活度计算理论的发展。

关键词: 电解质 理论模型 活度计算The calculate theoretical progress of Electrolyte solution activity inthe last 20 yearsClass: class 1 of 2009 chemical engineering and technology level name: WU Mingchuanstudent number:200910901090Abstract ：In recent years, the theory of electrolyte solution of active day by day, this paper introduces the recent 20 years in electrolyte solution activity calculation method and progress. According to the calculation of activity of people based principle, establish different theoretical model to calculate the activity coefficient of electrolyte. This article discusses some common theoretical model, introduced in recent years electrolyte activity calculation theory development. Keyword ： Electrolyte Theory model Activity calculation1 不同理论模型的电解质活度计算1．1微扰理论状态方程计算电解质的活度1.2 Bromley 模型以质量摩尔浓度计量单位计算多组分电解质水溶液中单一例子活度因子的Bromley 模型[1]为 i i m xF I I z A f ++-=5.05.021lg式中：m A 为Debye-Huckel 理论常熟；25C 和40C 时m A 的值分别为0.5100和0.5242[2]；i 为溶液中的第i 种离子；i Z 为第i 种离子的离子价；I 为溶液的离子强度。

电解质溶液活度系数的计算方法【摘要】：本文综述了近二十年电解质溶液活度系数计算方法的进展情况。

电解质溶液活度是溶液热力学研究的重要参数，它集中反映了指定溶剂中离子之间及粒子与溶剂之间的相互作用，对离子溶剂化、离子缔合及溶液结构理论的研究具有重要意义【1】。

因此，了解电解质溶液活度系数的计算方法意义非凡。

【关键词】：活度系数 ； 电解质溶液 ；计算方法Abstract: This paper reviews the last two decades the development of calculation methodsof the electrolyte solution activity coefficients. Electrolyte solution thermodynamic study of the activity is an important parameter, which has focused on the specified solvent and between the particles and solvent-ion interaction. Of ion solvation, ion association and solution structure of the theoretical study of great significance 【1】.Therefore, to understand the activity coefficients of electrolyte solution methods of calculating has special significance.Key words: activity coefficient ；electrolyte solution ；Calculation 1.引言近年来电解质溶液理论的发展较快，其研究已逐渐从经典理论和半经验模型向统计力学理论发展，电解质溶液活度计算理论也逐渐成为近期研究的热点。