用自准法测薄凸透镜焦距(2020年整理).pptx

实验一 用自准法测薄凸透镜焦距一、实验目的1、掌握简单光路的分析和调整方法2、了解、掌握自准法测凸透镜焦距的原理及方法3、掌握光的可逆性原理测透镜焦距的方法4、掌握光的可逆性原理的光路调节二、实验原理（一）光的可逆性原理当发光点（物）处在凸透镜的焦平面时，它发出的光线通过透镜后将成为一束平行光。

若用与主光轴垂直的平面镜将此平行光反射回去，反射光再次通过透镜后仍会聚于透镜的焦平面上，其会聚点将在发光点相对于光轴的对称位置上。

光的可逆性原理：当光线的方向返转时，它将逆着同一路径传播。

借此原理可测量薄凸透镜的焦距，实验原理见图1-1图1-1当物P在焦点处或焦平面上时，经透镜后光是平行光束，经平面镜反射再经透镜后成像于原物P处（记为Q）。

因此，P点到透镜中心O点的距离就是透镜的焦距f。

（二）自准法如图1-2所示，将物AB放在凸透镜的前焦面上，这时物上任一点发出的光束经透镜后成为平行光，由平面镜反射后再经透镜会聚于透镜的前焦平面上，得到一个大小与原物相同的倒立实像A´B´。

此时，物屏到透镜之间的距离就等于透镜的焦距f。

图1-2 自准法测薄透镜焦距光路图三、主要仪器及耗材1：白光源S（GY-6A） 6：三维调节架 (SZ-16)2：物屏P（SZ-14） 7：二维平移底座 (SZ-02)3：凸透镜L （f′=190 mm） 8：三维平移底座 (SZ-01)4：二维架（SZ-07）或透镜架（SZ-08） 9-10：通用5：平面镜M底座（SZ-04）四、实验内容和步骤（一）实验内容1、光学系统共轴的调节。

2、利用可逆性原理测薄透镜的焦距，分别记下P和L的位置a1、a2；则焦距为：3、将透镜转过1800，记下P和L的位置b1、b2；则焦距为4、综合焦距为：（二）实验步骤1、光路如图1-3所示，先对光学系统进行共轴调节，实验中，要求平面镜垂直于导轨；2、移动凸透镜，直至物屏上得到一个与物大小相等，倒立的实像；3、调M镜，并微动L，使像最清晰且与物等大（充满同一圆面积）；4、分别记下P和L的位置a1、a2；5、将P和L都转1800之后，重复做前4步；6、记下P和L新的位置b1、b2；7、计算：；图1-3 实验装置图五、数据处理与分析1、实验数据记录表1-1，也可自拟表格；2、按表格中所列各项利用高斯公式计算出透镜的焦距。

用自准法测薄凸透镜焦距
自准法是一种测量薄凸透镜焦距的方法，也称为自调整法或自匹配法。

这种方法利用光学成像原理，通过调整透镜与屏幕之间的距离，使得成像位置达到最清晰的状态，从而确定透镜的焦距。

实验中需要准备的器材有：薄凸透镜、调节屏幕、光源、卡尺、直梁器等。

首先，将调节屏幕、光源和薄凸透镜依次放置在同一条实验光路上，使得光源经过透镜后能够形成清晰的像。

接下来，先将透镜与调节屏幕之间的距离调至最短，此时光线聚焦出的图像距离透镜极近处，不清晰。

然后慢慢调整透镜与调节屏幕之间的距离，直到得到清晰的图像。

当图像清晰时，通过卡尺测量透镜到光源的距离和透镜到调节屏幕的距离，分别记为$s$和$s'$。

此时可以利用成像公式推导出透镜的焦距$f$：
$\frac{1}{f}=\frac{1}{s}+\frac{1}{s'}$
利用上述公式即可求解透镜的焦距。

需要注意的是，在实验中需要确保光线的稳定性，避免环境中产生的扰动对测量结果的影响。

此外，实验时需要注意透镜光学性能的限制，确保透镜为薄透镜并且成像光线的孔径足够小，以免误差产生。

自准法测量薄凸透镜的焦距简单易行，且精度较高，被广泛应用于实验教学和科研领域。

实验25 薄透镜焦距的测定教学目标重点与难点实验内容教学过程设计一。

讨论1．本实验介绍的测量薄凸透镜的方法有几种？请画出光路图。

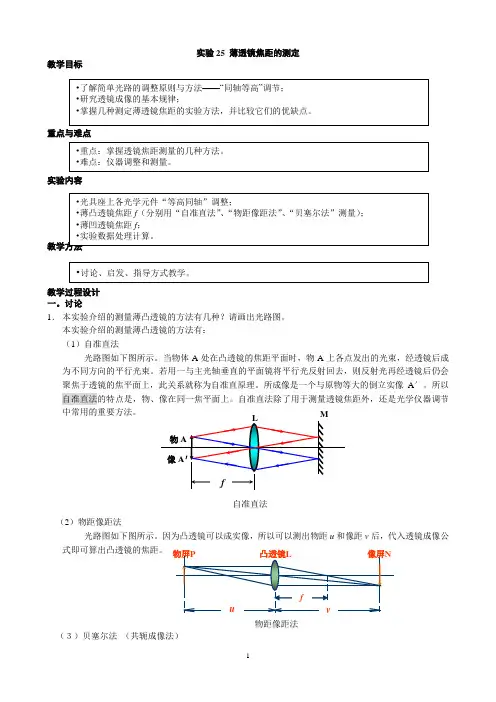
本实验介绍的测量薄凸透镜的方法有：（1）自准直法光路图如下图所示。

当物体A处在凸透镜的焦距平面时，物A上各点发出的光束，经透镜后成为不同方向的平行光束。

若用一与主光轴垂直的平面镜将平行光反射回去，则反射光再经透镜后仍会聚焦于透镜的焦平面上，此关系就称为自准直原理。

所成像是一个与原物等大的倒立实像A′。

所以自准直法的特点是，物、像在同一焦平面上。

自准直法除了用于测量透镜焦距外，还是光学仪器调节中常用的重要方法。

自准直法（2）物距像距法光路图如下图所示。

因为凸透镜可以成实像，所以可以测出物距u和像距v后，代入透镜成像公式即可算出凸透镜的焦距。

（３）贝塞尔法（共轭成像法）光路图如下图所示。

由凸透镜成像规律可知，如果物屏与像屏的相对位置l 保持不变，而且l >4f ，当凸透镜在物屏与像屏之间移动时，可实现两次成像。

透镜在x 1位置时，成倒立、放大的实像，；透镜在x 2位置时，成倒立、缩小的实像。

实验中，只要测量出光路图中的物屏与像屏的距离l 和透镜两次成像移动的距离d ，代入下式就可算出透镜的焦距。

224l d f l-=2． 如何测量凹透镜的焦距？凹透镜是发散透镜，所成像为虚像，不能用像屏接收。

为了测量凹透镜的焦距，常用辅助凸透镜与之组成透镜组，使能得到能用像屏接收的实像。

其测量原理如下光路图所示。

实物AB 经凸透镜L 1成像于A ′B ′。

在L 1和A ′B ′之间插入待测凹透镜L 2，就凹透镜L 2而言，虚物A ′B ′又成像于A ″B ″。

实验中，调整L 2及像屏至合适的位置，就可找到透镜组所成的实像A ″B ″。

因此可把O 2A ′看为凹透镜的物距u ，O 2A ″看为凹透镜的像距v ，则由成像公式可得 111u v f-+= （虚物的物距为负） u v f u v ⋅=- 由于u < v ，求出的凹透镜L 2的焦距f 为负值。

薄凸透镜焦距的测定1.自准法实验原理：如图1，当物体P处在凸透镜的焦平面上时,由 P发出光线通过透镜L折射后成平行光,如果在透镜后面放一个与透镜光轴垂直的平面反射镜M,此平行光经 M反射后再次通过透镜,仍会聚于透镜光轴的对称位置上。

也就是说,象相对于物为大小相等的倒立实象,物距、象距均等于该透镜的焦距.实验步骤:1.如图1所示，在导轨上放置物屏P、平面镜M，并使它们两者的距离比所测凸透镜的焦距大。

在物屏P和平面镜M之间放上被测量的凸透镜L。

2.适当调节光路，使物屏P发出的物光通过透镜后，由平面镜再反射回去，并再次通过透镜射向物屏P。

3.在导轨上，前后移动凸透镜，使物屏上产生倒立、等大、清晰的实像。

用纸片遮住平面镜，清晰的像应该消失。

记下凸透镜在导轨上位置L。

4.重复步骤（3）五次，共记下L六个数据，并读出P的位置，填入表格。

实验数据记录：1 2 3 4 5 6 平均Δ仪（cm）L(cm)P(cm)一．焦距的判断：放置好透镜和平面镜前后移动有孔的光屏，直到在屏上观察到清晰的等大像（此时应该能看清镜头纸纤维成的像），这是透镜光心与屏的距离就是焦距。

二．误差来源及解决方案：①由图此时的偏离光心，凸透镜前面相当于凸镜，起折射作用，后面相当于凹镜，起反射作用。

也就是不用经过的平面镜的反射即可在P’位置产生实相。

当撤去平面镜，此时P'依旧有像，而原图1 P'位置没有了像，所以根据这个方法可以知道实验时是否偏离光心。

而此时的像距小于焦距。

通过不断的移去和移回平面镜就可以把它调节的正常水平。

②在实际测量时，由于对成像刚清晰程度的判断不准确，可导致测量值产生一定的误差。

为了减小误差，常采用左右逼近法读数，即先使透镜由左向右移动，当像刚清晰时停止，记下透镜位置的读数；再使透镜自右向左移动，在像清晰时又得一读数，取这两次读数的平均值作为成像清晰时凸透镜的位置。

三．实验装置图：四．Δf的表达式2.物距像距法实验原理：一个凸透镜.从景物至镜片的距离,称物距；从镜片至所成投影之间的距离,称像距。