《平面与平面垂直的性质》
- 格式：ppt
- 大小：1.48 MB
- 文档页数：17
下载文档原格式
合集下载
第十二课时 平面与平面垂直的性质
（）求二面角 1 M BC D的正切值； （2）求CN与平面ABCD所成角的正切值；
（ 3 ）求CN与BD所成角的余弦值；
（4）求平面SBC与SDC所成角的正弦值。
S
M A B C
N
D
过 关 落 实
如图所示，四边形ABCD是边长为6的正方形， SA 平面ABCD，SA 8，M 是SA的中点， 过M 和BC的平面交SD于N。
（ 1 ）求二面角M BC D大小的正切值； （2）求CN与平面ABCD所成角的正切值；
（ 3 ）求CN与BD所成角的余弦值；
（4）求平面SBC与SDC所成角大小的正弦值。
S
M A B
Q
N E
D
F
C
小结
A
α a B β
线线垂直
线面垂直
α
β
线线平行 面面平行
面面垂直
A B
面面垂直 线面垂直
思考:若α ⊥β ，过平面α 内一点A 作平面β 的垂线，垂足为B，那么点 B在什么位置？
α
A
β
B
结论: 如果两个平面互相垂直，那么 经过一个平面内一点且垂直于另一 个平面的直线，必在这个平面内.
α A
β
B
概念巩固
判断正误
已知平面α⊥平面β,α∩
β＝l下列命题
(1)平面α内的任意一条直线必垂直于平面β （ ×）
a // b b a
a //
例3、如图，已知PA⊥平面ABC， 平面PAB⊥平面PBC，求证：BC⊥平面PAB
证明：过点A作AE⊥PB，垂足 P 为E， ∵平面PAB⊥平面PBC， 平面PAB∩平面PBC=PB， A ∴AE⊥平面PBC ∵BC 平面PBC ∴AE⊥BC ∵PA⊥平面ABC，BC 平面ABC ∴PA⊥BC ∵PA∩AE=A，∴BC⊥平面PAB B
（ 3 ）求CN与BD所成角的余弦值；
（4）求平面SBC与SDC所成角的正弦值。
S
M A B C
N
D
过 关 落 实
如图所示，四边形ABCD是边长为6的正方形， SA 平面ABCD，SA 8，M 是SA的中点， 过M 和BC的平面交SD于N。
（ 1 ）求二面角M BC D大小的正切值； （2）求CN与平面ABCD所成角的正切值；
（ 3 ）求CN与BD所成角的余弦值；
（4）求平面SBC与SDC所成角大小的正弦值。
S
M A B
Q
N E
D
F
C
小结
A
α a B β
线线垂直
线面垂直
α
β
线线平行 面面平行
面面垂直
A B
面面垂直 线面垂直
思考:若α ⊥β ，过平面α 内一点A 作平面β 的垂线，垂足为B，那么点 B在什么位置？
α
A
β
B
结论: 如果两个平面互相垂直，那么 经过一个平面内一点且垂直于另一 个平面的直线，必在这个平面内.
α A
β
B
概念巩固
判断正误
已知平面α⊥平面β,α∩
β＝l下列命题
(1)平面α内的任意一条直线必垂直于平面β （ ×）
a // b b a
a //
例3、如图，已知PA⊥平面ABC， 平面PAB⊥平面PBC，求证：BC⊥平面PAB
证明：过点A作AE⊥PB，垂足 P 为E， ∵平面PAB⊥平面PBC， 平面PAB∩平面PBC=PB， A ∴AE⊥平面PBC ∵BC 平面PBC ∴AE⊥BC ∵PA⊥平面ABC，BC 平面ABC ∴PA⊥BC ∵PA∩AE=A，∴BC⊥平面PAB B
人教版高中数学必修2《平面与平面垂直的性质》PPT课件
3，∴h＝
3 2.
在△BCD 中，BF＝BD·cos 60°＝2×12＝1，DF＝BD·sin 60°＝ 3，∴DC＝2 3，
故 S△BCD＝12BF·DC＝12×1×2 3＝ 3.
∴VD-BCG＝VG-BCD＝13S△BCD·h＝13× 3× 23＝12.
[方法技巧] (1)在有关垂直问题的证明过程中要注意线线垂直、线面垂直、面面垂直的 相互转化．因此，判定定理与性质定理的合理应用是证明垂直问题的关键． (2)空间问题转化成平面问题是解决立体几何问题的一个基本原则．解题时， 要通过几何图形自身的特点，如等腰(等边)三角形的“三线合一”、中位线定理、 菱形的对角线互相垂直等，得出一些题目所需要的条件．对于一些较复杂的问 题，注意应用转化思想解决问题．
【对点练清】 如图，在四棱锥 P-ABCD 中，平面 PAB⊥平面 ABCD，BC∥平 面 PAD，∠ABC＝90°，PA＝PB＝ 22AB.求证： (1)AD∥平面 PBC； (2)平面 PBC⊥平面 PAD. 证明：(1)∵BC∥平面 PAD，BC⊂平面 ABCD，平面 ABCD∩平面 PAD＝AD， ∴BC∥AD. ∵AD⊄平面 PBC，BC⊂平面 PBC，∴AD∥平面 PBC.
若①m⊥n，③n⊥β，④m⊥α 成立，则②α⊥β 一定成立； 若②α⊥β，③n⊥β，④m⊥α 成立，则①m⊥n 一定成立． ∴①③④⇒②(或②③④⇒①)． 答案：①③④⇒②(或②③④⇒①)
• 题型二 垂直关系的综合应用
• [探究发现]
• 试总结线线垂直、线面垂直、面面垂直之间的转化关 系．
提示：在线线垂直、线面垂直、面面垂直的相互转化中．每一种垂直的
判定都是从某一垂直开始转向另一垂直，最终达到目的，其转化关系如下：
2.3.4平面与平面的垂直的性质
性质
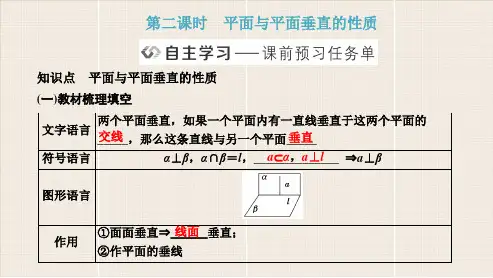
若两个平面垂直,则在一个平面内 性质定理：
垂直于它们交线的直线垂直于另一个平面.
在β内作直线BE⊥CD于B, 则∠ABE是二面角α-CD-β 的平面角 由α⊥β知,AB⊥BE ∴AB⊥β
A
D C B
E
又AB⊥CD 而BE和CD是β内的两条相交直线
面面垂直
线面垂直
举例
例： 已知
l , , ,
判定定理 判定定理
线线垂直
定义
线面垂直
性质定理
面面垂直
作业 1. 求证：两条异面直线不能同时
和一个平面垂直；
2. 求证：三个两两垂直的平面的 交线两两垂直.
平面与平面 垂直的性质
先直观感受平面与平面 垂直的情形
复习
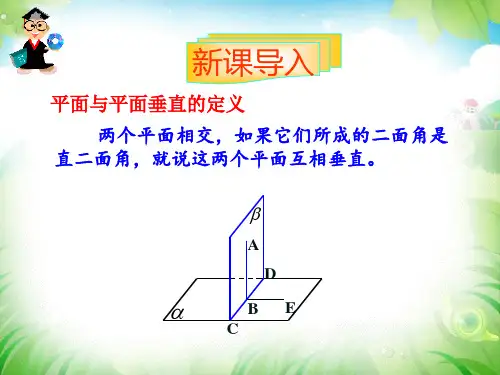
1.定义：两个平面相交，如果它们所成 的二面角是直二面角，则两个平面垂直
记作α⊥β
性质:
1.凡是直二面角都相等； 2.两个平面相交,可引成四个二面角,如果其中有一 个是直二面角,那么其他各个二面角都是直二面角.
复习
若一个平面经过另一个平面 2.判定定理： 的一条垂线,则这两个平面互相垂直.
D
A垂直
思考
(1) 黑板所在平面与地面所在平面垂直,你能 否在黑板上画一条直线与地面垂直? (2) 如图,长方体中, 平面A1ADD1与平面 ABCD垂直,直线A1A A1 垂直于其交线AD,平 面A1ADD1内的直线 A A1A与平面ABCD垂 直吗？ D1 B1 D B C C1
求证： l
l
m
n
a
b P
证明：在平面 a m，b n
平面与平面垂直的性质
面面垂直 图形表示:
C
线面垂直
A D
B
符号表示:
CD AB
AB AB CD AB CD B
定理剖析
1) 面面垂直线面垂直； （线是一个平面内垂直于两平面交线的 一条直线）
α
C
2）它为判定和作出线面垂直提供依据。
求证 : AB .
证明:在平面 内作BE⊥CD,
A D
垂足为B.
则∠ABE就是二面角 -CD- 的平面角 ∵
B C
E
, ∴AB⊥BE(平面与平面垂直的定义)
又由题意知AB⊥CD,且BE CD=B
∴AB⊥ (直线与平面垂直的判定定理)
定理
两个平面垂直，则一个平面内垂直于交线的直 线与另一个平面垂直．
D
C
B
定理的应用,你也可以
a. 求证: a
如图,已知 ,
b , , c ,
a
证明:过平面 内一点P作PA⊥ b 于A,作PB⊥ c 于B. ∵
a
∴PA⊥
∴a
A P
b
c
B
又
∴PA⊥ a
∵PB PA=P, PA , PB
3、平面与平面垂直的定义
两个平面相交，如果它们所成的二面角是 直二面角，就说这两个平面互相垂直。
4、平面与平面垂直的判定定理
一个平面过另一个平面的垂 线，则这两个平面垂直。
符号表示：
该命题正确吗？
b
b b
2.3.4平面与平面垂直的性质
面面垂直
性质定理 判定定理
线面垂直
1、平面与平面垂直的性质定理：两个平面 垂直，则一个平面内垂直于交线的直线与另 一个平面垂直。 2、证明线面垂直的两种方法： 线线垂直→线面垂直；面面垂直→线面垂直 3、线线、线面、面面之间的关系的转化是解 决空间图形问题的重要思想方法。
平面与平面垂直的性质定理
b
l
Ⅱ.概括结论
l bl
b 该命题正确吗？ 简述为移
如图，已知α ⊥β ，l⊥β ， l ，试判断直线l与平面α 的位 置关系，并说明理由.
α a m β
2013-1-16
例1
l
例2 如图，四棱锥P-ABCD的底面是 BC 矩形，AB=2， 2 ，侧面PAB是 等边三角形，且侧面PAB⊥底面ABCD. （1）证明：侧面PAB⊥侧面PBC； （2）求侧棱PC与底面ABCD所成的角.
P
A E
2013-1-16
D
B
C
例3：如图，AB是⊙O的直径，C是圆周上不同 于A，B的任意一点，平面PAC⊥平面ABC， (1)判断BC与平面PAC的位置关系，并证明。 (2)判断平面PBC与平面PAC的位置关系。
2.3.4《平面与平面 垂直的性质》
问题提出
1.平面与平面垂直的定义是什 么？如何判定平面与平面垂直？
定义和判定定理
2.平面与平面垂直的判定定理， 解决了两个平面垂直的条件问题； 反之，在平面与平面垂直的条件下， 能得到哪些结论？
2013-1-16
提出问题：
1、平面与平面垂直的定义
两个平面相交，如果它们所成的二面角是 直二面角，就说这两个平面互相垂直。
面面垂直的性质
解： 在内作垂直于 与 交线的直线b
, b
又 a , a / / b
a
b
即直线a与平面 平行
a / /
a ,b
探究: 已知平面 ， ，直线a ，且 ，
=AB,a // ,a AB , 试判断 直线a与平面 的位置关系.
思考1：对于三个平面 α ，β ，γ ，若α γ ， β γ ，α β l，那么直线l与平面γ 的位 置关系如何？为什么？
β
l
α b
a
γ
Ⅲ.知识应用
练习1：判断正误。 已知平面α ⊥平面β ,α ∩ β ＝l 下列命题
(1)平面α 内的任意一条直线必垂直于平面β （×） (2)垂直于交线l 的直线必垂直于平面β （× ）
3：如图，已知PA⊥平面ABC， 平面PAB⊥平面PBC，求证：BC⊥平面PAB
证明：过点A作AE⊥PB， P 垂足为E， ∵平面PAB⊥平面PBC， 平面PAB∩平面PBC=PB， A ∴AE⊥平面PBC ∵BC 平面PBC ∴AE⊥BC ∵PA⊥平面ABC，BC 平面ABC ∴PA⊥BC ∵PA∩AE=A，∴BC⊥平面PAB B
E
(1)EF//PD
A
F
D C
作业： p74，第3题
(2)BF⊥平面PAD
B
A 如果平面 α ⊥平面 β ,那么平面α 内一定存在直 线平行于平面 β
B如果平面α ⊥平面 β ,那么平面α 内所有直线都垂 直于平面 β C如果平面α 不垂直于平面 β，则平面 α 内一定不 存在直线垂直于平面 β D如果平面 α 、β 都垂直于平面M，且 交于直线 a，则 a ⊥平面M
α与
, b
又 a , a / / b
a
b
即直线a与平面 平行
a / /
a ,b
探究: 已知平面 ， ，直线a ，且 ，
=AB,a // ,a AB , 试判断 直线a与平面 的位置关系.
思考1：对于三个平面 α ，β ，γ ，若α γ ， β γ ，α β l，那么直线l与平面γ 的位 置关系如何？为什么？
β
l
α b
a
γ
Ⅲ.知识应用
练习1：判断正误。 已知平面α ⊥平面β ,α ∩ β ＝l 下列命题
(1)平面α 内的任意一条直线必垂直于平面β （×） (2)垂直于交线l 的直线必垂直于平面β （× ）
3：如图，已知PA⊥平面ABC， 平面PAB⊥平面PBC，求证：BC⊥平面PAB
证明：过点A作AE⊥PB， P 垂足为E， ∵平面PAB⊥平面PBC， 平面PAB∩平面PBC=PB， A ∴AE⊥平面PBC ∵BC 平面PBC ∴AE⊥BC ∵PA⊥平面ABC，BC 平面ABC ∴PA⊥BC ∵PA∩AE=A，∴BC⊥平面PAB B
E
(1)EF//PD
A
F
D C
作业： p74，第3题
(2)BF⊥平面PAD
B
A 如果平面 α ⊥平面 β ,那么平面α 内一定存在直 线平行于平面 β
B如果平面α ⊥平面 β ,那么平面α 内所有直线都垂 直于平面 β C如果平面α 不垂直于平面 β，则平面 α 内一定不 存在直线垂直于平面 β D如果平面 α 、β 都垂直于平面M，且 交于直线 a，则 a ⊥平面M
α与
高数数学必修一《8.6.3.2平面与平面垂直的性质》教学课件
1
AB＝AD＝ CD＝1，四边形ADEF是正方形，平面ADEF⊥平面ABCD.
2
证明：平面BCE⊥平面BDE.
1
2
证明：因为AB∥CD，AB⊥AD且AB＝AD＝ CD＝1，
所以BD＝BC＝ 2，CD＝2，所以BC⊥BD，
因为平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD＝AD，
四边形ADEF是正方形，ED⊥AD，ED⊂平面ADEF，所以ED⊥平面
平面内；③直线必须垂直于它们的交线．
跟踪训练1 如图，在三棱锥P-ABC中，PA⊥平面ABC，平面PAB⊥
平面PBC.
求证：BC⊥AB.
题型 2 垂直关系的综合应用
例2 如图，四棱锥P-ABCD，平面PAB⊥平面ABCD ，PA⊥AB，
AB∥CD，∠DAB＝90°，PA＝AD，DC＝2AB，E为PC中点．
2．线线、线面、面面垂直关系的综合应用．
第2课时 平面与平面垂直的性质
预学案
共学案
预学案
一、平面与平面垂直的性质定理❶
一个平面内
两个平面垂直，如果__________有一直线垂直于这两
文字语言
交线
个平面的________，那么这条直线与另一个平面垂直
α⊥β
α∩β=
ൢ⇒a⊥β
符号语言
a⊂α
____________
a⊥l
____________
ABCD，
因为BC⊂平面ABCD，所以BC⊥ED，
因为BD，ED⊂平面BDE，BD∩ED＝D，所以BC⊥平面BDE，
因为BC⊂平面BCE，所以平面BCE⊥平面BDE.
随堂练习
1．平面α⊥平面β，直线a∥α，则(
)
AB＝AD＝ CD＝1，四边形ADEF是正方形，平面ADEF⊥平面ABCD.
2
证明：平面BCE⊥平面BDE.
1
2
证明：因为AB∥CD，AB⊥AD且AB＝AD＝ CD＝1，
所以BD＝BC＝ 2，CD＝2，所以BC⊥BD，
因为平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD＝AD，
四边形ADEF是正方形，ED⊥AD，ED⊂平面ADEF，所以ED⊥平面
平面内；③直线必须垂直于它们的交线．
跟踪训练1 如图，在三棱锥P-ABC中，PA⊥平面ABC，平面PAB⊥
平面PBC.
求证：BC⊥AB.
题型 2 垂直关系的综合应用
例2 如图，四棱锥P-ABCD，平面PAB⊥平面ABCD ，PA⊥AB，
AB∥CD，∠DAB＝90°，PA＝AD，DC＝2AB，E为PC中点．
2．线线、线面、面面垂直关系的综合应用．
第2课时 平面与平面垂直的性质
预学案
共学案
预学案
一、平面与平面垂直的性质定理❶
一个平面内
两个平面垂直，如果__________有一直线垂直于这两
文字语言
交线
个平面的________，那么这条直线与另一个平面垂直
α⊥β
α∩β=
ൢ⇒a⊥β
符号语言
a⊂α
____________
a⊥l
____________
ABCD，
因为BC⊂平面ABCD，所以BC⊥ED，
因为BD，ED⊂平面BDE，BD∩ED＝D，所以BC⊥平面BDE，
因为BC⊂平面BCE，所以平面BCE⊥平面BDE.
随堂练习
1．平面α⊥平面β，直线a∥α，则(
)
人教版高一数学《2.3.4平面与平面垂直的性质》课件
2.长方体ABCD-A1B1C1D1中，平面A1ADD1与 平面ABCD垂直，平面A1ADD1内的直线A1A 与平面ABCD垂直吗?
D1 A1
D
A
C1 B1
C B
平面与平面垂直的性质定理
1. 两视个察平实面验垂直,则一
个平面视内察垂两直垂于直交平线面的直
线中与,另一个一平个面平内面的垂直直线.
l
与符另号一表个示平：面的有哪
例1 如下图所示，P是四边形ABCD所在平面外的一点，
ABCD是∠DAB＝60°且边长为a
的菱形．侧面PAD为正三角形，
其所在平面垂直于底面ABCD.
(1)若G为AD边的中点，求证： BG⊥平面PAD； (2)求证：AD⊥PB.
分析：①ABCD是边长为a的菱形；
②面PAD⊥面ABCD.
解答本题可先由面⊥面得线⊥面，再进一步得出线⊥线．
面面垂直
性质定理 判定定理
线面垂直
巩固提升:
1. 如图,已知平面 , , ，直线a满足
a , a ,试判断直线a与平面 的位置关系。
解:在 内作垂直于 与 交线的直线b,
因为 ,所以 b .
因为 a ,所以 a // b . 又因为 a ,所以a // .
a
b
即直线a与平面 平行
变式1 如图所示，α⊥β，CD⊂β，CD⊥AB， CE、EF⊂α，∠FEC＝90°.
求证：面EFD⊥面DCE.
证明：∵α⊥β，CD⊂β， CD⊥AB，α∩β＝AB，∴CD⊥α. 又∵EF⊂α，∴CD⊥EF. 又∠FEC＝90°，∴EF⊥EC. 又EC∩CD＝C，∴EF⊥面DCE. 又EF⊂面EFD，∴面EFD⊥面 DCE.
(2) 当 F 为 PC 的 中 点 时 ， 满 足 平 面 DEF⊥ 平 面 ABCD.取PC的中点F，连接DE、EF、DF，
D1 A1
D
A
C1 B1
C B
平面与平面垂直的性质定理
1. 两视个察平实面验垂直,则一
个平面视内察垂两直垂于直交平线面的直
线中与,另一个一平个面平内面的垂直直线.
l
与符另号一表个示平：面的有哪
例1 如下图所示，P是四边形ABCD所在平面外的一点，
ABCD是∠DAB＝60°且边长为a
的菱形．侧面PAD为正三角形，
其所在平面垂直于底面ABCD.
(1)若G为AD边的中点，求证： BG⊥平面PAD； (2)求证：AD⊥PB.
分析：①ABCD是边长为a的菱形；
②面PAD⊥面ABCD.
解答本题可先由面⊥面得线⊥面，再进一步得出线⊥线．
面面垂直
性质定理 判定定理
线面垂直
巩固提升:
1. 如图,已知平面 , , ，直线a满足
a , a ,试判断直线a与平面 的位置关系。
解:在 内作垂直于 与 交线的直线b,
因为 ,所以 b .
因为 a ,所以 a // b . 又因为 a ,所以a // .
a
b
即直线a与平面 平行
变式1 如图所示，α⊥β，CD⊂β，CD⊥AB， CE、EF⊂α，∠FEC＝90°.
求证：面EFD⊥面DCE.
证明：∵α⊥β，CD⊂β， CD⊥AB，α∩β＝AB，∴CD⊥α. 又∵EF⊂α，∴CD⊥EF. 又∠FEC＝90°，∴EF⊥EC. 又EC∩CD＝C，∴EF⊥面DCE. 又EF⊂面EFD，∴面EFD⊥面 DCE.
(2) 当 F 为 PC 的 中 点 时 ， 满 足 平 面 DEF⊥ 平 面 ABCD.取PC的中点F，连接DE、EF、DF，
平面与平面垂直的性质定理
证明:在平面 α 内作BE⊥CD,垂足为B。 则∠ABE就是二面角α-CD-β的平面 角。 又由题意知AB⊥CD,且BE CD=B
A D B C E
∵α⊥β, ∴AB⊥BE(平面与平面垂直的定义)
∴AB⊥α(直线与平面垂直的判定定理)
平面与平面垂直的性质定理
两个平面垂直，则一个平面内垂直于交线的直 线与另一个平面垂直． 符号表示:
B
∴AF⊥平面PBC
∩
例3．S为三角形ABC所在平面外一点，SA⊥平面 ABC，平面SAB⊥平面SBC。 求证：AB⊥BC。 S
证明：过A点作AD⊥SB于D点. ∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC， ∴ AD⊥BC.
A D C
又∵ SA ⊥ 平面ABC， ∴SA ⊥ BC. AD∩SA=A
2.3.4 平面与平面垂直的性质
复习回顾：
平面与平面垂直的定义 两个平面相交，如果它们所成的二面 角是直二面角，就说这两个平面互相垂直。
A D
B C
E
平面与平面垂直的判定定理
一个平面过另一个平面的垂线，则 这两个平面垂直。
符号表示：
b β α β b α
面面垂直
线面垂直
考思
α P
B
D C A
β
过P做PD⊥AB，垂足为D。 ∵PD⊥AB，∴PD⊥面β。 ∵过一点只能做一条直线与平面垂直。 ∴PC与PD必重合，即PC在面α内。
例1：如图:已知平面α，β， ⊥β,直线a满足 a⊥ β， a ，判断直线a与平面 的位置关系。
解:在 内作垂直于 与β 交线的直线b。 ∵ ⊥β ∴b ⊥β(平面与平面垂直的性质定理)
β ∵ ⊥β ∴a//b(直线与平面垂直的性质定理) 又∵a ∴a// (直线与平面平行的判定定理) 即直线a与平面 平行。
A D B C E
∵α⊥β, ∴AB⊥BE(平面与平面垂直的定义)
∴AB⊥α(直线与平面垂直的判定定理)
平面与平面垂直的性质定理
两个平面垂直，则一个平面内垂直于交线的直 线与另一个平面垂直． 符号表示:
B
∴AF⊥平面PBC
∩
例3．S为三角形ABC所在平面外一点，SA⊥平面 ABC，平面SAB⊥平面SBC。 求证：AB⊥BC。 S
证明：过A点作AD⊥SB于D点. ∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC， ∴ AD⊥BC.
A D C
又∵ SA ⊥ 平面ABC， ∴SA ⊥ BC. AD∩SA=A
2.3.4 平面与平面垂直的性质
复习回顾：
平面与平面垂直的定义 两个平面相交，如果它们所成的二面 角是直二面角，就说这两个平面互相垂直。
A D
B C
E
平面与平面垂直的判定定理
一个平面过另一个平面的垂线，则 这两个平面垂直。
符号表示：
b β α β b α
面面垂直
线面垂直
考思
α P
B
D C A
β
过P做PD⊥AB，垂足为D。 ∵PD⊥AB，∴PD⊥面β。 ∵过一点只能做一条直线与平面垂直。 ∴PC与PD必重合，即PC在面α内。
例1：如图:已知平面α，β， ⊥β,直线a满足 a⊥ β， a ，判断直线a与平面 的位置关系。
解:在 内作垂直于 与β 交线的直线b。 ∵ ⊥β ∴b ⊥β(平面与平面垂直的性质定理)
β ∵ ⊥β ∴a//b(直线与平面垂直的性质定理) 又∵a ∴a// (直线与平面平行的判定定理) 即直线a与平面 平行。
平面与平面垂直的性质
1.A. 2.B.
SUCCESS
THANK YOU
2024/1/5
B
C
又∵AF⊥PC,AF 面PAC ,面PBC∩面PAC=PC
∴AF⊥平面PBC
课堂小结
平面和平面垂直的性质定理：
如果两个平面相互垂直，那么在一个平面内 垂直于它们交线的直线垂直于另一个平面。
面面垂直
线面垂直
证明线面垂直的两种方法： 线线垂直→线面垂直；面面垂直→线面垂直
高考链接
1（2008 辽宁）如图，在棱长为1的正方体ABCD ABCD
的任意一条直线 (×) 有可能平行,相交但不垂直,异面。
6)一个平面内的已知直线必垂直于另一个平面
的无数条直线 (√)
7)一个平面内的任一条直线必垂直于另一个平
面 (×)
可能平行,可能相交但不垂直,可能在平面内。
8)过一个平面内任意一点作交线的垂线,则此垂 线必垂直于另一个平面 (√)
2.如图，四棱锥P-ABCD的底面是矩形， AB=2，BC 2，侧面PAB是等边三角形，且侧面 PAB⊥底面ABCD。 （1）证明：侧面PAB⊥侧面PBC； （2）求侧棱PC与底面ABCD所成的角。
中，AP=BP=b（ 0<b<1），截面PQEF∥ AD 截面
PQGH∥AD 。 (Ⅰ)证明：平面PQEF和平面PQGH互相垂直； (Ⅱ)证明：截面PQEF和截面PQGH面积之和是定值，并 求出这个值； (Ⅲ)若与平面PQEF所成的角为45°，求与平面PQGH所 成角的正弦值.
【解析】
习题答案
α P
B β
DC
A 过P做PD⊥AB，垂足为D。 ∵PD⊥AB，∴PD⊥面β。 ∵过一点只能做一条直线与平面垂直。 ∴PC与PD必重合，即PC在面α内。
SUCCESS
THANK YOU
2024/1/5
B
C
又∵AF⊥PC,AF 面PAC ,面PBC∩面PAC=PC
∴AF⊥平面PBC
课堂小结
平面和平面垂直的性质定理：
如果两个平面相互垂直，那么在一个平面内 垂直于它们交线的直线垂直于另一个平面。
面面垂直
线面垂直
证明线面垂直的两种方法： 线线垂直→线面垂直；面面垂直→线面垂直
高考链接
1（2008 辽宁）如图，在棱长为1的正方体ABCD ABCD
的任意一条直线 (×) 有可能平行,相交但不垂直,异面。
6)一个平面内的已知直线必垂直于另一个平面
的无数条直线 (√)
7)一个平面内的任一条直线必垂直于另一个平
面 (×)
可能平行,可能相交但不垂直,可能在平面内。
8)过一个平面内任意一点作交线的垂线,则此垂 线必垂直于另一个平面 (√)
2.如图，四棱锥P-ABCD的底面是矩形， AB=2，BC 2，侧面PAB是等边三角形，且侧面 PAB⊥底面ABCD。 （1）证明：侧面PAB⊥侧面PBC； （2）求侧棱PC与底面ABCD所成的角。
中，AP=BP=b（ 0<b<1），截面PQEF∥ AD 截面
PQGH∥AD 。 (Ⅰ)证明：平面PQEF和平面PQGH互相垂直； (Ⅱ)证明：截面PQEF和截面PQGH面积之和是定值，并 求出这个值； (Ⅲ)若与平面PQEF所成的角为45°，求与平面PQGH所 成角的正弦值.
【解析】
习题答案
α P
B β
DC
A 过P做PD⊥AB，垂足为D。 ∵PD⊥AB，∴PD⊥面β。 ∵过一点只能做一条直线与平面垂直。 ∴PC与PD必重合，即PC在面α内。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
线线平行 面面平行
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的
直线与另一个平面垂直.
符号表示:
bl
l
b
b
bl
简述为：
面面垂直
线面垂直
练习：
1、下列命题中错误的是（B ）
α A 如果平面 ⊥平面 β ,那么平面 α 内一定存在
直线平行于平面 β
内观垂察两直垂于直平交面线中的,一直个平线面与内 另一 个的位平直置线关面与系垂?另一直个. 平面的有哪些
l
符号表示：
b
Ⅱ.概括结论
bbbll 面bb简面述垂为：直该命题正确线吗？面垂直
Ⅲ.知识应用
练习1：判断正误。
已知平面α⊥平面β,α∩ β＝l下列命题
线线垂直 线面垂直 作PM ⊥ b于M，PN ⊥C于N.
因为 α⊥γ，β ⊥γ ，
所以 PM ⊥ α， PN ⊥ β. 因为 α ∩ β= a， 所以 PM ⊥ a， PN ⊥ a， γ 所以 a⊥γ.
αa β
cN P
已知：α⊥γ，β ⊥γ,α ∩ β= а,求证： a⊥γ.
证法二：
任取P∈a，过点P作b⊥γ.
解题反思
1、面面垂直的性质定理给我们提供了一 种证明线面垂直的方法
2、本题充分地体现了面面垂直与 线面 垂直之间的相互转化关系。
面面垂直
性质定理 判定定理
线面垂直
例 垂直于同一平面的两平面的交线垂直于这个平面。 已知：α⊥γ，β ⊥γ,α ∩ β= а,求证： a⊥γ. 证法一：
设α ∩ γ =b, β ∩ γ =c,在γ 内任取一点P，
因为α ⊥γ，
所以b α， 因为β ⊥γ，
同一法
因此b β， 故α ∩ β= b. 由已知 α∩ β= a， γ
αa Pβ b
所以a与 b重合，
所以a ⊥γ.
已知：α⊥γ，β ⊥γ,α ∩ β= а,求证： a⊥γ.
证法三：
设α⊥γ于b，β ⊥γ于c.
在α内作 b′ ⊥ b, 所以 b′ ⊥ γ.
D
D
折成
A
C
O
A
O
C
B
B
1、平面与平面垂直的性质定理：两个平面 垂直，则一个平面内垂直于交线的直线与另 一个平面垂直。
2、证明线面垂直的两种方法： 线线垂直→线面垂直；面面垂直→线面垂直
3、线线、线面、面面之间的关系的转化是解 决空间图形问题的重要思想方法。
线线垂直
小结
β A B αa
线面垂直
面面垂直
(2)判断平面PBC与平面PAC的位置关系。
(1)证明：∵ AB是⊙O的直径， P C是圆周上不同于A，B的任
意一点
∴∠ACB=90°∴BC⊥AC
又∵平面PAC⊥平面ABC，
C
平面PAC∩平面ABC＝AC,
BC 平面ABC
A
O
B
∴BC⊥平面PAC
(2)又∵ BC 平面PBC ，∴平面PBC⊥平面PAC
(1)平面α内的任意一条直线必垂直于平面β
（ ×）
(2)垂直于交线l的直线必垂直于平面β
（ ×）
(3)过平面α内任意一点作交线的垂线，则此
√ 垂线必垂直于平面β（ ）
例1：如图，AB是⊙O的直径，C是圆周上不同 于A，B的任意一点，平面PAC⊥平面ABC，
(1)判断BC与平面PAC的位置关系，并证明。
同理在β内作c′ ⊥ c,有c ′ ⊥ γ,
所线以线b′ ‖c平′, 行
线面垂直
又b′ β, c′ β, 所以 b′ ‖ β.
又 b′ α, α ∩ β=a,
αa β
所以 b′ ‖ a, 故 a ⊥ γ.
b′ c′
γ
bc
练习2：如图，已知PA⊥平面ABC， 平面PAB⊥平面PBC，求证：BC⊥平面PAB
提出问题：
1、平面与平面垂直的定义
两个平面相交，如果它们所成的二面角是 直二面角，就说这两个平面互相垂直。
2、平面与平面垂直的判定定理
一个平面过另一个平面的垂
线，则这两该个命平面题垂正直确。吗？
符号表示：
b
bb
平面与平面垂直的性质定理
两Ⅰ个. 观平察面垂实直验,则一个平面
②一个平面内的已知直线必垂直于另一个平面内的无 数条直线；
③一个平面内的任意一条直线必垂直于另一个平面；
④过一个平面内的任意一点做交线的垂线，则此垂线 必垂直于另一个平面。
A3 B 2 C1 D 0
B如果平面 α ⊥平面 β ,那么平面 α 内所有直
线都垂直于平面 β
α C如果平面 不垂直于平面 β ，则平面 α 内一
定不存在直线垂直于平面 β
D如果平面 α 、β 都垂直于平面M，且 α 与 β
交于直线 a，则 a ⊥平面M
2、已知两个平面垂直，下列命题中正确的有（B ）个
①一个平面内已知直线必垂直于另一个平面内的任意 直线；
证明：过点A作AE⊥PB，垂足 P 为E，
∵平面PAB⊥平面PBC，
平面PAB∩平面PBC=PB，
∴AE⊥平面PBC
A
C
∵BC 平面PBC ∴AE⊥BC
∵PA⊥平面ABC，BC 平面ABC
B
∴PA⊥BC
∵PA∩AE=A，∴BC⊥平面PAB
练习3：如图，以正方形ABCD的对角线AC为折 痕，使△ADC和△ABC折成相垂直的两个面， 求BD与平面ABC所成的角。