中考数学第二轮专题突破能力提升专题集训8动态几何问题试题

2021中考数学专题复习：压轴题动态几何问题专项训练题8（附答案详解）1．如图1，点P 、Q 分别是边长为4cm 的等边三角形ABC 的边AB 、BC 上的动点，点P 从顶点A ，点Q 从顶点B 同时出发，且它们的速度都为1cm/s ．（1）连接AQ 、CP 交于点M ，则在P ，Q 运动的过程中，证明ABQ ∆≌CAP ∆； （2）CMQ ∠会发生变化吗？若变化，则说明理由，若不变，则求出它的度数； （3）P 、Q 运动几秒时，PBQ ∆是直角三角形？（4）如图2，若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动，直线AQ 、CP 交点为M ，则CMQ ∠变化吗？若变化说明理由，若不变，则求出它的度数。

2．如图，已知抛物线的顶点坐标为M(1，4)，且经过点N(2，3)，与x 轴交于A 、B 两点(点A 在点B 左侧)，与y 轴交于点C ．(1)求抛物线的解析式及点A 、B 、C 的坐标；(2)若直线y=kx+t 经过C 、M 两点，且与x 轴交于点D ，探索并判断四边形CDAN 是怎样的四边形？并对你得到的结论予以证明；(3)直线y=mx+2与抛物线交于T ，Q 两点．是否存在这样的实数m ，使以线段TQ 为直径的圆恰好过坐标原点，若存在，请求出m 的值；若不存在，请说明理由．3．如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2－6x+8=0的两个根（OA＜OB）,点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D．（1）求出点A、点B的坐标.（2）请求出直线CD的解析式.（3）若点M为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B、P、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标；若不存在,请说明理由.4．如图，已知点A在数轴上对应的数为a，点B对应的数为b，且a，b满足()2a b++-=.20400（1）求点A与点B在数轴上对应的数a和b；（2）现动点P从点A出发，沿数轴向右以每秒4个单位长度的速度运动；同时，动点Q 从点B出发，沿数轴向左以每秒2个单位长度的速度运动，设点P的运动时间为t秒.①若点P和点Q相遇于点C, 求点C在数轴上表示的数；②当点P和点Q相距15个单位长度时，直接写出t的值.5．如图1，水平放置一个三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，∠ACB=90°，∠BAC=30°，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s的速度向右移动．（1）当点B于点O重合的时候，求三角板运动的时间；（2）三角板继续向右运动，当B点和E点重合时，AC与半圆相切于点F，连接EF，如图2所示．①求证：EF平分∠AEC；②求EF的长．6．如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC＝∠BCD．（1）求证：∠1+∠2＝90°；（2）若∠ABD的平分线与CD的延长线交于F，且∠F＝55°，求∠ABC；（3）若H是BC上一动点，F是BA延长线上一点，FH交BD于M，FG平分∠BFH，交DE于N，交BC于G．当H在BC上运动时（不与B点重合），试判断∠BAD+∠DMH 与∠DNG的数量关系，并说明理由．7．如图一，点C在线段AB上，图中有三条线段AB、AC和BC，若其中一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”．（1）填空：线段的中点这条线段的巧点（填“是”或“不是”或“不确定是”）（问题解决）和40，点C是线段AB的巧点，（2）如图二，点A和B在数轴上表示的数分别是20求点C在数轴上表示的数。

中考数学二轮专题复习动态几何综合题TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】中考数学二轮专题复习：动态几何综合题【简要分析】函数是中学数学的一个重要概念．加强对函数概念、图象和性质，以及函数思想方法的考查是近年中考试题的一个显着特点．大量涌现的动态几何问题，即建立几何中元素的函数关系式问题是这一特点的体现．这类题目的三乱扣帽子解法是抓住变化中的“不变”．以“不变”应“万变”．同时，要善于利用相似三角形的性质定理、勾股定理、圆幂定理、面积关系，借助议程为个桥梁，从而得到函数关系式，问题且有一定的实际意义，因此，对函数解析式中自变量的取值范围必须认真考虑，一般需要有约束条件．【典型考题例析】B、C三点的坐标分别为A（18，0）、B（18，6）、C（8，6），四边形OABC是梯形．点P、Q同时从原点出发，分别作匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC、CB向终点B运动，当这两点有一点到达自己的终点时，另一点也停止运动．（1）求出直线OC的解析式．（2）设从出发起运动了t秒，如果点Q的速度为每秒2个单位，试写出点Q的坐标，并写出此时t的取值范围．（3）设从出发起运动了t 秒，当P 、Q 两点运动的路程之和恰好等于梯形OABC 的周长的一半时，直线PQ 能否把梯形的面积也分成相等的两部分？如有可能，请求出t 的值；如不可能，请说明理由．分析与解答 （1）设OC 的解析式为y kx =，将C （8，6）代入，得34k =， ∴34y x =．（2）当Q 在OC 上运动时，设3(,)4Q m m ，依题意有2223()(2)4m m t +=，∴85m t =．故86(,)(05)55Q t t t ≤≤．当Q 在CB 上运动时，Q 点所走过的路程为2t ． ∵CO=10，∴210CQ t =-． ∴Q 点的横坐标为210812t t -+=-． ∴(22,6)(510)Q t t -<≤． （3）易得梯形的周长为44．①如图2-4-38，当Q 点在OC 上时，P 运动的路程为t ，则Q 运动的路程为(22)t -．过Q 作QM ⊥OA 于M ，则3(22)5QM t =-⨯．∴13(22)25OPQ S t t ∆=-⨯，1(1810)6842S =+⨯=四边形．假设存在t 值，使得P 、Q 两点同时平分梯形的周长和面积，则有131(22)84252t t =⨯=⨯，即2221400t t -+=． ∵22241400∆=-⨯<，∴这样的t 不存在．②如图2-4-39，当Q 点在BC 上时，Q 走过的路程为(22)t -， 故CQ 的长为：221012t t --=-．图2-4-38图2-4-39∴1()2OCQP S CQ OP =+梯形．11(12)6368422AB t t =⨯-+⨯=≠⨯， ∴这样的t 也不存在．综上所述，不存在这样的t 值，使得P 、Q 两点同时平分梯形的周长和面积． 例2： 如图2-5-40，在Rt △PMN 中，∠P=900，PM=PN ，MN=8㎝，矩形ABCD 的长和宽分别为8㎝和2㎝，C 点和M 点重合，BC 和MN 在一条直线上．令Rt △PMN 不动，矩形ABCD 沿MN 所在直线向右以每秒1㎝的速度移动（图2-4-41），直到C 点与N 点重合为止．设移动x 秒后，矩形ABCD 与△PMN 重叠部分的面积为y ㎝2．求y 与x 之间的函数关系式．分析与解答 在Rt △PMN 中，∵PM=PN ，∠P=900，∴∠PMN=∠PNM=450． 延长AD 分别交PM 、PN 于点G 、H ．过G 作GF ⊥MN 于F ，过H 作HT ⊥MN 于T （图2-4-42）． ∵DC=2㎝．∴MF=GF=2㎝， ∵MT=6㎝．因此矩形ABCD 以每秒1㎝的速度由开始向右移动到停止，和Rt △PMN 重叠部分的形状可分为下列三种情况：（1）当C 点由M 点运动到F 点的过程中（0≤x ≤2）．如图2-4-42所示，设CD 与PM 交于点E ，则重叠部分图形是Rt △MCE ，且MC=EC=x ．∴211(02)22y MC EC x x ==≤≤．（2）当C 点由F 点运动到T 点的过程中(26)x <≤， 如图2-4-43所示，重叠部分图形是直角梯形MCDG ． ∵,2MC x MF ==，∴FC=DG=x -2，且DC=2．N图2-4-42∴1()22(06)2y MC GD DC x x =+=-<≤（3）当C 点由T 点运动到N 点的过程中(68)x <≤， 如图2-4-44所示，设CD 与PN 交于点Q ， 则重叠部分图形是五边形MCQHG ． ∵MC x =，∴CN=CQ=8-x ，且DC=2．∴2111()(8)12(68)222y MN GH DC CN CQ x x =+-=--+<≤．说明：此题是一个图形运动问题，解答方法是将各个时刻的图形分别画出，将图形 则“动”这“静”，再设法分别求解．这种分类画图的方法在解动态几何题中非常有效，它可帮我们理清思路，各个击破． 【提高训练】 1．如图2-4-45，在ABCD 中，∠DAB=600，AB=5，BC=3，鼎足之势P 从起点D出发，沿DC 、CB 向终点B 匀速运动．设点P 所走过的路程为x ，点P 所以过的线段与绝无仅有AD 、AP 所围成图形的面积为y ，y 随x 的函数关系的变化而变化．在图2-4-46中，能正确反映y 与x 的函数关系的是（ ）2．如图2-4-47，四边形AOBC 为直角梯形，OB=%AC ，OC 所在直线方程为2y x =，平行于OC 的直线l 为：2y x t =+，l 是由A 点平移到B 点时，l 与直角梯形AOBC 两边所转成的三角形的面积记为S ．（1）求点C 的坐标．（2）求t 的取值范围．（3）求出S 与t 之间的函数关系式．3．如图2-4-48，在△ABC 中，∠B=900，点P 从点A 开始沿AB 边向点B 以1㎝/秒的速度移动，点Q 从点B 开始沿BC 边向点C 以2㎝/秒的速度移动．（1）如果P 、Q 分别从A 、B 同时出发，几秒后△PBQ 的面积等于8㎝2（2）如果P 、Q 分别从A 、B 同时出发，点P 到达点B 后又继续沿BC 边向点C 移动，点Q 到达点C 后又继续沿CA边向点A 移动，在这一整个移动过程中，是否存在点P 、Q ，使△PBQ 的面积等于9㎝2若存在，试确定P 、Q 的位置；若不存在，请说明理由．4．如图2-4-49，在梯形ABCD 中，AB=BC=10㎝，CD=6㎝，∠C=∠D=900． （1）如图2-4-50，动点P 、Q 同时以每秒1㎝的速度从点B 出发，点P 沿BA 、AD 、DC 运动到点C 停止．设P 、Q 同时从点B 出发t 秒时，△PBQ 的面积为1y （㎝2），求1y （㎝2）关于t （秒）的函数关系式．（2）如图2-4-51，动点P 以每秒1㎝的速度从点B 出发沿BA 运动，点E 在线段CD 上随之运动，且PC=PE ．设点P 从点B 出发t 秒时，四边形PADE 的面积为2y （㎝2）．求2y （㎝2）关于t （秒）的函数关系式，并写出自变量t 的取值范围．【答案】 1．A2．（1）C （1，2） （2）－10≤t ≤2（3）S 与t 的函数关系式为215(100)20S t t t =++-≤≤或211(02)4S t t t =-+≤≤3．（1）2秒或4秒（2）存在点P 、Q ，使得△PBQ 的面积等于9㎝2，有两种情况： ①点P 在AB 边上距离A 为3㎝，点Q 在BC 边上距离点B 为6㎝; ②点P 在BC 边上，距B 点3㎝时，此时Q 点就是A 点 4．（1）当点P 在BA 上运动时，21310y t =； 当点P 在AD 上运动时，130y =； 当点P 在DC 上运动时，190y t =-+（2）221299025BPC PEC ABCD y S S S t t ∆∆=--=-+梯形，自变量t 的取值范围是0≤t ≤5． .。

专题08 动态几何类压轴题一、单选题1．如图，在ABC 中，90ACB ∠=︒，4AC =，3BC =．线段PE 的两个端点都在AB 上，且1PE =，P 从点A 出发，沿AB 方向运动，当E 到达点B 时，P 停止运动，在整个运动过程中，空白部分面积DPEC S 四边形的大小变化的情况是（ ）A ．一直减小B ．一直增大C ．先增大后减小D ．先减小后增大【答案】C【分析】 设PD=x ，AB 边上的高为h ，求出h ，并运用相似三角形的性质求出AD ，构建二次函数，利用二次函数的性质解决问题即可．【详解】在Rt ABC ∆中，90ACB ∠=︒，4AC =，3BC =，5AB ∴===，设PD x =，则1205x ≤≤，AB 边上的高为h ，125AC BC h AB ==， //PD BC ， ADP ACB ∆∆∽∴， ∴PD AD BC AC=， 43AD x ∴=，53PA x = 221415122242333(4)2()23235353210△△APD CBE S S x x x x x x ∴+=+-=-+=-+， ()22233323()()32103210276△△△四边形ABC APD CBE DPEC S x S x S S ∴+-----+=-==， ∵203-<，∴32x≤<时，DPECS四边形随x的增大而增大，31225x<≤时，DPECS四边形随x的增大而减小，故选：C．【点睛】本题考查相似三角形的判定和性质，动点问题的函数图象，三角形面积，勾股定理等知识，解题的关键是构建二次函数，学会利用二次函数的增减性解决问题．2．如图，已知△ABC中，∠ACB=90°，∠BAC=30°，AB=6，点D为直线AB上一动点，将线段CD绕点C 逆时针旋转60°得到线段CE，连接ED、BE，当BE最小时，线段AD的值为（）A．5.5B．6C．7.5D．8【答案】C【分析】以BC为边作等边△BCF，连接DF，可证△BCE≌△FCD，可得BE=DF，则DF⊥AB时，DF的长最小，即BE的长最小，即可求解．【详解】如图，以BC为边作等边△BCF，连接DF，∵∠ACB=90°，∠BAC=30°，AB=6，∴∠ABC=60°，BC=3，∵将线段CD绕点C逆时针旋转60°得到线段CE，∴CD=CE，∠DCE=60°，∵△BCF是等边三角形，∴CF=BC=BF=3，∠BCF=∠DCE =60°，∴∠BCE=∠DCF，且BC=CF，DC=CE，∴△BCE≌△FCD(SAS)，∴ BE= DF，∴DF ⊥AB 时，DF 的长最小，即BE 的长最小，如图，此时作FD AB '⊥，∵FBD '∠=180°-60°-60°=60°，D F AB '⊥，∴ 1 1.52BD BF '==， ∴7.5AD AB BD '=+='，故选：C ．【点睛】本题考查了旋转的性质，全等三角形的判定与性质，直角三角形的性质，添加恰当的辅助线构造全等三角形是解题关键．二、解答题3．如图，在等腰直角三角形△ABC ，∠ABC=90°，AB=6，P 是射线AB 上一个动点，连接CP ，以CP 为斜边构造等腰直角△CDP （C 、D 、P 按逆时针方向），M 为CP 的中点，连接AD ，MB ．（1）当点P 在线段AB 上运动时，求证：△CDA ∽CMB ；（2）设AP x =，△ADP 的面积为y ．①当012x <<时，求y 关于x 的函数表达式；②记D 关于直线AC 的对称点为D ，若D 在△APC 的内部，求y 的取值范围．【答案】（1）见解析；（2）①2134y x x =-+；②189y << 【分析】 （1）根据等腰直角三角形的性质得BCM ACD ∠=∠，CB CM CA CD =，即可证明结论； （2）①分类讨论，当06x <≤时，或当612x <<时，过点D 作DE AB ⊥于点E ，根据（1）的相似三角形，得到AD=AP ，并且用x 表示出长度，即可求出函数表达式；②当点D 在APC △内部时，06x <<，过点P 作PN AC ⊥于点N ，利用面积法表示出PN 的长，得到x 的范围，即可求出y 的范围．【详解】解：（1）∵ABC 和CDP 是等腰直角三角形，∴45ACB DCP ∠=∠=︒，∴ACB ACP DCP ACP ∠-∠=∠-∠，即BCM ACD ∠=∠，∵ABC 和CDP 是等腰直角三角形，∴CB CA ==，CP CD = ∵M 是CP 的中点， ∴12CM CP =，∴21CM CD ==， ∴CB CM CA CD =， ∴CDA CMB ；（2）①∵M 是CP 中点， ∴12BM MC PC ==，若06x <≤，如图，过点D 作DE AB ⊥于点E ，∵AP x =，∴6PB x =-，∴PC = ∵DC DA MC MB=，∴2DC DA DP PC ==== ∵DE AB ⊥，∴12AE EP x ==，∴162DE x ===-， ∴21111632224ADP S AP DE x x x x ⎛⎫=⋅=⋅-=-+ ⎪⎝⎭； 若612x <<，如图，过点D 作DE AB ⊥于点E ，6BP x =-，PC =DC DA DP ====12AE EP x ==，162DE x ===-， ∴21111632224ADP S AP DE x x x x ⎛⎫=⋅=⋅-=-+ ⎪⎝⎭， 综上：2134y x x =-+； ②当点D 在APC △内部时，06x <<，点P 越往右，点D 离AC 越近，当点D 在PC 上时，过点P 作PN AC ⊥于点N ，∴DCA ACP PCB ∠=∠=∠，∴CP 为ACB ∠的角平分线，∴PN PB =，∵1131822ABC APC BPC S S S AC PN BC PB PN =+=⋅+⋅=+=，∴6PN PB ==，∴12AP AB PB =-=-，当126x -<<时，点D 在APC △内部，则根据2134y x x =-+，求出189y <<． 【点睛】本题考查相似三角形的综合题，解题的关键是掌握相似三角形的性质和判定，二次函数的几何运用，利用分类讨论的思想进行求解．4．如图，在平面直角坐标系中，直线3y x =-+与抛物线2y x bx c =-++交于A 、B 两点，点A 在x 轴上，点B 在y 轴上，点P 是抛物线上任意一点，过点P 作PQ ⊥y 轴，交直线AB 于点Q ，连接BP ，设点P 的横坐标为m ，△PQB 的边PQ 与PQ 边上的高之差为d ．（1）求此抛物线解析式.（2）求点Q 的横坐标（用含m 的代数式表示）；（3）∠BQP 为锐角.①求d 关于m 的函数关系式；②当△AOB 的顶点到PQ 的最短距离等于d 时，直接写出m 的值．【答案】（1）2y x 2x 3=-++；（2）22m m -；（3）①d m =-；②m =【分析】 （1）由直线解析式求解出A 、B 的坐标，再代入抛物线解析式求解即可；（2）由于PQ 垂直于y 轴，则P 、Q 的纵坐标相等，因此求出P 的纵坐标，再代入直线解析式求解Q 的横坐标即可；（3）①根据题中对d 的定义，分别求出PQ ，以及PQ 边上的高，再作差即可；②根据△AOB 的顶点到PQ 的最短距离等于d 时建立关于m 的一元二次方程求解，并注意运用条件判断合适的值即可．【详解】（1）由直线3y x =-+可知，A(3，0)，B(0，3)，将A(3，0)，B(0，3)代入2y x bx c =-++得： 9303b c c -++=⎧⎨=⎩，解得：23b c =⎧⎨=⎩， ∴抛物线的解析式为：2y x 2x 3=-++；（2）由题可知，P 、Q 的纵坐标相等，∵P 的横坐标为m ，且P 是抛物线上任意一点，∴P 的纵坐标为223y m m =-++，∴Q 的纵坐标为223y m m =-++，又∵Q 在直线上，∴将223y m m =-++代入3y x =-+得： 2233m m x -++=-+，解得：22x m m =-，∴Q 的横坐标为22m m -；（3）①由题意，()B P d PQ y y =--，由（2）可知： 2232Q P m P m m m m Q x x =-==---，()222332B P y m m m y m -+=+--=- ∴()B P d PQ y y m =--=-，∴d m =-；②由题可知：△AOB 为等腰直角三角形，其顶点为O ，则O 到PQ 的距离为223m m -++，当△AOB 的顶点到PQ 的最短距离等于d 时， 223m m m -++=-，解得：32m =， ∵∠BQP 为锐角，∴32m -=． 【点睛】本题考查二次函数与一次函数的综合运用，理解二次函数的性质，仔细分析题中表达的数量关系是解题关键．5．已知一次函数4y x =+的图象与二次函数()2y ax x =-的图象相交于()1,A b -和B ，点P 是线段AB 上的动点（不与A 、B 重合），过点P 作PC x ⊥轴，与二次函数()2y ax x =-的图象交于点C ．（1）求a 、b 的值；（2）如图1，M 为APC ∠内一点，且1PM =，E ，F 分别为边PA 和PC 上两个动点，求MEF 周长的最小值；（3）若PAC △是直角三角形，求点C 的坐标．【答案】（1）3b =，1a =；（2（3）()2,0C 或()3,3．【分析】∠1∠∠A∠∠∠∠∠∠b∠∠∠∠∠A∠∠∠∠∠∠∠a∠∠∠(2)∠∠∠M∠∠∠∠AB∠PC ∠∠∠∠,M M '''∠∠∠∠ ,,M M PM PM ''''''∠∠∠MEF∠∠∠∠∠∠∠∠ M M '''∠∠∠∠∠∠∠290M PM APC ∠=∠'=''︒∠∠∠ M M ==''='∠3∠∠∠PAC=90°∠∠ACP=90°∠∠∠∠∠∠∠【详解】解：∠1∠∠A 在直线y=x+4∠∠∠b=-1+4=3∠∠A∠∠∠∠∠-1∠3∠∠∠A∠∠∠∠∠y=ax(x -2)∠∠∠3=-a(-1-2)∠∠3=3a∠∠a=1∠∠3b =∠ 1a =∠∠2∠∠∠∠∠∠∠M ∠∠∠∠AB ∠PC ∠∠∠∠'M ∠''M ∠∠∠∠'''M M ∠'PM ∠''PM ∠∠MEF ∠∠∠∠∠∠∠'''M M ∠∠∠∠∠∠∠∠∠∠∠PM PM PM M PA APM MPC CPM ==∠=∠∠=∠''''''，，∠∠290M PM APC ∠=∠'=''︒,∠'''M M ===∠∠3∠∠(),4P m m +∠∠()2,2C m m m -∠ ∠∠∠PAC=90°∠∠222AP AC PC +=∠()()()()2222222112334m m m m m m ++++--=--∠ ∠∠1m =-∠∠∠∠∠2m =∠∠()2,0C ∠∠∠ACP=90°∠∠222AC PC AP +=∠()()()()2222221233421m m m m m m ++--+--=+∠ ∠∠1m =-∠∠∠∠∠3m =∠4m =∠∠∠∠∠∠()3,3C ∠∠∠()2,0C ∠()3,3∠【点睛】 本题考查二次函数与一次函数的综合运用，熟练掌握二次函数的图象与性质、一次函数的图象与性质、轴对称的性质、勾股定理的应用是解题关键．6．如图所示，直线AB 交x 轴于点(),0A a ，交y 轴于点()0,B b ，且a 、b ()240a -=． （1）如图1，若C 的坐标为()1,0-，且AH BC ⊥于点H ，AH 交OB 于点P ，试求点Р的坐标； （2）如图2，连接OH ，求证45OHP ∠=︒；（3）如图3，若点D 为AB 的中点，点M 为y 轴正半轴上一动点，连接MD ，过D 作DN DM ⊥交x 轴于N 点，当M 点在y 轴正半轴上运动的过程中，式子BDM ADN S S -△△的值是否发生改变？如发生改变，求出该式子的值的变化范围；若不改变，求该式子的值．【答案】（1）P 的坐标为()0,1-；（2）见解析；（3）S △BDM -S △ADN 的值不发生改变，等于4【分析】（1）先依据非负数的性质求得a 、b 的值，从而可得到OA=OB ，然后再∠COB=∠POA=90°，∠OAP=∠OBC ，最后，依据ASA 可证明∠OAP ≌△OBC ，得出OP=OC ，从而得出点P 的坐标；（2）过O 分别作OM ⊥CB 于M 点，作ON ⊥HA 于N 点，利用AAS 证明∠COM ≌△PON ，得出OM=ON ，再根据角平分线得到判定即可得出HO 平分∠CHA ，从而求出∠OHP ；（3）连接OD ，易证∠ODM ≌△ADN ，从而有S △ODM =S △ADN ，由此可得S △BDM -S △ADN =S △BDM -S △ODM =S △BOD =12S △AOB ． 【详解】解：（1()240a -=∴a+b=0，a -4=0，∴a=4，b=-4，则OA=OB=4．∵AH ⊥BC ，则∠AHC=90°，∠COB=90°，∴∠HAC+∠ACH=∠OBC+∠OCB=90°，∴∠HAC=∠OBC ．在∠OAP 和∠OBC 中， 90COB POA OA OB OAP OBC ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩∴△OAP ≌△OBC （AAS ）；∴OP=OC∵C 的坐标为()1,0-，∴OC=1∴OP=1∴P 的坐标为()0,1-（2）过O 分别作OM ⊥CB 于M 点，作ON ⊥HA 于N 点．在四边形OMHN 中，∠MON=360°-3×90°=90°，∴∠COM=∠PON=90°-∠MOP ．在∠COM 和∠PON 中，90COM PON OMC ONP OC OP ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩∴△COM ≌△PON （AAS ），∴OM=ON ．∵OM ⊥CB ，ON ⊥HA ，∴HO 平分∠CHA ，1452︒∴∠=∠=OHP CHA （2）S △BDM -S △ADN 的值不发生改变，等于4．理由如下：如图：连接OD ．∵∠AOB=90°，OA=OB ，D 为AB 的中点，∴OD ⊥AB ，∠BOD=∠AOD=45°，OD=DA=BD∴∠OAD=45°，∠MOD=90°+45°=135°，∴∠DAN=135°=∠MOD ．∵MD ⊥ND 即∠MDN=90°，∴∠MDO=∠NDA=90°-∠MDA ．在∠ODM 和∠ADN 中，,MDO NDA DOM DAN OD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ODM ≌△ADN （ASA ），∴S △ODM =S △ADN ， ∴12S ∆∆∆∆∆∆-=-==BDM ADN BDM ODM BOD AOB S S S S S ∴111144422S 22∆∆-=⨯⋅=⨯⨯⨯=BDM ADN S AO BO 【点睛】本题考查了全等三角形的判定与性质、角平分线的判定、二次根式及完全平方式的非负性等知识，在解决第（2）小题的过程中还用到了等积变换，而运用全等三角形的性质则是解决本题的关键．7．如图，已知等边ABC 的边长为16，点P 是AB 边上的一个动点（与点A 、B 不重合）．直线l 是经过点P 的一条直线，把ABC 沿直线l 折叠，点B 的对应点是点B '．（1）如图1，当8PB =时，若点B '恰好在AC 边上，则AB '的长度为_________；（2）如图2，当10PB =时，若直线//l AC ，则BB '的长度为_______；（3）如图3，点P 在AB 边上运动过程中，若直线l 始终垂直于AC ，ACB '△的面积是否变化？若变化，说明理由；若不变化，求出面积；（4）当12PB =时，在直线l 变化过程中，求ACB '△面积的最大值．【答案】（1）8或0；（2）（3）面积不变，（4）最大为96+【分析】（1）证明△APB′是等边三角形即可解决问题．（2）如图2中，设直线l 交BC 于点E ．连接BB′交PE 于O ．证明△PEB 是等边三角形，求出OB 即可解决问题．（3）如图3中，结论：面积不变．证明BB′∥AC 即可．（4）如图4中，当B′P ⊥AC 时，△ACB′的面积最大，设直线PB′交AC 于E ，求出B′E 即可解决问题．【详解】解：（1）如图1中，∵ABC 是等边三角形，∴60A ∠=︒，16AB BC CA ===，∵8PB =，∵8PB PB PA ==='，∵60A ∠=︒，∴APB '是等边三角形，∴8AB AP '==．当直线l 经过C 时，点B '与A 重合，此时0AB '=，故答案为8或0．（2）如图2中，设直线l 交BC 于点E ．连接BB '交PE 于O ．∵//PE AC ，∴60BPE A ∠=∠=︒，60BEP C ∠=∠=︒，∴PEB △是等边三角形，∵10PB =，且由于折叠，∴B ，B '关于PE 对称，∴BB PE '⊥，2BB OB '=，∴OP=12PB=5，∴OB =，∴BB '=故答案为（3）如图3中，结论：面积不变．连接BB ′，过点A 作AF ⊥BC ，垂足为F ，∵B ，B '关于直线l 对称，∴BB '⊥直线l ，∵直线l AC ⊥，∴//AC BB '，∴ACB ACB S S '=△△，∵BC=AB=AC=16，∴BF=8，∴=，∴1162ACB ACB S S '==⨯⨯= （4）如图4中，∵点B 和B′关于经过点P 的直线对称，∴B′到点P 的距离与点B 到点P 的距离相等，当B P AC '⊥时，ACB '△的面积最大，设直线PB '交AC 于E ，在Rt APE 中，∵4PA =，60PAE ∠=︒，∴AE=2，∴PE ==∵BP=B′P=12，∴12EB EP B P '=++'=∴(11612962ACB S '=⨯⨯+=+△ 【点睛】本题属于几何变换综合题，考查了等边三角形的性质和判定，轴对称变换，平行线的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考压轴题．8．已知抛物线2122y x x =-与x 轴交于点O 、A 两点，顶点为B ．（1）直接写出：A 点坐标________ ，B 点坐标_______ ，△ABO 的形状是_______；（2）如图，直线y x m =+(m<0)交抛物线于E 、F(E 在F 右边)，交对称轴于M ，交y 轴于N ．若EM -FN=MN ，求m 的值；（3）在(2)的条件下，y 轴上有一动点P ，当∠EPF 最大时，请直接写出此时P 点坐标___________【答案】（1）（4,0），（2，-2），等腰直角三角形；（2）52m =-；（3）（052-） 【分析】（1）令2122y x x =-中y=0，求出A 的坐标，由22112(2)242y x x x =--+=，求出顶点B 坐标，利用勾股定理的逆定理判定△ABO 是等腰直角三角形；（2）过点E 作EG ⊥y 轴于G ，过点F 作FH ⊥y 轴于H ，过点M 作MC ⊥y 轴于C ，设y x m =+（m ＜0）交x 轴于D ，先求出∠OND=45°，利用锐角三角函数可得FN=sin 45HF ︒，MN=sin 45CM ︒，EN=sin 45EG ︒，联立解析式求出点E 、F 的横坐标，最后根据已知等式即可列出方程，求出m ； （3）作以EF 为弦且与y 轴相切的圆D ，切点为P ，连接EP 、FP ，利用圆周角定理和三角形外角的性质先证此时∠EPF 最大，然后确定点P 的坐标，设点P 的坐标为（0，p ），用含p 的式子表示出DP 和DF ，列出方程即可求出结论．【详解】解：（1）令2122y x x =-中y=0，得21202x x -=， 解得x=0或x=4，∴A （4，0）； ∵22112(2)222y x x x =-=--， ∴顶点B 坐标为（2，-2）；连接AB 、OB ，∴22416OA ==，()()22224820AB =-+-=-，()()22220820OB =-+-=-，∴222OA AB OB =+，AB=OB ，∴△ABO 是等腰直角三角形，故答案为：（4,0），（2，-2），等腰直角三角形；（2）过点E 作EG ⊥y 轴于G ，过点F 作FH ⊥y 轴于H ，过点M 作MC ⊥y 轴于C ，设y x m =+（m ＜0）交x 轴于D将x=0代入y x m =+中，解得y=m ；将y=0代入y x m =+中，解得x=-m∴点N 的坐标为（0，m ），点D 的坐标为（-m ，0）∴ON=OD∴△OND 为等腰直角三角形∴∠OND=45°∴FN=sin 45HF ︒，MN=sin 45CM ︒，EN=sin 45EG ︒， ∴EM=EN －)EG CM - ∵抛物线2122y x x =-的对称轴为直线x=2 ∴CM=2 联立2122y x x y x m⎧=-⎪⎨⎪=+⎩消去y ，解得：x 1=3x 2=3+∴点F的横坐标为3-E的横坐标为3+∴HF=3-EG=3+∴3，MN=)321+=∵EM -FN=MN ，1+3-=解得：52m =-， 经检验，52m =-是原方程的解； （3）如下图所示，作以EF 为弦且与y 轴相切的圆D ，切点为P ，连接EP 、FP ，先证此时∠EPF 最大，在y 轴上任取一点P '，连接EP FP ''、，FP '与圆D 交于点C∴∠EPF=∠ECF∵∠ECF是△EP C'的外角∠∴∠ECF＞EP C'∴∠EPF＞EP F'∠即此时∠EPF最大，然后确定点P的坐标，设点P的坐标为（0，p），如下图所示，连接DP、DF，作EF的中垂线ST，交EF于S，交y轴于T，过点S作SK⊥y轴于K由（2）知52m =- ∴点E 的坐标为（5，52），点F 的坐标为（1，32-） ∴点S 的坐标为（3，12）， ∴OK=12，SK=3 由（2）知：∠SNO=45°，∵∠TSN=90°∴∠STK=45°∴△TSK 、△TDP 为等腰直角三角形∴TK=SK=3，TP=DP∴TP=TK ＋OK －OP=72p - ∴DP=72p -， ∴点D 的坐标为（72p -，p ）∴∵DP=DF∴72p -解得：52-或p=52∵∴ES=12EF=SK ∴以EF 为直径的圆与y 轴相离∴点P 必在以EF 为直径的圆的外边∴△EPF 为锐角三角形∴点D 在△EPF 内部，也必在S 的左上方∴点D 的纵坐标大于0，即p ＞0∴52∴点P 的坐标为（052）． 【点睛】此题考查的是二次函数、一次函数和圆的综合大题，掌握二次函数图象及性质、求一次函数解析式、等腰直角三角形的判定及性质、圆周角定理、锐角三角函数是解题关键．9．如图，已知在Rt ABC 中，90ACB ∠=︒，4AC BC ==，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，EDB ADC ∠=∠，过点E 作EF AD ⊥，垂足为点G ，交射线AC 于点F ．（1）如果点D 为边BC 的中点，求DAB ∠的正切值；（2）当点F 在边AC 上时，设CD x =，CF y =，求y 关于x 的函数解析式及定义域；（3）联结DF 如果CDF 与AGE 相似，求线段CD 的长．【答案】（1）1tan 3DAB ∠=；（2）()2402y x x =-+<≤；（3）-4、8-． 【分析】（1））过点D 作DH AB ⊥于H ，在Rt ACB 中，利用勾股定理解得AD 、AB 的长，再结合等积法，解得DH 、AH 的长即可解题；（2）根据相似三角形对应边成比例的性质，表示()444x EH x -=+， 再证明AFE BDE 由AF AE DB BE =即)4444x y x x --=-+得到与x 的关系； （3）根据相似三角形对应边成比例的性质，结合（2）中y 关于x 的函数解析式联立方程组，继而解得x 、y 的值即可解题．【详解】（1）过点D 作DH AB ⊥于H ，在Rt ACB 中，AD =AB ∴==142ADB SDB AC ∴=⋅= 12ADB S AB DH =⋅DH ∴=AH ==1tan 3DH DAB AH ∴∠==； （2）过E 作EH ⊥CB 于H∵EDB ADC ∠=∠，90C EHD ∠=∠=︒∴ACD EHD ． ∴AC EH CD DH = 即44EH x x EH=--． ∴()444x EH x -=+ ．∵EH ⊥CB ，90ACB ∠=︒，4AC BC ==∴)44x EB x -==+，AB =∴)44x AE x -=+ ∵EF AD ⊥，90C ∠=︒∴AFG ADC ∠=∠ ．∵EDB ADC ∠=∠∴AFG EDB ∠=∠．∵45FAE B ∠=∠=︒∴AFE BDE ． ∴AF AE DB BE =即)4444x y x x --=-+． 整理得，()2402y x x =-+<≤；（3）在Rt △MDB 中，DB=4-x,所以MD=MB=(4).2x - 在Rt △ADM 中，AM=AB 一MB=)(4).22x x -=+ 所以tan ∠DAB=44DM x AM x-=⋅+ 按照点F 的位置，分两种情况讨论△CDF 与△AGE 相似:①点F 在线段AC 上，此时y=4-2x.如图，如果∠FDC=∠DAB ，由tan ∠FDC=tan ∠DAB,得44y x x x-=⋅+ 结合y=4-2x ，整理，得x2+8x+16=0.解得-4 或--4 （舍去）, 如果∠CFD=∠DAB ，由tan ∠CFD=tan ∠DAB ，得4.4x x y x-=+ 结合y=4- -2x,整理，得x 2-16x+16=0.解得8x =-8+②点F 在线段AC 的延长线上，此时y=2x -4如图如果∠FDC=∠DAB,由44y x x x-=+结合y=2x -4，整理，得23160.x -=解得或3-（舍去） 如果∠CFD=∠DAB,44x x y x -=+与y=2x -4 整理，得238160.x x -+=此方程无解.综上，CD 的值为-4、8-． 【点睛】本题考查勾股定理、相似三角形的性质，涉及解二元一次方程组等知识，解题关键是根据题意利用相似三角形性质构造方程．10．如图，直线443y x =-+和x 轴、y 轴的交点分别为B 、C ，点A 的坐标是()2,0-．（1）试说明ABC 是等腰三角形；（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，MON △的面积为S ． ①求S 与t 的函数关系式；②设点M 在线段OB 上运动时，是否存在4S =的情形？若存在，求出对应的t 值；若不存在请说明理由； ③在运动过程中，当MON △为直角三角形时，求t 的值．【答案】（1）证明见解析；（2）①22455S t t =-+（02t <<），22455S t t =-（25t <≤）；②存在，(t s =；③5s 或25.8s 【分析】 （1）先求解,B C 的坐标，再求解,BC AB 的长度，从而可证明结论；（2）①过点N 作⊥ND x 轴于D ，则4sin 5ND BN OBC t =⋅∠=，分两种情况讨论，当02t <<时，当25t <≤时，分别画出符合题意的图形，再利用三角形的面积公式得到函数解析式即可；②分两种情况讨论，把4S =分别代入②中的两个函数解析式，再解方程即可得到答案；③分三种情况讨论；90∠=︒NMO 或90NOM ∠=︒或90MNO ∠=︒，再利用图形的性质与锐角三角函数可得答案．【详解】解：（1）将0y =代入443y x =-+，得3x =，∴点B 的坐标为3,0；将0x =代入443y x =-+，得4y =， ∴点C 的坐标为()0,4．在Rt OBC 中，∵4OC =，3OB =，∴5BC ==．又()2,0A -，∴5AB =，∴AB BC =，∴ABC 是等腰三角形．（2）∵5AB BC ==，故点M 、N 同时开始运动，同时停止运动．过点N 作⊥ND x 轴于D ， 则4sin 5ND BN OBC t =⋅∠=， ①当02t <<时（如图），2OM t =-，∴12S OM ND =⋅ ()14225t t =-⋅ 22455t t =-+． 当25t <≤时（如图），2OM t =-，∴12S OM ND =⋅ ()14225t t =-⋅ 22455t t =-． ②存在4S =的情形．当02t <<时∴ 224455t t -+=， 22100,t t ∴-+=()22411044036∴=--⨯⨯=-=-＜0，所以方程无解；当25t <≤时， ∴ 224455t t -=．解得11t =21t =（不合题意，舍去）．15t =+<，故当4S =时，(t =秒．③当MN x ⊥轴时，MON △为直角三角形．3cos 5MB BN MBN t =⋅∠=， 又5MB t =-． ∴355t t =-， ∴258t =． 当点M 、N 分别运动到点B 、C 时，MON △为直角三角形，5t =．当90MNO ∠=︒时，不合题意，舍去，故MON △为直角三角形时，258t =秒或5t =秒． 【点睛】本题考查了一次函数图象上点的坐标特征，勾股定理的应用，一元二次方程的解法，锐角三角函数的定义，等腰三角形的性质，直角三角形的性质，三角形的面积，分类讨论的思想，掌握分类讨论思想解决问题是解题的关键．11．如图，点O 在线段AB 上，OA =1，OB =3，以点O 为圆心、OA 为半径作∠O ，点M 在上运动．连接MB ，以MB 为腰作等腰Rt∠MBC ，使∠MBC =90°，M ，B ，C 三点按逆时针顺序排列．（1）当点M 在AB 上时，sin∠ACB =________________；（2）当BM 与∠O 相切时，求AM 的长；（3）连接AC ，求AC 长的取值范围．【答案】（1或2；（2）3；（3）46AC ≤≤． 【分析】（1）分当M 在AB 上和点M 和A 重合两种情况解答即可；（2）先证明△BMD ∽△BAM,然后根据相似三角形的性质列式解答即可；（3）如图：以B 为顶点、OB 为边向上方作等腰Rt △OBP ，连接CP ，OM ，有△BOM ≌△BPC （SAS ），PC=OM=1，则点C 在以点P 为圆心、1为半径的圆上，转化为“圆外一点到圆上的最值问题”，作射线AP ，交OP 于C 1、C 2两点，然后求得AC 1和AC 2的长即可解答．【详解】（1）①如图：当M 在AB 上时∵OA=OM=1∴AB=AO+OB=4,BM=OB -OM=2∵MB 为腰作等腰Rt∠MBC∴BC=BM=2=∠sin∠ACB =AB AC ==; ②如图：当M 和点A 重合时，AB=BC=4∴==∠sin∠ACB =AB AC ==综上，sin∠ACB 或2； （2）如图：∵BM 与∠O 相切∴∠BMO=90°==∠AB 是直径∠∠AMD=90°∠∠BMD+∠DMO=90°，∠AMO+∠DMO=90°，∴∠BMD=∠AMO∠OA=OM∠∠OAM=∠AMO∠∠OAM=∠BMD∠∠MBA=∠MBD∠△BMD ∽△BAM∴DM MB AM AB ===设AM=x ，则DM=2x2= ，解得x=3或x=-3（舍）；（3）以B 为顶点、OB 为边向上方作等腰Rt △OBP ，连接CP ，OM ，∴△BOM ≌△BPC （SAS ）∴PC=OM=1则点C 在以P 为圆心的M 上、1为半径的圆上，即求转化为“圆外一点到圆上的最值问题”，∴5=作射线AP ，交OP 于C 1、C 2两点，则A C 1=AP -P C 1=4, A C 2=AP+P C 2=6,∴46AC ≤≤．【点睛】本题属于几何综合题，考查了圆的性质、全等三角形的判定与性质、相似三角形的判定与性质以及锐角的三角函数，灵活应用所学知识成为解答本题的关键．12．如图，四边形ABCD 是矩形，点P 是对角线AC 上一动点（不与点C 和点A 重合），连接PB ，过点P作PF ⊥PB 交射线DA 于点F ，连接BF ．已知AD =CD=3，设CP 的长为x ．（1）线段BP 的最小值为________，当1x =时，AF =____________．（2）当动点P 运动到AC 的中点时，AP 与BF 的交点为G ，FP 的中点为H ，求线段GH 的长度． （3）若点P 在射线CA 上运动，点P 在运动的过程中，①试探究∠FBP 是否会发生变化？若不改变，请求出∠FBP 的大小；若改变，请说明理由．②若△AFP 是等腰三角形，直接写出x 的值．【答案】（1）2；（2；（3）①不发生变化，30； ②3或 【分析】（1）当BP 最小时，即BP AC ⊥，根据相似三角形的性质，可求得BP 的值，当x=1时，可得到BPN PMF ，由此可得出tan FBP ∠的值，继而得到AF 的值；（2）先证明BP 垂直平分AP ，得到PF =GH 是Rt FGP △的中线，即可得到GH 的长； （3）①过点P 作PN BC ⊥交AD 于点M ，可证明FMP PNB ，设,2x PC x PN ==，可求得NC 、MP 、BN 的长，tan =3FP MP FBP BP BN ∠==，即可求得∠FBP 的大小； ②分三种情况讨论即:当FA=FP ，AP=AF ，PA=PB 时，分别根据等腰三角形的性质解题．【详解】（1）当BP 最小时，A 与F 重合，即BP AC ⊥， 33AD CD ==6,30AC DAC ACB ∴=∠=∠=︒,在Rt ABC 与Rt APB △中，BAC PAB ∠=∠ABCAPB ∴ AB BP AC BC∴=36∴=2BP ∴= 作PM BC ⊥于N ，交AD 于M ，当x=1时，1522PN MP CN BN ====，， 90BNP PMF BPF ∠=∠=∠=︒,90,90FPM PFM FPM BPN ∴∠+∠=︒∠+∠=︒，PFM BPN ∴∠=∠，BPNPFM ∴，3MP FM BP BN NP FP ∴===，MF ∴=2663AF AM MF BN MF ∴=-=-=-==，故答案为：2，3； （2）P 为AC 的中点，3AP PC AB ∴===60ABP APB BAP ∴∠=∠=∠=︒在t R ABF 和t R PBF 中，AB=BP ，BF=BFt R ABF ∴≅t R PBF90AG PG AGB PGB ∴=∠=∠=︒，BF ∴垂直平分AP ，在t R BFP 中，303PBF BP ∠=︒=，PF ∴=取PF 的中点H ，连接GH ， H 为PF 中点，GH ∴为Rt PGF △的中线，12GH PF ∴==； （3）①不发生变化，30FBP ∠=︒，理由如下，作PM BC ⊥于点N ，交AD 于M ，,PBN FPM BPN PFM ∠=∠∠=∠，FMP PNB ∴，设,,,3,22x x CP x PN NC x MP BN x =∴===-=，3FP MP BP BN ∴== 30FBP ∴∠=︒；②当FA FP =时，BA BP =，ABP ∴为等边三角形,3AP AB ∴==，3x CP ∴==；当PA PF =时，12090APF ∠=︒>︒不符合题意；当AP=AD 时，75AFP APF ∠=∠=︒，75CBP CPB ∴∠=∠=︒，CP CB ∴==，即x =；综上所述，当3x =或AFP 是等腰三角形． 【点睛】本题考查矩形的性质、相似三角形的判定与性质、解直角三角形的应用、等腰三角形的判定与性质等知识，是重要考点，灵活运用分类讨论思想是解题关键．13．如图所示，在平面直角坐标系中，抛物线()230y ax bx a =++≠与x 轴交于点()1,0A -、()3,0B ，与y 轴交于点C ，点P 是第一象限内抛物线上的动点．（1）求抛物线的解析式；（2）连接BC 与OP ，交于点D ，求当PD OD的值最大时点P 的坐标； （3）点F 与点C 关于抛物线的对称轴成轴对称，当点P 的纵坐标为2时，过点P 作直线//PQ x 轴，点M 为直线PQ 上的一个动点，过点M 作MN x ⊥轴于点N ，在线段ON 上任取一点K ，当有且只有一个点K 满足135FKM ∠=︒时，请直接写出此时线段ON 的长．【答案】（1）2y x 2x 3=-++；（2）315,24⎛⎫⎪⎝⎭；（3）7+3+【分析】（1）直接利用待定系数法求解即可； （2）过P 作PG ∥y 轴，交BC 于点G ，则可构造出相似三角形，将PD OD 转换为PG OC求解即可； （3）分两种情况讨论，连接FM ，以FM 为斜边，作等腰直角△FHM ，当以H 为圆心FH 为半径作圆H ，与x 轴相切于K ，此时有且只有一个点K 满足∠FKM=135°，设点H （x ，y ），由“AAS”可证△FHE ≌△HMQ ，可得HE=QM=y -3，HQ=EF=x -2，由勾股定理可求y 的值，可求点M 坐标，即可求解．【详解】（1）将()1,0A -、()3,0B 代入抛物线解析式得：030933a b a b =-+⎧⎨=++⎩，解得：12a b =-⎧⎨=⎩， ∴抛物线的解析式为：2y x 2x 3=-++；（2）如图所示，作PG ∥y 轴，交BC 于点G ，则△DPG ∽△DOC ， ∴PD PG OD OC=， 由题可知：()0,3C ，设直线BC 的解析式为：y kx b =+，将()3,0B ，()0,3C 代入得：303k b b +=⎧⎨=⎩，解得：13k b =-⎧⎨=⎩，∴直线BC 的解析式为：3BC y x =-+，3OC =，设P 的坐标为()223m,m m -++，则G 的坐标为()3m,m -+， ∴23PG m m =-+， ∴223932433m PD PG m m OD OC ⎛⎫--+ ⎪-+⎝⎭===， ∴当32m =时，PD OD 有最大值，将32m =代入抛物线解析式得：154y =， ∴点P 的坐标为31524⎛⎫⎪⎝⎭，；（3）①当M 在F 右侧时，如图所示，连接FM ，以FM 为斜边构造等腰直角△FHM ，当以H 为圆心，FH 为半径作圆H ，与x 轴相切于K 时，此时有且只有一个K 点满足∠FKM=135°，此时，连接HK ，交PM 于点Q ，延长CF 交于HK 于E ，则HK ⊥x 轴，设H （x ，y ），由题可知，抛物线的对称轴为直线x=1，∵点F 与点C 关于抛物线的对称轴对称，∴点F 的坐标为（2，3），CF ∥x 轴，∴CF ∥PM ，∴HK ⊥CF ，HK ⊥PM ，∴∠FEH=∠HQM=90°，∵∠FHE+∠MHE=90°，∠FHE+∠HFE=90°，∴∠HFE=∠MHQ ，又∵HF=HM ，∴△HFE ≌△MHQ （AAS ），∴HE=QM=y -3，HQ=FE=x -2，而HQ=HK -QK=y -2，∴y -2=x -2，即：x=y ，∴FE=y -2，∵222FH FE HE =+，FH=HK=y ，∴()()22223y y y =-+-，解得：5y =，5y =-（舍去）∴532QM =-=，523FE =-=，∴点M 的坐标为()72,，∴7ON =+；②当M 在F 左侧时，如图所示，同①的过程，可证得△HFE ≌△MHQ ，此时设H 的坐标为（x ，y ），显然有，HE=QM=y -3，HQ=FE=2-x ，而HQ=HK -QK=y -2，∴y -2=2-x ，即：4-y=x ，∴FE=y -2，∵222FH FE HE =+，FH=HK=y ，∴()()22223y y y =-+-，同理解得：5y =，∴532QM =-=，523FE =-=，∴点M 的坐标为()32,-，∴3ON =+综上，线段ON 的长为7+3+【点睛】本题考查二次函数综合问题，考查了待定系数法求解析式，二次函数的性质，全等三角形的判定与性质，圆的相关性质，以及相似三角形的判定与性质等，添加恰当的辅助线构造全等三角形是解题关键． 14．如图，在矩形ABCD 中，AB =6，BC =8，点O 为对角线AC 的中点，动点P 从点A 出发沿AC 向终点C 运动，同时动点Q 从点B 出发沿BA 向点A 运动，点P 运动速度为每秒2个单位长度，点Q 运动速度为每秒1个单位长度，当点P 到达点C 时停止运动，点Q 也同时停止运动，连结PQ ，设点P 运动时间为t （t ＞0）秒．（1）cos∠BAC= ．（2）当PQ⊥AC时，求t的值．（3）求△QOP的面积S关于t的函数表达式，并写出t的取值范围．（4）当线段PQ的垂直平分线经过△ABC的某个顶点时，请直接写出t的值．【答案】（1）35；（2）1813t=秒；（3）22434512(0)552434512(5)552S t t tS t t t⎧=-+<<⎪⎪⎨⎪=-+-<≤⎪⎩；（4）当2t=或t=秒时，线段PQ的垂直平分线经过△ABC的某个顶点．【分析】（1）利用勾股定理先求得AC的长，即可求解；（2）在Rt△ABC中，利用余弦函数构建方程即可求解；（3）过P作PE⊥AQ于点E，过O作OF⊥AQ于点F，分52t<<，52t=和552t<≤三种情况讨论，利用三角形面积公式即可求解；（4）分线段PQ的垂直平分线经过点C时，经过点A时，经过点B时，三种情况讨论，求得结论即可．【详解】（1）在Rt△ABC中，AB=6，BC=8，10=，∴63 cos105ABBACAC∠===；故答案为：35；（2）当PQ⊥AC时，∵AP=2t，AQ=6t-，∴在Rt△ABC中，∴23cos 65AP t PAQ AQ t ∠===-， 解得：1813t =秒， 经检验，1813t =是方程的解， ∴1813t =(秒)； （3）过P 作PE ⊥AQ 于点E ，过O 作OF ⊥AQ 于点F ，在Rt △ABC 中，AB =6，BC =8，AC 10=， ∴4sin 5BC BAC AC ∠==，4sin 25PE PE PAE AP t ∠===，4sin 55OF OF OAF AO ∠===， ∴PE=85t ，OF=4， ①当502t <<时， ()()2POQ AOQ APQ 1184346461222555t S S S t t t t =-=-⨯--⨯=-+， 即24341255S t t =-+(502t <<)； ②当52t =时，POQ 不存在； ③当552t <≤时，()()2POQ APQ AOQ 1814346641225255t S S S t t t t =-=-⨯--⨯=-+-， 即24341255S t t =-+-(552t <≤)；综上，△QOP 的面积S 关于t 的函数表达式是22434512(0)552434512(5)552S t t t S t t t ⎧=-+<<⎪⎪⎨⎪=-+-<≤⎪⎩； （4）①当线段PQ 的垂直平分线经过点C 时，PC=QC=102t -，在Rt △QBC 中，222QB BC QC +=，∴()2228102t t +=-，解得：203t -=(负值已舍)； ②当线段PQ 的垂直平分线经过点A 时，AQ=AP ，即62t t -=，解得：2t =；③当线段PQ 的垂直平分线经过点B 时，过P 作PG ⊥BC 于点G ，3sin 5AB PG ACB AC PC ∠===，4cos 5BC PG ACB AC GC ∠===， ∴PG=()36102655t t -=-，CG=()48102855t t -=-， BG= BC -CG=888855t t ⎛⎫--= ⎪⎝⎭， 在Rt △BPG 中，222BG PG BP +=， 即22286655t t t ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭， 整理得：215721800t t -+=， ()2247241518056160b ac =-=--⨯⨯=-<，方程无解，∴线段PQ 的垂直平分线不会经过点B ，综上，当2t =或203t -=秒时，线段PQ 的垂直平分线经过△ABC 的某个顶点． 【点睛】本题考查了矩形性质，解直角三角形，线段垂直平分线性质等知识，主要考查学生分析问题和解决问题的能力，题目比较典型，但是有一定的难度．15．问题探究：如图，在Rt △ABC 和Rt △DEC 中，∠ACB =∠DCE =90°，∠CAB =∠CDE =60°，点D 为线段AB 上一动点，连接BE ．（1）求证：△ADC ∽△BEC ．（2）求证：∠DBE =90°．拓展延伸：把问题探究中的“点D 为线段AB 上一动点”改为“点D 为直线AB 上一动点”，其他条件不变，若点M 为DE 的中点，连接BM ，且有AD =1，AB =4，请直接写出BM 的长度．【答案】（1）见解析；（2）见解析；拓展延伸：BM ．【分析】（1）先证得∠ACD =∠BCE ，再利用tan 60BC CE AC CD ︒===AC BC CD CE=，即可证明结论； （2）由（1）的结论得∠CAD =∠CBE ，即可证明；拓展延伸：分D 在线段AB 上和D 在BA 延长线上两种情况讨论，利用△ADC ∽△BEC 的 性质求得BE 的长，再利用直角三角形的性质即可求解．【详解】（1）∵∠ACB =∠DCE =90°，∴∠ACD+∠BCD =∠BCE+∠BCD =90°，∴∠ACD =∠BCE ，∵∠CAB =∠CDE =60°，∴tan 60BC CE AC CD ︒===AC BC CD CE=， ∴△ADC ∽△BEC ；（2）由（1）得：∠CAD =∠CBE ，∴∠CBE +∠CBA =∠CAD +∠CBA =90°，∴∠DBE =90°；拓展延伸：在Rt △ABC 中，∠ACB =90°，∠CAB =60°，AB =4，∴AC=2，BC =由（1）得：△ADC ∽△BEC ， ∴AC AD BC BE=， ∵AD =1，∴由（2）得：∠DBE =90°，∵点M 为DE 的中点，∴BM=12DE ； ①当D 在线段AB 上时，如图：在Rt △BDE 中，BD=AB -AD=4-1=3，，∴DE ==∴BM=12 ②当D 在BA 延长线上时，如图：在Rt △BDE 中，BD=AB+AD=4+1=5，，∴DE ==∴BM=12综上，BM【点睛】本题考查了相似三角形的判定和性质，特殊角的三角函数值，勾股定理，等腰三角形的性质，直角三角形的性质，证明△ADC ∽△BEC 是本题的关键．16．如图，在△ABC 中，AB ＝BC ＝AC ＝12cm ，点D 为AB 上的点，且BD ＝34AB ，如果点P 在线段BC 上以3cm /s 的速度由B 点向终点C 运动，同时，点Q 在线段CA 上由C 点向终点A 运动．当一点到达终点时，另一点也随之停止运动．（1）如（图一）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，△BPD 与△CQP 是否全等，请说明理由．（2）如（图二）若点Q 的运动速度与点P 的运动速度相等（点P 不与点B 和点C 重合），连接点A 与点P ，连接点B 与点Q ，并且线段AP ，BQ 相交于点F ，求∠AFQ 的度数．（3）若点Q 的运动速度为6cm /s ，当点Q 运动几秒后，可得到等边△CQP ？【答案】（1）BPD CQP ≌，证明见解析；（2）60︒（3）43【分析】 （1）根据时间和速度求得BP 、CQ 的长，根据SAS 判定两个三角形全等．（2）利用第（1）小题的方法可证得ABP BCQ ≌，BAP CBQ ∠=∠，根据三角形外角性质可得APB PAC C ∠=∠+∠，根据等边三角形性质和三角形内角和定理可得18060BFP CBQ APB ∠=︒-∠-∠=︒，根据对顶角性质可得AFQ ∠的度数．（3）设点Q 运动时间是x 秒，根据CP CQ =列一元一次方程，根据任意一角为60︒的等腰三角形是等边三角形，即可求出答案．【详解】（1）BPD CQP ≌．证明：点P 在线段BC 上以3cm /s 的速度由B 点向终点C 运动，经过1s 后，∠133BP =⨯=，∠点Q 的运动速度与点P 的运动速度相等，∠3CQ BP ==，∠AB ＝BC ＝AC ＝12cm ，BD ＝34AB ， ∠ABC 是等边三角形，60B C ∠=∠=︒，31294BD =⨯=， ∠1239PC BC BP =-=-=，在BDP △和CPQ 中，BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∠BPD CQP ≌（SAS ）．（2）解：∠点Q 的运动速度与点P 的运动速度相等，∠BP CQ =，∠AB ＝BC ＝AC ，∠ABC 是等边三角形，60BAC ABC C ∠=∠=∠=︒，∠在ABP △和BCQ △中，AB BC ABC C BP CQ =⎧⎪∠=∠⎨⎪=⎩∠ABP BCQ ≌，∠BAP CBQ ∠=∠；在BPF △中，180()BFP CBQ APB ∠=︒-∠+∠，∵=CBQ APB CBQ CAP C ∠+∠∠+∠+∠，∵=60CBQ CAP BAP CAP ∠+∠∠+∠=︒，60C ∠=°，∴=6060=120CBQ APB ∠+∠︒+︒︒，∴180()=180120=60BFP CBQ APB ∠=︒-∠+∠︒-︒︒，∴=60AFQ BFP ∠∠=︒（对顶角相等）．（3）解：设点Q 运动时间是x 秒，若CP CQ =，可列方程：1236x x -=， 解得：43x =． ∵在CQP 中，CP CQ =，=60C ∠︒， ∴当43x =秒时，CQP 是等边三角形（任意角是60︒的等腰三角形是等边三角形）． ∴当点Q 运动43秒后，可得到等边CQP ． 【点睛】。

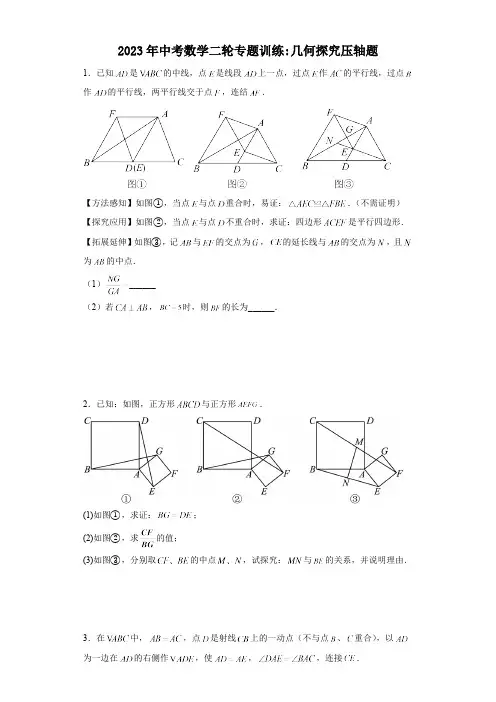
2023年中考数学二轮专题训练:几何探究压轴题1．已知是的中线，点是线段上一点，过点作的平行线，过点作的平行线，两平行线交于点，连结．【方法感知】如图①，当点与点重合时，易证：．（不需证明）【探究应用】如图②，当点与点不重合时，求证：四边形是平行四边形．【拓展延伸】如图③，记与的交点为，的延长线与的交点为，且为的中点．（1）______（2）若，时，则的长为______．2．已知：如图，正方形与正方形．(1)如图①，求证：；(2)如图②，求的值；(3)如图③，分别取的中点，试探究：与的关系，并说明理由．3．在中，，点是射线上的一动点（不与点、重合），以为一边在的右侧作，使，，连接．(1)如图1，当点在线段上，且时，那么________度；(2)设，．①如图2，当点D在线段上，时，请你探究与之间的数量关系，并证明你的结论；②如图3，当点D在线段的延长线上，时，请将图3补充完整；写出此时与之间的数量关系，并说明理由．4．已知，为等边三角形，点在边上．【基本图形】如图1，以为一边作等边三角形，连结．可得（不需证明）．【迁移运用】如图2，点是边上一点，以为一边作等边三角．求证：．【类比探究】如图3，点是边的延长线上一点，以为一边作等边三角．试探究线段，，三条线段之间存在怎样的数量关系，请写出你的结论并说明理由．5．综合与实践二轮复习中，刘老师以“最值问题”为专题引导同学们进行复习探究．问题模型：等腰三角形，，，(1)探究：如图，点为等腰三角形底边上一个动点，连接，则的最小值为______，判断依据为______；(2)探究：在探究的结论下，继续探究，作的平分线交于点，点，分别为，上一个动点，求的最小值；(3)探究：在探究的结论下，继续探究，点为线段上一个动点，连接，将顺时针旋转，得到线段，连接，求线段的最小值．6．问题提出（1）如图1，在中，，，将其折叠，使点B落在边上的处，折痕经过点C，交于点D，则的度数为___________；问题探究（2）如图2，正方形的一条对称轴l交于点H，点E在l上，连接．若正方形的边长为2，，求线段的长．问题解决（3）如图3，有一块三角形空地经测量，米，．现要过点C边修建一条小路，满足，点A关于的对称点为D，连接交于点E．若米，请利用所学知识，求的长．7．已知是等腰直角三角形，，(1)如图1，是等腰直角三角形，点D在的延长线上，，连接，求证：；(2)如图2，点F是斜边上动点，点G是延长线上动点，总有，探究的数量关系，并说明理由；(3)如图3，点H是一点，连接FH，若，，，直接写出的面积为____________（用m，n表示）．8．课本再现如图1，在等边中，为边上一点，为上一点，且，连接与相交于点．(1)与的数量关系是______，与构成的锐角夹角的度数是______．深入探究(2)将图1中的延长至点，使，连接，，如图2所示．求证：平分．（第一问的结论，本问可直接使用）迁移应用(3)如图3，在等腰中，，，分别是边，上的点，与相交于点．若，且，求的值．．四边形中，，为上一点，连、．(1)平分，，①如图1，求证：；②如图2，若平分，交于F，交于N，，(2)在（1）的条件下求的值；，当,时，试探究与的数量关系，证明你的结论．，在中，，为的中点，连接，，试猜想与的数量关系，并加以证(1)独立思考：请解答老师提出的问题；(2)实践探究：希望小组受此问题的启发，将沿着（F为的中点）所在直线折叠，如图②，点C的对应点为，连接并延长交于点G，请判断与的数量关系，并加以证明．问题解决：智慧小组突发奇想，将沿过点对应点为，使于点，折痕交于点，连接，交于点组提出一个问题：若此的面积为20，边长，，求图中阴影部分（四边形）的面积．请你思考此问题，直接写出结果．．问题提出：已知矩形，点为上的一点，，交于点．将绕点顺时针旋转得到，则与有怎样的数量关系．【问题探究】探究一：如图，已知正方形，点为上的一点，，交于点．（1）如图1，直接写出的值；（2）将绕点顺时针旋转到如图所示的位置，连接、，猜想与的数量关系，并证明你的结论；探究二：如图，已知矩形，点为上的一点，，交于点．，若四边形为矩形，，将绕点顺时针旋转得到、的对应点分别为、点，连接、，则的值是否随着的变化而变化．若变化，请说明变化情况；若不变，请求出的值．【一般规律】如图，若四边形为矩形，，其它条件都不变，将绕点顺时针旋转得到，连接，，请直接写出与的数量12．定义：有一个角是直角的平行四边形叫做矩形．(1)根据定义判矩形已知：如图1，在平行四边形中，是它的两条对角线，．求证：平行四边形是矩形．(2)动手操作有发现如图2，在矩形中，是的中点，将沿折叠后得到，点在矩形内部，延长交于点．猜想线段与有何数量关系?并证明你的结论．(3)类比探究到一般如图3，将(2)中的矩形改为平行四边形，其它条件不变，(2)中的结论是否仍然成立，请说明理由．(4)解决问题巧应用如图4，保持(2)中的条件不变，若点是的中点，且，请直接写出矩形的面积．13．在中，，，点P是平面内不与点A，C重合的任意一点，连接，将线段绕点P逆时针旋转α得到线段，连接，，.(1)观察猜想如图①，当时，的值是_______，直线与直线相交所成的较小角的度数是________．(2)类比探究如图②，当时，请写出的值及直线与直线相交所成的较小角的度数，并就图②的情形说明理由．14．（1）（问题背景）如图1，在等边中，点M是边上一点，连接，以为边作等边（A，M，N按逆时针方向排列），连接，求证：（2）（变式探究）如图2，已知，指出图中的另外一对相似三角形并进行证明；（3）（拓展应用）如图3，在和中，，，点D在边上，求的值．15．（1）【操作发现】如图1，四边形都是矩形，，，小明将矩形绕点C顺时针转，如图2所示．若的值不变，请求出的值，若变化，请说明理由．在旋转过程中，当点E、F在同一条直线上时，画出图形并求出的长度．）【类比探究】，中，，，为中点，为平面内一个动点，且，将线段绕点D逆时针旋转得到，则四边形面积的最大值为．（直接写出结果），在矩形中，，动点射线方向移动，作关于直线的对称，设点的运动时间为．(1)若．①如图2，当点落在上时，求证：，②是否存在异于图2的时刻，使得是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．(2)当P点不与C点重合时，若直线与直线相交于点M，且当时存在某一时刻有结论成立，试探究：对于的任意时刻，结论“”总是成立？请说明理由．．在正方形中，是边上一点（点不与点、重合），连结．感知：如图①，过点作交于点．求证．探究：如图②，取的中点，过点作交于点，交于点．（1）求证：．（2）连结，若，求的长．应用如图③，取的中点，连结．过点作交于点，连结、．若，求四边形的面积．18．点在四边形的对角线上，直角三角板绕直角顶点旋转，其边、分别交、边于点、．操作发现：如图①，若四边形是正方形，当时，可知四边形是正方形，显然．当与不垂直时，判断确定、之间的数量关系；______．（直接写出结论即可）类比探究：如图②，若四边形是矩形，试说明．拓展应用：如图③，改变四边形、的形状，其他条件不变，且满足，，，时，求的值．参考答案：1．【拓展延伸】（1）；（2）2．(2)(3)，3．(1)90(2)①，证明见解析；②，5．(1)；点到直线的距离垂线段最短(2)(3)6．（1）；（2）；（3）米7．(2)(3)8．(1)；60°(3)39．(1)(2)(3)10．(1)，(2)，(3)11．[问题探究]探究一：(1)；(2)，探究二：．[一般规律]12．(2)，(3)成立，(4)13．(1)1，；(2)，，14．（2）（3）；15．（1）①不变，；②或；（2）24 16．(1)②存在，的值为2或6或(2)对于的任意时刻，结论“”总是成立，17．（（2）2应用：918．操作发现：；类比探究：拓展应用：。

2021年九年级数学中考二轮复习《动态的几何问题》专题突破训练（附答案）1．如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是边BC上的任意一点，把BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为（）A．152B．223C．294D．82．如图，已知△ABC中，∠ACB=90°，∠BAC=30°，AB=6，点D为直线AB上一动点，将线段CD绕点C逆时针旋转60°得到线段CE，连接ED、BE，当BE最小时，线段AD的值为（）A．5.5 B．6 C．7.5 D．83．如图，已知正方形ABCD的边长为4，点E是AB边上一动点，连接ED，将ED绕点E顺时针旋转90°到EF，连接DF，CF，则DF+CF的最小值是（）A．42B．210C．53D．454．如图，在Rt△ABC中，∠ABC=90°，AB=2，BC=4，点D是BC上的一点，BD=1，点P是AC上的一个动点，连接DP，将线段DP绕点D顺时针旋转90°得到线段DQ，连接BQ，则线段B Q长的最小值是（）A．1 B．2 C．35D．5．如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q 从点A 同时出发以每秒2cm 的速度向点C 运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ 是以PQ 为底的等腰三角形时，运动的时间是（ ）A ．2sB ．3sC ．4sD ．6s6．如图，在四边形ABCD 中，//AD BC ，6AD =，16BC =，E 是BC 的中点．点P 以每秒1个单位长度的速度从点A 出发，沿AD 向点D 运动；点Q 同时以每秒3个单位长度的速度从点C 出发，沿CB 向点B 运动．点P 停止运动时，点Q 也随之停止运动．若以点,,,P Q E D 为顶点的四边形是平行四边形，则点P 运动的时间为（ ）A ．1B ．72C ．2或72D ．1或72 7．如图，在菱形ABCD 中，5AB cm =，120ADC =∠︒，点E 、F 同时由A 、C 两点出发，分别沿AB 、CB 方向向点B 匀速移动（到点B 为止），点E 的速度为1/cm s ，点F 的速度为2/cm s ，经过t 秒DEF ∆为等边三角形，则t 的值为（ ）A ．34 B ．43 C ．32 D ．538．已知：如图①，长方形ABCD 中，E 是边AD 上一点，且AE =6cm ，AB =8cm ，点P 从B 出发，沿折线BE ﹣ED ﹣DC 匀速运动，运动到点C 停止．P 的运动速度为2c m/s ，运动时间。

2023年中考数学高频考点突破- -二次函数动态几何问题1．如图，在平面直角坐标系中，二次函数的图象与轴交于、两点，点在原点的左则，点的坐标为，与轴交于点，点是直线下方的抛物线上一动点．（1）求这个二次函数的表达式；（2）求出四边形的面积最大时的P点坐标和四边形ABPC的最大面积；2．已知直线y＝kx＋b（k≠0）过点F（0，1），与抛物线y＝14x2相交于B、C两点．（1）如图，当点C的横坐标为1时，求直线BC的表达式；（2）在（1）的条件下，点M是直线BC上一动点，过点M作y轴的平行线，与抛物线交于点D，是否存在这样的点M，使得以M、D、O、F为顶点的四边形为平行四边形？若存在，求出点M 的坐标；若不存在，请说明理由．3．已知:如图，二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点，（1）求这个二次函数的解析式（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6.求点B的坐标。

4．如图，抛物线y＝x2+bx+c与直线y＝12x﹣3交于，B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC△x轴于点C，交AB于点D.（1）求抛物线对应的函数解析式；（2）以O，A，P，D为顶点的平行四边形是否存在若存在，求点P的坐标；若不存在，说明理由.5．如图，在平面直角坐标系中，抛物线y=−12x2+bx+c与x轴交于B，C两点，与y轴交于点A，直线y=−12x+2经过A，C两点，抛物线的顶点为D，对称轴与x轴交于点E．（1）求此抛物线的解析式；（2）求ΔDAC的面积；（3）在抛物线上是否存在一点P，使它到x轴的距离为4，若存在，请求出点P的坐标，若不存在，则说明理由．6．已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．7．如图，在平面直角坐标系xOy中，抛物线y＝ax2﹣45x+c与直线y＝25x+25交于A、B两点，已知点B的横坐标是4，直线y＝25x+25与x、y轴的交点分别为A、C，点P是抛物线上一动点．（1）求抛物线的解析式；（2）若点P在直线y＝25x+25下方，求△PAC的最大面积；（3）设M是抛物线对称轴上的一点，以点A、B、P、M为顶点的四边形能否成为平行四边形？若能，求出点P的坐标；若不能，请说明理由．8．二次函数y=ax2+2x-1与直线y=2x-3交于点P（1，b）。

2024年九年级数学中考复习——反比例函数-动态几何问题1．如图，在矩形ABCD 中，已知点A （2，1），且AB ＝4，AD ＝3，把矩形ABCD 的内部及边上，横、纵坐标均为整数的点称为靓点，反比例函数y＝（x ＞0）的图象为曲线L ．（1）若曲线L 过AB 的中点．①求k 的值．②求该曲线L 下方（包括边界）的靓点坐标．（2）若分布在曲线L 上方与下方的靓点个数相同，求k 的取值范围．2．如图，在平面直角坐标系中，一次函数 与反比例函数 相交于点 ，与 轴相交于点 ，点 的横坐标为-2.（1）求 的值；（2）直接写出当 且 时， 的取值范围；（3）设点 是直线AB 上的一点，过点 作 轴，交反比例函数 的图象于点 .若以A ，O ，M ，N 为顶点的四边形为平行四边形，求点 的坐标.k x12y x =-+2(0)k y x x=<B x A B k 0x <12y y <x M M //MN x 2(0)k y x x=<N M3．如图，在平面直角坐标系中，OA ⊥OB ，AB ⊥x 轴于点C ，点A （，1）在反比例函数y ＝ 的图象上．（1）求反比例函数y ＝ 的表达式； （2）在x 轴上是否存在一点P ，使得S △AOP ＝S △AOB ，若存在，求所有符合条件点P 的坐标；若不存在，简述你的理由．4．如图，点 ， 在 轴上，以 为边的正方形 在 轴上方，点 的坐标为 ，反比例函数 的图象经过 的中点 ， 是 上的一个动点，将 沿 所在直线折叠得到 .（1）求反比例函数 的表达式； （2）若点 落在 轴上，求线段 的长及点 的坐标.k x k x12A B x AB ABCD x C (14)，(0)k y k x=≠CD E F AD DEF EF GEF (0)k y k x=≠G y OG F5．如图，已知反比例函数y＝（x ＞0）的图象经过点A （4，2），过A 作AC ⊥y 轴于点C ．点B 为反比例函数图象上的一动点，过点B 作BD ⊥x 轴于点D ，连接AD ．直线BC 与x 轴的负半轴交于点E ．（1）求k 的值；（2）连接CD ，求△ACD 的面积；（3）若BD ＝3OC ，求四边形ACED 的面积．6．已知：如图1，点是反比例函数图象上的一点．（1）求的值和直线的解析式；（2）如图2，将反比例函数的图象绕原点逆时针旋转后，与轴交于点，求线段的长度；（3）如图3，将直线绕原点逆时针旋转，与反比例函数的图象交于点，求点的坐标．k x(4)A n ，8(0)y x x=>n OA 8(0)y x x =>O 45︒y M OM OA O 45︒8(0)y x x=>B B7．已知：反比例函数的图像过点A （ ， ），B （ ， ）且 （1）求m 的值；（2）点C 在x 轴上，且 ，求C 点的坐标；（3）点Q 是第一象限内反比例函数图象上的动点，且在直线AB 的右侧，设直线QA ，QB 与y 轴分别交于点E 、D ，试判断DE 的长度是否变化，若变化请说明理由，若不变，请求出长度.8．规定：在平面直角坐标系中，横坐标与纵坐标均为整数的点，叫做整点，点，在反比例函数的图象上；（1）m= ；（2）已知，过点、D 点作直线交双曲线于E 点，连接OB ，若阴影区域（不包括边界）内有4个整点，求b 的取值范围．m y x =1x 121m --2x 45m-120x x +=16ABC s ∆=()22A ，()1B m ，()0k y x x=>0b >()40C b -，()0b ，()0k y x x=>9．已知，矩形OCBA 在平面直角坐标系中的位置如图所示，点C 在x 轴的正半轴上，点A 在y 轴的正半轴上，已知点B 坐标为（3，6），反比例函数的图象经过AB 的中点D ，且与BC 交于点E ，顺次连接O ，D ，E ．（1）求m 的值及点E 的坐标；（2）点M 为y 轴正半轴上一点，若△MBO 的面积等于△ODE 的面积，求点M 的坐标；（3）平面直角坐标系中是否存在一点N ，使得O ，D ，E ，N 四点顺次连接构成平行四边形？若存在，请直接写出N 的坐标；若不存在，请说明理由．10．如图，点P 为函数与函数图象的交点，点P 的纵坐标为4，轴，垂足为点B ．（1）求m 的值；（2）点M 是函数图象上一动点，过点M 作于点D ，若，求点M的坐标．m y x=1y x =+()0m y x x=>PB x ⊥()0m y x x =>MD BP ⊥12tan PMD ∠=11．如图，在平面直角坐标系中，直线与轴、轴分别交于点、，与双曲线交于点，直线分别与直线和双曲线交于点、．（1）求和的值；（2）当点在线段上时，如果，求的值；（3）点是轴上一点，如果四边形是菱形，求点的坐标．12．如图，等边和等边的一边都在x 轴上，双曲线经过的中点C 和的中点D ．已知等边的边长为4．（1）求k 的值；（2）求等边的边长；（3）将等边绕点A 任意旋转，得到等边，P 是的中点（如图2所示），连结，直接写出的最大值．xOy 34l y x b =+：x y A B x k H y =：922P ⎛⎫ ⎪⎝⎭，x m =H E D k b E AB ED BO =m C y BCDE C OAB AEF ()0k y k x=>OB AE OAB AEF AEF AE F '' E F ''BP BP13．如图，点A 、B 是反比例函数y ＝ 的图象上的两个动点，过A 、B 分别作AC ⊥x 轴、BD ⊥x 轴，分别交反比例函数y ＝－ 的图象于点C 、D ，四边形ACBD 是平行四边形. （1）若点A 的横坐标为－4.①直接写出线段AC 的长度；②求出点B 的坐标；（2）当点A 、B 不断运动时，下列关于□ACBD 的结论：①□ACBD 可能是矩形；②□ACBD 可能是菱形；③□ACBD 可能是正方形；④□ACBD 的周长始终不变；⑤□ACBD 的面积始终不变.其中所有正确结论的序号是 .8x2x14．在平面直角坐标系 中，正比例函数 与反比例函数 的图象相交于点 与点Q ． （1）求点Q 的坐标；（2）若存在点 ，使得 ，求c 的值； （3）过点 平行于x 轴的直线，分别与第一象限内的正比例函数 、反比例函数数 的图象相交于点 、点 ，当 时，请直接写出a 的取值范围．15．在平面直角坐标系中，直线y=x+2与x 轴交于点A ，与y 轴交于点B ，并与反比例函数y=（k≠0）的图象在第一象限相交于点C ，且点B 是AC 的中点xOy ()1110y k x k =≠()2220k y k x=≠(11)P ，(0)C c ，2PQC S = (0)M a ，()1110y k x k =≠()2220k y k x =≠()11A x y ，()22B x y ，1252x x +≤kx（1）如图1，求反比例函数y=（k≠0）的解析式；（2）如图2，若矩形FEHG 的顶点E 在直线AB 上，顶点F 在点C 右侧的反比例函数y=（k≠0）图象上，顶点H ，G 在x 轴上，且EF=4．①求点F 的坐标；②若点M 是反比例函数的图象第一象限上的动点，且在点F 的左侧，连结MG ，并在MG 左侧作正方形GMNP ．当顶点N 或顶点P 恰好落在直线AB 上，直接写出对应的点M 的横坐标．16．如图，动点P 在函数y （x ＞0）的图象上，过点P 分别作x 轴和y 轴的平行线，交函数y 的图象于点A 、B ，连接AB 、OA 、OB ．设点P 横坐标为a ．（1）直接写出点P 、A 、B 的坐标（用a 的代数式表示）；（2）点P 在运动的过程中，△AOB 的面积是否为定值？若是，求出此定值；若不是，请说明理由；（3）在平面内有一点Q （，1），且点Q 始终在△PAB 的内部（不包含边），求a 的取值范围．k xk x 3x =1x =-1317．如图1，一次函数y ＝kx ﹣3（k≠0）的图象与y 轴交于点B ，与反比例函数y＝（x ＞0）的图象交于点A （8，1）．（1）求出一次函数与反比例函数的解析式；（2）点C 是线段AB 上一点（不与A ，B 重合），过点C 作y 轴的平行线与该反比例函数的图象交于点D ，连接OC ，OD ，AD ，当CD 等于6时，求点C 的坐标和△ACD 的面积；（3）在（2）的前提下，将△OCD 沿射线BA 方向平移一定的距离后，得到△O'CD'，若点O 的对应点O'恰好落在该反比例函数图象上（如图2），求出点O'，D'的坐标．18．如图1所示，已知 图象上一点 轴于点 ，点 ，动点 是 轴正半轴点 上方的点，动点 在射线AP 上，过点 作AB 的垂线，交射线AP 于点 ，交直线MN 于点 ，连结AQ ，取AQ 的中点 . m x6(0)y x x=>P PA x ⊥，(0)A a ，(0)(0)B b b >，M y B N B D Q C（1）如图2，连结BP ，求 的面积；（2）当点 在线段BD 上时，若四边形BQNC 是菱形，面积为 .①求此时点Q ，P 的坐标；②此时在y 轴上找到一点E ，求使|EQ-EP|最大时的点E 的坐标.19．已知反比例函数y=的图象经过点A （6，1）．（1）求该反比例函数的表达式；（2）如图，在反比例函数y=在第一象限的图象上点A 的左侧取点C ，过点A 作x 轴的垂线交x 轴于点H ，过点C 作y 轴的垂线CE ，垂足为点E ，交直线AH 于点D ．①过点A 、点C 分别作y 轴、x 轴的垂线，两条垂线相交于点B ，求证：O 、B 、D 三点共线；②若AC=2CO ，求证：∠OCE=3∠CDO ．PAB Q k xk x20．如图，一次函数与反比例函数的图象交于点和，与y 轴交于点C ．（1） ， ；（2）过点A 作轴于点D ，点P 是反比例函数在第一象限的图象上一点，设直线与线段交于点E ，当时，求点P 的坐标．（3）点M 是坐标轴上的一个动点，点N 是平面内的任意一点，当四边形是矩形时，求出点M 的坐标．21．如图1，将函数的图象T 1向左平移4个单位得到函数的图象T 2，T 2与y 轴交于点．（1）若，求k 的值（2）如图2，B 为x 轴正半轴上一点，以AB 为边，向上作正方形ABCD ，若D 、C 恰好落在T 1上，线段BC 与T 2相交于点E①求正方形ABCD 的面积；②直接写出点E 的坐标．114y k x =+22k y x=()2A m ，()62B --，1k =2k =AD x ⊥OP AD Δ41ODE ODAC S S =四边形：：ABMN ()0k y x x =>()44k y x x =>-+()0A a ，3a =22．如图1，直线的图像与x 轴、y 轴分别交于A 、B 两点，点D 是线段AB 上一点，过D 点分别作OA 、OB 的垂线，垂足分别是C 、E ，矩形OCDE 的面积为4，且．（1）求D 点坐标；（2）将矩形OCDE 以1个单位/秒的速度向右平移，平移后记为矩形MNPQ ，记平移时间为t 秒．①如图2，当矩形MNPQ 的面积被直线AB 平分时，求t 的值；②如图3，当矩形MNPQ 的边与反比例函数的图像有两个交点，记为T 、K ，若直线TK 把矩形面积分成1：7两部分，请直接写出t 的值．23．如图1，在平面直角坐标系中，点，点，直线与反比例函数的图象在第一象限相交于点，26y x =-+CD DE >12y x=()40A -，()04B ，AB ()0k y k x=≠()6C a ，（1）求反比例函数的解析式；（2）如图2，点是反比例函数图象上一点，连接，试问在x 轴上是否存在一点D ，使的面积与的面积相等，若存在，请求点D 的坐标；若不存在，请说明理由；（3）新定义：如图3，在平面内，如果三角形的一边等于另一边的3倍，这两条边中较长的边称为“麒麟边”，两条边所夹的角称为“麒麟角”，则称该三角形为“麒麟三角形”，如图所示，在平面直角坐标系中，为“麒麟三角形”， 为“麒麟边”， 为“麒麟角”，其中A ，B 两点在反比例函数 图象上，且A 点横坐标为，点C 坐标为，当为直角三角形时，求n 的值．24．如图1，已知点A （a ，0），B （0，b ），且a 、b 满足 +（a +b +3）2＝0，平等四边形ABCD的边AD 与y 轴交于点E ，且E 为AD 中点，双曲线y ＝经过C 、D 两点． （1）a ＝ ，b ＝ ；（2）求D 点的坐标；（3）点P 在双曲线y ＝ 上，点Q 在y 轴上，若以点A 、B 、P 、Q 为顶点的四边形是平行四边形，试求满足要求的所有点Q 的坐标；（4）以线段AB 为对角线作正方形AFBH （如图3），点T 是边AF 上一动点，M 是HT 的中点，MN ⊥HT ，交AB 于N ，当T 在AF 上运动时， 的值是否发生改变？若改变，求出其变化范围；若()6E m ，()0k y k x=≠CE AE ，ACD ACE ABC AB BAC ∠n y x=1-()02，ABC k x k xMN HT不改变，请求出其值，并给出你的证明．25．在平面直角坐标系中，已知点，点.（1）若将沿轴向右平移个单位，此时点恰好落在反比例函数的图象上，求的值；（2）若绕点按逆时针方向旋转度.①当时，点恰好落在反比例函数图象上，求的值；②问点能否同时落在(1)中的反比例函数的图象上?若能，直接写出的值；若不能，请说明理由.26．如图，已知直线与双曲线交第一象限于点．（1）求点的坐标和反比例函数的解析式；（2）将点绕点逆时针旋转至点，求直线的函数解析式；（3）在（2）的条件下，若点C 是射线上的一个动点，过点作轴的平行线，交双曲线xOy ()A -()60B -，OAB x m A y =m OAB O α()0α180<<α30= B k y x=k A B ，α2y x =(0)k y k x=≠(4)A m ，A O A 90︒B OB OB C y的图像于点，交轴于点，且，求点的坐标．27．如图，一次函数的图象与反比例函数的图象交于点，与y 轴交于点B ．（1）求a ，k 的值；（2）直线CD 过点A ，与反比例函数图象交于点C ，与x 轴交于点D ，AC ＝AD ，连接CB ．①求△ABC 的面积；②点P 在反比例函数的图象上，点Q 在x 轴上，若以点A ，B ，P ，Q 为顶点的四边形是平行四边形，请求出所有符合条件的点P 坐标．28．如图1，反比例函数与一次函数的图象交于两点，已知．（1）求反比例函数和一次函数的表达式；（2）一次函数的图象与轴交于点，点（未在图中画出）是反比例函数图象上的一个动点，若，求点的坐标：(0)k y k x=≠D x E 23DCO DEO S S = ：：C 112y x =+()0k y x x =>()3A a ，k y x=y x b =+A B ，()23B ，y x b =+x C D 3OCD S = D（3）若点是坐标轴上一点，点是平面内一点，是否存在点，使得四边形是矩形？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．29．如图，已知直线y=-2x 与双曲线y=（k<0）上交于A 、B 两点，且点A 的纵坐标为-2 （1）求k 的值；（2）若双曲线y= （k<0）上一点C 的纵坐标为 ，求△BOC 的面积；（3）若A 、B 、P 、Q 为顶点组成的四边形为正方形，直接写出过点P 的反比例函数解析式。

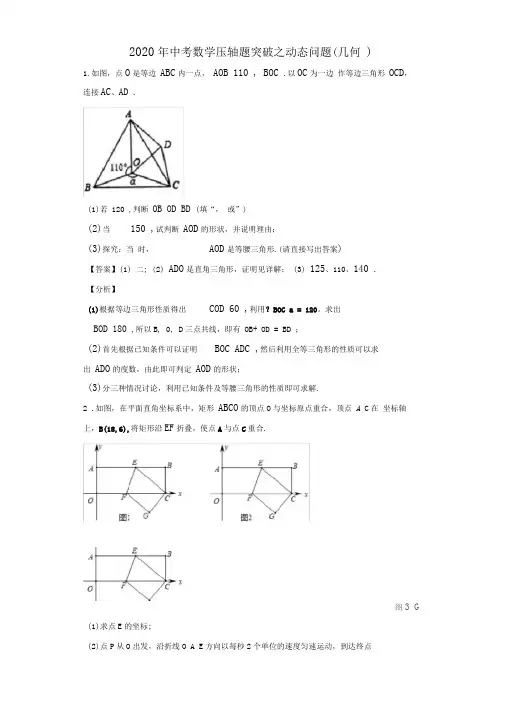
2020年中考数学压轴题突破之动态问题(几何)1.如图，点O是等边ABC内一点，AOB 110 , BOC .以OC为一边作等边三角形OCD，连接AC、AD .(1)若120 ,判断OB OD BD (填“，或”)(2)当150 ,试判断AOD的形状，并说明理由；(3)探究：当时，AOD是等腰三角形.(请直接写出答案)【答案】(1) 二; (2) ADO是直角三角形，证明见详解；(3) 125、110、140 .【分析】(1)根据等边三角形性质得出COD 60 ,利用？BOC a = 120。

求出BOD 180 ,所以B, 0, D三点共线，即有OB+ OD = BD ；(2)首先根据已知条件可以证明BOC ADC ,然后利用全等三角形的性质可以求出ADO的度数，由此即可判定AOD的形状；(3)分三种情况讨论，利用已知条件及等腰三角形的性质即可求解.2 .如图，在平面直角坐标系中，矩形ABCO的顶点O与坐标原点重合，顶点A C在坐标轴上，B(18,6),将矩形沿EF折叠，使点A与点C重合.图3 G(1)求点E的坐标;(2)P O O A E2E时停止运动，设P的运动时间为t, VPCE的面积为S,求S与t的关系式，直接写出t 的取值范围;3(3)在(2)的条件下，当PA=]PE 时，在平面直角坐标系中是否存在点Q,使得以点P 、E 、G Q 为顶点的四边形为平行四边形？若不存在，请说明理由；若存在，请求出点Q 的坐标.【答案】(1) E (10, 6); (2) S= -8t+54 (0<t<3)或 S=-6t+48 (3vtW8)； (3)存 在，Q (14.4 , -4.8 )或(18.4 , -4.8 ). 【详解】解：(1)如图 1,矩形 ABO, B (18, 6),• .AB=18 BC=6,设 AE=x,贝U EC=x BE=18-x,Rt^EBC 中，由勾股定理得： EB"+BC 2=EC 2,(18-x) 2+62=x 2, x=10,即 AE=10,①当P 在OA 上时，0WtW3,如图 2,=18X 6-1X10(62) — - X8X6 - 1X 18X2t , 2 2 2=-8t+54 ,②当P 在AE 上时，3<t<8,如图3,S = S 矩形 OABC S △ PAE -S △ BEC -S △OPCj• •E ( 10, 6);(2)分两种情况：S=1PE?BC=1 X 6X(16-2t)=3 (16-2t ) =-6t+48 ;2 2(3)存在，由PA=3PE可知：P在AE上，如图4,过G作GHLOC于H,2•.AP+PE=10.•.AP=6 PE=4,设OF=y,则FG=y, FC=18-y,由折叠得：/ CGFW AOF=90 ,由勾股定理得：FC2=FC+CG,•. ( 18-y) 2=y2+62,y=8,•.FG=8 FC=18-8=10,1FC?GH= 1FG?CG221X10XGH= 1 X6X8,22GH=4.8,由勾股定理得：FH=J82 4 82 =6.4 ,• .OH=8+6.4=14.4,.•.G ( 14.4 , -4.8 ),•・•点P、E G Q为顶点的四边形为平行四边形，且PE=4,.•.Q ( 14.4 , -4.8 )或(18.4 , -4.8 ). k ,3.如图1,平面直角坐标系xoy中，A(-4, 3),反比例函数y —(k 0)的图象分别x交矩形ABOC勺两边AC, BC于E, F (E, F不与A重合)，沿着EF将矩形ABO所叠使A, D重合.②若折叠后点 D 落在矩形ABOCrt （不包括边界），求线段CE 长度的取值范围.（2）若折叠后，△ ABD 是等腰三角形，请直接写出此时点 D 的坐标.7 . 23 3. 11 3.【答案】（1）①EC= 2;②3 CE 4； （2）点D 的坐标为（一,一）或（一，一）88 2 5 5【详解】,k k解：(1)①由题意得E(k,3) , F( 4,-), 3 4k kk 0 ,则 EC — , FB 一, 3 4AF 3 一， 417(12 k) 4 3 1 3 4(12 k) 3..由 A(-4, 3)得：AC 4, AB 3,,AC 4一 --- 一,AB 3 AE AC AF AB '又A=Z A,・ .△AE% AACB ・ •/AEF4 ACB ・ •.EF// CB如图2,连接AD 交EF 于点H ,••• AE.AE （1）①如图2,当点D 恰好在矩形 ABOC 勺对角线BC 上时，求CE 的长；②由折叠得EF 垂直平分AD,••• /AHE 90 ,则 EAH AEF又• BAD EAH BAC 90 ,BAD AEF ，・ .△AE% ABAQAE AF 口"AB AE 4--- ----- ,则 ----- ------ -，AB BD BD AF 34 3 9 BDAB - 3 - 3 4 4设 AF=x,贝U FB=3— x, FD=AF=x 在Rt^BDF 中，由勾股定理得：FB 2 BD 2 FD 2，r i图2由折叠的性质得： •••D 在 BC 上， ,AE AHEC DH 1 EC AC 2AH=DH 1,则 AE EC 2;即(3 x)2x 2 ,解得:如图，当D 落在BO 上时，: EAF ABD 90 ,B力。

2021年九年级数学中考二轮复习《动态几何问题》专题突破训练（附答案）1．如图，在直角三角形ABC 中，∠ACB =90°，AB =5cm ，BC =4cm ．动点P 从点A 出发，沿线段AB 向终点B 以5cm /s 的速度运动，同时动点Q 从点A 出发沿射线AC 以5cm /s 的速度运动，当点P 到达终点时，点Q 也随之停止运动；连接PQ ，设△APQ 与△ABC 重叠部分图形的面积为S （cm 2），点P 运动的时间为t （s ）（t ＞0）．（1）直接写出AC = cm ；（2）当点A 关于直线PQ 的对称点A '落在线段BC 上时，求t 的值；（3）求S 与t 之间的函数关系式；（4）若M 是PQ 的中点，N 是AB 的中点，当MN 与BC 平行时，t = ；当MN 与AB 垂直时，t = ．2．如图，矩形ABCD 中，P 是边AD 上的一动点，联结BP 、CP ，过点B 作射线交线段CP 的延长线于点E ，交边AD 于点M ，且使得ABE CBP =∠∠，如果2AB =，5BC =，AP x =，PM y =（1）求y 关于x 的函数解析式，并写出它的定义域；（2）当4AP =时，求 tan EBP ∠；（3）如果EBC ∆是以EBC ∠为底角的等腰三角形，求AP 的长3．如图，平行四边形ABCO 位于直角坐标系中，O 为坐标原点，点(8,0)A -，点()3,4C BC 交y 轴于点.D 动点E 从点D 出发，沿DB 方向以每秒1个单位长度的速度终点B 运动，同时动点F 从点O 出发，沿射线OA 的方向以每秒2个单位长度的速度运动，当点E 运动到点B 时，点F 随之停止运动，运动时间为 t （秒）．（1）用t 的代数式表示： BE = ________， OF = ________（2）若以A ，B ，E ，F 为顶点的四边形是平行四边形时，求t 的值．（3）当BEF 恰好是等腰三角形时，求t 的值．4．在△ABC 中，AB =AC ，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作△ADE ，使AD =AE ，∠DAE =∠BAC ，连接CE ．（1）如图1，当点D 在线段BC 上，如果∠BAC =90°，则∠BCE 为多少？说明理由； （2）设∠BAC =α，∠BCE =β．①如图2，当点D 在线段BC 上移动，则α，β之间有怎样的数量关系？请说明理由； ②当点D 在直线BC 上移动，则α，β之间有怎样的数量关系？请直接写出你的结论，不需证明．5．问题情境：如图1，已知正方形ABCD与正方形CEFG，B、C、G在一条直线上，M是AF 的中点，连接DM，EM．探究DM，EM的数量关系与位置关系．小明的思路是：小明发现AD//EF，所以通过延长ME交AD于点H，构造△EFM和△HAM全等，进而可得△DEH是等腰直角三角形，从而使问题得到解决，请你参考小明同学的思路，探究并解决下列问题：（1）猜想图1中DM、EM的数量关系，位置关系．（2）如图2，把图1中的正方形CEFG绕点C旋转180°，此时点E在线段DC的延长线上，点G落在线段BC上，其他条件不变，（1）中结论是否成立？请说明理由；（3）我们可以猜想，把图1中的正方形CEFG绕点C旋转任意角度，如图3，（1）中的结论（“成立”或“不成立”）拓展应用：将图1中的正方形CEFG绕点C旋转，使D，E，F三点在一条直线上，若AB＝13，CE＝5，请画出图形，并直接写出MF的长．6．如图，已知抛物线y＝﹣x2+bx+c经过点A（﹣1，0），B（3，0），与y轴交于点C，点P 是抛物线上一动点，连接PB，PC．（1）求抛物线的解析式；（2）如图1，当点P在直线BC上方时，过点P作PD上x轴于点D，交直线BC于点E．若PE＝2ED，求△PBC的面积；（3）抛物线上存在一点P，使△PBC是以BC为直角边的直角三角形，求点P的坐标．7．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB ∠＝ °，线段BD 、CE 之间的数量关系是 ；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．8．如图，⊙O 的半径为5，弦BC ＝6，A 为BC 所对优弧上一动点，△ABC 的外角平分线AP 交⊙O 于点P ，直线AP 与直线BC 交于点E ．（1）如图1，①求证：点P 为BAC 的中点；②求sin ∠BAC 的值；（2）如图2，若点A 为PC 的中点，求CE 的长；（3）若△ABC 为非锐角三角形，求PA •AE 的最大值．9．如图1，已知△ABC 中，∠ACB ＝90°，AC ＝BC ＝6，点D 在AB 边的延长线上，且CD ＝AB ．（1）求BD 的长度；（2）如图2，将△ACD 绕点C 逆时针旋转α（0°＜α＜360°）得到△A'CD'．①若α＝30°，A'D'与CD 相交于点E ，求DE 的长度；②连接A'D 、BD'，若旋转过程中A'D ＝BD'时，求满足条件的α的度数．（3）如图3，将△ACD 绕点C 逆时针旋转α（0°＜α＜360°）得到△A'CD'，若点M 为AC 的中点，点N 为线段A'D'上任意一点，直接写出旋转过程中线段MN 长度的取值范围．10．如图，P 是等边ABC 内的一点，且5PA =，4PB =，3PC =，将APB △绕点B 逆时针旋转，得到CQB △．（1）求点P 与点Q 之间的距离；（2）求BPC ∠的度数；（3）求ABC 的面积ABC S．11．如图，在矩形ABCD 中，6AB cm =，8BC cm =，如果点E 由点B 出发沿BC 方向向点C 匀速运动，同时点F 由点D 出发沿DA 方向向点A 匀速运动，它们的速度分别为2/cm s 和1/cm s ，FQ BC ⊥，分别交AC ，BC 于点P 和Q ，设运动时间为()04ts t <<．（1）连接EF ，若运动时间t =_______s 时，62EF cm =；（2）连接EP ，当EPC 的面积为23cm 时，求t 的值；（3）若EQP ADC ∽△△，求t 的值．12．如图，边长为32的正方形ABCD 中，P 是对角线AC 上的一个动点（点P 与A 、C不重合），连接BP ，将BP 绕点B 顺时针旋转90°得到BQ ，连接QP ，QP 与BC 交于点E ，其延长线与AD （或AD 延长线）交于点F ．（1）连接CQ ，证明：CQ AP =；（2）设AP x =，CE y =，试写出y 关于x 的函数关系式，并写出自变量x 的取值范围； （3）试问当P 点运动到何处时，PB PE +的值最小，并求出此时CE 的长．（画出图形，直接写出答案即可）13．已知：O 是ABC ∆的外接圆，且,60,AB BC ABC D =∠=︒为O 上一动点． （1）如图1，若点D 是AB 的中点，求DBA ∠的度数．（2）过点B 作直线AD 的垂线，垂足为点E ．①如图2，若点D 在AB 上．求证CD DE AE =+．②若点D 在AC 上，当它从点A 向点C 运动且满足CD DE AE =+时，求ABD ∠的最大值．14．抛物线239344y x x =--与x 轴交于点A ，与y 轴交于点B ．线段OA 上有一动点P (不与O A 、重合)，过点P 作y 轴的平行线交直线AB 于点C ，交抛物线于点M （1）求直线AB 的解析式；（2）点N 为线段AB 下方抛物线上一动点，点D 是线段AB 上一动点；①若四边形CMND 是平行四边形，证明：点M N 、横坐标之和为定值；②在点P N D 、、运动过程中，平行四边形CMND 的周长是否存在最大值？若存在，求出此时点D 的坐标，若不存在，说明理由15．如图，在平面直角坐标系中，点C 在x 轴上，90,10cm,6cm OCD D AO OC CD ︒∠=∠====．（1）请求出点A 的坐标．（2）如图（2），动点P Q 、以每秒1cm 的速度分别从点O 和点C 同时出发，点P 沿OA AD DC 、、运动到点C 停止，点Q 沿CO 运动到点O 停止，设P Q 、同时出发t 秒． ①是否存在某个时间t （秒），使得OPQ △为直角三角形？若存在，请求出值；若不存在，请说明理由．②若记POQ △的面积为()2cm y ，求()2cm y 关于t （秒）的函数关系式． 16．已知，点O 是等边ABC 内的任一点，连接OA ，OB ，OC ．（Ⅰ）如图1所示，已知150AOB ∠=︒，120BOC ∠=︒，将BOC 绕点C 按顺时针方向旋转60︒得ADC ．①求DAO ∠的度数：②用等式表示线段OA ，OB ，OC 之间的数量关系，并证明；（Ⅱ）设AOB α∠=，BOC β∠=．①当α，β满足什么关系时，OA OB OC ++有最小值？并说明理由；②若等边ABC 的边长为1，请你直接写出OA OB OC ++的最小值．17．如图，在正方形ABCD 中，AB =4，动点P 从点A 出发，以每秒2个单位的速度，沿线段AB 方向匀速运动，到达点B 停止．连接DP 交AC 于点E ，以DP 为直径作⊙O 交AC 于点F ，连接DF 、PF ．（1）则△DPF 是 三角形；（2）若点P 的运动时间t 秒．①当t 为何值时，点E 恰好为AC 的一个三等分点；②将△EFP 沿PF 翻折，得到△QFP ，当点Q 恰好落在BC 上时，求t 的值．18．已知四边形ABCD 为矩形，对角线AC 、BD 相交于点O ，AD AO =．点E 、F 为矩形边上的两个动点，且60EOF ∠=︒．（1）如图1，当点E 、F 分别位于AB 、AD 边上时，若75OEB ∠=︒，求证：AD BE =；（2）如图2，当点E 、F 同时位于AB 边上时，若75OFB ∠=︒，试说明AF 与BE 的数量关系；（3）如图3，当点E 、F 同时在AB 边上运动时，将OEF 沿OE 所在直线翻折至OEP ，取线段CB 的中点Q ．连接PQ ，若()20AD a a =>，则当PQ 最短时，求PF 之长．19．如图，在△ABC中，AB＝BC＝AC＝12cm，点D为AB上的点，且BD＝34AB，如果点P在线段BC上以3cm/s的速度由B点向终点C运动，同时，点Q在线段CA上由C点向终点A运动．当一点到达终点时，另一点也随之停止运动．（1）如（图一）若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP 是否全等，请说明理由．（2）如（图二）若点Q的运动速度与点P的运动速度相等（点P不与点B和点C重合），连接点A与点P，连接点B与点Q，并且线段AP，BQ相交于点F，求∠AFQ的度数．（3）若点Q的运动速度为6cm/s，当点Q运动几秒后，可得到等边△CQP？20．如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．（1）若△BPQ与△ABC相似，求t的值；（2）试探究t为何值时，△BPQ是等腰三角形；（3）试探究t为何值时，CP＝CQ；（4）连接AQ，CP，若AQ⊥CP，求t的值．21．如图1，在正方形ABCD 中，4AB m =，点P 从点D 出发，沿DA 向点A 匀速运动，速度是1/cm s ，同时，点Q 从点A 出发，沿AB 方向，向点B 匀速运动，速度是2/cm s ，连接PQ 、CP 、CQ ，设运动时间为()(02)t s t <<．()1是否存在某一时刻，使得//PQ BD 若存在，求出t 的值；若不存在，说明理由； ()2设PQC △的面积为()2S cm ，求S 与t 之间的函数关系式；()3如图2，连接AC ，与线段PQ 相交于点M ，是否存在某一时刻t ，使QCM S ：4PCM S =：5？若存在，直接写t 的值；若不存在，说明理由．22．如图，在 RtΔABC 中，∠C=90°，BC=5cm ，tanA 512=．点 M 在边 AB 上，以 2 cm/s 的速度 由点B 出发沿BA 向点A 匀速运动；同时点N 在边AC 上，以1 cm/s 的速度由A 出发沿AC 向点C 匀速运动．当点M 到达A 点时，点M ，N 同时停止运动．连接MN ，设点M 运动的时间为t (单位：s)．（1）求AB 的长；（2）当t 为何值时，ΔAMN 的面积为△ABC 面积的326； （3）是否存在时间t ，使得以A ，M ，N 为顶点的三角形与ΔABC 相似？若存在，求出时间t 的值；若不存在，请说明理由．23．如图，抛物线y ＝ax 2+bx+3与x 轴交于A ，B 两点，且点B 的坐标为(2，0)，与y 轴交于点C ，抛物线对称轴为直线x 12=-．连接AC ，BC ，点P 是抛物线上在第二象限内的一个动点．过点P 作x 轴的垂线PH ，垂足为点H ，交AC 于点Q ．过点P 作PG ⊥AC 于点G ． （1）求抛物线的解析式．（2）求PQG 周长的最大值及此时点P 的坐标．（3）在点P 运动的过程中，是否存在这样的点Q ，使得以B ，C ，Q 为顶点的三角形是等腰三角形？若存在，请写出此时点Q 的坐标；若不存在，请说明理由．24．如图，直线1:1l y kx =+与x 轴交于点D ，直线2:l y x b =-+与x 轴交于点A ，且经过定点(1,5)B -，直线1l 与2l 交于点(2,)C m ．（1）求k 、b 和m 的值；（2）求ADC ∆的面积；（3）在x 轴上是否存在一点E ，使BCE ∆的周长最短？若存在，请求出点E 的坐标；若不存在，请说明理由；（4）若动点P 在线段DA 上从点D 开始以每秒1个单位的速度向点A 运动，设点P 的运动时间为t 秒．是否存在t 的值，使ACP ∆为等腰三角形？若存在，直接写出t 的值；若不存在，清说明理由．25．如图，已知抛物线2()30y ax bx a =++≠与x 轴交于点(1,0)A 和点(3,0)B -，与y 轴交于点C ．（1）求抛物线的解析式；（2）设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使CMP ∆为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由； （3）作直线BC ，若点(,0)D d 是线段BM 上的一个动点（不与B 、M 重合），过点D 作x 轴的垂线交抛物线于点F ，交BC 于点E ，当BDE CEF S S ∆∆=时，求d 的值．26．正方形ABCD 和等腰Rt DEF △共顶点D ，90DEF ∠=︒，DE EF =，将DEF 绕点D 逆时针旋转一周．（1）如图1，当点F 与点C 重合时，若2AD =，求AE 的长；（2）如图2，M 为BF 中点，连接AM 、ME ，探究AM 、ME 的关系，并说明理由； （3）如图3，在（2）条件下，连接DM 并延长交BC 于点Q ，若22AD DE ==，在旋转过程中，CQ 的最小值为_________．27．综合与探究 如图，抛物线245y x bx c =++经过点()0,4A ，()10B ,，与x 轴交于另一点C （点C 在点B 的右侧），点()P m n ,是第四象限内抛物线上的动点．（1）求抛物线的函数解析式及点C 的坐标；（2）若APC △的面积为S ，请直接写出S 关于m 的函数关系表达式，并求出当m 的值为多少时，S 的值最大？最大值为多少？（3）是否存在点P ，使得PCO ACB ∠=∠？若存在，求出点P 的坐标；若不存在，请说明理由．28．某学校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程： 操作发现：（1）如图1，分别以AB 和AC 为边向△ABC 外侧作等边△ABD 和等边△ACE ，连接BE ､CD ，请你完成作图并证明BE =CD ．（要求：尺规作图，不写作法但保留作图痕迹）类比探究：（2）如图2，分别以AB 和AC 为边向△ABC 外侧作正方形ABDE 和正方形ACFG ，连接CE ､BG ，则线段CE ､BG 有什么关系？说明理由．灵活运用：（3）如图3，在四边形ABCD 中，AC 、BD 是对角线，AB =BC ，∠ABC =60°，∠ADC =30°，AD =3，BD =5，求CD 的长．参考答案1．（1）3；（2）38t =；（3）当305t <≤时，210S t =；当315t <≤时，215309S t t =-+-；（4）38；58．2．（1）4y x x =-．定义域为25x <≤；（2）34；（3）4或53+ 3．（1）5－t ，2t ；（2）3t =或133t =；（3）53t =或910t = 4．（1）90°；（2）①α＋β＝180°；②点D 在直线BC 上移动，α＋β＝180°或α＝β．5．（1）DM ⊥EM ，DM ＝ME ；（2）结论成立；（3）成立；拓展应用： 6．（1）y ＝﹣x 2+2x +3；（2）3；（3）点P 的坐标为（1，4）或（﹣2，﹣5）7．（1）60BD CE ，＝；（2）45CEB BD ∠︒＝，；（3）CE 的长为或8．（1）①证明；②3sin 5BAC ∠=；（2）CE =；（3）80.9．（1）﹣（2）﹣；②45°或225°；（3）﹣＋310．（1）4PQ =；（2）150BPC ∠=︒；（3）9ABC S=． 11．（1）23；（2）2；（3）212．（1）见解析；（2）2(06)6y x x =-+<<；（3）P 位置如图所示，此时PB PE +的值最小，6CE =-13．（1）30DBA ∠=；（2）①；②当点D 运动到点I 时ABI ∠取得最大值，此时30ABD ∠=．14．（1）334y x =-；（2）①证明；②存在；点D 的坐标为111111,,3434⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭；． 15．（1）(8,6)A ．（2）①存在，40 s 9t =或者50 s 9t =．②233(010)10S t t t =-+<<． 16．（1）①90°；②线段OA ，OB ，OC 之间的数量关系是OA 2+OB 2=OC 2，证明；（2）①当α=β=120°时，OA+OB+OC 有最小值．证明；②线段OA+OB+OC ．17．(1)等腰直角;(2)①当t 为1时，点E 恰好为AC 的一个三等分点；．18．（1）证明；（2）2AF BE =；（3）.FP =19．（1）BPD CQP ≌；（2）60︒（3）4320．（1）1或3241；（2）23或89或6457；（3；（4）78． 21．()1存在，43t =；()2228(02)S t t t =-+<<；()3存在，1t = 22．（1）13cm ；（2）t=2或92s ；（3）存在，15637t =或16938t =s23．（1）y 12=-x 212-x+3；（2）)9108，P(32-，218)；（3）存在，Q 1(，+3)，Q 2(﹣1，2)24．（1）12k =，4b =，2m =；（2）6；（3存在，8(7E ，0)；（4）存在，6-4或2．25．（1）223y x x =--+；（2）存在，P (-或(1,-或(1,6)-或5(1,)3-；（3）12d -=26．（1）AE =（2）AM ME =，AM ME ⊥；（3）227．（1）2424455x x y -+=；点C 的坐标为（5，0）；（2）当m ＝52时，S 的值最大，最大值为252；（3）存在点P ，使得使得∠PCO ＝∠ACB ．点P 的坐标为（2，－125）. 28．（1）；（2）CE=BG ；（3）CD=4。

【2019赢在中考】数学二轮专题解读与强化训练专题08 动态型问题动态型问题是以点、线、面(如三角形、四边形)的运动为情境，探索和发现其中规律和结论的中考题型，由于图形的运动，导致题目的条件不断改变，随之相应的数量关系和结论也可能改变，这样就出现一个事件中蕴含着多个数学问题，既独立又有联系，使题目无论从考查知识上，还是解决方法上都具有较强的综合性，以达到培养和考查学生的观察、试验、空间想象、分析综合等解决问题的能力，在全国的中考试卷中常作为压轴题出现，类型有：(1)点的运动，(2)线的运动，(3)面(如三角形、四边形)的运动．解决动态问题的思维与方法：(1)认清问题中的静态图形和动态图形，并确定动态图形的起始位置和终止位置；(2)画出不同时刻动态图形与静态图形形成的几何图形，这样就能达到由“动”变“静”，再设法分别求解问题．考向一点的运动型问题例1．（2018年广东省广州市）如图，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．（1）求∠A+∠C的度数．（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由．（3）若AB=1，点E在四边形ABCD内部运动，且满足，求点E运动路径的长度．【考点】等边三角形的判定与性质，勾股定理的逆定理，多边形内角与外角，弧长的计算，旋转的性质【思路点拨】（1）根据四边形内角和为360度，结合已知条件即可求出答案.（2）将△BCD绕点B逆时针旋转60°，得到△BAQ，连接DQ（如图），由旋转性质和等边三角形判定得△BDQ是等边三角形，由旋转性质根据角的计算可得△DAQ是直角三角形，根据勾股定理得AD2+AQ2=DQ2，即AD2+CD2=BD2.（3）将△BCE绕点B逆时针旋转60°，得到△BAF，连接EF(如图)，由等边三角形判定得△BEF是等边三角形，结合已知条件和等边三角形性质可得AE2=EF2+AF2，即∠AFE=90°，从而得出∠BFA=∠BEC=150°，从而得出点E是在以O为圆心，OB为半径的圆周上运动，运动轨迹为BC，根据弧长公式即可得出答案.【解题过程】解：（1）在四边形ABCD中，∠B=60°，∠D=30°，∴∠A+∠C=360°-∠B-∠C=360°-60°-30°=270°.（2）如图，将△BCD绕点B逆时针旋转60°，得到△BAQ，连接DQ，∵BD=BQ，∠DBQ=60°，∴△BDQ是等边三角形，∴BD=DQ，∵∠BAD+∠C=270°，∴∠BAD+∠BAQ=270°，∴∠DAQ=360°-270°=90°，∴△DAQ是直角三角形∴AD2+AQ2=DQ2，即AD2+CD2=BD2（3）如图，将△BCE绕点B逆时针旋转60°，得到△BAF，连接EF，∵BE=BF，∠EBF=60°，∴△BEF是等边三角形，∴EF=BE，∠BFE=60°，∵AE2=BE2+CE2∴AE2=EF2+AF2∴∠AFE=90°∴∠BFA=∠BFE+∠AFE=60°+90°=150°，∴∠BEC=150°，则动点E在四边形ABCD内部运动，满足∠BEC=150°，以BC为边向外作等边△OBC，则点E是以O为圆心，OB为半径的圆周上运动，运动轨迹为BC，∵OB=AB=1，则BC= =【名师点睛】此题考查了学生对等边三角形的判定与性质，勾股定理的逆定理，多边形内角与外角，弧长的计算，旋转的性质等知识点的综合运用能力．考向二线的运动型问题例2．如图，矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足方程|x﹣15|+=0（OA＞OC），直线y=kx+b分别与x轴、y轴交于M、N两点，将△BCN沿直线BN折叠，点C恰好落在直线MN上的点D处，且tan∠CBD=（1）求点B的坐标；（2）求直线BN的解析式；（3）将直线BN以每秒1个单位长度的速度沿y轴向下平移，求直线BN扫过矩形AOCB的面积S关于运动的时间t（0＜t≤13）的函数关系式．【思路点拨】（1）由非负数的性质可求得x、y的值，则可求得B点坐标；（2）过D作EF⊥OA于点E，交CB于点F，由条件可求得D点坐标，且可求得=，结合DE∥ON，利用平行线分线段成比例可求得OM和ON的长，则可求得N点坐标，利用待定系数法可求得直线BN的解析式；（3）设直线BN平移后交y轴于点N′，交AB于点B′，当点N′在x轴上方时，可知S 即为▱BNN′B′的面积，当N′在y轴的负半轴上时，可用t表示出直线B′N′的解析式，设交x轴于点G，可用t表示出G点坐标，由S=S四边形BNN′B′﹣S△OGN′，可分别得到S与t的函数关系式．【解题过程】解：（1）∵|x﹣15|+=0，∴x=15，y=13，∴OA=BC=15，AB=OC=13，∴B（15，13）；（2）如图1，过D作EF⊥OA于点E，交CB于点F，由折叠的性质可知BD=BC=15，∠BDN=∠BCN=90°，∵tan∠CBD=，∴=，且BF2+DF2=BD2=152，解得BF=12，DF=9，∴CF=OE=15﹣12=3，DE=EF﹣DF=13﹣9=4，∵∠CND+∠CBD=360°﹣90°﹣90°=180°，且∠ONM+∠CND=180°，∴∠ONM=∠CBD，∴=，∵DE∥ON，∴==，且OE=3，∴=，解得OM=6，∴ON=8，即N（0，8），把N、B的坐标代入y=kx+b可得，解得，∴直线BN的解析式为y=x+8；（3）设直线BN平移后交y轴于点N′，交AB于点B′，当点N′在x轴上方，即0＜t≤8时，如图2，由题意可知四边形BNN′B′为平行四边形，且NN′=t，∴S=NN′•OA=15t；当点N′在y轴负半轴上，即8＜t≤13时，设直线B′N′交x轴于点G，如图3，∵NN′=t，∴可设直线B′N′解析式为y=x+8﹣t，令y=0，可得x=3t﹣24，∴OG=3t﹣24，∵ON=8，NN′=t，∴ON′=t﹣8，∴S=S四边形BNN′B′﹣S△OGN′=15t﹣（t﹣8）（3t﹣24）=﹣t2+39t﹣96；综上可知S与t的函数关系式为S=．【名师点睛】本题为一次函数的综合应用，涉及非负数的性质、待定系数法、矩形的性质、三角函数的定义、折叠的性质、平行线分线段成比例、平移的性质及分类讨论思想等知识．在（1）中注意非负数的性质的应用，在（2）中求得N点的坐标是解题的关键，在（3）中确定出扫过的面积是解题的关键．本题考查知识点较多，综合性较强，难度较大考向三面的运动型问题例3．（2018年黑龙江省绥化）如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣4，1），B（﹣1，﹣1），C（﹣3，3）．（每个小方格都是边长为1个单位长度的正方形）（1）将△ABC先向上平移2个单位长度，再向右平移4个单位长度得到△A1B1C1（点A、B、C的对应点分别为点A1、B1、C1），画出平移后的△A1B1C1；（2）将△A1B1C1绕着坐标原点O顺时针旋转90°得到△A2B2C2（点A1、B1、C1的对应点分别为点A2、B2、C2），画出旋转后的△A2B2C2；（3）求△A1B1C1在旋转过程中，点C1旋转到点C2所经过的路径的长．（结果用含π的式子表示）【考点】轨迹；作图﹣平移变换；作图﹣旋转变换【思路点拨】（1）分别将点A、B、C的纵坐标加2，横坐标加4，即可得到A1、B1、C1的坐标，连接A1C1，B1C1，A1B1即可，（2）利用网格和旋转的性质画出△A2B2C2即可，（3）利用勾股定理求出OC1的长，再根据弧长公式即可求得答案．【解题过程】解：（1）根据题意得：A1（0，3），B1（3，1），C1（1，5），连接A1C1，B1C1，A1B1如下图：（2）利用网格和旋转的性质画出△A2B2C2如上图所示，（3）∵C1（1，5），∴OC1=，∴点C1旋转到点C2所经过的路径的长为：=．【名师点睛】本题考查作图﹣旋转变换，轨迹，作图﹣平移变换，解题的关键是：平移，旋转后对应点的坐标表示出来，及弧长公式的正确运用．一、选择题1.（2018年天津市）如图，在正方形中，，分别为，的中点，为对角线上的一个动点，则下列线段的长等于最小值的是（）A. B. C. D.2.（2018年广东省中考数学试题）如图，点P是菱形ABCD边上的一动点，它从点A出发沿在A→B→C→D路径匀速运动到点D，设△PAD的面积为y，P点的运动时间为x，则y 关于x的函数图象大致为（）A．B．C．D．3.（2018年新疆乌鲁木齐市）如图①，在矩形ABCD中，E是AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止；点Q从点B沿BC运动到点C时停止，速度均为每秒1个单位长度．如果点P、Q同时开始运动，设运动时间为t，△BPQ的面积为y，已知y 与t的函数图象如图②所示．以下结论：①BC=10；②cos∠ABE=；③当0≤t≤10时，y=t2；④当t=12时，△BPQ是等腰三角形；⑤当14≤t≤20时，y=110﹣5t中正确的有（）A．2个 B．3个C．4个D．5个4.（2018年河南省）如图1，点F从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，图2是点F运动时，△FBC的面积y（cm2）随时间x（s）变化的关系图象，则a的值为（）A． B．2 C． D．25.（2018年四川省泸州市）在平面直角坐标系内，以原点O为圆心，1为半径作圆，点P在直线y=上运动，过点P作该圆的一条切线，切点为A，则PA的最小值为（）A．3 B．2 C． D．二、填空题6.（2018年河南省）如图，在△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，其中点B的运动路径为，则图中阴影部分的面积为．7.（2018年浙江省衢州市）定义：在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的γ（a，θ）变换．如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A1B1C1就是△ABC经γ（1，180°）变换后所得的图形．若△ABC经γ（1，180°）变换后得△A1B1C1，△A1B1C1经γ（2，180°）变换后得△A2B2C2，△A2B2C2经γ（3，180°）变换后得△A3B3C3，依此类推……△A n﹣1B n﹣1C n﹣1经γ（n，180°）变换后得△A n B n C n，则点A1的坐标是，点A2018的坐标是．8.（2018年河南省）如图，∠MAN=90°，点C在边AM上，AC=4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为．9.（2018年内蒙古呼和浩特市）如图，已知正方形ABCD，点M是边BA延长线上的动点（不与点A重合），且AM＜AB，△CBE由△DAM平移得到．若过点E作EH⊥AC，H为垂足，则有以下结论：①点M位置变化，使得∠DHC=60°时，2BE=DM；②无论点M运动到何处，都有DM=HM；③无论点M运动到何处，∠CHM一定大于135°．其中正确结论的序号为．10.（2018年四川省达州市）如图，Rt△ABC中，∠C=90°，AC=2，BC=5，点D是BC边上一点且CD=1，点P是线段DB上一动点，连接AP，以AP为斜边在AP的下方作等腰Rt△AOP．当P从点D出发运动至点B停止时，点O的运动路径长为．11.（2018年甘肃省兰州市（a卷））如图，M、N是正方形ABCD的边CD上的两个动点，满足AM=BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是．三、解答题12.如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）画出△ABC绕点O逆时针旋转90°后的△A2B2C2；（3）在（2）的条件下，求线段BC扫过的面积（结果保留π）．13.（2018年北京市）如图，Q是与弦AB所围成的图形的内部的一定点，P是弦AB上一动点，连接PQ并延长交于点C，连接AC．已知AB=6cm，设A，P两点间的距离为xcm，P，C两点间的距离为y1cm，A，C两点间的距离为y2cm．小腾根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小腾的探究过程，请补充完整：（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；x/cm 0 1 2 3 4 5 6y1/cm 5.62 4.67 3.76 2.65 3.18 4.37y2/cm 5.62 5.59 5.53 5.42 5.19 4.73 4.11 （2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；（3）结合函数图象，解决问题：当△APC为等腰三角形时，AP的长度约为cm．14.（2018年浙江省杭州市临安市）如图，△OAB是边长为2+的等边三角形，其中O是坐标原点，顶点B在y轴正方向上，将△OAB折叠，使点A落在边OB上，记为A′，折痕为EF．（1）当A′E∥x轴时，求点A′和E的坐标；（2）当A′E∥x轴，且抛物线y=﹣x2+bx+c经过点A′和E时，求抛物线与x轴的交点的坐标；（3）当点A′在OB上运动，但不与点O、B重合时，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明理由．15.（2018年四川省达州市）矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y=（k＞0）的图象与边AC交于点E．（1）当点F运动到边BC的中点时，求点E的坐标；（2）连接EF，求∠EFC的正切值；（3）如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式．16.（2018年四川省绵阳市）如图，已知△ABC的顶点坐标分别为A（3，0），B（0，4），C（﹣3，0）．动点M，N同时从A点出发，M沿A→C，N沿折线A→B→C，均以每秒1个单位长度的速度移动，当一个动点到达终点C时，另一个动点也随之停止移动，移动的时间记为t秒．连接MN．（1）求直线BC的解析式；（2）移动过程中，将△AMN沿直线MN翻折，点A恰好落在BC边上点D处，求此时t 值及点D的坐标；（3）当点M，N移动时，记△ABC在直线MN右侧部分的面积为S，求S关于时间t的函数关系式．。

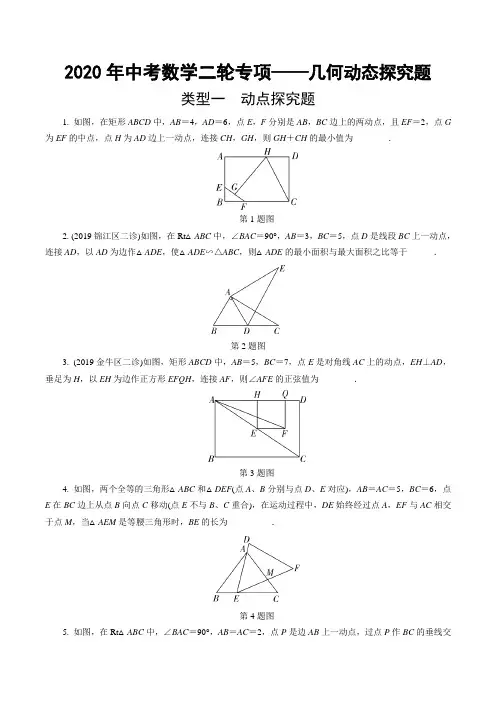
2020年中考数学二轮专项——几何动态探究题类型一动点探究题1. 如图，在矩形ABCD中，AB＝4，AD＝6，点E，F分别是AB，BC边上的两动点，且EF＝2，点G 为EF的中点，点H为AD边上一动点，连接CH，GH，则GH＋CH的最小值为________．第1题图2. (2019锦江区二诊)如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点D是线段BC上一动点，连接AD，以AD为边作△ADE，使△ADE∽△ABC，则△ADE的最小面积与最大面积之比等于______．第2题图3. (2019金牛区二诊)如图，矩形ABCD中，AB＝5，BC＝7，点E是对角线AC上的动点，EH⊥AD，垂足为H，以EH为边作正方形EFQH，连接AF，则∠AFE的正弦值为________．第3题图4. 如图，两个全等的三角形△ABC和△DEF(点A、B分别与点D、E对应)，AB＝AC＝5，BC＝6，点E在BC边上从点B向点C移动(点E不与B、C重合)，在运动过程中，DE始终经过点A，EF与AC相交于点M，当△AEM是等腰三角形时，BE的长为__________．第4题图5. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝2，点P是边AB上一动点，过点P作BC的垂线交BC 于点D ，点F 与点B 关于直线PD 对称，连接AF ，当△AFC 是等腰三角形时，BD 的长为________．第5题图6. (2018成都黑白卷)如图，△ABC 内接于半径为2的⊙O ，∠ABC ＝45°，∠ACB ＝60°，点D 为AB ︵的中点，点M 、N 分别是CD 、AC 上的动点，则MA ＋MN 的最小值为________．第6题图7. 如图，在矩形ABCD 中，点E 是对角线AC 上的动点，连接BE ，MN 是BE 的垂直平分线，分别交AB 、BC 于点M 、N ，连接EM 、EN .过点E 作EF ⊥AD 于点F ，已知AB ＝1，BC ＝2.若△AEM 是直角三角形，则EF 的长为________．第7题图8. 如图，在矩形ABCD 中，AC 和BD 交于点O ，点E 是边BC 上的动点，连接EO 并延长交AD 于点F ，连接AE ，已知AB ＝1，BC ＝3，若△AEF 是等腰三角形，则DF 的长为________．第8题图9. 如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝2，BC ＝3，点M 是直线BC 上一动点，且∠CAM ＋∠CBA ＝45°，则BM 的长为________．第9题图10. (2019锦江区一诊)如图，矩形OABC的边OC在x轴上，边OA在y轴上，A点坐标为(0，2)．点D 是线段OC上的一个动点，连接AD，以AD为边作矩形ADEF，使边EF过点B，连接OF.当点D与点C 重合时，所作矩形ADEF的面积为6.在点D的运动过程中，当线段OF有最小值时，直线OF的解析式为________．第10题图类型二平移探究题1. 如图，矩形ABCD中，点E是BC边上一点，连接AE，将△ABE向右平移得到△DCF，连接AF.若四边形AEFD为菱形，AF＝45，BE∶EC＝3∶2，则AD长为________．第1题图2．如图，在Rt△AOB中，OA＝2，OB＝4，点E在OB上，且∠OAE＝∠OB A.将△AEO沿AO方向向右平移得到△A′E′O′，连接A′B、BE′.当A′B＋BE′取得最小值时，则EE′的长是________．第2题图3. 如图，在Rt△ABC中，AB＝AC＝2，∠A＝90°，D是AB延长线上一点，过点B在AD上方作射线BE，使得∠DBE＝45°.将△ABC沿射线BE平移，得到△A′B′C′，其中点A，B，C的对应点分别是A′，B′，C′，连接A′B，C′B，则A′B＋C′B的最小值是________ .第3题图4. (2018成都黑白卷)如图，在▱ABCD中，AB＝6，∠BAD＝45°，∠ABD＝75°，点E为线段BD边上一动点，连接AE，第一步：将△AED剪下平移到△BGC处；第二步：将△ABE剪下平移到△DCF处；第三步：将△BGC沿BC的中垂线翻转180°后得到△CG′B；第四步：将△CFD沿DC的中垂线翻转180°后得到△DF′C，连接F′G′；当点E在BD上移动时，F′G′的最小值为________．第4题图类型三旋转探究题1. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2，AC＝6，在AC上取一点D，使AD＝4，将线段AD 绕点A按顺时针方向旋转，点D的对应点是点P，连接BP，取BP的中点F，连接CF，在旋转过程中，CF的最大长度是________．第1题图2. 在Rt △ABC 中，∠ACB ＝90°，tan ∠BAC ＝12.点D 在边AC 上(不与A ，C 重合)，连接BD ，F 为BD 中点．若BC ＝6，点D 在边AC 的三等分点处，将线段AD 绕点A 旋转，点F 始终为BD 中点，则线段CF 长度的最大值是________．第2题图3. 如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝4，AC ＝3，点D ，E 分别是AB ，AC 的中点，点G ，F 在BC 边上(均不与端点重合)，DG ∥EF .将△BDG 绕点D 顺时针旋转180°，将△CEF 绕点E 逆时针旋转180°，拼成四边形MGFN ，则四边形MGFN 周长l 的取值范围是________．第3题图4. (2019高新区二诊)如图，△ABC ，△EFG 分别是边长为2和233的等边三角形，D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ，当△EFG 绕点D 旋转一周时，点M 经过的路径长为________．第4题图5. 如图，△ABC 和△CDE 都是等腰直角三角形(∠ACB ＝∠DCE ＝90°)．保持△ABC 固定不动，将△CDE 绕点C 顺时针旋转一周，连接AD 、AE 、BD ，直线AE 与BD 相交于点H ，点P 、M 、N 分别是AD 、AB 、DE 的中点，若AC ＝4，CD ＝2，则在旋转过程中，△PMN 的面积的最大值为________．第5题图类型四折叠探究题1. 如图，在矩形ABCD中，AB＝6，AD＝8，E是AB的中点，点F是BC边上的动点，将△EBF沿EF 所在的直线折叠到△EGF的位置，连接GD，则GD的最小值是______．第1题图2. 如图，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点分别在AB、BC上(含端点)，且AB＝6，BC＝10.设AE＝x，则x的最大值和最小值的和是______．第2题图3. (2019淮安)如图，在矩形ABCD中，AB＝3，BC＝2，H是AB的中点，将△CBH沿CH折叠，点B 落在矩形内点P处，连接AP，则tan∠HAP＝________．第3题图4. (2019金牛区二诊)如图，在等腰直角三角形ABC 中，∠ACB ＝90°，在△ABC 内有一点P ，已知∠1＝∠2＝∠3，将△BCP 以直线PC 为对称轴翻折，使点B 与点D 重合，PD 与AB 交于点E ，连接AD ，将△APD 的面积记为S 1，将△BPE 的面积记为S 2，则S 2S 1的值为________．第4题图5. 如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝6，点D 是边BC 的中点，点E 是边AB 上任意一点(点E 不与点B 重合)，沿DE 翻折△DBE ，使点B 落在点F 处，连接AF ，则线段AF 的长取最小值时，BF 的长为________．第5题图6. (2019都江堰区一诊)如图，已知在△ABC 中，AB ＝AC ，BC ＝8，D 、E 两点分别在边BC 、AB 上，将△ABC 沿着直线DE 翻折，点B 正好落在边AC 上的点M 处，并且AC ＝4AM ，设BD ＝m ，那么∠ACD 的正切值是______．(用含m 的代数式表示)第6题图7. (2019成华区二诊)已知一个矩形纸片ABCD ，AB ＝12，BC ＝6，点E 在BC 边上，将△CDE 沿DE 折叠，点C 落在C ′处，DC ′，EC ′分别交AB 于点F ，G ，若GE ＝GF ，则sin ∠CDE 的值为________．第7题图8. (2019成都黑白卷)如图，在平行四边形ABCD 中，点E 为AD 边的中点，将△ABE 沿BE 翻折，得到△FBE ，连接DF 并延长交BC 于点G ，若BE ＝AD ＝10，平行四边形ABCD 的面积为60，则FG ＝ ________．第8题图9. 如图，四边形ABCD是矩形纸片，AB＝2，对折矩形纸片ABCD，使AD与BC重合，折痕为EF，展开后再过点B折叠矩形纸片，使点A落在EF上的点N处，折痕BM与EF相交于点Q，再次展平，连接BN，MN，延长MN交BC于点G.P为线段BM上一动点，H是BN的中点，则PN＋PH的最小值是______．第9题图10. 如图，四边形纸片ABCD中，AD⊥AB，AB∥DC，AB＝6，AD＝CD＝3，点E，F分别在线段AB，AD上，将△AEF沿EF翻折，点A的落点记为P.当P落在四边形ABCD内部时，PD的最小值为______．第10题图参考答案类型一 动点探究题1. 9 【解析】如解图，由题意可知，点G 在以点B 为圆心，1为半径的14圆弧上运动．作点C 关于AD 的对称点C ′，连接C ′B 交AD 于点H ，交以点B 为圆心，1为半径的圆于点G ，由两点之间线段最短，此时C ′B 的值最小，最小值为BC 2＋CC ′2＝62＋82＝10，∵GH ＋CH ＝GH ＋C ′H ＝BC ′－BG ＝9，∴GH ＋CH 的最小值为9.第1题解图2. 925【解析】如解图，∵点D 为BC 边上一动点，∴AD 的最小值为AD 1，最大值为AD 2，∵在Rt △ABC 中，AB ＝3，BC ＝5，∴AC ＝52－32＝4，∵S △ABC ＝AB ·AC 2＝BC ·AD 12，解得AD 1＝125，∵AD 2为最大值4，∴最小面积与最大面积之比＝(125∶4)2＝925.第2题解图3. 513【解析】∵四边形EFQH 是正方形，∴∠EHA ＝90°，设HE ＝HQ ＝x ，AH ＝y ，∵四边形ABCD 是矩形，∴∠D ＝90°，∴HE ∥CD ，AD ∥EF ，∴△AHE ∽△ADC ，∴HE CD ＝AH AD ，即x 5＝y 7，设x ＝5k ，则y ＝7k ，∵四边形EFQH 是正方形，∴HQ ∥EF ，∴∠AFE ＝∠QAF ，在Rt △AQF 中，AF ＝（5k ）2＋（12k ）2＝13k ，∴sin ∠AFE ＝sin ∠QAF ＝QF AF ＝5k 13k ＝513. 4. 1或116【解析】∵∠AEF ＝∠B ＝∠C ，且∠AME ＞∠C ，∴∠AME ＞∠AEF ，∴AE ≠AM ；①当AE ＝EM 时，则△ABE ≌△ECM ，∴CE ＝AB ＝5，∴BE ＝BC －EC ＝6－5＝1；②当AM ＝EM 时，则∠MAE ＝∠MEA ，∴∠MAE ＋∠BAE ＝∠MEA ＋∠CEM ，即∠CAB ＝∠CEA ，又∵∠C ＝∠C ，∴△CAE ∽△CBA ，∴CE CA ＝AC BC ，∴CE ＝AC 2CB ＝256，∴BE ＝BC －EC ＝6－256＝116.综上所述，BE 的长是1或116. 5. 22或2－1 【解析】∵在Rt △ABC 中，AB ＝AC ＝2，∴BC ＝2 2.①当AF ＝CF 时，∠F AC ＝∠C ＝45°，∴∠AFC ＝90°，∴AF ⊥BC ，∴BF ＝CF ＝12BC ＝2，∵直线PD 垂直平分BF ，∴BD ＝12BF ＝22；②当CF ＝CA ＝2时，BF ＝BC －CF ＝22－2，∵直线PD 垂直平分BF ，∴BD ＝12BF ＝2－1；③当AF ＝AC 时，点F 与点B 重合(舍去)．综上所述，BD 的长为22或2－1. 6. 6 【解析】如解图，连接OA 、OC ，∵∠ABC ＝45°，OA ＝OC ＝2，∴∠AOC ＝90°，∴AC ＝2OA ＝22，在CB 上取一点A ′，使CA ′＝CA ，∵∠ACB ＝60°，∴△A ′CA 为等边三角形，过点A ′作A ′N ′⊥AC 于点N ′，∵点D 为AB ︵的中点，∴CD 为∠ACB 的平分线，∴点A 与点A ′关于直线CD 对称，连接A ′M ，∴A ′M＝AM ，即AM ＋MN ＝A ′M ＋MN ，根据直线外一点到直线上的所有连线中，垂线段最短，∴A ′N ′的长即为MA ＋MN 的最小值，∵A ′C ＝AC ＝22，∠ACB ＝60°，∴A ′N ′＝A ′C ·sin60°＝22×32＝6，即MA ＋MN 的最小值为 6.第6题解图7. 13或5－255【解析】如解图①，当∠AME ＝90°时，易知四边形AMEF 是矩形，且四边形BMEN 是正方形．∵ME ∥BC ，∴AM ME ＝AB BC ＝12，∴AM ＋BM ＝AM ＋2AM ＝1，则EF ＝AM ＝13；如解图②，当∠AEM ＝90°时，易证△AEM ∽△ABC ，∴AE ME ＝AB CB ＝12，∴ME ＝2AE ，则BM ＝ME ＝2AE ，AM ＝5AE ，∴AB ＝AM ＋BM ＝2AE ＋5AE ＝1，解得AE ＝5－2.又∵EF ∥CD ，∴EF AE ＝CD AC ＝15，∴EF ＝55(5－2)＝5－255.综上，若△AEM 是直角三角形，则EF 的长为13或5－255.图① 图②第7题解图 8. 43或1或1－63 【解析】如解图①，当AE ＝AF 时，设BE ＝DF ＝a ，则AF ＝AE ＝3－a .在Rt △ABE中，由AE 2＝AB 2＋BE 2得(3－a )2＝12＋a 2，解得a ＝43；如解图②，当AE ＝EF 时，设BE ＝DF ＝a ，则AF ＝3－a ，由AF ＝2BE ，得3－a ＝2a ，解得a ＝1；如解图③，当AF ＝EF 时，设BE ＝DF ＝a ，则AF ＝EF ＝3－a .由∠F AE ＝∠FEA ＝∠AEB 可得AB ＝AG ＝1，易知EG ＝BE ＝a ，∴FG ＝3－2a .在Rt △AFG 中，由AF 2＝AG 2＋FG 2得(3－a )2＝12＋(3－2a )2，解得a ＝1－63或a ＝1＋63(不符合题意，舍去)．综上，若△AEF 是等腰三角形，则DF 的长为43或1或1－63.图① 图② 图③第8题解图 9. 135或175【解析】①当M 在线段BC 上时，如解图，过点M 作MH ⊥AB 于点H ，∵∠CAM ＋∠CBA ＝45°，∠ACB ＝90°，∴∠BAM ＝45°.∵AC ＝2，BC ＝3，∴AB ＝13.∵Rt △BHM ∽Rt △BCA ，∴MH AC ＝BH BC＝BM BA .设MH ＝2x ，则2x 2＝BH 3＝BM 13，∴BH ＝3x ，BM ＝13x ，在Rt △AHM 中，AH ＝MH ＝2x ，∵AB ＝BH ＋AH ＝13，∴5x ＝13，x ＝135，BM ＝13x ＝135；②当M 在BC 延长线上时，如解图，则∠CAM ′＋∠CBA ＝45°，又∵∠CAM ＋ ∠CBA ＝45°，∴∠CAM ＝∠CAM ′.又∵AC ⊥BM ′，∴CM ＝CM ′.由①得CM ＝BC －BM ＝25，∴BM ′＝175；③当M 在CB 的延长线上时，不存在∠CAM ＋∠CBA ＝45°.综上所述，BM 的长为135或175.第9题解图10. y ＝113x 【解析】当点D 与点C 重合时，如解图，过F 作FG ⊥y 轴于点G ，连接OF ，∵S △ABC ＝12S 矩形 AOCB ＝12S 矩形ADEF ＝3，∴S 矩形AOCB ＝6，∵A 点坐标为(0，2)，∴OA ＝2，∴OC ＝3，∵∠F AD ＝90°，易得△FGA ∽△AOD ，∴FG AO ＝AG DO ，即FG AG ＝AO DO ＝23，设|FG |＝2a ，|AG |＝3a 由勾股定理得OF ＝OG 2＋FG 2＝（2＋3a ）2＋（2a ）2＝13a 2＋12a ＋4，令t ＝13a 2＋12a ＋4，∴t ＝13a 2＋12a ＋4＝13(a ＋613)2＋4，∴当a ＝－613时，t 有最小值．∴|FG |＝|2×(－613)|＝1213，|AG |＝|3×(－613)|＝1813，点F 的横坐标为1213，纵坐标为1813＋2＝4413，设OF 解析式为y ＝kx (k ≠0)，求得k ＝113，故函数的解析式为y ＝113x .第10题解图类型二 平移探究题1. 5 【解析】∵四边形AEFD 为菱形，∴AE ＝EF ，∵将△ABE 向右平移得到△DCF ，∴BE ＝CF ，AB ＝CD ，∵BE ∶EC ＝3∶2，设BE ＝3k ，EC ＝2k ，∴BC ＝EF ＝5k ，∴AE ＝5k ，∵四边形ABCD 是矩形，∴AD ＝BC ，AB ＝CD ，∠B ＝90°，∴AB ＝AE 2－BE 2＝4k ，∴AB 2＋BF 2＝AF 2，即(4k )2＋(8k )2＝(45)2，∴k ＝1，∴AD ＝BC ＝5.2. 67 【解析】∵OA ＝2，OB ＝4，∠OAE ＝∠OBA ，∠EOA ＝∠AOB ＝90°，∴△OAE ∽△OBA ，∴OA OB ＝OE OA ，即24＝OE 2，解得OE ＝1，如解图，过点A 作AB ′⊥OA ，并使AB ′＝BE ＝3.易证△AB ′A ′≌△EBE ′，∴B ′A ′＝BE ′，∴A ′B ＋BE ′＝A ′B ＋B ′A ′.当点B 、A ′、B ′在同一条直线上时，A ′B ＋B ′A ′最小，即此时A ′B ＋BE ′取得最小值．易证△AB ′A ′∽△OBA ′，∴AA ′OA ′＝AB ′OB ＝34，∴AA ′OA ＝37，AO ＝2，∴AA ′＝37×2＝67，∴EE ′＝AA ′＝67.第2题解图3. 25 【解析】如解图，作射线CC ′，AA ′，AA ′交BC ′于点O ，过点C 作CF ∥AB 交AA ′于F ，连接BF ，由平移性质得AA ′∥BE ∥CC ′，∵∠EBD ＝45°，∴∠F AB ＝∠C ′CF ＝45°，∵Rt △ABC 中，AB ＝AC ，∠CAB ＝90°，∴易得四边形ABFC 是正方形，∴∠FCB ＝45°，∴∠C ′CB ＝90°，∵A ′C ′＝BF ，∠A ′OC ′＝∠FOB ，∠C ′A ′O ＝∠BFO ＝45°，∴△A ′OC ′≌△FOB ，∴BO ＝C ′O ，∴CO ＝C ′O ＝BO ，延长FC 到G ，使得CG ＝CF ，连接A ′G ，则CO 是△FGA ′的中位线，∴A ′G ＝2CO ＝BC ′，∴BC ′＋BA ′＝BA ′＋A ′G ，∴当点B 、A ′、G 在同一条直线上时，BG 取得最小值，那A ′B ＋C ′B 取得最小值．∵在Rt △GFB 中，BF ＝AC ＝2，FG ＝2CF ＝4，∴BG ＝25，∴A ′B ＋C ′B 的最小值为2 5.第3题解图 4. 32＋62 【解析】由翻转可得△BG ′C ≌△CGB ≌△DEA ，∴CG ′＝AE ，∠BCG ′＝EAD ，同理可得CF ′＝AE ，∠DCF ′＝∠BAE ，∴∠BCG ′＋∠DCF ′＝∠EAD ＋∠BAE ＝45°，在平行四边形ABCD 中，∠BAD ＝∠BCD ＝45°，∴∠G ′CF ′＝∠G ′CB ＋∠BCD ＋∠DCF ′＝90°.∴△G ′CF ′为等腰直角三角形，由勾股定理可得F ′G ′＝2CG ′＝2AE ，当AE ⊥BD 时，AE 的值最小，即此时F ′G ′的值最小，∵△AED ≌△BGC ，△ABE ≌△DCF ，且∠AED ＝∠AEB ＝90°，∴∠BGC ＝∠AED ＝90°，∠DFC ＝∠AEB ＝90°，∴BG ∥DF ，又∵BG ＝AE ＝DF ，∴四边形BGFD 为矩形，如解图，过点B 作BM ⊥AD 于点M ，在Rt △ABM 中，∵∠BAM ＝∠ABM ＝45°，AB ＝6，∴AM ＝BM ＝6×22＝3，∵∠ABD ＝75°，∴∠DBM ＝∠ABD －∠ABM ＝75°－45°＝30°，∴∠ADB ＝60°，∴在Rt △DBM 中，BD ＝BM sin60°＝2，MD ＝BM tan60°＝1，∴AD ＝AM ＋MD ＝1＋3，∵S △BAD ＝12BD ·AE ＝12AD ·BM ，即2AE ＝(1＋3)×3.∴AE ＝3＋32，∴F ′G ′的最小值为32＋62.第4题解图类型三 旋转探究题1. 10＋2 【解析】如解图，取AB 的中点M ，连接MF 和CM ，∵在Rt △ABC 中，∠ACB ＝90°，AC＝6，BC ＝2，∴AB ＝AC 2＋BC 2＝210.∵M 为AB 中点，∴CM ＝12AB ＝10，∵将线段AD 绕点A 按顺时针方向旋转，点D 的对应点是点P ，∴AP ＝AD ＝4，∵M 为AB 中点，F 为BP 中点，∴FM ＝12AP ＝2.当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大，此时CF ＝CM ＋FM ＝10＋2.第1题解图2. 4＋35 【解析】如解图①，当AD ＝13AC 时，取AB 的中点M ，连接MF 和CM ，∵∠ACB ＝90°，tan ∠BAC ＝12，且BC ＝6，∴AC ＝12，AB ＝6 5.∵M 为AB 中点，∴CM ＝35，∵AD ＝13AC ，∴AD ＝4.∵M 为AB 中点，F 为BD 中点，∴FM ＝12AD ＝2，∴当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大，此时CF ＝CM ＋FM ＝2＋35；如解图②，当AD ＝23AC 时，取AB 的中点M ，连接MF 和CM ，同理可得CF 的最大值为4＋35，综上，线段CF 的长度的最大值为4＋3 5.第2题解图3. 7＜l ＜17 【解析】如解图，过点A 作AH ∥DG ，∵DG ∥EF ，∴DG ∥EF ∥AH ，∵点D 为AB 的中点，将△BDG 绕点D 顺时针旋转180°后到△ADM 的位置，∴BG ＝AM ，MG ∥AH 且MG ＝AH ，同理CF ＝AN ，NF ∥AH 且NF ＝AH ，∴四边形MGFN 是平行四边形，∴MN ＝GF ＝AM ＋AN ＝BG ＋CF .在Rt △ABC 中，∵AB ＝4，AC ＝3，∴由勾股定理得BC ＝5，即MN ＋GF ＝5，在△ABH 中，由三角形的三边关系可得AB －BH ＜AH ＜AB ＋BH ，同理AC －CH ＜AH ＜AC ＋CH ，两式相加得AB ＋AC －(BH ＋CH )＜2AH ＜AB ＋AC ＋(BH ＋CH )，∴4＋3－5＜2AH ＜4＋3＋5，即2＜2AH ＜12，l ＝MG ＋GF ＋NF ＋MN ＝2AH ＋BC ，∵BC ＝5，2＜2AH ＜12，∴7＜l ＜17.第3题解图4. 4π3【解析】如解图，连接AD 、DG .∵△ABC 和△EFG 均是等边三角形，D 分别是BC 和EF 的中点，∴BD ＝CD ，DE ＝DF ，∴AD ⊥BC ，GD ⊥EF ，∴∠ADC ＝∠GDF ＝90°，∴∠ADG ＝∠CDF ，∵AD CD＝DG DF＝tan60°，∴△ADG ∽△CDF ，∴∠DAG ＝∠DCF ，∴∠AMC ＝90°，∴点M 的轨迹是以AC 为直径的圆，且来回共两个三分之一圆，∴点M 运动的路径长为4π3.第4题解图5. 92【解析】∵△ABC 和△CDE 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，∴AC ＝BC ，CE ＝CD ，∠ACB ＋∠BCE ＝∠BCE ＋∠ECD ，∴∠ACE ＝∠BCD ，∴△ACE ≌△BCD ，∴AE ＝BD ，∠CAE ＝∠CBD ，∴∠HBA ＋∠HAB ＝∠HBC ＋∠CBA ＋∠HAB ＝∠CBA ＋∠CAB ＝90°，∴BD ⊥AE .∵P ，M 分别是AD ，AB的中点，∴PM ∥BD ，且PM ＝12BD ，同理，PN ∥AE ，且PN ＝12AE ，∴PM ⊥PN ，PM ＝PN ，∴△PMN 是等腰直角三角形，∴S △PMN ＝12PM 2＝18BD 2，∴当BD 最大时，△PMN 的面积最大，∵△CDE 绕点C 旋转，∴点D 在以C 为圆心，CD 为半径的圆上，∴当点D 在BC 的延长线上时，BD 最大，此时BD ＝AC ＋CD ＝6，∴△PMN 面积的最大值为18×62＝92.第5题解图类型四 折叠探究题1. 73－3 【解析】如解图，由EG ＝EB ＝3，可得当点G 在DE 上时，此时GD 的值最小，根据折叠的性质，△EBF ≌△EGF ，∴EG ⊥GF ，EG ＝EB ，∵E 是AB 边的中点，AB ＝6，∴AE ＝EG ＝3，∵AD ＝8，∴Rt △ADE 中，DE ＝82＋32＝73，∴GD ＝73－3.第1题解图2. 8 【解析】设折痕为PQ ，点P 在AB 边上，点Q 在BC 边上．如解图①，当点Q 与点C 重合时，AE 最小，根据翻折对称性可得EC ＝BC ＝10，在Rt △CDE 中，CE 2＝ED 2＋CD 2，即102＝(10－AE )2＋62，解得AE ＝2，即x ＝2；如解图②，当点P 与点A 重合时，AE 最大，根据翻折对称性可得AE ＝AB ＝6，即x ＝6，所以x 的最大值和最小值的和是8.图① 图②第2题解图 3. 43 【解析】如解图，连接PB 交CH 于点E .在Rt △BCH 中，BC ＝2，BH ＝12AB ＝32，∵△PCH 是由△BCH 折叠得到的，∴PB ⊥CH ，BE ＝PE ，PH ＝HB .∴∠HPB ＝∠HBP .∵AH ＝BH ，∴AH ＝PH .∴∠P AH ＝∠APH .∴∠APH ＋∠BPH ＝12(∠P AB ＋∠APB ＋∠ABP )＝90°.∴AP ∥CH ，∴tan ∠HAP ＝tan ∠BHC ＝BC BH ＝43.第3题解图 4. 12 【解析】如解图，连接BD ，延长CP 交BD 于点F ，由翻折可知CF ⊥BD ，BF ＝DF ，∠BPF ＝∠DPF ，∵∠1＝∠2＝∠3，△ABC 是等腰直角三角形，∴∠1＋∠ACP ＝∠2＋∠ACP ＝90°，∠2＋∠PBC ＝∠3＋∠PBC ＝45°，∴∠APC ＝90°，∠DPF ＝45°，DF ＝FB ＝PF ，∴△APC ≌△CFB ，∴AP ＝CF ，CP＝BF ＝PF ，∴AP ＝BD ，∴四边形ADBP 是平行四边形，∴S 2S 1＝12.第4题解图5. 1255【解析】由题意得：DF ＝DB ，∴点F 在以D 为圆心，BD 长为半径的圆上，如解图，连接AD 交⊙D 于点F .此时AF 的值最小，∵点D 是边BC 的中点，∴CD ＝BD ＝3，由勾股定理得：AD 2＝AC 2＋CD 2，∵AC ＝4，∴AD ＝5，∵FD ＝3，∴F A ＝5－3＝2，即线段AF 长的最小值是2，连接BF ，过点F 作FH ⊥BC 于点H ，∵∠ACB ＝90°，∴FH ∥AC ，∴△DFH ∽△DAC ，∴DF DA ＝DH DC ＝HF CA ，即35＝DH 3＝HF 4，∴HF ＝125，DH ＝95，∴BH ＝245，∴BF ＝BH 2＋HF 2＝1255.第5题解图6. 10m －253【解析】如解图，作AH ⊥BC 于点H ，MG ⊥BC 于点G ，连接EM 、MD 、BM ，∵AB ＝AC ，BC ＝8，AH ⊥BC ，∴CH ＝4，∵AC ＝4AM ，∴CM ∶AC ＝3∶4，∵AH ∥MG ，∴CG HC ＝CM AC ＝34，即CG 4＝34，解得CG ＝3，∴BG ＝5，∴DG ＝m －5，由翻折的性质可知MD ＝BD ＝m ，在Rt △MGD 中，依据勾股定理可知：MG ＝MD 2－GD 2＝m 2－（m －5）2＝10m －25，∴tan ∠ACD ＝tan ∠ACG ＝MG CG ＝10m －253.第6题解图 7. 1010 【解析】设CE ＝x ，则BE ＝6－x .根据折叠的对称性可知DC ′＝DC ＝12，C ′E ＝CE ＝x .在△FC ′G 和△EBG 中，⎩⎪⎨⎪⎧∠C ′＝∠B ＝90°∠FGC ′＝∠EGB GF ＝GE，∴△FC ′G ≌△EBG (AAS)．∴FC ′＝BE ＝6－x .∴DF ＝12－(6－x )＝6＋x .连接FE ，在Rt △FC ′E 和Rt △EBF 中，⎩⎪⎨⎪⎧FC ′＝BE EF ＝EF，∴Rt △FC ′E ≌Rt △EBF (HL)．∴FB ＝EC ′＝x .∴AF ＝12－x .在Rt △ADF 中，AD 2＋AF 2＝DF 2，即36＋(12－x )2＝(6＋x )2，解得x ＝4.∴CE ＝4.在Rt △CDE 中，DE 2＝DC 2＋CE 2，则DE ＝410.∴sin ∠CDE ＝CE DE ＝1010. 8. 2 【解析】∵将△ABE 沿BE 翻折，得到△FBE ，∴AE ＝EF ，∠AEB ＝∠FEB ，∴∠AEB ＝12(180°－∠DEF )，∵E 为AD 边的中点，∴AE ＝DE ，∴DE ＝EF ，∴∠EDF ＝∠EFD ，∴∠EDF ＝12(180°－∠DEF )，∴∠AEB ＝∠EDF ，∴BE ∥DG ，∵四边形ABCD 是平行四边形，∴DE ∥BG ，∴四边形BEDG 为平行四边形，∴DE ＝BG ，DG ＝BE ＝10，∵四边形ABCD 是平行四边形，且面积等于60，AE ＝DE ，∴S △ABE ＝14S ▱ABCD ＝15，如解图，连接AF 交BE 于H ，则AH ⊥BE ，AH ＝HF ，∵BE ＝10，∴AH ＝3，∴AF ＝6，∵BE ∥DG ，∴AF ⊥DG ，∴DF ＝AD 2－AF 2＝8，∴FG ＝DG －FD ＝2.第8题解图9. 3 【解析】如解图，连接AN ，∵∠ABM ＝∠MBN ＝30°，∠BNM ＝∠BAM ＝90°，∴∠BMG ＝∠BNM －∠MBN ＝90°－30°＝60°，∴∠MBG ＝∠ABG －∠ABM ＝90°－30°＝60°，∴∠BGM ＝180°－60°－60°＝60°，∴∠MBG ＝∠BMG ＝∠BGM ＝60°，∴△BMG 为等边三角形，∵点N 是MG 的中点，∴BN ⊥MG ，∵BG＝BM ＝AB cos ∠ABM ＝433，∴BN ＝BG ·sin60°＝433×32＝2，根据题意易知E 点和H 点关于BM 对称，∴PH ＝PE ，∴P 与Q 重合时，PN ＋PH 的值最小，此时PN ＋PH ＝PN ＋PE ＝EN ，∵EN ＝BN 2－BE 2＝22－（2÷2）2＝3，∴PN ＋PH ＝3，∴PN ＋PH 的最小值是 3.第9题解图10. 35－6【解析】如解图①，设A的对应点为P1，连接ED，过P1作PP1⊥ED于点P，∴在Rt△P1PD 中，DP1＞DP，∴当点A的对应点P落在线段ED上时，此时PD有最小值，即当EP取最大值时，PD有最小值，而点E在线段AB上，∴当点E与点B重合时，如解图②，即EP最大，从而此时PD取得最小值，在Rt△ADB中，BD＝AB2＋AD2＝35，∵PB＝AB＝6，∴DP＝BD－BP＝35－6.图①图②第10题解图。

2024陕西中考数学二轮专题训练题型八几何测量问题类型一与锐角三角函数有关的几何测量【类型解答】与锐角三角函数有关的几何测量应用题近10年解答题中考查3次，分值为6分或7分．考查特点：设问均为底部不可及的测量问题，且都是通过在两个直角三角形中解决问题．1.西安奥体中心体育馆是第十四届全运会的主场馆之一，其顶部有16个角舒展绽放，像盛开的花瓣．某日，家住附近的小华和小明想测量其中一个角顶部距离地面的高度AB，由于施工，点B周围设有20米宽的禁行区域MN.如图所示，小明先在距离点M60米远的D处用测倾器CD测得顶部A的仰角为30°，然后小华在距离点N30米远的F处用测倾器EF测得顶部A的仰角为45°，已知测倾器的高CD＝EF＝1.5米，点D、M、B、N、F在同一条直线上，CD、EF均垂直于DF，求角顶部距离地面的高度A B.(结果用根号表示)第1题图2.某广场的平面示意图大致如图所示，小明和小凯想用测量知识测量广场的南北长度．首先，他们在广场最北边选取一点A，测得建筑物最西端M位于点A南偏东37°方向，然后沿着广场边缘向东行走10m，到达点B，测得该建筑物最东端N位于点B南偏东45°方向．已知建筑物东西长度MN为60m，且点M、N在广场的最南端边上，求该广场的南北长度．(结果精确到1m．参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，2≈1.41)第2题图3.[真实问题情境]如图①，是一个手动饸饹机的实物图，图②是其示意图，已知手柄的长度AB＝36cm，BD＝4cm，支架的高度EF＝33cm.抬至最高时与水平方向的夹角∠ABC约为52°，A、C、E、F四点共线．(结果精确到0.1cm，参考数据：sin52°≈0.79，cos52°≈0.62，tan52°≈1.28)(1)求饸饹机手柄上的点A到水平面GF的距离；(2)李师傅压制饸饹时，某一时刻AB与水平方向的夹角为30°，则手柄AB上点A的高度降低了多少？第3题图类型二与相似三角形有关的几何测量【类型解读】与相似三角形有关的几何测量应用题近10年解答题考查6次．考查特点：以利用“标杆”测高、中心投影、平行投影、镜面反射或固定视角等问题为背景，设问多为测量高度.1.大约公元前600年，几何学家泰勒斯第一个测量出了金字塔的高度．如图①，他首先测量了金字塔正方形底座的边长为230米，然后他站立在沙地上的点B′处，请人不断测量他的影子B′C′，当他的影子B′C′和身高A′B′相等时，立刻测量出该金字塔塔尖P的影子A与相应底棱中点B的距离约为22.2米，此时点A与点B的连线恰好与相应的底棱垂直，即正方形底座中心O与A和B在一条直线上，聪明的小明根据老师的讲述，迅速画出图②所示的测量金字塔高度的平面图形，请你根据这个平面图形计算出该金字塔的高度．第1题图2.小唯想利用所学的知识测量学校旗杆的高度，一天下午，她和学习小组来到旗杆前，由于旗杆下面有旗杆台，到旗杆底部的距离无法测量到，于是她们先在旗杆周围的空地上选择一点E并放置小平面镜，小唯沿着BE方向移动到点D处，她恰好在小平面镜内看到旗杆顶端A的像，此时测得DE＝0.8m，然后小唯拿着自制的直角三角板FMN在BE方向移动，在点G处用眼睛观察到斜边FM与点A在同一条直线上，测得DG＝7.4m．已知直角三角板的直角边MN＝9cm，FN＝12cm，小唯的眼睛与地面的距离CD＝FG＝1.6m，AB、CD、FG、MN均垂直于BG，求旗杆的高度A B.(平面镜大小忽略不计)第2题图3.如图，河岸旁种植了两排平行的树，且每排每两棵树之间的距离为3m，为测量这两排树之间的距离PQ，小明先在中间两棵树QP的延长线上选取一点A，恰好发现点A、树B、树C在一条直线上，然后小明后退10m到达点D处，发现点D、树E、树F在一条直线上．已知PQ所在的直线垂直于两岸的树，且两排树均用图中的黑点表示，求河岸旁两排树之间的距离PQ.第3题图类型三与全等三角形有关的几何测量1.如图所示，物体从一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，求旗杆的高度OM和物体在荡绳索过程中离地面的最低点的高度MN.第1题图2.(北师九下P22活动二改编)如图所示，小明与小华计划测量学校春晖楼的高度A B.小明先站在点E处，用测倾器EF测得求实楼CD的顶端D的仰角为α，然后走到点C处，用测倾器CG测得春晖楼AB的顶端B的仰角为β，发现α＋β＝90°.已知AB、EF、CD均垂直于AC，EF＝CG＝1.6m，CE＝25.2m，求实楼的高CD＝31.6m，两栋楼之间的距离AC＝30m，求春晖楼的高度A B.第2题图类型四与勾股定理有关的几何测量1.[数学文化](北师八上P15习题1.4T5改编)《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐.问水深，葭长各几何？”题意是：有一个池塘，其底面是边长为10尺的正方形，一棵芦苇AB生长在它的中央，高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B 恰好碰到岸边的B′(如图).水深和芦苇长各多少尺？第1题图2.一天，小明带着弟弟去图书大厦买书，已知该图书大厦装有一个自动感应门，当人体进入感应范围内，感应门会自动打开，小明发现门打开时，自己和弟弟距离门的位置不相同，于是小明利用所学的知识计划测量该感应门的最大感应范围．小明先站在D处，门恰好自动打开，然后小明后退，让弟弟去打开门，发现当弟弟站在点F处时，门恰好自动打开，且小明发现自己与弟弟所站的位置中间相隔2个地砖．已知小明的身高CD＝1.6m，弟弟的身高EF＝1.3m，感应器距离地面的高度AB＝2.5m，每个地砖的宽度为15cm，AB、CD、EF 均垂直于BD，求该感应门的最大感应距离AC(或AE)．第2题图参考答案类型一与锐角三角函数有关的几何测量1.解：如解图，连接CE 交AB 于点G ，由题知，CD 、EF 均垂直于DF ，且CD ＝EF ，第1题解图∴四边形CDFE 为矩形，∴CE ＝DF ＝60＋20＋30＝110.在Rt △AGE 中，∵∠AEG ＝45°，∴AG ＝EG .设AG ＝EG ＝x ，∵在Rt △ACG 中，∠ACG ＝30°，∴CG ＝AG tan30°＝3x ，∴3x ＋x ＝110，解得x ＝553－55，∵CD ＝EF ＝1.5，∴BG ＝1.5，∴AB ＝AG ＋BG ＝553－55＋1.5＝(553－53.5)米．答：该角顶部距离地面的高度AB 为(553－53.5)米．2.解：如解图，过点A 作AE ⊥MN 于点E ，过点B 作BF ⊥MN 于点F ，则四边形ABFE 是矩形，由题意可知∠EAM ＝37°，∠FBN ＝45°，设FM ＝x ，则EM ＝10＋x ，FN ＝60＋x ，在Rt △BFN 中，∵∠FBN ＝45°，∴BF ＝FN ＝60＋x .∴AE ＝BF ＝60＋x .在Rt △AEM 中，∵∠EAM ＝37°，∴tan ∠EAM ＝EM AE ＝10＋x 60＋x≈0.75，解得x ＝140，∴AE ＝60＋140＝200m ，答：该广场的南北长度约为200m.第2题解图3.(1)解：在Rt △ABC 中，∵∠ACB ＝90°，∠ABC ＝52°，AB ＝36cm ，∴AC ＝AB ·sin52°≈36×0.79＝28.44cm.∵BD ⊥DE ，BD ⊥BC ，BC ⊥AF ，∴四边形BDEC 是矩形．∴CE ＝BD ＝4cm.又∵EF ＝33cm ，∴AF ＝AC ＋CE ＋EF ＝28.44＋4＋33＝65.44≈65.4cm.答：饸饹机手柄上的点A 到水平面GF 的距离约为65.4cm ；(2)由(1)知，AC ＝28.44cm ，当∠ABC ＝30°时，AC ＝AB ·sin ∠ABC ＝36×12＝18cm ，∴手柄AB 上点A 的高度降低了28.44－18≈10.4cm.类型二与相似三角形有关的几何测量1.解：由题意可知，△POA ∽△A ′B ′C ′，∴PO OA ＝A ′B ′B ′C ′.∵A ′B ′＝B ′C ′，∴OP ＝OA.∵金字塔正方形底座的边长为230，点O 为正方形的对称中心，点B 为正方形边上的中点，∴OB ＝115，∴OA ＝OB ＋AB ＝115＋22.2＝137.2，∴OP ＝137.2.答：金字塔的高度约为137.2米．2.解：如解图，延长FN 交AB 于点H ，则FH ⊥AB ，∴四边形FGBH 是矩形，由题意可知△ABE ∽△CDE ，△MFN ∽△AFH ，∴AB CD ＝BE DE ，AH FH ＝MN FN ＝912＝34.设AB ＝x ，则AH ＝x －1.6，则x 1.6＝BE 0.8，∴BE ＝0.5x ，∴FH ＝BG ＝GD ＋DE ＋BE ＝7.4＋0.8＋0.5x ＝8.2＋0.5x ，∴x －1.68.2＋0.5x ＝34，解得x ＝12.4，答：旗杆的高度AB 为12.4m.第2题解图3.解：设AP ＝x ，由题意可知，BP ＝3，PE ＝6，CQ ＝6，FQ ＝9，EP ∥FQ ，∴△APB ∽△AQC ，△DPE ∽△DQF ，∴AP AQ ＝BP CQ ＝36＝12，∴AQ ＝2AP ＝2x ，∴DP ＝x ＋10，DQ ＝2x ＋10，∴DP DQ ＝PE FQ ，即x ＋102x ＋10＝69＝23，解得x ＝10，∴PQ ＝10，答：河岸旁两排树之间的距离PQ 为10m.类型三与全等三角形有关的几何测量1.解：如解图，过点A作AE⊥OM于点E，过点B作BF⊥OM于点F，∵∠AOE＋∠BOF＝∠BOF＋∠OBF＝90°，∴∠AOE＝∠OBF.在△AOE和△OBF中，OEA＝∠BFOAOE＝∠OBF，＝OB∴△AOE≌△OBF(AAS)，∴OE＝BF，AE＝OF，∴OE＋OF＝AE＋BF＝CD＝17，∴2EO＋EF＝17.∵EF＝EM－FM＝AC－BD＝10－3＝7，∴EO＝5，∴AE＝12，∴在Rt△AOE中，OA＝OE2＋AE2＝13.∵OM＝OE＋EM＝15，∴MN＝15－13＝2.答：旗杆的高度OM为15米，物体在荡绳索过程中离地面的最低点的高度MN为2米．第1题解图2.解：如解图，延长GF交AB于点H，∵AB⊥AC，EF⊥AC，CD⊥AC，EF＝CG，∴四边形AEFH、四边形EFGC、四边形ACGH均为矩形．∴HG＝AC，∠BHG＝∠FGD＝90°.∴α＋∠FDG＝90°.∵α＋β＝90°，∴∠FDG＝β.即∠D＝∠BGH.又∵EF＝CG＝1.6m，CD＝31.6m，AC＝30m，∴HG＝30m，GD＝CD－CG＝30m，在△BHG和△FGD中，BHG＝∠FGD，＝GDBGH＝∠D∴△BHG≌△FGD(ASA)．∴BH＝FG＝CE＝25.2m.∴AB＝BH＋AH＝BH＋EF＝26.8m.答：春晖楼的高度AB为26.8m.第2题解图类型四与勾股定理有关的几何测量1.解：设水深x尺，则芦苇长(x＋1)尺．由题意得x2＋52＝(x＋1)2.解得x＝12.∴x＋1＝13.答：水深12尺，芦苇长13尺．2.解：如解图，过点C作CG⊥AB于点G，过点E作EH⊥AB于点H，则四边形EFBH和四边形CDBG是矩形，由题意可知DF＝30cm＝0.3m，GH＝CD－EF＝0.3m，AC＝AE，设BF＝x，则BD＝CG＝0.3＋x，在Rt△AEH中，∵AH＝2.5－1.3＝1.2m，∴AE2＝x2＋1.22，在Rt△ACG中，∵AG＝2.5－1.6＝0.9m，∴AC2＝(0.3＋x)2＋0.92.∵AC＝AE，∴(0.3＋x)2＋0.92＝x2＋1.22，∴AC＝1.5m，答：该感应门的最大感应距离AC(或AE)为1.5m.第2题解图。

一、三年中考概况；近年来运动问题是以三角形或四边形为背景，用运动的观点来探究几何图形变化规律的问题．这类题的特点是：图形中的某些元素(如点、线段、角等)或整个图形按某种规律运动，图形的各个元素在运动变化过程中相互依存，相互制约．考查学生的分类讨论、转化、数形结合、函数与方程等思想方法.二、马年中考策略；“动点型问题〞题型繁多、题意创新，考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等，是近几年中考题的热点和难点。

解决动点问题的关键是“动中求静〞.点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体，运动变化为主线，集多个知识点为一体，集多种解题思想于一题. 这类题综合性强，能力要求高，它能全面的考查学生的实践操作能力，空间想象能力以及分析问题和解决问题的能力.动态几何特点－－－－问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性〔特殊角、特殊图形的性质、图形的特殊位置。

〕动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

解决运动型问题常用的数学思想是方程思想，数学建模思想，函数思想，转化思想等；常用的数学方法有：分类讨论法，数形结合法等.三、三年中考回放；类型一建立动点问题的函数解析式〔或函数图象〕例1 〔2022•兰州〕如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，那么以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为〔〕例2〔2022湖南衡阳〕如图，P是正方形ABCD的边AD上一个动点，AE⊥BP，CF⊥BP，垂足分别为点E、F，AD=4〔2〕过点P作PM∥FC交CD于点M，点P在何位置时线段DM最长，并求出此时DM的值例3 〔2022•荆门〕如右图所示，等腰梯形ABCD，AD∥BC，假设动直线l垂直于BC，且向右平移，设扫过的阴影局部的面积为S，BP为x，那么S关于x的函数图象大致是〔〕类型四：面动几何型问题(1)如图①，当AB∥CB′时，设A′B′与CB相交于D.求证：△A′CD是等边三角形；(3)如图③，设AC的中点为E，A′B′的中点为P，AC＝a，连接EP，当θ＝________°时，EP的长度最大，最大值为________．(3)连接CP，那么CP＝12A′B′＝12×2a＝a.∵EC＋PC≥EP，∴EP≤12a＋a＝32a，当点P还是AB中点时，例5 〔2022•攀枝花〕如图10，在平面直角坐标系中，四边形ABCD是梯形，AB ∥CD,点B〔10,0〕，C〔7,4〕,直线l经过A、D两点，且sin∠DAB=22,动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B以每秒5个单位的速度沿B C D→→的方向向点D运动.过点P作PM 垂直于x轴，与折线A D C→→相交于点M。

2020年中考数学热点专练八动态几何问题（江苏版）（解析版）专题导读动态几何问题，是近年来的热点问题.它几乎成了每个城市中考试卷中的亮点，拿到一套试卷，总是习惯先看看有没有关于动态几何的问题.动态几何问题也就是关于图形运动的一类问题，它主要是牵扯到图形的三种变换：平移、旋转、轴对称及动点问题.当然考查图形的运动问题有小题，也有大题，小题主要分布在选择和填空的最后一两个题，也就是小压轴题，解答题中也会有关于图形的运动问题，主要有两类，一类是关于平移、旋转、轴对称的作图，这个比较简单，我们这里就不说了；另一类就是我们介绍的重点一一研究图形在运动过程中产生的一些图形性质上的变化和不变的情况.这几乎成了压轴题基本上共同的特点.中考要求中考要求课程标准和中考说明都要求学生要具备一定的用运动观点分析问题的能力.学会在运动变化中寻求不变的图形性质.学会运用函数的观点研究关于图形运动中性质的变化情况.专题集训考向1图形的运动与最值1.（2019江苏省连云港市）如图，在矩形ABCD中，AB=4,AD=3,以点C为圆心作。

与直线相切，点P是QC±一个动点，连接AP交于点T,则业的最大值是AT2.（2019江苏省无锡市）如图，在AABC中，AB=AC=5,BC=4逐，D为边AB上一动点（3点除外），以CD为一边作正方形CDEF,连接8E,则ABDE面积的最大值为.3.（2019江苏省宿迁市）如图，ZMAN^60°,若△ABC的顶点3在射线AM上，且A3=2,点。

在射线AN上运动，当AABC是锐角三角形时，BC的取值范围是.4.（2019江苏省宿迁市）如图，正方形ABCQ的边长为4,E为BC上一点，且BE=1,F为AB边上的一个动点，连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为.5.(2019江苏省扬州市)如图，己知等边△ABC的边长为8,点F是边上的一个动点(与点A、B不重合).直线1是经过点P的一条直线，把△ABC沿直线1折叠，点B的对应点是点B'.(1)如图1,当PB=4时，若点可恰好在AC边上，则菌，的长度为；(2)如图2,当PB=5时，若直线1〃AC,则33,的长度为；(3)如图3,点P在AB边上运动过程中，若直线1始终垂直于AC,AACB'的面积是否变化？若变化，说明理由；若不变化，求出面积；(4)当PB=6时，在直线1变化过程中，求可面积的最大值.6.(2019江苏省苏州市)已知矩形ABCD AB=5cm,点F为对角线AC上的一点，且AP =26cm.如图①，动点M从点A出发，在矩形边上沿着的方向匀速运动(不包含点C).设动点M的运动时间为I(s),A4PM的面积为S(enF),S与f的函数关系如图②所示:(1)直接写出动点M的运动速度为cm/s,BC的长度为cm-,(2)如图③，动点M重新从点A出发，在矩形边上，按原来的速度和方向匀速运动.同时，另一个动点N从点£＞出发，在矩形边上沿着D t C t B的方向匀速运动，设动点N的运动速度为v(cm/s).已知两动点M、N经过时间x(s)在线段BC上相遇(不包含点C),动点N相遇后立即停止运动，记此时AARW与AZJRV的面积为5]（＜?麻）,$2（伽2）.①求动点N运动速度v（cm/s）的取值范围；②试探究S] .S?是否存在最大值.若存在，求出S|・S2的最大值并确定运动速度时间x的值;若不存在，请说明理由.(B®)7.（2019江苏省扬州市）如图，四边形A3CD是矩形，A3=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,ZG=90°.点M在线段AB上，且AM=a,点P沿折线AQ-DG运动，点Q沿折线BC-CG运动（与点G不重合），在运动过程中始终保持线段PQ//AQ.设PQ与AB之间的距离为x.（1）若a=12.①如图1,当点F在线段AD上时，若四边形AMQF的面积为48,则x的值为；②在运动过程中，求四边形AMQP的最大面积；（2）如图2,若点P在线段ZJG上时，要使四边形AMQP的面积始终不小于50,求a的取值范围.考向2动点与函数的结合问题1.(2019江苏省连云港市)如图，在平面直角坐标系xOy中，抛物线L：y^x+bx+c过点C(0,-3),与抛物线£2：-lx2-旦t+2的一个交点为A,且点A的横坐标为2,点22P、Q分别是抛物线3、3上的动点.(1)求抛物线3对应的函数表达式；(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形，求出点F的坐标；(3)设点R为抛物线3上另一个动点，且CA平分ZPCR.若OQ//PR,求出点。

2021年中考数数学阶段复习巩固与提升微专题《几何动态问题》高频考题专题提升练习一． 选择题.1. 如图，将平行四边形ABCD 沿对角线BD 折叠，使点A 落在点A′处，若∠1=∠2=50°，则∠A′的度数为（ ）A ．130°B ．120°C ．105°D ．100°2. 如图，在矩形ABCD 中，BC=8，CD=6，将△ABE 沿BE 折叠，使点A 恰好落在对角线BD 上的点F 处，则EF 的长是（ ）A ．3B ．524C ．5D ．1689 3. 如图，在四边形ABCD 中，∠BAD=130°，∠B=∠D=90°，点E ，F 分别是线段BC ，DC 上的动点．当△AEF 的周长最小时，则∠EAF 的度数为（ ）A．90°B．80C．70°D．60°4.如图，在Rt△ABC中，∠ACB=90°，BC=2，将△ABC绕顶点C逆时针旋转得到△A′B′C，使点B′落在AC边上，设M是A′B′的中点，连接BM，CM，则△BCM的面积为（）A．1B．2C．3D．45. 在矩形ABCD中，AB=3，AD=5，如图所示，使点A落在BC边上的A'处，折痕为PQ，当点A在BC边上移动时，折痕的端点P，Q也随之移动，若限定点P，Q 分别在AB、AD上移动，则点A在BC边上可移动的最大距离为（）A.1B. 2C.3D.46.如图，已知四边形ABCD是边长为4的正方形，E为AB的中点，将△DAE 绕点D沿逆时针方向旋转后得到△DCF，连接EF，则EF的长为（）A．23B．25C．26D．2107. 如图，菱形ABCD 中，AB=2，∠D=120°，E 是对角线AC 上的任意一点，则BE+21CE 的最小值为（ ）A ．3B ．2C ．23+1D ．3+18. 如图，将矩形ABCD 绕点A 逆时针旋转至矩形AB′C′D′位置，此时AC′的中点恰好与D 点重合，AB′交CD 于点E ，则旋转角的度数为（ ）A ．30°B ．45°C ．60°D ．90°二．填空题.9. 如图，在矩形ABCD 中，AB=3，AD=5，点E 在DC 上，将矩形ABCD 沿AE 折叠，点D 恰好落在BC 边上的点F 处，那么cos ∠EFC 的值是 ．10. 如图，点C 坐标为(2，,5),点A 的坐标为(7,0)，⊙C 的半为√10,点B 在⊙C 上一动点,OB+√55AB 的最小值为 。

2024海南中考数学二轮专题训练几何图形动点型综合题(小题破大题)模型再现：自旋转型全等模型1.如图，在矩形ABCD中，点E是BC上一动点，连接DE，点F是DE上一点，DF＝CE，BC＝DE.求证：AF⊥DE.【思维教练】由矩形ABCD的性质可知∠ADF＝∠DEC，由BC＝DE，得AD＝DE，再由已知条件DF＝CE，即可证得△ADF≌△DEC，可得∠AFD＝∠C＝90°，即可得证．第1题图模型再现：一线三垂直型相似模型2.如图，在矩形ABCD中，AB＝4，BC＝5，E是BC边上的一个动点，DF⊥AE，垂足为点F，若AE＝BC，求tan∠FCE的值．【思维教练】要求tan∠FCE的值，先过点F作BC的垂线，构造直角三角形，再结合矩形的性质和相似三角形的性质列出比例关系，即可求解．第2题图模型再现：8字型相似模型3.如图，在矩形ABCD 中，E 是BC 边上一动点，AE ⊥BD ，垂足为点F ，连接DE .若BE ＝12BC ，求cos ∠AED 的值．【思维教练】要求cos ∠AED 的值，即要求Rt △EFD 中EF ED的值，结合矩形的性质和相似三角形的性质即可得出EF ＝13AE ＝13DE .第3题图模型再现：正A 字型相似模型4.如图，在矩形ABCD 中，AB ＝3，BC ＝5，E 是AD 上一个动点，连接BD ，O 是对角线BD 的中点，连接OE ，AO ，当OE ＝DE 时，求AE 的长．【思维教练】由矩形ABCD 的性质和勾股定理，可得BD 的长，再通过角度之间的等量关系转换，得△ODE ∽△ADO ，结合相似的性质对应边成比例得出AE 的长．第4题图1.四边形ABCD是边长为2的正方形，E是AB的中点，连接DE，点F是射线BC上一动点(不与点B重合)，连接AF，交DE于点G.(1)如图①，当点F是BC边的中点时，求证：△ABF≌△DAE；(2)如图②，当点F与点C重合时，求AG的长；(3)在点F运动的过程中，当线段BF为何值时，AG＝AE？请说明理由．第1题图备用图2.已知，如图①，在▱ABCD中，点E是AB中点，连接DE并延长，交CB的延长线于点F.(1)求证：△ADE≌△BFE；(2)如图②，点G是边BC上任意一点(点G不与点B、C重合)，连接AG交DF于点H，连接HC，过点A作AK∥HC，交DF于点K.①求证：HC＝2AK；②当点G是边BC的中点时，恰有HD＝n·HK(n为正整数)，求n的值．第2题图1.如图，边长为1的正方形ABCD中，点K在AD上，连接BK，过点A，C作BK的垂线，垂足分别为M，N，点O是正方形ABCD的中心，连接OM，ON.第1题图(1)求证：△ABM≌△BCN；(2)请判定△OMN的形状，并说明理由；(3)若点K在线段AD上运动(不包括端点)，当AK＝13时，求△OMN的面积．2.如图①，在正方形ABCD中，M是AD的中点，点E是边AB上的一个动点，连接EM并延长交射线CD于点F，过点M作EF的垂线交射线BC于点G，连接EG、FG.(1)求证：△AME≌△DMF；(2)在点E的运动过程中，探究：①tan∠GEF的值是否发生变化？若不变，求出这个值；②如图②，把正方形ABCD改为矩形(AB<BC)，BC＝4，AB＝k，其他条件不变，当△GEF 为等边三角形时，试求k的值．第2题图3.在矩形ABCD中，AB＝6，BC＝8，P为对角线BD上一点，连接PC，过点P作PG⊥PC 交直线AB于点G，交直线BC于点H.(1)如图①，若BG＝PC，求证：△BHG≌△PHC；(2)如图②，当点G在线段AB的延长线上时，连接GC.①作CE⊥BD于点E，求CE的长；②设PD＝m，当△PCG的面积为503时，求m的值．第3题图4.如图，P是边长为1的正方形ABCD对角线BD上一动点(P与B、D不重合)，∠APE＝90°，且点E在BC边上，AE交BD于点F.(1)求证：△PAB≌△PCB；(2)在点P的运动过程中，APAE的值是否改变？若不变，求出它的值；若改变，请说明理由；(3)设DP＝x，当x为何值时，AE∥PC，并判断此时四边形PAFC的形状．第4题图5.正方形ABCD的边长为4，E是CB上的一个动点，过点D作DF⊥DE，交BA的延长线于点F，EF交对角线AC所在的直线于点M，DE交AC于点N.(1)求证：△ECD≌△FAD；(2)设CE＝x，当x为何值时，△AMF的面积为1；(3)随着点E在射线CB上的运动，NA·MC的值是否会发生变化？若不变，请求出NA·MC 的值，若变化，请说明理由．第5题图6.如图，在正方形ABCD中，AB＝17，点E是边BC上一个动点(点E不与点B，点C重合)，连接AE，过点B作BF⊥AE，垂足为点G，交DC于点F.(1)求证：△ABE≌△BCF；(2)过点E作EH⊥AE交∠DCM的平分线于点H，连接FH，判断四边形BFHE的形状，并说明理由；(3)在(2)的条件下，若sin∠EHC＝513，求线段FG的长．第6题图参考答案小题破大题1.证明：∵四边形ABCD 是矩形，∴∠C ＝90°，AD ＝BC ，AD ∥BC ，∴∠ADF ＝∠DEC ，∵BC ＝DE ，∴DE ＝AD ，在△ADF 和△DEC 中，＝DEADF ＝∠DEC ＝CE，∴△ADF ≌△DEC (SAS)，∴∠AFD ＝∠C ＝90°，∴AF ⊥DE .2.解：如解图，过点F 作FM ⊥BC 于点M .∵AE ＝BC ＝5，AB ＝4，∴BE ＝3，即CE ＝BC －BE ＝2，∵四边形ABCD 是矩形，且DF ⊥AE ，∴∠B ＝∠DFA ＝90°，∵∠BAF ＋∠FAD ＝∠FAD ＋∠FDA ＝90°，∴∠BAE ＝∠FDA ，又∵AE ＝BC ＝DA ，∴△ABE ≌△DFA (AAS)，∴BE ＝FA ＝3，∴EF ＝AE －FA ＝2，∵四边形ABCD 是矩形，∴AB ⊥BC ，∴AB ∥FM ，∴△ABE ∽△FME ，∴AB FM ＝AE FE ＝BE ME，∴4FM ＝52＝3ME。

2020年中考数学二轮专项——几何动态探究题类型一动点探究题1. 如图，在矩形ABCD中，AB＝4，AD＝6，点E，F分别是AB，BC边上的两动点，且EF＝2，点G 为EF的中点，点H为AD边上一动点，连接CH，GH，则GH＋CH的最小值为________．第1题图2. (2019锦江区二诊)如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点D是线段BC上一动点，连接AD，以AD为边作△ADE，使△ADE∽△ABC，则△ADE的最小面积与最大面积之比等于______．第2题图3. (2019金牛区二诊)如图，矩形ABCD中，AB＝5，BC＝7，点E是对角线AC上的动点，EH⊥AD，垂足为H，以EH为边作正方形EFQH，连接AF，则∠AFE的正弦值为________．第3题图4. 如图，两个全等的三角形△ABC和△DEF(点A、B分别与点D、E对应)，AB＝AC＝5，BC＝6，点E在BC边上从点B向点C移动(点E不与B、C重合)，在运动过程中，DE始终经过点A，EF与AC相交于点M，当△AEM是等腰三角形时，BE的长为__________．第4题图5. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝2，点P是边AB上一动点，过点P作BC的垂线交BC 于点D ，点F 与点B 关于直线PD 对称，连接AF ，当△AFC 是等腰三角形时，BD 的长为________．第5题图6. (2018成都黑白卷)如图，△ABC 内接于半径为2的⊙O ，∠ABC ＝45°，∠ACB ＝60°，点D 为AB ︵的中点，点M 、N 分别是CD 、AC 上的动点，则MA ＋MN 的最小值为________．第6题图7. 如图，在矩形ABCD 中，点E 是对角线AC 上的动点，连接BE ，MN 是BE 的垂直平分线，分别交AB 、BC 于点M 、N ，连接EM 、EN .过点E 作EF ⊥AD 于点F ，已知AB ＝1，BC ＝2.若△AEM 是直角三角形，则EF 的长为________．第7题图8. 如图，在矩形ABCD 中，AC 和BD 交于点O ，点E 是边BC 上的动点，连接EO 并延长交AD 于点F ，连接AE ，已知AB ＝1，BC ＝3，若△AEF 是等腰三角形，则DF 的长为________．第8题图9. 如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝2，BC ＝3，点M 是直线BC 上一动点，且∠CAM ＋∠CBA ＝45°，则BM 的长为________．第9题图10. (2019锦江区一诊)如图，矩形OABC的边OC在x轴上，边OA在y轴上，A点坐标为(0，2)．点D 是线段OC上的一个动点，连接AD，以AD为边作矩形ADEF，使边EF过点B，连接OF.当点D与点C 重合时，所作矩形ADEF的面积为6.在点D的运动过程中，当线段OF有最小值时，直线OF的解析式为________．第10题图类型二平移探究题1. 如图，矩形ABCD中，点E是BC边上一点，连接AE，将△ABE向右平移得到△DCF，连接AF.若四边形AEFD为菱形，AF＝45，BE∶EC＝3∶2，则AD长为________．第1题图2．如图，在Rt△AOB中，OA＝2，OB＝4，点E在OB上，且∠OAE＝∠OB A.将△AEO沿AO方向向右平移得到△A′E′O′，连接A′B、BE′.当A′B＋BE′取得最小值时，则EE′的长是________．第2题图3. 如图，在Rt△ABC中，AB＝AC＝2，∠A＝90°，D是AB延长线上一点，过点B在AD上方作射线BE，使得∠DBE＝45°.将△ABC沿射线BE平移，得到△A′B′C′，其中点A，B，C的对应点分别是A′，B′，C′，连接A′B，C′B，则A′B＋C′B的最小值是________ .第3题图4. (2018成都黑白卷)如图，在▱ABCD中，AB＝6，∠BAD＝45°，∠ABD＝75°，点E为线段BD边上一动点，连接AE，第一步：将△AED剪下平移到△BGC处；第二步：将△ABE剪下平移到△DCF处；第三步：将△BGC沿BC的中垂线翻转180°后得到△CG′B；第四步：将△CFD沿DC的中垂线翻转180°后得到△DF′C，连接F′G′；当点E在BD上移动时，F′G′的最小值为________．第4题图类型三旋转探究题1. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2，AC＝6，在AC上取一点D，使AD＝4，将线段AD 绕点A按顺时针方向旋转，点D的对应点是点P，连接BP，取BP的中点F，连接CF，在旋转过程中，CF的最大长度是________．第1题图2. 在Rt △ABC 中，∠ACB ＝90°，tan ∠BAC ＝12.点D 在边AC 上(不与A ，C 重合)，连接BD ，F 为BD 中点．若BC ＝6，点D 在边AC 的三等分点处，将线段AD 绕点A 旋转，点F 始终为BD 中点，则线段CF 长度的最大值是________．第2题图3. 如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝4，AC ＝3，点D ，E 分别是AB ，AC 的中点，点G ，F 在BC 边上(均不与端点重合)，DG ∥EF .将△BDG 绕点D 顺时针旋转180°，将△CEF 绕点E 逆时针旋转180°，拼成四边形MGFN ，则四边形MGFN 周长l 的取值范围是________．第3题图4. (2019高新区二诊)如图，△ABC ，△EFG 分别是边长为2和233的等边三角形，D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ，当△EFG 绕点D 旋转一周时，点M 经过的路径长为________．第4题图5. 如图，△ABC 和△CDE 都是等腰直角三角形(∠ACB ＝∠DCE ＝90°)．保持△ABC 固定不动，将△CDE 绕点C 顺时针旋转一周，连接AD 、AE 、BD ，直线AE 与BD 相交于点H ，点P 、M 、N 分别是AD 、AB 、DE 的中点，若AC ＝4，CD ＝2，则在旋转过程中，△PMN 的面积的最大值为________．第5题图类型四折叠探究题1. 如图，在矩形ABCD中，AB＝6，AD＝8，E是AB的中点，点F是BC边上的动点，将△EBF沿EF 所在的直线折叠到△EGF的位置，连接GD，则GD的最小值是______．第1题图2. 如图，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点分别在AB、BC上(含端点)，且AB＝6，BC＝10.设AE＝x，则x的最大值和最小值的和是______．第2题图3. (2019淮安)如图，在矩形ABCD中，AB＝3，BC＝2，H是AB的中点，将△CBH沿CH折叠，点B 落在矩形内点P处，连接AP，则tan∠HAP＝________．第3题图4. (2019金牛区二诊)如图，在等腰直角三角形ABC 中，∠ACB ＝90°，在△ABC 内有一点P ，已知∠1＝∠2＝∠3，将△BCP 以直线PC 为对称轴翻折，使点B 与点D 重合，PD 与AB 交于点E ，连接AD ，将△APD 的面积记为S 1，将△BPE 的面积记为S 2，则S 2S 1的值为________．第4题图5. 如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝6，点D 是边BC 的中点，点E 是边AB 上任意一点(点E 不与点B 重合)，沿DE 翻折△DBE ，使点B 落在点F 处，连接AF ，则线段AF 的长取最小值时，BF 的长为________．第5题图6. (2019都江堰区一诊)如图，已知在△ABC 中，AB ＝AC ，BC ＝8，D 、E 两点分别在边BC 、AB 上，将△ABC 沿着直线DE 翻折，点B 正好落在边AC 上的点M 处，并且AC ＝4AM ，设BD ＝m ，那么∠ACD 的正切值是______．(用含m 的代数式表示)第6题图7. (2019成华区二诊)已知一个矩形纸片ABCD ，AB ＝12，BC ＝6，点E 在BC 边上，将△CDE 沿DE 折叠，点C 落在C ′处，DC ′，EC ′分别交AB 于点F ，G ，若GE ＝GF ，则sin ∠CDE 的值为________．第7题图8. (2019成都黑白卷)如图，在平行四边形ABCD 中，点E 为AD 边的中点，将△ABE 沿BE 翻折，得到△FBE ，连接DF 并延长交BC 于点G ，若BE ＝AD ＝10，平行四边形ABCD 的面积为60，则FG ＝ ________．第8题图9. 如图，四边形ABCD是矩形纸片，AB＝2，对折矩形纸片ABCD，使AD与BC重合，折痕为EF，展开后再过点B折叠矩形纸片，使点A落在EF上的点N处，折痕BM与EF相交于点Q，再次展平，连接BN，MN，延长MN交BC于点G.P为线段BM上一动点，H是BN的中点，则PN＋PH的最小值是______．第9题图10. 如图，四边形纸片ABCD中，AD⊥AB，AB∥DC，AB＝6，AD＝CD＝3，点E，F分别在线段AB，AD上，将△AEF沿EF翻折，点A的落点记为P.当P落在四边形ABCD内部时，PD的最小值为______．第10题图参考答案类型一 动点探究题1. 9 【解析】如解图，由题意可知，点G 在以点B 为圆心，1为半径的14圆弧上运动．作点C 关于AD 的对称点C ′，连接C ′B 交AD 于点H ，交以点B 为圆心，1为半径的圆于点G ，由两点之间线段最短，此时C ′B 的值最小，最小值为BC 2＋CC ′2＝62＋82＝10，∵GH ＋CH ＝GH ＋C ′H ＝BC ′－BG ＝9，∴GH ＋CH 的最小值为9.第1题解图2. 925【解析】如解图，∵点D 为BC 边上一动点，∴AD 的最小值为AD 1，最大值为AD 2，∵在Rt △ABC 中，AB ＝3，BC ＝5，∴AC ＝52－32＝4，∵S △ABC ＝AB ·AC 2＝BC ·AD 12，解得AD 1＝125，∵AD 2为最大值4，∴最小面积与最大面积之比＝(125∶4)2＝925.第2题解图3. 513【解析】∵四边形EFQH 是正方形，∴∠EHA ＝90°，设HE ＝HQ ＝x ，AH ＝y ，∵四边形ABCD 是矩形，∴∠D ＝90°，∴HE ∥CD ，AD ∥EF ，∴△AHE ∽△ADC ，∴HE CD ＝AH AD ，即x 5＝y 7，设x ＝5k ，则y ＝7k ，∵四边形EFQH 是正方形，∴HQ ∥EF ，∴∠AFE ＝∠QAF ，在Rt △AQF 中，AF ＝（5k ）2＋（12k ）2＝13k ，∴sin ∠AFE ＝sin ∠QAF ＝QF AF ＝5k 13k ＝513. 4. 1或116【解析】∵∠AEF ＝∠B ＝∠C ，且∠AME ＞∠C ，∴∠AME ＞∠AEF ，∴AE ≠AM ；①当AE ＝EM 时，则△ABE ≌△ECM ，∴CE ＝AB ＝5，∴BE ＝BC －EC ＝6－5＝1；②当AM ＝EM 时，则∠MAE ＝∠MEA ，∴∠MAE ＋∠BAE ＝∠MEA ＋∠CEM ，即∠CAB ＝∠CEA ，又∵∠C ＝∠C ，∴△CAE ∽△CBA ，∴CE CA ＝AC BC ，∴CE ＝AC 2CB ＝256，∴BE ＝BC －EC ＝6－256＝116.综上所述，BE 的长是1或116. 5. 22或2－1 【解析】∵在Rt △ABC 中，AB ＝AC ＝2，∴BC ＝2 2.①当AF ＝CF 时，∠F AC ＝∠C ＝45°，∴∠AFC ＝90°，∴AF ⊥BC ，∴BF ＝CF ＝12BC ＝2，∵直线PD 垂直平分BF ，∴BD ＝12BF ＝22；②当CF ＝CA ＝2时，BF ＝BC －CF ＝22－2，∵直线PD 垂直平分BF ，∴BD ＝12BF ＝2－1；③当AF ＝AC 时，点F 与点B 重合(舍去)．综上所述，BD 的长为22或2－1. 6. 6 【解析】如解图，连接OA 、OC ，∵∠ABC ＝45°，OA ＝OC ＝2，∴∠AOC ＝90°，∴AC ＝2OA ＝22，在CB 上取一点A ′，使CA ′＝CA ，∵∠ACB ＝60°，∴△A ′CA 为等边三角形，过点A ′作A ′N ′⊥AC 于点N ′，∵点D 为AB ︵的中点，∴CD 为∠ACB 的平分线，∴点A 与点A ′关于直线CD 对称，连接A ′M ，∴A ′M＝AM ，即AM ＋MN ＝A ′M ＋MN ，根据直线外一点到直线上的所有连线中，垂线段最短，∴A ′N ′的长即为MA ＋MN 的最小值，∵A ′C ＝AC ＝22，∠ACB ＝60°，∴A ′N ′＝A ′C ·sin60°＝22×32＝6，即MA ＋MN 的最小值为 6.第6题解图7. 13或5－255【解析】如解图①，当∠AME ＝90°时，易知四边形AMEF 是矩形，且四边形BMEN 是正方形．∵ME ∥BC ，∴AM ME ＝AB BC ＝12，∴AM ＋BM ＝AM ＋2AM ＝1，则EF ＝AM ＝13；如解图②，当∠AEM ＝90°时，易证△AEM ∽△ABC ，∴AE ME ＝AB CB ＝12，∴ME ＝2AE ，则BM ＝ME ＝2AE ，AM ＝5AE ，∴AB ＝AM ＋BM ＝2AE ＋5AE ＝1，解得AE ＝5－2.又∵EF ∥CD ，∴EF AE ＝CD AC ＝15，∴EF ＝55(5－2)＝5－255.综上，若△AEM 是直角三角形，则EF 的长为13或5－255.图① 图②第7题解图 8. 43或1或1－63 【解析】如解图①，当AE ＝AF 时，设BE ＝DF ＝a ，则AF ＝AE ＝3－a .在Rt △ABE中，由AE 2＝AB 2＋BE 2得(3－a )2＝12＋a 2，解得a ＝43；如解图②，当AE ＝EF 时，设BE ＝DF ＝a ，则AF ＝3－a ，由AF ＝2BE ，得3－a ＝2a ，解得a ＝1；如解图③，当AF ＝EF 时，设BE ＝DF ＝a ，则AF ＝EF ＝3－a .由∠F AE ＝∠FEA ＝∠AEB 可得AB ＝AG ＝1，易知EG ＝BE ＝a ，∴FG ＝3－2a .在Rt △AFG 中，由AF 2＝AG 2＋FG 2得(3－a )2＝12＋(3－2a )2，解得a ＝1－63或a ＝1＋63(不符合题意，舍去)．综上，若△AEF 是等腰三角形，则DF 的长为43或1或1－63.图① 图② 图③第8题解图 9. 135或175【解析】①当M 在线段BC 上时，如解图，过点M 作MH ⊥AB 于点H ，∵∠CAM ＋∠CBA ＝45°，∠ACB ＝90°，∴∠BAM ＝45°.∵AC ＝2，BC ＝3，∴AB ＝13.∵Rt △BHM ∽Rt △BCA ，∴MH AC ＝BH BC＝BM BA .设MH ＝2x ，则2x 2＝BH 3＝BM 13，∴BH ＝3x ，BM ＝13x ，在Rt △AHM 中，AH ＝MH ＝2x ，∵AB ＝BH ＋AH ＝13，∴5x ＝13，x ＝135，BM ＝13x ＝135；②当M 在BC 延长线上时，如解图，则∠CAM ′＋∠CBA ＝45°，又∵∠CAM ＋ ∠CBA ＝45°，∴∠CAM ＝∠CAM ′.又∵AC ⊥BM ′，∴CM ＝CM ′.由①得CM ＝BC －BM ＝25，∴BM ′＝175；③当M 在CB 的延长线上时，不存在∠CAM ＋∠CBA ＝45°.综上所述，BM 的长为135或175.第9题解图10. y ＝113x 【解析】当点D 与点C 重合时，如解图，过F 作FG ⊥y 轴于点G ，连接OF ，∵S △ABC ＝12S 矩形 AOCB ＝12S 矩形ADEF ＝3，∴S 矩形AOCB ＝6，∵A 点坐标为(0，2)，∴OA ＝2，∴OC ＝3，∵∠F AD ＝90°，易得△FGA ∽△AOD ，∴FG AO ＝AG DO ，即FG AG ＝AO DO ＝23，设|FG |＝2a ，|AG |＝3a 由勾股定理得OF ＝OG 2＋FG 2＝（2＋3a ）2＋（2a ）2＝13a 2＋12a ＋4，令t ＝13a 2＋12a ＋4，∴t ＝13a 2＋12a ＋4＝13(a ＋613)2＋4，∴当a ＝－613时，t 有最小值．∴|FG |＝|2×(－613)|＝1213，|AG |＝|3×(－613)|＝1813，点F 的横坐标为1213，纵坐标为1813＋2＝4413，设OF 解析式为y ＝kx (k ≠0)，求得k ＝113，故函数的解析式为y ＝113x .第10题解图类型二 平移探究题1. 5 【解析】∵四边形AEFD 为菱形，∴AE ＝EF ，∵将△ABE 向右平移得到△DCF ，∴BE ＝CF ，AB ＝CD ，∵BE ∶EC ＝3∶2，设BE ＝3k ，EC ＝2k ，∴BC ＝EF ＝5k ，∴AE ＝5k ，∵四边形ABCD 是矩形，∴AD ＝BC ，AB ＝CD ，∠B ＝90°，∴AB ＝AE 2－BE 2＝4k ，∴AB 2＋BF 2＝AF 2，即(4k )2＋(8k )2＝(45)2，∴k ＝1，∴AD ＝BC ＝5.2. 67 【解析】∵OA ＝2，OB ＝4，∠OAE ＝∠OBA ，∠EOA ＝∠AOB ＝90°，∴△OAE ∽△OBA ，∴OA OB ＝OE OA ，即24＝OE 2，解得OE ＝1，如解图，过点A 作AB ′⊥OA ，并使AB ′＝BE ＝3.易证△AB ′A ′≌△EBE ′，∴B ′A ′＝BE ′，∴A ′B ＋BE ′＝A ′B ＋B ′A ′.当点B 、A ′、B ′在同一条直线上时，A ′B ＋B ′A ′最小，即此时A ′B ＋BE ′取得最小值．易证△AB ′A ′∽△OBA ′，∴AA ′OA ′＝AB ′OB ＝34，∴AA ′OA ＝37，AO ＝2，∴AA ′＝37×2＝67，∴EE ′＝AA ′＝67.第2题解图3. 25 【解析】如解图，作射线CC ′，AA ′，AA ′交BC ′于点O ，过点C 作CF ∥AB 交AA ′于F ，连接BF ，由平移性质得AA ′∥BE ∥CC ′，∵∠EBD ＝45°，∴∠F AB ＝∠C ′CF ＝45°，∵Rt △ABC 中，AB ＝AC ，∠CAB ＝90°，∴易得四边形ABFC 是正方形，∴∠FCB ＝45°，∴∠C ′CB ＝90°，∵A ′C ′＝BF ，∠A ′OC ′＝∠FOB ，∠C ′A ′O ＝∠BFO ＝45°，∴△A ′OC ′≌△FOB ，∴BO ＝C ′O ，∴CO ＝C ′O ＝BO ，延长FC 到G ，使得CG ＝CF ，连接A ′G ，则CO 是△FGA ′的中位线，∴A ′G ＝2CO ＝BC ′，∴BC ′＋BA ′＝BA ′＋A ′G ，∴当点B 、A ′、G 在同一条直线上时，BG 取得最小值，那A ′B ＋C ′B 取得最小值．∵在Rt △GFB 中，BF ＝AC ＝2，FG ＝2CF ＝4，∴BG ＝25，∴A ′B ＋C ′B 的最小值为2 5.第3题解图 4. 32＋62 【解析】由翻转可得△BG ′C ≌△CGB ≌△DEA ，∴CG ′＝AE ，∠BCG ′＝EAD ，同理可得CF ′＝AE ，∠DCF ′＝∠BAE ，∴∠BCG ′＋∠DCF ′＝∠EAD ＋∠BAE ＝45°，在平行四边形ABCD 中，∠BAD ＝∠BCD ＝45°，∴∠G ′CF ′＝∠G ′CB ＋∠BCD ＋∠DCF ′＝90°.∴△G ′CF ′为等腰直角三角形，由勾股定理可得F ′G ′＝2CG ′＝2AE ，当AE ⊥BD 时，AE 的值最小，即此时F ′G ′的值最小，∵△AED ≌△BGC ，△ABE ≌△DCF ，且∠AED ＝∠AEB ＝90°，∴∠BGC ＝∠AED ＝90°，∠DFC ＝∠AEB ＝90°，∴BG ∥DF ，又∵BG ＝AE ＝DF ，∴四边形BGFD 为矩形，如解图，过点B 作BM ⊥AD 于点M ，在Rt △ABM 中，∵∠BAM ＝∠ABM ＝45°，AB ＝6，∴AM ＝BM ＝6×22＝3，∵∠ABD ＝75°，∴∠DBM ＝∠ABD －∠ABM ＝75°－45°＝30°，∴∠ADB ＝60°，∴在Rt △DBM 中，BD ＝BM sin60°＝2，MD ＝BM tan60°＝1，∴AD ＝AM ＋MD ＝1＋3，∵S △BAD ＝12BD ·AE ＝12AD ·BM ，即2AE ＝(1＋3)×3.∴AE ＝3＋32，∴F ′G ′的最小值为32＋62.第4题解图类型三 旋转探究题1. 10＋2 【解析】如解图，取AB 的中点M ，连接MF 和CM ，∵在Rt △ABC 中，∠ACB ＝90°，AC＝6，BC ＝2，∴AB ＝AC 2＋BC 2＝210.∵M 为AB 中点，∴CM ＝12AB ＝10，∵将线段AD 绕点A 按顺时针方向旋转，点D 的对应点是点P ，∴AP ＝AD ＝4，∵M 为AB 中点，F 为BP 中点，∴FM ＝12AP ＝2.当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大，此时CF ＝CM ＋FM ＝10＋2.第1题解图2. 4＋35 【解析】如解图①，当AD ＝13AC 时，取AB 的中点M ，连接MF 和CM ，∵∠ACB ＝90°，tan ∠BAC ＝12，且BC ＝6，∴AC ＝12，AB ＝6 5.∵M 为AB 中点，∴CM ＝35，∵AD ＝13AC ，∴AD ＝4.∵M 为AB 中点，F 为BD 中点，∴FM ＝12AD ＝2，∴当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大，此时CF ＝CM ＋FM ＝2＋35；如解图②，当AD ＝23AC 时，取AB 的中点M ，连接MF 和CM ，同理可得CF 的最大值为4＋35，综上，线段CF 的长度的最大值为4＋3 5.第2题解图3. 7＜l ＜17 【解析】如解图，过点A 作AH ∥DG ，∵DG ∥EF ，∴DG ∥EF ∥AH ，∵点D 为AB 的中点，将△BDG 绕点D 顺时针旋转180°后到△ADM 的位置，∴BG ＝AM ，MG ∥AH 且MG ＝AH ，同理CF ＝AN ，NF ∥AH 且NF ＝AH ，∴四边形MGFN 是平行四边形，∴MN ＝GF ＝AM ＋AN ＝BG ＋CF .在Rt △ABC 中，∵AB ＝4，AC ＝3，∴由勾股定理得BC ＝5，即MN ＋GF ＝5，在△ABH 中，由三角形的三边关系可得AB －BH ＜AH ＜AB ＋BH ，同理AC －CH ＜AH ＜AC ＋CH ，两式相加得AB ＋AC －(BH ＋CH )＜2AH ＜AB ＋AC ＋(BH ＋CH )，∴4＋3－5＜2AH ＜4＋3＋5，即2＜2AH ＜12，l ＝MG ＋GF ＋NF ＋MN ＝2AH ＋BC ，∵BC ＝5，2＜2AH ＜12，∴7＜l ＜17.第3题解图4. 4π3【解析】如解图，连接AD 、DG .∵△ABC 和△EFG 均是等边三角形，D 分别是BC 和EF 的中点，∴BD ＝CD ，DE ＝DF ，∴AD ⊥BC ，GD ⊥EF ，∴∠ADC ＝∠GDF ＝90°，∴∠ADG ＝∠CDF ，∵AD CD＝DG DF＝tan60°，∴△ADG ∽△CDF ，∴∠DAG ＝∠DCF ，∴∠AMC ＝90°，∴点M 的轨迹是以AC 为直径的圆，且来回共两个三分之一圆，∴点M 运动的路径长为4π3.第4题解图5. 92【解析】∵△ABC 和△CDE 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，∴AC ＝BC ，CE ＝CD ，∠ACB ＋∠BCE ＝∠BCE ＋∠ECD ，∴∠ACE ＝∠BCD ，∴△ACE ≌△BCD ，∴AE ＝BD ，∠CAE ＝∠CBD ，∴∠HBA ＋∠HAB ＝∠HBC ＋∠CBA ＋∠HAB ＝∠CBA ＋∠CAB ＝90°，∴BD ⊥AE .∵P ，M 分别是AD ，AB的中点，∴PM ∥BD ，且PM ＝12BD ，同理，PN ∥AE ，且PN ＝12AE ，∴PM ⊥PN ，PM ＝PN ，∴△PMN 是等腰直角三角形，∴S △PMN ＝12PM 2＝18BD 2，∴当BD 最大时，△PMN 的面积最大，∵△CDE 绕点C 旋转，∴点D 在以C 为圆心，CD 为半径的圆上，∴当点D 在BC 的延长线上时，BD 最大，此时BD ＝AC ＋CD ＝6，∴△PMN 面积的最大值为18×62＝92.第5题解图类型四 折叠探究题1. 73－3 【解析】如解图，由EG ＝EB ＝3，可得当点G 在DE 上时，此时GD 的值最小，根据折叠的性质，△EBF ≌△EGF ，∴EG ⊥GF ，EG ＝EB ，∵E 是AB 边的中点，AB ＝6，∴AE ＝EG ＝3，∵AD ＝8，∴Rt △ADE 中，DE ＝82＋32＝73，∴GD ＝73－3.第1题解图2. 8 【解析】设折痕为PQ ，点P 在AB 边上，点Q 在BC 边上．如解图①，当点Q 与点C 重合时，AE 最小，根据翻折对称性可得EC ＝BC ＝10，在Rt △CDE 中，CE 2＝ED 2＋CD 2，即102＝(10－AE )2＋62，解得AE ＝2，即x ＝2；如解图②，当点P 与点A 重合时，AE 最大，根据翻折对称性可得AE ＝AB ＝6，即x ＝6，所以x 的最大值和最小值的和是8.图① 图②第2题解图 3. 43 【解析】如解图，连接PB 交CH 于点E .在Rt △BCH 中，BC ＝2，BH ＝12AB ＝32，∵△PCH 是由△BCH 折叠得到的，∴PB ⊥CH ，BE ＝PE ，PH ＝HB .∴∠HPB ＝∠HBP .∵AH ＝BH ，∴AH ＝PH .∴∠P AH ＝∠APH .∴∠APH ＋∠BPH ＝12(∠P AB ＋∠APB ＋∠ABP )＝90°.∴AP ∥CH ，∴tan ∠HAP ＝tan ∠BHC ＝BC BH ＝43.第3题解图 4. 12 【解析】如解图，连接BD ，延长CP 交BD 于点F ，由翻折可知CF ⊥BD ，BF ＝DF ，∠BPF ＝∠DPF ，∵∠1＝∠2＝∠3，△ABC 是等腰直角三角形，∴∠1＋∠ACP ＝∠2＋∠ACP ＝90°，∠2＋∠PBC ＝∠3＋∠PBC ＝45°，∴∠APC ＝90°，∠DPF ＝45°，DF ＝FB ＝PF ，∴△APC ≌△CFB ，∴AP ＝CF ，CP＝BF ＝PF ，∴AP ＝BD ，∴四边形ADBP 是平行四边形，∴S 2S 1＝12.第4题解图5. 1255【解析】由题意得：DF ＝DB ，∴点F 在以D 为圆心，BD 长为半径的圆上，如解图，连接AD 交⊙D 于点F .此时AF 的值最小，∵点D 是边BC 的中点，∴CD ＝BD ＝3，由勾股定理得：AD 2＝AC 2＋CD 2，∵AC ＝4，∴AD ＝5，∵FD ＝3，∴F A ＝5－3＝2，即线段AF 长的最小值是2，连接BF ，过点F 作FH ⊥BC 于点H ，∵∠ACB ＝90°，∴FH ∥AC ，∴△DFH ∽△DAC ，∴DF DA ＝DH DC ＝HF CA ，即35＝DH 3＝HF 4，∴HF ＝125，DH ＝95，∴BH ＝245，∴BF ＝BH 2＋HF 2＝1255.第5题解图6. 10m －253【解析】如解图，作AH ⊥BC 于点H ，MG ⊥BC 于点G ，连接EM 、MD 、BM ，∵AB ＝AC ，BC ＝8，AH ⊥BC ，∴CH ＝4，∵AC ＝4AM ，∴CM ∶AC ＝3∶4，∵AH ∥MG ，∴CG HC ＝CM AC ＝34，即CG 4＝34，解得CG ＝3，∴BG ＝5，∴DG ＝m －5，由翻折的性质可知MD ＝BD ＝m ，在Rt △MGD 中，依据勾股定理可知：MG ＝MD 2－GD 2＝m 2－（m －5）2＝10m －25，∴tan ∠ACD ＝tan ∠ACG ＝MG CG ＝10m －253.第6题解图 7. 1010 【解析】设CE ＝x ，则BE ＝6－x .根据折叠的对称性可知DC ′＝DC ＝12，C ′E ＝CE ＝x .在△FC ′G 和△EBG 中，⎩⎪⎨⎪⎧∠C ′＝∠B ＝90°∠FGC ′＝∠EGB GF ＝GE，∴△FC ′G ≌△EBG (AAS)．∴FC ′＝BE ＝6－x .∴DF ＝12－(6－x )＝6＋x .连接FE ，在Rt △FC ′E 和Rt △EBF 中，⎩⎪⎨⎪⎧FC ′＝BE EF ＝EF，∴Rt △FC ′E ≌Rt △EBF (HL)．∴FB ＝EC ′＝x .∴AF ＝12－x .在Rt △ADF 中，AD 2＋AF 2＝DF 2，即36＋(12－x )2＝(6＋x )2，解得x ＝4.∴CE ＝4.在Rt △CDE 中，DE 2＝DC 2＋CE 2，则DE ＝410.∴sin ∠CDE ＝CE DE ＝1010. 8. 2 【解析】∵将△ABE 沿BE 翻折，得到△FBE ，∴AE ＝EF ，∠AEB ＝∠FEB ，∴∠AEB ＝12(180°－∠DEF )，∵E 为AD 边的中点，∴AE ＝DE ，∴DE ＝EF ，∴∠EDF ＝∠EFD ，∴∠EDF ＝12(180°－∠DEF )，∴∠AEB ＝∠EDF ，∴BE ∥DG ，∵四边形ABCD 是平行四边形，∴DE ∥BG ，∴四边形BEDG 为平行四边形，∴DE ＝BG ，DG ＝BE ＝10，∵四边形ABCD 是平行四边形，且面积等于60，AE ＝DE ，∴S △ABE ＝14S ▱ABCD ＝15，如解图，连接AF 交BE 于H ，则AH ⊥BE ，AH ＝HF ，∵BE ＝10，∴AH ＝3，∴AF ＝6，∵BE ∥DG ，∴AF ⊥DG ，∴DF ＝AD 2－AF 2＝8，∴FG ＝DG －FD ＝2.第8题解图9. 3 【解析】如解图，连接AN ，∵∠ABM ＝∠MBN ＝30°，∠BNM ＝∠BAM ＝90°，∴∠BMG ＝∠BNM －∠MBN ＝90°－30°＝60°，∴∠MBG ＝∠ABG －∠ABM ＝90°－30°＝60°，∴∠BGM ＝180°－60°－60°＝60°，∴∠MBG ＝∠BMG ＝∠BGM ＝60°，∴△BMG 为等边三角形，∵点N 是MG 的中点，∴BN ⊥MG ，∵BG＝BM ＝AB cos ∠ABM ＝433，∴BN ＝BG ·sin60°＝433×32＝2，根据题意易知E 点和H 点关于BM 对称，∴PH ＝PE ，∴P 与Q 重合时，PN ＋PH 的值最小，此时PN ＋PH ＝PN ＋PE ＝EN ，∵EN ＝BN 2－BE 2＝22－（2÷2）2＝3，∴PN ＋PH ＝3，∴PN ＋PH 的最小值是 3.第9题解图10. 35－6【解析】如解图①，设A的对应点为P1，连接ED，过P1作PP1⊥ED于点P，∴在Rt△P1PD 中，DP1＞DP，∴当点A的对应点P落在线段ED上时，此时PD有最小值，即当EP取最大值时，PD有最小值，而点E在线段AB上，∴当点E与点B重合时，如解图②，即EP最大，从而此时PD取得最小值，在Rt△ADB中，BD＝AB2＋AD2＝35，∵PB＝AB＝6，∴DP＝BD－BP＝35－6.图①图②第10题解图。