当前位置：文档之家 › 堆芯一维中子扩散方程的数值解法(通用型)

堆芯一维中子扩散方程的数值解法(通用型)

  • 格式：pdf
  • 大小：44.77 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

CANDU反应堆物理数值计算技术

CANDU反应堆物理数值计算技术

RFSP 程序中使用的是 POWDERPUFS-V 的栅元程序 。 2． 超栅元计算
由 于 CANDU 反 应 堆 的 堆 芯 内 部 存 在 的 一 系 列 反 应 性 控制装置和结构材料与燃 料 通道 成 正 交 垂 直方 位 ， 因 此 在对 基 本 栅 元 计 算 时 ，无 法 考 虑 它 们 的 影 响 ，必 须 建 立 一 种 反 应 堆 基 本 单 元 模 型 ：使 用 笛 卡 儿 坐 标 ，采 用 一 种 超 栅 元 计 算 模 型 （ 参见图 2 ）。 该模型由基本栅元和垂直于栅元的反应性装 置组成 ， 然后计算反应性 装 置 对最 接 近 的 相邻 网 格 区 域中 基 本的栅元特性的改变 （ 增 加 的 截 面 ）， 最 后 得 到 反应 性 装 置 相 应对基本栅元造成的增量截 面 ， 用 于 堆 芯模 拟 中 的 反应 性 装 置的反应性计算 。 栅元的综合截面＝栅元的基本截面＋反应性设备增量截面 计算程序 ：MUTICELL （ 扩散程序 ） 此外 ，DRAGON 也可计算反应性装置的反应性 。
1. RFSP 中的节点模型 RFSP 程序采用有限差分法求解中子扩散方程 。 首先 ，要引
入一系列网格点将堆芯离散化 ，这里使用全堆芯 48×32×40（X,Y,
Z）网格模型 。 所有的反应性控制装置和结构材料都被包含在模
型中 ，诸如 ：调节棒和调节棒导向管 、停堆棒和停堆棒导向管 、轻 水区域控制器、2 号停堆系统的毒物喷嘴等。
量分布：
●求解两群三维的有限差分中子扩散方程 ●使用通量绘图的方法进行谐波拟合 RFSP 能进行燃料管理计算，按照给定的时间步长和该时间
段的换料通道 ，模拟反应堆的运行历史 ，这就是 RFSP 命名的由 来。
赞 Fi(t)， 所以 堆芯棒束 i 的燃耗为 ωi(t) ， 棒束所在位置的通量为 Φ 赞 Fi(t)△t。 然后调用 当前堆芯中每个棒束的燃耗 ωi(t+△t)=ωi(t)+Φ

第四章：均匀反应堆的临界理论

第四章：均匀反应堆的临界理论

一、反射层节省
在芯部包有反射层以后，芯部临界大小尺寸的减少量通常可以用
反射层节省 来表示。 对于圆柱形反应堆，反射层节省通常分别用径向和轴向的反射层节 省来表示，即
反射层对临界的影响可以用反射层节省这个量来表示。它表示反应堆由 于加上反射层所引起的临界尺寸的减少。因此，可以把有反射层反应堆 的几何曲率用芯部外形尺寸增大2δ 后的等效裸堆的几何曲率来表示。
1 2 2 1 L Bg
不泄漏几率
k k P
1
L
1
再次说明，k1是有效增殖系数
1 B: PL 2 2 1 L Bg
反应堆的中子泄漏不仅与扩散长度有关，而且与
几何曲率有关。从前面平板状反应堆的例子中可以看 到，当反应堆体积增大时，Bg2就减小，因而正如所预 料的那样，不泄漏几率也就增大。 同样，扩散长度 L 愈大，意味着中子自产生到 被吸收所穿行的距离也愈大，因而从反应堆中泄漏出 去的几率也就增大，不泄漏几率PL就要减小
2 对于给定的曲率 Bg ，对芯部半径为 R0 的球形裸堆有
2 Bg R0
2
R B g
2 0

2
设具有反射层时芯部的临界半径为R，则


Bg
R

R
对有反射层的球形堆有
2 Bg (
)2
可以把有反射层的球形堆的几何曲率用一个尺寸等于 R 的等效 裸堆的几何曲率来表示
芯部
反 射 层 反 射 层
k<1，调整k∞使 其临界
① 带有反射层的球形堆
考虑一个芯部半径为R，带有厚度为T（包括外推距离在内）的反射层 的球形堆。采用球坐标系，并把坐标远点取在球心上。根据中子通量 密度在堆内处处为有限值的条件，得到芯部方程

核反应堆物理基础第3章

核反应堆物理基础第3章

中子从dV内泄漏的总数应等于以上三项之和，这样，单位时间， 单位体积泄漏出去的中子数
L D D D x x y y z z
（3-15）
若护散系数D与空间位置无关，那么便得到
u Ae
r / L
Ce
r/L
因此
er / L er / L (r ) A C r r
式中A，C为两个待定常数，可以由边界条件确定 C必须为零，否则当r趋于无限大时，φ便变为无限大 常数A由中子源条件求出
r 0
J (r ) D
d 1 1 DA 2 e r / L dr rL r
s dA 2 2 J dA (r )e s r cos sin drd d 4 0 0 0
z
s dA 2 2 J dA (r )e s r cos sin drd d 4 0 0 0
z
其中， J z
得
A
SL 2D
最后得中子通量密度
( x)
SL x / L e 2D
根据对称性，只需将式中的x用 x 代替，源平面 左边介质内的中子通量密度即可得到。
第三章 单速中子扩散
§3.1 单速中子扩散方程
§3.2
§3.3
非增殖介质内中子扩散方程的解 扩散长度
§3.4 与能量相关的中子扩散方程

基本概念
中子角密度:
n(t , r, v, )
中子角通量密度:
n(t , r, v, )v (t , r, v, )
稳态情况
中子角密度: 中子角通量密度: 一、中子流密度:
如果之间有一夹角

第三章 中子扩散理论

第三章 中子扩散理论
J z (r ) J z (r ) J z (r )
s (r )
3 z
J z (r ) 叫做z方向的中子流密度或净中子流密度，若dA的取向
与x轴垂直，沿着x方向穿过dA平面单位面积净中子数Jx为
J x (r )
s ( r )
3 x
同样，沿着y方向穿过dA平面单位面积净中子数Jy为
推导中并没有考虑中子源的贡献，中子流密度的贡献只 是来自中子与介质核的散射碰撞 在强中子源两三个平均自由程的区域内，斐克定律不 适用。
3.2 非增殖介质内中子扩散方程的解
稳态单能的中子扩散方程
D2 (r ) a (r ) S (r ) 0
无源情况下，即除中子源所在的位置以外的无源区域,扩散 方程有以下形式: 1 D (r ) 2 2 2 2 L ( r ) 0 (r ) (r ) 0 或 k2 L2
第三章 中子扩散理论
中子在介质中的输运过程中 的运动状态由位置矢量r(x,y,z), 能量 E, 和运动方向Ω表示。 Ω通过极角θ 和方位角φ 来 表示
dS r 2 sin dd d 2 sin dd 2 r r
中子角密度函数n(r,E, Ω)定义： 方向 Ω的表示 在r处单位体积内和能量为E的 单位能量间隔内，运动方向为 Ω的单位立体角内的中子数目。 中子角通量密度定义为: ( r, E, ) n( r , E, )v( E ) 对中子角密度和中子角通量密度积分便可得到与运动方向无 关的标量中子密度和标量中子通量密度
4

tr d
6 dx
0
d dx
x 0
30 2tr
应用输运理论和扩散理论的 外推距离求得的扩散方程的解

一维对流扩散方程的数值解法

一维对流扩散方程的数值解法

一维对流扩散方程的数值解法对流-扩散方程是守恒定律控制方程的一种模型方程，它既是能量方程的表示形式，同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。

因此，以对流-扩散方程为例，来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。

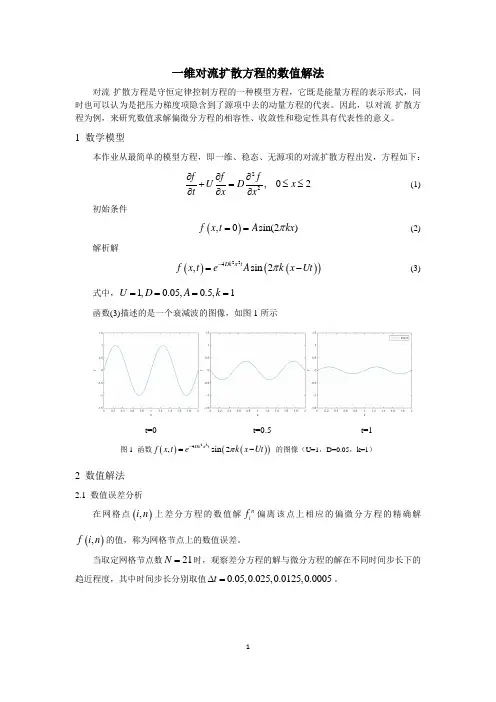
1 数学模型本作业从最简单的模型方程，即一维、稳态、无源项的对流扩散方程出发，方程如下： 22, 02f f fU D x t x x∂∂∂+=≤≤∂∂∂ (1)初始条件 (),0sin(2)f x t A kx π==(2)解析解()()()224,sin 2Dk tf x t eA k x Ut ππ-=-(3)式中，1,0.05,0.5,1U D A k ====函数(3)描述的是一个衰减波的图像，如图1所示t=0 t=0.5 t=1图1 函数()()()224,sin 2Dk tf x t ek x Ut ππ-=- 的图像（U=1，D=0.05，k=1）2 数值解法2.1 数值误差分析在网格点(),i n 上差分方程的数值解ni f 偏离该点上相应的偏微分方程的精确解(),f i n 的值，称为网格节点上的数值误差。

当取定网格节点数21N =时，观察差分方程的解与微分方程的解在不同时间步长下的趋近程度，其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。

（a ）21,0.05N t =∆= （b ）21,0.025N t =∆=（c ）21,0.0125N t =∆= （d ）201,0.0005N t =∆=图2 数值误差随步长的变化情况从图2的(a)~(d)可以定性的看出，数值误差与步长的大小有关。

在满足稳定性条件的前提下，数值误差随着时间步长的减小而减小，同时，图（d ）表示增大网格的分辨率也有助于减小网格误差。

为了对数值误差有一个定量的认识，接下来取定时间步长为0.0005t ∆=，分别算出11,21,41,61,81,101,121,161N =时，指标E =1所示。

第3章反应堆物理设计计算

第3章反应堆物理设计计算

常用的反射层材料有：水、重水、石墨和铍等。
19
反射层节省
在芯部包有反射层以后，芯部临界大小的减少量称为反射层 节省，用δ表示。 对圆柱形反应堆： 径向反射层 节省：
2.405 2 2 Bc Br2 Bz R H eff eff
2 2
r Reff R

29
压水堆的非均匀化计算
（1）堆芯最基本单元的栅元均匀化。 空间均匀化：将栅元等效成简单的一维圆柱，能 量和能群简并，采用多群近似。 计算方法：输运方程→碰撞概率法；Sn直接离散 →中子通量按能量的分布φn,i。 （2）利用栅元均匀化结果对燃料组件进行均匀化、并 群计算。 计算方法：穿透概率法、直接离散。按通量-体积 权重，并群求出组件的均匀化少群常数。 （3）利用得到的少群常数，做全堆芯的扩散计算， 求出keff和功率、中子通量分布。 计算方法：有限差分、节块法。 少群常数并非不变，受燃料密度影响很大。 30
(r, z) r R 0
z
z 0
(r , z )
z
H 2
0
0
r
r 0
0
8
有限高圆柱形均匀裸堆

几何曲率：
2 B2 R H

临界时其高度H与半径R须满足：
B2 k 1 2.405 2 ( ) ( )2 R H L2
中子通量密度分布不均匀系数

中子通量密度分布不均匀系数定义为堆芯最大热中子通量密 度与堆芯平均热中子通量密度的比值，即：
max KV
最大中子通量密度 平均中子通量密度
(r, z)dv 1 (r, z)dv V dv
V V V

哈尔滨工业大学计算传热学第四章扩散方程的数值解法及其应用资料重点

哈尔滨工业大学计算传热学第四章扩散方程的数值解法及其应用资料重点

1
y
xw
TP
aETE
aNTN
aSTS
1
y
xw
Tf
Scxy
kB
kB
所以对第三类边界条件不仅有附加常数源项，而且还有 附加源项的斜率项
aPTP aETE aNTN aSTS (Sc•ad Sc )xy
aP aE 0 aN aS (Sp•ad Sp )xy
Sp•ad
y xy
a)算术平均线性分布
ke
kp
xe+ xe
kE
xe xe
e
••
•
W
Pxe xe E
xe
b)调和平均
qe
TE TP
xe
ke
TE Te
xe
kE
Te Tp
xe
kp
TE
xe
kE
TP
xe
kP
ke
kP kExe xek p xekE
当 xe xe
kP kE
算术平均
ke
kP
kE 2
kP 2
第四章 扩散方程的数值解法及其应用
§4.1 一维稳态导热
1 • d [kF(x) dT ] S 0
F (x) dx
dx
F(x)：与坐标系和截面形状有关的计算因子
S：内热源。
w
e
△x
e d
dT
[kF (x) ]dx
w dx
dx
e
F (x) • Sdx 0
w
•
W
xw
•
P
xe
•
E
keFe
W PE
ap
Fe k e
xe

反应堆物理数值计算

反应堆物理数值计算

核科学与技术学院
25
Harbin Engineering University
四个节块共32个系数，需32个方程。 1. 四个相邻节块平均中子通量密度，可建立四个方程。
2. 节块间平均偏通通量密，可建立四个方程。
核科学与技术学院
26
Harbin Engineering University
3. 交界面上平均偏中子通量密度对应的净中子流，确定 四个方程
从而得
（5-158）
（5-159）
核科学与技术学院 12
Harbin Engineering University
则（5-159）式可表示为
（5-161）
（5-162）
核科学与技术学院
13
Harbin Engineering University
比较上述两式，可知
（5-163）
上式结合双曲函数定义及（5-135）式通过更复杂的运算， 由（5-138）及（5-140）可得（5-145）式，其系数矩阵为
4. 节块界面偏中子通量连续，确定四个方程
核科学与技术学院
27
Harbin Engineering University
5. 交界面上偏净中子流连续，确定四个方程
核科学与技术学院
28
Harbin Engineering University
6. 角点处连续性条件，确定七个方程。
核科学与技术学院
29
令 则
同理可得v、w方向上类似的横向积分中子通量密度方程。 （5-177）式是非齐次方程，对泄漏项源，采用二次函 数逼近。
核科学与技术学院
18
Harbin Engineering University

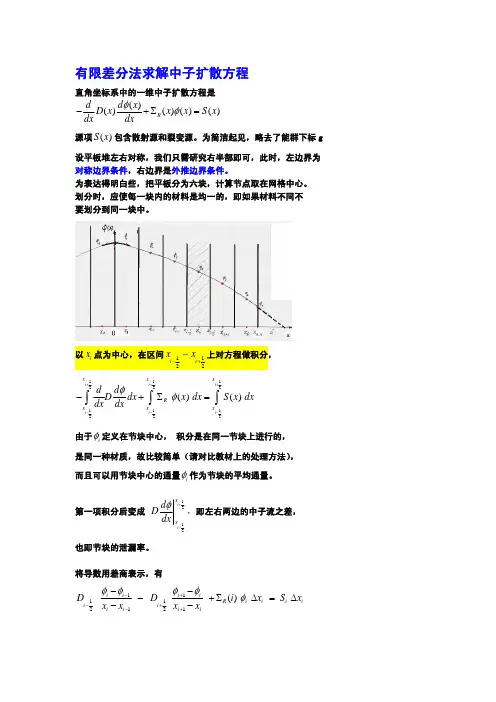
一维平板有限差分法

一维平板有限差分法

有限差分法求解中子扩散方程 直角坐标系中的一维中子扩散方程是()()()()()R d d x D x x x S x dx dxφφ−+Σ= 源项()S x 包含散射源和裂变源。

为简洁起见，略去了能群下标g 设平板堆左右对称，我们只需研究右半部即可，此时，左边界为 对称边界条件，右边界是外推边界条件。

为表达得明白些，把平板分为六块，计算节点取在网格中心。

划分时，应使每一块内的材料是均一的，即如果材料不同不要划分到同一块中。

111222111222 () () i i i i i i x xx R x x x d d D dx x dx S x dx dx dx φφ+++−−−−+Σ=∫∫∫ 由于i φ定义在节块中心， 积分是在同一节块上进行的，是同一种材质，故比较简单（请对比教材上的处理方法）， 而且可以用节块中心的通量i φ作为节块的平均通量。

第一项积分后变成 1212i i x x d D dxφ+−，即左右两边的中子流之差， 也即节块的泄漏率。

将导数用差商表示，有 11111122() i i i i R i i i i i i i i i i D D i x S x x x x x φφφφφ−+−+−+−−−+ΣΔ=Δ−−其中 1122i i i x xx +−Δ=− 扩散系数12 i D −和 12 i D +的取值点，正好是两个节块的交界面，故D 应该取两个相邻节块的某种平均值（可以取为简单的算术 平均值，也可以更精细地加以处理求出等效的平均值）。

上式经整理得到：11122211111211 () + i i i i R i i i i i i i i i i i i i i D D D i x x x x x x x D S x x x φφφ−−+−−−++++−⎡⎤⎡⎤⎢⎥⎢⎥+++ΣΔ⎢⎥⎢⎥−−−⎢⎥⎢⎥⎣⎦⎣⎦−⎡⎤⎢⎥=Δ⎢⎥−⎢⎥⎣⎦令112 / ()i i i i a Dx x −−=−− 112, / ()i i i i i R i i ii i ic D x x b a cd S x ++=−−=Σ−−=Δ 则差分方程可以写成i-1 i i+1 i i i i a b c d φφφ++=这4个系数都是由材料的核截面以及网格尺寸决定的，当堆的材料、 尺寸和网格划分情况都确定后，它们都是已知常数。

第3章-中子扩散理论

第3章-中子扩散理论
第3章 中子扩散理论
主讲：马续波
maxb@
华北电力大学核科学与工程学院
1
堆内链式裂变反应过程实质：中子在介质内不断的产生、
运动和消亡的过程
反应堆物理的核心问题之一：确定堆内中子通量密度按空 间和能量的分布 第二章通过求解中子慢化方程，解决了中子通量密度按能 量的分布， φ (E)～ E，即中子能谱
19
场论知识
• 数量场φ的梯度
• 向量场 J 的散度 div J J
算子
grad
i j k x y z 2 2 2 x y z
2 2 2 2
20
2、菲克定律的推导
– 确定性方法(Deterministic method)
• 数学模型用数学物理方程表示，然后采用数值方法求解 • 优点：计算快速，相对精确等

• 缺点：模型简化，大型多维问题需大量计算时间及存储空间等
• 典型方法：离散纵标法（SN） – 非确定性方法(蒙特卡罗方法，Monte Carlo method)： • 基于统计理论，通过计算机的随机模拟来跟踪中子在介质中的运动 • 优点：计算精确，可以模拟三维复杂几何模型 • 缺点：对于深穿透问题（Deep-penetration），计算非常耗时
6
2、中子状态的描述
中子状态: 位置矢量 r (x,y,z)、能量E(或运 动速度v)、运动方向、 时间 （7个）
：单位矢量，模等 于1，方向表示中子的 运动方向，通过极角 和方位角来表示
7
中子角密度：在r处单位体积内和能量为E的单位能量间
隔内，运动方向为 的单位立体角内的中子数目。
由于中子与原子核的无规则碰撞，中子在介质内的运动是一种 杂乱无章的具有统计性质的运动，即初始在堆内某一位置具有某 种能量及某一运动方向的中子，在稍晚些时候，将运动到堆内另 一位置以另一能量和另一运动方向出现。这一现象称为中子在介 质内的输运过程（Transport）。描述这一过程的精确方程为玻 尔兹曼输运方程（Boltzmann equation）。 输运理论：微观粒子(中子、光子、电子、离子和分子等)在介 质中的迁移统计规律的数学理论；不是研究个别粒子的运动，而

第4章 扩散方程数值解法

第4章 扩散方程数值解法
2013-7-10
e
E N-1 N
第4章 扩散方程的数值解法及应用
8
aPTP aETE aW TW b
aE Ae ( x) / (d x e P (d x e E

从i=2到N-1，遍历所有控制容积，得线性代数方程组：
(

aW Aw ( x) / (d x w P (d x e W
aPP aEE aW W b
aE e Ae / (d x e , aW w Aw / (d x w
aP aW aE SP AP Dx , b Sc AP Dx
到此为止，只剩下界面物性λe，λw取值问题了。
2013-7-10 第4章 扩散方程的数值解法及应用 4
MODULE CASEDATA USE PARAM REAL H,D REAL*8 GAM(NI),SP(NI),SC(NI),AF(NI) END MODULE
SUBROUTINE GRID USE MESH ! ----------控制容积界面位置-----------DX=XL/(N-2.) ! 控制容积的宽度 XU(2)=0 ! The first CV面编号为2 DO I=3,N XU(I)=XU(I-1)+DX ENDDO !------- 节点坐标计算 -----------X(1)=XU(2) DO I=2,N-1 X(I)=0.5*(XU(I)+XU(I+1)) ENDDO X(N)=XU(N) END SUBROUTINE
2013-7-10
第4章 扩散方程的数值解法及应用
12
SUBROUTINE COEF USE COEFDATA; USE MESH; USE CASEDATA INTEGER P,E Real*8 gamw,afw,dltax_w,RE,AFE,DIFF,CV GAMW=GAM(1) Afw=AF(2) Dltax_W=X(2)-X(1) AW(2)=GAMW*Afw/Dltax_W ! 第1个内节点的西界面总传导系数 DO I=2,N-1 P=I ; E=P+1 Re=(XU(E)-X(P))/(GAM(P)+1.0e-30)+(X(E)-XU(E))/(GAM(E)+1.0e-30) ! 热阻 计算 DIFF=AF(E)/Re AE(P)=DIFF ; AW(E)=DIFF CV= 0.5* (XU(E)-XU(P)) * ( AF(P)+AF(E)) AP(P)=AE(P)+AW(P)-SP(P)*CV CON(P)=SC(P)*CV ENDDO END SUBROUTINE

反应堆物理分析 第二章：单速中子扩散理论

反应堆物理分析 第二章：单速中子扩散理论

x, y, z 0 x y z y x 0 0 z 0
x r sin cos y r sin sin z dr cos
s JZ 4
中子温度相同，单速
r, v, nr v
单速中子扩散方程
§2.1
单速中子扩散方程
分子的扩散现象“斐克扩 散定律”。 中子的扩散主要是中子与 介质原子核散射碰撞的结果。 中子总是从密度高的地方
向密度低的地方扩散。
§2.1.1
斐克定律
表示穿过某一取向表面的净流量,描述中子的 泄漏或流动
的介质交界面上，垂直于分
界面的中子流密度相等，中 子通量密度相等。
在分界面上所有沿正x（或负x）方向穿过A介质的中子数 必定等于在同一方向穿过介质B的中子数，（因为在分界面上 不能有中子的积累或消耗），即
Jx A Jx B
J x A J x Bc
两式相减便可得到
D
d dx
稳态扩散方程
D2 a S 0
无源，S＝0
k2
2

D
a
扩散长度
D a 0
2
1 D L 2 k a
2
k 0
2

2

L
2
0
曲率！
表：2-1
（1）无限介质内点源的情况 Point Source in an Infinite Medium
代 入
①
可以得出

0 2 0


2
0
exp(t r )[0 ( )0 cos ] cos sin drdd z

第四章 中子扩散理论1re

第四章 中子扩散理论1re

J zdA每z 秒自上方穿过dAz的中子数
一. 单能中子扩散方程
反应堆原理
Jz dAz
S(r
)e
sr
xy平面上方
co sdA z 4r 2
dV
dV r2 sin drdd (ϕ0为圆点处的中子通量密度)
JzdAz
s dA z 4
2/ 2 (r )esr
000
cossin drdd
J
z
S( r )dV
dV内散射的中子被散射到dAz方 cos dA Z
向上的概率：
4r 2
e e 射向dAz方向的中子最终到达dAz tr
sr
的概率：
每秒自dV内散射出来到达dAz的中子数：
S(
r
)e
s
r
cos dA z 4r 2
dV
推导斐克定律示意图
设
J
z
每秒自上方(沿-z方向)穿过垂直于z轴的单位面积的中子数。
第四章 中子扩散理论
反应堆原理
求解反应堆内中子密度或中子通量密度分布的方法：
Ⅰ 确定性方法：根据问题建立数学模型，得到一个或一组确定的数 学物理方程，然后对这些方程精确求解。
Ⅱ 非确定性方法：通过计算机的随机模拟来模拟每个中子在介质中的 运动的历史，然后对获取的信息加以分析。
描述中子输运过程的方程：
反应堆原理
《反应堆原理》
第四章 中子扩散理论-I
目录
反应堆原理
1 单能中子扩散方程 2 非增殖介质内中子扩散方程的解
3 扩散长度、慢化长度和徙动长度
第四章 中子扩散理论
反应堆原理
初始在反应堆内某一位置具有某种能量及某一运动方向的中子， 在稍晚些时候，将运动到堆内的另一位置以另一能量和另一运动方向 出现，这一现象称为中子在介质内的输运过程。

一维两群堆心数值计算

一维两群堆心数值计算

一维两群堆芯数值计算目录：一、题目分析 (2)二、公式推导 (2)1.原始方程 (2)2.划分网格 (3)3.写出离散方程 (3)三、编程计算 (4)四、结果分析 (4)五、程序代码 (8)作者：郭凯成5070209245一、题目分析如题所述，计算一维反应堆的有效增值系数和两群中子通量密度分布及功率密度，解题思路如下：先写出双群扩散方程，将一维反应堆离散化，推导出网格节点扩散方程，运用源迭代或外迭代法和中子通量密度迭代或内迭代法将扩散方程编写为C++程序。

C++程序应能计算不同的结块宽度以及不同组件布置，计算结果处理，运用origin软件将两群通量分布数据以及功率分布数据绘制成图，在不同数据对比图中了解结果，根据对比结果和计算结果再做进一步讨论。

二、公式推导1.原始方程在无外源情况下，反应堆一维双群扩散方程依据书本（5-12）式可以写成：快中子扩散方程一：慢中子扩散方程二：快中子源项方程三：有效增值系数估算方程四：功率方程五：2.划分网格1 1 1 1 1 1 1 1 1 1 1 1 1堆芯长度为260 cm，结块宽度为，网格数为n，共n+1各节点，令i=0,1,2...n。

j 为迭代次数3.写出离散方程方程一：方程二：方程三：方程四：方程五：其中，,,,,,，K[i]=，k[i]=将上述四个方程用C++编程计算，设置变量网格数为n，每个网格填入的组件类型（1、2、3），可以用源迭代和中子通量密度迭代法求解出、、P[i]及。

输出数据到文件中，用origin软件绘制出不同组件布置下的快中子、慢中子和功率通量分布。

三、编程计算编程代码见（五），初值组件数n设为26,组件分布为：3 3 3 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 2 2 2 2 3 3 3 3布置11 1 1 1 12 2 2 23 3 3 3 3 3 3 3 2 2 2 2 1 1 1 1 1布置2四、结果分析程序输出结果如下截图：布置1计算结果布置2计算结果分布图绘制如下：图1 布置1快慢中子分布图图2 布置2快慢中子分布图布置1：keff=1.23273 布置2：keff=1.16337通量分布展平情况图如下：图3 快中子通量展平图图4 慢中子通量展平图功率分布图如下：图5 布置1、2功率图及展平比较从图1、2都可以看出快中子和慢中子的中子通量分布接近余弦曲线分布，且快中子通量大于慢中子，快中子分布曲线比慢中子更陡，不均匀性更大。

压水堆堆芯Pin-by-pin计算扩散系数的计算方法研究

压水堆堆芯Pin-by-pin计算扩散系数的计算方法研究

1 扩散系数的计算方法研究
根据扩散理论中的菲克定律[2]可以得到被广泛使用的
扩散系数的定义：
D= 1
3Σ tr
式中：Σt
r
——
均匀化输运截面，单位cm-1。
(2)
根据通量体积权重法可以得到栅格计算中Pin-by-pin
均匀化少群扩散系数的归并方法有如下两种：
(1)对多群细区输运截面采用通量体积权重方法归并得
A Vi h
φhA r r dr
dr
(5)
D hom i,h
=
1 3Σ hom
tr,i , h
(6)
hom
∑ ∫ ( ) φ D hom
h∈g Vi i,h
D = i,g
A
∑ ∫ ( ) φ h∈g Vi h
A h
r
r dr dr
(7)
通量体积权重方法是简单地把扩散系数视为一种均
匀化截面进行归并，无法保证中子泄漏率守恒。在保证栅
组件中出现的各栅元的几何结构如图1所组件类型特征值参考解特征值误差pcm棒功率均方根误差rms方法1方法2方法3uox1109740860319403384030uox1cr066526563118857481755635184uox1ba087311355728737032953500282uox21244109604010504394038uox2cr080341572716358371525726160uox2ba103878313524232582493037234mox072460124749012885061229462moxcr073342115750412015201142467moxba069578134049213805081326469表1kaist单组件问题的七群扩散计算结果表2kaist单组件问题的七群简化球谐函数计算结果表3棋盘式多组件问题的七群扩散计算结果与简化球谐函数计算结果组件类型特征值参考解特征值误差pcm棒功率均方根误差rms方法1方法2方法3uox1109740380224802436021uox1cr066526322015833491453199153uox1ba087311214518423151932057176uox2124410420265302940025uox2cr080341324114033641293207166uox2ba103878190315820471661775147mox072460669290713304649256moxcr073342568301615316555256moxba069578761283806298746254棋盘式多组件问题特征值特征值误差pcm棒功率均方根误差rms扩散方法简化球谐函数方法方法1方法2方法3方法1方法2方法3unpoisoned09561332756857829223624909367534486807374moxpoisoned09557434056349826211648894371515487768387uoxpoisoned075473412285374329397302462341407353466339heavilypoisoned08185531846851705147615647367362458506398科技创新导报2020no13scienceandtechnologyinno

点堆动力学方程的数值解法

点堆动力学方程的数值解法

（ 4）
（ 它们分别是 n(t ) 和C i t ) 在步长h两端的导数值
三、点堆动力学方程的数值解法 3、厄密特多项式方法
t t1 为方便起见，作变量代换 t t1 h , 即 h
于是t的时间间隔（t1,t2）就变化为关于τ 的 时间间隔（0,1）,故点堆方程可写成
1 dn a( )n( ) i Ci ( ) h d i 1 dCi bi ( )n( ) i Ci ( ) h dt
学号：
报告人：
对于这些不同的差分方程是否都同样有效， 同样可靠，而且能得到同样的计算结果呢？
答案是否定的。事实上，性质不同的，数值结果 不同。
如何判断和分析差分方程有效性和可靠性 就成为非常必要和现实的问题了。
差分格式与原微分方程的相容性
利用差分格式求解的收敛性
差分格式的稳定性
1、相容性
I
I
二、三性与点堆动力学方程的刚性
4、刚性（stiff）微分方程
二、三性与点堆动力学方程的刚性
4、刚性（stiff）微分方程 该方程的根全部是实数，并满足
如果1 I
1 1 2 2 I I I 1 l
1
三、堆动力学方程的数值解法
Rn2 i i Ci 2 F Ri n2 U i i Ci 2 Vi k Ck 2 Gi
k i i
（10）
三、点堆动力学方程的数值解法 3、厄密特多项式方法
R R1 R2 R3 R 4 R5 R 6 1 2 3 4 5 6 U1 V1 V1 V1 V1 V1 V2 U 2 V2 V2 V2 V2 V3 V3 U 3 V3 V3 V3 V4 V4 V4 U 4 V4 V4 V5 V5 V5 V5 U 5 V5 V6 V6 V6 V6 V6 U 6

一维两群堆芯数值计算

一维两群堆芯数值计算

通量分布：
-6-
功率分布：
第三组：
迭代步长 堆芯布置 计算时间(精确到秒) 外迭代次数 有效增殖系数 0.1 3 3 3 3 3 3 3 3 3 3 3 3 3 t=219 k=100 keff=1.068060
通量分布：
-7-
功率分布：
第四组：
迭代步长 堆芯布置 计算时间(精确到秒) 外迭代次数 有效增殖系数 0.1 1 2 3 1 2 3 3 1 3 2 1 3 2 t=165 k=93 keff=1.149930
一维两群堆芯数值计算
简介：
本课题的目的是用数值计算的方法算出在燃料组件不同排列情 况下一维两群堆芯的 keff、中子通量分布及功率分布。
问题详述：
一个一维的反应堆，长度为 260 cm（13*20cm） 。左右边界条件 为零通量边界条件如图 1 所示。
1
1
1
1
1
1
1
1
1
1
1
1
1
图 1. 一维堆芯示意图
g 1
G
g
keff
Q(r )
g 1, 2, , G Q(r ) ( f ) g g (r )
g 1 G
本题为一维两群，因此r x , G 2, 即g 1, 2。 其中1代表快群，代表慢群。 2 我们利用源迭代法，人为将中子分代求解，以下公式中角标i表示中 子代数。将之前的公式离散化，可得：
其中i 0, 1, 2,
。
-2-
对于每一代中子的求解，我们采用高斯-塞德尔迭代法。 对快群，有：

（i )(j ) 1
D1 1x 2 (i 1) （i )(j 1) （i )(j ) ( x) [1 ( x 1) 1 ( x 1) Q ( x)] r ,1x 2 2 D1 D1keff
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

10-11-17 下午1:11
F:\my_matlab\core_1D.m
3 of 3
flux_fast=tdma(a1,b1,c1,d1);%解出快群. %慢群 d2=[]; for i=1:N for j=1:n d2(j+(i-1)*n)=E12(m(i))*flux_fast(j+(i-1)*n)*dx; end end d2(1)=d2(1)+2*f_left*D(m(1),2)/dx; d2(N*n)=d2(N*n)+2*f_right*D(m(N),2)/dx; flux_slow=tdma(a2,b2,c2,d2);%解出慢群. for i=1:N for j=1:n Q_new(j+(i-1)*n)=flux_fast(j+(i-1)*n)*vEf(m(i),1)+flux_slow(j+(i-1)*n)*vEf(m(i),2); end end %更新源项. keff_new=sum(Q_new)*dx/(sum(Q_old)*dx/keff_old);%更新keff. e_keff=abs((keff_new-keff_old)/(keff_new+eps)); keff_old=keff_new; e_Q=max(abs((Q_new-Q_old)./(Q_new+eps))); Q_old=Q_new; cycle=cycle+1;%记录循环次数. if e_keff<error_keff && e_Q<error_Q break; end end %归一化. flux_fast=flux_fast/(sum(flux_fast)); flux_slow=flux_slow/(sum(flux_slow)); Q=Q_new'; Q=N*L*Q/(dx*sum(Q)); keff=keff_new; end
10-11-17 下午1:11
F:\my_matlab\core_1D.m
2 of 3
end a1(1)=3*D(m(1),1)/dx+Ea(m(1),1)*dx+E12(m(1))*dx; a1(N*n)=3*D(m(N),1)/dx+Ea(m(N),1)*dx+E12(m(N))*dx; for i=1:N b1=[b1,-(D(m(i),1)/dx)*ones(1,n)]; end for i=1:N-1 b1(i*n)=-2*D(m(i),1)*D(m(i+1),1)/((D(m(i),1)+D(m(i+1),1))*dx); end for i=1:N c1=[c1,(-D(m(i),1)/dx)*ones(1,n)]; end for i=1:N-1 c1(i*n+1)=-2*D(m(i),1)*D(m(i+1),1)/((D(m(i),1)+D(m(i+1),1))*dx); end %三对角矩阵系数的对角系数向量计算-慢群 a2=[];b2=[];c2=[]; for i=1:N a2=[a2,(Ea(m(i),2)*dx+2*D(m(i),2)/dx)*ones(1,n)]; end for i=1:N-1 a2(i*n)=Ea(m(i),2)*dx+(D(m(i),2)^2+3*D(m(i),2)*D(m(i+1),2))/((D(m(i),2)+D(m(i+1),2))*dx); a2(i*n+1)=Ea(m(i+1),2)*dx+(D(m(i+1),2)^2+3*D(m(i),2)*D(m(i+1),2))/((D(m(i),2)+D(m(i+1),2))*dx); end a2(1)=3*D(m(1),2)/dx+Ea(m(1),2)*dx; a2(N*n)=3*D(m(N),2)/dx+Ea(m(N),2)*dx; for i=1:N b2=[b2,(-D(m(i),2)/dx)*ones(1,n)]; end for i=1:N-1 b2(n*i)=-2*D(m(i),2)*D(m(i+1),2)/((D(m(i),2)+D(m(i+1),2))*dx); end for i=1:N c2=[c2,(-D(m(i),2)/dx)*ones(1,n)]; end for i=1:N-1 c2(i*n+1)=-2*D(m(i),2)*D(m(i+1),2)/((D(m(i),2)+D(m(i+1),2))*dx); end %迭代计算 while(1) %快群 d1=[]; d1=Q_old*dx/keff_old; d1(1)=d1(1)+2*f_left*D(m(1),1)/dx; d1(N*n)=d1(N*n)+2*f_right*D(m(1),1)/dx;
10-11-17 下午1:11
F:\my_matlab\core_1D.m
1 of 3
function [keff flux_fast flux_slow Q]=core_1D(m) %m为燃料排布,L为结块长度,N为结块数目,n为每个结块划分份额. %材料参数. Ea=[1.071240E-02 9.389003E-02 8.915481E-03 9.007146E-02 1.033911E-02 9.685340E-02 9.920272E-03 9.850721E-02 1.033911E-02 9.685340E-02 9.616552E-03 9.824058E-02 3.064667E-03 4.777252E-02 8.603110E-03 7.853440E-02]; vEf=[4.334360E-03 1.029336E-01 6.260639E-03 1.217170E-01 4.769662E-03 1.141428E-01 5.251954E-03 1.232079E-01 4.769662E-03 1.141428E-01 5.555385E-03 1.264411E-01 0.000000E+00 0.000000E+00 6.160544E-03 1.207603E-01]; E12=[1.771023E-02 1.812268E-02 1.770407E-02 1.776033E-02 1.770407E-02 1.785182E-02 2.090091E-02 1.708523E-02]; D=[1.378098E+00 3.437887E-01 1.373819E+00 3.542306E-01 1.376979E+00 3.443704E-01 1.376071E+00 3.457435E-01 1.376979E+00 3.443704E-01 1.375501E+00 3.472169E-01 1.134501E+00 2.587405E-01 1.407447E+00 0.3670093E+0]; L=20;n=20;N=length(m); dx=L/n;%等边距划分,dx为每份宽度. Q_old=10*ones(1,N*n);keff_old=1.7;%设置初始值. error_keff=1e-6;error_Q=1e-5;%方程收敛验收系数. cycle=0;%存储计算循环次数. f_left=0;f_right=0;%边界条件. %三对角矩阵系数的对角系数向量计算-快群. a1=[];b1=[];c1=[]; for i=1:N a1=[a1,(Ea(m(i),1)*dx+E12(m(i))*dx+2*D(m(i),1)/dx)*ones(1,n)]; end for i=1:N-1 a1(i*n)=(Ea(m(i),1)+E12(m(i)))*dx+(D(m(i),1)^2+3*D(m(i),1)*D(m(i+1),1))/((D(m(i),1)+D(m(i+1),1)) *dx); a1(i*n+1)=(Ea(m(i+1),1)+E12(m(i+1)))*dx+(D(m(i+1),1)^2+3*D(m(i),1)*D(m(i+1),1))/((D(m(i),1)+D(m (i+1),1))dx);