当前位置：文档之家 › 数学分析课件PPT之十一章反常积分

数学分析课件PPT之十一章反常积分

  • 格式：ppt
  • 大小：1.13 MB
  • 文档页数：61

下载文档原格式

  / 61

合集下载

反常重积分课件

反常重积分课件

无界函数的反常重积分 设 D 为 R 2 上的有界区域，点 P0 D ， f ( x, y) 在 D \{P0 } 上有定义， 但在点 P0 的任何去心邻域内无界。这时 P0 称为 f 的奇点。 设 为内部含有 P0 的、面积为零的闭曲线，记 为它所包围的区 域。并设二重积分
D\
f ( x, y)dxdy
为定义在 D 上的函数。积分 f ( x, y)dxdy 当 p 2 时收敛；当 p 2 时发
D
散。 当 D 为扇形区域
a r ,
时，上述结论也成立。
( , [0, 2π ])
定理 13.4.1（比较判别法） 设 D 为 R 2 上具有分段光滑 边界的无界区域，在 D 上成立 0 f ( x, y) g( x, y) 。那么 （1） 当 g ( x, y)dxdy 收敛时， f ( x, y)dxdy 也收敛；

R
dx e
x
R
( x y )
dy lim e e dx x 0 R
R
R 0
1 1 e2 x e x R dx lim (1 e 2 R ) e 2 R e R 。 R 2 2
D\
f ( x, y)dxdy 的极限存在，就称 f ( x, y) 在 D 上可积，并记
f ( x, y)dxdy lim f ( x, y)dxdy ，
D ( ) 0 D\
这个极限值称为无界函数 f ( x, y) 在 D 上的反常二重积分，这时也称无 界函数的反常二重积分 f ( x, y)dxdy 收敛。如果右端的极限不存在，


a
dx

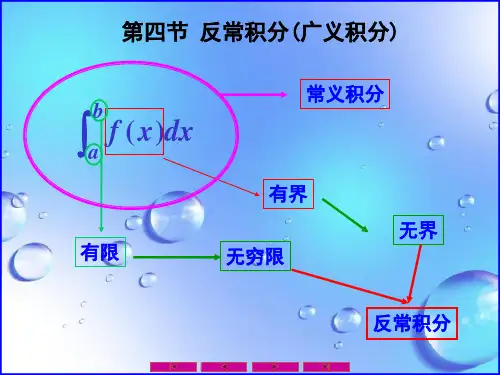
《反常积分课件》课件

《反常积分课件》课件
PPT,a click to unlimited possibilities
汇报人：PPT
目录
反常积分的定义
反常积分的定义：反常积分是一种特殊的积分，它包括无穷积分和瑕积分两种类型。
无穷积分：当积分区间为无穷大时，称为无穷积分。
瑕积分：当积分区间为有限时，但积分函数在积分区间内有无穷多个间断点，称为瑕积 分。 反常积分的求解方法：反常积分的求解方法包括积分判别法、积分变换法、积分估计法 等。
反常积分的证明方法
直接证明法：通 过直接计算反常 积分的值来证明
间接证明法：通过 证明反常积分的极 限存在来证明
积分变换法：通过 积分变换来证明反 常积分的性质与定 理
级数展开法：通过 级数展开来证明反 常积分的性质与定 理
物理中的应用实例
计算电场强度：利用反常积 分求解电场强度
计算引力场强度：利用反常 积分求解引力场强度
反常积分的分类
无穷积分：积分区间为无穷大
瑕积分：积分区间为有限，但积分函数在积分区间内有无穷多个间断点
瑕积分的推广：积分区间为有限，但积分函数在积分区间内有无穷多个间断点，且间 断点处函数值趋于无穷大
积分函数在积分区间内有无穷多个间断点，且间断点处函数值趋于无穷大，但积分区 间为有限
反常积分的特点
反常积分的难点解析
反常积分的 定义和性质
反常积分的 收敛性判断
反常积分的 计算方法
反常积分的 应用实例
反常积分的易错点分析
积分函数的选择：注意函数 的连续性和可积性
积分方法的选择：注意积分 方法的适用条件和计算技巧
积分区间的选取：注意区间 的端点和区间内的函数值
积分结果的验证：注意积分 结果的正确性和合理性

11-2——华东师范大学数学分析课件PPT

11-2——华东师范大学数学分析课件PPT

f ( x) dx 收敛，则 f ( x) dx 也收敛，并 有
a
a
a f ( x) dx a f ( x) dx.
数学分析 第十一章 反常积分
高等教育出版社
§2 无穷积分的性质与收敛判别
无穷积分的性质
非负函数无穷积分 的收敛判别法
一般函数无穷积分的 收敛判别法
非负函数无穷积分的收敛判别法
u1
u1
数学分析 第十一章 反常积分
高等教育出版社
§2 无穷积分的性质与收敛判别
无穷积分的性质
非负函数无穷积分 的收敛判别法
又因为 f ( x) 2 f ( x)dx u2 h( x)dx u2 g( x)dx ,
u1
证 设F(u)
u
f ( x)dx,
u [a, ),
则
f ( x)dx
a
a
收敛的充要条件是存在极限 lim F(u). 由函数
u
极限的柯西准则,此等价于
0, G a, u1, u2 G,
数学分析 第十一章 反常积分
高等教育出版社
F (u1) F (u2 ) ,
后退 前进 目录 退出
无穷积分的性质
非负函数无穷积分 的收敛判别法
一般函数无穷积分的 收敛判别法
定理11.1（无穷积分收敛的柯西准则）
无穷积分
f ( x)dx
收敛的充要条件是:
a
0, G a, 当 u1, u2 G 时,
u1 f ( x)dx u2 f ( x)dx u2 f ( x)dx .
a
a
高等教育出版社
§2 无穷积分的性质与收敛判别
无穷积分的性质
非负函数无穷积分 的收敛判别法

《反常积分课件》课件

《反常积分课件》课件
对函数f(x)在[a, b]上，当b->+∞或a->-∞时，求极 限∫f(x)dx。
瑕点在积分区间内的反常 积分定义为
对函数f(x)在[a, b]上，当存在c∈(a,b)使得 f(c)=∞时，求极限∫f(x)dx。
反常积分的分类
无穷区间上的反常积分分为两种：发 散和收敛。
瑕点在积分区间内的反常积分也分为 两种：瑕积分发散、瑕积分收敛。
03
CATALOGUE
反常积分的收敛性判断
收敛性的定义
收敛性的定义
一个反常积分 $int_{a}^{infty} f(x) dx$ 或 $int_{-infty}^{b} f(x) dx$ 在实数轴上的极 限存在时，称该反常积分是收敛的。
收敛与发散
如果反常积分存在极限，则称该反常积分是收敛的；否则，称该反常积分是发散的。
CATALOGUE
反常积分在数学分析中的地位和作用
在数学分析中的地位
反常积分是数学分析中一个重要的概念，它是对经典积分的扩展，使得积 分理论更加完整和广泛。
反常积分在解决一些经典积分无法处理的问题时发挥了关键作用，为数学 分析提供了更强大的工具。
反常积分是实数完备性的重要组成部分，对于实数理论的完善和发展具有 重要意义。
收敛与无穷小
当 $f(x)$ 在 $x to infty$ 或 $x to -infty$ 时，如果 $f(x)$ 是无穷小量，则反常积分 可能收敛。
收敛性的判断方法
判断方法一
判断方法二
判断方法三
通过比较判别法来判断反常积分的收 敛性。如果 $f(x) leq g(x)$ 且 $int_{a}^{infty} g(x) dx$ 是收敛的， 那么 $int_{a}^{infty} f(x) dx$ 也一定 是收敛的。

数学分析之十一章反常积分

数学分析之十一章反常积分

于是: a 0
dx
a
lim
a2 x2 0 0
dx a2 x2
1 a
lim
0
arcsin
x a a c
o
lim
0
arcsin
a
a
a
0c
arcsin
1
2
a a x
图5-7-1
例5 : 讨论反常积分
1 1
dx x2
的收敛性
.
解
:
被积函数f
(x)
1 x2
在积分区间[1,1]上除x
0外连续,
f (x)dx
0
都收敛, 则称上述两无穷积分之和为函数 f (x)在
区间(, +)上无穷积分.记作 f (x)dx ,即
0
f (x)dx f (x)dx f (x)dx
0
0
b
lim f (x)dx lim f (x)dx (3)
a a
b 0
这时, 也称无穷积分 f (x)dx 收敛;
a
b
a
( )
22
y
y
1
1 x2
obx
注:
为方便起见,
把
lim F
b
(x)ba
记作F
( x)a .
例2 : 计算无穷积分 te ptdt ( p是常数,且p 0). 0
解:
te ptdt lim b te ptdt
0
b 0
lim
b
t p
e pt
b 0
1 p
b
e
pt
dt
1 dx x
又
b 1
1 dx 2 x

课件：反常积分

课件：反常积分

dx发
散,
1
1
1 x
dx也
发
散.
思考题(2)
求位于x轴上方,直线x 1右侧,曲线y 2 1 x2
下方的平面图形的面积.
解
所求面积
1
1
2 x
2
dx
2arctan
x 1
22
4
.
2
三、小结与教学要求:
◆掌握无穷限的广义积分
a
f
( x)dx,
b
f
( x)dx,
f
(
x
)dx.
◆掌握无界函数的广义积分（瑕积分）
若lim b ta t
f
( x)dx存在,
则称此极限为f ( x)在(a,b]上的反常积分, 记作ab f ( x)dx,
即
b
a
f ( x)dx
b
lim
ta t
f ( x)dx,
此时,也称广义积分收敛; 否则,称广义积分发散.
类似地, 设f ( x)在[a,b)上连续, 点b为f ( x)的瑕点,
若lim t tb a
f
( x)dx存在,
则称此极限为f ( x)在[a,b)上的反常积分, 记作ab f ( x)dx,
即
b
a
f ( x)dx
t
lim
tb a
f ( x)dx.
此时,也称广义积分收敛; 否则,称广义积分发散.
若f ( x)在[a,b]上除c点外处处连续,且c为瑕点,则定义
b
a
x
1
,
(2) p 1,
1 1 x p dx
x1 1
p
p
1

反常积分法课件

反常积分法课件

3、
0
x ne xdx（
n 为自然数
）；4、
2 dx 0 (1 x)2
；
5 、 2 xdx ； 1 x1
6 、
x ln x 0 (1 x 2 )2
dx
；
7 、
1
ln
n
xdx
.
0
三 、 求 当 k 为何值时
， 广 义 积 分 b dx a (x a)k
(b a)
收 敛 ？ 又 k 为何值时 ， 这 广 义 积 分 发 散 ？
的瑕点是哪几点？
01
02
思考题解答
1
ln
x
0
x
dx 1
积分
x0,可能x 的 瑕1 点是
lim lnx lim1 1, x1
x014x 1 x1 x
03
的瑕1点l是nx dx
0 x1
x0.
不是瑕点,
练习题
一、填空题：
1、广义积分 dx 当_______时收敛；当______ 时
1 xp 发散；
0 1x2
6、 广 义 积 分x f(t)d的 t 几 何 意 义 是 ______________
________________________.
二、判别下列各广义积分的收敛性，如果收敛，则计
算广义积分的值：
1、 e pt cosh tdt 0
( p 1) ； 2、 dx
；
x2 2x 2
1
因此当q 1时反常积分收敛，其值为 1 ； 1q
当q 1时反常积分发散.
例6 计算反常积分
2 dx .
1 x ln x
2
1
dx x ln x

27-反常积分省公开课一等奖全国示范课微课金奖PPT课件

27-反常积分省公开课一等奖全国示范课微课金奖PPT课件

15第15页
当
a
为瑕点时,
b
a
f
(x)dx [F(x)]ba
F(b) lim xa
F(x)
当
b
为瑕点时,
b
a
f
(x)dx [F(x)]ba
lim
xb
F(x) F(a)
例例47
计算反常积分
a
0
1 dx a2 x2
解 因为 lim 1 , xa a2 x2
所以点a为被积函数瑕点
a
0
1 a2 x2
1)]1
lim
x
1 2
ln
x2 x2 1
1 2
ln
2
பைடு நூலகம்
1 2
ln
2.
8第8页
a
f
(x)dx [F(x)]a
lim
x
F (x)
F(a)
例例34
讨论反常积分
a
1 xp
dx
(a>0)的敛散性
解 当 p1 时,
a
1 xp
dx
a
1 x
dx [ln
x]
a
当 p<1 时,
a
1 xp
dx [11 p
x1
p]
b
a
f
(
x)dx
lim
ta
b
t
f
(x)dx
lim [F
ta
(x)]bt
F(b) lim F(t) F(b) lim F(x)
ta
xa
可采取简记形式
b
a
f
(x)dx
[F(x)]ba
F (b)

《数学分析》第11章 反常积分ppt课件

《数学分析》第11章 反常积分ppt课件

f ( x)dx 收敛, 则可得
c g( x)dx
收敛,从而
a
a2
a g( x)dx 收敛.反之,若 a g( x) dx 收敛, 可得
3c g( x)dx 收敛,从而
f ( x)dx 收敛.
a2
a
(ii)由 lim f ( x) 0, 存在 G a, 使 x G, 有 x g( x) f (x) 1 , g( x)
的积分
R
m gR 2 x2
dx
lim
r
r R
mgR x2
2
dx
mgR.
由机械能守恒定律可求初速度 v0 至少应使
1 2
mv02
mgR.
用 g 9.81(m / s2) , R 6.371 106 (m) 代入,得
v0 2gR 11.2 (km / s).
例2 圆柱形桶的内壁高为 h,内半径为 R,桶底有
ln u,
,q1 q 1,
故当 0 q 1 时,
1 dx 0 xq
lim
u0
1 dx u xq
1
1
; q
当 1 q 时,
1 0
dx xq
发散.
同样, 若 f (x) 的原函数为 F (x), 瑕积分的牛顿-莱
布尼茨公式写作
b a
f
(x)
dx
F(x)
b a
F (b)
F (a
)
F (b) lim F (u). ua
a f ( x) dx 与 b f ( x) dx (b a ),
同时收敛或同时发散，且
f ( x)dx
b f ( x)dx
f ( x)dx.

《数学分析》第十一章反常积分

《数学分析》第十一章反常积分

《数学分析》第十一章反常积分首先，我们来讨论无界函数的积分。

对于一个在区间[a,b)上定义的无界函数f(x)，其积分可以表示为：∫f(x)dx = lim(ξ→b-)∫f(x)dx，其中ξ是趋于b的数列。

这种积分的定义方式是将区间[a,b)划分为有限多个子区间并对每个子区间的积分进行求和，然后再取极限。

如果极限存在且有限，则称该反常积分收敛；若极限不存在或为无穷大，则称该反常积分发散。

接下来，我们来讨论无界区间上的积分。

对于一个定义在区间(-∞,a)或(a,∞)上的无界函数f(x)，其积分可以表示为：∫f(x)dx = lim(ξ→±∞)∫f(x)dx，其中ξ是趋于±∞的数列。

这种积分的定义方式与上述无界函数的积分类似，即将区间划分为有限多个子区间并对每个子区间的积分进行求和，然后取极限。

同样地，如果极限存在且有限，则该反常积分收敛；若极限不存在或为无穷大，则该反常积分发散。

在讨论反常积分时，还需考虑奇点的分类。

奇点是指函数在一些点上不满足积分条件的情况。

常见的奇点包括无界点、端点以及间断点。

对于无界点，通常情况下我们可以通过取极限的方式来处理；而对于端点，需要分别对两个方向上的积分进行讨论，并判断两个反常积分是否收敛；对于间断点，要分别对间断点左、右两侧的积分进行求和，并判断两个反常积分是否收敛。

在实际应用中，我们常常需要计算一些函数的反常积分，比如Gaussian函数的积分、Beta函数的积分等。

这些积分在数学、物理、工程等领域都有广泛的应用。

在计算这些积分时，我们可以利用换元法、分部积分法等积分技巧来简化计算过程，并帮助判断反常积分的收敛性。

总之，反常积分是对于不满足黎曼积分条件的函数取极限得到的积分。

本章介绍了无界函数的积分、无界区间上的积分以及奇点的分类等内容。

通过学习本章的内容，我们能够更好地理解和应用反常积分的概念和方法。

《数学分析》第十一章反常积分1

《数学分析》第十一章反常积分1

《数学分析》第十一章反常积分1《数学分析》第十一章反常积分1第十一章反常积分在数学分析中，我们经常研究的是定义在有界闭区间上的函数的积分，这些函数在有界闭区间上的积分被称为定积分。

但是，在实际应用中，有时会遇到一些函数在一些点上的值没有定义，或者函数在一些有界闭区间上的积分不存在，这就引出了反常积分的概念。

反常积分是对于在有界闭区间上不满足定积分条件的函数进行积分，也可以看作是对定积分的扩充。

反常积分分为无穷积分和广义积分两种类型。

一、无穷积分如果函数f(x)在区间[a,+∞)上定义，而对于任意的x∈[a,+∞)，f(x)都是有定义的，那么这样的函数f(x)在[a,+∞)上的积分称为无穷积分。

记作∫[a,+∞) f(x)dx如果函数f(x)在区间(-∞,a]上定义，而对于任意的x∈(-∞,a]，f(x)都是有定义的，那么这样的函数f(x)在(-∞,a]上的积分称为无穷积分。

记作∫(-∞,a] f(x)dx在计算无穷积分时，常常使用变量替换或者部分积分等方法。

二、广义积分如果函数f(x)在区间[a,b]上除了其中一点x=c外都是有定义的，而在x=c处f(x)的定义和c的极限存在，那么这样的函数f(x)在[a,b]上的积分称为广义积分。

记作∫[a,b] f(x)dx如果函数f(x)在区间[a,b)上除了其中一点x=b外都是有定义的，而在x=b处f(x)的定义和b的极限存在，那么这样的函数f(x)在[a,b)上的积分称为广义积分。

记作∫[a,b) f(x)dx如果函数f(x)在区间(a,b]上除了其中一点x=a外都是有定义的，而在x=a处f(x)的定义和a的极限存在，那么这样的函数f(x)在(a,b]上的积分称为广义积分。

记作∫(a,b] f(x)dx如果函数f(x)在区间(a,b)上除了其中一点x=a和x=b外都是有定义的，而在x=a和x=b处f(x)的定义和a、b的极限存在，那么这样的函数f(x)在(a,b)上的积分称为广义积分。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x
a


当 p 1时

a
1 xp
dx

x1 p 1 pa

,


a1 p p 1
,
p 1 p 1
所以无穷积分
dx a xp
当p 1时收敛, 其值为 ap1 p1. 当p 1时发散.
练习1.确定下列无穷积分是否收敛，若收敛算出它的值.
(1)
1
e
x
dx
(2)
1
1 x4
dx
(3)
1
1 dx x
解：
(1)
1be x dx

e x
b 1
1 eb
lim (1
b

eb
)

1

lim
b
1 eb
1
故
1
e
x
dx收敛，且
1
e
xdx

1
(2)
b 1
1 x4
dx


1 3x3
b 1

1 3

1 3
b3
lim (1 b 3

1 3b3
)

1 1 lim 3 3 b
1 b3

1 3
故
1
1 x4
dx收敛，且
1
1 x4
dx

1 3
(3)
1
1 dx lim
x
b
b 1
1 dx x
又
b 1
1 dx 2 x
a
b a
(1)
这时也称无穷积分 f (x)dx 收敛; 若上述极 a
限不存在, 就称无穷积分 f (x)dx 发散, 这时记
号

f
a
( x)dx不再表示数值了。
a
例如：
1 0 1 x2
dx

lim
b
b 0
1 1 x2
dx

lim arctan
向是开口的，即这时的积
分区间为[1，+∞），
01
故b
1,则A的面积为
b 1
1 x2
dx
[
1 x
]1b
1 1 b
y

1 x2
bx
显然当b改变时，曲边梯形的面积也随之改变，
故b 时，即lim b
b 1
1 x2
dx

lim (1
b
1) b

1
则所求曲边梯形的面积为1
t p
e
pt
0

1 p2
e pt
0


1 p
lim
t
te
pt
0
1 p2
(0 1)

1 p2
例3 :
证明无穷积分
a
dx xp
(a 0).
当p 1时收敛, 当p 1时发散.
证: 当 p = 1时

a
dx xp

a
dx x

ln
b
xb0
lim arctanb b
y
1
y

1
1 x
2


2
o
b
x
类似地, 设函数 f (x)在区间(, b]上连续, 取a < b,
如果极限
b
lim f (x)dx
a a
存在, 则称此极限为函数
f
(x)在无穷区间(,
b]上无穷积分,
记作
b

f
( x)dx,
x
b 1

2
b 2
lim (2 b 2)
b
故
1
1 dx发散 x
练习2：计算无穷积分
(1)
0
xe
x2
dx
（2）
1 e
ln x x
dx
解(1):
0
xex
2
dx
[
1 2
ex2
]0


1 2
(0 1)

1 2
练习4：求下列无穷积分：
b
f
( x)dx,即
b
b
f (x)dx lim
f (x)dx
a
a
0 a
0
都收敛, 则称上述两无穷积分之和为函数 f (x)在
区间(, +)上无穷积分.记作 f (x)dx ,即

0

f (x)dx f (x)dx f (x)dx


0
0
b
lim f (x)dx lim f (x)dx (3)
a a
b 0
(1)

xe

x2 2
dx
(2)
0
e
x
dx
定义2: 设函数 f (x)在区间(a, b]上连续, 而在点 a 的 右邻域内无界, 取 > 0.如果极限
b
lim f (x)dx
0 a
存在,
则称此极限为无界函数 f (x)在(a, b]上的反常积分.
仍然记作
dx

lim
b
b1 0 1 x2
dx

lim arctan
a
x0a

lim arctan
b
xb0
lim arctan a lim arctan b
a
b
a



2
)


2


y
y

1
1 x
2
obx
注:
为方便起见,
把
lim F
b
(
x)ba
即
b
b
f (x)dx lim f (x)dx

a a
(2)
这时也称无穷积分
b

f (x)dx 收敛;
若上述
极限不存在, 就称无穷积分b f (x)dx 发散.
设函数 f (x)在区间(, +)上连续, 如果无穷积分
0
f (x)dx 和

f (x)dx

记作F
( x)a .
例2 : 计算无穷积分 te ptdt ( p是常数,且p 0). 0
解:
te ptdt lim b te ptdt
0
b 0

blim
t p
e

pt

b 0

1 p
b
e
pt
dt

0


这时, 也称无穷积分 f (x)dx 收敛;
否则就称
无穷积分 f (x)dx 发散.
例1：计算无穷积分

1
dx x
2
.
解：
dx 1 x2

0 dx 1 x2

dx 0 1 x2
lim a
01 a1 x2
第十一章反常积分
11.1 反常积分概念 11.2 无穷积分的收敛性质与判别 11.3 瑕积分的性质与收敛判别
11.1 反常积分概念
一、 引例 二、两类反常积分的定义
一. 引入
例：
求曲线y

1 x2
, x轴及直线x
1，右边所围成的“开口
曲边梯形”的面积。
y
解：由于这个图形不是封闭的
曲边梯形,而在x轴的正方
二、两类反常积分的定义.
定义1: 设函数 f (x)在区间[a, +)上连续, 取b > a,
如果极限 lim b f (x)dx 存在, b a
则称此极限为函数 f (x)在无穷区间[a, +)上
的无穷限反常积分, 记作 f (x)dx,即 a

b
f (x)dx lim f (x)dx