数学拓展校本课程 第二讲 速算与巧算

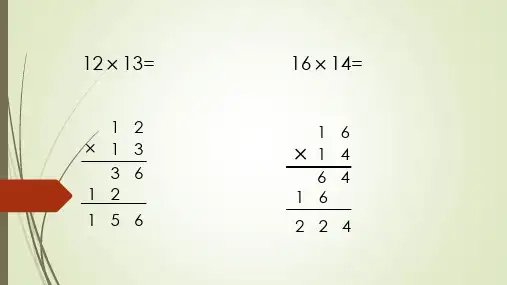
第2讲速算与巧算计算是数学的基础，小学生要学好数学，必须具有过硬的计算本领。

准确、快速的计算能力既是一种技巧，也是一种思维训练，既能提高计算效率、节省计算时间，更可以锻炼记忆力，提高分析、判断能力，促进思维和智力的发展。

我们在三年级已经讲过一些四则运算的速算与巧算的方法，本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。

例1：四年级一班第一小组有10名同学，某次数学测验的成绩（分数）如下：86，78，77，83，91，74，92，69，84，75。

求这10名同学的总分。

例1所用的方法叫做加法的基准数法。

这种方法适用于加数较多，而且所有的加数相差不大的情况。

作为“基准”的数（如例1的80）叫做基准数，各数与基准数的差的和叫做累计差。

由例1得到：总和数=基准数×加数的个数+累计差，平均数=基准数+累计差÷加数的个数。

在使用基准数法时，应选取与各数的差较小的数作为基准数，这样才容易计算累计差。

同时考虑到基准数与加数个数的乘法能够方便地计算出来，所以基准数应尽量选取整十、整百的数。

练习：1.求下面10个数的总和：165，152，168，171，148，156，169，161，157，149。

2.某车间有9个工人加工零件，他们加工零件的个数分别为：68，91，84，75，78，81，83，72，79。

他们共加工了多少个零件？例2 某农场有10块麦田，每块的产量如下（单位：千克）：462，480，443，420，473，429，468，439，475，461。

求平均每块麦田的产量。

练习：1.农业科研小组测定麦苗的生长情况，量出12株麦苗的高度分别为（单位：厘米）：26，25，25，23，27，28，26，24，29，27，27，25。

求这批麦苗的平均高度。

2.计算：13＋16＋10+11＋17＋12＋15＋12＋16＋13＋12=求一位数的平方，在乘法口诀的九九表中已经被同学们熟知，如7×7＝49（七七四十九）。

＊＊＊＊＊校本课程数学计算方法第一讲生活中几十乘以几十巧算方法1.十几乘十几:口诀：头乘头，尾加尾，尾乘尾.例：12×14=？解：1×1=1２＋４＝６２×４＝８12×14=168注：个位相乘,不够两位数要用0占位。

２。

头相同，尾互补(尾相加等于10）：口诀:一个头加１后，头乘头，尾乘尾。

例：23×27=？解：２＋１＝３２×３＝６３×７＝2123×27=621注：个位相乘，不够两位数要用0占位。

３.第一个乘数互补，另一个乘数数字相同：口诀:一个头加１后,头乘头，尾乘尾。

例：37×44=？解：3+1=44×4=167×4=2837×44=1628注：个位相乘，不够两位数要用0占位。

４。

几十一乘几十一:口诀:头乘头，头加头，尾乘尾。

例：21×41=？解:2×4=82+4=61×1=121×41=861５。

11乘任意数：口诀：首尾不动下落，中间之和下拉.例：11×23125=？解：2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注：和满十要进一。

６.十几乘任意数：口诀：第二乘数首位不动向下落，第一因数的个位乘以第二因数后面每一个数字,加下一位数，再向下落.例:13×326=？解：13个位是33×3+2=113×2+6=123×6=1813×326=4238注：和满十要进一.第二讲常用巧算速算中的思维与方法（1）【顺逆相加】用“顺逆相加”算式可求出若干个连续数的和。

例如著名的大数学家高斯（德国）小时候就做过的“百数求和”题,可以计算为1+2 +……+99+100所以,1＋2＋3＋4＋……＋99＋100=101×100÷2=5050“3+5+7+………＋97+99=？3+5＋7＋……＋97+99=（99＋3）×49÷2= 2499。

校本:《速算与巧算》教学设计教学内容：速算与巧算教学目标：1、掌握速算与巧算的方法，提高学生的计算能力和思维能力。

2、选用合理、灵活的计算方法，简便运算过程，化繁为简，化难为易，使计算又快又准确。

教学过程：一、巧算激趣。

1、出示三组巧算题，学生随意指，教师张口说出答案。

72―27= 34×11= 72＋27=63―36= 25×11= 75＋57=53―35= 36×11= 97＋79=82―28= 125×11= 82＋29=92―29= 215×11= 67＋76=61―16= 324×11= 58＋85=95―59= 1234×11= 37＋73=二、导入新课。

同学们，知道老师是怎么算的吗？想和老师一样“神机妙算”吗？让我们一起步入今天的巧算天地。

（出示课题）三、探究新知。

（一）学习第一组：72―27= 63―36= 53―35= 82―28=①仔细观察，这组题有什么特征？②学生观察后，发言，说出自己的发现。

③教师介绍：倒转数的概念。

经过观察发现，被减数是81，减数是18，减数是被减数的十位和个位交换位置而得来的。

我们就把18叫做81的倒转数。

例如，23是32的倒转数，59是95的倒转数。

④学生计算这组题的答案。

⑤仔细观察答案，你发现了什么？⑥学生思考片刻，举手发言。

⑦教师引导，小结算法。

计算：721－27=（7－2）×9=45小结：一个数和它的倒转数的差，只要将将十位与个位上的两个数字的差乘以9，所得的积就是这两个数的差。

⑧学生验证。

（二）学习第二组，乘11的巧数34×11 635×11①列式计算：34×11。

②观察答案，你发现什么？通过观察34×11=374 635×11=6985的计算结果。

发现它们具有如下特点: 3 4 ×11 = 374 6 3 5 ×11 = 69853 74 6 9 8 5乘11的那个数从右边起，每相邻位上的数字相加占一位，高位和个位各占一位。

第02讲速算与巧算（下）教学目标：1、进一步巩固对五大运算律、运算性质、方法和技巧等知识的掌握，提升进行速算和巧算熟练度；2、运用速算与巧算知识，解决相关的实际生活问题；3、培养学员速算方面的意识，为变身小小CEO做准备。

教学重点：进一步巩固五大运算律、运算性质、方法和技巧等知识的掌握，提升进行速算和巧算熟练度。

教学难点：运用速算与巧算知识，解决相关的实际生活问题。

教学过程：【复习与提升】层层高1、计算：（1）251×4＋﹙753－251﹚×2（2）25×70-5×28×2+4×5×7解析部分：第一步：引导学员对于此题中的各个算式进行结构分析，对于之前所学的速算巧算方式进行初步回顾，与各个算式结合起来，进行尝试计算操作。

第二步：根据题中各个算式的具体结构特点，对于算式进行相应的计算，可以有“（1）251×4＋﹙753－251﹚×2=251×4+251×6-251×2=251×8=2008；（2）25×70-5×28×2+4×5×7=25×10×7-5×2×4×7+4×5×7=（250-40+20）×7=1610”第三步：最后引导学员对于此题的算式结构特点进行回顾总结，找出进行速算和巧算的一些规律特点，进一步加深对于速算和巧算的认识和理解。

参考答案：（1）251×4＋﹙753－251﹚×2=251×4+251×6-251×2=251×8=2008（2）25×70-5×28×2+4×5×7=25×10×7-5×2×4×7+4×5×7=（250-40+20）×7=1610层层高2、计算：(1) 44×555＋55×666 (2) 2014×20152015－2015×20142014 参考答案：（1）44×555＋55×666=4×5×11×111+5×6×11×111=50×11×111=61050 （2）2014×20152015－2015×20142014=2014×2015×10001-2015×2014×10001=0层层高3、计算：（1）9999×5555－2222×9999（2）（1234＋2341＋3412＋4123）÷（1＋2＋3＋4）参考答案：（1）9999×5555－2222×9999=（10000-1）×3333=33330000-3333=33326667 （2）（1234＋2341＋3412＋4123）÷（1＋2＋3＋4）=11110÷10=1111层层高4、计算：（1）9999×2222+3333×3334（2）9999×8888-3332×3333参考答案：（1）9999×2222+3333×3334=9999×2222+3333×（3333+1）=9999×2222+3333×3333+3333=9999×2222+9999×1111+3333=9999×3333+3333=33330000 （2）9999×8888-3332×3333=9999×8888-（3333-1）×3333=9999×8888-3333×3333+3333 =9999×8888-9999×1111+3333=（10000-1）×7777+3333=77770000-7777+3333=77765556层层高5、计算：（1）（1+3+5+......+99）×（2+4+6+ (100)（2）100×99－99×98＋98×97－97×96＋……＋2×1参考答案：（1）（1+3+5+……+99）×（2+4+6+……+100）=（1+99）×50÷2×（2+100）×50÷2=2500×2550=6375000（2）100×99－99×98＋98×97－97×96＋……＋2×1=2×（99+97+95+……+3+1）=2×2500=5000【课堂总结】对于综合算式的速算和巧算：（1）首先，根据复杂算式的结构特点对其进行一定变形处理向凑整或者配对等方向靠近；（2）然后，根据具体的巧算方向采取凑整或者配对等方式对算式进行计算；（3）最后，检查一下计算过程中的合理性以及出现错误与否。

第2讲 速算与巧算【知识概述】小数、分数、整数的四则混合运算一样，都是按先乘除，后加减的顺序进行。

整数运算中的定律和性质，在分数运算中同样适用。

乘法分配律是最常见的一种运算定律。

另外，分数的运算技巧和方法主要有凑整法、裂项法、代数法等。

运算定律和性质1．加法运算定律：a ＋b ＝b ＋a(a ＋b)＋c ＝a ＋(b ＋c)2．乘法运算规律：a ×b ＝b ×a(a ×b)×c ＝a ×(b ×c)a ×(b ＋c) ＝a ×b ＋a ×c3．带符号搬家1）在加减混合运算中，交换任意两个数的位置，结果不变，但要注意符号要跟着数一起走。

a －b ＋c ＝a ＋c －b a ＋b －c ＝a －c ＋b2）在乘除混合运算中，交换任意两个数的位置，结果不变，但要注意符号要跟着数一起走。

a ÷b ÷c ＝a ÷c ÷b a ÷b ×c ＝a ×c ÷b4．添括号、去括号添加括号原则： a ＋b ＋c ＝a ＋(b ＋c) a ×b ×c ＝ a ×(b ×c)a ＋b －c ＝a ＋(b －c) a ×b ÷c ＝ a ×(b ÷c)a －b －c ＝a －(b ＋c) a ÷b ÷c ＝ a ÷(b ×c)a －b ＋c ＝a －(b －c) a ÷b ×c ＝ a ÷(b ÷c)【典型例题】例1 )851741()731375.3(--- 【思路点拨】按照四则混合运算法则计算，需要通分，再做分数的加减法，计算比较复杂。

通过观察算式两个括号中有731和741、3.375和851可以试图用先去括号，再添括号凑整进行简便计算。

第二讲速算与巧算（二）一、乘法中的巧算1. 两数的乘积是整十、整百、整千的，要先乘.为此，要牢记下面这三个特殊的等式：5×2=1025×4=100125×8=1000例1 计算①123×4×25②125×2×8×25×5×4解：①式=123×（4×25）=123×100＝12300②式=（125×8）×（25×4）×（5×2）=1000×100×10=10000002. 分解因数，凑整先乘。

例2计算①24×25②56×125③125×5×32×5解：①式=6×（4×25）=6×100=600②式=7×8×125=7×（8×125）=7×1000=7000③式=125×5×4×8×5=（125×8）×（5×5×4）=1000×100=1000003. 应用乘法分配律。

例3 计算①175×34＋175×66②67×12+67×35＋67×52+6解：①式=175×（34+66）=175×100=17500②式=67×（12＋35＋52＋1）＝67×100＝6700（原式中最后一项67可看成67×1）例4 计算①123×101 ②123×99解：①式=123×（100＋1）=123×100＋123＝12300＋123=12423②式=123×（100-1）=12300-123=121774. 几种特殊因数的巧算。

第2讲速算与巧算（二）上一讲咱们介绍了一类两位数乘法的速算方式，这一讲讨论乘法的“同补”与“补同”速算法。

两个数之和等于10，则称这两个数互补。

在整数乘法运算中，常会碰到像72×78，26×86等被乘数与乘数的十位数字相同或互补，或被乘数与乘数的个位数字相同或互补的情况。

72×78的被乘数与乘数的十位数字相同、个位数字互补，这种式子咱们称为“头相同、尾互补”型；26×86的被乘数与乘数的十位数字互补、个位数字相同，这种式子咱们称为“头互补、尾相同”型。

计算这两类题目，有超级简捷的速算方式，别离称为“同补”速算法和“补同”速算法。

例1 （1）76×74＝？（2）31×39＝？分析与解：本例两题都是“头相同、尾互补”类型。

（1）由乘法分派律和结合律，取得76×74＝（7＋6）×（70+4）＝（70＋6）×70＋（7＋6）×4＝70×70＋6×70＋70×4＋6×4＝70×（70＋6＋4）＋6×4＝70×（70＋10）＋6×4＝7×（7+1）×100＋6×4。

于是，咱们取得下面的速算式：（2）与（1）类似可取得下面的速算式：由例1看出，在“头相同、尾互补”的两个两位数乘法中，积的末两位数是两个因数的个位数之积（不够两位时前面补0，如1×9＝09），积中从百位起前面的数是被乘数（或乘数）的十位数与十位数加1的乘积。

“同补”速算法简单地说就是：积的末两位是“尾×尾”，前面是“头×（头+1）”。

咱们在三年级时学到的15×15，25×25，…，95×95的速算，实际上就是“同补”速算法。

例2 （1）78×38＝？（2）43×63＝？分析与解：本例两题都是“头互补、尾相同”类型。

四年级奥数部分第二讲 速算与巧算整数乘除法的速算与巧算，一条最基本的原则就是“凑整”。

要达到“凑整”的目的，就要将一些数分解、变形，再运用乘法的交换律、结合律、分配律以及四则运算中的一些规则，把某些数组合到一起，使复杂的计算过程简便化。

一、乘法中的巧算1.凑整法：两数的乘积是整十、整百、整千的，要先乘.5×2=10 25×4=100 125×8=1000 625×8＝5000 625×16＝10000 例1 计算①123×4×25 ② 125×2×8×25×5×4999999⨯⨯ ()=-⨯⨯10001999 ()=-⨯99000999………………再次转化为()101-()=⨯-=-=98901101989010989018901092.分解因数，凑整先乘。

乘法结合律：(a ×b)×c=a ×(b ×c)例 2计算① 24×25 ② 56×125 ③ 125×5×32×53.应用乘法分配律。

乘法分配律：(a＋b)×c=ac＋bc例3 计算① 175×34＋175×66 ②67×12+67×35＋67×52+6 （1）999＋999×999例4 计算① 123×101 ② 123×994.几种特殊因数的巧算。

例5一个数×10，数后添0；一个数×100，数后添00；一个数×1000，数后添000；以此类推。

如：15×10=15015×100=150015×1000＝15000例6一个数×9，数后添0，再减此数；一个数×99，数后添00，再减此数；一个数×999，数后添000，再减此数；…以此类推。

第2讲 速算与巧算（裂项法）1、分数裂项法将算式中的项进行拆分，使拆分后的项可前后抵消，这种拆项计算称为裂项法。

裂项分为分数裂项和整数裂项，常见的裂项方法是将数字分拆成两个或多个数字单位的和或差。

遇到裂项的计算题时，要仔细的观察每项的分子和分母，找出每项分子分母之间具有的相同的关系，找出共有部分，裂项的题目无需复杂的计算，一般都是中间部分消去的过程，这样的话，找到相邻两项的相似部分，让它们消去才是最根本的。

(1)对于分母可以写作两个因数乘积的分数，即1a b ⨯形式的，这里我们把较小的数写在前面，即a b <，那么有1111()a b b a a b =-⨯- (2)对于分母上为3个或4个连续自然数乘积形式的分数，即：1(1)(2)n n n ⨯+⨯+，1(1)(2)(3)n n n n ⨯+⨯+⨯+形式的，我们有：裂差型裂项的三大关键特征：（1）分子全部相同，最简单形式为都是1的，复杂形式可为都是x(x 为任意自然数)的，但是只要将x 提取出来即可转化为分子都是1的运算。

（2）分母上均为几个自然数的乘积形式，并且满足相邻2个分母上的因数“首尾相接”（3）分母上几个因数间的差是一个定值。

2、整数裂项法：裂项思想是：瞻前顾后，相互抵消。

例如：1223344950⨯+⨯+⨯++⨯=_________；设S ＝1223344950⨯+⨯+⨯++⨯1×2×3＝1×2×32×3×3＝2×3×（4－1）＝2×3×4－1×2×3 3×4×3＝3×4×（5－2）＝3×4×5－2×3×449×50×3＝49×50×（51－48）=49×50×51－48×49×50 3S ＝1×2×3＋2×3×3＋3×4×3＋…＋49×50×3＝49×50×51 S ＝49×50×51÷3＝41650例1：111111223344556++++=⨯⨯⨯⨯⨯ 。

目录第一讲速算与巧算（一）一、凑十法同学们已经知道，下面的五组成对的数相加之和都等于101＋9＝10，2＋8＝10，3＋7＝10，4＋6＝10，5＋5＝10巧用这些结果，可以使计算又快又准。

例1计算1＋2＋3＋4＋5＋6＋7＋8＋9＋10解：对于这道题，当然可以从左往右逐步相加：1＋2＝3，3＋3＝6，6＋4＝10，10＋5＝15，15＋6＝21，21＋7＝28，28＋8＝36，36＋9＝45，45＋10＝55这种逐步相加的方法，好处是可以得到每一步的结果，但缺点是麻烦、容易出错；而且一步出错，以后步步都错。

若是利用凑十法，就能克服这种缺点。

二、凑整法同学们还知道，有些数相加之和是整十、整百的数，如：1＋19＝20，11＋9＝30，2＋18＝20，12＋28＝40，3＋17＝20，13＋37＝50，4＋16＝205＋15＝20，15＋55＝70，6＋14＝20，16＋64＝80，7＋13＝20，17＋73＝90，8＋12＝20又如：15＋85＝100，14＋86＝100，25＋75＝100，24＋76＝100，35＋65＝100，34＋66＝100等等。

巧用这些结果，可以使那些较大的数相加又快又准。

像10、20、30、40、50、60、70、80、90、100等等这些整十、整百的数就是凑整的目标。

例2计算1＋3＋5＋7＋9＋11＋13＋15＋17＋19解：这是求1到19共10个单数之和，用凑整法做：例3计算2＋4＋6＋8＋10＋12＋14＋16＋18＋20解：这是求2到20共10个双数之和，用凑整法做：例4计算2＋13＋25＋44＋18＋37＋56＋75解：用凑整法：三、用已知求未知利用已经获得较简单的知识来解决面临的更复杂的难题这是人们认识事物的一般过程，凑十法、凑整法的实质就是这个道理，可见把这种认识规律用于计算方面，可使计算更快更准。

下面再举两个例子。

例5计算：1＋2＋3＋4＋5＋6＋7＋8＋9＋10＋11＋12＋13＋14＋15＋16＋17＋18＋19＋20解：由例2和例3，已经知道从1开始的前10个单数之和以及从2开始的前10个双数之和，巧用这些结果计算这道题就容易了。