江苏省灌云县四队中学苏教数学必修四《任意角的三角函数2》教案

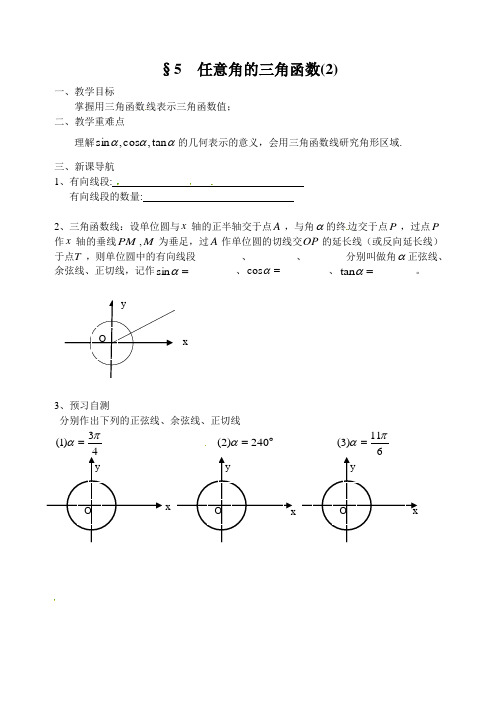
§5 任意角的三角函数(2)一、教学目标 掌握用三角函数线表示三角函数值；二、教学重难点理解αααtan ,cos ,sin 的几何表示的意义，会用三角函数线研究角形区域.三、新课导航1、有向线段:有向线段的数量:2、三角函数线：设单位圆与x 轴的正半轴交于点A ，与角α的终边交于点P ，过点P 作x 轴的垂线PM ,M 为垂足，过A 作单位圆的切线交OP 的延长线（或反向延长线）于点T ，则单位圆中的有向线段_________、_________、________分别叫做角α正弦线、余弦线、正切线，记作=αsin _________、=αcos _________、=αtan ________。

3、预习自测分别作出下列的正弦线、余弦线、正切线 43)1(πα=︒=240)2(α 611)3(πα=x yO x y O y O y O xx四、合作探究：活动1、利用三角函数线比较下列各式的大小︒︒57cos ,57sin )1( （2）3cos ,2cos ,1cos活动2、利用单位圆作出符合下列条件的角的终边（1）23sin =α （2）1cos 2α=- （3）1tan =α活动3、在单位圆中用阴影表示满足1cos 2>α的角α的终边所在区域,并写出角α的集合.五、知识网点六、反思§5 任意角的三角函数(2)作业班级___________姓名_____________学号__________日期_________得分 _________1、 下列关系式中不正确的是（1）01sin < （2）0)690cos(>-。

（3）0)35tan(>-π 2、 若[)πα2,0∈ ，则满足 3cos 2=α的α=3、 利用正弦线比较5.1sin ,2.1sin ,1sin 的大小 （用“<”连接）4、 函数x x x x y tan tan cos cos +=的值域为5、 写出函数x x f cos )(=的定义域为 .6、 若sin sin =αβ，则的,αβ的关系是7、作出下列各角的正弦线、余弦线、正切线；11(1);6π 2(2)3π-8、利用单位圆分别写出符合下列条件的角的集合：（1）21sin -=α （2）21sin ->α9、根据条件利用单位圆写出θ的取值范围：（1）2cos 2<θ （2）23sin 21<≤θ10、若θ为锐角（单位为弧度），利用单位圆及三角函数线，试比较 θ,θsin ,θtan 三者之间的大小关系.错题剖析:。

1.1.1 任意角（2）
教学目标
1．熟练掌握象限角与非象限角的集合表示；
2．会写出某个区间上角的集合。

教学重、难点
区间角的表示。

教学过程
复习：
1．角的分类：按旋转方向分；按终边所在位置分。

2．与角α同终边的角的集合S 表示。

3．练习：把下列各角写成360(0360)k αα⋅+≤<o o
的形式，并指出它们所在的象限或终边位置。

（1）135-o ； （2）1110o ； （3）540-o ．
新课讲解
1．轴线角的集合表示
例1：写出终边在y 轴上的角的集合。

拓展：（1）终边在x 轴线的角的集合怎么表示？
（2）所有轴线角的集合怎么表示？
例2：写出第一象限角的集合M ．
提问：第二、三、四象限角的集合又怎么表示？
例3 写出(0)y x x =±≥所夹区域内的角的集合。

课堂练习
1．若角β的终边在第一象限或第三象限的角平分线上，则角β的集合是 ．
2．若角α与β的终边在一条直线上，则α与β的关系是 ．
3．（思考）若角α与β的终边关于x 轴对称，则α与β的关系是 ． 若角α与β的终边关于y 轴对称，则α与β的关系是 ．
若角α与β的终边关于原点对称，则α与β的关系是 ．
课堂小结
1．非象限角（轴线角）的集合表示；
2．区间角集合的书写。

教学后记。

课题：任意角的三角函数教学目的：要求学生掌握任意角的正弦、余弦、正切的定义；掌握三角函数值在各象限内的符号；会求已知终边上一点的角的三角函数值.教学重点：理解三角函数的定义，能确定三角函数值在各象限内的符号教学过程：一、问题情境：初中学过的锐角的正弦、余弦、正切的定义是什么？当角推广到任意角后，角的正弦、余弦、正切又怎样定义呢？二、建构数学1.任意角的正弦、余弦、正切的定义设α是一个任意角，在α的终边上任取（异于原点的）．．．．．．．一点P（x,y）则P与原点的距离（图示见P11，可于空白处自行补图）比值yr叫做α的正弦，记作：ysinα=r比值xr叫做α的余弦，记作：xcosα=r比值yx叫做α的正切，记作：ytanα=x说明：（1）三角函数值与点的选择无关.（2）由于r2=x2+y2,∴r≥|x|,且r≥|y|故|sinα|≤1且|cosα|≤12.三角函数的定义域3.三角函数值在各个象限内的符号（1）图示符号规律：（2）注意点：①凡是终边相同的角的三角函数值相等；②如果终边在坐标轴上，上述定义同样适用；③三角函数是以“比值”为函数值的函数；④r>0，而x,y 的正负是随象限的变化而不同，故三角函数的符号应由角所在的象限确定.三、数学应用1、例题教学例1. 已知α的终边经过点P(2,-3)，分别求α的正弦、余弦、正切值.变式⑴ 已知角α的终边经过P(4,-3),求2sin α+cos α的值.变式⑵ 已知角α的终边经过P(4a,-3a),(a ≠0) 求2sin α+cos α的值.例2. 求下列各角的正弦、余弦、正切值⑴ 0 ⑵2π ⑶π ⑷ 32π例3．确定下列三角函数值的符号：（1）cos 7π12 ; (2)sin(-465°) ; (3) tan 11π3例4.若sin α<0且tan α<0,试确定α为第几象限角.2、学生练习：课本15页1,2,3,4,5,6 四、回顾反思五、作业。

课 题：1.1.1 任意角（二）教学目的：1．巩固角的形成，正角、负角、零角等概念，熟练掌握掌握所有与α角终边相同的角（包括α角）、象限角、区间角、终边在坐标轴上的角的表示方法；2．掌握所有与α角终边相同的角（包括α角）、象限角、终边在坐标轴上的角的表示方法；3．体会运动变化观点，逐渐学会用动态观点分析解决问题；教学重点：象限角、终边在坐标轴上的角的表示方法；教学难点：终边在坐标轴上的角的集合表示；授课类型：新授课课时安排：1课时教 具：多媒体、实物投影仪内容分析：通过复习回顾，使学生进一步理解角的概念，象限角的概念.通过具体的例子，使学生掌握终边在坐标轴上的角和终边不在坐标轴上的角的集合表示以及符号语言的运用.教学过程：一、复习引入：1．角的概念的推广⑴“旋转”形成角 ABαO一条射线由原来的位置OA ，绕着它的端点O 按逆时针方向旋转到另一位置OB ，就形成角α．旋转开始时的射线OA 叫做角α的始边，旋转终止的射线OB 叫做角α的终边，射线的端点O 叫做角α的顶点．⑵．“正角”与“负角”“0角”我们把按逆时针方向旋转所形成的角叫做正角，把按顺时针方向旋转所形成并⑶意义用“旋转”定义角之后，角的范围大大地扩大了。

3︒ 还有零角 一条射线，没有旋转角的概念推广以后，它包括任意大小的正角、负角和零角．2．“象限角”角的顶点合于坐标原点，角的始边合于x 轴的正半轴，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角（角的终边落在坐标轴上，则此角不属于任何一个象限）3．终边相同的角结论：所有与α终边相同的角连同α在内可以构成一个集合：{}Z k k S ∈⋅+==,360| αββ即：任何一个与角α终边相同的角，都可以表示成角α与整数个周角的和。

⑷注意以下四点：(1)Z k ∈(2) α是任意角；(3)0360⋅k 与α之间是“+”号，如0360⋅k -30°，应看成0360⋅k +(-30°)；(4)终边相同的角不一定相等，但相等的角，终边一定相同，终边相同的角有无数多个，它们相差360°的整数倍．二、讲解新课：例1写出终边在y 轴上的角的集合（用0到360度的角表示）.解：∵ 在0°～360°间，终边在y 轴的正半轴上的角为90°，终边在y 轴的负半轴上的角为270°，∴终边在y 正半轴、负半轴上所有角分别是：S 1={α|α=k ⋅360︒+90︒,k ∈Z}；S 2={α|α=k ⋅360︒+270︒,k ∈Z}探究：怎么将二者写成统一表达式？∵S 1={α|α=k ⋅360︒+90︒,k ∈Z}={α|α=2k ⋅180︒+90︒,k ∈Z}；S 2={α|α=k ⋅360︒+270︒,k ∈Z}={α|α=2k ⋅180︒+180︒+90︒,k ∈Z}={α|α=(2k+1)⋅180︒+90︒,k ∈Z}；∴终边在y 轴上的角的集合是：S=S 1 S 2={α|α=2k ⋅180︒+90︒,k ∈Z} {α|α=(2k+1)⋅180︒+90︒,k ∈Z}={α|α=180︒的偶数倍+90︒,k ∈Z} {α|α=180︒的奇数倍+90︒,k ∈Z}={α|α=180︒的整数倍+90︒,k ∈Z}={α|α=n ⋅180︒+90︒,n ∈Z}引申：写出所有轴上角的集合{α|α=k ⋅360︒, k ∈Z} {α|α=k ⋅360︒+180︒,k ∈Z} {α|α=k ⋅180︒,k ∈Z}{α|α=k ⋅360︒+90︒,k ∈Z} {α|α=k ⋅360︒+270︒,k ∈Z} {α|α=k ⋅180︒+90︒,k ∈Z}{α|α=k ⋅90︒, k ∈Z} {α|α=k ⋅90︒+45︒, k ∈Z} {α|α=k ⋅45︒, k ∈Z}(最后两个可以根据实际情况处理)例2．用集合的形式表示象限角第一象限的角表示为{α|k ⋅360︒<α<k ⋅360︒+90︒，（k ∈Z ）}；第二象限的角表示为{α|k ⋅360︒+90︒<α<k ⋅360︒+180︒，（k ∈Z ）}；第三象限的角表示为{α|k ⋅360︒+180︒<α<k ⋅360︒+270︒，（k ∈Z ）}；第四象限的角表示为{α|k ⋅360︒+270︒<α<k ⋅360︒+360︒，（k ∈Z ）}；或{α|k ⋅360︒-90︒<α<k ⋅360︒，（k ∈Z ）}。

§1.2.1 任意角的三角函数（二）学习目标：⒈理解有向线段的意义及其方向、数值的规定．⒉能够利用单位圆中的有向线段表示任意角α的正弦、余弦和正切函数值．⒊在从图形角度考察三角函数的过程中，体会数形结合的基本数学思想方法．教学重点：角α的正弦、余弦和正切的几何表示——单位圆中的三角函数线．教学难点：当角α为第二、三象限角时的正切线． 教学方法：讲授、讨论．教具准备：用《几何画板》演示单位圆中的三角函数线． 教学过程：一、复习:1.上节课我们学习了任意角三角函数的定义，请同学们回忆该定义．设任意角α的终边与单位圆交于点(,)P x y ，那么： ⑴ y 叫做α的正弦，记作sin α，即sin y α=； ⑵ x 叫做α的余弦，记作cos α，即cos x α=； ⑶ y x叫做α的正切，记作tan α，即tan y xα=．2.任意角三角函数可以看成是自变量为实数的函数，它们的定义域各是怎样的集合？正弦、余弦函数的定义域都是实数集R ，正切函数的定义域是{|2,}2x x k k Z ππ≠+∈．3.三角函数值的符号是随着角的位置变化而变化的，请说明三角函数值在各象限的符号．三角函数值在各象限内取正值的规律：一全二弦三切四余． 4.三角函数值有“周而复始”的变化规律，即角α的终边每绕原点旋转一周，函数值将重复出现．从那里可以体现这一点呢？终边相同的角的同一三角函数值相等． 5.课前练习:1.(课时训练P5练习3)答案:{-2,0,2}引申: 求函数|sin |cos |tan |sin |cos |tan x x x y x x x=++的值域.2.已知角α的终边落在直线y ＝2x 上，求sin α的值．解析:(1)当角的终边在第一象限时，在角的终边上取点P(1，2)，55252sin 521|OP |22＝＝　得　＝＋＝由α．(2)当角的终边在第三象限时，在角的终边上取点Q(一l ，一2)，55252sin 521|OQ |22＝－－＝　得　＝）＋（－）（－＝由α．上节课我们从“数”的角度认识了任意角的三角函数，本节课我们从图形的角度来考察任意角的三角函数，即任意角三角函数的几何表示——单位圆中的三角函数线． （I ）新课引入：问题1.我们能否通过适当的选取点P 的位置而将上述三个表达式简化一些呢？可以将点P 取在使线段OP 的长1r =的特殊位置上，这样我们就可以得到用直角坐标系内点的坐标表示的锐角三角函数：sin MP b OP α==，cos OM a OP α==，tan MP bOA aα==． ⒈单位圆在直角坐标系中，我们把以原点O 为圆心，以单位长度为半径的圆成为单位圆． ⒉任意角三角函数我们可以利用单位圆定义任意角的三角函数．如图，任意角α的终边与单位圆交于点(,)P x y ，那么：⑴ y 叫做α的正弦，记作sin α，即sin y α=； ⑵ x 叫做α的余弦，记作cos α，即cos x α=；⑶yx叫做α的正切，记作tan α，即tan yxα=． （用《几何画板》演示）如图，角α的终边与单位圆交于点(,)P x y，过点P作x轴的垂线，垂足为M．根据三角函数的定义得==；|||||sin|MP yα==．OM xα|||||cos|为了实现“以形示数”，我们应该用图中的哪些线段来表示点P的坐标y，x呢？应该用线段MP，OM来表示点P的坐标y,x．那么我们就要给线段MP，OM规定一个符号了．显然，使线段MP，OM的符号与点P的坐标y，x的符号一致是最理想的．你能否给线段MP，OM规定一个适当的方向，使它们的取值与点P的坐标y，x一致？请同学们观察线段MP，OM的方向与点P的坐标y，x的关系．（用《几何画板》演示）3.有向线段为了使线段MP，OM的符号与点P的坐标y，x的符号一致，应该以坐标轴的方向为标准，即以坐标轴的方向来规定线段MP，OM的方向．我们把规定了方向的线段称为有向线段．有向线段的端点有始点、终点之分．规定：当角α的终边不在坐标轴上时，线段OM以O为始点、M 为终点；线段MP 以M 为始点、P 为终点． 4.单位圆中的三角函数线规定：当线段OM 与x 轴同向时，OM 的方向为正向，且有正值x ；当线段OM 与x 轴反向时，OM 的方向为负向，且有负值x ．当线段MP 与y 轴同向时，MP 的方向为正向，且有正值y ；当线段MP 与y 轴反向时，MP 的方向为负向，且有负值y ．其中x ，y 为点P 的坐标．在上述规定之下，无论是哪一种情况都有sin MP y α==，cos OM x α==．那么，如何用有向线段来表示角α的正切呢？ 你能根据tan y MP x OMα==在单位圆中作出一条用于表示正切值的有向线段吗？请同学们阅读课本P14第三自然段．（用《几何画板》演示）过(1,0)A 作单位圆的切线，这条切线必然平行于y 轴，设它与角α的终边（当α为第一、四象限角时）或其反向延长线（当α为第二、三象限角时）相交于点T ．根据正切函数的定义和相似三角形的指示，借助有向线段OA 、AT 可以得到tan yAT xα==．这三条与单位圆有关的有向线段MP 、OM 、AT ，分别叫做角α的正弦线、余弦线、正切线，统称为三角函数线.现在，我们在角α的终边不在坐标轴上的前提下定义了三角函数线．那么，当角α的终边落在坐标轴上时，各三角函数线将会怎样呢？当角α的终边与x轴重合时，正弦线、余弦线分别变成一个点，此时角α的正弦值和正切值都是0；当角α的终边与y轴重合时，余弦线变成一个点，正切线不存在，此时角α的正切值不存在．由此进一步验证得:例1.作出下列各角的正弦线、余弦线. （1）6π；（2）32π；（3）－65π；（4）－49π.解析:作角α的正弦线的关键是画出单位圆和角α的终边.（1） （2） （3） （4）各个圆中的有向线段MP 、OM 分别表示各个角的正弦线、余弦线.练习:作出下列各角的正弦线、余弦线、正切线. （1）6π；（2）32π；（3）－65π；（4）－49π.解析:作角α的正弦线的关键是画出单位圆和角α的终边.（1） （2） （3） （4） 各个圆中的有向线段OT 分别表示各个角的正切线.例2.在单位圆中画出适合cos α≤－21的角α终边的范围，并由此写出角α的集合.分析:首先作出满足cos α=－21的角的终边，然后根据已知条件确定角α终边的范围.解析:作直线x =－21交单位圆于C 、D 两点，连结OC 与OD ，则OC 与OD 围成的 区域（如图阴影部分所示）即为角 α终边的范围.故满足条件的角α的集合为 {α|2k π+3π2≤α≤2k π+3π4，k ∈Z}.说明：三角函数线可以用来求出满足形如f （α）≥m 或f （α）≤m 的三角函数的角α的范围.练习1:利用正切函数线解不等式3tan x .答案: 利用图象知，所求解为[,),32k k k Z ππππ++∈2.(课时训练P6练习7)根据下列条件,写出θ的取值范围:(1)tan 1θ>- ; (2)1sin 22θ-≤< .分析:①作出边界值的三角函数线的终边; ②根据已知条件确定角终边的范围.解析: (1)如图(1),θ的取值范围为,.42k k k Z πππθπ-<<+∈(2)如图(2), θ的取值范围为2263k k πππθπ-≤<+或2722,36k k k Z πππθπ+<≤+∈.利用单位圆中的三角函数线，我们可以直观的得到三角函数的一些简单性质．如：⑴|sin ||cos |1αα+≥，其中等号当且仅当2k πα=()k Z ∈时成立； ⑵设02πα<<，则sin tan ααα<<．图1试试证明一下吧!~(1)若θ为锐角，则有2cos sin 1πθθ<+<.证法一：如图1，在扇形OAB 中，∠AOB=900，OA=1，在弧AB 上任取一点P ，连OP ，设∠AOP=θ.过点P 作PD ⊥OA 于D ，PC ⊥OB 于C.则PD=θsin ，PC=θcos ，由图形知，PD+PC>OP=1，PC<弧PB ， PD<弧PA ，所以PC+PD<弧AB=2π， 即2cos sin 1πθθ<+<.证法二：如图2，（假设同方法一）易知， S 三角形OAB <S 四边形OAPB <S 扇形OAB ， 而S 四边形OAPB =S 三角形OAP + S 三角形OBP =)cos (sin 21θθ+， S 三角形OAB =21，S 扇形OAB =4π， 所以，2cos sin 1πθθ<+<.⑵设02πθ<<，则sin tan θθθ<<．证明;S 三角形OAB <S 四边形OAPB <S 扇形OAB <S 三角形OAT ， 111sin tan 222OA OA OA θθθ⨯⨯<⨯⨯<⨯⨯ , ∴sin tan θθθ<< .（Ⅲ）课后练习：课本19P 练习； 25P 习题1.2 B 组 ⒋．图2图1 T（Ⅳ）课时小结：⒈用有向线段表示三角函数值，是三角函数与指数函数、对数函数和幂函数所不同的地方．⒉正弦线、余弦线、正切线分别是正弦、余弦、正切函数的一种几何表示．它们都是与单位圆有关的平行于坐标轴的有向线段，各点的字母是特定的．⒊三角函数线在求解关于三角函数的不等式、三角函数图象的作图等方面也有广泛的应用．（Ⅴ）课后作业：⒈课本P练习⒉19⒉预习课本P～23P，思考下列问题：21⑴同一个角的不同三角函数之间有哪些关系？你能证明这些关系吗？⑵已知角 的一个三角函数值，怎样求另外两个三角函数的值？⑶你能总结一下证明三角恒等式的方法吗？板书设计：。

4-1.2.1 任意角的三角函数（二）【课题】：任意角的三角函数线【学情分析】：（适用于平行班）三角函数是中学数学的重要内容之一，而三角函数线的概念及其应用不仅体现了数形结合的数学思想，又贯穿整个三角函数的教学.借助三角函数线可以推出三角函数公式，求解三角函数不等式，探索三角函数的图像和性质，……可以说,三角函数线是研究三角函数的有利工具.学习本节前,学生已经掌握任意角三角函数的定义,三角函数值在各象限的符号,以及诱导公式一,为三角函数线的寻找做好了知识准备.【教学目标】：（1）复习三角函数的定义、定义域与值域、符号、及诱导公式；（2）掌握利用单位圆中的有向线段分别表示任意角的正弦、余弦、正切函数值，对三角函数的定义域、值域有更深的理解；（3）能利用三角函数线解决一些简单的三角函数问题，如利用三角函数线比较两个同名三角函数值的大小及表示角的范围；（4）培养学生善于观察、勇于探索的数学能力，学习转化思想，提高解题能力.【教学重点】：三角函数线的作法及其简单应用.【教学难点】：利用与单位圆有关的有向线段，将任意角的正弦、余弦、正切函数值分别用它们的几何形式表示出来.【教学突破点】：通过对有向线段的复习，分解教学难点，同时引导学生动手画图操作，通过观察、分析，获得新知.【教法、学法设计】：（1）教法选择：“引出问题、温故知新、分解难点、引导讨论、巩固应用”——启发式教学（2）学法选择：类比，达到知识迁移；动手实验，以理解知识；分析讨论，学会应用知识. 【课前准备】：课件起点，正弦线和正切线以此线段与坐标轴的公共点为起点，其中点A为定点（1，0）.六、巩固训练，提高能力例1 作出下列各角的正弦线、余弦线、正切线：（1）3π；（2）136π-．学生先做,然后投影展示一个学生的作品,并强调三角函数线的位置和方向.解：图略．例2 利用三角函数线比较下列各组数的大小：(1)32sinπ与54sinπ;(2) cos32π与cos54π; (3) tan32π与tan54π解：如图可知：32sinπ>54sinπcos32π>cos54πtan32π< tan54π学生先做，教师引导学生利用三角函数线解题，并投影展示一个学生作品，强调数形结合思想．例3利用三角函数线画出适合下列条件的角α的终边：（1）21sin=α；（2）21cos-=α；（3）1tan=α.共同分析（1），设角α的终边与单位圆交于P(yx,),则αsin=y,所以要作出满足21sin=α的角的终边，只要在单位圆上找出纵坐标为21的巩固练习,准确掌握三角函数线的作法.巩固新知，提高运用知识的能力体会三角函数线的用处和实质.逆向思维,灵活运用三角函数线,并为利用三角函数线求解三角函数不等式(组)作铺垫.oBAT2T1P2 P1M2M1。

四队中学教案纸 （ 学科： 高一数学 ）备课时间教学课题教时计划2教学课时2教学 目标 1.正确寻找角之间的关系，选用恰当的公式解决问题；2.能将简单的几何问题化归为三角问题，培养学生的数学转换能力及分析问题的能力。

重点难点选用恰当的方法解决问题选用恰当的方法解决问题教学过程（一）复习：()T αβ±公式及变形公式.（二）新课讲解：例1：在非直角ABC ∆中，（1）求证：tan tan tan tan tan tan A B C A B C ++=；（2）若,,A B C 成等差数列，且tan tan 23A C =+，求ABC ∆的三内角大小。

（1）证明：∵A B C π++=，∴tan()tan A B C +=-， ∴tan tan tan tan()(1tan tan )A B C A B A B ++=+-tan C +tan (1tan tan tan )tan C A B C C =--+ tan tan tan A B C =；（2）解：,,A B C 成等差数列，∴2B A C =+， 又A B C π++= ， ∴60B =， ∴120A C +=，tan tan tan()(1tan tan )A C A C A B +=+-∴3[1(23)]=--+33=+， 又∵tan tan 23A C =+，tan 1tan 23A C =⎧⎪⎨=+⎪⎩∴ 或tan 23tan 1A C ⎧=+⎪⎨=⎪⎩所以，456075A B C ⎧=⎪=⎨⎪=⎩或756045A B C ⎧=⎪=⎨⎪=⎩．例2：已知2tan()5αβ+=，1tan()44πβ-=，求tan()4πα+的值。

解：tan()4πα+tan[()()]4παββ=+--tan()tan()41tan()tan()4παββπαββ+--=++-213542122154-==+⨯． 【变题】：已知2cot 2,tan()3ααβ=-=-，求tan(2)βα-的值。

高中数学 第1章《三角函数》任意角的三角函数(2)教学案
苏教版必修4
教学目标：了解如何运用与单位圆有关的有向线段，将任意角的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来，并能作出三角函数线。

促进学生对数形结合
思想的理解与感悟。

教学重点：三角函数线的探究与作法 教学难点：三角函数线的探究与作法
教学过程：
一、问题情境：
设点P(x,y)是α终边上的任意一点(r=22x y +)，
sin α=_____,cos α=_____,tan α=_____.
问题：三角函数的几何表示又如何呢？
二、学生活动：
探究：1、为简化上式可令r=____,则sin α=_____,cos α=_____,tan α=_____.此时，点P 的位置在哪？可如何取得？
2、在上述条件下，若α是锐角，sin α=____=_____,cos α=____=______,
tan α=____=_____.若α是任意角，结论还成立吗？
3、如何解决这个问题？
三、知识建构：
1、有向线段：
有向线段的数量：
2、正弦线：
3、余弦线：
4、正切线：
x y O M P
四、知识运用：
例1、比较大小：（1）sin1______sin60°（2）c os 4
7
π______cos
5
7
π
练习：书 P15 7、 8
五、回顾反思：
知识：思想方法：
六、作业布置：
书P22 习题1.2 2（2）（4）、 3。

第六课时 任意角的三角函数(二)教学目标：理解并掌握终边相同的角的同一三角函数值相等，使学生认识到规律是客观存在的，只要用心去找，认真寻求，就不难发现，不难认识.客观世界中的事物也是这样，要善于发现规律，认识规律，掌握规律，利用规律，按照事物的发展规律去办事.教学重点：各种三角函数在各象限内的符号，终边相同的角的同一三角函数值相等. 教学难点：各种三角函数在各象限内的符号. 教学过程： Ⅰ.复习回顾任意角三角函数的定义 Ⅱ.讲授新课三角函数的定义告诉我们，各三角函数值实质上是个比值，因此，各三角函数在各象限内的符号，取决于x 、y 的符号(因为r 恒大于零).因为P 点在第一、第二象限时，纵坐标y ＞0，P 点在第三、第四象限时，纵坐标y ＜0，所以正弦函数值对于第一、第二象限角是正的，对于第三、第四象限角是负的.请同学们仿照我们讨论正弦函数值在各象限内符号的方法，回答余弦函数值在各象限内的符号.余弦函数值的正负取决于P 点横坐标x 的正负，因为P 点在第一、第四象限时，横坐标x ＞0，P 点在第二、第三象限时，横坐标x ＜0，所以余弦函数值对于第一、第四象限角是正的，对于第二、第三象限角是负的.对于正切函数值，其正负怎样确定呢?正切函数值 yx 的正负，取决于x 、y 的符号是否相同.因为P 点在第一象限时，x 、y 同正，P 点在第三象限时，x 、y 同负，此时 yx ＞0，P 点在第二、第四象限时，x 、y 异号，此时 yx ＜0，所以正切函数值对于第一、第三象限角是正的，对于第二、第四象限角是负的.Ⅲ.例题分析［例1］确定下列三角函数值的符号(1)cos250° （2）sin （－π4 ） （3）tan （－672°） （4）tan 11π3 解：(1)∵250°是第三象限角，∴cos250°＜0(2)∵－π4 是第四象限角，∴sin （－π4 ）＜0(3)tan （－672°）＝tan （48°－2×360°）＝tan48° 而48°是第一象限角，∴tan （－672°）＞0(4)tan 11π3 ＝tan （5π3 ＋2π）＝tan 5π3 而5π3 是第四象限角，∴tan 11π3 ＜0.［例2］如果点P （2a ，－3a )(a ＜0)在角θ的终边上，求sin θ、cos θ、tan θ的值.分析：依据点P （2a ，－3a )(a ＜0)坐标，可以在一直角三角形中利用任意角的三角函数定义求.解：如图，点P （2a ，－3a )(a ＜0)在第二象限，且r ＝－13 a ， ∴sin θ＝－3a r ＝－3a －13a＝31313 cos θ＝2a r ＝2a －13a ＝－21313tan θ＝－3a 2a ＝－32［例3］已知角θ的终边在直线y ＝－3x 上，求10sin θ＋3cos θ的值.分析：依据θ的终边在直线y ＝－3x 上，可设出其终边上任一点P （m ，－3m ），再对m ＞0与m ＜0分别讨论.解：设P （m ，－3m )是θ终边上任一点，则 r ＝x 2＋y 2 ＝m 2＋（－3m ）2 ＝10 |m | 当m ＞0时，r ＝10 m .∴sin θ＝－3m 10m ＝－31010，1cos θ ＝10mm ＝10∴10sin θ＋3cos θ ＝－310 ＋310 ＝0当m ＜0时，r ＝－10 m ∴sin θ＝3m 10m＝310101cos θ＝－10m m ＝－10 ∴10sin θ＋3cos θ ＝310 －310 ＝0综上，得10sin θ＋3cos θ＝0Ⅳ.课堂练习课本P 16练习 4、5、6、7、8. Ⅴ.课时小结本节课我们重点讨论了三角函数在各象限内的符号，这是我们日后学习的基础，经常要用，请同学们熟记.Ⅵ.课后作业课本P23习题4、5、6.任意角的三角函数(二) 1．已知角θ的终边过点P（－4a，3a)a≠0，则2sinθ＋cosθ的值是（）A.25 B.－25 C.25或－25 D.不确定2．设A是第三象限角，且|sin A2|＝－sinA2，则A2是（）A.第一象限角B.第二象限角C.第三象限角D.第四象限角3．sin2cos3tan4的值（）A.大于0B.小于0C.等于0D.不确定4．已知|cosθ|＝cosθ，|tanθ|＝－tanθ，则θ2的终边在（）A.第二、四象限B.第一、三象限C.第一、三象限或x轴上D.第二、四象限或x轴上5．若sinθ·cosθ＞0，则θ是第象限的角.6．若α的余弦线为0，则它的正弦线的长度为.7．角α（0＜α＜2π）的正弦线与余弦线的长度相等且符号相同，则α的值为.8．已知α是第三象限角，试判定sin（cosα)·cos(sinα)的符号.9．已知：P（－2，y）是角α终边上一点，且sinα＝－55，求cosα的值.10．已知角α的终边经过P（8m，6m）(m≠0)，求log2|1cosα－tanα|的值.任意角的三角函数(二)答案1．C 2．D 3．B 4．D 5．一、三 6．1 7．π4 或5π48．已知α是第三象限角，试判定sin （cos α)·cos(sin α)的符号.分析：依据α是第三象限角可得cos α＜0且－1＜cos α＜0，与sin α＜0 且－1＜sin α＜0，进而确定式子sin （cos α)·cos(sin α)的符号. 解：∵α是第三象限角∴－1＜cos α＜0，－1＜sin α＜0， ∴sin(cos α)＜0，cos(sin α)＞0. ∴sin(cos α)·cos(sin α)＜09．已知：P （－2，y ）是角α终边上一点，且sin α＝－55，求cos α的值. 由P （－2，y ）且sin α＝－55＜0知y ＜0 又22)2(y y+-＝－55，y 2＋4＝5y 2，y 2＝1∴y ＝－1 ∴cos α＝242y +-＝52-＝－25510．已知角α的终边经过P （8m ，6m ）(m ≠0)，求log 2|1cos θ －tan α|的值.分析：依据点P （8m ，6m ）(m ≠0)的坐标，求出1cos θ 及tan α的值，进而求出log 2|1cos θ－tan α|的值.解：∵P （8m ，6m )(m ≠0)，∴r ＝10|m | 当m ＞0时，r ＝10m∴1cos θ ＝54 ，tan α＝34 ， ∴log 2|1cos θ －tan α|＝log 212 ＝－1 当m ＜0时，r ＝－10m ∴1cos θ ＝－54 ，tan α＝34 ， ∴log 2|1cos θ －tan α|＝log 22＝1 综上，得log 2|1cos θ －tan α|＝⎩⎨⎧<>-)0( 1)0( 1m m。