2014年河南省普通高中毕业班高考适应性模拟练习文科数学试题
- 格式:doc
- 大小:2.63 MB
- 文档页数:8

2014年普通高等学校招生全国统一考试模拟卷(一)文科数学一、选择题:(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.) 1. 已知集合2{|320}A x x x =-+<,41{|log }2B x x =>,则( )A .AB ⊆ B .B A ⊆C .R A C B R =D .AB =∅2。
已知复数521i i z +=,则它的共轭复数z 等于( )A .2i -B .2i -+C .2i +D .2i --3。
.命题“2cos sin ,,2>-⎥⎦⎤⎢⎣⎡∈∃x x x ππ”的否定是( )A .2cos sin ,,2<-⎥⎦⎤⎢⎣⎡∈∀x x x ππB .2cos sin ,,2≤-⎥⎦⎤⎢⎣⎡∈∀x x x ππC .2cos sin ,,2≤-⎥⎦⎤⎢⎣⎡∈∃x x x ππD .2cos sin ,,2<-⎥⎦⎤⎢⎣⎡∈∃x x x ππ 4.已知,αβ是两个不同的平面,下列四个条件中能推出//αβ的是( )①在一条直线,,a a a αβ⊥⊥, ③存在两条平行直线,,,,//,//a b a b a b αββα⊂⊂;②存在一个平面,,γγαγβ⊥⊥; ④存在两条异面直线,,,,//,//a b a b a b αββα⊂⊂。
A.①③B.②④C.①④D.②③5.已知平面向量,m n 的夹角为,6π且3,2m n ==,在ABC ∆中,22AB m n =+,26AC m n =-,D 为BC 中点,则AD =( )A.2B.4 C 。
6 D 。
86.能够把圆O :1622=+y x 的周长和面积同时分为相等的两部分的函数称为圆O 的“和谐函数",下列函数不是..圆O 的“和谐函数"的是( ) A .3()4f x xx =+B .5()15x f x n x-=+ C .()xx f x ee -=+D .()tan 2x f x =7.已知sin α+错误!cos α=错误!,则tan α=( ) A .错误! B .错误! C .- 错误! D .-错误! 8.已知等比数列{}na 的前An 项和为nS ,且1352a a +=,2454aa +=,则n n S a =( )A .14n - B .41n- C .12n - D .21n-9.执行如图所示的程序框图后,输出的值为4,则P 的取值范围是 ( )A . 715816P <≤ B.1516P >C . 715816P ≤< D. 3748P <≤1 0.已知实数,x y 满足2102101x y x y x y -+≥⎧⎪--≤⎨⎪+≤⎩,则347x y +-的最大值为( )A .11B .12C .13D .14 11.设双曲线C 的中心为点O ,若有且只有一对相交于点O ,所成的角为60°的直线A 1B 1和A 2B 2,使11A B =22A B ,其中A 1,B 1和A 2,B 2分别是这对直线与双曲线C 的交点,则该双曲线的离心率的取值范围是( )(A)2323⎛⎤ ⎥ ⎝⎦(B)2323⎡⎫⎪⎢⎪⎣⎭(C)33⎛⎫+∞ ⎪ ⎪⎝⎭ (D )233⎡⎫+∞⎪⎢⎪⎣⎭ 12.已知函数()3111,0,36221,,112x x f x x x x ⎧⎡⎤-+∈⎪⎢⎥⎣⎦⎪=⎨⎛⎤⎪∈ ⎥⎪+⎝⎦⎩,函数()()sin 220,6g x a x a a π⎛⎫=-+> ⎪⎝⎭若存在[]12,0,1x x ∈,使得()()12f x g x =成立,则实数a 的取值范围是( )A 。
2014年河南省普通高中毕业班高考适应性测试数学(文)试卷一、选择题:本大题共12小题,每小题5分。
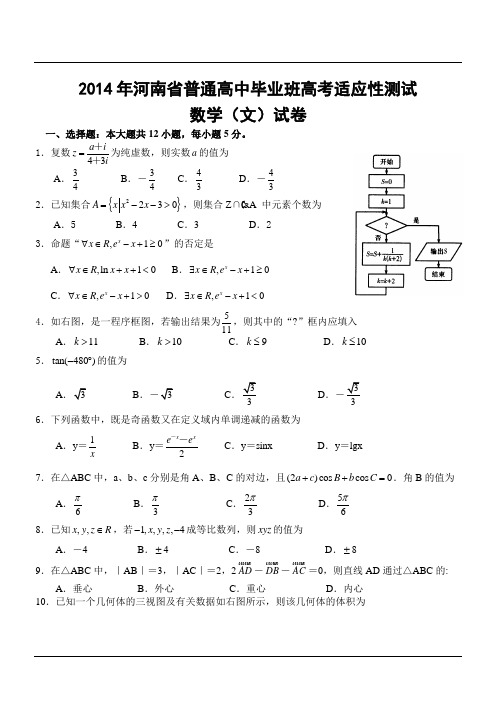
1.复数43a iz i =++为纯虚数,则实数a 的值为A .34B .-34C .43D .-432.已知集合{}2230A x x x =-->,则集合Z ∩C R A 中元素个数为A .5B .4C .3D .2 3.命题“,10x x R e x ∀∈-+≥”的否定是A .,ln 10x R x x ∀∈++<B .,10x x R e x ∃∈-+≥C .,10x x R e x ∀∈-+>D .,10x x R e x ∃∈-+<4.如右图,是一程序框图,若输出结果为511,则其中的“?”框内应填入 A .11k > B .10k > C .9k ≤ D .10k ≤5.tan(480)-︒的值为A .B .-CD 6.下列函数中,既是奇函数又在定义域内单调递减的函数为A .y =1xB .y =2x xe e -- C .y =sinx D .y =lgx7.在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且(2)cos cos 0a c B b C ++=.角B 的值为 A .6π B .3π C .23π D .56π8.已知,,x y z R ∈,若1,,,,4x y z --成等比数列,则xyz 的值为A .-4B .±4C .-8D .±8 9.在△ABC 中,|AB |=3,|AC |=2,2AD u u u r -DB uu u r -AC uuu r=0,则直线AD 通过△ABC 的: A .垂心 B .外心 C .重心 D .内心 10.已知一个几何体的三视图及有关数据如右图所示,则该几何体的体积为A .2 B.3 CD.311.已知圆22213x y a +=与双曲线2221(0,0)x a b a b>>2y -=的右支交于A ,B 两点,且直线AB 过双曲线的右焦点,则双曲线的离心率为 A. BC .2D . 312.已知函数0,(),0.x x f x x x ≤⎧=⎨>⎩+2,ln 若函数()y f x k =-的零点恰有四个,则实数k 的取值范围为A .(1,2]B .(1,2)C .(0,2)D .(0,2] 二、填空题:本大题共4小题,每小题5分.13.实数x ,y 满足条件40,220,00,x y x x y ≤⎧⎪≥⎨⎪≥≥⎩+--y +,则x -y 的最小值为_________.14.已知数列{n a }的通项公式为n a =32,n n n n ,⎧⎨⎩-11-为偶数,为奇数.则其前10项和为____________.15.在平面直角坐标系xOy 中,F 是抛物线C :2x =2py (p >0)的焦点,M 是抛物线C 上位于第一象限内的任意一点,过M ,F ,O 三点的圆的圆心为Q ,点Q 到抛物线C 的准线的距离为34.则抛物线C 的方程为___________16.已知四棱锥P -ABCD 的底面是边长为a 的正方形,所有侧棱长相等且等于2a ,若其外接球的半径为R ,则aR等于____________三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知函数()()2sin()(0,f x x πϕϕπ=+∈的一条对称轴为16x =.(Ⅰ)求ϕ的值,并求函数()f x 的单调增区间;(Ⅱ)若函数()f x 与x 轴在原点右侧的交点横坐标从左到右组成一个数列{n a },求数列{11n n a a +}的前n 项和n S . 18.(本小题满分12分)如图,在直三棱柱ABC -A 1B 1C 1中,∠ACB =90°,E ,F ,D 分别是AA 1,AC ,BB 1的中点,且CD ⊥C 1D . (Ⅰ)求证:CD ∥平面BEF ;(Ⅱ)求证:平面BEF ⊥平面A 1C 1D .19.(本小题满分12分) 为了构建和谐社会建立幸福指标体系,某地区决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).(Ⅰ)求研究小组的总人数;(Ⅱ)若从研究小组的公务员和教师中随机选3人撰写研究报告,求其中恰好有1人来自教师的概率.20.(本小题满分12分)过点C (0的椭圆2221x a b 2y +=(0a b >>)的离心率为12,椭圆与x 轴交于(),0A a 和(),0B a -两点,过点C 的直线l 与椭圆交于另一点D ,并与x 轴交于点P ,直线AC 与直线BD 交于点Q .(Ⅰ)当直线l 过椭圆的右焦点时,求线段CD 的长;(Ⅱ)当点P 异于点B 时,求证:OP uu u r ·OQ uuu r为定值.21.(本小题满分12分)函数()f x 的定义域为D ,若存在闭区间[a ,b]⊆D ,使得函数()f x 满足:(1)()f x 在[a ,b]内是单调函数;(2)()f x 在[a ,b]上的值域为[ka ,kb],则称区间[a ,b]为()y f x =的“和谐k 区间”.(Ⅰ)试判断函数2()g x x =,()ln h x x =是否存在“和谐2区间”,若存在,找出一个符合条件的区间;若不存在,说明理由.(Ⅱ)若函数()x f x e =存在“和谐k 区间”,求正整数k 的最小值;请考生在第22、23、24三题中任选一题做答.如果多做。

中原名校2014年高考仿真模拟统一考试(文数答案)17.解:(1)由1323244,=221=+a a a a a a 得,又()=+解得:2q = 12n n a -\= n b n \=………………………………………………………………(6分)(2)12(21)2n+1nn c n =+-()………………………………………………………(8分)\23111222.......21335(21)(21)n n s n n =+++++++创-? 2(12)111111(1.......)1223352121n n n -=+-+-++---+1n 222n+1n +=-+……(12分)……………………………………(2分)2800(60=160K 5分)\能在犯错误不超过0.001的前提下认为该校学生的数学与化学成绩有关系(6分) (2)设其他学生为丙和丁,4人分组的所有情况如下:(甲乙,丙丁),(甲丙,乙丁),(甲丁,乙丙),(乙丙,甲丁),(乙丁,甲丙),(丙丁,甲乙)基本事件共六种, 记“学生甲分到负责收集成绩组,学生乙分到负责数据处理”为事件A,则A 包含的基本事件为(甲丙,乙丁),(甲丁,乙丙)共两种21()63P A == ………………………………………………………………(12分)19. 解:(1) 证明:设ACBD O =,连接OH ,在ACF ∆中,因为OA OC =,CH HF =, 所以//OH AF ,又因为AF ⊄平面BDGH ,OH ⊂平面BDGH ,所以//OH 平面BDGH . ………………………………………………(6分) (2)解:因为四边形ABCD 是正方形,所以AC BD ⊥. 又因为平面BDEF ⊥平面ABCD ,平面BDEF 平面ABCD BD =,且AC ⊂平面ABCD ,所以AC ⊥平面BDEF . 得 AC ⊥平面BDEF ………………………………………(8分) 则H 到平面BDEF 的距离为CO 的一半又因为AO =,三角形BEF的面积132BEF S ∆=⨯⨯=所以1132E BHF B EFH V V --==⨯=………………………………………………(12分) 20. 解:(1)设动点P 坐标为(,)x y ,当2x ≠±时,由条件得:22y y x x ⋅=-+1-4,化简得221(2)4x y x =≠±+ 曲线E 的方程为,221(2)4x y x =≠±+,………………4分(说明:不写2x ≠±的扣1分)⎪⎪⎩⎪⎪⎨⎧=+-=145622y x ky x ,化简得:02564512)4(22=--+ky y k所以090MAN ∠=,所以MAN ∠的大小为定值 …………………………(8分)(Ⅱ)121||||2S AB y y =⋅-1|22|2=⋅+==令224,(4),4,k t t k t +=≥∴=-S∴=22432536252(2536)2572(),()t t t t t f t f t t t t -----+'=∴==4,()0t f t '≥∴<()y f t ∴=在[)4,+∞上单调递减.10036()(4)416f t f -∴≤== 由4t =,得K=0,此时S 有最大值16…………………(12分) 21. 解:(1)2'()()'()xf x f x F x x -=因为'()()0xf x f x ->在(0,)+ 上恒成立 所以'()0F x >在(0,)+ 上恒成立所以()F x 的单增区间是(0,)+ ,无单减区间………………………………………(3分) (2)1'()2(0)f x ax x x=+> 因为'()()0xf x f x ->在(0,)+ 上恒成立所以21(2)(ln )0x ax x ax x+-+>在(0,)+ 上恒成立 即2ln 1x a x->在(0,)+ 上恒成立………………………………………(4分) 设2ln 1()x h x x -= 则332ln '()xh x x-= 令'()0h x =得32x e =当32(0,)x e Î时,'()0h x >;当32(,)x e ? 时,'()0h x < 故函数()h x 在32(0,)e 上单调递增,在32(,)e + 上单调递减, 所以32max 31()()2h x h e e==,所以312a e >.…………………………………(8分) (3)因为0x 是()f x 的零点,所以0()0f x = 由(1)知,()F x 在(0,)+ 上单调递增, 所以当0(0,)x x Î时,0()()F x F x <,即00()()0f x f x x x <=所以当0(0,)x x Î时,()0f x <因为0,(0,)m n x Î,所以()0,()0f m f n <<,且()(),()()F m F m n F n F m n <+<+ 即()()()(),f m f m n f n f m n m m n n m n++<<++ 所以()()()()()mf m n nf m n f m f n f m n m n m n+++<+=+++所以()1()()f m n f m f n +<+…………………………………………………………………(12分)22. 解:(I)连接BC ,则90=∠=∠APE ACB , 即B 、P 、E 、C 四点共圆. ∴CBA PEC ∠=∠又A 、B 、C 、D 四点共圆, ∴PDF CBA ∠=∠∴PDF PEC ∠=∠ …………………………(5分)(II)∵PDF PEC ∠=∠,∴F 、E 、C 、D 四点共圆,∴PD PC PF PE ⋅=⋅,又24)102(2=+⨯=⋅=⋅PA PB PD PC ,24=⋅PF PE …………………………(10分)23.解:(I)由θθρcos 4sin2=,得θρθρcos 4)sin (2=所以曲线C 的直角坐标方程为x y 42=…………………………(4分)两点对应的参数分别为t 1+t 22-当2a =时,|AB |的最小值为4 …………………………(10分)13+ 得:313ax -? 即42ax -#当0a >时,42x a a-#原不等式的解集是{}12x x-#4122aa ìïï-=-ïï\íïï=ïïïî,无解; 当0a <时,24x aa#-原不等式的解集是{}12x x-#4221aa ìïï-=ïï\íïï=-ïïïî,得2a =- ……………………………………………………………………………………………(5分)(2)由题:2121()()11()2222x x f x f x g x x x -++++-===-++解得:11k k <->或…………………………………………………………………(10分)。

2014届高三毕业班第二次模拟考试 数学(文)参考答案 一、选择题二、填空题三、解答题18.(Ⅰ)解:依题意,得,解得. ·······3分 19.(1)∵底面,∴ 又∴面 ∴······① , ·······3分 又,且是的中点,∴·········② 由①②得面 ∴. 又 ∴面 ∴平面平面 ······ 6分 (2)∵是的中点,∴. ·····9分. ····· 12分 (II)当时,直线与椭圆交于两点的坐标分别为 , 设y轴上一点,满足, 即, ∴解得或(舍), 则可知满足条件,若所求的定点M存在,则一定是P点. ·······6分 下面证明就是满足条件的定点. 设直线交椭圆于点,. 由题意联立方程 ·······8分 , ·······9分 ∴ . ·······11分 ∴ ,即在y轴正半轴上存在定点满足条件. ·······12分 (II). ①由(1)知,是函数的极值点, 又函数与有相同极值点,是函数的极值点, ,解得. ·······4分 经验证,当时,函数在时取到极小值,符合题意. ·······5分 ②, 易知,即. ···6分 由①知, 当时,;当时,. 故在上为减函数,在上为增函数. , 而. . ·······7分 当,即时,对于,不等式恒成立. , . ·······9分当,即时,对于,不等式恒成立. , ······11分 综上,所求实数的取值范围为. ·······12分 23.解:(1)直线即直线的直角坐标方程为,点在直线上。

河南省实验中学2014届高三二测模拟卷数学(文科)【试卷综析】试卷贴近中学教学实际,在坚持对五个能力、两个意识考查的同时,注重对数学思想与方法的考查,体现了数学的基础性、应用性和工具性的学科特色.以支撑学科知识体系的重点内容为考点来挑选合理背景,考查更加科学.试卷从多视角、多维度、多层次地考查数学思维品质,考查考生对数学本质的理解,考查考生的数学素养和学习潜能.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】1.集合P={3,4,5},Q={6,7},定义},|),{(*Q b P a b a Q P ∈∈=,则Q P *的子集个数为A .7B .12C .32D .64 【知识点】集合及运算. A1【答案解析】D 解析:()()()()()(){}*=3,63,74,64,75,65,7P Q ,,,,,,所以P*Q 中有6个元素,所以P*Q 的子集个数为62=64,故选D.【思路点拨】由P*Q 定义得P*Q 中元素个数为6,所以P*Q 的子集个数为62=64. 【题文】2.已知复数2ii ia b -=+(a ,b ∈R ,i 为虚数单位),则2a b -= A. 1 B. 2 C. 3 D.4【知识点】复数的运算. L4 【答案解析】C 解析:由2ii i a b -=+得121232a a i i a b b =-⎧-=-+⇒⇒-=⎨=-⎩, 故选C.【思路点拨】利用复数乘法及复数相等条件,得a,b 值,从而求得a-2b 值. 【题文】3. “p 或q ”为真命题是“p 且q ”为真命题的 A .充要条件 B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 【知识点】充分条件;必要条件. A2【答案解析】C 解析:因为命题:若“p 或q ”为真命题则“p 且q ”为真命题,是假命题;而命题:若“p 且q ”为真命题则p 或q ”为真命题,是真命题.所以“p 或q ”为真命题是“p 且q ”为真命题的必要不充分条件.故选C.【思路点拨】根据:若p 则q 为假命题,若q 则p 为真命题时,p 是q 的必要不充分条件得结论.【题文】4.一个几何体的三视图如图所示,则该几何体的体积是A .6B .8C .10D .12 【知识点】空间几何体的三视图. G2【答案解析】D 解析:该几何体是两个全等的斜四棱 柱对接而成的几何体,其中每个四棱柱是底面邻边长分 别为3, 2的长方形,高为1,所以该几何体的体积为:2321⨯⨯⨯=12.故选D.【思路点拨】由几何体的三视图得该几何体的结构,该几何体是两个全等的斜四棱 柱对接而成的几何体,进而求得该几何体的体积.【题文】5.已知数阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛333231232221131211aa aa a aa a a 中,每行的3个数依次成等差数列,每列的3个数也依次成等差数列,若822=a ,则这9个数的和为A .16B .32C .36D .72 【知识点】等差数列. D2【答案解析】D 解析:根据等差数列的性质得: 11121312212223223,3a a a a a a a a ++=++=,313233323a a a ++=,且122232223a a a a ++=,所以这9个数的和为:()122232223339872a a a a ++=⨯=⨯=,故选D.【思路点拨】根据等差数列的性质求解.【题文】6.如图所示的程序框图,它的输出结果是A .3B .4C .5D .6 【知识点】算法与程序框图. L1【答案解析】 C 解析:由框图可知循环的结果依次为:(1)90,2k α==,(2)135,3,k α==(3)180,4,k α== (4)225,5k α== ,此时满足sin cos αα<,所以输出k=5,故选C.【思路点拨】依次写出循环结果可得输出的k 值. 【题文】7.已知三个数2,m ,8构成一个等比数列,则圆锥曲线2212x y m +=的离心率为A .2B .C.2或D.2或2【知识点】等比数列;圆锥曲线. D3 H5 H6【答案解析】 C 解析:因为2,m ,8构成等比数列,所以2164,m m =⇒=±当m=4时,圆锥曲线2212x y m +=;当m=-4时,圆锥曲线2212x y m +=为双曲C.【思路点拨】由2,m ,8成等比数列得m 值,由m 值确定圆锥曲线2212x y m +=是椭圆还是双曲线,进而求得相应的离心率.【题文】8.若0≥a ,0≥b ,且当⎪⎩⎪⎨⎧≤+≥≥100y x y x 时,恒有≤+by ax 1,则以b a ,为坐标的点),(b a P 所形成的平面区域的面积是 A .21 B .4π C .1 D .2π 【知识点】简单的线性规划;不等式恒成立. E5 E1【答案解析】 C 解析:不等式组001x y x y ≥⎧⎪≥⎨⎪+≤⎩表示的区域是以点(0,0),(1,0),(0,1)为顶点的三角形及其内部,当a,b 中有的取0时,满足条件得点是点或线段,其面积为0,当a>0,b>0时,要恒有≤+by ax 1,即恒有111x y a b +≤,则1111ab⎧≥⎪⎪⎨⎪≥⎪⎩,解得0101a b <≤⎧⎨<≤⎩,所以以b a ,为坐标的点),(b a P 所形成的平面区域的面积是111⨯=,故选C.【思路点拨】若0≥a ,0≥b ,且当⎪⎩⎪⎨⎧≤+≥≥100y x y x 时,恒有≤+by ax 1,则直线1ax by +=在不等式组001x y x y ≥⎧⎪≥⎨⎪+≤⎩表示的区域的上方,由此得 a,b 满足的条件.【题文】9.在平行四边形ABCD 中,1,60AD BAD =∠=,E 为CD 的中点.若12AD BE ⋅= ,则AB 的长为 A.12 B.1 C .32D .2 【知识点】向量的线性运算;向量的数量积. F1 F3【答案解析】D 解析:设AB 长为x ,则CE 长12x ,又1,,2BC AD CE BA == 所以12BE BC CE AD BA =+=+ ,所以12AD BE AD AD BA ⎛⎫⋅=⋅+ ⎪⎝⎭()21111cos12022AD AD BA x =+⋅=+⨯⨯⨯ =14x -=12,所以x=2,故选D.【思路点拨】 根据向量加法的三角形法则,将BE 用,AB AD表示,再利用向量数量积的定义式求线段ABG 的长.【题文】10.过抛物线)0(22>=p px y 的焦点F ,斜率为34的直线交抛物线于A ,B 两点,若(1)AF FB λλ=>,则λ的值为A .5B .4C .34 D .25 【知识点】抛物线及其几何性质;直线与圆锥曲线. H7 H8【答案解析】B 解析:不妨取p=2,则直线AB 方程为4x-3y-4=0,代入抛物线方程消去x 得2340y y --=,解得124,1y y ==-. 因为(1)AF FB λλ=>,所以设A ()()12,4,,1xB x -,又F (1,0),所以()()121,41,1x x λ--=--,所以44λλ-=-⇒=, 故选B.【思路点拨】把直线AB 方程代入抛物线方程消去x ,解得点A,B 的纵坐标,用坐标表示条件(1)AF FB λλ=>,利用A,B 的纵坐标求得λ值.【题文】11.已知函数()f x 对定义域R 内的任意x 都有()f x =(4)f x -,且当2x ≠时,其导函数()f x '满足()2()xf x f x ''>,若24a <<,则有A. 2(2)(3)(l o g)af f fa << B. 2(3)(log )(2)a f f a f << C. 2(l o g )(3)(2)af a f f<< D. 2(log )(2)(3)a f a f f << 【知识点】函数的对称性、单调性. B1 B3【答案解析】C 解析:由()f x =(4)f x -得()()22f x f x +=-,所以函数()f x 图像关于x=2对称,由()2()xf x f x ''>得()()20x f x '->,所以x>2时,()0f x '>,所以()f x 是()2,+∞的增函数,因为2<a<4,所以224,1log 2a a ><<, 2log a 关于x=2的对称的数是24log a -,且224log 3a <-<,所以24log a -<3<2a,所以选C.【思路点拨】根据题设条件得函数()f x 的对称性和单调性,利用对称性把自变量取值化到 同一单调区间上,再利用单调性得结论.【题文】12.函数[]11,0,2()1(2),(2,)2x x f x f x x ⎧--∈⎪=⎨-∈+∞⎪⎩,则下列说法中正确命题的个数是①函数()ln(1)y f x x =-+有3个零点; ②若0x >时,函数()k f x x ≤恒成立,则实数k 的取值范围是3,2⎡⎫+∞⎪⎢⎣⎭; ③函数()f x 的极大值中一定存在最小值,④)(),2(2)(N k k x f x f k ∈+=,对于一切[)0,x ∈+∞恒成立.A .1B .2C .3D .4【知识点】分段函数的图像;函数的零点;不等式恒成立;函数的极值. B1 B9 E1 【答案解析】B 解析:函数()()[]*11121,22,2,2n f x x n x n n n N -⎡⎤=---∈-∈⎣⎦ 其图像为① 函数()ln(1)y f x x =-+的零点个数,即函数()y f x =与函数()ln 1y x =+的交点个数,由由图可知两函数交点个数是2,故①不正确;②因为函数()y f x =的极大值点是*21,x n n N =-∈,极大值是112n -,所以0x >时,函数()kf x x≤恒成立,即11121,2122n n k n k n ---≥⇒≥-在*n N ∈时恒成立,因为1212n n --在2n =时有最大值32,所以32k ≥,故②正确;③由函数()y f x =的图像可知,函数()f x 的极大值中不存在最小值故③不正确;④由函数解析式可知,当[]*22,2,x k k k N ∈-∈时,()()2222,22x k k k +∈-⎡⎤⎣⎦,所以()()()211222122212k k k f x k x k k -⎡⎤+=⋅-+-⋅-⎣⎦()()111212k x k f x -⎡⎤=---=⎣⎦,当0k =时,显然成立,故④正确.所以选B. 【思路点拨】变形已知函数得()()[]*11121,22,2,2n f x x n x n n n N -⎡⎤=---∈-∈⎣⎦, 由图像可知①、③不正确;对于②由不等式恒成立条件求k 范围即可;对于④将2(2),()k f x k k N +∈的表达式求出,其与()f x 表达式相同,故④正确.二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题纸的相应位置. 【题文】13.若非零向量,满足||||=,0)2(=⋅+,则a 与b 的夹角为______. 【知识点】向量的数量积;向量的夹角. F3【答案解析】120解析:由()22(2)22cos 0a b b a b ba b b θ+⋅=⋅+=+=及a b = 得1cos 2θ=-,因为[]0,θπ∈,所以120θ=【思路点拨】由向量向量数量积的运算律,及向量数量积的定义公式求解.【题文】14.函数()sin cos f x x x =+,在各项均为正数的数列{}n a 中对任意的*n N ∈都有()()n n f a x f a x +=-成立,则数列{}n a 的通项公式可以为(写一个你认为正确的)______【知识点】数列与函数. D1【答案解析】34n a n π⎛⎫=-⎪⎝⎭,*n N ∈ 解析:()4f x x π⎛⎫=+ ⎪⎝⎭,因为()()n n f a x f a x +=-,所以n a 是函数()f x 的对称轴,由42x k πππ+=+()k Z ∈得函数()f x 的对称轴为()4x k k Z ππ=+∈,取*1,k n n N =-∈得34n a n π⎛⎫=-⎪⎝⎭,*n N ∈. 【思路点拨】根据题设条件得n a 是函数()f x 的对称轴,因此求出函数()f x 的对称轴即可. 【题文】15.将一颗骰子先后投掷两次分别得到点数b a 、,则直线0=+by ax 与圆2)2(22=+-y x 有公共点的概率为_______.【知识点】古典概型. K2【答案解析】712 解析:a b ≤≤,而点(),a b 共有6636⨯=种,其中满足a b ≤的有21种,所以所求概率为2173612=. 【思路点拨】基本事件总数为6636⨯=,满足直线0=+by ax 与圆2)2(22=+-y x 有公共点的基本事件数为21,所以所求概率为2173612=. 【题文】16.已知四棱柱1111D C B A ABCD -中,侧棱⊥1AA 底面ABCD ,且21=AA ,底面ABCD 的边长均大于2,且︒=∠45DAB ,点P 在底面ABCD 内运动,且在AB ,AD 上的射影分别为M ,N ,若|PA|=2,则三棱锥MN D P 1-体积的最大值为______.【知识点】三棱锥的体积;正弦定理;两角和与差的三角函数;二倍角公式. G1 C5 C6【答案解析】13解析:1111233P D MN D PMN PMN PMN V V S AA S --∆∆==⨯⨯=,因为︒=∠45DAB ,,PN AD PM AB ⊥⊥所以135MPN ∠= 且PMN ∆的外接圆直径为PA=2,设,PMN θ∠=则45PNM θ∠=-,由正弦定理得:()2sin 45,PN 2sin PM θθ=-= ,所以()11sin1352sin 452sin 222PMN S PM PN θθ∆=⋅⋅=⨯-⨯⨯()()45sin cos sin sin θθθθθ-=- 2sin cos sin θθθ=-=1242πθ⎛⎫+- ⎪⎝⎭,当2428πππθθ+=⇒=时PMN S ∆,故三棱锥MN D P 1-体积的最大值为13.【思路点拨】因为1111233P D MN D PMN PMN PMN V V S AA S --∆∆==⨯⨯=,所以只需求PMN ∆面积的最大值,因为︒=∠45DAB ,,PN AD PM AB ⊥⊥所以135MPN ∠=且PMN ∆的外接圆直径为PA=2,设,PMN θ∠=则45PNM θ∠=-,由正弦定理得:()2sin 45,PN 2sin PM θθ=-= ,所以()11sin1352sin 452sin 222PMN S PM PN θθ∆=⋅⋅=⨯-⨯⨯()()45sin cos sin sin θθθθθ-=- 2sin cos sin θθθ=-=12242πθ⎛⎫+- ⎪⎝⎭,当2428πππθθ+=⇒=时PMN S ∆,故三棱锥MN D P 1-体积的最大值为13. 三、解答题:本大题共6个小题,共70分.解答应写文字说明、证明过程或演算步骤 【题文】17.(本小题满分12分)在ABC ∆中,已知角A 、B 、C 所对的边分别为a 、b 、c ,直线1:10l ax y ++=与直线()222:40l b c bc x ay +-++=互相平行(其中4a ≠).(I )求角A 的值, (II )若22,,sin cos 2232A C B B ππ+⎡⎫∈+⎪⎢⎣⎭求的取值范围. 【知识点】两条直线的位置关系;三角函数的求值、化简;解三角形. H2 C7 C8 【答案解析】(I )3π;(II )171,324⎡⎫--⎪⎢⎣⎭解析:(I )由12l l 得()2224a b c bc a =+-≠, 即222b c a bc +-=,--------2分所以2221cos 22b c a A bc +-==,又()0,A π∈,所以3A π=.---------5分 (II )2sincos 22A C B ++2221cos 1cos 2cos 2cos 1222B B B B +=+-=+- 22111172cos cos 2cos 22832B B B ⎛⎫=+-=+- ⎪⎝⎭,--------8分因为2,23B ππ⎡⎫∈⎪⎢⎣⎭,所以1cos ,02B ⎛⎤∈- ⎥⎝⎦,-----9分 所以21172cos 832B ⎛⎫+- ⎪⎝⎭171,324⎡⎫∈--⎪⎢⎣⎭,------11分即2sincos 22A C B ++的取值范围为171,324⎡⎫--⎪⎢⎣⎭.------12分 【思路点拨】(I )由两直线平行则对应系数比相等得222b c a bc +-=,再由余弦定理得A值;(II )利用三角公式将2sincos 22A C B ++化为21172cos 832B ⎛⎫+- ⎪⎝⎭,由角B 范围得 cos B 范围,从而求得2sin cos 22A CB ++的取值范围. 【题文】18.(本小题满分12分) 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人. (Ⅰ)求第七组的频率;(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm 以上(含180cm )的人数; (Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,x y ,事件=E {5x y -≤},事件F ={15->x y },求() P E F .【知识点】频率分布直方图;用样本估计总体;古典概型. I2 K2【答案解析】(Ⅰ)0.06;(Ⅱ)中位数174.5, 身高在180cm 以上(含180cm )的人数144人; (Ⅲ)715.解析:(Ⅰ)第六组的频率为40.0850=,所以第七组的频率为:10.085(0.00820.0160.0420.06)0.06--⨯⨯++⨯+=; ………4分(Ⅱ)身高在第一组[155,160)的频率为0.00850.04⨯=, 身高在第二组[160,165)的频率为0.01650.08⨯=, 身高在第三组[165,170)的频率为0.0450.2⨯=, 身高在第四组[170,175)的频率为0.0450.2⨯=,由于0.040.080.20.320.5++=<,0.040.080.20.20.520.5+++=> 估计这所学校的800名男生的身高的中位数为m ,则170175<<m 由0.040.080.2(170)0.040.5+++-⨯=m 得174.5=m所以可估计这所学校的800名男生的身高的中位数为174.5 …………………………6分 由直方图得后三组频率为0.060.080.00850.18++⨯=,所以身高在180cm 以上(含180cm )的人数为0.18800144⨯=人. ………………8分 (Ⅲ)第六组[180,185)的人数为4人,设为,,,a b c d ,第八组[190,195]的人数为2人, 设为,A B ,则有,,,,,,ab ac ad bc bd cd ,,,,,,,,aA bA cA dA aB bB cB dB AB 共15种情况,因事件=E {5x y -≤}发生当且仅当随机抽取的两名男生在同一组,所以事件E 包含的基本事件为,,,,,,ab ac ad bc bd cd AB 共7种情况,故7()15P E =. ……………………10分由于max 19518015x y -=-=,所以事件F ={15->x y }是不可能事件,()0P F =, 由于事件E 和事件F 是互斥事件,所以7()()()15P E F P E P F =+=………12分 【思路点拨】(Ⅰ)由第七组的频率等于1减去其它七组的频率求得;(Ⅱ)依次求出每组的频率,由于前3组的频率和0.32<0.5,前4组的频率和0.52>0.5,所以估计身高中位数()170,175m ∈,由0.040.080.2(170)0.040.5+++-⨯=m 得174.5=m ,所以可估计这所学校的800名男生的身高的中位数为174.5 .又由直方图可知身高在180cm 以上(含180cm )的 频率为0.18,所以估计该校的800名男生的身高在180cm 以上(含180cm )的人数为0.18800144⨯=人. (Ⅲ)先求出第六组、第八组的人数分别为4人、2人,用列举法写出从这六人中随机抽取两人共有15种情况,其中满足E 中条件的有7种,满足F 中条件的有0种,由于事件E 、F 是互斥事件,所以7()()()15P E F P E P F =+=. 【题文】19.(本题满分12分)如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =6,BC =4,AB =2,E 、F 分别在BC 、AD 上,EF ∥AB .现将四边形ABEF 沿EF 折起,使得平面ABEF ⊥平面EFDC .(Ⅰ) 当1BE =,是否在折叠后的AD 上存在一点P ,且AP PD λ=,使得CP ∥平面ABEF ?若存在,求出λ的值;若不存在,说明理由;(Ⅱ) 设BE =x ,问当x 为何值时,三棱锥A -CDF 的体积有最大值?并求出这个最大值.【知识点】折叠形;线面平行的判定;函数的最值. G4 G5 B3 【答案解析】(Ⅰ) 存在P 使得满足条件CP ∥平面ABEF ,且此时32λ=,理由:略; (Ⅱ)当x =3时,A CDF V -有最大值,最大值为3.解析:(Ⅰ)存在P 使得满足条件CP ∥平面ABEF ,且此时32λ=.…………… 2分 下面证明:当32λ=时,即此时32AP PD = ,可知35AP AD =,过点P 作MP ∥FD ,与AF 交于点M ,则有35MP FD =,又FD =5,故MP =3,又因为EC =3,MP ∥FD ∥EC ,故有MP //=EC ,故四边形MPCE 为平行四边形,所以PC ∥ME ,又CP ⊄平面ABEF ,ME ⊂平面ABEF ,故有CP ∥平面ABEF 成立.……………………… 6分(Ⅱ)因为平面ABEF ⊥平面EFDC ,平面ABEF 平面EFDC =EF ,又AF ⊥EF ,所以AF ⊥平面EFDC .由已知BE =x ,所以AF =x (0<x …4),FD =6-x .故222111112(6)(6)[(3)9](3)332333A C D F V x x x x x x -=⋅⋅⋅-⋅=-=--+=--+.所以,当x =3时,A CDF V -有最大值,最大值为3.【思路点拨】(Ⅰ)在平面EFCD 内作CN DF ⊥于N,在平面ADF 内作NP DF ⊥交AD 于P ,可证明平面CNP 平行于平面ABEF ,从而CP ∥平面ABEF ,所以点P 为所求点,进一步求得λ值;(Ⅱ) 由已知BE =x 得AF =x (0<x …4),FD =6-x .故222111112(6)(6)[(3)9](3)332333A CD FV x x x x x x -=⋅⋅⋅-⋅=-=--+=--+.所以,当x =3时,A CDF V -有最大值,最大值为3. 【题文】20.(本小题满分12分)已知函数xe xf =)(,若函数)(xg 满足)()(x g x f ≥恒成立,则称)(x g 为函数)(x f 的下界函数.(1)若函数kx x g =)(是)(x f 的下界函数,求实数k 的取值范围;(2)证明:对任意的2≤m ,函数x m x h ln )(+=都是)(x f 的下界函数.A B C D E F E F A BC D【知识点】导数的应用. B12【答案解析】(1) e k ≤≤0;(2)证明:略. 解析:(1)若kx x g =)(为xe xf =)(的下界函数,易知0<k 不成立,而0=k 必然成立.当0>k 时,若kx x g =)(为xe xf =)(的下界函数,则)()(xg x f ≥恒成立,即0≥-kx e x 恒成立.-------(2分)令kx e x x-=)(ϕ,则k e x x-=')(ϕ.易知函数)(x ϕ在)ln ,(k -∞单调递减,在),(ln +∞k 上单调递增.-------(4分)由0)(≥x ϕ恒成立得0ln )(ln )(min ≥-==k k k k x ϕϕ,解得e k ≤<0.综上知e k ≤≤0.---------(6分)(2) 由(1)知函数ex x G =)(是xe xf =)(的下界函数,即)()(x G x f ≥恒成立, 若2≤m ,构造函数)0(ln )(>--=x m x ex x F ,--------(8分) 则11()ex F x e x x -'=-=,易知02)1()(min ≥-==m eF x F , 即x m x h ln )(+=是ex xG =)(的下界函数,即)()(x h x G ≥恒成立.-----(11分)所以)()()(x h x G x f ≥≥恒成立,即2≤m 时,x m x h ln )(+=是=)(x f xe 的下界函数.--------(12分)【思路点拨】(1)因为直线y=kx 恒过定点(0,0),由图像可知当直线y=kx 自x 轴开始绕原点逆时针旋转到与曲线x y e =相切时满足条件,所以只需求过(0,0)与曲线xy e =相切的切线的斜率,利用导数求此斜率;(2)即证: ln xe x m -≥在2m ≤时恒成立.由(1)知函数ex x G =)(是x e x f =)(的下界函数,只需证函数x m x h ln )(+=是ex x G =)(的下界函数,构造函数)0(ln )(>--=x m x ex x F , 则11()ex F x e x x-'=-=,又2≤m ,故易知02)1()(m i n ≥-==m eF x F ,即x m x h ln )(+=是ex xG =)(的下界函数,即)()(x h x G ≥恒成立.所以)()()(x h x G x f ≥≥恒成立,即2≤m 时,x m x h ln )(+=是=)(x f xe 的下界函数.【题文】21.(本小题满分12分)已知2212221x y F F a b+=、是椭圆的左、右焦点,O 为坐标原点,点P ⎛- ⎝⎭在椭圆上,线段PF 2与y 轴的交点M 满足20PM F M += ; (I )求椭圆的标准方程;(II ) O 是以12F F 为直径的圆,一直线:l y kx m =+ 与相切,并与椭圆交于不同的两点A 、B.当23,34OA OB AOB λλ⋅=≤≤∆ 且满足时,求面积S 的取值范围.【知识点】椭圆及其几何性质. H5【答案解析】(I )2212x y +=;(II23s ≤≤. 解析:(I )因为20,PM F M == 所以点M 是线段2PF 的中点,所以OM 是12PF F ∆的中位线,又12OM F F ⊥,所以112PFF F ⊥, 所以2222211112c a b a b c=⎧⎪⎪+=⎨⎪⎪=+⎩,解得2222,1,1a b c ===所以椭圆方程为2212x y +=.--------5分 (II )因为圆O 与直线l1=,即221m k =+由2212x y y kx m ⎧+=⎪⎨⎪=+⎩消去y 得()222124220k x kmx m +++-= 因为直线l 与椭圆相交于两个不同点,所以200k ∆>⇒>,设()()1122,,,A x y B x y ,则122412km x x k +=-+,2212222221212m k x x k k -⋅==++,---7分()()()2212121212y y kx m kx m k x x km x x m =++=+++=2211k k-+ 212122112k OA OB x x y y k λ+⋅=+==+ ,所以222133124k k +≤≤+,解得2112k ≤≤S=112AB ⨯==-------10分设42u kk =+,则332,s ,244u u ⎡⎤≤≤=∈⎢⎥⎣⎦因为s 在u ∈3,24⎡⎤⎢⎥⎣⎦上单调递增,()32243s s ⎛⎫== ⎪⎝⎭,所以:243s ≤≤. ------12分 【思路点拨】(Ⅰ)由20PM F M +=得点M 是线段2PF 的中点,所以OM 是12PF F ∆的中位线,又12OM F F ⊥,所以112PF F F ⊥,所以2222211112c a b a b c=⎧⎪⎪+=⎨⎪⎪=+⎩,解得2222,1,1a b c === 所以椭圆方程为2212x y +=.(Ⅱ)由圆O 与直线l 相切,得221m k =+ 由2212x y y kx m ⎧+=⎪⎨⎪=+⎩消去y 得()222124220k x kmx m +++-=,由200k ∆>⇒>, 设()()1122,,,A x y B x y ,则122412km x x k +=-+,2212222221212m k x x k k-⋅==++,从而 12y y =2211k k -+,所以212122112k OA OB x x y y k λ+⋅=+==+ ,所以222133124k k +≤≤+, 解得2112k ≤≤ ,所以S=112AB ⨯=设42u kk =+,则332,s ,244u u ⎡⎤≤≤=∈⎢⎥⎣⎦因为s 在u ∈3,24⎡⎤⎢⎥⎣⎦上单调递增,()322443s s ⎛⎫== ⎪⎝⎭23s ≤≤. 请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分。

2014届高三第一次适应性考试数学(文)试题 本试卷分第I卷(选择题)和第II卷(非选择题)两部分.其中第II卷第22~24题为选考题,其他题为必考题. 第I卷 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.将答案直接填涂在答题卷上. 1.已知集合,则( ) (A) (B) (C) (D) 2.复数的模为( ) (A) (B) (C) (D) 3.曲线在点(1,0)处的切线方程为( ) (A) (B) (C) (D) 4.椭圆的离心率为( ) (A) (B) (C) (D) 5.在中,,则( ) (A) (B) (C) (D) 6.执行右面的程序框图,如果输入的是6,那么输出的是( ) (A)120 (B)720 (C)1440 (D)5040 7.在一个几何体的三视图中,正视图和俯视图如右图所示, 则相应的侧视图可以为( ) 8.设,则( ) (A) (B) (C) (D) 9.设为等差数列的前项和,,则( ) (A) (B) (C) (D) 10.设抛物线的焦点为,直线过且与交于两点.若,则的方程为( ) (A) (B) (C) (D) 11.已知函数,下列结论中错误的是( ) (A)若是的极小值点,则在区间单调递减 (B)函数的图象是中心对称图形 (C) (D)若是的极值点,则 12.已知函数y=f(x) 的周期为2,当x时 f(x)=x2,那么函数y=f(x) 的图像与函数y=的图像的交点共有( ) (A)8个 (B)9个 (C)10个 (D)1个 第II卷 本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分,共20分.将答案直接填写在答题卷上. 13.从中任取两个不同的数,则取出的两个数之差的绝对值为的概率是 . 14.若满足约束条件,则的最小值为 . 15.等比数列{an}的前n项和为Sn,若S3+3S2=0,则公比q= . 16.已知直三棱柱的个顶点都在球的球面上.若,,则球的直径为 . 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.将解答直接答在答题卷上. 17.(本小题满分12分) 设向量. (Ⅰ)若,求的值; (Ⅱ)设函数,求的最大值. 18.(本小题满分12分) 如图,四棱锥中,底面为平行四边形., 底面. (I)证明:; (II)设,求棱锥的高. (本小题满分12分) 近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸,呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机对入院50人进行了问卷调查,得到了如下的列联表. (Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人? (Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率; (Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量,并回答有多大把握认为心肺疾病与性别有关? 下面的临界值表供参考: (本小题满分12分) 在平面直角坐标系中,已知圆在轴上截得线段长为,在轴上截得线段长为. (I)求圆心的轨迹方程; (II)若点到直线的距离为,求圆的方程. (本小题满分12分) 设函数. (Ⅰ)若,求的单调区间; (Ⅱ)若当时,求的取值范围. 请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分. (本小题满分10分)选修4-1:几何证明选讲 如图,分别为的边上的点,且不与的顶点重合.已知的长为m,的长为n,的长是关于的方程的两个根. (Ⅰ)证明:四点共圆; (Ⅱ)若,且,求所在圆的半径. 23.(本小题满分10分)选修4-4:坐标系与参数方程 在直角坐标系中,曲线C1的参数方程为(为参数), M是C1上的动点,P点满足,P点的轨迹为曲线C2 (Ⅰ)求C2的方程; (Ⅱ)在以为极点,x轴的正半轴为极轴的极坐标系中,射线与C1的异于极点的交点为A,与C2的异于极点的交点为B,求. 24.(本小题满分10分)选修4-5:不等式选讲 设函数,其中. (Ⅰ)当时,求不等式的解集; (Ⅱ)若不等式的解集为 ,求的值.扶沟高中2013-2014学年度(上)高三第一次考试(适应性) 文数参考答案 一、选择题: 题号123456789101112答案BDADBBDBACAC二、填空题: 13. 14. 15. 16. 18.解:(Ⅰ?)因为, 由余弦定理得 从而BD2+AD2=AB2,故BDAD 又PD底面ABCD,可得BDPD 所以BD平面PAD. 故PABD (Ⅱ)过D作DE⊥PB于E,由(I)知BC⊥BD,又PD⊥底面, 所以BC⊥平面PBD,而DE平面PBD,故DE⊥BC,所以DE⊥平面PBC 由题设知PD=1,则BD=,PB=2, 由DEPB=PDBD得DE=,即棱锥的高为 (Ⅱ) 21.解:(Ⅰ)时,,。
高中三年级模拟考试数学(文科)注意事项:1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷l 至3页,第Ⅱ卷3至5页。
2.答卷前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成,答在本试卷上无效。
4.考试结束后,将本试题和答题卡一并交回。
第I卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{}{}=<<=-+>,则A B=()A x xB x x x|02,|(1)(1)0A。
(0,1) B.(1,2) C.( -∞,-l)U(0,+∞)D.(-∞,—l)U(l,+∞)i+对应的点位于()(2)在复平面内,复数22A.第一象限B.第二象限C.第三象限D.第四象限(3)如图,一个封闭的长方体,它的六个表面各标出A、B、C、D、E、F这六个字母,现放成下面三种不同的位置,所看见的表面上的字母已表明,则字母A、B、C对面的字母依次分别为( )A 。
E.D 。
F B. F 。
D.E C 。
E.F 。
D D. D.E.F (4)将函数sin y x =的图象上所有点向右平行移动10π个单位长度,再把所得的各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是 ( ) A . sin(2)10y x π=-B .sin(2)5y x π=-C . sin()220x y π=-D 。
sin()210x y π=-(5)设n S 是公差不为0的等差数列 {}n a 的前n 项和,且124,,S S S 成等比数列,则21a a 等于 ( )A .1B .2C .3D .4(6)在△ABC 中,内角A ,B,C 的对边分别是a ,b,c ,若223,sin 23sin a b bc C B -==,则A= ( )A 。
30 B 。
60 C.120D. 150(7)过P (2,0)的直线 l 被圆22(2)(3)9x y -+-=截得的线段长为2时,直线的斜率为 ( ) A 。
4545输出河南省实验中学2014届高三二测模拟卷数学(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合P={3,4,5},Q={6,7},定义},|),{(*Q b P a b a Q P ∈∈=,则Q P *的子集个数为A .7B .12C .32D .642.已知复数2ii ia b -=+(a ,b ∈R ,i 为虚数单位),则2a b -= A. 1 B. 2 C. 3 D.4 3. “p 或q ”为真命题是“p 且q ”为真命题的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 4.一个几何体的三视图如图所示,则该几何体的体积是A .6B .8C .10D .125.已知数阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛333231232221131211aa aa a aa a a 中,每行的3个数依次成等差数列,每列的3个数也依次成等差数列,若822=a ,则这9个数的和为A .16B .32C .36D .72 6.如图所示的程序框图,它的输出结果是A .3B .4C .5D .67.已知三个数2,m ,8构成一个等比数列,则圆锥曲线2212x y m +=的离心率为A .B. C.或 D8.若0≥a ,0≥b ,且当⎪⎩⎪⎨⎧≤+≥≥100y x y x 时,恒有≤+by ax 1,则以b a ,为坐标的点),(b a P 所形成的平面区域的面积是 A .21 B .4π C .1 D .2π 9.在平行四边形ABCD 中,1,60AD BAD =∠=,E 为CD 的中点.若12AD BE ⋅=, 则AB 的长为A.12 B.1 C .32D .2 10.过抛物线)0(22>=p px y 的焦点F ,斜率为34的直线交抛物线于A ,B 两点,若)1(>=λλFB AF ,则λ的值为A .5B .4C .34 D .25 11.已知函数()f x 对定义域R 内的任意x 都有()f x =(4)f x -,且当2x ≠时,其导函数()f x '满足()2()xf x f x ''>,若24a <<,则有A. 2(2)(3)(l o g)af f fa << B. 2(3)(log )(2)a f f a f << C. 2(l o g )(3)(2)af a f f<< D. 2(log )(2)(3)a f a f f << 12.函数[]11,0,2()1(2),(2,)2x x f x f x x ⎧--∈⎪=⎨-∈+∞⎪⎩,则下列说法中正确命题的个数是①函数()ln(1)y f x x =-+有3个零点; ②若0x >时,函数()k f x x ≤恒成立,则实数k 的取值范围是3,2⎡⎫+∞⎪⎢⎣⎭; ③函数()f x 的极大值中一定存在最小值,④)(),2(2)(N k k x f x f k ∈+=,对于一切[)0,x ∈+∞恒成立.A .1B .2C .3D .4二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题纸的相应位置. 13.若非零向量b a ,满足||||b a =,0)2(=⋅+b b a ,则与的夹角为______.14.函数()sin cos f x x x =+,在各项均为正数的数列{}n a 中对任意的*n N ∈都有()()n n f a x f a x +=-成立,则数列{}n a 的通项公式可以为(写一个你认为正确的)______15.将一颗骰子先后投掷两次分别得到点数b a 、,则直线0=+by ax 与圆2)2(22=+-y x 有公共点的概率为_______.16.已知四棱柱1111D C B A ABCD -中,侧棱⊥1AA 底面ABCD ,且21=AA ,底面ABCD 的边长均大于2,且︒=∠45DAB ,点P 在底面ABCD 内运动,且在AB ,AD 上的射影分别为M ,N ,若|PA|=2,则三棱锥MN D P 1-体积的最大值为______.三、解答题:本大题共6个小题,共70分.解答应写文字说明、证明过程或演算步骤17.(本小题满分12分)在ABC ∆中,已知角A 、B 、C 所对的边分别为a 、b 、c ,直线1:10l ax y ++=与直线()222:40l b c bc x ay +-++=互相平行(其中4a ≠).(I )求角A 的值, (II )若22,,sin cos 2232A C B B ππ+⎡⎫∈+⎪⎢⎣⎭求的取值范围.18.(本小题满分12分) 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.(Ⅰ)求第七组的频率; (Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm 以上(含180cm )的人数;(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,x y ,事件=E {5x y -≤},事件F ={15->x y },求()P E F .19.(本题满分12分)如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =6,BC =4,AB =2,E 、F 分别在BC 、AD 上,EF ∥AB .现将四边形ABEF 沿EF 折起,使得平面ABEF ⊥平面EFDC .(Ⅰ) 当1BE =,是否在折叠后的AD 上存在一点P ,且AP PD λ=,使得CP ∥平面ABEF ?若存在,求出λ的值;若不存在,说明理由;(Ⅱ) 设BE =x ,问当x 为何值时,三棱锥A -CDF 的体积有最大值?并求出这个最大值.20.(本小题满分12分)已知函数xe xf =)(,若函数)(xg 满足)()(x g x f ≥恒成立,则称)(x g 为函数)(x f 的下界函数.(1)若函数kx x g =)(是)(x f 的下界函数,求实数k 的取值范围;A B C D EFE F A B CD(2)证明:对任意的2≤m ,函数x m x h ln )(+=都是)(x f 的下界函数.21.(本小题满分12分)已知2212221x y F F a b +=、是椭圆的左、右焦点,O 为坐标原点,点P ⎛- ⎝⎭在椭圆上,线段PF 2与y 轴的交点M 满足20PM F M +=; (I )求椭圆的标准方程;(II )O 是以12F F 为直径的圆,一直线:l y kx m =+与相切,并与椭圆交于不同的两点A 、B.当23,34OA OB AOB λλ⋅=≤≤∆且满足时,求面积S 的取值范围.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分。
河南省实验中学2014届高三二测模拟卷数学(文科)【试卷综析】试卷贴近中学教学实际,在坚持对五个能力、两个意识考查的同时,注重对数学思想与方法的考查,体现了数学的基础性、应用性和工具性的学科特色.以支撑学科知识体系的重点内容为考点来挑选合理背景,考查更加科学.试卷从多视角、多维度、多层次地考查数学思维品质,考查考生对数学本质的理解,考查考生的数学素养和学习潜能.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】1.集合P={3,4,5},Q={6,7},定义},|),{(*QbPabaQP∈∈=,则QP*的子集个数为A.7 B.12 C.32 D.64 【知识点】集合及运算. A1【答案解析】D 解析:()()()()()(){}*=3,63,74,64,75,65,7P Q,,,,,,所以P*Q 中有6个元素,所以P*Q的子集个数为62=64,故选D.【思路点拨】由P*Q定义得P*Q中元素个数为6,所以P*Q的子集个数为62=64.【题文】2.已知复数2iiiab-=+(a,b∈R,i为虚数单位),则2a b-=A.1B.2C.3D.4【知识点】复数的运算. L4【答案解析】C 解析:由2iiiab-=+得121232aa i i a bb=-⎧-=-+⇒⇒-=⎨=-⎩,故选C.【思路点拨】利用复数乘法及复数相等条件,得a,b值,从而求得a-2b值.【题文】3. “p或q”为真命题是“p且q”为真命题的A.充要条件 B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件【知识点】充分条件;必要条件. A2【答案解析】C 解析:因为命题:若“p或q”为真命题则“p且q”为真命题,是假命题;而命题:若“p且q”为真命题则p或q”为真命题,是真命题.所以“p或q”为真命题是“p且q”为真命题的必要不充分条件.故选C.【思路点拨】根据:若p则q为假命题,若q则p为真命题时,p是q的必要不充分条件得开始0k =45α=sin cos ?αα<是45αα=+1k k =+否输出k 结束结论.【题文】4.一个几何体的三视图如图所示,则该几何体的体积是 A .6 B .8 C .10 D .12 【知识点】空间几何体的三视图. G2【答案解析】D 解析:该几何体是两个全等的斜四棱 柱对接而成的几何体,其中每个四棱柱是底面邻边长分 别为3, 2的长方形,高为1,所以该几何体的体积为:2321⨯⨯⨯=12.故选D.【思路点拨】由几何体的三视图得该几何体的结构,该几何体是两个全等的斜四棱柱对接而成的几何体,进而求得该几何体的体积.【题文】5.已知数阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛333231232221131211aa aa a aa a a中,每行的3个数依次成等差数列,每列的3个数也依次成等差数列,若822=a ,则这9个数的和为 A .16 B .32 C .36 D .72 【知识点】等差数列. D2【答案解析】D 解析:根据等差数列的性质得:11121312212223223,3a a a a a a a a ++=++=,313233323a a a ++=,且122232223a a a a ++=,所以这9个数的和为:()122232223339872a a a a ++=⨯=⨯=,故选D.【思路点拨】根据等差数列的性质求解.【题文】6.如图所示的程序框图,它的输出结果是 A .3 B .4 C .5D .6【知识点】算法与程序框图. L1 【答案解析】 C 解析:由框图可知循环的结果依次为:(1)90,2k α==,(2)135,3,k α==(3)180,4,k α==(4)225,5k α==,此时满足sin cos αα<,所以输出k=5,故选C.【思路点拨】依次写出循环结果可得输出的k 值. 【题文】7.已知三个数2,m ,8构成一个等比数列,则圆锥曲线2212x y m +=的离心率为A .2 B ..2或.2或2【知识点】等比数列;圆锥曲线. D3 H5 H6【答案解析】 C 解析:因为2,m ,8构成等比数列,所以2164,m m =⇒=±当m=4时, 圆锥曲线2212x y m +=为椭圆,其离心率为2;当m=-4时,圆锥曲线2212x y m +=为双曲,故选C.【思路点拨】由2,m ,8成等比数列得m 值,由m 值确定圆锥曲线2212x y m +=是椭圆还是双曲线,进而求得相应的离心率.【题文】8.若0≥a ,0≥b ,且当⎪⎩⎪⎨⎧≤+≥≥100y x y x 时,恒有≤+by ax 1,则以b a ,为坐标的点),(b a P 所形成的平面区域的面积是 A .21 B .4π C .1 D .2π【知识点】简单的线性规划;不等式恒成立. E5 E1【答案解析】 C 解析:不等式组001x y x y ≥⎧⎪≥⎨⎪+≤⎩表示的区域是以点(0,0),(1,0),(0,1)为顶点的三角形及其内部,当a,b 中有的取0时,满足条件得点是点或线段,其面积为0,当a>0,b>0时,要恒有≤+by ax 1,即恒有111x ya b +≤,则1111a b ⎧≥⎪⎪⎨⎪≥⎪⎩,解得0101a b <≤⎧⎨<≤⎩,所以以b a ,为坐标的点),(b a P 所形成的平面区域的面积是111⨯=,故选C.【思路点拨】若0≥a ,0≥b ,且当⎪⎩⎪⎨⎧≤+≥≥100y x y x 时,恒有≤+by ax 1,则直线1ax by +=在不等式组001x y x y ≥⎧⎪≥⎨⎪+≤⎩表示的区域的上方,由此得 a,b 满足的条件.【题文】9.在平行四边形ABCD 中,1,60AD BAD =∠=,E 为CD 的中点.若12AD BE ⋅=,则AB 的长为A.12B.1 C .32 D .2【知识点】向量的线性运算;向量的数量积. F1 F3【答案解析】D 解析:设AB 长为x ,则CE 长12x ,又1,,2BC AD CE BA ==所以 12BE BC CE AD BA=+=+,所以12AD BE AD AD BA ⎛⎫⋅=⋅+ ⎪⎝⎭ ()21111cos12022AD AD BA x =+⋅=+⨯⨯⨯=14x -=12,所以x=2,故选D.【思路点拨】 根据向量加法的三角形法则,将BE 用,AB AD 表示,再利用向量数量积的定义式求线段ABG 的长.【题文】10.过抛物线)0(22>=p px y 的焦点F ,斜率为34的直线交抛物线于A ,B 两点,若(1)AF FB λλ=>,则λ的值为A .5B .4C .34D .25【知识点】抛物线及其几何性质;直线与圆锥曲线. H7 H8【答案解析】B 解析:不妨取p=2,则直线AB 方程为4x-3y-4=0,代入抛物线方程消去x得2340y y --=,解得124,1y y ==-. 因为(1)AF FB λλ=>,所以设A()()12,4,,1x B x -,又F (1,0),所以()()121,41,1x x λ--=--,所以44λλ-=-⇒=,故选B.【思路点拨】把直线AB 方程代入抛物线方程消去x ,解得点A,B 的纵坐标,用坐标表示条件(1)AF FB λλ=>,利用A,B 的纵坐标求得λ值.【题文】11.已知函数()f x 对定义域R 内的任意x 都有()f x =(4)f x -,且当2x ≠时,其导函数()f x '满足()2()xf x f x ''>,若24a <<,则有A. 2(2)(3)(log )a f f f a <<B. 2(3)(log )(2)a f f a f <<C. 2(log )(3)(2)a f a f f <<D. 2(log )(2)(3)a f a f f <<【知识点】函数的对称性、单调性. B1 B3【答案解析】C 解析:由()f x =(4)f x -得()()22f x f x +=-,所以函数()f x 图像关于x=2对称,由()2()xf x f x ''>得()()20x f x '->,所以x>2时,()0f x '>,所以 ()f x 是()2,+∞的增函数,因为2<a<4,所以224,1log 2a a ><<, 2log a 关于x=2的对称的数是24log a-,且224log 3a <-<,所以24log a-<3<2a,所以选C.【思路点拨】根据题设条件得函数()f x 的对称性和单调性,利用对称性把自变量取值化到同一单调区间上,再利用单调性得结论.【题文】12.函数[]11,0,2()1(2),(2,)2x x f x f x x ⎧--∈⎪=⎨-∈+∞⎪⎩,则下列说法中正确命题的个数是①函数()ln(1)y f x x =-+有3个零点;②若0x >时,函数()k f x x ≤恒成立,则实数k 的取值范围是3,2⎡⎫+∞⎪⎢⎣⎭;③函数()f x 的极大值中一定存在最小值,④)(),2(2)(N k k x f x f k∈+=,对于一切[)0,x ∈+∞恒成立. A .1 B .2 C .3 D .4【知识点】分段函数的图像;函数的零点;不等式恒成立;函数的极值. B1 B9 E1【答案解析】B 解析:函数()()[]*11121,22,2,2n f x x n x n n n N -⎡⎤=---∈-∈⎣⎦其图像为函数()ln(1)y f x x =-+的零点个数,即函数()y f x =与函数()ln 1y x =+的交点个数,由由图可知两函数交点个数是2,故①不正确;②因为函数()y f x =的极大值点是*21,x n n N =-∈,极大值是112n -,所以0x >时,函数()k f x x ≤恒成立,即11121,2122n n k n k n ---≥⇒≥-在*n N ∈时恒成立,因为1212n n --在2n =时有最大值32,所以32k ≥,故②正确;③由函数()y f x =的图像可知,函数()f x 的极大值中不存在最小值故③不正确;④由函数解析式可知,当[]*22,2,x k k k N ∈-∈时,()()2222,22x k k k +∈-⎡⎤⎣⎦,所以()()()211222122212k k k f x k x k k -⎡⎤+=⋅-+-⋅-⎣⎦ ()()111212k x k f x -⎡⎤=---=⎣⎦,当0k =时,显然成立,故④正确.所以选B.【思路点拨】变形已知函数得()()[]*11121,22,2,2n f x x n x n n n N -⎡⎤=---∈-∈⎣⎦,由图像可知①、③不正确;对于②由不等式恒成立条件求k 范围即可;对于④将2(2),()k f x k k N +∈的表达式求出,其与()f x 表达式相同,故④正确.二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题纸的相应位置. 【题文】13.若非零向量b a ,满足||||b a =,0)2(=⋅+b b a ,则a 与b 的夹角为______. 【知识点】向量的数量积;向量的夹角. F3【答案解析】120 解析:由()22(2)22cos 0a b b a b ba b b θ+⋅=⋅+=+=及a b=得1cos 2θ=-,因为[]0,θπ∈,所以120θ=【思路点拨】由向量向量数量积的运算律,及向量数量积的定义公式求解.【题文】14.函数()sin cos f x x x =+,在各项均为正数的数列{}n a 中对任意的*n N ∈都有()()n n f a x f a x +=-成立,则数列{}n a 的通项公式可以为(写一个你认为正确的)______【知识点】数列与函数. D1【答案解析】34n a n π⎛⎫=- ⎪⎝⎭,*n N ∈ 解析:()4f x x π⎛⎫=+ ⎪⎝⎭,因为()()n n f a x f a x +=-,所以na 是函数()f x 的对称轴,由42x k πππ+=+()k Z ∈得函数()f x 的对称轴为()4x k k Z ππ=+∈,取*1,k n n N =-∈得34n a n π⎛⎫=- ⎪⎝⎭,*n N ∈. 【思路点拨】根据题设条件得na 是函数()f x 的对称轴,因此求出函数()f x 的对称轴即可.【题文】15.将一颗骰子先后投掷两次分别得到点数b a 、,则直线0=+by ax 与圆2)2(22=+-y x 有公共点的概率为_______.【知识点】古典概型. K2【答案解析】712 解析:a b≤⇒≤,而点(),a b 共有6636⨯=种,其中满足a b ≤的有21种,所以所求概率为2173612=. 【思路点拨】基本事件总数为6636⨯=,满足直线0=+by ax 与圆2)2(22=+-y x 有公共点的基本事件数为21,所以所求概率为2173612=.【题文】16.已知四棱柱1111D C B A ABCD -中,侧棱⊥1AA 底面ABCD ,且21=AA ,底面ABCD 的边长均大于2,且︒=∠45DAB ,点P 在底面ABCD 内运动,且在AB ,AD 上的射影分别为M ,N ,若|PA|=2,则三棱锥MN D P 1-体积的最大值为______.【知识点】三棱锥的体积;正弦定理;两角和与差的三角函数;二倍角公式. G1 C5 C6【答案解析】213- 解析:1111233P D MN D PMN PMN PMNV V S AA S --∆∆==⨯⨯=,因为︒=∠45DAB ,,PN AD PM AB ⊥⊥所以135MPN ∠=且PMN ∆的外接圆直径为PA=2,设,PMN θ∠=则45PNM θ∠=-,由正弦定理得:()2sin 45,PN 2sin PM θθ=-=,所以()112sin1352sin 452sin 222PMN S PM PN θθ∆=⋅⋅=⨯-⨯⨯=()()2sin 45sin cos sin sin θθθθθ-=-2sin cos sin θθθ=-=21sin 2242πθ⎛⎫+- ⎪⎝⎭,当2428πππθθ+=⇒=时PMN S ∆有最大值212-, 故三棱锥MN D P 1-体积的最大值为213-.【思路点拨】因为1111233P D MN D PMN PMN PMNV V S AA S --∆∆==⨯⨯=,所以只需求PMN ∆面积的最大值,因为︒=∠45DAB ,,PN AD PM AB ⊥⊥所以135MPN ∠=且PMN ∆的外接圆直径为PA=2,设,PMN θ∠=则45PNM θ∠=-,由正弦定理得:()2sin 45,PN 2sin PM θθ=-=,所以()112sin1352sin 452sin 222PMN S PM PN θθ∆=⋅⋅=⨯-⨯⨯=()()245sin cos sin sin θθθθθ-=-2sin cos sin θθθ=-=12242πθ⎛⎫+- ⎪⎝⎭,当2428πππθθ+=⇒=时PMN S ∆有最大值12, 故三棱锥MN D P 1-体积的最大值为.三、解答题:本大题共6个小题,共70分.解答应写文字说明、证明过程或演算步骤 【题文】17.(本小题满分12分)在ABC ∆中,已知角A 、B 、C 所对的边分别为a 、b 、c ,直线1:10l ax y ++=与直线()222:40l b c bc x ay +-++=互相平行(其中4a ≠).(I )求角A 的值, (II )若22,,sin cos 2232A C B B ππ+⎡⎫∈+⎪⎢⎣⎭求的取值范围.【知识点】两条直线的位置关系;三角函数的求值、化简;解三角形. H2 C7 C8【答案解析】(I )3π;(II )171,324⎡⎫--⎪⎢⎣⎭ 解析:(I )由12l l 得()2224a b c bc a =+-≠,即222b c a bc +-=,--------2分所以2221cos 22b c a A bc +-==,又()0,A π∈,所以3A π=.---------5分 (II )2sin cos 22A C B ++2221cos 1cos 2cos 2cos 1222B B B B +=+-=+-22111172cos cos 2cos 22832B B B ⎛⎫=+-=+-⎪⎝⎭,--------8分 因为2,23B ππ⎡⎫∈⎪⎢⎣⎭,所以1cos ,02B ⎛⎤∈- ⎥⎝⎦,-----9分所以21172cos 832B ⎛⎫+- ⎪⎝⎭171,324⎡⎫∈--⎪⎢⎣⎭,------11分 即2sin cos 22A C B ++的取值范围为171,324⎡⎫--⎪⎢⎣⎭.------12分【思路点拨】(I )由两直线平行则对应系数比相等得222b c a bc +-=,再由余弦定理得A值;(II )利用三角公式将2sin cos 22A C B++化为21172cos 832B ⎛⎫+- ⎪⎝⎭,由角B 范围得cos B 范围,从而求得2sin cos 22A CB ++的取值范围.【题文】18.(本小题满分12分) 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人. (Ⅰ)求第七组的频率;(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm 以上(含180cm )的人数; (Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,x y ,事件=E {5x y -≤},事件F ={15->x y },求()P E F .【知识点】频率分布直方图;用样本估计总体;古典概型. I2 K2【答案解析】(Ⅰ)0.06;(Ⅱ)中位数174.5, 身高在180cm 以上(含180cm )的人数144人;(Ⅲ)715.解析:(Ⅰ)第六组的频率为40.0850=,所以第七组的频率为:10.085(0.00820.0160.0420.06)0.06--⨯⨯++⨯+=; ………4分 (Ⅱ)身高在第一组[155,160)的频率为0.00850.04⨯=, 身高在第二组[160,165)的频率为0.01650.08⨯=, 身高在第三组[165,170)的频率为0.0450.2⨯=, 身高在第四组[170,175)的频率为0.0450.2⨯=,由于0.040.080.20.320.5++=<,0.040.080.20.20.520.5+++=> 估计这所学校的800名男生的身高的中位数为m ,则170175<<m 由0.040.080.2(170)0.040.5+++-⨯=m 得174.5=m所以可估计这所学校的800名男生的身高的中位数为174.5 …………………………6分 由直方图得后三组频率为0.060.080.00850.18++⨯=,所以身高在180cm 以上(含180cm )的人数为0.18800144⨯=人. ………………8分 (Ⅲ)第六组[180,185)的人数为4人,设为,,,a b c d ,第八组[190,195]的人数为2人, 设为,A B ,则有,,,,,,ab ac ad bc bd cd ,,,,,,,,aA bA cA dA aB bB cB dB AB 共15种情况, 因事件=E {5x y -≤}发生当且仅当随机抽取的两名男生在同一组,所以事件E 包含的基本事件为,,,,,,ab ac ad bc bd cd AB 共7种情况,故7()15P E =. (10)分 由于max 19518015x y -=-=,所以事件F ={15->x y }是不可能事件,()0P F =,由于事件E 和事件F 是互斥事件,所以7()()()15P E F P E P F =+=………12分【思路点拨】(Ⅰ)由第七组的频率等于1减去其它七组的频率求得;(Ⅱ)依次求出每组的频率,由于前3组的频率和0.32<0.5,前4组的频率和0.52>0.5,所以估计身高中位数()170,175m ∈,由0.040.080.2(170)0.040.5+++-⨯=m 得174.5=m ,所以可估计这所学校的800名男生的身高的中位数为174.5 .又由直方图可知身高在180cm 以上(含180cm )的 频率为0.18,所以估计该校的800名男生的身高在180cm 以上(含180cm )的人数为0.18800144⨯=人. (Ⅲ)先求出第六组、第八组的人数分别为4人、2人,用列举法写出从这六人中随机抽取两人共有15种情况,其中满足E 中条件的有7种,满足F 中条件的有0种,由于事件E 、F 是互斥事件,所以7()()()15P EF P E P F =+=.【题文】19.(本题满分12分)如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =6,BC =4,AB =2,E 、F 分别在BC 、AD 上,EF ∥AB .现将四边形ABEF 沿EF 折起,使得平面ABEF ⊥平面EFDC .(Ⅰ) 当1BE =,是否在折叠后的AD 上存在一点P ,且AP PD λ=,使得CP ∥平面ABEF ?若存在,求出λ的值;若不存在,说明理由;(Ⅱ) 设BE =x ,问当x 为何值时,三棱锥A -CDF 的体积有最大值?并求出这个最大值.【知识点】折叠形;线面平行的判定;函数的最值. G4 G5 B3【答案解析】(Ⅰ) 存在P 使得满足条件CP ∥平面ABEF ,且此时32λ=,理由:略;(Ⅱ)当x =3时,A CDFV -有最大值,最大值为3.解析:(Ⅰ)存在P 使得满足条件CP ∥平面ABEF ,且此时32λ=.…………… 2分下面证明:当32λ=时,即此时32AP PD=,可知35AP AD =,过点P 作MP ∥FD ,与AF 交于点M ,则有35MP FD =,又FD =5,故MP =3,又因为EC =3,MP ∥FD ∥EC ,故有MP //=EC ,故四边形MPCE 为平行四边形,所以PC ∥ME ,又CP ⊄平面ABEF ,ME ⊂平面ABEF ,故有CP ∥平面ABEF 成立.……………………… 6分 (Ⅱ)因为平面ABEF ⊥平面EFDC ,平面ABEF 平面EFDC =EF ,又AF ⊥EF ,所以AF ⊥平面EFDC .由已知BE =x ,所以AF =x(0<x4),FD =6-x .故222111112(6)(6)[(3)9](3)332333A CDF V x x x x x x -=⋅⋅⋅-⋅=-=--+=--+.所以,当x=3时,A CDFV -有最大值,最大值为3.【思路点拨】(Ⅰ)在平面EFCD 内作CN DF ⊥于N,在平面ADF 内作NP DF ⊥交AD 于P ,可证明平面CNP 平行于平面ABEF ,从而CP ∥平面ABEF ,所以点P 为所求点,进一步求得λ值;(Ⅱ) 由已知BE =x得AF =x(0<x4),FD =6-x .故222111112(6)(6)[(3)9](3)332333A CDF V x x x x x x -=⋅⋅⋅-⋅=-=--+=--+.所以,当x=3时,A CDFV -有最大值,最大值为3.【题文】20.(本小题满分12分)A B C D E F E FA BC D已知函数xe xf =)(,若函数)(xg 满足)()(x g x f ≥恒成立,则称)(x g 为函数)(x f 的下界函数.(1)若函数kx x g =)(是)(x f 的下界函数,求实数k 的取值范围; (2)证明:对任意的2≤m ,函数x m x h ln )(+=都是)(x f 的下界函数. 【知识点】导数的应用. B12【答案解析】(1) e k ≤≤0;(2)证明:略. 解析:(1)若kx x g =)(为xe xf =)(的下界函数,易知0<k 不成立,而0=k 必然成立.当0>k 时,若kx x g =)(为x e x f =)(的下界函数,则)()(x g x f ≥恒成立,即0≥-kx e x 恒成立.-------(2分)令kx e x x-=)(ϕ,则k e x x -=')(ϕ.易知函数)(x ϕ在)ln ,(k -∞单调递减,在),(ln +∞k 上单调递增.-------(4分)由0)(≥x ϕ恒成立得0ln )(ln )(min ≥-==k k k k x ϕϕ,解得e k ≤<0.综上知e k ≤≤0.---------(6分)(2) 由(1)知函数ex x G =)(是xe xf =)(的下界函数,即)()(x G x f ≥恒成立,若2≤m ,构造函数)0(ln )(>--=x m x ex x F ,--------(8分)则11()ex F x e x x -'=-=,易知02)1()(min ≥-==m e F x F ,即x m x h ln )(+=是ex x G =)(的下界函数,即)()(x h x G ≥恒成立.-----(11分)所以)()()(x h x G x f ≥≥恒成立,即2≤m 时,x m x h ln )(+=是=)(x f xe 的下界函数.--------(12分)【思路点拨】(1)因为直线y=kx 恒过定点(0,0),由图像可知当直线y=kx 自x 轴开始绕原点逆时针旋转到与曲线x y e =相切时满足条件,所以只需求过(0,0)与曲线xy e =相切的切线的斜率,利用导数求此斜率;(2)即证: ln xe x m -≥在2m ≤时恒成立.由(1)知函数ex x G =)(是x e x f =)(的下界函数,只需证函数x m x h ln )(+=是ex x G =)(的下界函数,构造函数)0(ln )(>--=x m x ex x F , 则11()ex F x e x x -'=-=,又2≤m ,故易知2)1()(min ≥-==m e F x F ,即x m x h ln )(+=是ex x G =)(的下界函数,即)()(x h x G ≥恒成立.所以)()()(x h x G x f ≥≥恒成立,即2≤m 时,x m x h ln )(+=是=)(x f xe 的下界函数.【题文】21.(本小题满分12分)已知2212221x y F F a b +=、是椭圆的左、右焦点,O 为坐标原点,点1,2P ⎛⎫- ⎪ ⎪⎝⎭在椭圆上,线段PF 2与y 轴的交点M 满足20PM F M +=; (I )求椭圆的标准方程; (II )O 是以12F F 为直径的圆,一直线:l y kx m =+与相切,并与椭圆交于不同的两点A 、B.当23,34OA OB AOBλλ⋅=≤≤∆且满足时,求面积S 的取值范围.【知识点】椭圆及其几何性质. H5【答案解析】(I )2212x y +=;(II)243s ≤≤. 解析:(I )因为20,PM F M ==所以点M 是线段2PF 的中点, 所以OM 是12PF F ∆的中位线,又12OM F F ⊥,所以112PF F F ⊥,所以2222211112c a b a b c =⎧⎪⎪+=⎨⎪⎪=+⎩,解得2222,1,1a b c === 所以椭圆方程为2212x y +=.--------5分(II )因为圆O 与直线l1=,即221m k =+由2212x y y kx m ⎧+=⎪⎨⎪=+⎩消去y 得()222124220k x kmx m +++-=因为直线l 与椭圆相交于两个不同点,所以200k ∆>⇒>,设()()1122,,,A x y B x y ,则122412kmx x k +=-+,2212222221212m k x x k k -⋅==++,---7分 ()()()2212121212y y kx m kx m k x x km x x m =++=+++=2211k k -+212122112k OA OB x x y y k λ+⋅=+==+,所以222133124k k +≤≤+,解得2112k ≤≤S=112AB ⨯==-------10分设42u kk =+,则332,s ,244u u ⎡⎤≤≤=∈⎢⎥⎣⎦ 因为s 在u ∈3,24⎡⎤⎢⎥⎣⎦上单调递增,()322443s s ⎛⎫==⎪⎝⎭,所以:23s ≤≤. ------12分【思路点拨】(Ⅰ)由20PM F M +=得点M 是线段2PF 的中点,所以OM 是12PF F ∆的中位线,又12OM F F ⊥,所以112PF F F ⊥,所以2222211112c a b a b c =⎧⎪⎪+=⎨⎪⎪=+⎩,解得2222,1,1a b c === 所以椭圆方程为2212x y +=.(Ⅱ)由圆O 与直线l 相切,得221m k =+由2212x y y kx m ⎧+=⎪⎨⎪=+⎩消去y 得()222124220k x kmx m +++-=,由200k ∆>⇒>,设()()1122,,,A x y B x y ,则122412kmx x k +=-+,2212222221212m k x x k k -⋅==++,从而 12y y =2211k k -+,所以212122112k OA OB x x y y k λ+⋅=+==+,所以222133124k k+≤≤+,CA解得2112k ≤≤ ,所以S=()2212121111422AB k x x x x ⨯=++-()()4242241k k k k +++设42u k k =+,则3232,s ,,24214u u u u ⎡⎤≤≤=∈⎢⎥+⎣⎦ 因为s 在u ∈3,24⎡⎤⎢⎥⎣⎦上单调递增,()3622443s s ⎛⎫== ⎪⎝⎭,所以:6243s ≤≤. 请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分。
开封市2014届高三第二次模拟考试高二数学试题(文科)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第(22)- (23)题为选考题,其他题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名,准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号,非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卷面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题专上把所选题目对应的题号涂黑。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集{}0U =,1,2,3,4,集合{}{}1,2,2,3,4A B ==,则的子集个数是A. 2B. 4C.8D.162.已知复数2(1)(2)()z a a i a R =-+-∈,则“1a =”是“z 为纯虚数”的 A. 充分非必蕞条件 B .必要非充分条件C .充要条件 D.既非充分又非必要条件 3.在一次独立性检验中,得出2×2列联表如下:且最后发现,两个分类变量X 和y 没有任何关系,则m 的可能值是A .200B .720C .100D .1804.已知函数23,0()tan ,02x x f x x x π<⎧⎪=⎨-≤<⎪⎩,则(())4f f π= A .2 B .1 C .-2 D .-15.几何体的三视图如图所示,则这个几何体的体积为 A .4 B .6 C .12 D .186.在等比数列{}n a 中,若48,a a 是方程2430x x -+=的两根,则6a 的值是A. B .CD .3± 7.设函数())cos(2)()2f x x x πϕϕϕ=+++<,且其图象关于直线x=0对称,则 A. ()y f x =的最小正周期为π,且在(0,)2π上为增函数 B .()y f x =的最小正周期为2π,且在(0,)4π上为增函数 C .()y f x =的最小正周期为π,且在(0,)2π上为减函数 D. ()y f x =的最小正周期为2π,且在(0,)4π上为减函数8存在直线x m =±与双曲线22221(0,0)x y a b a b-=>>相交于A 、B 、C 、D 四点,若四边形ABCD 为正方形,则双曲线离心率的取值范围为.A.)+∞ B .)+∞ C. D.3± 9.若曲线与曲线在交点(0,m )处有公切线,则a+b=A .1B .2C .3D .410.如图是某算法的程序框图,则程序运行后输出的T 是A .1B .2C .3D .411.在平行四边形ABCD 中,1,60AD BAD =∠=,E 为CD 的中点.若12AD BE ⋅=, 则AB 的长为 A.12 B.1 C .32D .2 12.函数[]11,0,2()1(2),(2,)2x x f x f x x ⎧--∈⎪=⎨-∈+∞⎪⎩,则下列说法中正确命题的个数是①函数()ln(1)y f x x =-+有3个零点; ②若0x >时,函数()k f x x ≤恒成立,则实数k 的取值范围是3,2⎡⎫+∞⎪⎢⎣⎭; ③函数()f x 的极大值中一定存在最小值,④()2(2),()f x kf x k k N =+∈,对于一切[)0,x ∈+∞恒成立. A .1 B .2 C .3 D .4第Ⅱ卷本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答,第(22)题~第(24)题为选考题,考生根据要求做答。