【核按钮】2015高考新课标数学(理)课时作业：10.1 算法与程序框图]

温馨提示：此题库为Word 版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，关闭Word 文档返回原板块。

考点41 算法与程序框图、基本算法语句、算法案例一、选择题1.(2015·四川高考文科·T6)执行如图所示的程序框图,输出S 的值为 ( )（A ）（B （C ）12- （D ）12 【解题指南】按照框图给定的运算顺序,依次循环运算,当k=5时,停止循环.【解析】选D.按照程序框图依次循环运算,当k=5时,停止循环,当k=5时,S=sin =.2.(2015·安徽高考文科·T7)执行如图所示的程序框图(算法流程图),输出的n 为 ( )A.3B.4C.5D.6【解题指南】利用循环结构逐次计算,直到退出循环,输出结果。

【解析】选B。

执行第一次循环体32,n=2;此时|a-1.414|=|1.5-1.414|=0.086≥0.005;执行第二次循环体75,n=3;此时|a-1.414|=|1.4-1.414|=0.014≥0.005;执行第三次循环体1712,n=4;此时|a-1.414|<0.005,此时不满足判断条件，输出n=4，故选B。

3. (2015·北京高考理科·T3)执行如图所示的程序框图,输出的结果为( )A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)【解析】选B.x=1,y=1,k=0;s=0,t=2,x=0,y=2,k=1;s=-2,t=2,x=-2,y=2,k=2;s=-4,t=0,x=-4,y=0,k=3.输出(-4,0).4. (2015·北京高考文科·T5)执行如图所示程序框图,输出的k 值为 ( )A.3B.4C.5D.6【解析】选B 。

10,3,;2k a q ===3,12a k == ; 3,24a k ==；3,38a k == ；3,416a k == 。

第九章算法初步、统计与统计案例、概率第一节算法的概念与程序框图1．算法具有确切性，其确切性是指( )A．算法一定包含输入、输出B．算法的每个步骤是具体的、可操作的C．算法的步骤是有限的D．以上说法都不正确答案：B2．(2013·北京卷)执行如图所示的程序框图，输出的S值为( )A ．1 B.23 C.1321 D.610987解析：执行一次循环后S ＝23，i ＝1，执行第二次循环后，S ＝1321，i ＝2≥2，退出循环体，输出S 的值为1321.答案：C3．(2013·石家庄模拟)已知流程图如图所示，该程序运行后，为使输出的b值为16，则循环体的判断框内①处应填( )A．2 B．3 C．5 D．7解析：当a＝1时，进入循环，此时b＝21＝2；当a＝2时，再进入循环，此时b＝22＝4；当a＝3时，再进入循环，此时b＝24＝16，所以当a＝4时，应跳出循环，得循环满足的条件为a≤3，故选B.答案：B4．(2012·合肥模拟)如上图所示，该程序框图所输出的结果是( )A．32 B．62 C．63 D．64答案：D5．(2012·东北三校联考)如图，若依次输入的x 分别为56π，π6，相应输出的y 分别为y 1，y 2，则y 1，y 2的大小关系是( )A ．y 1＝y 2B ．y 1>y 2C ．y 1<y 2D ．无法确定解析：由程序框图可知，当输入的x 为5π6时，sin 5π6>cos 5π6成立，所以输出的y 1＝sin 5π6＝12；当输入的x 为π6时，sin π6>cos π6不成立，所以输出的y 2＝cos π6＝32，所以y 1<y 2.故选C.答案：C6．(2013·福建卷)阅读如图所示的程序框图，若输入的k ＝10，则该算法的功能是( )A．计算数列{2n－1}的前10项和B．计算数列{2n－1}的前9项和C．计算数列{2n－1}的前10项和D．计算数列{2n－1}的前9项和解析：第一次循环：S＝1，i＝2，i<10；第二次循环：S＝3，i＝3，i<10；第三次循环：S＝7，i＝4，i<10……第九次循环：S＝29－1，i＝10，i＝10.第十次循环：S＝210－1，i＝11，i>10，输出S.根据选项，S＝－2101－2，故为数列{2n－1}的前10项和．故选A.答案：A7．(2013·重庆卷)执行如图所示的程序框图，如果输出s＝3，那么判断框内应填入的条件是( )A．k≤6 B．k≤7 C．k≤8 D．k≤9解析：当k ＝2时，s ＝log 23，当k ＝3时，s ＝log 23·log 34，当k ＝4时，s ＝log 23·log 34·log 45.由s ＝3，得lg 3lg 2×lg 4lg 3×lg 5lg 4×…×k ＋lg k＝3，即lg(k ＋1)＝3lg 2，所以k ＝7.再循环时，k ＝7＋1＝8，此时输出s ，因此判断框内应填入“k ≤7”．故选B.答案：B8．(2013·浙江卷)若某程序框图如上页图所示，则该程序运行后输出的值等于________．解析：当k ＝5时，输出S .此时，S ＝1＋11×2＋12×3＋13×4＋14×5＝1＋1－12＋12－13＋13－14＋14－15＝2－15＝95.答案：959．(2012·德阳模拟)下图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图．已知图甲中从左向右第一组的频数为4 000.在样本中记月收入在[)1 000，1 500，[1 500,2 000)，[2 000,2 500)，[2 500，3 000)，[3 000,3 500)，[3 500,4 000]的人数依次为A 1，A 2，…，A 6.图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图，则样本的容量n ＝________ ；图乙输出的S ＝__________(用数字作答)．解析：∵月收入在[1 000,1 500)的频率为0.000 8×500＝0.4，且有4 000人，∴样本的容量n ＝4 0000.4＝10 000，由图乙知输出的S ＝A 2＋A 3＋…＋A 6＝10 000－4 000＝6 000.答案：10 000 6 00010．(2013·南京二模)如图是一个算法流程图，其输出的n 值是________． 解析：程序运行如下：第一次循环：S ＝1＋3＝4，n ＝2； 第二次循环：S ＝1＋3＋6＝10，n ＝3； 第三次循环：S ＝1＋3＋6＋9＝19，n ＝4； 第四次循环：S ＝1＋3＋6＋9＋12＝31，n ＝5； 此时S ＝31＞20，故退出循环体，输出n ＝5. 答案：511．(2013·韶关二模)执行如图的程序框图，若p ＝4，则输出的S ＝________.解析：根据流程图所示的顺序可知：该程序的作用是计算S ＝12＋14＋18＋…＋12p .因为S ＝12＋14＋18＋…＋12p ＝1－12p .所以p ＝4.所以S ＝1516.答案：1516次记为(x1，y1)，(x2，y2)，…，(x n，y n)，…(1)若程序运行中输出的某个数组是(t，－6)，则t＝________________；(2)程序结束时，共输出(x，y)的组数为__________．解析：(1)按框图，x是公比为3的等比数列的项，y是公差为－2的等差数列的项，当y＝－6时，为第4项，这时x是等比数列的第4项，即t＝27.(2)n是公差为2的等差数列的项，当n＞2 012时，最大的项数为1 006，即输出(x，y)共1 006组．答案：(1)27 (2)1 00613．下图是某算法的程序框图，则程序运行后输出的结果是________．解析：第一次，s＝0＋(－1)1＋1＝0，n＝2；第二次，s＝0＋(－1)2＋2＝3，n＝3；第三次，s＝3＋(－1)3＋3＝5，n＝4；第四次，s＝5＋(－1)4＋4＝10>9，终止循环，输出结果10.答案：1014．执行下图所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________．解析：把l＝2，m＝3，n＝5代入y＝70l＋21m＋15n得y＝278，此时y＝278>105，第一次循环y＝278－105＝173，此时y＝173>105，再循环，y＝173－105＝68＜105，输出68，结束循环．答案：68。

第十二章算法初步、复数学案70算法与程序框图导学目标：1.了解算法的含义，了解算法的思想.2.理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构．自主梳理1．算法通常是指按照一定规则解决某一类问题的________和________的步骤．这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成．2．程序框图又称________，是一种用________、________及____________来准确、直观地表示算法的图形．通常程序框图由________和________组成，一个或几个程序框的组合表示算法中的一个步骤；________带方向箭头，按照算法进行的顺序将________连结起来．3．顺序结构是由________________________组成的，这是任何一个算法都离不开的基本结构．其结构形式为4．条件结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式．其结构形式为5．循环结构是指__________________________________________________________．反复执行的步骤称为________．循环结构又分为________________和________________．其结构形式为6．算法的五个特征：概括性、逻辑性、有穷性、不惟一性、普遍性． 自我检测1．(2010·陕西)如图所示是求样本x 1，x 2，…，x 10平均数x 的程序框图，图中空白框中应填入的内容为( )A ．S ＝S ＋x nB ．S ＝S ＋x nnC ．S ＝S ＋nD ．S ＝S ＋1n第1题图 第2题图2．(2010·全国)如果执行如图所示的框图，输入N ＝5，则输出的数等于( ) A .54B .45C .65D .563．(2011·北京)执行如图所示的程序框图，输出的s 值为( ) A ．－3B ．－12C .13D ．2第3题图第4题图4．(2011·山东)执行如图所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________.探究点一算法的顺序结构例1已知点P(x0，y0)和直线l：Ax＋By＋C＝0，求点P(x0，y0)到直线l的距离d，写出其算法并画出程序框图．变式迁移1阅读如图的程序框图，若输入的a、b、c分别是21、32、75，则输出的a、b、c分别是()A．75、21、32B．21、32、75C．32、21、75 D．75、32、21探究点二 算法的条件结构例2 (2011·杭州模拟)函数y ＝⎩⎪⎨⎪⎧－2 (x>0)0 (x ＝0)2 (x<0)，写出求该函数的函数值的算法，并画出程序框图．变式迁移2 给出一个如图所示的程序框图，若要使输入的x 值与输出的y 值相等，则这样的x 值的个数是( )A ．1B ．2C ．3D ．4探究点三 算法的循环结构例3 写出求1×2×3×4×…×100的一个算法并画出程序框图.变式迁移3 (2011·天津和平区模拟)在如图所示的程序框图中，当程序被执行后，输出s的结果是______．1．程序框图主要包括三部分：(1)表示相应操作的框；(2)带箭头的流程线；(3)框内外必要的文字说明，读懂程序框图要从这三个方面研究．流程线反映了流程执行的先后顺序，主要看箭头方向，框内外文字说明表明了操作内容．2．两种循环结构的区别：(1)执行情况不同：当型循环是先判断条件，当条件成立时才执行循环体，若循环条件一开始就不成立，则循环体一次也不执行．而直到型循环是先执行一次循环体，再判断循环条件，循环体至少要执行一次．(2)循环条件不同：当型循环是当条件成立时循环，条件不成立时停止循环，而直到型循环是当条件不成立时循环，直到条件成立时结束循环．(满分：75分)一、选择题(每小题5分，共25分)1．中山市的士收费办法如下：不超过2公里收7元(即起步价7元)，超过2公里的里程每公里收2.6元，另每车次超过2公里收燃油附加费1元(不考虑其他因素)．相应收费系统的程序框图如图所示，则①处应填()A．y＝7＋2.6x B．y＝8＋2.6xC．y＝7＋2.6(x－2) D．y＝8＋2.6(x－2)第1题图第2题图2．(2010·福建)阅读如图所示的程序框图，运行相应的程序，输出的i值等于() A．2 B．3 C．4 D．53．(2010·浙江)某程序框图如图所示，若输出的S＝57，则判断框内为()A．k>4? B．k>5? C．k>6? D．k>7?第3题图第4题图4．(2010·辽宁)如果执行如图所示的程序框图，输入n＝6，m＝4，那么输出的p等于() A．720 B．360 C．240 D．1205．阅读下面的程序框图，则输出的S等于()A．14 B．20 C．30 D．55二、填空题(每小题4分，共12分)6．(2011·浙江)若某程序框图如图所示，则该程序运行后输出的k的值是__________．第6题图第7题图7．执行如图所示的程序框图，输出的T＝________.8．(2010·江苏改编)如图是一个程序框图，则输出的S的值是________．三、解答题(共38分)9．(12分)(2011·包头模拟)对一个作直线运动的质点的运动过程观测了8次，第i次观测得到的数据为a i，具体如下表所示：i 1 2 3 4 5 6 7 8a i40 41 43 43 44 46 47 48在对上述统计数据的分析中，一部分计算见如图所示的程序框图(其中a是这8个数据的平均数)，求输出的S的值．10．(12分)(2011·汕头模拟)已知数列{a n}的各项均为正数，观察程序框图，若k＝5，k＝10时，分别有S＝511和S＝1021.(1)试求数列{a n}的通项；(2)令b n＝2a n，求b1＋b2＋…＋b m的值．11．(14分)已知某算法的程序框图如图所示，若将输出的(x，y)值依次记为(x1，y1)，(x2，y 2)，…，(x n ，y n )，…，(1)若程序运行中输出一个数组是(9，t)，求t 的值； (2)求程序结束时，共输出(x ，y)的组数； (3)求程序结束时，输出的最后一个数组．学案70 算法与程序框图自主梳理1．明确 有限 2.流程图 程序框 流程线 文字说明 程序框 流程线 流程线 程序框 3.若干个依次执行的步骤 5.从某处开始，按照一定的条件反复执行某些步骤的情况 循环体 当型(WHILE 型) 直到型(UNTIL 型)自我检测1．A [由循环结构的程序框图可知需添加的运算为S ＝x 1＋x 2＋…＋x 10的累加求和．] 2．D [第一次运行N ＝5，k ＝1，S ＝0，S ＝0＋11×2，1<5成立，进入第二次运行；k ＝2，S ＝11×2＋12×3，2<5成立，进入第三次运行；k ＝3，S ＝11×2＋12×3＋13×4，3<5成立，进入第四次运行；k ＝4，S ＝11×2＋12×3＋13×4＋14×5，4<5成立，进入第五次运行；k ＝5，S ＝11×2＋12×3＋13×4＋14×5＋15×6＝1－16＝56，5<5不成立，此时退出循环，输出S.]3．D [由框图可知i ＝0，s ＝2→i ＝1，s ＝13→i ＝2，s ＝－12→i ＝3，s ＝－3→i ＝4，s ＝2，循环终止，输出s ，故最终输出的s 值为2.]4．68解析 当输入l ＝2，m ＝3，n ＝5时，不满足l 2＋m 2＋n 2＝0，因此执行：y ＝70l ＋21m ＋15n ＝70×2＋21×3＋15×5＝278.由于278>105，故执行y ＝y －105，执行后y ＝278－105＝173，再执行一次y＝y－105后y的值为173－105＝68，此时68>105不成立，故输出68.课堂活动区例1解题导引顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．程序框图中一定包含顺序结构．解算法如下：第一步，输入x0，y0及直线方程的系数A，B，C.第二步，计算Z1＝Ax0＋By0＋C.第三步，计算Z2＝A2＋B2.第四步，计算d＝|Z1|.Z2第五步，输出d.程序框图：变式迁移1A[由程序框图中的各个赋值语句可得x＝21，a＝75，c＝32，b＝21，故a、b、c分别是75、21、32.]例2解题导引求分段函数函数值的程序框图的画法，如果是分两段的函数，则需引入一个判断框；如果是分三段的函数，则需引入两个判断框．解算法如下：第一步，输入x；第二步，如果x>0，则y ＝－2；如果x ＝0，则y ＝0；如果x<0，则y ＝2；第三步，输出函数值y.相应的程序框图如图所示．变式迁移2 C [本问题即求函数y ＝⎩⎪⎨⎪⎧ x 2，x ≤2，2x －3，2<x ≤5，1x ，x>5的值．若x ≤2，由x 2＝x 得，x ＝1或0；若2<x ≤5，由x ＝2x －3得，x ＝3；若x>5，由x ＝1x得，x ＝±1，不符合． 故符合要求的x 值有3个．] 例3 解题导引 数学中的累加、累乘、累差等重复性操作可以用循环结构来实现．循环结构分当型和直到型两种，二者的区别是：前者是，当满足条件时执行循环体，而后者是“直到”条件满足时结束循环．解 第一步，设S 的值为1.第二步，设i 的值为2.第三步，如果i ≤100执行第四步，否则转去执行第七步．第四步，计算S 乘i 并将结果赋给S.第五步，计数i 加1并将结果赋给i.第六步，转去执行第三步．第七步，输出S 的值并结束算法．根据自然语言描述，程序框图如下：变式迁移3 286 解析 数列{a n }：4,7,10，…为等差数列，令a n ＝4＋(n －1)×3＝40，得n ＝13，∴s ＝4＋7＋…＋40＝(4＋40)×132＝286. 课后练习区1．D [根据题意可知x>2时，收费应为起步价7元＋超过2公里的里程收费2.6(x －2)元＋燃油附加费1元＝8＋2.6(x －2)．]2．C [由框图可知i ＝1，s ＝1×21＝2；i ＝2，s ＝2＋2×22＝10；i ＝3，s ＝2＋2×22＋3×23>11，i ＝i ＋1＝3＋1＝4.]3．A [当k ＝1时，k ＝k ＋1＝2，S ＝2×1＋2＝4；当k ＝2时，k ＝k ＋1＝3，S ＝2×4＋3＝11；当k ＝3时，k ＝k ＋1＝4，S ＝2×11＋4＝26；当k ＝4时，k ＝k ＋1＝5，S ＝2×26＋5＝57.此时S ＝57，循环结束，k ＝5，所以判断框中应为“k>4？”．]4．B [由框图可知：当n ＝6，m ＝4时，第一次循环：p ＝(6－4＋1)×1＝3，k ＝2.第二次循环：p ＝(6－4＋2)×3＝12，k ＝3.第三次循环：p ＝(6－4＋3)×12＝60，k ＝4.第四次循环：p ＝(6－4＋4)×60＝360，此时k ＝m ，终止循环．输出p ＝360.]5．C [第一次循环：S ＝12；第二次循环：S ＝12＋22；第三次循环；S ＝12＋22＋32；第四次循环：S ＝12＋22＋32＋42＝30.]6．5解析 初始值：k ＝2，执行“k ＝k ＋1”得k ＝3，a ＝43＝64，b ＝34＝81，a>b 不成立； k ＝4，a ＝44＝256，b ＝44＝256，a>b 不成立；k ＝5，a ＝45＝1 024，b ＝54＝625，a>b 成立，此时输出k ＝5.7．30解析 按照程序框图依次执行为S ＝5，n ＝2，T ＝2；S ＝10，n ＝4，T ＝2＋4＝6；S ＝15，n ＝6，T ＝6＋6＝12；S ＝20，n ＝8，T ＝12＋8＝20；S ＝25，n ＝10，T ＝20＋10＝30>S ，输出T ＝30.8．63解析 当n ＝1时，S ＝1＋21＝3；当n ＝2时，S ＝3＋22＝7；当n ＝3时，S ＝7＋23＝15；当n ＝4时，S ＝15＋24＝31；当n ＝5时，S ＝31＋25＝63>33.故S ＝63.9．解 该程序框图即求这组数据的方差，∵a ＝44，(2分)∴S ＝18∑8i ＝1 (a i －a )2＝18[(40－44)2＋(41－44)2＋…＋(48－44)2]＝7.(12分)10．解 由题中框图可知S ＝1a 1a 2＋1a 2a 3＋…＋1a k a k ＋1， ∵数列{a n }是等差数列，设公差为d ，则有1a k a k ＋1＝1d (1a k －1a k ＋1)， ∴S ＝1d (1a 1－1a 2＋1a 2－1a 3＋…＋1a k －1a k ＋1) ＝1d (1a 1－1a k ＋1)．(4分) (1)由题意可知，k ＝5时，S ＝511；k ＝10时，S ＝1021. ∴⎩⎨⎧ 1d (1a 1－1a 6)＝511，1d (1a 1－1a 11)＝1021，解得⎩⎪⎨⎪⎧ a 1＝1，d ＝2或⎩⎪⎨⎪⎧a 1＝－1，d ＝－2(舍去)． 故a n ＝a 1＋(n －1)d ＝2n －1.(8分)(2)由(1)可得b n ＝2a n ＝22n －1，∴b 1＋b 2＋…＋b m＝21＋23＋…＋22m －1＝2(1－4m )1－4＝23(4m －1)． (12分)11．解 (1)循环体运行结果如下： 输出(1，0)n ＝3x ＝3y ＝－2n<2 011 输出(3，－2)n ＝5x ＝9y ＝－4n<2 011 输出(9，－4)n ＝7x ＝27y ＝－6n<2 011∴输出数组(9，t)中的t 值是－4.(4分)(2)计数变量n 的取值为：3,5,7，…，构成等差数列，由3＋(m －1)×2＝2 011.解得m ＝1 005，由于当m＝1 005时，n＝2 011，循环体还要执行一遍，会输出第1 006个数组，然后n＝2 013>2 011，跳出循环体．故共输出1 006个数组．(8分)(3)程序输出的数组(x n，y n)按输出的先后顺序，横坐标x n组成一个等比数列{x n}，首项x1＝1，公比q＝3.纵坐标组成一个等差数列{y n}，首项y1＝0，公差d＝－2.∴x1 006＝31 005，y1 006＝－2×1 005＝－2 010.故程序结束时，输出的最后一个数组是(31 005，－2 010)．(14分)。

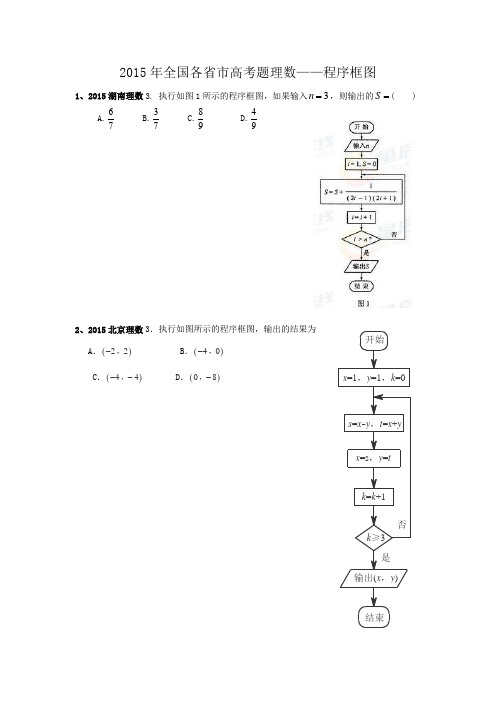
2015年全国各省市高考题理数——程序框图1、2015湖南理数3. 执行如图1所示的程序框图，如果输入3n =，则输出的S =( ) A.67 B.37 C.89 D.492、2015北京理数3．执行如图所示的程序框图，输出的结果为 A ．()22-，B ．()40-，C ．()44--，D ．()08-，开始x =1，y =1，k =0s =x -y ，t =x +y x =s ，y =t k =k +1k ≥3输出(x ，y )结束是否3、2015天津理数（3）阅读右边的程序框图，运行相应的程序，则输出S的值为（A）-10（B）6（C）14（D）184、2015江苏4.根据如图所示的伪代码，可知输出的结果S为________.5、2015福建理数6、阅读如图所示的程序框图，运行相应的程序，则输出的结果为A.2B.1C.0D.16、2015新课标Ⅰ理数（9）执行右面的程序框图，如果输入的t=0.01，则输出的n=（A）5 （B）6 （C）7 （D）87、2015陕西理数8. 根据右边的框图，当输入x为2006时，输出的yA.2B.4C.10D.288、2015新课标II理数（8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入a,b分别为14,18，则输出的a=A.0B.2C.4D.149、2015四川理数3.执行如图所示的程序框图，输出S 的值是（ ）A.- C.-12 D.1210、2015重庆理数7、执行如图所示的程序框图，若输入K 的值为8，则判断框图可填入的条件是A 、34s ≤B 、56s ≤ C 、1112s ≤ D 、2524s ≤11、2015山东理数（13）执行右边的程序框图，输出的T 的值为 .13、2015安徽理数13.执行如图所示的程序框图（算法流程图），输出的n为参考答案：1、B2、B3、B4、 75、C6、C7、C8、B9、D10、C 11、11613、4。

【优化方案】2015年高考数学第十章第4课时算法与程序框图、基本算法语句知能演练轻松闯关新人教A版[基础达标])1．(2014·某某某某市模拟考试) 若某程序框图如图所示，则该程序运行后输出的值是( )A．2 B．3C．4 D．5解析：选C.逐次运行的结果是n＝3，i＝2；n＝4，i＝3；n＝2，i＝4.故输出的值是4.2．(2014·某某东营一模)运行下面框图输出的S是254，则(1)应为( )A．a≤5? B．a≤6?C．a≤7? D．a≤8?解析：选C.循环第一次：S＝2，a＝2；第二次：S＝6，a＝3；第三次：S＝14，a＝4；第四次：S＝30，a＝5；第五次：S＝62，a＝6；第六次：S＝126，a＝7；第七次：S＝254，a＝8；此时，应结束循环，所以a≤7.3．(2014·某某某某一模)执行如图所示的程序框图，若输出结果为3，则可输入的实数x值的个数为( )A ．1B ．2C ．3D ．4 解析：选C.本题为分段函数f (x )＝⎩⎪⎨⎪⎧x 2－1，x ≤2，log 2x ，x >2.又输出结果为3，则可输入的实数x的值可为－2，2，8.4．(2013·高考某某卷)执行两次如图所示的程序框图，若第一次输入的a 的值为－1.2，第二次输入的a 的值为1.2，则第一次，第二次输出的a 的值分别为( )A ．0.2，0.2B ．0.2，0.8C ．0.8，0.2D ．0.8，0.8解析：选C.由程序框图可知：当a ＝－1.2时，∵a <0， ∴a ＝－1.2＋1＝－0.2，a <0，a ＝－0.2＋1＝0.8，a >0.∵0.8<1，输出a ＝0.8. 当a ＝1.2时，∵a ≥1，∴a ＝1.2－1＝0.2. ∵0.2<1，输出a ＝0.2. 5．(2014·某某某某市模拟考试) 阅读程序框图，运行相应的程序，输出的结果为( )A.1311 B.2113C.813 D.138解析：选D.逐次运行的结果是x ＝1，y ＝1，z ＝2；x ＝1，y ＝2，z ＝3；x ＝2，y ＝3，z＝5；x ＝3，y ＝5，z ＝8；x ＝5，y ＝8，z ＝13；x ＝8，y ＝13，z ＝21，此时输出的结果y x ＝138.6．(2014·某某某某市诊断性检测) 某算法的程序框图如图所示，执行该算法后输出的结果i 的值为( )A ．4B ．5C ．6D ．7 解析：选C.第一次循环S ＝1，满足S <30，所以P ＝0＋1＝1，S ＝1＋1＝2，i ＝1＋1＝2； 第二次循环S ＝2，满足S <30，所以P ＝1＋2＝3，S ＝2＋3＝5，i ＝2＋1＝3； 第三次循环S ＝5，满足S <30，所以P ＝3＋3＝6，S ＝5＋6＝11，i ＝3＋1＝4； 第四次循环S ＝11，满足S <30，所以P ＝6＋4＝10，S ＝11＋10＝21，i ＝4＋1＝5； 第五次循环S ＝21，满足S <30，所以P ＝10＋5＝15，S ＝21＋15＝36，i ＝5＋1＝6； 第六次循环S ＝36，不满足S <30，输出的i ＝6.7. (2013·高考某某卷)阅读如图所示的程序框图，若输入的k ＝10，则该算法的功能是( )A ．计算数列{2n －1}的前10项和B ．计算数列{2n －1}的前9项和C ．计算数列{2n－1}的前10项和D ．计算数列{2n－1}的前9项和 解析：选A.S ＝0，i ＝1； S ＝1＋2×0＝1＝20，i ＝2；S ＝1＋2×1＝1＋2＝20＋21，i ＝3；S ＝1＋2×3＝20＋21＋22，i ＝4；…观察得到对应数列的通项公式为a n ＝2n －1.k ＝10时，i >10时输出，说明是求前10项的和．8．运行如图所示的程序框图，若输出的结果为137，则判断框中应该填的条件是( )A ．k >5B ．k >6C ．k >7D ．k >8解析：选B.第一次运行S ＝1＋11×2，k ＝2；第二次运行S ＝1＋11×2＋12×3，k ＝3；…；第n 次运行S ＝1＋11×2＋12×3＋…＋1n （n ＋1）＝137，k ＝n ＋1，此时结束循环，得n ＝6，故判断框中应该填入“k >6”．9．(2013·高考某某卷)如图是一个算法的流程图，则输出的n 的值是________．解析：算法流程图执行过程如下： n ＝1，a ＝2，a <20； a ＝8，n ＝2，a <20； a ＝26，n ＝3，a >20， 输出n ＝3. 答案：310．(2013·高考某某卷)执行如图所示的程序框图，若输入n 的值为4，则输出s 的值为________．解析：第一步运算结果：s ＝1，i ＝2(i ≤4成立)；第二步运算结果：s ＝2，i ＝3(i ≤4成立)；第三步运算结果：s ＝4，i ＝4(i ≤4成立)；第四步运算结果：s ＝7，i ＝5(i ≤4不成立)，程序结束，故输出s 的值为7.答案：711．(2013·高考某某卷) 阅读如图所示的程序框图，运行相应的程序，若输入m 的值为2, 则输出的结果i ＝________．解析：m ＝2，A ＝1，B ＝1，i ＝0.第一次：i ＝0＋1＝1，A ＝1×2＝2，B ＝1×1＝1，A>B ； 第二次：i ＝1＋1＝2，A ＝2×2＝4，B ＝1×2＝2，A>B ； 第三次：i ＝2＋1＝3，A ＝4×2＝8，B ＝2×3＝6，A>B ； 第四次：i ＝3＋1＝4，A ＝8×2＝16，B ＝6×4＝24，A<B. 终止循环，输出i ＝4. 答案：4 12．(2014·某某某某一模)输入x ＝5，运行如图所示的程序之后得到的y 等于________．I N PUTx IFx <0THE Ny ＝(x ＋1)*(x ＋1) ELSEy ＝(x －1)*(x －1) E ND IF P R I N Ty E ND解析：y ＝f (x )＝⎩⎪⎨⎪⎧（x ＋1）2，x <0，（x －1）2，x ≥0， ∴f (5)＝(5－1)2＝16. 答案：16[能力提升])1．(2014·某某某某市质量预测) 执行如图所示的程序框图，若输入x ＝2，则输出y 的值为( )A．5 B．9C．14 D．41解析：选D.第一次循环后：x＝5，y＝14；第二次循环后：x＝14，y＝41，此时|x－y|>9，终止循环，故输出y的值为41.2．执行如图所示的程序框图([x]表示不超过x的最大整数)，则输出S的值为( )A．4 B．5C．7 D．9解析：选C.初始条件：S＝0，n＝0，逐次计算结果是S＝0；n＝1，S＝[1]＝1；n＝2，S＝1＋[2]＝2；n＝3，S＝2＋[3]＝3；n＝4，S＝3＋[4]＝5；n＝5，S＝5＋[5]＝7，此时n＝5满足输出条件，输出S＝7.3．(2012·高考某某卷)如图所示是用模拟方法估计圆周率π值的程序框图，P表示估计结果，则图中空白框内应填入( )A．P＝N1 000B．P＝4N1 000C．P＝M1 000D．P＝4M1 000解析：选D.∵x i ，y i 为0～1之间的随机数，构成以1为边长的正方形面，当x 2i ＋y 2i ≤1时，点(x i ，y i )均落在以原点为圆心，以1为半径且在第一象限的14圆内，当x 2i ＋y 2i >1时对应点落在阴影部分中(如图所示)．∴有N M ＝1－π4π4，N π＝4M －M π，π(M ＋N)＝4M ，π＝4M1 000. 4．(2013·高考某某卷) 某程序框图如图所示，若该程序运行后输出的值是95，则( )A ．a ＝4B ．a ＝5C ．a ＝6D ．a ＝7解析：选A.法一：由程序框图及最后输出的值是95可知：当k ＝1时，S ＝1，k >a 不成立，故S ＝1＋11×2＝32，k ＝2>a 不成立，故S ＝32＋12×3＝53，k ＝3>a 不成立，故S ＝53＋13×4＝74，k ＝4>a 不成立，故S ＝74＋14×5＝95，此时k ＝5>a 成立，所以a ＝4.法二：由程序框图可知：S ＝1＋11×2＋12×3＋…＋1k （k ＋1）＝1＋1－12＋12－13＋…＋1k －1k ＋1＝1＋1－1k ＋1＝2－1k ＋1，由S ＝95，得2－1k ＋1＝95，解得k ＝4，故由程序框图可知k ＝4>a 不成立，k ＝5>a 成立，所以a ＝4.5．(2014·某某东营模拟)如图是判断“美数”的流程图，在[30，40]内的所有整数中，“美数”的个数是________．解析：依题意可知，题中的“美数”包括12的倍数与能被3整除但不能被6整除的数，由此不难得知，在[30，40]内的“美数”有3×11、3×12、3×13三个数．答案：36．(2013·高考某某卷)阅读如图所示的程序框图，运行相应的程序，输出的结果i ＝________．解析：程序框图的执行流程及中间结果如下：第一步：a ＝10，i ＝1，a ≠4，a 不是奇数，a ＝102＝5，i ＝2；第二步：a ≠4，a 是奇数，a ＝3×5＋1＝16，i ＝3；第三步：a ≠4，a 不是奇数，a ＝162＝8，i ＝4；第四步；a ≠4，a不是奇数，a ＝82＝4，i ＝5；第五步，a ＝4，这时跳出循环，输出i ＝5.答案：5。

2015全国新课标I数学（理）试题及解析满分:班级：_________ 姓名：_________ 考号：_________一、单选题（共12小题）1。

设得数z满足，则|z|=( )A．1B．C．D．22.（ )A．B．C．D．3.设命题( ）A．B．C．D．4。

投篮测试中，每人投3次，至少投中2次才能通过测试，已知某同学每次投篮投中的概率为0。

6，且各次投篮是否投中相互独立，则该同学能过测试的概率为( )A．0。

648B．0.432C．0。

36D．0。

3125.已知是双曲线上的一点，是的两个焦点。

若，则的取值范围是（）A．B．C．D．6.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依恒内角,下周八尺,高五尺.问：积及为米几何？”其意思为:“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺,米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3,估算出堆放斛的米约有（）A．14斛B．22斛C．36斛D．66斛7.设D为所在平面内一点，，则( )A．B．C．D．8.函数的部分图像如图所示，则的单调递减区间为（ )A．B．C．D．9。

执行下面的程序框图，如果输入的,则输出的（）A．5B．6C．7D．810。

的展开式中，的系数是（）A．10B．20C．30D．6011.圆柱被一个平面截去一部分后与半球（半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为，则( ）A．1B．2C．4D．812.设函数=,其中a1，若存在唯一的整数，使得，则的取值范围是( ）A．B．C．D．二、填空题(共4小题）13。

若函数为偶函数，则 .14。

一个圆经过椭圆的三个顶点，且圆心在x轴的正半轴上,则该圆的标准方程为。

15.若x，y满足约束条件则的最大值为 .16。

在平面四边形ABCD中，，，则AB的取值范围是。