经典算法例题分析
- 格式:pptx
- 大小:8.43 MB
- 文档页数:39
几种常见的算法案例分析算法不仅是数学及其应用的重要的组成局部,也是计算机科学的重要根底,其中算法的重要思想在几种常见的算法例案中得以较好的表达。
本文从几种常见算法案例出发,来探究一下算法的内涵。
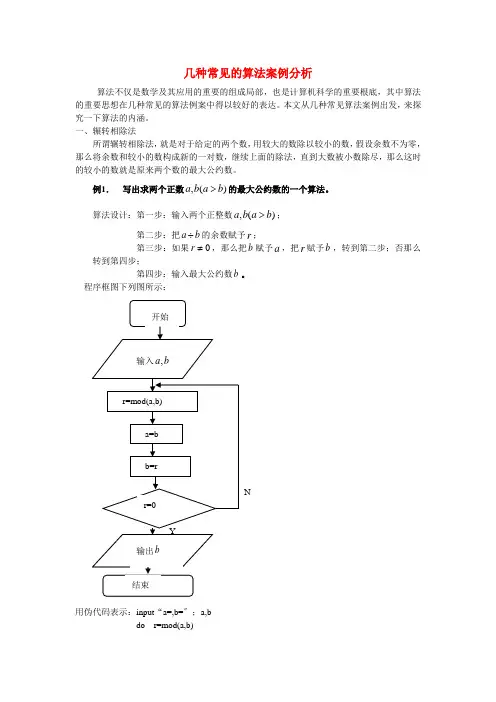
一、辗转相除法所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数,假设余数不为零,那么将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,那么这时的较小的数就是原来两个数的最大公约数。
例1. 写出求两个正数,()a b a b >的最大公约数的一个算法。
算法设计:第一步:输入两个正整数,()a b a b >;第二步:把a b ÷的余数赋予r ;第三步:如果0r ≠,那么把b 赋予a ,把r 赋予b ,转到第二步;否那么转到第四步;第四步:输入最大公约数b 。
程序框图下列图所示:用伪代码表示:input “a=,b=〞;a,bdo r=mod(a,b)a=bb=rloop until r=0print bend二、更相减损术所谓更相减术,就是对于给定的两个数,以其中较大的数减去较小的数,然后将差和较小的数构成一对新数,再用较大的数减去较小的数,反复执行此步骤,直到差数和较小的数相等,此时相等的两个数就是原两个数的最大公约数。
在我国古代的<<九章算术>>中有这样的描述“约分术曰:可半者半之,不可半者会置分母分子之数,以少减多,更相损减,求其等也,以等数约之。
〞意思是说如果分母、分子都是偶数,那么先除以2;如果不全是偶数,便将分子与分母互减,以少减多,直到得出最大公约数为止,用最大公约数约分子与分母,便可使分数最简。
如果两个数都是偶数,也不除以2,直接求最大公约数。
这是一种多么奇妙的方法啊,我们古代人在许多方面都比西方先进,这是值得我们自豪的。
以上题为例,算法可以这样来设计:第一步:输入两个正整数,()a b a b >;第二步:假设a 不等于b ,那么执行第三步;否那么执行第五步;第三步:把a b -的差赋予r ;第四步:如果b r >,那么把b 的值赋予a ,否那么把r 的值赋予a ,执行第二步; 第五步:输出最大公约数b 。

卡车更新问题(第二届选拔赛第三题,即设备更新问题)【试题】某人购置了一辆新卡车, 从事个体运输业务. 给定以下各有关数据:R[t], t=1,2,...,k, 表示已使用过 t 年的卡车, 再工作一年所得的运费, 它随 t 的增加而减少, k (k≢20) 年后卡车已无使用价值.U[t], t=1,...,k, 表示已使用过 t 年的卡车, 再工作一年所需的维修费, 它随 t 的增加而增加.C[t], t=1,2,...,k, 表示已使用过 t 年的旧卡车, 卖掉旧车, 买进新车, 所需的净费用, 它随 t 的增加而增加. 以上各数据均为实型, 单位为"万元".设某卡车已使用过 t 年,①如果继续使用, 则第 t+1 年回收额为 R[t]-U[t],②如果卖掉旧车,买进新车, 则第 t+1 年回收额为 R[0]-U[0]-C[t] .该运输户从某年初购车日起,计划工作 N (N<=20) 年, N 年后不论车的状态如何,不再工作. 为使这 N 年的总回收额最大, 应在哪些年更新旧车? 假定在这 N 年内, 运输户每年只用一辆车, 而且以上各种费用均不改变.输入: 用文件输入已知数据, 格式为:第 1 行: N (运输户工作年限)第 2 行: k (卡车最大使用年限, k≢20 )第 3 行: R[0] R[1] ... R[k]第 4 行: U[0] U[1] ... U[k]第 5 行: C[0] C[1] ... C[k]输出: 用文本文件按以下格式输出结果:第 1 行: W ( N 年总回收额 )第 2--N+1 行: 每行输出 3 个数据:年序号 ( 从 1 到 N 按升序输出 );是否更新 ( 当年如果更新,输出 1, 否则输出 0);当年回收额 ( N 年回收总额应等于 W ).例: 设给定以下数据:N=4, k=5,i: 0 1 2 3 4 5R[i]: 8 7 6 5 4 2U[i]: 0.5 1 2 3 4 5C[i]: 0 2 3 5 8 10则正确的输出应该是24.51 0 7.52 1 5.53 1 5.54 0 6.0【分析】这是动态规划的一个典型的例题.由题意可知,用过t年的卡车,继续使用一年的收益为d[t]=R[t]-U[t],更换新车后一年的收益为e[t]=R[0]-U[0]-C[t]. 我们采用倒推分析的方法.F[j,t]表示已经使用了t年的卡车, 在第j年不论继续使用还是更新,到第N年为止,可能得到的最大收益. 规定当j>N时, F[j,t]≡0. 如果在第j年更新,则收益为p=e[t]+F[j+1,1]; 如果仍使用旧车,则收益为 q=d[t]+F[j+1,t+1]. 这里,e[t]或d[t]为第j年的收益, F[j+1,1]或F[j+1,t+1]为从第j+1年到第N年在不同条件下的最大收益.显然,F[j,t]=Max(p,q).这就是所需要的计算公式.在下面的程序中,数组g[j,t]用于记录使用过t年的车,在第j年的选择方案,g[j,t]=1表示更换新车,g[j,t]=0表示仍使用旧车.【参考程序】program tjcoi2_3; { Write By Li Xuewu }type arr20=array[0..20] of real;var rr,uu,cc,d,e:arr20;f:array [0..22,0..21] of real;g:array [0..22,0..21] of integer;i,j,k,k2,n,t:integer;file1:string[20];p,q:real;text2,text3:text;procedure init;var i:integer;beginwriteln('Input filename:');readln(file1);assign(text2,file1); reset(text2);readln(text2,n); readln(text2,k);for i:=0 to k do read(text2,rr[i]); readln(text2);for i:=0 to k do read(text2,uu[i]); readln(text2);for i:=0 to k do read(text2,cc[i]); readln(text2);close(text2);for i:=0 to k dobegin d[i]:=rr[i]-uu[i]; e[i]:=d[0]-cc[i]; end;end;procedure result3;var i:integer;beginwriteln('enter filename for output:');readln(file1);assign(text3,file1); rewrite(text3);writeln(text3,f[1,1]:8:3);writeln(text3,' 1 0', e[0]:8:2); t:=1;for i:=2 to n doif g[i,t]=1 thenbegin writeln(text3,i:2,' 1',e[t]:8:2); t:=1 endelsebegin writeln(text3,i:2,' 0',d[t]:8:2); t:=t+1; end ; writeln(f[1,1]:8:3);writeln(' 1 0',e[0]:8:2); t:=1;for i:=2 to n doif g[i,t]=1 thenbegin writeln(i:2,' 1',e[t]:8:2); t:=1 endelsebegin writeln(i:2,' 0',d[t]:8:2); t:=t+1; end ;close(text3);end;begin {main}init;for i:=0 to n dofor j:=0 to k do g[i,j]:=1;for i:=0 to k do f[n+1,i]:=0;for i:=1 to n+1 do f[i,k+1]:=-100;for j:=n downto 2 dobegink2:=k;if j<k then k2:=j-1;for t:=1 to k2 dobeginp:=e[t]+f[j+1,1]; q:=d[t]+f[j+1,t+1]; f[j,t]:=p; g[j,t]:=1;if q>p thenbegin g[j,t]:=0; f[j,t]:=q; end; end;end;f[1,1]:=d[0]+f[2,1];result3;end.省刻度尺问题program e04_06;label 10;type arr40=array [0..40]of byte;var a,b,c,d:arr40;i,j, k,kz,r,m,t1,t2:byte;done: boolean;procedure result;var file1:string[20];text2:text;i,j,w:integer;beginwriteln('enter filename for output:');readln (file1);assign(text2,file1); rewrite(text2);writeln(k:2);for i:=1 to k do write(a[i]:4);writeln;for i:=1 to m do writeln(i:2, c[i]:4,d[i]:4);writeln(text2,k:2);for i:=1 to k do write(text2,a[i]:4);writeln(text2);for i:=1 to m do writeln(text2,i:2, c[i]:4,d[i]:4);close(text2);done:=true;halt;end;procedure init1;var i:integer;beginfor i:=0 to 40 do b[i]:=0; c:=b; d:=b;for i:=2 to k do a[i]:=0;a[0]:=0; a[k+1]:=m; a[1]:=1;end;procedure find2(r,t1,t2:integer);var i,j,j2,v1,v2,t,t3,t4,temp:integer;begin {1}for i:=t1 to t2 dobegin {2}a[r]:=i;if (r<k) and (i<t2) thenbegin t3:=i+1; find2(r+1,t3,t2); end;if r=k thenbegin{3}if ((kz=1)or(kz=3)) and (k>2) thenbegintemp:=a[2];for j:=2 to k-1 do a[j]:=a[j+1];a[k]:=temp;end;for j:=1 to m do b[j]:=0;for j:=0 to k dofor j2:=j+1 to k+1 dobegint:=a[j2]-a[j];if b[t]=0 thenbeginb[t]:=1; c[t]:=a[j]; d[t]:=a[j2];end;end;done:=true; j:=0;repeat j:=j+1 until (b[j]=0)or(j>m);if j<=m then done:=false;if done then result;end;{3}end; {2}end; {1}begin{main}writeln('inptu L:(L<=40 and L>3)'); readln(m); k:=0;repeat k:=k+1 until ((k+2)*(k+1) div 2) >= m; 10: init1;for kz:=1 to 3 docase kz of1: begin{*}a[2]:=m-2;if k=2then find2(2,a[2],a[2])elsebeginr:=3; t1:=2; t2:=m-3;find2(r,t1,t2);end;end;{*}2: begin{**}a[2]:=2;r:=3; t1:=3; t2:=m-1;if t2<t1 then t2:=t1;find2(r,t1,t2);end;{**}3: begin{***}a[2]:=m-1;r:=3; t1:=2; t2:=m-2;if t2<t1 then t2:=t1;find2(r,t1,t2);end;{***}end;{case}k:=k+1; goto 10;end.排列问题输入整数N(<15),输出1..N的全部不同排列的总数,当N<=6时,还要输出全部排列. int p[30];int pr1(int n){ int i,m,j, t,j1,j2;for (i=n;i>0 && p[i]>=p[i+1];i--);if(i<=0) return 0;for(j=i+1,t=i+1;t<=n && p[i]<p[t];t++)j=t;m=p[i];p[i]=p[j];p[j]=m;for (j1=i+1,j2=n;j1<j2;j1++,j2--)m=p[j1],p[j1]=p[j2],p[j2]=m;return 1;}main() /*n!*/{int j,t,n,m;long num;printf("input n:\n");scanf("%d",&n);for (j=1;j<=n;j++) p[j]=j;t=1; num=0;while (t>0) /***/{if (n<=6){for(j=1;j<=n;j++) printf("%d ",p[j]);printf("\n");}num++;t=pr1(n);}printf("num=%ld\n",num);}取奇数游戏{ 该游戏规则如下: 操作者先输入一个奇数N(<200)表示N个石子. 设计算机为A 方,操作者为B 方, 双方轮流取石子,每次取1-3个. 最后取到石子总数为奇数的一方获胜. 编制程序使计算机有较多的获胜机会,}unit lxw022;typesetab=set of 0..200;varevena,evenb,odda,oddb:setab;i,j,n,na,nb,k,kz,r,t:integer;ab,ll:char;procedure init0(var n:integer);beginclrscr;gotoxy(1,1);writeln('***************************************');writeln(' 取奇数游戏规则如下: ');writeln(' 1.操作者先输入一个奇数N(<200).');writeln(' 2.设计算机为A 方,操作者为B 方,双方轮流取数,每次取1-3个.');writeln(' 3.最后取到奇数的一方为胜方. ');writeln('***************************************');n:=400;while not odd(n)or(n>200) dobegingotoxy(10,7);writeln('输入一个奇数N(<200):');gotoxy(10,8); readln(n);end;end;procedure prt1;begingotoxy(1,17);writeln(' 总计计算机已取得操作手已取得剩余');gotoxy(50,19);writeln(' ');gotoxy(1,19);writeln(' ',n,' ',na,' ',nb,' ',r);end;procedure prt2(var ll:char);begingotoxy(10,21);if odd(na) then writeln('可惜, 你输了!')else writeln ('祝贺你的成功!');gotoxy(10,22);writeln('再玩一次吗? (Y/N)');gotoxy(10,23); readln(ll);end;procedure aget(var r,t,na:integer);var k,kz:integer;beginkz:=0; k:=0;while (k<3)and(kz=0)and(k<r) dobegink:=k+1;if (not odd(na+k))and(r-k in evena) thenbegin kz:=1; t:=k end;if (odd(na+k))and(r-k in odda) thenbegin kz:=1; t:=k end;end;if kz=0 then t:=1;gotoxy(50,14);writeln(' 计算机这次取',t,' 个.');na:=na+t; r:=r-t;end;procedure bget(var r,t,nb,i:integer);begint:=0;while not(t in[1,2,3])or(t>r) dobegingotoxy(30,13); writeln(' ');gotoxy(2,13);writeln('第',i:2,' 轮: 输入你的选择(1/2/3) 并且不得超过',r);gotoxy(5,14); write(' ');gotoxy(5,14); readln(t); gotoxy(20,14);if not(t in[1,2,3])or(t>r)then write('数据错! 请重新输入.')else write(' ');end;nb:=nb+t; r:=r-t;end;begin{main}ll:='y';while (ll='Y')or(ll='y') dobegin{2}init0(n);r:=n;{ 1. 建立获胜策略集EVENA,EVENB,ODDA,ODDB }evena:=[4,5]; evenb:=[0,1,2,3];odda:=[0,1]; oddb:=[2..5];for i:=6 to n dobegin{3}nb:=0;if not odd(i) then nb:=1;kz:=0; k:=0;while (k<3)and(kz=0) dobegink:=k+1;if odd(nb+k)and (i-k in odda) then kz:=1;if (not odd(nb+k))and(i-k in evena) then kz:=1;end;if kz=0then evena:=evena+[i]else evenb:=evenb+[i];nb:=0;if odd(i) then nb:=1;kz:=0; k:=0;while (k<3)and(kz=0) dobegink:=k+1;if odd(nb+k)and (i-k in odda) then kz:=1;if (not odd(nb+k))and(i-k in evena) then kz:=1;end;if kz=0then odda:=odda+[i]else oddb:=oddb+[i];end;{3}{ 2. 开始取数. }na:=0; nb:=0; t:=0; ab:=' ';while not (ab in ['a','b','A','B']) dobegingotoxy(10,9);writeln('输入: "谁先开始(A/B) ?" A: 计算机, B:操作手.');gotoxy(10,10); readln(ab);end;i:=1;if (ab='B')or(ab='b') then bget(r,t,nb,i);repeatif r>0 thenbegin {5}aget(r,t,na);prt1;if r>0 then bget(r,t,nb,i);i:=i+1;end;{5}until r=0;gotoxy(3,16); writeln(' 最后结果:');prt1; prt2(ll);end{2}end.{main}unit Unit1;interfaceusesWindows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs;typeTForm1 = class(TForm)private{ Private declarations }public{ Public declarations }end;varForm1: TForm1;implementation{$R *.DFM}end.取石子游戏任给N堆石子,两人(游戏者与计算机)轮流从任一堆中任取,计算机先取,取最后一颗石子胜.#include <stdio.h>unsigned int a[11];int n;void init1(){int i;printf("input n(2--10):"); scanf("%d",&n);for (i=1;i<=n;i++){printf("input No.%d Number of stone:\n",i);scanf("%d",&a[i]);}}void status(){int i;printf("Now remainder:\n");for (i=1;i<=n;i++) printf(" No.%d rem: %u \n",i,a[i]);}unsigned int sum1(){unsigned int s; int i;s=0;for(i=1;i<=n;i++) s+=a[i];return s;}unsigned int xorall(){unsigned int s; int i;s=0;for (i=1;i<=n;i++) s^=a[i];return s;}main(){unsigned int t;int i,s,e;init1();while (sum1()){if (xorall()==0){for (i=1;i<=n;i++)if(a[i]>0){printf("computer take 1 from No.%d \n",i);a[i]--; goto loop2;}}elsefor (i=1;i<=n;i++){ s=a[i]-(xorall()^a[i]) ;if (s>0){printf("computer take %u from No.%d \n",s,i);a[i]^=xorall();goto loop2;}}loop2:;if(sum1()==0){printf("computer win!"); break;}status();while (1){printf("Input your selection(examp. 1 2 means take 2 from No.1):\n");scanf("%d %u",&e,&t);if ((e>=1)&&(e<=n)&&(a[e]>=t)){a[e]-=t; goto loop1;}elseprintf("data error! re-input...\n");}loop1:;if(sum1()==0){printf("you win!"); break;}}}跳马问题16.(*)( 6_24 p.197 )int map[12][12], status[12][12],kp;int c[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-2,1},{-2,-1},{-1,2},{-1,-2}};void prt(int a[][12]) /* 打印棋盘状态 */{int i,j,i2,j2;printf("\n");for (i=2;i<=9;i++){ for (j=2;j<=9;j++) printf("%4d",a[i][j]);printf("\n");}}void status2(void) /* 计算棋盘各点条件数 */{ int i,j,k,i2,j2,kz;for(i=0;i<12;i++)for(j=0;j<12;j++)status[i][j]=100;for(i=2;i<=9;i++)for(j=2;j<=9;j++){kz=0;for (k=0;k<=7;k++){i2=i+c[k][0];j2=j+c[k][1];if (map[i2][j2]<50) kz++;}status[i][j]=kz;}prt(status);}void sort1(int b1[],int b2[]) /* 对8个可能的方向按条件数排序 */ {int i,j,mini,t; /*b1[]记录状态值(升序),b2[]记录排序后的下标 */ for (i=0;i<7;i++){mini=i;for (j=i+1;j<=7;j++)if (b1[j]<b1[mini]) mini=j;t=b1[i];b1[i]=b1[mini];b1[mini]=t;t=b2[i];b2[i]=b2[mini];b2[mini]=t;}}void init1(void) /* 初始化 */{int i,j,k;for(i=0;i<12;i++)for(j=0;j<12;j++)map[i][j]=100;for(i=2;i<=9;i++)for(j=2;j<=9;j++)map[i][j]=0;status2();}void search(int i2,int j2) /* 利用递归回溯进行搜索 */ {int b1[8],b2[8],i,i3,j3;kp++;if(kp==65){prt(map); exit(0); }for(i=0;i<=7;i++){b2[i]=i;b1[i]=status[i2+c[i][0]][j2+c[i][1]];}sort1(b1,b2);for(i=0;i<=7;i++){i3=i2+c[b2[i]][0]; j3=j2+c[b2[i]][1];if (map[i3][j3]==0){ map[i3][j3]=kp; search(i3,j3); map[i3][j3]=0; }}kp--;}main(){init1();map[5][2]=1; kp=1;search(5,2);}运行结果:2 3 4 4 4 4 3 23 4 6 6 6 6 4 34 6 8 8 8 8 6 44 6 8 8 8 8 6 44 6 8 8 8 8 6 44 6 8 8 8 8 6 43 4 6 6 6 6 4 32 3 4 4 4 4 3 232 17 42 3 34 19 44 541 2 33 18 43 4 35 2016 31 64 53 38 59 6 451 40 61 58 63 52 21 3630 15 54 39 60 37 46 755 12 57 62 51 48 25 2214 29 10 49 24 27 8 4711 56 13 28 9 50 23 2617. ( ex 6_32 p.201 选择排序,利用递归实现 ) void select(int a[],int begin,int n){int i,t,min;min=begin;for (i=begin+1;i<n;i++)if(a[i]<a[min]) min=i;t=a[begin]; a[begin]=a[min]; a[min]=t;if (begin<n-1)select(a,begin+1,n);}main(){int a[10]={5,6,7,99,1,2,0,45,21,-97};int i,n=10;for(i=0;i<=n-1;i++) printf("%5d ",a[i]);printf("\n");select(a,0,n);for(i=0;i<=n-1;i++)printf("%5d ",a[i]);printf("\n");}18.( ex 6_25 p.202 二分查找,递归方法 )void binsearch(int b[],int x,int low,int high){int mid;if (low>high){printf("\n%d dosn't exists in the array!\n",x);exit(0);}mid=(low+high)/2;if(x==b[mid]){printf("OK! b[%d]=%d\n",mid,x);exit(0);}if(x>b[mid])binsearch(b,x,mid+1,high);elsebinsearch(b,x,mid,high-1);}main(){int a[10]={2,3,4,5,7,10,20,40,50,100};int key,n=10;;printf("input a number for search:\n");scanf("%d",&key);binsearch(a,key,0,n-1);}信息学 (计算机) 奥林匹克训练题 (中级部分)天津师范大学李学武编 1997.7.1. 给定等式 A B C D E 其中每个字母代表一个数字,且不同数字对应不D F G 同字母。

算法设计与分析习题答案算法设计与分析是计算机科学中一个重要的领域,它涉及到算法的创建、优化以及评估。
以下是一些典型的算法设计与分析习题及其答案。
习题1:二分查找算法问题描述:给定一个已排序的整数数组,编写一个函数来查找一个目标值是否存在于数组中。
答案:二分查找算法的基本思想是将数组分成两半,比较中间元素与目标值的大小,如果目标值等于中间元素,则查找成功;如果目标值小于中间元素,则在左半部分继续查找;如果目标值大于中间元素,则在右半部分继续查找。
这个过程会不断重复,直到找到目标值或搜索范围为空。
```pythondef binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return Trueelif arr[mid] < target:low = mid + 1else:high = mid - 1return False```习题2:归并排序算法问题描述:给定一个无序数组,使用归并排序算法对其进行排序。
答案:归并排序是一种分治算法,它将数组分成两半,分别对这两半进行排序,然后将排序好的两半合并成一个有序数组。
```pythondef merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half): if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1arr = [38, 27, 43, 3, 9, 82, 10]merge_sort(arr)print("Sorted array is:", arr)```习题3:动态规划求解最长公共子序列问题问题描述:给定两个序列,找到它们的最长公共子序列。
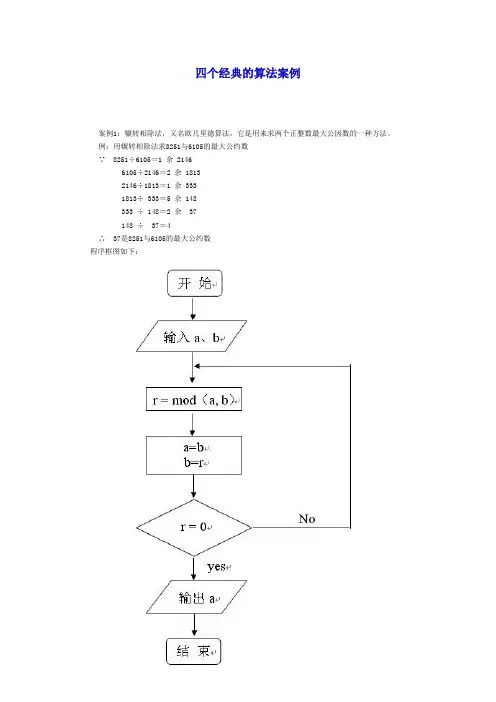
四个经典的算法案例案例1:辗转相除法,又名欧几里德算法,它是用来求两个正整数最大公因数的一种方法。
例:用辗转相除法求8251与6105的最大公约数∵ 8251÷6105=1 余 21466105÷2146=2 余 18132146÷1813=1 余 3331813÷ 333=5 余 148333 ÷ 148=2 余 37148 ÷ 37=4∴ 37是8251与6105的最大公约数程序框图如下:其中 r = mod(a, b) r表示a÷b的余数案例2:秦九韶算法,它是中国南宋时期数学家秦九韶提出的,用来解决多项式的求值问题,在西方被称作霍纳算法。
首先看一道例题:求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法:f(x)可表示为f(x)=({[(2x―5)x―4]x+3}x―6)x+7于是令 V0=5则 V1=2V0―5=2×5―5=5V2=V1X―4=5×5―4=21V3=V2X+3=21×5+3=108V4=V3X―6=108×5―6=534V5=V4X+7=534×5+7=2677∴ f(5) = 2677秦九韶算法只用到乘法、加法两个简单运算,不需要乘方运算,它是多项式求值的简化算法。
下面看程序框图,其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3:排序:是一种基本并且常用的算法,排序的算法很多,可以参阅课本,这里不再叙述。
案例4:进位制例:画程序框图,表示把k进制数a(共有n位),转化为十进制数b的过程框图如下:其中:t = GET a│i│ t表示a右数第i位利用上面的算法,把2进制数110011化为十进制的数即:1×20+1×21+0×22+0×23+1×24+1×25= 51以上是四个经典算法,大家可以从中体会算法的基本思想和算法的基本结构,并尝试用算法的基本语句描述它。

经典算法题解经典算法题解涵盖了各种计算机科学和编程领域的经典问题。
这些题目不仅具有代表性,而且在算法设计和分析方面具有较高的价值。
以下是一些经典算法题解的例子:1. 动态规划:动态规划是一种解决复杂问题的方法,通过将问题分解成子问题,并求解子问题的最优解,从而找到原问题的最优解。
经典动态规划问题包括背包问题、最长公共子序列(LCS)问题、最长递增子序列(LIS)问题等。
2. 贪心算法:贪心算法是一种解决复杂问题的方法,它总是选择局部最优解,以期望达到全局最优解。
经典贪心算法问题包括哈夫曼编码问题、最小生成树(Kruskal算法、Prim算法等)、最短路径(Dijkstra算法等)等。
3. 分治算法:分治算法是一种解决复杂问题的方法,它将原问题分解成规模较小的子问题,并在子问题上求解,最后合并子问题的解得到原问题的解。
经典分治算法问题包括归并排序、快速排序、归并查找等。
4. 回溯算法:回溯算法是一种解决复杂问题的方法,它通过递归的方式,从一条路线上不断地尝试,直到找到一条可行的路径。
经典回溯算法问题包括八皇后问题、数独问题、背包问题等。
5. 深度优先搜索(DFS)和广度优先搜索(BFS):DFS和BFS 是解决复杂问题的搜索算法,它们通过搜索树或图的方式,寻找问题的解。
经典DFS和BFS问题包括无序集合问题、图的遍历、最短路径等。
6. 字符串匹配算法:字符串匹配算法是解决在文本中查找某个子串的问题。
经典字符串匹配算法包括朴素匹配算法、KMP算法、Boyer-Moore算法等。
7. 数据结构:数据结构是解决计算机科学问题的重要工具。
经典数据结构问题包括链表、栈、队列、树、图等数据结构的操作和应用。
8. 算法复杂度分析:算法复杂度分析是研究算法时间复杂度和空间复杂度的问题。
经典算法复杂度分析问题包括大O标记、大Ω标记、大Ω标记、大Ω标记等。
这些经典算法题解对于提高编程能力和解决实际问题具有很大的帮助。
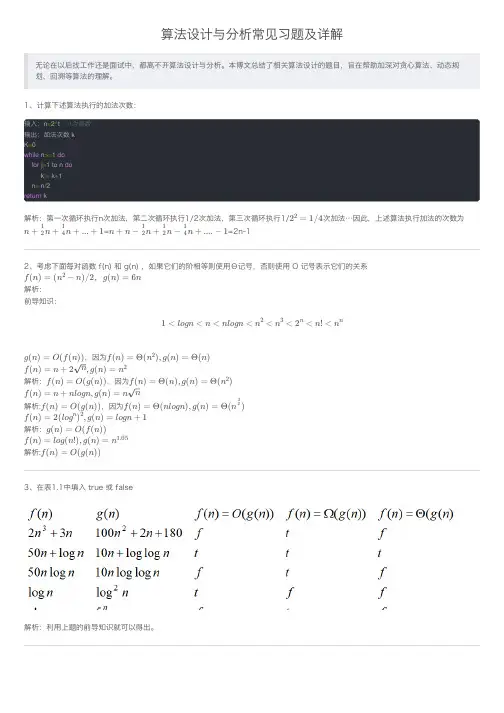
算法设计与分析常见习题及详解⽆论在以后找⼯作还是⾯试中,都离不开算法设计与分析。
本博⽂总结了相关算法设计的题⽬,旨在帮助加深对贪⼼算法、动态规划、回溯等算法的理解。
1、计算下述算法执⾏的加法次数:输⼊:n =2^t //t 为整数输出:加法次数 k K =0while n >=1 do for j =1 to n do k := k +1 n = n /2return k解析:第⼀次循环执⾏n次加法,第⼆次循环执⾏1/2次加法,第三次循环执⾏1/次加法…因此,上述算法执⾏加法的次数为==2n-12、考虑下⾯每对函数 f(n) 和 g(n) ,如果它们的阶相等则使⽤Θ记号,否则使⽤ O 记号表⽰它们的关系解析:前导知识:,因为解析:,因为解析:,因为解析:解析:3、在表1.1中填⼊ true 或 false解析:利⽤上题的前导知识就可以得出。
2=21/4n +n +21n +41...+1n +n −n +21n −21n +41....−1f (n )=(n −2n )/2,g (n )=6n1<logn <n <nlogn <n <2n <32<n n !<n ng (n )=O (f (n ))f (n )=Θ(n ),g (n )=2Θ(n )f (n )=n +2,g (n )=n n 2f (n )=O (g (n ))f (n )=Θ(n ),g (n )=Θ(n )2f (n )=n +nlogn ,g (n )=n nf (n )=O (g (n ))f (n )=Θ(nlogn ),g (n )=Θ(n )23f (n )=2(log ),g (n )=n 2logn +1g (n )=O (f (n ))f (n )=log (n !),g (n )=n 1.05f (n )=O (g (n ))4、对于下⾯每个函数 f(n),⽤f(n) =Θ(g(n))的形式,其中g(n)要尽可能简洁,然后按阶递增序排列它们(最后⼀列)解析:最后⼀个⽤到了调和公式:按阶递增的顺序排列:、、、、、、、、、(n −2)!=Θ((n −2)!)5log (n +100)=10Θ(logn )2=2n Θ(4)n 0.001n +43n +31=Θ(n )4(lnn )=2Θ(ln n )2+3n logn =Θ()3n 3=n Θ(3)n log (n !)=Θ(nlogn )log (n )=n +1Θ(nlogn )1++21....+=n1Θ(logn )=∑k =1nk 1logn +O (1)1++21....+n 15log (n +100)10(lnn )2+3n logn log (n !)log (n )n +10.001n +43n +313n 22n (n −2)!5、求解递推⽅程前导知识:主定理前导知识:递归树:例⼦:递归树是⼀棵节点带权的⼆叉树,初始递归树只有⼀个结点,标记为权重W(n),然后不断进⾏迭代,最后直到树种不再含有权为函数的结点为⽌,然后将树根结点到树叶节点的全部权值加起来,即为算法的复杂度。

贪心算法经典例题引言贪心算法是一种常见的算法策略,它在求解问题时每一步都选择当前状态下的最优解,从而最终得到全局最优解。
本文将介绍一些经典的贪心算法例题,帮助读者更好地理解贪心算法的思想和应用。
背景知识在讨论贪心算法之前,我们先了解一些背景知识。
1. 贪心算法的特点贪心算法具有以下特点: - 每一步都选择当前状态下的最优解; - 不进行回溯;- 不保证能得到全局最优解,但通常能得到较优解; - 算法运行效率高。
2. 贪心算法的适用情况贪心算法适用于满足以下条件的问题: - 具有最优子结构性质:问题的最优解包含子问题的最优解; - 贪心选择性质:局部最优解能导致全局最优解; - 没有后效性:当前的选择不会影响后续的选择。
经典例题1:找零钱问题问题描述假设有1元、5元、10元、20元、50元、100元面值的纸币,如何用最少的纸币数量找零给顾客?对于找零问题,贪心算法可以得到最优解。
具体步骤如下: 1. 首先,我们选择最大面额的纸币进行找零。
2. 然后,将选择的纸币数量减去顾客需找的金额,得到剩余金额。
3. 重复步骤1和步骤2,直到剩余金额为0。
实现代码int[] denominations = {100, 50, 20, 10, 5, 1};int[] counts = new int[denominations.length];int amount = 168;for (int i = 0; i < denominations.length; i++) {counts[i] = amount / denominations[i];amount %= denominations[i];}System.out.println("找零纸币面额及数量:");for (int i = 0; i < denominations.length; i++) {if (counts[i] > 0) {System.out.println(denominations[i] + "元:" + counts[i] + "张");}}分析与总结通过贪心算法,我们可以得到找零纸币的最优解。

c++贪心算法经典例题和详解贪心算法(Greedy Algorithm)是一种优化问题解决方法,其基本思想是每一步都选择当前状态下的最优解,以期望达到全局最优解。
贪心算法的特点是每一步都要做出一个局部最优的选择,而这些局部最优选择最终构成了全局最优解。
下面是一个经典的贪心算法例题以及详解:例题:活动选择问题(Activity Selection Problem)假设有一个需要在同一时段使用同一个资源的活动集合,每个活动都有一个开始时间和结束时间。
设计一个算法,使得能够安排最多数量的互不相交的活动。
# 输入:-活动的开始时间数组`start[]`。
-活动的结束时间数组`end[]`。
# 输出:-选择的互不相交的活动的最大数量。
# 算法详解:1. 首先,将活动按照结束时间从小到大排序。
2. 选择第一个活动,并将其加入最终选择的集合中。
3. 对于剩下的活动,选择下一个结束时间最早且与前一个活动不冲突的活动。
4. 重复步骤3,直到所有活动都被选择。
```cpp#include <iostream>#include <algorithm>#include <vector>using namespace std;// 定义活动结构体struct Activity {int start, end;};// 比较函数,用于排序bool compareActivities(Activity a, Activity b) {return a.end < b.end;}// 贪心算法解决活动选择问题void activitySelection(vector<Activity>& activities) {// 按照结束时间排序sort(activities.begin(), activities.end(), compareActivities);// 第一个活动总是被选中cout << "Selected activity: (" << activities[0].start << ", " << activities[0].end << ")" << endl;// 选择其余活动int lastSelected = 0;for (int i = 1; i < activities.size(); i++) {// 如果当前活动的开始时间大于等于上一个选择的活动的结束时间,则选择该活动if (activities[i].start >= activities[lastSelected].end) {cout << "Selected activity: (" << activities[i].start << ", " << activities[i].end << ")" << endl;lastSelected = i;}}}int main() {vector<Activity> activities = {{1, 2}, {3, 4}, {0, 6}, {5, 7}, {8, 9}, {5, 9}};cout << "Activities before sorting:" << endl;for (const Activity& activity : activities) {cout << "(" << activity.start << ", " << activity.end << ") ";}cout << endl;activitySelection(activities);return 0;}```在这个例子中,我们首先定义了一个活动的结构体`Activity`,然后编写了一个比较函数`compareActivities` 用于排序。

快速排序经典例题快速排序是一种经典的排序算法,它能够在平均情况下以O(n log n)的时间复杂度对一个数组进行排序。
快速排序的核心思想是通过一次划分操作将待排序数组分成两个部分,其中一部分的所有元素都小于等于划分元素,另一部分的所有元素都大于划分元素,然后对这两部分分别进行递归排序。
下面我们将通过一个经典的例题来详细介绍快速排序的算法流程。
假设我们有一个包含n个整数的数组,我们的目标是将它们按照非降序进行排序。
下面是一个简单的例题:例题:给定一个数组[9, 7, 5, 11, 12, 2, 14, 3, 10, 6],请使用快速排序算法将其进行排序。
解题步骤如下:1. 选择一个划分元素pivot。
在这个例题中,我们可以选择数组的第一个元素9作为pivot。
2. 根据划分元素将数组分成两个部分。
遍历数组,将小于等于pivot的元素放在数组左侧,将大于pivot的元素放在数组右侧。
在这个例题中,我们得到的划分结果如下:[5, 2, 3, 6, 7, 9, 14, 12, 10, 11]3. 对划分结果的左右两部分进行递归排序。
我们分别对左侧的子数组[5, 2, 3, 6, 7]和右侧的子数组[14, 12, 10, 11]进行递归排序。
4. 重复步骤1到步骤3,直到每个子数组只包含一个元素或是空数组。
5. 合并排序后的子数组。
最后,将排序后的子数组进行合并,我们得到最终的排序结果为:[2, 3, 5, 6, 7, 9, 10, 11, 12, 14]快速排序的时间复杂度主要取决于划分的效果。
在最坏情况下,每次划分都将数组划分成一个元素和n-1个元素两部分,这种情况下快速排序的时间复杂度为O(n^2)。
然而,在平均情况下,快速排序的时间复杂度为O(n log n)。
快速排序是一种原地排序算法,即不需要额外的空间来存储排序结果。
通过交换数组元素来实现排序,因此它的空间复杂度为O(log n)。
然而,在最坏情况下,快速排序需要O(n)的额外空间来进行递归调用。

经典算法试题及答案题目一:找出旋转排序数组中的最小值题目描述:假设按照升序排序的数组在预先未知的某个点上进行了旋转。
例如,数组 `[0,1,2,4,5,6,7]` 可能变为`[4,5,6,7,0,1,2]`。
请找出并返回数组中的最小元素。
说明:- 原数组是一个升序排序的数组- 数组中可能包含重复的元素- 你的算法应该具有 O(log n) 的时间复杂度答案解析:这个问题可以通过二分查找的方法来解决。
以下是详细的解题步骤:1. 初始化两个指针 `left` 和 `right` 分别指向数组的开头和结尾。
2. 当 `left` 小于 `right` 时,执行以下步骤:- 找到中间位置 `mid`。
- 如果 `nums[mid]` 大于 `nums[right]`,则最小值在 `mid+1` 到 `right` 之间,更新 `left = mid + 1`。
- 如果 `nums[mid]` 小于 `nums[right]`,则最小值在 `left` 到 `mid` 之间,更新 `right = mid`。
- 如果 `nums[mid]` 等于 `nums[right]`,则无法判断最小值的位置,需要减少 `right`。
3. 当 `left` 等于 `right` 时,返回 `nums[left]`。
代码实现:```pythondef findMin(nums):left, right = 0, len(nums) - 1while left < right:mid = left + (right - left) // 2if nums[mid] > nums[right]:left = mid + 1elif nums[mid] < nums[right]:right = midelse:right -= 1return nums[left]```题目二:合并两个有序链表题目描述:将两个有序链表合并为一个新的有序链表。

决策树id3算法例题经典一、决策树ID3算法例题经典之基础概念决策树ID3算法就像是一个超级聪明的小侦探,在数据的世界里寻找线索。
它是一种用来分类的算法哦。
比如说,我们要把一群小动物分成哺乳动物和非哺乳动物,就可以用这个算法。
它的基本思想呢,就是通过计算信息增益来选择特征。
就好比是在一堆乱糟糟的东西里,先找到那个最能区分开不同类别的特征。
比如说在判断小动物的时候,有没有毛发这个特征可能就很关键。
如果有毛发,那很可能就是哺乳动物啦。
二、经典例题解析假设我们有这样一个数据集,是关于一些水果的。
这些水果有颜色、形状、是否有籽等特征,我们要根据这些特征来判断这个水果是苹果、香蕉还是橙子。
首先看颜色这个特征。
如果颜色是红色的,那可能是苹果的概率就比较大。
但是仅仅靠颜色可不够准确呢。
这时候就需要计算信息增益啦。
通过计算发现,形状这个特征对于区分这三种水果的信息增益更大。
比如说圆形的可能是苹果或者橙子,弯弯的可能就是香蕉啦。
再考虑是否有籽这个特征。
苹果和橙子有籽,香蕉没有籽。
把这个特征也加入到决策树的构建当中,就可以更准确地判断出到底是哪种水果了。
三、决策树ID3算法的优缺点1. 优点这个算法很容易理解,就像我们平常做选择一样,一步一步来。
它的结果也很容易解释,不像有些复杂的算法,结果出来了都不知道怎么回事。
它不需要太多的计算资源,对于小数据集来说,速度很快。
就像小马拉小车,轻松就能搞定。
2. 缺点它很容易过拟合。
就是在训练数据上表现很好,但是一到新的数据就不行了。
比如说我们只根据训练数据里的几个苹果的特征构建了决策树,新的苹果稍微有点不一样,就可能判断错了。
它只能处理离散型的数据。
如果是连续型的数据,就需要先进行离散化处理,这就多了一道工序,比较麻烦。
四、实际应用场景1. 在医疗领域,可以用来判断病人是否患有某种疾病。
比如说根据病人的症状、年龄、性别等特征来判断是否得了感冒或者其他疾病。
就像医生的小助手一样。
贪心算法经典例题贪心算法是一种求解最优问题的算法思想,其核心理念是每一步都选择当前最优的策略,从而达到全局最优解。
贪心算法可以应用于许多经典问题,下面将介绍几个常见的贪心算法经典例题及相关参考内容。
1. 会议室安排问题题目描述:给定一组会议的开始时间和结束时间,求解如何安排会议,使得尽可能多的会议可以在同一时间段内进行。
解题思路:贪心算法可以通过每次选择结束时间最早的会议来求解。
首先将会议按照结束时间排序,选择第一个会议作为首先安排的会议,然后依次选择后续结束时间不冲突的会议进行安排。
相关参考内容:- 《算法导论》第16章:贪心算法(ISBN: 9787115265955)- 《数据结构与算法分析》第13章:贪心算法(ISBN: 9787302483626)2. 零钱兑换问题题目描述:给定一定面额的硬币,求解如何用最少的硬币数量兑换指定金额的零钱。
解题思路:贪心算法可以通过每次选择面额最大且不超过目标金额的硬币来求解。
从面额最大的硬币开始,尽可能多地选择当前面额的硬币,并减去已经选择的硬币金额,直到金额为0。
相关参考内容:- 《算法导论》第16章:贪心算法(ISBN: 9787115265955)- 《算法4》第1章:基础(ISBN: 9787302444627)3. 区间调度问题题目描述:给定一组区间,求解如何选择尽可能多的不重叠区间。
解题思路:贪心算法可以通过每次选择结束时间最早的区间来求解。
首先将区间按照结束时间排序,选择第一个区间作为首先选择的区间,然后依次选择后续结束时间不与已经选择的区间重叠的区间进行选择。
相关参考内容:- 《算法导论》第16章:贪心算法(ISBN: 9787115265955)- 《数据结构与算法分析》第13章:贪心算法(ISBN: 9787302483626)4. 分糖果问题题目描述:给定一组孩子和一组糖果,求解如何分配糖果,使得最多的孩子能够得到满足。
解题思路:贪心算法可以通过每次选择糖果最小且能满足当前孩子的糖果来求解。
决策树算法例题经典
案例1:购物产品推荐。
假设当前我们需要进行购物产品推荐工作,用户可以选择若干项属性,例如品牌、价格、颜色、是否有折扣等等,在已知一些样本的基础上,构
建一棵决策树,帮助用户快速得到最佳购买推荐。
如果用户选择的品牌为A,则直接推荐产品P3;如果选择品牌为B,
则继续考虑价格,如果价格低于100,则推荐产品P1,否则推荐产品P2。
如果用户选择的品牌为C,则直接推荐产品P4。
当然,这只是一个简单的例子,实际应用场景中可能会有更多的属性
和样本。
因此,在构建决策树时需要考虑选取最优特征,避免过度拟合等
问题。
案例2:疾病预测。
假设有一组医学数据,其中包括患者的年龄、性别、身高、体重、血
压等指标以及是否患有糖尿病的标签信息。
我们希望构建一个决策树来帮
助医生快速判断患者是否可能患有糖尿病。
如果患者年龄大于45岁,则进一步考虑体重,如果体重高于120kg,则判断为高风险群体;否则判断为低风险群体。
如果患者年龄不超过45岁,则直接判断为低风险群体。
当然,这只是一个简单的例子,实际应用场景中可能会有更多的指标
和样本。
因此,在构建决策树时需要考虑选取最优特征,避免过度拟合等
问题。
贪心算法经典例题贪心算法是一种基于当前最优解的选择方法,它的思想在算法设计中占有重要地位。
贪心算法常被用于解决许多问题,如背包问题、区间覆盖问题等。
在本文中,我们将介绍一种经典的贪心算法例题。
例题描述假设有一组有限数量的钞票,其面额分别为1元、5元、10元、50元、100元、500元、1000元、5000元。
现在需要用这些钞票凑出一个给定的金额。
编写一个函数,返回最少需要几张钞票。
分析这个问题可以用贪心算法来解决。
根据贪心策略,我们应该选择面额最大的钞票,使其不超过目标金额。
如果目标金额减去选定的钞票面额后仍然大于0,则继续选择面额最大的钞票,反之,选择面额次大的钞票,直到凑出目标金额。
每次选择的钞票数量加1,最终得到的数量即为所需钞票的最小数量。
代码实现下面是这个例题的代码实现:```pythondef min_coin_count(target_amount, coins):# 从大到小排序coins.sort(reverse=True)# 计数器count = 0# 遍历所有钞票面额for coin in coins:# 计算当前钞票最多可以用几张max_count = target_amount // coin# 更新计数器和目标金额count += max_counttarget_amount -= max_count * coinreturn count```测试我们用以下代码对这个函数进行测试:```pythonamount = 427coins = [1, 5, 10, 50, 100, 500, 1000, 5000]print(min_coin_count(amount, coins)) # 输出结果为 7```结果说明,我们可以用七张钞票凑出 427 元,这是最小的钞票数量。
总结贪心算法作为一种常用的算法思想,在算法设计中具有重要作用。
本文介绍了一种经典的贪心算法例题,并给出了具体的代码实现和测试。
算法递归典型例题实验一:递归策略运用练习三、实验项目1.运用递归策略设计算法实现下述题目的求解过程。
题目列表如下:(1)运动会开了N天,一共发出金牌M枚。
第一天发金牌1枚加剩下的七分之一枚,第二天发金牌2枚加剩下的七分之一枚,第3天发金牌3枚加剩下的七分之一枚,以后每天都照此办理。
到了第N天刚好还有金牌N枚,到此金牌全部发完。
编程求N和M。
(2)国王分财产。
某国王临终前给儿子们分财产。
他把财产分为若干份,然后给第一个儿子一份,再加上剩余财产的1/10;给第二个儿子两份,再加上剩余财产的1/10;……;给第i 个儿子i份,再加上剩余财产的1/10。
每个儿子都窃窃自喜。
以为得到了父王的偏爱,孰不知国王是“一碗水端平”的。
请用程序回答,老国王共有几个儿子?财产共分成了多少份?源程序:(3)出售金鱼问题:第一次卖出全部金鱼的一半加二分之一条金鱼;第二次卖出乘余金鱼的三分之一加三分之一条金鱼;第三次卖出剩余金鱼的四分之一加四分之一条金鱼;第四次卖出剩余金鱼的五分之一加五分之一条金鱼;现在还剩下11条金鱼,在出售金鱼时不能把金鱼切开或者有任何破损的。
问这鱼缸里原有多少条金鱼?(4)某路公共汽车,总共有八站,从一号站发轩时车上已有n位乘客,到了第二站先下一半乘客,再上来了六位乘客;到了第三站也先下一半乘客,再上来了五位乘客,以后每到一站都先下车上已有的一半乘客,再上来了乘客比前一站少一个……,到了终点站车上还有乘客六人,问发车时车上的乘客有多少?(5)猴子吃桃。
有一群猴子摘来了一批桃子,猴王规定每天只准吃一半加一只(即第二天吃剩下的一半加一只,以此类推),第九天正好吃完,问猴子们摘来了多少桃子?(6)小华读书。
第一天读了全书的一半加二页,第二天读了剩下的一半加二页,以后天天如此……,第六天读完了最后的三页,问全书有多少页?(7)日本著名数学游戏专家中村义作教授提出这样一个问题:父亲将2520个桔子分给六个儿子。
决策树算法例题经典决策树是一种常用的机器学习算法,用于处理分类和回归问题。
它通过对数据集进行划分,构建一个树状模型来进行决策。
在这篇文章中,我将介绍一个经典的决策树算法的例子,并详细解释其原理和实现方法。
假设我们有一个数据集,里面包含了一些患有乳腺癌的病人的信息。
每个病人的信息都有一些特征,比如年龄、乳房厚度、肿块大小等。
我们的任务是根据这些特征预测病人是否患有乳腺癌。
首先,我们需要选择一个合适的划分准则来构建决策树。
常用的划分准则有信息增益、信息增益比、基尼指数等。
在本例中,我们选择使用信息增益作为划分准则。
接下来,我们需要计算每个特征的信息增益。
信息增益是根据特征划分前后的熵变化来衡量的。
熵是一个用于度量系统无序程度的指标,越大表示越无序,越小表示越有序。
在本例中,我们可以通过计算患有乳腺癌和未患有乳腺癌的病人的比例来计算熵。
然后,我们选取信息增益最大的特征作为当前节点的划分特征。
这样可以使得划分后的子集的熵最小化,从而提高分类的准确性。
接着,我们递归地对每个子集进行上述操作,直到满足停止条件。
停止条件可以是子集中只有一类样本或没有更多的特征可供选择划分。
在实现决策树算法时,我们需要解决一些问题。
首先,如何选择划分特征。
上述例子中我们选择了信息增益最大的特征作为划分特征,但也可以选择其他准则。
其次,如何处理缺失值。
在实际应用中,数据集中可能会有一些缺失值,我们需要考虑如何处理这些缺失值。
最后,如何处理连续型特征。
决策树算法本质上是一个离散型算法,对于连续型特征,我们需要进行离散化处理。
决策树算法是一种简单但有效的机器学习算法,可以用于处理分类和回归问题。
它具有可解释性好、易于理解和实现等优点,在实际应用中得到了广泛的应用。
然而,决策树算法也存在一些限制,比如容易过拟合、适应性较差等。
为了提高决策树算法的性能,可以使用集成学习方法,如随机森林、梯度提升树等。
总之,决策树算法是一种经典的机器学习算法,本文介绍了它的原理和实现方法,并给出了一个实际应用的例子。
10个经典的算法问题与解决方案算法问题是计算机科学中非常重要的一部分,对于准备面试或提升自己的技能都是很有帮助的。
下面列举了10个经典的算法问题及其解决方案:1.两数之和(Two Sum)问题描述:给定一个整数数组和一个目标值,找出数组中和为目标值的两个数。
解决方案:使用哈希表记录每个数字的索引,然后遍历数组,查找目标值减当前数的差是否存在于哈希表中。
2.盛最多水的容器(Container With Most Water)问题描述:给定一个非负整数数组,数组中的每个表示一条柱子的高度,找出两个柱子,使得它们与x轴构成的容器可以容纳最多的水。
解决方案:维护两个指针,分别指向数组的开始和结尾,计算当前指针所指的两条柱子之间的面积,并更新最大面积。
然后移动指向较小柱子的指针,重复计算直到两个指针相遇。
3.三数之和(3Sum)问题描述:给定一个整数数组,找出数组中所有不重复的三个数,使得它们的和为0。
解决方案:首先对数组进行排序,然后固定一个数字,使用双指针在剩余的数字中寻找另外两个数使得它们的和为相反数。
4.最大子序和(Maximum Subarray)问题描述:给定一个整数数组,找到一个具有最大和的连续子数组(子数组最少包含一个元素)。
解决方案:使用动态规划的思想,从数组的第一个元素开始依次计算以当前位置结尾的子数组的最大和,并保存最大值。
5.二分查找(Binary Search)问题描述:给定一个排序的整数数组和一个目标值,使用二分查找算法确定目标值是否存在于数组中,并返回其索引。
解决方案:通过比较目标值与数组的中间元素来确定目标值是在左半部分还是右半部分,并更新搜索范围进行下一轮查找。
6.背包问题(Knapsack Problem)问题描述:给定一组物品和一个背包,每个物品都有自己的重量和价值,在不超过背包容量的情况下,找到一个组合使得总价值最大化。
解决方案:使用动态规划的思想,定义一个二维数组表示背包容量和物品数量,从左上角开始计算每个格子可以放置的最大价值。