最新位移与时间地关系2

高中物理匀变速直线运动的位移与时间关系2教案 新课标 人教版 必修1 教学目标:1. 进一步理解匀变速直线运动的速度公式和位移公式。

2. 能较熟练地应用速度公式和位移公式求解有关问题。

3. 能推导匀变速直线运动的位移和速度关系式，并会应用它进行计算。

4. 掌握匀变速直线运动的两个重要要推论。

5．能灵活应用匀变速直线运动的规律进行分析和计算。

学习重点: 1. as v v t 2202=-2. 推论1：S 2-S 1=S 3-S 2=S 4-S 3=…=S n -S n-1=△S=aT 23．推论2：v v t =2学习难点: 推论1主要内容:一、匀变速直线运动的位移和速度关系1．公式：as v v t 2202=-2．推导：3．物理意义：【例一】发射枪弹时，枪弹在枪筒中的运动可以看做匀加速运动，如果枪弹的加速度大小是5×105m ／s ，枪筒长0．64米，枪弹射出枪口时的速度是多大?【例二】一光滑斜面坡长为l0m ，有一小球以l0m ／s 的初速度从斜面底端向上运动，刚好能到达最高点，试求：小球运动的加速度。

二、匀变速直线运动三公式的讨论1．三个方程中有两个是独立方程，其中任意两个公式可以推导出第三式。

2．三式中共有五个物理量，已知任意三个可解出另外两个，称作“知三解二”。

3．Vo 、a 在三式中都出现，而t 、Vt 、s 两次出现。

4．已知的三个量中有Vo 、a 时，另外两个量可以各用一个公式解出，无需联立方程．5．已知的三个量中有Vo 、a 中的一个时，两个未知量中有一个可以用一个公式解出，另一个可以根据解出的量用一个公式解出。

6．已知的三个量中没有Vo 、a 时，可以任选两个公式联立求解Vo 、a 。

7．不能死套公式，要具体问题具体分析(如刹车问题)。

【例三】一个滑雪的人，从85 m 长的山坡上匀变速滑下，初速度是1．8 m ／s ，末速度是5．0 m ／s ，他通过这段山坡需要多长时间？三、匀变速直线运动的两个推论1．匀变速直线运动的物体在连续相等的时间(T)内的位移之差为一恒量。

匀变速直线运动的位移与时间的关系【考点归纳】（1）匀变速直线运动的位移与时间的关系式：x＝v0t+at2。

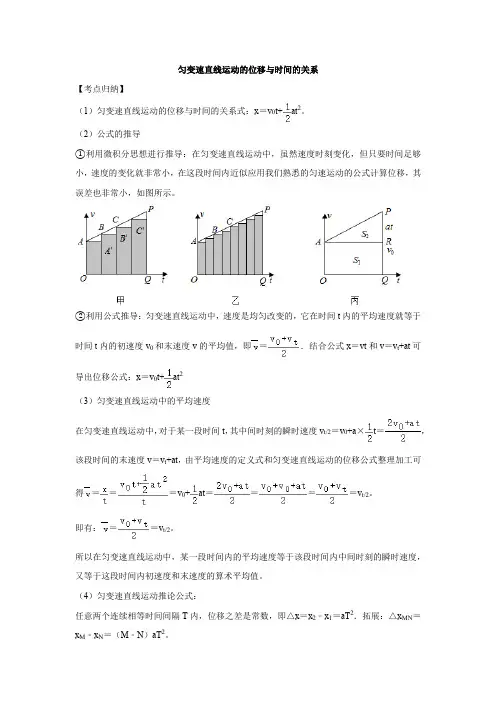
（2）公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示。

②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即＝．结合公式x＝vt和v＝v t+at可导出位移公式：x＝v0t+at2（3）匀变速直线运动中的平均速度在匀变速直线运动中，对于某一段时间t，其中间时刻的瞬时速度v t/2＝v0+a×t＝，该段时间的末速度v＝v t+at，由平均速度的定义式和匀变速直线运动的位移公式整理加工可得＝＝＝v0+at＝＝＝＝v t/2。

即有：＝＝v t/2。

所以在匀变速直线运动中，某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度，又等于这段时间内初速度和末速度的算术平均值。

（4）匀变速直线运动推论公式：任意两个连续相等时间间隔T内，位移之差是常数，即△x＝x2﹣x1＝aT2．拓展：△x MN＝x M﹣x N＝（M﹣N）aT2。

推导：如图所示，x1、x2为连续相等的时间T内的位移，加速度为a。

【命题方向】例1：对基本公式的理解汽车在平直的公路上以30m/s的速度行驶，当汽车遇到交通事故时就以7.5m/s2的加速度刹车，刹车2s内和6s内的位移之比（）A.1：1B.5：9C.5：8D.3：4分析：求出汽车刹车到停止所需的时间，汽车刹车停止后不再运动，然后根据位移时间公式求出2s内和6s内的位移。

解：汽车刹车到停止所需的时间＞2s所以刹车2s内的位移＝45m。

t0＜6s，所以刹车在6s内的位移等于在4s内的位移。

＝60m。

所以刹车2s内和6s内的位移之比为3：4．故D正确，A、B、C错误。

位移和时间的关系位移和时间的关系是物理学中非常重要的概念，在研究物体的运动与变化时起着至关重要的作用。

位移是物体从一个位置移动到另一个位置的变化量，而时间则是这个过程所经历的时间长度。

在这篇文档中，我们将深入探讨位移和时间之间的关系。

1. 位移和时间的定义•位移：位移是指物体从初始位置到最终位置的变化量，用矢量表示。

在一维运动中，位移可以用一个数值表示，它包含了大小和方向。

在二维和三维运动中，位移需要用多个分量表示。

•时间：时间是一个基本的物理量，描述了事件发生的顺序和持续的时间长度。

时间通常用标准单位秒来表示。

2. 位移与时间的关系位移和时间之间的关系可以通过速度来描述。

速度是位移与时间之比，用于衡量物体在单位时间内移动的距离。

在一维运动中，速度可以用以下公式表示：$$ 速度 = \\frac{位移}{时间} $$速度可以有正负两种情况，正表示物体向正方向移动，负表示物体向负方向移动。

速度的单位通常是米/秒（m/s）。

3. 位移与时间的图示为了更直观地了解位移和时间之间的关系，我们可以绘制位移-时间图表。

图表上横坐标表示时间，纵坐标表示位移。

根据物体的速度和方向的不同，位移-时间图表可以呈现出不同的形状。

•匀速直线运动：如果物体以恒定的速度沿直线运动，位移-时间图将是一条直线，并且斜率等于速度。

•匀加速直线运动：如果物体在匀加速条件下运动，位移-时间图将是一条曲线。

曲线的斜率逐渐增加，代表速度在不断改变。

4. 位移与时间的实例下面以一些实际例子来探讨位移和时间之间的关系：•车辆行驶：假设一辆汽车以恒定速度60 km/h向前行驶，我们可以计算不同时间内的位移。

例如，1小时后，汽车的位移为60公里。

如果我们只知道位移，也可以通过位移除以速度来计算所花费的时间。

•自由落体：当物体自由下落时，其位移与时间之间也存在关系。

根据重力加速度的定义，物体下落的位移与时间的平方成正比。

可以使用下面的公式计算位移：$$ 位移 = \\frac{1}{2} \\cdot g \\cdot t^2 $$其中，g是重力加速度，t是时间。

位移与时间的关系位移与时间的关系是物理学中一个重要的概念，在描述物体运动时起着关键作用。

位移是指物体从一个位置到另一个位置的变化，而时间是指这个变化所经历的时长。

研究位移与时间的关系可以帮助我们更好地理解和描述物体的运动规律。

本文将详细探讨位移与时间的关系，并且探讨在不同情况下这种关系的特点和规律。

一、匀速直线运动情况下的位移与时间关系在匀速直线运动中，物体的速度保持恒定，因此它的位移与时间的关系是线性的。

根据物体的匀速直线运动的定义，位移与时间的比值等于物体的速度。

例如，如果一个物体以每秒10米的速度匀速向前运动，那么它在1秒钟内的位移将为10米，在2秒钟内的位移为20米。

可以看出，位移与时间成正比，位移和时间的比例关系由速度来决定。

二、加速度运动情况下的位移与时间关系在加速度运动中，物体的速度在单位时间内发生变化，因此它的位移与时间的关系不再是线性的。

根据牛顿第二定律，物体的加速度等于力对物体施加的作用力。

在这种情况下，位移和时间之间的关系由物体的加速度来决定。

在匀加速直线运动中，物体的速度随时间线性变化，位移与时间的关系呈现二次函数的形式。

具体而言，位移与时间的关系可以用以下公式表示：s = ut + (1/2)at^2其中s表示位移，u表示初始速度，t表示时间，a表示加速度。

这个公式表明，在匀加速直线运动中，位移与时间的平方成正比，与时间一次方成正比，与初始速度无关。

三、自由落体情况下的位移与时间关系自由落体是指物体在无空气阻力作用下由高处自由下落的运动。

在自由落体中，物体的加速度近似为地球上的重力加速度。

根据这个特点，位移与时间的关系可以用以下公式表示：s = (1/2)gt^2其中s表示位移，g表示重力加速度，t表示时间。

这个公式表明，在自由落体运动中，位移与时间的平方成正比。

四、周期性运动情况下的位移与时间关系在周期性运动中，物体经过一段时间后按照相同的模式重复运动。

这种情况下，位移与时间的关系呈现周期性变化的特点。

匀变速直线运动位移与时间的关系知识集结知识元匀变速直线运动的位移与时间的关系知识讲解匀变速直线运动的位移与时间的关系式：x=v0t+at2．公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示．②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即．结合公式x=vt和v=v0+at可导出位移公式：x=v0t+ at2例题精讲匀变速直线运动的位移与时间的关系例1.一个物体由静止开始做匀加速直线运动，第1s内的位移是1m，物体在第3s内的位移是（）A．2m B．3m C．5m D．8m例2.为了测定某轿车在平直路上启动阶段的加速度（轿车启动时的运动可近似看成是匀加速直线运动），某人拍摄一张在同一底片上多次曝光的照片，如图所示，如果拍摄时每隔2s曝光一次，轿车车身总长为4.5m，那么这辆轿车的加速度为（）A．1m/s2B．2.25m/s2C．3m/s2D．4.25m/s2例3.2015年9月2日，“抗战专列”在武汉地铁4号线亮相，引得乘车市民纷纷点赞．若该地铁列车先从甲站开始做初速度为零、加速度大小为a的匀加速直线运动，通过位移L后，立即做加速度大小也为a的匀减速直线运动，恰好到乙站停下．则列车从甲站到乙站所用时间为（）A．B．2C．2D．4当堂练习单选题练习1.一个物体在水平直线上做匀加速直线运动，初速度为3m/s，经过4s它的位移为24m，则这个物体运动的加速度等于（）A．1.5m/s2B．2m/s2C．4m/s2D．0.75m/s2练习2.小球以某一较大初速度冲上一足够长光滑斜面，加速度大小为5m/s2则小球在沿斜面上滑过程中最后一秒的位移是（）A．2.0m B．2.5m C．3.0m D．3.5m练习3.“蛟龙号”是我国首台自主研制的作业型深海载人潜水器，它是目前世界上下潜能力最强的潜水器．假设某次海试活动中，“蛟龙号”完成海底任务后竖直上浮，从上浮速度为v时开始计时，此后“蛟龙号”匀减速上浮，经过时间t上浮到海面，速度恰好减为零，则“蛟龙号”在t0（t0<t）时刻距离海平面的深度为（）A．B．C．D．练习4.一个物体由静止开始做匀加速直线运动，第1s内的位移是1m，物体在第3s内的位移是（）A．2m B．3m C．5m D．8m练习5.为了测定某轿车在平直路上启动阶段的加速度（轿车启动时的运动可近似看成是匀加速直线运动），某人拍摄一张在同一底片上多次曝光的照片，如图所示，如果拍摄时每隔2s曝光一次，轿车车身总长为4.5m，那么这辆轿车的加速度为（）A．1m/s2B．2.25m/s2C．3m/s2D．4.25m/s2练习6.2015年9月2日，“抗战专列”在武汉地铁4号线亮相，引得乘车市民纷纷点赞．若该地铁列车先从甲站开始做初速度为零、加速度大小为a的匀加速直线运动，通过位移L后，立即做加速度大小也为a的匀减速直线运动，恰好到乙站停下．则列车从甲站到乙站所用时间为A．B．2C．2D．4。

位移与时间关系公式位移与时间关系公式是描述物体在运动过程中位移与时间之间的数学关系的公式。

在物理学中，位移通常用符号Δx表示，表示物体从初始位置到最终位置之间的距离。

时间用符号t表示，表示物体运动所经过的时间。

位移与时间之间的关系可以通过速度来描述。

速度是物体在单位时间内所经过的位移。

如果物体的速度是恒定的，那么位移与时间之间的关系可以用简单的公式来表示。

当物体的速度恒定时，位移与时间之间的关系可以用以下公式表示：Δx = v × t其中，Δx表示位移，v表示速度，t表示时间。

这个公式的意思是物体的位移等于物体的速度乘以物体运动所经过的时间。

如果物体的速度不是恒定的，那么位移与时间之间的关系就需要通过速度的变化来描述。

在这种情况下，可以使用平均速度来表示位移与时间之间的关系。

平均速度是物体在一段时间内的位移与时间的比值。

如果物体在时间t1内的位移为x1，在时间t2内的位移为x2，那么位移与时间之间的关系可以用以下公式表示：Δx = (x2 - x1) / (t2 - t1)这个公式的意思是物体的位移等于物体在时间t2和t1之间的位移差除以时间t2和t1之间的时间差。

除了上述的线性关系，位移与时间之间的关系还可以通过其他的函数关系来描述。

例如，当物体的加速度恒定时，位移与时间之间的关系可以用以下公式表示：Δx = v0 × t + (1/2) × a × t^2其中，Δx表示位移，v0表示物体的初始速度，t表示时间，a表示物体的加速度。

这个公式的意思是物体的位移等于物体的初始速度乘以时间加上物体的加速度乘以时间的平方的一半。

除了上述的公式，位移与时间之间的关系还可以通过其他的函数关系来描述，这些函数关系会因物体运动的特性而不同。

例如，当物体的加速度不恒定时，位移与时间之间的关系可以通过物体的加速度函数来描述。

总结起来，位移与时间之间的关系可以通过不同的公式来描述，这些公式的选择取决于物体运动的特性以及速度和加速度是否恒定。