电场的能量能量密度

电磁场的能量与功率计算电磁场是我们生活中常见的一种物理现象，它包括电场和磁场两个部分。

电磁场的能量与功率计算是电磁学中的一个重要内容，它帮助我们理解电磁场的特性和应用。

本文将从电磁场能量的计算和功率的计算两个方面进行探讨。

一、电磁场能量的计算电磁场能量的计算是通过对电场和磁场的能量密度进行积分得到的。

首先，我们来看电场能量的计算。

电场能量密度表示单位体积内的电场能量，它的计算公式为：\[u_e = \frac{1}{2}\varepsilon_0E^2\]其中，\(u_e\)为电场能量密度，\(\varepsilon_0\)为真空介电常数，\(E\)为电场强度。

在计算电场能量时，我们需要将电场能量密度进行积分。

假设电场是由一个点电荷产生的，电场能量的计算公式为：\[W_e = \int u_e dV = \frac{1}{2}\varepsilon_0\int E^2 dV\]其中，\(W_e\)为电场能量，\(dV\)为体积元素。

接下来，我们来看磁场能量的计算。

磁场能量密度表示单位体积内的磁场能量，它的计算公式为：\[u_m = \frac{1}{2\mu_0}B^2\]其中，\(u_m\)为磁场能量密度，\(\mu_0\)为真空磁导率，\(B\)为磁感应强度。

与电场能量类似，计算磁场能量时也需要将磁场能量密度进行积分。

假设磁场是由一个线圈产生的，磁场能量的计算公式为：\[W_m = \int u_m dV = \frac{1}{2\mu_0}\int B^2 dV\]其中，\(W_m\)为磁场能量。

通过以上的计算公式，我们可以得到电场和磁场的能量。

电磁场的总能量为电场能量和磁场能量之和：\[W_{em} = W_e + W_m\]二、电磁场功率的计算电磁场的功率表示单位时间内电磁场传递的能量，它的计算公式为：\[P = \frac{dW}{dt}\]其中，\(P\)为电磁场功率，\(dW\)为电磁场传递的能量的微小变化量，\(dt\)为时间的微小变化量。

静电场是由带电粒子的分布和运动引起的一种电力学现象。

它的能量
与能量密度是电力学中的重要概念，可以用来描述静电场的强弱和能
量分布。

静电场的能量是指静电场中带电粒子所携带的能量。

这些能量可以在
静电场中传递和转化，但是总能量是不变的。

静画场的能量密度是指单位体积内静电场的能量。

在静电场中，能量
密度越大，静电场就越强。

反之，能量密度越小，静电场就越弱。

举个例子，假设有两个电荷相互作用，一个带正电荷，一个带负电荷。

如果电荷的电量越大，那么静电场的能量就越大，能量密度也就越大。

如果电荷的电量越小，那么静电场的能量就越小，能量密度也就越小。

静电场的能量和能量密度是相互影响的，因此在研究静电场时，通常
要同时考虑这两个概念。

电场能量密度公式
电场能量密度是指一个电场中每单位体积所存在的电能量的大小。

电场能量密度的表达式为：U = 1/2 ρE2，它的单位是电子伏特的平方，其中ρ是电荷密度，E是电场强度。

电场能量密度可以用来计算在一定体积中有多少电能量。

例如，如果电场强度为5伏/厘米，电荷密度为5伏/厘米，则电场能量密度为25电子伏特的平方。

这意味着，在1立方厘米的体积中存在25电子伏特的电能量。

电场能量密度的另一个用途是计算电容器的工作能量。

电容器的电容量C可以用电容器的电场能量密度U来计算：U = 1/2Cv2，其中v是电压。

如果电容器的电压为5伏，那么电容器的工作能量就是25伏特的平方，也就是1/2Cv2。

电场能量密度不仅可以用来计算电能量和电容器的工作能量，还可以用来计算电磁场的能量。

如果电磁场的电场强度为E，磁场强度为H，则电磁场的能量密度可以表示为U = 1/2(E2 + H2)。

电场能量密度的量纲是电子伏特的平方，它可以用来计算一定体积中的电能量、电容器的工作能量和电磁场的能量。

因此，电场能量密度是电力学中非常重要的概念，在电子设备和电力系统的设计中都被广泛使用。

平均磁场能量密度（）平均电场能量密度。

平均磁场能量密度（H）平均电场能量密度（E）在电磁学中，磁场能量密度和电场能量密度是描述电磁场能量分布的重要参数。

平均磁场能量密度（H）和平均电场能量密度（E）是两个关键概念，用于解释电磁场的能量特性。

首先，我们来讨论平均磁场能量密度（H）。

磁场能量密度指的是磁场中单位体积的能量。

磁场能量密度与磁场强度（H）的平方成正比。

在一个恒定的磁场中，磁场能量密度可以通过求解磁场强度的平方并乘以一个常数来计算。

平均磁场能量密度表示一个时间段内磁场能量密度的平均值。

接下来，我们来探讨平均电场能量密度（E）。

电场能量密度指的是电场中单位体积的能量。

电场能量密度与电场强度（E）的平方成正比。

在一个恒定的电场中，电场能量密度可以通过求解电场强度的平方并乘以一个常数来计算。

平均电场能量密度表示一个时间段内电场能量密度的平均值。

平均磁场能量密度（H）和平均电场能量密度（E）在电磁学中扮演着重要的角色。

它们的计算可以帮助我们了解电磁场的能量分布情况，并为电磁场的应用提供理论基础。

同时，在电磁波的传播中，平均磁场能量密度（H）和平均电场能量密度（E）的比值也决定了电磁波的传播速度和传播性质。

总结而言，平均磁场能量密度（H）和平均电场能量密度（E）是描述电磁场能量分布的重要参数。

它们的计算可以帮助我们了解电磁场的能量特性，并为电磁场的应用提供理论基础。

在编写文章时，我们需要确保标题与内容相符，避免涉及广告信息和侵权争议，并注意排除不适宜展示的敏感词或其他不良信息。

同时，文章的结构应当清晰，段落完整，使得读者能够流畅地理解和阅读。

电能密度和磁能密度
电能密度和磁能密度是物理学中一个重要的概念，它们可以研究物质间相互作用的机制。

它们两个都是电磁学里最基本的概念，也是物理学中的重要概念。

电能密度是指电场的能量分布密度，它描述了单位体积内单位时间内所承受的电能量。

它
可以用矢量E表示，它的强度可以用V/m来衡量，静电场中，它仅在电场影响之外有效，
它可以定义为单位体积内所承受的电能量总和，它可以通过驱动电位来计算出来，它以牛
顿/千万伏特每立方厘米为单位计算。

磁能密度，即磁场能量密度，是指在某一点植物中所存在的磁场能量，它可以用矢量B表示，用斯坦比/立方米表示强度，它的单位为牛顿/千万伏特每立方厘米，它主要用来衡量
物体与场之间的互作用，其值受到场的强度和磁密度的影响，当场强度变化和磁密度变化时，磁能密度也随之改变。

电能密度和磁能密度都是电磁学最基本的概念，他们都可以研究物质之间的相互作用机制。

在相互影响下，它们的值发生变化，也控制了物质间的相互作用，电磁学研究中有着重要
的地位。

静电场中的能量静电场是一种由电荷积聚所形成的电场，具有辐射状的特点。

在静电场中，电荷之间会相互作用，并产生电势能和电场能量。

本文将探讨静电场中的能量转化和计算方法。

一、静电场的基本概念静电场是由带电粒子或物体所产生的电场，其特点是电荷不进行移动，所以称为“静电”场。

静电场的强度与电荷的分布有关，通常通过电场强度来描述。

电场强度的方向与电荷的正负性及其位置有关。

二、电静场能量的定义在静电场中，电荷之间由于存在电场而具有势能。

电静场能量是静电场中电荷与电场之间相互作用而具有的能量，用符号U表示。

电静场能量可以用来描述电荷在电场中的粒子之间的相互作用。

三、电势能的计算公式电势能是静电场中电荷所具有的能量，它可以通过电荷的电势差来计算。

根据电势能的定义，可以得到电荷在静电场中的电势能计算公式：U = k * q1 * q2 / r其中，U为电势能，k为电场常数（通常取为 8.99 × 10^9 N·m^2/C^2），q1和q2为两个电荷的大小，r为两个电荷之间的距离。

四、静电场能量的转化静电场能量可以在电荷之间进行转化，也可以转化为其他形式的能量。

例如，当两个电荷之间产生电势差时，静电场能量可以转化为电动势能，从而使电荷发生位移。

静电场能量也可以转化为热能，当电荷在与其他物质接触时，静电场能量的转化会产生热量。

五、电场能量密度电场能量密度是指静电场中单位体积内的能量。

在某一点的电场能量密度可以通过以下公式计算：u = 1/2 * ε * E^2其中，u为电场能量密度，ε为真空介质常数（通常取为 8.85 ×10^-12 C^2/N · m^2），E为电场强度。

六、电场能量的保守性静电场能量是保守的，即不随着电荷的移动而改变。

这是因为在静止的电荷之间，电场是由静电荷产生的，而静电荷的电场是不随时间变化的，所以电场能量保持不变。

七、实际应用静电场的能量在日常生活和工业生产中有着广泛的应用。

电场的能量公式
电场能量的公式是w=1/2q²/c，其中w表示电场能量，q表示电荷量，c表示电容。

这个公式表明，电场能量等于电场能量密度对电场所处空间的积分。

在点电荷产生的静电场中，电场能量正比于点电荷的带电量的平方。

对于平行板电容器，电场能量的表达式可以改写为Eₑ=CU²/2，其中Eₑ表示电场能量，C表示平行板电容器的电容，U表示两板间电势差。

在静电场中，我们通常只讨论在静电场中的能量分布。

在均匀线性介质中，总能量W=1/2 * E · D。

这些公式提供了对电场能量在空间中的分布以及电容储存能量的量化的理解和应用。

电场能量和磁场能量的转化问题一、引言电场和磁场是物理学中非常重要的概念，它们可以相互作用，相互转化。

其中，电场能量和磁场能量的转化问题是一个非常有趣的问题。

本文将围绕这个问题展开讨论。

二、电场能量1. 电势能和电场能量在静电学中，一个带点粒子在电势为V的点处具有电势能E=qV，其中q为粒子的电荷量。

当带点粒子从一个位置移动到另一个位置时，它所具有的电势能发生了变化。

这种变化可以用下面的公式来表示：ΔE=q(V2-V1)其中ΔE表示电势能变化量，V2和V1分别表示粒子所处位置的电势。

在涉及多个带点粒子时，我们需要考虑它们之间相互作用产生的总体效应。

这就需要引入电场概念。

对于一个静止不动的带点粒子，在某个空间点处所受到的力可以用下面公式来表示：F=qE其中F为力大小，q为粒子荷量，E为该空间点处的电场强度。

我们可以将这个公式推广到多个带点粒子之间相互作用的情况下：F=∑qiEi其中qi为第i个粒子的电荷量，Ei为该空间点处的电场强度。

这个公式说明了电场力是所有带点粒子之间相互作用的结果。

由于电势能和电场强度之间存在着一定的关系，我们可以将它们转化为电场能量。

对于一个体积为V的空间区域，其中所存储的电场能量可以用下面公式来表示：W=1/2ε∫E^2dV其中ε为真空介质常数，E为该空间区域内任意一点处的电场强度。

这个公式说明了电场能量与空间中电场强度分布有关。

2. 电场能量密度对于一个给定体积V内部的所有点，我们可以定义它们各自所存储的单位体积内平均电场能量为u。

这样，我们就得到了一个新概念——电场能量密度。

u=W/V=1/2εE^2其中W表示体积V内所存储的总电场能量。

三、磁场能量1. 磁感应强度和磁通量在静磁学中，一个带磁物质在磁感应强度B处具有磁势能E=mB，其中m为物质的磁矩。

当带磁物质从一个位置移动到另一个位置时，它所具有的磁势能发生了变化。

这种变化可以用下面的公式来表示：ΔE=m(B2-B1)其中ΔE表示磁势能变化量，B2和B1分别表示物质所处位置的磁感应强度。

静电场能量密度静电场是指电荷静止或者以恒定速度运动时所产生的电场。

在静电场中，电荷之间存在作用力，这个作用力产生的能量就是静电能。

而在静电场中，电场能量密度则是描述单位体积内的能量。

静电场能量密度的计算公式是：\[ U_E = \frac{1}{2} \varepsilon_0 E^2 \]其中，\( U_E \) 表示单位体积内的静电场能量密度，\( \varepsilon_0 \) 是真空电容率，而 \( E \) 则代表电场强度。

根据这个公式，可以看出电场强度越大，静电场能量密度也越大。

在物理学中，静电场能量密度的概念可以用来研究和分析电磁场的能量分布情况。

在不同的电场分布情况下，静电场能量密度也会有所变化。

例如，在均匀电场中，电场强度处处相等，那么静电场能量密度也是均匀分布的。

此时，可以通过计算单位体积内的能量，来求得整个电场的总能量。

而在非均匀电场中，电场强度和静电场能量密度则会随着位置的不同而不同。

此时，需要将空间划分为微小体积，然后对每个微小体积内的能量密度进行计算，最后进行积分求和，得到整个电场的总能量。

除此之外，在介质存在的情况下，静电场能量密度的计算公式还会发生变化。

考虑到介质极化的影响，公式可以改写为：\[ U_E = \frac{1}{2} \varepsilon E^2 \]其中，\( \varepsilon \) 表示介质的电容率。

这个公式表明了在介质存在时，静电场能量密度与电场强度的关系。

总结起来，静电场能量密度是描述单位体积内静电场能量的物理量。

通过对电场强度和介质电容率的计算，可以得到静电场能量密度在不同电场分布和介质环境下的数值。

这一概念在电磁学和物理学的研究中有着重要的应用和意义。

电容与电介质介电常数与电场能量与电场能量密度之间的关系电容是电学中一个重要的概念，它描述了电路元件对电荷的存储能力。

而电介质介电常数则是衡量电介质的极化能力，它与电场能量和电场能量密度之间存在紧密的关系。

首先，让我们回顾一下电容的概念。

电容是电路元件对电荷存储能力的度量，用单位电压下的电容量来表示。

在一个理想的理论电容器中，电容量的计算公式为C = Q/V，其中C表示电容量，Q表示电荷量，V表示电压。

这意味着当电容器的电压增加时，可以存储的电荷量也会增加。

然而，在实际的应用中，电容器常常由电介质填充，以增加电容量。

电介质介电常数是衡量电介质极化能力的物理量，用εr来表示。

理想情况下，如果电介质介电常数为1，则电介质对电场几乎没有影响。

但是，在实际情况下，绝大多数电介质都有介电常数大于1，这意味着它们能够存储更多的电荷。

因此，对于一个实际的电容器而言，其电容量的计算公式可以表示为C = εrε0A/d，其中ε0表示真空中的介电常数，A表示电容器的极板面积，d表示极板之间的距离。

由此可见，电介质介电常数的增加会导致电容量的增加。

现在，让我们思考一下电场能量与电场能量密度之间的关系。

在电磁学中，电场能量是电场对电荷进行的功的总和。

假设一个点电荷q在电场E中移动一个距离d，那么它所受到的力F等于qE，因此电场对电荷所做的功W等于F·d = qEd。

由此可见，电场能量与电荷量、电场强度和电位移之间存在紧密的联系。

而电场能量密度则是单位体积内的电场能量，用u表示。

它表示了电场能量在空间中的分布情况。

对于一个电容器而言，它的电场能量密度可以表示为u =1/2εE²，其中ε表示电介质介电常数，E表示电场强度。

这意味着电场能量密度的大小与电介质的极化能力和电场强度成正比。

综上所述，电容与电介质介电常数与电场能量和电场能量密度之间存在着密切的关系。

电介质的介电常数决定了电容器的电容量，而电场能量和电场能量密度则分别与电介质的极化能力和电场强度有关。

电场强度与电场能量密度关系的探讨电场强度和电场能量密度是电场的基本性质，对于理解电场及其应用至关重要。

本文将探讨电场强度与电场能量密度之间的关系，并从微观和宏观的角度进行分析。

首先，我们先来了解一下电场强度和电场能量密度的概念。

电场强度是指单位正电荷在电场中受力的大小，通常用E表示，它是描述电场强弱的物理量。

而电场能量密度是指单位体积内电场能量的大小，通常用u表示，它是描述电场能量分布的物理量。

从微观的角度来看，电场强度与电场能量密度是密切相关的。

在电场中，带电粒子受到电场力的作用，这个作用力与电场强度成正比，即F=qE，其中F表示力，q表示电荷量，E表示电场强度。

当电场强度增大时，力的大小也会增大，即电场对带电粒子的作用更强烈。

而电场能量密度则与电场强度的平方成正比，即u=εE²/2，其中ε表示电介质的介电常数。

可以看到，电场能量密度随着电场强度的增大而增大，说明电场强度越大，电场中的能量分布越密集。

从宏观的角度来看，电场强度与电场能量密度之间也存在着一定的关系。

在一个封闭的电场中，电场能量保持不变，因此电场能量密度与电场强度之间存在着反比关系。

当电场强度增大时，电场能量密度减小；反之，当电场强度减小时，电场能量密度增大。

这是因为电场能量主要储存在电场中的介质中，电场强度的增加会导致电荷粒子更加密集地堆积在电场中的介质中，进而减小了单位体积内的电场能量密度。

总结起来，电场强度与电场能量密度之间存在着复杂的关系。

从微观角度来看，电场强度增大会导致电场力增大，电场能量密度也随之增大；从宏观角度来看，电场强度增大会导致电场能量密度减小，而电场强度减小则会导致电场能量密度增大。

这种关系是电场能量传递和转化的基础，也是电场相互作用的重要表现。

最后，需要注意的是，电场强度和电场能量密度是相互联系的两个概念，它们在电场的研究和应用中都起着重要的作用。

对于理解电场的能量分布和电荷间相互作用的机制，深入研究电场强度与电场能量密度的关系具有重要的意义。

电场能量密度公式
电场能量密度公式为：W=(1/2)UQ。

电场能量密度即单位体积内的电场能量。

静电场的能量是静电场的一个重要特征，对于静电场的能量，一般电磁学教材在讲述这一基本概念时，利用电容器的储能来说明能量定域在电场中，电场中的电介质要受到电场力的作用。

电场是电荷及变化磁场周围空间里存在的一种特殊物质。

这种物质与通常的实物不同，它虽然不是由分子原子所组成的，但它却是客观存在的特殊物质，具有通常物质所具有的力和能量等属性。

电场的力的性质表现为：电场对放入其中的电荷有作用力，这种力称为电场力。

电场的能的性质表现为：当电荷在电场中移动时，电场力对电荷做功，说明电场具有能量。

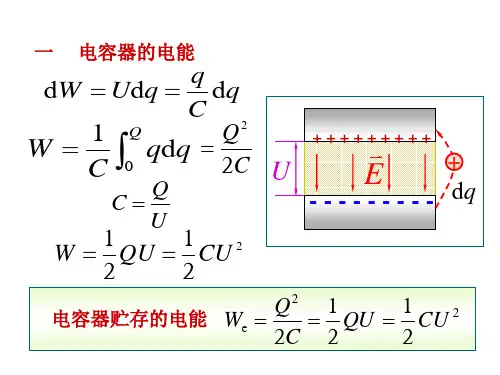
7-7 电场能量与能量密度一、4个重要基本公式①电介质下的电容C与真空下的电容C0的关系:C=C0εr②电场能量W e=12QU=12CU²③能量密度w e=12εE²=12DE④能量密度与电场能量的关系W e=w eVdV(V是电场体积，如果是平面采用二重积分)二、真空环境下与有介质环境下的各物理量间的关系引入：如图所示，已知真空下平行板电容器σ0，E0,U0,D0,C0,W e0,平行板电容器两板间距为d，求下面两种情况下电容器插入相对电容率为εr的σ，E,U,D,C,W e①充电后断开电源②充电后保持两板的电压不变①E=E0εr σ=Eε=E0εεr=E0ε0=σ0U=Ed=E0dεr=U0εrD=Eε=E0εrε0εr =E0ε0=σ0C=εr C0W e=12CU²=12εr C0(U0εr)²=W e0εr②保持电压不变，则：U=U0E=U0d =Ud=E0D= Eε=E0ε0εr=σ0εrσ=Eε=D=σ0εrC=εr C0W e=εr W e0小结：1、电容器的电容与电压大小无关，只和电介质相对电容率有关2、平行板电容器由于电荷增加而增加的能量，大于插入介质损失的能量，所以电场能量增加拓展：1、电位移矢量沿任何一个闭合曲面的通量为0，表明曲面内自由电荷代数和为0（D与E方向一致）2、介质中的电位移矢量和自由电荷与极化电荷的分布有关3、在自由电荷分布不发生变化时，含电介质的电容器电容一定是真空状态下的1ε0三、两个重要模型1、带电球壳电容器模型模型简述：如图所示,球形电容器的内、外半径分别为R 1和R 2,所带电荷为±Q .若在两球壳间充以电容率为ε的电介质，问此电容器贮存的电场能量为多少？解：根据笔记7-1，得到r 处的电场强度大小为E=Q4πεr能量密度w e =12× Q4πεr 2×ε=Q 232π2εr 那么根据第一幕的公式4，得到W e = w e V dV = dW e =Q 28πε drr ²R 2R 1=Q 28πε(1R 1−1R 2)回到笔记7-5的孤立导体，R 2趋近于无穷大，得到W e =Q 28πε1R 1是孤立导体的电场能量2、带电圆柱电容器模型模型简述：如图圆柱形电容器，中间是空气，空气的击穿场强是E b ，电容器外半径R 2.在空气不被击穿的情况下，内半径R 1为多少，可使电容器存储能量最多？解：根据7-3笔记得到任意圆柱面r 的电场强度是E=λ2πε0r带入击穿场强有λmax =E b 2πε0R 1 求出电容器电压U= λ2πε0r dr R 2R 1=λ2πε0ln R2R1根据能量公式得到W e =λl 2λ2πε0ln R 2R 1=λ²l 4πε0ln R 2R 1带入λmax =E b 2πε0R 1 得到：W e =πε0E b ²R 1²lnR 2R 1求导求出R 1取得的值使得W e 最大。