当前位置：文档之家 › 16-3波的能量 波的能量密度

16-3波的能量 波的能量密度

  • 格式：ppt
  • 大小：798.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

波的能量知识

波的能量知识


A0 r0 r y= cos ω (t − ) r u
r1
式中r为离开波源的距离，A0为r = r0处的振幅。
小结： 小结： 波动能量 u 1 x 2 2 2 d dV内： Wk = ρdVA ω sin ω (t − ) 2 u dV 1 x S 2 2 2 dW p = ρdVA ω sin ω ( t − ) 2 u x 2 2 2 dW = ρdVA ω sin ω (t − ) u 不守恒 dW 1 2 2 平均能量密度： 平均能量密度： w = = ρω A dV 2 1 2 2 2 能流密度（波强）： 能流密度（波强）： I = ρ A ω u ∝ A 2
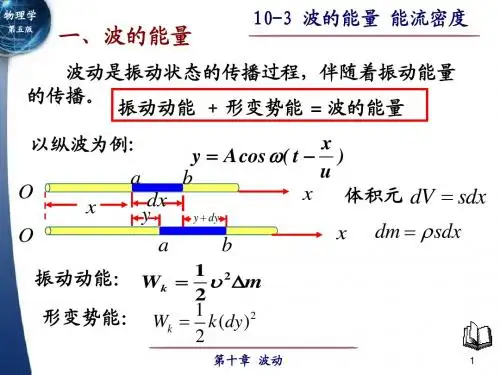
10、3 波的能量 能流密度 一 波动能量的传播 1 波的能量 波的传播是能量的传播， 波的传播是能量的传播，传播 过程中,媒质中的质点由不动到动， 过程中,媒质中的质点由不动到动， 具只动能 W K ,媒质形变具只势能 W P .
以固体棒传播纵波为例分析波动能量的传播. 固体棒传播纵波为例分析波动能量的传播 传播纵波为例分析波动能量的传播
u= E
2
Sdx = dV dy ∂y 考虑到 y 是 x 和 t 的函数，故 应是 dx ∂x ∂y ω x 1 2 ∂y 2 = A sin ω (t − ) dW P = u ρdV ( ) 而 ∂x u u 2 ∂x
ρ
E = u2ρ
1 x 2 2 2 dWP = ρdVA ω sin ω(t − ) 2 u
E 纵波 u = 固体： 固体：
ρ ρ
G 横波 u =
弹性模量
杨氏模量： 杨氏模量：
应力 F S E= = 应变 ∆L L
x d W = ρ d VA ω sin ω (t − ) u (2) 任一体积元都在不断地接收和 ) 放出能量，即不断地传播能量. 放出能量，即不断地传播能量 任一体 积元的机械能不守恒. 积元的机械能不守恒 波动是能量传递 的一种方式 .
大学物理 波的能量 惠更斯原理

大学物理 波的能量 惠更斯原理

u = Y
由于： 由于： 势能
1 dEP = ( ρdV ) A 2ω 2 sin 2 ω (t − x / u ) 2
ρ
1 2 2 2 与动能相同 dEk = ( ρdV ) A ω sin ω (t − x / u ) 2 k=0、±1、±2、…最大， 最大， 当：ω(t-x/u)=(2k+1) ̟/2 最大
ω(t-x/u)=k̟ k=0、±1、±2……最小。 最小。
Ek、EP
同时达到最大 平衡位置处 同时达到最小 最大位移处
6
3.波动的能量
dE = dEk + dEP
= ( ρdV ) A ω sin ω (t别 • 振动能量中 k、EP相互转换，系统机械 振动能量中E 相互转换， 能守恒。 能守恒。 •波动能量中 k、EP同时达到最大，同时 波动能量中E 同时达到最大， 波动能量中 为零，总能量随时间周期变化。 为零，总能量随时间周期变化。
7.3 7.4
波的能量 惠更斯原理
1
一、波的动能、势能和能量 波的动能、
在波传播的过程中， 在波传播的过程中，振源的能量通过弹性介质传 播出去，介质中各质点在平衡位置附近振动， 播出去，介质中各质点在平衡位置附近振动，介质中 各部分具有动能，同时介质因形变而具有势能。 各部分具有动能，同时介质因形变而具有势能。 波动传播的过程也是能量传递的过程。 波动传播的过程也是能量传递的过程。
1.波动的动能
纵波为例： 以均匀细棒中传播的 纵波为例： 取一体积元 dV， ， 质量为ρdV, 质量为 质元振动速度为v。 质元振动速度为
2
ρdV
dm = ρdV
波函数
y = A cos ω (t − x / u) 质元振动速度 v = ∂y = − Aω sin ω (t − x / u ) ∂t 动能 1 2 dEk = dm v 2 1 2 2 2 = ( ρdV ) A ω sin ω (t − x / u ) 2
16-3 波的能量 能流密度

16-3 波的能量 能流密度


讨论 1）在波动传播的媒质中，任一体积元的动能、 ）在波动传播的媒质中，任一体积元的动能、 势能、总机械能均随x, 作周期性变化 且变化是同 作周期性变化， 势能、总机械能均随 t作周期性变化，且变化是同 相位的 相位的. 体积元在平衡位置时，动能、 体积元在平衡位置时，动能、势能和总机械能 均最大. 均最大 体积元的位移最大时，三者均为零. 体积元的位移最大时，三者均为零
第十六章 机械波动理论 弹性势能
16-3 波的能量 能流密度 16O O
1 2 dW P = k (dy ) 2 dy F 胡克定律 =Y S dx
x
F
dx
SY k= F = YS dx dx 2 1 1 Y dy 2 dW P = k (d y ) = YS d x u= 2 2 ρ dx ∂y ω 1 dy 2 x 2 = ρu dV ( ) = A sin ω (t − ) 2 dx ∂x u u 1 x 2 2 2 = ρdVA ω sin ω (t − ) 2 u
16-3 波的能量 能流密度 16-
s2
s1
r1
r2
即
w 1 uS1 = w 2 uS2 1 1 2 2 2 ρ A1 ω u 4π r1 = ρ A22ω 2 u 4π r22 2 2 A0 r0 r A1 r2 y= cos ω (t − ) = r u A2 r1
处的振幅。 式中r为离开波源的距离， 式中 为离开波源的距离，A0为r=r0处的振幅。 为离开波源的距离
O O
x
dx
x
y + dy
y
x
第十六章 机械波动理论
16-3 波的能量 能流密度 16-
O O
x
大学物理-波的能量

大学物理-波的能量


x
y + ∆y
x y = Acosω(t − ) 1）体积元的动能 ） u ∂y x v = = − Aω sin ω(t − ) ∂t u
1 1 x 2 2 2 2 ∆Ek = ∆mi v = ρ∆VA ω sin ω(t − ) 2 2 u
2）体积元的势能 ∆E ）
x
∆x
u
1 x 2 2 2 ρ∆VA ω sin ω(t − ) P = 2 u
形变最小 →0， ， 振动速度最小 →0
y
r u
a
b
x
形变最大， 形变最大，振动 速度最大
r u
y
B P A Q
x
质元A 质元 质元P 质元 质元B 质元 质元Q 质元
（填吸收、释放）能量 填吸收、释放） 填吸收、释放） （填吸收、释放） 能量 填吸收、释放） （填吸收、释放） 能量 （填吸收、释放）能量 填吸收、释放）
结论：在波动过程中能量以波的形式沿 x 方向以 u 向
前传播着。 前传播着。
2、平均能量密度--- 能量密度在一个时间周期内的平均值 、平均能量密度
1 T 2 2 2 x 1 2 2 w = ∫ ρA ω sin ω(t − )dt = ρA ω T 0 u 2
为了定量描述波动过程中能量的传播， 为了定量描述波动过程中能量的传播，引入能流和 能流密度的概念 3、能流---单位时间内通过介质中某面积的能量 、能流 单位时间内通过介质中某面积的能量
形变最小形变最大形变最大振动速度最大填汲取释放能量填汲取释放填汲取释放填汲取释放能量填汲取释放填汲取释放能量填汲取释放能量能流和能流密度波强二能流和能流密ep为了精确地描述波的能量分布为了精确地描述波的能量分布引入能量密度1能量密度介质中单位体积中的波动能量能量密word版本能量密度描述了介质中各点能量即振动能量的分布能量密度描述了介质中各点能量即振动能量由上式可知波的能量密度是随介质的空间坐标能量密度是随介质的空间坐标由上式可知争论
机械波的几个概念

机械波的几个概念

二、波的干涉
两个频率相同,振动方向相同,相差恒 定的波源发出的波的叠加。
波源的振动：
y10 A10 cos(t 1 ) s1
r1
p
y20 A20 cos(t 2 ) s2
r2
Ｐ点的振动：
y1
A1 cos(t
1
2r1 )
y2
A2
cos(t
2
2r2
)
令：
2
1
2
(
r2
r1
)
由叠加原理Ｐ点： y y1 y2 Acos(t )
表
dE dEk
明：
dEk
dVA22 sin2
(t
x) u
１、总能量随时间作周期性变化。
２、波动能量与振动能量有显著不同;振
动中动能与势能相位差为 ,波动中
动、势能同相。
2
３、波动是能量传播的形式。
二、能量密度
１、定义:单位体积介质中的波动能量.
w dE A22 sin2 (t x )
dV
3、其他情况合振幅在最大值与最小值之间。
综上：同频率,同方向,相位差恒定的两 列波,在相遇区域内,某些点处振动始终加 强,另一些点处的振动始终减弱,这一现象 称为波的干涉。
例1.波源A、B具有相同的振动方向和振幅,
初相差为,设沿A、B联线相向发出两列
简谐波,频率均为100Hz,波速为430米/ 秒已知A在原点,B在X=30米处.
2 Acos 2 x
2、各点作同频率的谐振动；
各点作频率相同、振幅不同的谐振动。
三、驻波的特征：
1、波节和波腹： 振幅为 2Acos 2 x
cos 2 x 0
振幅为0 ——波节
大学物理[下册]波动习题课

大学物理[下册]波动习题课



将沿oy轴的负方向运动. 0 / 3
y
(
x,
t)
Acos[(t x ) u
0.1cos[500(t
0 ] x / 5000)


/
3]m
o
A/2 y
(2)在距原点7.5m处质点的运动方程.
y 0.1cos[500t 13 /12]m
t=0时该点的振动速度
15-5 波源作简谐运动,周期为0.02s,若该振动以100m.s-1的速度沿直 线传播,设t=0时,波源处的质点经平衡位置向正方向运动,求:(1)距波 源15.0m和5.0m处质点的运动方程和初相;(2)距波源分别为16.0m和 17.0m的两质点间的相位差.
解: (1)由题意知:T=0.02s,u=100m.s-1,可得
解: (1)已知波动方程为 y 0.20cos2.50t xm
与一般表达式 y Acos(t x / u) 0
比较,得 A 0.20m,u 2.5m s1, 0 0 / 2 1.25HZ u / 2.0m
(2)绳上的质点振动速度
15-9波动的能量与那些物理量有关?比较波动的能量与 简谐运动的能量.
从波的能量密度公式可知 w A22 sin 2 t x / u
波动的能量不但与体积有关,且与,A,,u.
波动的能量与简谐运动的能量有显著的不同,在简谐 运动系统中,动能和势能有/2的相位差,系统的机械 能是守恒的.在波动中,动能和势能的变化是同相位 的,对任何体积元来说,系统的机械能是不守恒的.
15-11波的干涉的产生条件是什么?若两波源所发出的波的 振动方向相同,频率不同,则它们在空间叠加时,加强和减弱 是否稳定?
10-3 波的能量能流密度

10-3 波的能量能流密度


平均能量密度
一个周期内能量密度的平均值。 一个周期内能量密度的平均值。
第十章 波动
5
物理学
第五版
1010-3 波的能量 能流密度
1 T 1 T x 2 2 2 w = ∫ wdt = ∫0 ρA ω sin ω( t − u )dt T 0 T T 1 x 2 2 2π ρA ω ∫0 sin ( t − )dt = T =π ω T T u T 1 1 x π 2 2 2 2 2π w = ρA ω = ρA ω ∫0 sin ( t − )d( t ) π T u T 2
1 A2ω2 x 2 = YSdx sin [ω(t − )] 2 2 u u
1 x 2 2 2 Wp = ρ A ω sin [ω(t − )]∆V = W k 2 u
第十章 波动
3
物理学
第五版
1010-3 波的能量 能流密度 体积中质点的总能量： 考虑 ∆V 体积中质点的总能量：
2 2 2
x W = Wk +Wp= ρA ω sin ω( t − )∆V u 说明： 说明：
∫
π
0
sin 2 θ ⋅ dθ = π 2
第十章 波动
6
物理学
第五版
1010-3 波的能量 能流密度 二、波的能流和能流密度 波的能流和能流密度
u
∆S
能流: 能流:单位时间内通过介质中某一 截面的能量。 截面的能量。 p = wu∆S 平均能流：在一个周期内能流的平均值。 平均能流：在一个周期内能流的平均值。
物理学
第五版
一、波的能量 波的能量
1010-3 波的能量 能流密度
波动是振动状态的传播过程， 波动是振动状态的传播过程，伴随着振动能量 的传播。 的传播。 振动动能 + 形变势能 = 波的能量 以纵波为例: 以纵波为例:
波的能流密度强度公式

波的能流密度强度公式

波的能流密度强度公式全文共四篇示例，供读者参考第一篇示例：波是一种能够传播能量的物理现象，它可以在任何介质中传播，比如空气中的声波、水中的水波等。

波的传播是由波的能流密度决定的，而波的能流密度强度可以用一定的数学公式来描述。

在本文中，我们将介绍波的能流密度强度公式以及它的作用和应用。

波的能流密度强度公式描述了波在向前传播过程中所携带的能量的密度。

波的传播是通过波的振动传递能量的，而波的振动会导致介质中的粒子发生振动，从而传递能量。

波的振动会产生波动，而波动的能量密度就是波的能流密度强度公式要描述的内容。

波的能流密度强度公式可以表示为：\[ S = \frac{1}{2} \cdot v \cdot \rho \cdot A \cdot \omega^2 \]S表示波的能流密度强度，单位是瓦特每平方米（W/m^2）；v 表示波的传播速度，单位是米每秒（m/s）；ρ表示介质的密度，单位是千克每立方米（kg/m^3）；A表示波动的幅度，单位是米（m）；ω表示波的角频率，单位是弧度每秒（rad/s）。

以上就是波的能流密度强度的公式，它描述了波在传播过程中所携带的能量的密度。

根据这个公式，我们可以计算出波在传播过程中的能量密度，从而了解波的能量传输情况。

波的能流密度强度公式是描述波在传播过程中所携带的能量密度的重要工具，它可以帮助我们深入理解波动的物理本质和传播规律。

通过研究波的能流密度强度，我们可以更好地掌握波的传播特性，进一步推动物理学和工程学等领域的发展和进步。

希望本文的介绍对您有所帮助，谢谢阅读！第二篇示例：波的能流密度强度公式是描述波的能量传播强度的一种数学表达式。

在物理学中，波是一种传播能量和动量的方式，而波的能流密度强度则表示单位面积或单位时间内通过的能量。

波的能流密度强度公式可以通过波的振幅、频率、波长等参数来表达，不同类型的波可以有不同的能流密度强度公式。

在本文中，我们将主要探讨波的能流密度强度公式的基本概念和应用。

波的能量

波的能量


I S u I 2 2 A2 2u
通常
I 2 2 zA2 2
I 1 A2 2u
2
z u 是表征介质特性的一个常量，
——称为介质的特性阻抗
说明：
S u I 2 2 A2 2u
上式根据平面简谐波得到的结论， 但是波的强度与波的振幅、波的频率的 平方成正比的结论对任何弹性波都成立. 波的能量密度表征媒质中某点质元的
一．有波传播时媒质质元的能量
（以平面纵波在固体细长棒中的传播为例）
设有一截面积为 S ，密度为 ρ 的固体细棒，
一平面纵波沿棒长方向传播。
a
b u
o●●
S
x●
●
x
x x
选棒长的方向为 x 轴，在棒上距 o 点 x 处附近 取一长为 Δx 质元 ab ，
a
b u
o●●
S
x●
x
x x

a
W 1 mv2 K2
1 V 2 A2 sin2 (t 2 x )
2

0
1）求势能：
a
b u
o●●

x●
d
●
x
x x
t
a
b u
时
o●
刻
y●
●
y y
x
当有纵波传播时，在应力作用下质元 ab 发生线变,
设 t 时刻质元 ab 正被拉长，
由图上几何关系，质元 ab 长度变化为 Δy
能量的大小. 能流密度表征媒质中某点， 能量传播的多少和快慢.
例:波动的能量与那些物理量有关?比较波动的能量与 简谐运动的能量.
答: 1 V 2 A2
2
物理波的能量

物理波的能量


=
3
cos
4πt
(2)以距a点5m处的b点为坐标原 点写出波动方程。
b.
u .a 5m
x
解：(1)以a点为原点在x轴上任取一点P，坐标为x
ya = 3 cos 4πt y =3 cos 4πt +
x
20
(2)以b点为坐标原点
wk
wp
2 A2
sin
2 [ (t
x )] u
平均能量密度（对时间平均)
w 1 T A2 2 sin 2[(t x)]dt
T0
u
w
=
1 2
ρAω2
2
三、波的强度
能流P :单位时间内垂直通过某一截面的 P = w S u 能量称为波通过该截面的能流，或叫能通量。
显然能流是随时间周期性变化的。但它总为正值
(t+
d u
)
π
2
]
y
=
A cos[ω
(
t
+
d u
x u
)
π
2
]
例6、波速 u =400m/s, t = 0 s时刻的波形如图所示。
{ 写出波动方程。
t= 0 (o点)
得：
y 0
=
2
=
A
2
v0
＞0 0=
π
3
2
o
y(m)
4 5
p
u
x (m)
{ t =0
(p点)
2π
=
y 0
=
0
v0＜ 0
p
0
d
λ
得：
平均能流P : 能流在一个周期内的平均值。 P = S w u 波的强度 I（能流密度）:
大学物理-波的能量能流密度

大学物理-波的能量能流密度


04
电磁波中的能量传播
电磁波概述
电磁波定义
电磁波是由电场和磁场交替变化而产生 的一种波动现象，可以在真空中或物质 中传播。
VS
电磁波分类
根据频率和波长的不同，电磁波可分为无 线电波、红外线、可见光、紫外线、X射线、 γ射线等。
电磁波中电场和磁场能量关系
电场能量
电磁波中电场能量与电场强度的平方成正比，即$W_e = frac{1}{2} epsilon_0 E^2$，其中 $epsilon_0$为真空介电常数，$E$为电场强度。
行波
与驻波不同，行波是向前传播的波形 。在行波中，质点的振动方向与波的 传播方向垂直（横波）或平行（纵波 ）。行波传递能量和动量。
02
能量传播与能流密度
能量传播方式
机械波
通过介质中质点的振动和相互作用传播能量，如声波、水波 等。
电磁波
通过电场和磁场的交替变化传播能量，如光波、无线电波等 。
能流密度定义及表达式
磁场能量
电磁波中磁场能量与磁场强度的平方成正比，即$W_m = frac{1}{2} mu_0 H^2$，其中 $mu_0$为真空磁导率，$H$为磁场强度。
总能量
电磁波的总能量等于电场能量和磁场能量之和，即$W = W_e + W_m$。
电磁波中能量传播特点
01
能流密度矢量
电磁波中的能量传播可以用能流密度矢量$vec{S}$来描述 ，其方向垂直于电磁波的传播方向，大小等于单位时间内 通过单位面积的能量。
光学领域应用
光的传播
01
光波的能量能流密度决定了光的亮度、颜色和温度等特性，是
光学研究的基础。
激光技术
Hale Waihona Puke 02激光具有高能量能流密度的特点，被广泛应用于切割、焊接、

大学物理,课后习题,答案

第十八章 波 动1、一横波沿绳子传播，其波的表达式为 x)2- t 100050ππcos(.y = (SI) 求: (1) 波的振幅、波速、频率和波长。

(2) 绳子上各质点的最大振动速度和最大振动加速度。

(3) 在m .x 201=处和m .x 702=处二质点振动的位相差。

解：（1）)0.02 (100cos 05.0) 2 100cos(05.0x t x t y -=-=πππ m A 05.0=∴,υππω 2 100 ==502/100==⇒ππυ(HZ) )(501-⋅=s m u , )(15050m u===υλ(2) ) 2 100sin(10005.0πππ-⨯-==∂∂t v tY, )(7.15510005.01max -⋅==⨯=s m v ππ) 2 100cos()100(05.02 22x t a t Yπππ-⨯-==∂∂∴ 8.4934500)100(05.022m ax ==⨯=ππa )(2-⋅s m(3)ππλπϕ=-=-=∆12.07.022 12x x2、一平面简谐波沿ｘ轴正向传播，波的振幅cm A 10=，波的圆频率-1s rad 7 ⋅=πω，当s .t 01=时，cm x 10=处的a 质点正通过其平衡位置向ｙ轴负方向运动，而cm x 20=处的ｂ质点正通过cm y 5=点向ｙ轴正方向运动。

设该波波长10c m>λ，求该平面波的表达式。

解：设波动方程为：)2 7cos(1.0πϕπλ⋅-+=xt Yt=1(s)时， 05.0)2 7cos(1.0 ,0)2 7cos(1.02.01.0=⋅-+==⋅-+=πϕππϕπλλ b a Y Y∵0<a v ⇒ ππϕππλk 22 721.0+=⋅-+ ① ∵ 0>b v ， ⇒ ππϕππλk 22 732.0+-=⋅-+ ② 且m 1.0 >λ，故b a ,两质点的位相差π2<①-②得：5λ=1.2， 即 λ=0.24（m ） 代入①得：πϕ317-= 所以 波动方程为：) 7cos(1.031325πππ+-=x t Y 3、图示一平面简谐波在0=t 时刻的波形图，求： （1）该波的波动方程； （2）Ｐ处质点的振动方程。

电磁波的能量密度与能量传递

电磁波的能量密度与能量传递电磁波是一种由电场和磁场相互作用而形成的能量传播现象。

在物质中，电磁波的能量密度与能量传递是一个非常重要的概念。

本文将探讨电磁波的能量密度、能量传递以及与之相关的一些重要应用。

一、电磁波的能量密度电磁波的能量密度是指单位体积内电磁波所携带的能量。

根据电磁波的性质，我们可以得出电磁波的能量密度与电场强度和磁场强度的关系。

根据麦克斯韦方程组，电磁波的能量密度可以表示为：能量密度= 0.5 * ε0 * E^2 + 0.5 * μ0 * B^2其中，ε0和μ0分别是电场和磁场的介质常数，E和B分别是电场强度和磁场强度。

电磁波的能量密度与电场强度和磁场强度的平方成正比，这意味着电磁波的能量密度与电磁场的强度密切相关。

当电磁场的强度增加时，能量密度也会增加，反之亦然。

二、电磁波的能量传递电磁波的能量传递是指电磁波能量从一个地方传递到另一个地方的过程。

在电磁波的传播过程中，能量以波的形式传递，从而实现能量的传递。

电磁波的能量传递是通过电场和磁场之间的相互作用完成的。

当电磁波传播时，电场和磁场会相互耦合，形成电磁波的传播。

电磁波的能量主要集中在电场和磁场的交界处，即电磁波的传播方向。

电磁波的能量传递速度是光速，即299,792,458米/秒。

这是因为电磁波是由电场和磁场相互作用而形成的，而电场和磁场的相互作用是瞬时的，因此电磁波的传播速度也是瞬时的。

三、电磁波的应用电磁波的能量密度与能量传递在现代科学和技术中有着广泛的应用。

以下是一些重要的应用领域：1. 通信技术：无线电、电视、手机等通信技术都是基于电磁波的传播原理。

电磁波的能量密度和能量传递决定了通信信号的传输质量。

2. 医学影像学：医学影像学中的X射线、CT扫描、核磁共振等技术都是基于电磁波的能量传递原理。

电磁波的能量密度和能量传递决定了医学影像的清晰度和准确性。

3. 太阳能利用：太阳能是一种清洁、可再生的能源，其利用过程依赖于电磁波的能量密度和能量传递。

波的能量密度

波的能量密度一、引言波是自然界中广泛存在的物理现象，其能量密度是描述波能量分布的重要参数。

本文将介绍波的能量密度的概念、计算方法以及应用领域。

二、波的能量密度的概念1.定义波的能量密度是指单位体积内所包含的波动能量。

在电磁学中，电磁场中每个点上单位时间内通过单位面积传递的电磁能量称为辐射通量密度，而辐射通量密度除以光速就可以得到电磁场中每个点上单位体积内所包含的电磁辐射能量，即电磁场中的辐射能密度。

2.单位波的能量密度通常用J/m³或者W/m³来表示。

三、计算方法1.机械波对于机械波，其能量密度可以表示为：u = 1/2ρv²其中，u为机械波在介质中传播时所具有的单位体积内储存的总功率；ρ为介质的质量密度；v为机械波在介质中传播时所具有的速率。

2.电磁波对于电磁波，其能量密度可以表示为：u = εE²/2 + 1/2μB²其中，u为电磁波在介质中传播时所具有的单位体积内储存的总功率；ε为介质的介电常数；E为电场强度；μ为介质的磁导率；B为磁感应强度。

四、应用领域1.辐射治疗医学上常用的X射线、γ射线等电离辐射对人体组织产生伤害，而这些伤害与辐射通量密度和能量密度有关。

因此，在医学上，需要精确测量出辐射通量密度和能量密度，以便控制辐射剂量。

2.光学领域在光学领域中，波的能量密度是描述光强的重要参数。

例如，在太阳能电池中，需要精确测量出太阳光的能量密度以确定其转换效率。

3.声学领域在声学领域中，波的能量密度是描述声音强度的重要参数。

例如，在音频设备中，需要精确测量出声音波的能量密度以确定其音质和音响效果。

五、结论波的能量密度是描述波能量分布的重要参数，其计算方法不同于不同类型的波。

在医学、光学和声学领域中，波的能量密度被广泛应用于测量和控制波的强度和剂量。

波的能流密度

近来在超声延时方面有新的发展，因为它的波速比电磁波速低。 近来在超声延时方面有新的发展，因为它的波速比电磁波速低。
10
超声波、 • 超声波、次声波
* 次声波
特点一 频率在10 频率在 －4～20赫芝之间 赫芝之间 的机械波，人耳听不到。 的机械波，人耳听不到。 特点二 由于它具有衰减极小的特点， 由于它具有衰减极小的特点， 衰减极小的特点 具有远距离传播的突出特点。 具有远距离传播的突出特点。 已形成现代声学的一个新的 分支—次声学 次声学。 分支 次声学。 因为大气湍流、火山爆发、地震、 因为大气湍流、火山爆发、地震、 陨石落地、雷暴、 陨石落地、雷暴、磁暴等大规模自 用途 然活动中，都有次声波产生，因此， 然活动中，都有次声波产生，因此， 它是研究地球、海洋、 它是研究地球、海洋、大气等大规 模运动的有力的工具。 模运动的有力的工具。
y
∆y
A B
o o
A
∆x
B
2
质元形变： 质元形变：
2
∂y 1 ∂y [(∆x) + (∆y) ] − ∆x = ∆x1+ − ∆x ≈ 2 ∂x ∂x 质元的形变势能： 质元的形变势能： 2 1 ∂y = 1 FdxA 2 k 2 sin 2 (ω t − kx ) dE p ≈ F × 2 ∂x 2 ∂x
1 ε = T
∫
T
0
εdt =
ρA2ω 2
T
∫
T
0
1 sin (ω t − kx)dt = ρA 2ω 2 2
2
4
二、波的能流密度 波的强度 单位时间内通过截面 单位时间内通过截面 S 的能量等于体积 uS中的 中的 能量，称为能流 能流。 能量，称为能流。 E = ε uS 单位时间内通过垂直于波的传播方向的 通过垂直于波的传播方向的单位面 单位时间内通过垂直于波的传播方向的单位面 上的能量叫做能流密度 能流密度。 积上的能量叫做能流密度。 r dE 写成矢量式： J= = ε u 写成矢量式： J = ε u dS 一个周期内能流密度大小的平均值称为波的强度 波的强度。 一个周期内能流密度大小的平均值称为波的强度。

电磁波衰减

[吸收系数]absorption coefficient 又称“衰减系数”当电磁波进入岩石中时，由于涡流的热能损耗，将使电磁波的强度随进入距离的增加而衰减，这种现象又称为岩石对电磁波的吸收作用。

吸收或衰减系数β的大小和电磁波角频率ω、岩石导电率σ、岩石导磁率μ、岩石介电系数ε有关，1)1(2222-+=δωσμεωβ。

在导体中则简化为：2ωμσβ=。

第十六章机械波和电磁波振动状态的传播就是波动,简称波.激发波动的振动系统称为波源16-1机械波的产生和传播1. 机械波产生的条件(1)要有作机械振动的物体,亦即波源.(2)要有能够传播这种振动的介质波源处质点的振动通过弹性介质中的弹性力，将振动传播开去，从而形成机械波。

波动（或行波)是振动状态的传播，是能量的传播，而不是质点的传播。

◆ 质点的振动方向和波的传播方向相互垂直,这种波称为横波.◆ 质点的振动方向和波的传播方向相互平行,这种波称为纵波.2.波阵面和波射线● 在波动过程中,振动相位相同的点连成的面称为波阵面（wave surface）● 波面中最前面的那个波面称为波前（wave front）● 波的传播方向称为波线（wave line）或波射线波面波线平面波球面波3. 波的传播速度由媒质的性质决定与波源情况无关● 液体和气体中纵波传播速度B－介质体变弹性模量ρ－介质密度●在固体中G－介质切变模量Y－介质杨氏模量4.波长和频率● 一个完整波的长度,称为波长.● 波传过一个波长的时间,叫作波的周期● 周期的倒数称为频率.振动曲线波形曲线图形研究对象某质点位移随时间变化规律某时刻，波线上各质点位移随位置变化规律物理意义由振动曲线可知周期T. 振幅A 初相φ0某时刻方向参看下一时刻由波形曲线可知该时刻各质点位移,波长λ，振幅 A只有 t=0 时刻波形才能提供初相某质点方向参看前一质点特征对确定质点曲线形状一定曲线形状随 t 向前平移16-2 平面简谐波波动方程● 前进中的波动,称为行波.● 描述介质中各质点的位移随时间变化的数学函数式称为行波的波动表式(或波动方程)设坐标原点的振动为：O 点运动传到 p 点需用时相位落后所以 p点的运动方程：1.平面简谐波的波动表式定义 k 为角波数又因此下述表达式等价：为波的相位● 波在某点的相位反映该点媒质的“运动状态”，所以简谐波的传播也是媒质振动相位的传播。

波的能量概述

次声波：
频率低于20Hz的机械波（如地震、火山爆发、陨石落地、
雷暴等发出…）
(1)声强：
指声波的波强，即声波的平均能流密度
I 1 2 A2 u
2
(2) 声强级：
以人耳刚能听到的声强
I 0 1012 w m2为标准，
则声强级
IL lg I ( 贝 尔 ) 10 lg I ( 分 贝 dB)
I0
y
在横波中，产生切变
y
o
x
x
y
x
x
h
lim tg
x h
x0
y x
y x
u
A s in
t
x u
0
u
G
E p
dV
1 2
G
y x
2
1 2
dV2 A2
s in 2
(t
x) u
0
2
３、dV内的总波动能量
dE dEk dEp
以上讨论说明：
(dV
) A2 2
s in 2 [ (t
(3)声功率: 单位时间里通过某一面积的声波的能量,亦即声波的能流。
(4)响度:
人耳对声音强弱的主观感觉.其既与声强有关也与频率有关。
(5)声压:
在声波传播的空间里，某一点在某一瞬时的压强P与没有 声波时的静压强P0之差dP=P- P0，叫做该点该瞬时的声压。
10
因空气波为疏密波，故声压可正、可负，其单位为“帕斯 卡”。
（Ｄ）
12
例 5－6 一平面简谐波，频率为300Ｈｚ，波速为340ｍ／ｓ， 在截面积为 3.00×10－2 ｍ2 的管内空气中传播，若在10ｓ内通 过截面的能量为 2.70×106Ｊ，求 （1）通过截面的平均能流； （2）波的平均能流密度； （3）波的平均能量密度。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

I 四、声强及声强级 LI 10 lg dB I0
16.4 波的能量
波的能量密度
概念检测
在同一介质中两列频率相同的平面简谐波的强 度之比I1 / I2 = 4，则两列波的振幅之比A1 / A2是
A.1/4 B. 1/2 C. 2 D.4
16.4 波的能量
波的能量密度
例：一球面波源的功率为 100W，则距波源 10m 处， 波的能流密度 I 是多少？
16.4 波的能量
波的能量密度
1 2 弹性势能 dEp k (dy ) 2 dy F E S dx 弹性回复力F dy F ES ES dx k dx
F = kdy
dy 2 1 1 ES 2 2 1 dEp k (dy ) (dy ) EdV ( ) 2 dx 2 dx 2
16.3.2 波的能量密度
x dE A (dV ) sin (t ) u
2 2 2
能量密度：单位体积媒质中的能量
dE x 2 2 2 w A sin (t ) dV u
平均能量密度： 能量密度在一个周期T 内的平均值
1 T 2 2 2 x w A sin (t )dt T 0 u 1 2 2 w A 媒质中并不积累能量 2
16.4 波的能量
波的能量密度
16.3 波的能量和能量密度
16.3.1 波的能量 16.3.2 波的能量密度 16.3.3 能流和能流密度 16.3.4 声强及声强级
16.4 波的能量
波的能量密度
16.3.1 波的能量
振动动能 弹性势能
x 棒中波动的表达式 y A cos (t ) u a b
I LI lg I0
贝尔（B）
I LI 10 lg I0
分贝（ dB ）
16.4 波的能量
波的能量密度
ቤተ መጻሕፍቲ ባይዱ
几种声音近似的声强、声强级和响度
声源 引起痛觉的声音 炮声 交通繁忙的街道 声强 W/m2 1 10-1 10-5 声强级dB 120 110 70 震耳 响 响度
通常的谈话
耳语 树叶的沙沙声 引起听觉的最弱声音
体积元总能量不守恒，随时间作周期性变化。 对于给定的时刻，所有体积元的总能量又随x 作周期性变化。
16.4 波的能量
波的能量密度
概念检测
波的能量随平面简谐波传播，下列几种说法中正确 的是
A.因简谐波传播到的各介质体积元均作简谐振动， 故其能量守恒 B.各介质体积元在平衡位置处的动能，势能最大， 总能量最大 C.各介质体积元在平衡位置处的动能最大，势能最小 D.各介质体积元在最大位移处的势能最大，动能为0 B
解：
P P I 2 S 4r
1 100 2 4 4 10
（W •m2 ）
16.4 波的能量
波的能量密度
例：有一波在介质中传播，其波速u=103 m/s，振幅 A=1.0104m，波频 =103Hz，若介质的密度为 800 kg/m3，求： ①.该波的平均能流密度； ②.1分钟内垂直通过一面积 S = 410 4 m2的总能量。 解：
0.027 P 2.7 103W 10
P 2.7 10 3 2 I 0.09W / m S 0.03 I 0.09 4 2.6 10 W u 340
2I A u 7 1 2 120 10 5 1 . 27 10 m 5 3 3 2π 5 10 1 10 1.5 10
1
16.4 波的能量
波的能量密度
用声音成像——B超检查
16.4 波的能量
波的能量密度
16.3.4 声强及声强级
在弹性介质中传播的机械纵波，一般统称为声波 可闻声波 : 次声波: 20 ~ 20000 Hz < 20 Hz
波的能量密度
球面波的振幅 1 1 2 2 u A1 S1 u 2 A22 S 2 2 2
r2
r1
S1
2 4πr1
S2
2 4πr2
A1r1 A2 r2
设r1=1m， A1 =A，在距点波源r 处的振幅为 A / r r 处的 相位比点波源落后 r / u
A r 球面简谐波的波函数： y cos (t ) r u
E ISt
1.58 10 4.0 10 60
5
4
3792 J
16.4 波的能量
波的能量密度
例：一平面简谐波，频率为300Hz，波速为340m/s， 在截面面积为0.03m2的管内空气中传播，若在10s内 通过截面的能量为0.027J，求： （2）波的平均能流密度； （1）通过截面的平均能流； （3）波的平均能量密度。
16.4 波的能量
波的能量密度
例题 用聚焦超声波的方法，可以在液体中产生 平均能流密度为120kw/cm2的大功率超声波。设 波源作简谐振动，频率为500kHz，液体的密度为 1g/cm3，声速为1500m/s。求液体质点振动的振幅。
解 由平均能流密度
液体质点振动的振幅
1 2 2 I A u 2
16.4 波的能量
波的能量密度
概念检测
一平面简谐波在弹性介质中传播，在介质质元 从平衡位置运动到最大位移处的过程中
A.它的动能转换成势能 B.它的势能转换成动能 C.它把自已的能量传给相邻的一段质元， 其能量逐渐增大 D.它把自已的能量传给相邻的一段质元， 其能量逐渐减小 D
16.4 波的能量
波的能量密度
o x x+dx y o a x
y+dy
b x
dx+dy
16.4 波的能量

波的能量密度
振动动能 体积元ab振动速度
体积元的振动动能
y x v A sin (t ) t u
1 2 dEk (dm) v 2 dm=dV=Sdx
1 x 2 2 2 dEk ( dV ) A sin (t ) 2 u
1 y 2 EdV ( ) 2 x
16.4 波的能量
波的能量密度
y A x sin t x u u
u
E

1 x 2 2 2 dEp ( dV ) A sin (t ) 2 u

体积元的总机械能
dE dEk dEp
x dE A (dV ) sin (t ) u
10-6
10-10 10-11 10-12
60
20 10 0
正常
轻 极轻
16.4 波的能量
波的能量密度
小
一、波的能量
结
1 x 2 2 2 dEk dEp ( dV ) A sin (t ) 2 u x 2 2 2 二、波的能量密度 w A sin (t ) u 1 三、能流和能流密度 P uSw uSA2 2 2 1 2 2 I w u A u 2
16.4 波的能量
波的能量密度
平均能流密度矢量：
通过与波的传播方向垂直的单位面积的 平均能流称为平均能流密度，用 I 表示。 I 的大小为
P 1 2 2 I w u A u 2 S
I 的方向就是波速 u 的方向
1 2 2 I w u A u 2
——又称为波的强度
2 2 2
16.4 波的能量
波的能量密度
1 x 2 2 2 dEk dEp ( dV ) A sin (t ) y 2 u x 2 2 2 dE A (dV ) sin (t ) t
u
动能和势能同相位地随时间变化，它们在任 一时刻都有完全相同的值。 体积元在平衡位置( y = 0 )时，动能、势能 和总机械能均最大 体积元的位移最大(y = A)时，三者均为零
超声波:
> 20000 Hz
声强：声波的平均能流密度
1 2 2 I A u 2
能够引起人们听觉的声强范围：
1012 W/m2 1 W/m2
16.4 波的能量
波的能量密度
声强级：
规定声强I0=1012 wm2（频率为1000Hz）为测定 声强的标准，使用对数标度。 某声强为I的声强级为LI
16.4 波的能量
波的能量密度
16.3.3 能流和能流密度
能流：单位时间内通过媒质中某一面积的能量
u S P
u
在单位时间内通过垂直于波速截面 S 的能量:
通过S 面积的平均能流
x P u S w uSA sin (t ) u
2 2 2
1 2 2 uS A P uSw 2
1 I A 2 2u 2
2
2 2 2
I 2 A u
2 800 10 (1.0 10 10 )
2 3 4 3 2
1.58 10 w m
5
-2
16.4 波的能量
波的能量密度
②.1 分钟内垂直通过一面积 S = 4104 m2的总能量。
单位：W/m2
16.4 波的能量
波的能量密度
平面波的振幅
在均匀不吸收能量的媒质中传播的平面波 在行进方向上振幅不变。 因为
I1S1 I 2 S2
S1 S2 S
S1
u
S2
1 1 2 2 2 2 u A1 S1 u A2 S 2 2 2
平面波振幅相等：
A1 A2
16.4 波的能量