C常用矩阵子函数
- 格式:docx
- 大小:14.57 KB
- 文档页数:4


矩阵连乘问题描述:给定n 个矩阵12n {A ,A ,,A } ,其中i A 与1i A +是可乘的,1,2,,1i n =-。
考察这n 个矩阵的连乘积12n A A A 。
由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。
这种计算次序可以用加括号的方式来确定。
若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少?代码:#include<stdio.h>const int MAX=100;//静态变量,控制矩阵大小int n;//定义相乘矩阵 的个数int p[MAX+1],m[MAX][MAX],s[MAX][MAX];void matrixChain(){for(int i=1;i<=n;i++) //填主对角线d1{m[i][i]=0;}for(int r=2;r<=n;r++)//填次对角线dr(r=2~n){for(int i=1;i<=n-r+1;i++)//填次对角线的各个元素{int j=i+r-1;//计算次对角线dr 上第i 行的元素的列标 m[i][j]=m[i+1][j]+ p[i-1]*p[i]*p[j];//用计算Ai(Ai+1…Aj)的次数作为m[i][j]的初始值s[i][j]=i;//保存分界点for(int k=i+1;k<j;k++){//用m[i][k]和m[k+1][j]计算m[i][j]的新值 int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];if(t<m[i][j]){m[i][j]=t;s[i][j]=k;}}}}}void tb(int i,int j,int s[MAX][MAX]){//根据s[][]记录的各个子段的最优解,将其输出if(i==j) return;tb(i,s[i][j],s);tb(s[i][j]+1,j,s);printf("Multiply A%d,%dand A%d,%d\n",i,s[i][j],s[i][j]+1,j); }int main(){printf("Please input the number of n...\n");scanf("%d",&n);for(int i=0;i<=n;i++)scanf("%d",&p[i]);matrixChain();//调用函数tb(1,n,s);printf("%d\n",m[1][n]);//输出最优解printf("\n\n\n");for(int i=1;i<=n;i++)//输出矩阵的m[][]的值{for(int j=1;j<=n;j++){printf("%d\t",m[i][j]);}printf("\n");}printf("\n\n\n");for(int i=1;i<=n;i++)//输出矩阵的s[][]的值{for(int j=1;j<=n;j++){printf("%d\t",s[i][j]);}printf("\n");}return 0;}输出结果:。

c语⾔⼆次函数拟合,⼆次函数拟合算法
⼆次函数拟合算法
原理:
在给定⼀组数据序列(x i,y i),i=0,1,2…m,⽤⼆次多项式拟合这组数据时,设
p(x)=a0+a1x+a2x2,则根据拟合函数与数据序列的均⽅误差最⼩原则,可以得到⼆次多项式函数拟合的矩阵计算⽅程如下所⽰:(
m x i
m
i=1
x i2
m
i=1
x i
m
i=1
x i2
m
i=1
x i3
m
i=1
x i2
m
i=1
x i3
m
i=1
x i4
m
i=1
)(
a0
a1
a2
)= (
y i
m
i=1
x i y i
m
i=1
x i2y i
m
i=1
)
在我们的计算库伦效应实例中,Y即为每个Cycle对应的DischargeC/ChargeC的⽐值,X即
为每个Cycle对应的数字。
代码中定义的三个矩阵XX,AA,YY则分别对应原理公式中等式左边X系数矩阵,A系数矩阵
以及等式右边包含Y系数的矩阵。
具体步骤:
1:先将矩阵中需要的所有量计算出来,并且存放在XX,AA,YY三个矩阵中。
2:为了求得系数矩阵AA,我们需要先把XX矩阵求逆,然后与YY矩阵相乘。
函数MRinv
即为矩阵求逆的函数,返回时存放其逆矩阵。
3:得到系数矩阵AA之后,即得到了拟合好的⼆次函数,将此⼆次函数输出在Excel表中。
具体代码实现:步骤1对应代码:。

C语言常用算法归纳应当掌握的一般算法一、基本算法:交换、累加、累乘二、非数值计算常用经典算法:穷举、排序(冒泡,选择)、查找(顺序即线性)三、数值计算常用经典算法:级数计算(直接、简接即递推)、一元非线性方程求根(牛顿迭代法、二分法)、定积分计算(矩形法、梯形法)四、其他:迭代、进制转换、矩阵转置、字符处理(统计、数字串、字母大小写转换、加密等)、整数各数位上数字的获取、辗转相除法求最大公约数(最小公倍数)、求最值、判断素数(各种变形)、数组元素的插入(删除)、二维数组的其他典型问题(方阵的特点、杨辉三角形)详细讲解一、基本算法1.交换(两量交换借助第三者)例1、任意读入两个整数,将二者的值交换后输出。
main(){ int a,b,t;scanf("%d%d",&a,&b);printf("%d,%d\n",a,b);t=a; a=b; b=t;printf("%d,%d\n",a,b);}【解析】程序中加粗部分为算法的核心,如同交换两个杯子里的饮料,必须借助第三个空杯子。
假设输入的值分别为3、7,则第一行输出为3,7;第二行输出为7,3。
其中t为中间变量,起到“空杯子”的作用。
注意:三句赋值语句赋值号左右的各量之间的关系!【应用】例2、任意读入三个整数,然后按从小到大的顺序输出。
main(){ int a,b,c,t;scanf("%d%d%d",&a,&b,&c);/*以下两个if语句使得a中存放的数最小*/if(a>b){ t=a; a=b; b=t; }if(a>c){ t=a; a=c; c=t; }/*以下if语句使得b中存放的数次小*/if(b>c) { t=b; b=c; c=t; }printf("%d,%d,%d\n",a,b,c);}2.累加累加算法的要领是形如“s=s+A”的累加式,此式必须出现在循环中才能被反复执行,从而实现累加功能。

当涉及到指针和矩阵操作时,我们可以编写一个函数来求解一个 n 阶矩阵中的最大元素和最小元素的值。
下面是用 C 语言编写的一个示例函数:```c#include <stdio.h>// 定义矩阵的维度#define N 3// 求解矩阵中的最大元素值int findMaxElement(int *matrix, int size) {int max = *matrix;for (int i = 1; i < size; i++) {if (*(matrix + i) > max) {max = *(matrix + i);}}return max;}// 求解矩阵中的最小元素值int findMinElement(int *matrix, int size) {int min = *matrix;for (int i = 1; i < size; i++) {if (*(matrix + i) < min) {min = *(matrix + i);}}return min;}int main() {int matrix[N][N] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};int *ptr = &matrix[0][0]; // 获取矩阵的指针int max = findMaxElement(ptr, N * N);int min = findMinElement(ptr, N * N);printf("最大元素值为: %d\n", max);printf("最小元素值为: %d\n", min);return 0;}```在这个示例中,我们首先定义了一个 3x3 的矩阵 `matrix`,然后获取了矩阵的指针 `ptr`,并将其传递给 `findMaxElement` 和 `findMinElement` 函数来找到最大元素和最小元素的值。


#include "stdafx.h"#include <stdlib.h>//结构体typedef struct{double ** mat;int row;int col;}Matrix;void InitialMatrix(Matrix *T, int row,int col); //只分配空间不初始化;void InitialMatrixZero(Matrix *T,int row, int col); //初始化为0void InitialMatrixRand(Matrix *T,int row, int col); //初始化为50以内随机正整数void InputMatrix(Matrix *T); //键盘输入矩阵void DestroyMatrix(Matrix *T); // 释放矩阵空间void PrintfMatrix(Matrix *T); //矩阵输出int AddMatrix(Matrix *A,Matrix *B,Matrix *C); // 矩阵加int MinusMatrix(Matrix *A,Matrix *B,Matrix *C); // 矩阵减int MultiMatrix(Matrix *A,Matrix *B,Matrix *C); //矩阵乘法double MeanMatrix(Matrix *T); //矩阵元素均值int SubMatrix(Matrix *T1,Matrix *T2,int BeginRow,int BeginCol,int EndRow,int EndCol); //求T1的子矩阵T2;测试程序参考界面如下所示:矩阵函数测试,请选择功能,输入对应的数字:***************************************************1:输入一个矩阵,求矩阵均值;2:产生一个随机数矩阵,求矩阵均值;3:输入两个个矩阵,求矩阵和;4:输入两个个矩阵,求矩阵差;5:输入两个个矩阵,求矩阵积;6:产生两个个随机数矩阵,求矩阵和;7:产生两个个随机数矩阵,求矩阵差;8:产生两个个随机数矩阵,求矩阵积;9:求矩阵的子阵,如矩阵的2-4行,1-3列的子阵;0:结束!#include <stdio.h>#include <stdlib.h>//结构体typedef struct {double **mat;int row;int col;} Matrix;//函数声明void InitialMatrix(Matrix *T, int row, int col);void InitialMatrixZero(Matrix *T, int row, int col);void InitialMatrixRand(Matrix *T, int row, int col);void InputMatrix(Matrix *T);void DestroyMatrix(Matrix *T); // 释放矩阵空间void PrintfMatrix(Matrix *T); //矩阵输出int AddMatrix(Matrix *A, Matrix *B, Matrix *C); // 矩阵加int MinusMatrix(Matrix *A, Matrix *B, Matrix *C); // 矩阵减int MultiMatrix(Matrix *A, Matrix *B, Matrix *C); //矩阵乘法double MeanMatrix(Matrix *T); //矩阵元素均值//int SubMatrix(Matrix *T1, Matrix *T2, int BeginRow, int BeginCol, int EndRow, int EndCol); //求T1的子矩阵T2;void NMatrix(void);//求逆矩阵//主函数int main(){int inputevent;//int i, j;int row, col;Matrix T;Matrix A;Matrix B;Matrix C;printf(" 矩阵函数测试,请选择功能,输入对应的数字:\n");printf(" ***************************************************\n\n"); printf("1:输入一个矩阵,求矩阵均值;\n");printf("2:产生一个随机数矩阵,求矩阵均值;\n");printf("3:输入两个个矩阵,求矩阵和;\n");printf("4:输入两个个矩阵,求矩阵差;\n");printf("5:输入两个矩阵,求矩阵积;");printf("\n6:产生两个随机数矩阵,求矩阵和;\n");printf("7:产生两个随机数矩阵,求矩阵差;\n");printf("8:产生两个随机数矩阵,求矩阵积;\n");printf("9:求矩阵的子阵,如矩阵的2-4行D,1-3列的子阵;\n");printf("10:输入一个方阵,求其逆矩阵\n");printf("0:结束!\n");printf("\n\n选择:");scanf("%d", &inputevent);while (inputevent != 0){if (inputevent == 1) {printf("您要输入的矩阵的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&T, row, col);InitialMatrixZero(&T, T.row, T.col);InputMatrix(&T);printf("\n矩阵的平均值为:\n%lf\n\n", MeanMatrix(&T));DestroyMatrix(&T);}if (inputevent == 2) {printf("输入您要产生的矩阵的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&T, row, col);InitialMatrixRand(&T, row, col);MeanMatrix(&T);PrintfMatrix(&T);printf("\n矩阵的平均值为:\n%lf\n\n", MeanMatrix(&T));DestroyMatrix(&T);}if (inputevent == 3) {printf("您要输入的矩阵A的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixZero(&A, A.row, A.col);InputMatrix(&A);printf("您要输入的矩阵B的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixZero(&B, B.row, B.col);InputMatrix(&B);InitialMatrix(&C, B.row, B.col);InitialMatrixZero(&C, C.row, C.col);if (AddMatrix(&A, &B, &C) == 1) {printf("\n\n矩阵的和为:A*B\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 4) {printf("您要输入的矩阵A的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixZero(&A, A.row, A.col);InputMatrix(&A);printf("您要输入的矩阵B的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixZero(&B, B.row, B.col);InputMatrix(&B);InitialMatrix(&C, B.row, B.col);InitialMatrixZero(&C, C.row, C.col);if (MinusMatrix(&A, &B, &C) == 1) {printf("\n矩阵的差为:A-B=\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 5) {int able;printf("您要输入的矩阵A的行数和列数e.g: 5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixZero(&A, A.row, A.col);InputMatrix(&A);printf("您要输入的矩阵B的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixZero(&B, B.row, B.col);InputMatrix(&B);InitialMatrix(&C, A.row, B.col);InitialMatrixZero(&C, C.row, C.col);able = MultiMatrix(&A, &B, &C);if (able == 1) {printf("\n积为:A*B\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 6) {printf("您要产生的矩阵A的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixRand(&A, row, col);printf("A为:\n\n");PrintfMatrix(&A);printf("您要产生的矩阵B的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixRand(&B, row, col);printf("B为:\n\n");PrintfMatrix(&B);InitialMatrix(&C, A.row, A.col);InitialMatrixZero(&C, C.row, C.col);if (AddMatrix(&A, &B, &C) == 1) {printf("\n矩阵的和为:A+B=\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 7) {printf("您要产生的矩阵A的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixRand(&A, row, col);printf("您要产生的矩阵B的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixRand(&B, row, col);InitialMatrix(&C, A.row, A.col);InitialMatrixZero(&C, C.row, C.col);if (MinusMatrix(&A, &B, &C) == 1) {printf("\n矩阵的差为:A-B=\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 8) {printf("您要产生的矩阵A的行数和列数e.g:5,6: \n");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixRand(&A, row, col);printf("A为:\n\n");PrintfMatrix(&A);printf("您要产生的矩阵B的行数和列数e.g:5,6: \n");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixRand(&B, row, col);printf("B为:\n\n");PrintfMatrix(&B);InitialMatrix(&C, A.row, A.col);InitialMatrixZero(&C, C.row, C.col);if (MultiMatrix(&A, &B, &C) == 1) {printf("\n积为:A*B=\n\n");PrintfMatrix(&C);;}else printf("\n\n无法计算;\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 9) printf("对不起,该函数尚在完善中\n\n");if (inputevent == 10) NMatrix();if (inputevent == 0)break;printf(" 矩阵函数测试,请选择功能,输入对应的数字:\n");printf(" ***************************************************\n\n"); printf("1:输入一个矩阵,求矩阵均值;\n");printf("2:产生一个随机数矩阵,求矩阵均值;\n");printf("3:输入两个个矩阵,求矩阵和;\n");printf("4:输入两个个矩阵,求矩阵差;\n");printf("5:输入两个矩阵,求矩阵积;");printf("\n6:产生两个随机数矩阵,求矩阵和;\n");printf("7:产生两个随机数矩阵,求矩阵差;\n");printf("8:产生两个随机数矩阵,求矩阵积;\n");printf("9:求矩阵的子阵,如矩阵的2-4行D,1-3列的子阵;\n");printf("10:输入一个方阵,求其逆矩阵\n");printf("0:结束!\n");printf("\n\n选择:");scanf("%d", &inputevent);}return 0;}//其他函数void InitialMatrix(Matrix *T, int row, int col){//printf("分配内存中......\n");int i;int succ = 1;//T=(Matrix *)malloc(sizeof(Matrix));T->row = row;T->col = col;T->mat = (double **)malloc(T->row * sizeof(double *));if (T->mat == NULL) {succ = 0;}else {for (i = 0; i < T->row; i++) {T->mat[i] = (double *)malloc(T->col * sizeof(double));if (T->mat[i] == NULL) {succ = 0;break;}}//if(succ==1)// printf("内存分配成功|;?\n");//else printf("内存分配失败;\n");}}void InitialMatrixZero(Matrix *T, int row, int col) { //printf("矩阵初始化为零中......\n");int i, j;for (i = 0; i < row; i++)for (j = 0; j < col; j++)T->mat[i][j] = 0;//printf("矩阵初始化为零矩阵成功;\n"); }void InitialMatrixRand(Matrix *T, int row, int col) { int i, j;for (i = 0; i < row; i++)for (j = 0; j < col; j++)(*T).mat[i][j] = rand() % 50;}void InputMatrix(Matrix *T) {printf("输入矩阵:\n");int i, j;for (i = 0; i < (*T).row; i++)for (j = 0; j < (*T).col; j++)scanf("%lf", &(*T).mat[i][j]);}void DestroyMatrix(Matrix *T){int i;for (i = 0; i < (*T).row; i++)free((*T).mat[i]);}void PrintfMatrix(Matrix *T){int i, j;for (i = 0; i < (*T).row; i++){for (j = 0; j < (*T).col; j++)printf("%lf ", (*T).mat[i][j]);printf("\n");}}int AddMatrix(Matrix *A, Matrix *B, Matrix *C){int i, j;if ((*A).row == (*B).row && (*A).col == (*B).col){for (i = 0; i < (*A).row; i++)for (j = 0; j < (*A).col; j++)(*C).mat[i][j] = (*A).mat[i][j] + (*B).mat[i][j];for (i = 0; i < (*A).row; i++)for (j = 0; j < (*A).col; j++)return 1;}else {printf("这两个矩阵不能相加!\n");return 0;}}int MinusMatrix(Matrix *A, Matrix *B, Matrix *C){int i, j;if ((*A).row == (*B).row && (*A).col == (*B).col){for (i = 0; i < (*A).row; i++)for (j = 0; j < (*A).col; j++)(*C).mat[i][j] = (*A).mat[i][j] - (*B).mat[i][j];return 1;}elseprintf("这两个矩阵不能相减!\n");return 0;}int MultiMatrix(Matrix *A, Matrix *B, Matrix *C){int i=0, j=0;int k = 0;if ((*A).col == (*B).row){for (i = 0; i < (*A).row; i++) {for (j = 0; j < (*B).col; j++)for(k=0;k <(A->col);k++)(*C).mat[i][j] += (*A).mat[i][k] * (*B).mat[k][j];}return 1;}elseprintf("这两个矩阵不能相乘!\n");return 0;}double MeanMatrix(Matrix *T) //矩阵元素均值{double mean;double sum = 0;int i, j;for (i = 0; i < (*T).row; i++)for (j = 0; j < (*T).col; j++)sum += (*T).mat[i][j];mean = sum / ((*T).row*(*T).col);return mean;}void NMatrix(void){#define M 20#define N 20int i,j,m,n;float y=1.0;float a[M][2 * M];float b[N][2 * N];float t, x;int k, T;printf("输入方阵的维数:\n"); //请输入方阵,即行和列相等的矩阵。
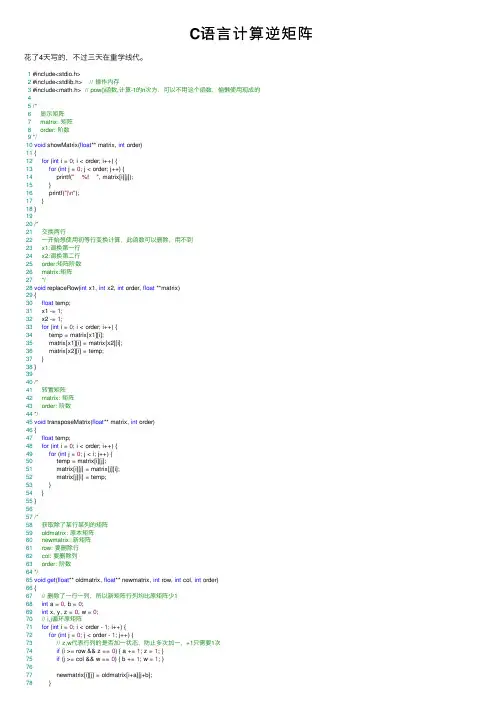
C语⾔计算逆矩阵花了4天写的,不过三天在重学线代。
1 #include<stdio.h>2 #include<stdlib.h> // 操作内存3 #include<math.h> // pow()函数,计算-1的n次⽅,可以不⽤这个函数,偷懒使⽤现成的45/*6显⽰矩阵7 matrix: 矩阵8 order: 阶数9*/10void showMatrix(float** matrix, int order)11 {12for (int i = 0; i < order; i++) {13for (int j = 0; j < order; j++) {14 printf(" %f ", matrix[i][j]);15 }16 printf("|\n");17 }18 }1920/*21交换两⾏22⼀开始想使⽤初等⾏变换计算,此函数可以删除,⽤不到23 x1:调换第⼀⾏24 x2:调换第⼆⾏25 order:矩阵阶数26 matrix:矩阵27*/28void replaceRow(int x1, int x2, int order, float **matrix)29 {30float temp;31 x1 -= 1;32 x2 -= 1;33for (int i = 0; i < order; i++) {34 temp = matrix[x1][i];35 matrix[x1][i] = matrix[x2][i];36 matrix[x2][i] = temp;37 }38 }3940/*41转置矩阵42 matrix: 矩阵43 order: 阶数44*/45void transposeMatrix(float** matrix, int order)46 {47float temp;48for (int i = 0; i < order; i++) {49for (int j = 0; j < i; j++) {50 temp = matrix[i][j];51 matrix[i][j] = matrix[j][i];52 matrix[j][i] = temp;53 }54 }55 }5657/*58获取除了某⾏某列的矩阵59 oldmatrix: 原本矩阵60 newmatrix: 新矩阵61 row: 要删除⾏62 col: 要删除列63 order: 阶数64*/65void get(float** oldmatrix, float** newmatrix, int row, int col, int order)66 {67// 删除了⼀⾏⼀列,所以新矩阵⾏列均⽐原矩阵少168int a = 0, b = 0;69int x, y, z = 0, w = 0;70// i,j循环原矩阵71for (int i = 0; i < order - 1; i++) {72for (int j = 0; j < order - 1; j++) {73// z,w代表⾏列的是否加⼀状态,防⽌多次加⼀,+1只需要1次74if (i >= row && z == 0) { a += 1; z = 1; }75if (j >= col && w == 0) { b += 1; w = 1; }7677 newmatrix[i][j] = oldmatrix[i+a][j+b];78 }79 a = 0;b = 0;80 z = 0;w = 0;81 }82 }8384/*85计算⾏列式86 matrix: 矩阵87 order: 阶数88*/89float calc(float** matrix, int order)90 {91// 递归求⾏列式值92float num=0;93int i, j;94if (order == 2) {95// 如果是⼆阶直接获取值96 num = matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0];97 }98else {99// 创建更⼩⼆维数组100 order -= 1;101float** matrixlow = (float**)malloc(sizeof(float*) * order);102for (i = 0; i < order; i++) {103 matrixlow[i] = (float*)malloc(sizeof(float) * order);104 }105 order += 1;106107// 循环展开第⼀⾏108for (j = 0; j < order; j++) {109110get(matrix, matrixlow, 0, j, order);111// 此处开始递归,调⽤⾃⾝函数112 num += matrix[0][j] * pow(-1, j) * calc(matrixlow, order - 1); 113 }114115// 释放内存116for (i = 0; i < order-1; ++i)free(*(matrixlow + i));117 }118119return num;120 }121122123/*124主函数125*/126int main()127 {128int order; // 矩阵阶数129int i, j;130float det;131132// 获取矩阵阶133 printf("输⼊矩阵阶:");134 scanf("%d", &order);135136 printf("输⼊的阶是:%d\n\n", order);137138// 申请⼆维数组内存139float** matrix = (float**)malloc(sizeof(float*) * order);140for (i = 0; i < order; i++) {141 matrix[i] = (float*)malloc(sizeof(float) * order);142 }143144// 获取输⼊145for (i = 0; i < order; i++) {146for (j = 0; j < order; j++) {147 printf("位置:( %d , %d)请输⼊数据:",i + 1,j + 1);148 scanf("%f", &matrix[i][j]);149 }150 }151152// 计算并显⽰det153 det = calc(matrix, order);154 printf("\ndet值为:%f",det);155// 0不能做除数156if (det == 0)157 printf("\n矩阵接近奇异值,结果可能不准确!");158 printf("\n\n");159160// 显⽰输⼊矩阵161 printf("\n输⼊的矩阵是:\n\n");162 showMatrix(matrix, order);163164// 申请⼆维数组存储结果165float** Rmatrix = (float**)malloc(sizeof(float*) * order);166for (i = 0; i < order; i++) {167 Rmatrix[i] = (float*)malloc(sizeof(float) * order);168 }169170171// 开始计算172if (order == 2) {173// 阶数为⼆直接运⾏公式174float n = 1 / (matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]);175 Rmatrix[0][0] = n * matrix[1][1];176 Rmatrix[0][1] = -n * matrix[0][1];177 Rmatrix[1][0] = -n * matrix[1][0];178 Rmatrix[1][1] = n * matrix[0][0];179 }180else {181// 转置矩阵并显⽰182 transposeMatrix(matrix, order);183 printf("\n\n转置后为:\n\n");184 showMatrix(matrix, order);185186// 循环求i,j位的代数余⼦式187for (i = 0; i < order; i++) {188for (j = 0; j < order; j++) {189// 申请⼆维数组190 order -= 1;191float** matrixlow = (float**)malloc(sizeof(float*) * order);192for (int t = 0; t < order; t++) {193 matrixlow[t] = (float*)malloc(sizeof(float) * order);194 }195 order += 1;196197// 获取除了i,j⾏的值组成⾏列式198get(matrix, matrixlow, i, j, order);199// 计算⾏列式值除以det200 Rmatrix[i][j] = pow(-1, i + j) * calc(matrixlow, order - 1) / det; 201202// 释放内存203for (int t = 0; t < order-1; ++t)free(*(matrixlow + t));204 }205 }206207 }208209// 显⽰逆矩阵210 printf("\n\n逆矩阵为:\n\n");211 showMatrix(Rmatrix, order);212213214//// 释放⼆维数组215for (i = 0; i < order; ++i)free(*(matrix + i));216for (i = 0; i < order; ++i)free(*(Rmatrix + i));217218return0;219 }。

C语言二维数组作为函数的参数C语言中,数组是一种非常常用的数据类型。
除了一维数组,C语言还支持二维数组,即数组的数组。
在函数中,我们可以使用二维数组作为参数来传递数组的内容。
本文将详细介绍如何在C语言中使用二维数组作为函数的参数,并给出一些实例来帮助理解。
1.二维数组的基本概念在C语言中,二维数组可以看作是一个由行和列组成的矩阵。
每个元素都可以通过两个下标来确定,第一个下标表示行号,第二个下标表示列号。
例如,一个int类型的二维数组arr可以用arr[i][j]来表示第i行第j列的元素。
2.二维数组作为函数参数的声明在函数声明中,为了传递二维数组,我们需要指定数组的列数。
其一般格式如下:```cvoid functionName(type arrayName[][columnSize], int rowSize);```其中,functionName是函数的名称,type是数组元素的类型,arrayName是要传递的二维数组名称,columnSize是数组的列数,rowSize是数组的行数。
3.二维数组作为函数参数的传递当我们把一个二维数组作为参数传递给函数时,实际上是把数组的地址传给了函数。
因此,在函数中可以通过修改数组元素来改变数组的内容。
4.二维数组作为函数参数的实例下面是一个简单的例子,展示了如何使用二维数组作为函数参数。
```c#include <stdio.h>void printMatrix(int matrix[][3], int rowSize)int i, j;for (i = 0; i < rowSize; i++)for (j = 0; j < 3; j++)printf("%d ", matrix[i][j]);}printf("\n");}int maiint matrix[2][3] = {{1, 2, 3}, {4, 5, 6}};printMatrix(matrix, 2);return 0;```在上面的例子中,我们定义了一个名为`printMatrix`的函数,其参数为一个二维数组和一个行数。


C语言常用基本词汇及其他提示语运算符与表达式:1.constant 常量2. variable 变量3. identify 标识符4. keywords 关键字5. sign 符号6. operator 运算符7. statement语句8. syntax 语法9. expression 表达式10. initialition 初始化11. number format 数据格式12 declaration 说明13. type conversion 类型转换14.define 、definition 定义条件语句:1.select 选择2. expression 表达式3. logical expression 逻辑表达式4. Relational expression 关系表达式5.priority优先6. operation运算7.structure 结构循环语句:1.circle 循环2. condition 条件3. variant 变量4. process过程5.priority优先6. operation运算数组:1. array 数组2. reference 引用3. element 元素4. address 地址5. sort 排序6. character 字符7. string 字符串8. application 应用函数:1.call 调用2.return value 返回值3.function 函数4. declare 声明5. `parameter 参数6.static 静态的7.extern 外部的指针:1. pointer 指针2. argument 参数3. array 数组4. declaration 声明5. represent 表示6. manipulate 处理结构体、共用体、链表:1 structure 结构2 member成员3 tag 标记4 function 函数5 enumerate 枚举6 union 联合(共用体)7 create 创建8 insert 插入9 delete 删除10 modify 修改文件:1、file 文件2、open 打开3、close 关闭4、read 读5、write 写6、error 错误序号主要章节常用英汉对照词汇备注1 运算符与表达式(operator and expression )汉语英语常量constant变量variable标识符identify关键字keywords符号sign运算符operator语句statement语法syntax表达式Expression初始化Initialization数据格式number format说明Declaration类型转换type conversion定义Define 、definition2 条件语句(conditionstatement) 选择select表达式expression逻辑表达式logical expression关系表达式Relational expression 优先priority运算operation结构structure3 循环语句(circle statement) 循环circle条件condition变量variant过程process优先priority运算operation4 函数(function) 调用call返回值return value函数function声明declare参数parameter静态的static外部的extern5 数组和指针(array and pointer) 数组array 引用reference元素element地址address排序sort字符character字符串string应用application指针pointer参数argument数组array声明declaration表示represent处理manipulate6 结构体、共用体(structures 、union )结构structure 成员member标记tag函数function枚举enumerate联合( 共用体) union创建create插入insert删除delete修改modify7 文件(file) 文件file打开open关闭close读read写write错误errorProgram Design 程序设计writing program 编写程序standardize vt.使标准化coding the program 编程simplify vt.单一化,简单化programming 程序revision n.校订,修正programmer n.程序员occupy vt.占领,住进logic n.逻辑,逻辑学BASIC 初学者通用符号指令代码machine code 机器代码teaching language 教学语言debug n.DOS命令,调试simplicity n.单纯,简朴compactness a.紧凑的,紧密的timesharing system 分时系统description n.描述,说明interactive language 交互式语言break n.中断manufacturer n.制造业者structure chart 结构图dialect n.方言,语调the program flow 程序流expense n.费用,代价manager module 管理模块uniformity n.同样,划一worder module 工作模块archaic a.己废的,古老的mainmodule 主模块sufficient a.充分的,足够的submodule 子模块data processing 数据处理modify v.修正,修改business application 商业应用outline n.轮廓,概要scientific application 科学应用compose分解lexical a.字典的,词汇的code 代码non-programmer n.非编程人员node vt改为密码notation n.记号法,表示法,注释pseudocode n.伪代码verbosity n.唠叨,冗长commas n.逗点逗号record n.记录documentation 文档subrecord n.子记录flowchart/flow 程表/流程data division 数据部visual a.视觉的procedure division 过程部represent vt.表现,表示,代表comprise vt.包含构成structured techniques结构化技术operator n.运算符,算子straightforward a.笔直的,率直的commercial package 商业软件包subroutine n.子程序generator n.产生器,生产者driver module 驱动模块mathematician n.专家line by line 逐行operator n.作符translate vt.翻译,解释forerunner n.先驱modular 摸块化ancestor n.祖宗cumbersome a.讨厌的,麻烦的teaching programming 编程教学lengthy a.冗长的,漫长的alter vi./vt.改变flaw n.缺点裂纹devclop vt.发达separate a.各别的recompile v.编译assist n.帮助cycle n.循环technician n.技师remove vt.移动,除去straight line 直线category n.种类,类项rectangle n.长方形,矩形P-code p代码virtrally ad.事实上symology n.象征学象征的使用register n.寄存器to summaries 总之,总而言之by convention 按照惯例cyptic n.含义模糊的,隐藏的diamond-shaped a,菱形的bracket n.括号decision n判断obviate 除去,排除terminal n. a终端机,终端的keyword n.关键字card reader 阅读器underline vt.下划线translator program 译程序monadic a. monad(单位)的Programming 程序设计dec/binary n.二进制source language 源语shift 变化,转移,移位machine language 机器overflow n.溢出machine instruction 机器指令arithmetic n.算术,算法computer language 计算机语composite symbol 复合型符号.assembly language 汇编语assignment n.赋值floating point number浮点数proliferation n.增服high-level language高级语pointer n.指针natural language 自然语言array n.数组矩阵,source text 源文本subscript n.下标intermediate language 中间语言type conversion 类型转换software development 软件开发address arithmetic 地址运算map vt.映射,计划denote vt.指示,表示maintenance cost 维护费用subprogram n.子程序legibility n.易读性,易识别separate compilation 分离式编泽amend vt.修正,改善alphabetic a.照字母次序的consumer n.消费者digit n.数字位数enormous a.巨大的,庞大的numeric expression 数值表达式reliability n.可信赖性,可信度tap n.轻打,轻敲,选择safety n.安全,安全设备print zone 打印区property n.财产,所有权column n.列correctness n.正确,functionality n.机能semicolon n.分号portable a.叮携带的,可搬运的survey n.概观.altoggle n.肘节开关task n.作,任务declaration n.宣告说明source program 源程序mufti-dimension array 多维数组object program 目标程序其他提示语:CPU(Center Processor Unit)中央处理单元mainboard主板RAM(random accessmemory)随机存储器(内存)ROM(Read Only Memory)只读存储器Floppy Disk软盘Hard Disk硬盘CD-ROM光盘驱动器(光驱)monitor监视器keyboard键盘mouse鼠标chip芯片CD-R光盘刻录机HUB集线器Modem= MOdulator-DEModulator,调制解调器P-P(Plug and Play)即插即用UPS(Uninterruptable Power Supply)不间断电源BIOS(Basic-input-OutputSystem)基本输入输出系统CMOS(Complementary Metal-Oxide-Semiconductor)互补金属氧化物半导体setup安装uninstall卸载wizzard向导OS(Operation Systrem)操作系统OA(Office AutoMation)办公自动化exit退出edit编辑copy复制cut剪切paste粘贴delete删除select选择find查找select all全选replace替换undo撤消redo重做program程序license许可(证)back前一步next下一步finish结束folder文件夹Destination Folder目的文件夹user用户click点击double click双击right click右击settings设置update更新release发布data数据data base数据库DBMS(Data Base Manege System)数据库管理系统view视图insert插入object对象configuration配置command命令document文档POST(power-on-self-test)电源自检程序cursor光标attribute属性icon图标service pack服务补丁option pack功能补丁Demo演示short cut快捷方式exception异常debug调试previous前一个column行row列restart重新启动text文本font字体size大小scale比例interface界面function函数access访问manual指南active激活computer language计算机语言menu菜单GUI(graphical user interfaces )图形用户界面template模版page setup页面设置password口令code密码print preview打印预览zoom in放大zoom out缩小pan漫游cruise漫游full screen全屏tool bar工具条status bar状态条ruler标尺table表paragraph段落symbol符号style风格execute执行graphics图形image图像Unix用于服务器的一种操作系统Mac OS苹果公司开发的操作系统OO(Object-Oriented)面向对象virus病毒file文件open打开colse关闭new新建save保存exit退出clear清除default默认LAN局域网WAN广域网Client/Server客户机/服务器ATM( AsynchronousTransfer Mode)异步传输模式Windows NT微软公司的网络操作系统Internet互联网WWW(World Wide Web)万维网protocol协议HTTP超文本传输协议FTP文件传输协议Browser浏览器homepage主页Webpage网页website网站URL在Internet的WWW服务程序上用于指定信息位置的表示方法Online在线Email电子邮件ICQ网上寻呼Firewall防火墙Gateway网关HTML超文本标识语言hypertext超文本hyperlink超级链接IP(Address)互联网协议(地址)SearchEngine搜索引擎TCP/IP用于网络的一组通讯协议Telnet远程登录IE(Internet Explorer)探索者(微软公司的网络浏览器) Navigator引航者(网景公司的浏览器)multimedia多媒体ISO国际标准化组织ANSI美国国家标准协会able 能activefile 活动文件addwatch 添加监视点allfiles 所有文件allrightsreserved 所有的权力保留altdirlst 切换目录格式andfixamuchwiderrangeofdiskproblems 并能够解决更大范围内的磁盘问题andotherinFORMation 以及其它的信息archivefileattribute 归档文件属性assignto 指定到autoanswer 自动应答autodetect 自动检测autoindent 自动缩进autosave 自动存储availableonvolume 该盘剩余空间badcommand 命令错badcommandorfilename 命令或文件名错batchparameters 批处理参数binaryfile 二进制文件binaryfiles 二进制文件borlandinternational borland国际公司bottommargin 页下空白bydate 按日期byextension 按扩展名byname 按名称bytesfree 字节空闲callstack 调用栈casesensitive 区分大小写causespromptingtoconfirmyouwanttooverwritean 要求出现确认提示,在你想覆盖一个centralpointsoftwareinc central point 软件股份公司changedirectory 更换目录changedrive 改变驱动器changename 更改名称characterset 字符集checkingfor 正在检查checksadiskanddisplaysastatusreport 检查磁盘并显示一个状态报告chgdrivepath 改变盘/路径node 节点npasswd UNIX的一种代理密码检查器,在提交给密码文件前,它将对潜在的密码进行筛选。
CC++中多维数组做参数情况的详细解释我⼤⼆刚学完C语⾔,之后⽤来写矩阵分析的时候想把⼆维矩阵直接传到函数⾥,结果出现了问题:形参实参类型不⼀致,⽆法通过编译!随后我就尝试各种⽅法(改变形参或者实参的格式),虽然最后通过了不过当时还是没理解原理。
后来⾃⼰把原因分析出来了,现在把它写出来,希望对碰到同样问题的朋友有所帮助。
转载请注明出处,谢谢!⼏个跟参数有关的知识:C/C++的函数形参可以是普通类型、指针、引⽤。
传值⽅式有两种:值传递(包括指针)、引⽤。
传参时从左往右,结合时从右往左,这个很重要(函数默认值与此有关)。
参数是指针时,我们⼀般通过两种⽅式实现读写:①移动指针 p++ ② p+i(⽬标位置)或者 p[i],等同于寻址的⽅式实现,他们实现时在内存⾥的操作:⼀维 p+0(p[0]) p+1(p[1]) p+2(p[2]) ······ p+(n-1) (p[n-1]) 由于作图不太⽅便,下⾯的讲解就不附图了。
1、⼀维数组(指针)做参数⼀般指针做参数我就不多说了,专门搜这种问题的⼈应该都懂。
下⾯说⼀下⼀维数组:⼀般传参情况:字符串、整型数组(举个特例,实际上字符串是字符型数组)。
字符串,我们⼀般⽤下⾯这种⽅式:bool PrintStr(char* str)//char str[]也⼀样{if (NULL == str || "" == str){return false;}for (int i = 0; i < strlen(str);i++)//就不考虑效率了,注意不要⽤sizeof{cout << str[i] << " ";}while ('\0' != *str)//通过指针{cout << *str++ << " ";}return true;}2、⼆维数组做参数在⼀维中我们看到,遍历数组时必须有终⽌条件,可以是某种标志也可以规定移动次数。
c语言中的矩阵摘要:一、矩阵的概念与作用1.矩阵的定义2.矩阵在C语言中的作用二、C语言中矩阵的表示方法1.行优先表示法2.列优先表示法3.二维数组表示法三、矩阵的基本操作1.矩阵的初始化2.矩阵的访问与修改3.矩阵的运算a.矩阵的加法b.矩阵的减法c.矩阵的乘法d.矩阵的转置四、常用的矩阵处理函数1.矩阵的求和2.矩阵的求差3.矩阵的乘积4.矩阵的转置函数五、C语言中矩阵的应用1.图像处理2.数据存储与处理3.机器学习与人工智能正文:C语言中的矩阵是一种用于处理数据的数学结构,广泛应用于图像处理、数据存储与处理、机器学习与人工智能等领域。
矩阵是一个由行和列组成的矩形阵列,可以用于表示线性方程组、线性变换等。
在C语言中,矩阵有多种表示方法,包括行优先表示法、列优先表示法以及二维数组表示法。
行优先表示法是按照行来排列元素,先存储第一行的元素,再存储第二行的元素,依此类推。
列优先表示法则是按照列来排列元素,先存储第一列的元素,再存储第二列的元素,依此类推。
而二维数组表示法则是将矩阵看作一个二维数组,数组的行数表示矩阵的行数,数组的列数表示矩阵的列数。
矩阵在C语言中有许多基本操作,包括矩阵的初始化、访问与修改以及运算。
矩阵的初始化是指为矩阵的每个元素赋予一个初始值。
矩阵的访问与修改是指通过下标访问矩阵的元素并对其进行修改。
矩阵的运算包括矩阵的加法、减法、乘法以及转置。
在C语言中,我们可以通过编写相应的函数来实现这些操作。
C语言中矩阵处理函数是处理矩阵的常用工具。
常用的矩阵处理函数包括矩阵的求和、求差、乘积以及转置函数。
这些函数可以帮助我们更方便地处理矩阵数据,提高编程效率。
总的来说,C语言中的矩阵是一种强大的数据结构,通过矩阵,我们可以解决许多实际问题。
c++坐标系之间的变换坐标系是计算机图形学和几何处理中常用的概念,它用于描述和表示空间中的点位置。
在坐标系之间进行变换是计算机图形学和几何处理中的一项重要任务。
本篇文章将介绍C语言中实现坐标系之间变换的方法和技巧。
一、坐标系的基本概念1. 坐标系表示坐标系通常用坐标轴、原点和单位长度来表示。
在平面直角坐标系中,x轴和y轴将平面分成四个象限,原点表示坐标系的原点,单位长度通常表示为1个单位长度。
在三维空间直角坐标系中,x轴、y轴和z轴将空间分成八个部分,原点表示坐标系的原点,单位长度通常表示为1个单位长度。
2. 坐标系变换坐标系变换包括平移、旋转、缩放、反射等操作。
这些操作可以通过矩阵变换或四元数等方法来实现。
矩阵变换是将一个坐标系转换到另一个坐标系的过程,通常使用齐次坐标表示。
四元数是一种表示三维空间中点的方法,它包含了点的位置、速度和方向的信息。
二、C语言实现坐标系变换的方法1. 矩阵变换矩阵变换是实现坐标系变换的一种常用方法。
在C语言中,可以使用矩阵来表示变换矩阵,通过矩阵运算来实现坐标系的变换。
具体实现过程如下:(1)定义一个4x4的矩阵,用于表示变换矩阵;(2)根据需要,设置矩阵中的元素值;(3)使用矩阵乘法,将原点和目标点进行变换。
下面是一个简单的示例代码,实现了平移变换:```c#include <stdio.h>#define SCALE 1.0 // 缩放因子void translate(double matrix[4][4], double tx, double ty) {matrix[0][0] = SCALE; matrix[0][1] = 0.0; matrix[0][2] = 0.0; matrix[0][3] = tx;matrix[1][0] = 0.0; matrix[1][1] = SCALE; matrix[1][2] = 0.0; matrix[1][3] = ty;matrix[2][0] = 0.0; matrix[2][1] = 0.0; matrix[2][2]= 1.0; matrix[2][3] = 0.0;}int main() {double origin[3]; // 原点坐标double target[3]; // 目标点坐标double matrix[4][4]; // 变换矩阵origin[0] = 0.0; origin[1] = 0.0; origin[2] = 0.0; // 原点坐标设置target[0] = 5.0; target[1] = 5.0; target[2] = 5.0; // 目标点坐标设置translate(matrix, 2.0, 3.0); // 平移距离为2个单位长度,方向为x轴向右和y轴向上// 将原点和目标点进行变换,并输出结果printf("Origin: (%f, %f, %f)\n", origin[0], origin[1], origin[2]);printf("Target: (%f, %f, %f)\n", target[0], target[1], target[2]);return 0;}```该示例代码中,定义了一个4x4的矩阵`matrix`,用于表示平移变换矩阵。
第六章矩阵矩阵函数及函数矩阵函数及函数矩阵第一节矩阵多项式、最小多项式定义:设nn m m mm CA a a a a p ⨯--∈++++=,)(0111λλλλ m m1-则称E a A a A a A a A p m m 011)(++++=- 为A 的矩阵多项式.块i ⎥⎤⎢⎡λλ1例1:设J i 为d i 阶Jordan ii J ⎥⎥⎥⎢⎢⎢=1 iidd i ⨯⎦⎣λJ d di ()例2:设J 为Jordan 标准形, J =diag(J 1, J 2, , J r ), 则:diag J J J J =))(,),(),((g )(21r p p p p 例3:设A 为n 阶矩阵, J 为其Jordan 标准形, A =PJP -1=P diag(J 1, J 2, , J r )P -1,则:11--== (以上表达式称为p (A )的Jordan 表示)21))(,),(),((diag )()(PJ p J p J p P P J Pp A p r 例4:设34,12)(-+-=p λλλλ1020*********-⎥⎥⎤⎢⎡=⎥⎥⎤⎢⎡=PP A 200311⎦⎢⎣⎦⎢⎣-⎥⎤⎢⎢⎡-=⎥⎤⎢⎡=-111010,0011101P P 其中:⎥⎥⎦⎢⎣-⎥⎥⎦⎢⎢⎣-110101则:=-)()(1PJ Pp A p ⎤⎡-⎤⎡'⎤⎡0100)2()2(0110p p ⎥⎥⎦⎢⎢⎣-⎥⎥⎦⎢⎢⎣⎥⎥⎦⎢⎢⎣-=0110111)2(000)2(010101p p ⎥⎤⎢⎡--=⎥⎥⎤⎢⎢⎡''-'''-'=98901)2()2()2()2(00)2(p p p p p ⎥⎦⎢⎣⎦⎣+1099)2()2()2()2(p p p p定义:设0111)(,a a a a p C A m m m m nn ++++=∈--⨯λλλλ 若-满足则称(λ)为A 的化零多项式.0)(0111=++++=-E a A a A a A a A p m m mm p 定理:设是A 的化零多项)det()(,A E D CA nn -=∈⨯λλ则式,即D (A ) =0. (Hamilton Hamilton--Cayley 定理)))))证明:设J =diag(J 1(λ1), J 2(λ2), , J r (λr )) 是A 的若当标准型,即A =PJP -1=P diag(J 1, J 2, , J r )P -1, 则:1211))(,),(),((diag )()(--==PJ D J D J D P P J PD A D r)()()(λλλλf p id i i -=⇒id 即: Jordan 块的最小多项式为其初等因子.ii J )()(λλλψ-=⇒定理:设, 则:的任一化零多项式都能被nn CA ⨯∈(1)A 的任化零多项式都能被ψA (λ)整除;(2)A 的最小多项式ψA (λ)是唯一的;(3)相似矩阵的最小多项式相同证明:(1) 设f (λ)为A 的化零多项式, 则∃多项式q (λ)及次数小于ψA (λ)次数的多项式r (λ),使)()()()(λλλψλr q f A +=⇒)()()()(=+=A r A q A A f A ψ即: r (λ)也是A 的化零多项式. 从而r (λ) =0, 否则与ψA (λ)为A 0)(=A r 再由⇒)(=A A ψ的最小多项式矛盾,因为r (λ)的次数<ψA (λ)的次数.(2)(2)设ψA (λ)及ξA (λ)都为A 的最小多项式, 则ψA (λ)能被ξA (λ)整除, ξA (λ)也能被ψA (λ)整除,从而ψA (λ) =ξA (λ).(3) 设B =P -1AP , A 和B 的最小多项式为p (λ)和q (λ). 由B =-1)=-1=0,P AP 知:p (B ) P p (A )P 0, 从而p (λ)是B 的化零多项式, p (λ)的次数≥q (λ)的次数.同理, q (λ)的次数≥p (λ)的次数.))所以p (λ)的次数=q (λ)的次数.从而, p (λ) =q (λ).定理:定理:设分别是的最小多项式,则A 的最小多项式是)(,),(),(),,,,(diag 2121λψλψλψs s A A A A =s A A A ,,,21 的最低公倍式.)(,),(),(21λψλψλψs 证明:设是A 的最小多项式, 则:)(λψA 0))(,),(),((diag )(21==s A A A A A A A A ψψψψ 于是: , 即0)(,,0)(,0)(21===s A A A A A A ψψψ )(λψA ))是的化零多项式⇒是的公倍式.s A A A ,,,21 )(,λψs )(λψA ),(),(21λψλψ⇒若不是的公倍式,:)(,),(),(21λψλψλψs )(λψA 则0)(≠A A ψ另一方面, 若是的最低公倍式,则: .从而是A 的化零多项式. 次数)(λψA )(,),(),(21λψλψλψs 0)(=A A ψ)(λψA 更低的多项式必定不是的公倍式,从而不是A 的化零多项式.定理得证.)(,),(),(21λψλψλψs ⎥⎤⎢⎢⎡=⎥⎤⎢⎡---=11621例5:⎥⎥⎦⎢⎣→⎥⎥⎦⎢⎢⎣--11411301)1(J A 2)1()(-=λλψA ⇒⎤⎡-⎤⎡-1111⎥⎥⎦⎢⎢=→⎥⎥⎢⎢--=01017215)2(J A ⎥⎢⎣⎥⎦⎢⎣-212662)1()(λλλψ+=A ⇒J d 第二节矩阵函数及其Jordan 表示定义:设A 的最小多项式为,)()()()(2121sd s d d A λλλλλλλψ---= 其中为A 的互异特征值. 若函数f (x )具有足够多且下列s λλλ,,,21 d d d m +++= 阶的导数值,个值),,2,1(),(,),(),()1(s i ff f i d i i i ='-λλλs 21都有确定的值,则称f (x )在A 的影谱上有定义.-⎡-111例1:⎥⎥⎤⎢⎢⎡--=⎥⎥⎤⎢⎢-=112103,0340B A ⎥⎦⎢⎣-⎥⎦⎢⎣30201p(x)不唯一例2:⎤⎡⎤⎡⎥⎤⎡11012002⎥⎥⎥⎦⎢⎢⎢-=⎥⎥⎥⎦⎢⎢⎢==⎥⎥⎢⎢⎢-=-101001,22,3111111P J PJP A ⎣⎣⎦⎣⎤⎡⎤⎡'010)2()2(f f ⎥⎥⎥⎦⎢⎢⎢--=⎥⎥⎥⎢⎢⎢=-110111,)2()2()(1P f f J f ⎣⎦⎣⎤⎡00)2(f ⎥⎥⎥⎢⎢⎢'+'-'''-'==-2222)2()2()2()2()()(1f f f f P J Pf A f ⎦⎣)()()()(f f f fA e At cos 例3:求f (A )的Jordan 表示, 并计算e , e , cos A⎡50⎥⎥⎤⎢⎢⎡=⎥⎥⎦⎤⎢⎢⎡==⎥⎥⎤⎢⎢--=-13000120,2123,130903025171P J PJP A ⎦⎣⎣⎦⎣⎡1⎥⎥⎤⎢⎢⎡--=⎥⎥⎦⎤⎢⎢'=-50320100,2()2()2()3()(1P f f f J f ⎡''⎦⎣⎣)f ⎥⎥⎤⎢⎢'-'-+==-21520290)3(0)2(250)2(15)2()()(1f f f f P J Pf A f ⎦⎣)()()(f f f⎡⎥⎥⎤⎢⎢--+=⎥⎥⎦⎤⎢⎢⎡--=1510900250)151(,140900250162232222322t e te e te t e e e e ee e e tt t t t At A ⎥⎦⎢⎣⎣)(⎤⎡-()2sin(250)2sin(15)2cos((⎥⎥⎦⎢⎢⎣+-=)2sin(15)2cos(0)2sin(90)3cos(0)cos(A •用矩阵函数Jordan 表示计算f (A )的一般步骤:(1) 求A 的Jordan 标准形J ; (2) 求f (J );(3) 由AP =PA 计算变换矩阵P ; (4) 求f (A ) =Pf (J )P -1;(5) x Pf J P -1A ).()将具体f ()代入f ()即可求出f ()定理:设f (x )与g (x )在A 的影谱上有定义, 则:f (A ) =g (A ) ⇔f (x )与g (x )在A 的影谱上有相同的值第三节矩阵函数的多项式表示定义:设n 阶矩阵A 的最小多项式为,)()()()(2121sd s d d A λλλλλλλψ---= , 函数f (x )在A 的影谱上有定义, m -1次多项式s d d d m +++= 21满足1110)(--+++=m m a a a p λλλ 为什么是m -1次?1,,1,0;,,2,1),()()()(-===i i k i k d k s i fp λλ从而:1110)()(--+++==m m Aa A a E a A p A f 称f (A )的以上表达式为f (A )的多项式表示.⎡0例1: 设, 求矩阵函数f (A )的多项式表示,⎥⎤⎢=11102A 并计算e At⎥⎥⎦⎢⎢⎣-311解:前已求得, A 的Jordan 标准形为:⎥⎥⎤⎢⎢⎡=020012J 因此, 其最小多项式为(x ) =(x -2)2⇒m =2 ⇒⎥⎦⎢⎣200ψA 110)()(a x p x a a x p ='⇒+=满足:⎨⎧''-=⇒⎨⎧''=+=)2(2)2()2(2)2(010a f f a f a a p ⎩=⎩==)2()2()2(11f f a p从而:AE A a E a A 2222'+'-=+=f f f f )()]()([)(10此即f (A )的多项式表示. 将E 和A 代入, 可得:⎤⎡⎥⎢''-'=)2()2()2()2(00)2()(f f f f f A f ⎥⎥⎦⎢⎢⎣'+'-')2()2()2()2(f f f f 与第一节例4t 的结果相同⎡当f (x ) =e tx时, f (2) =e 2t , f'(x ) =t e 2t , 从而⎥⎥⎤⎢⎢-=t t t t e et At110012⎥⎦⎢⎣+-t t⎡1例2: 设, 求矩阵函数f (A )的多项式表示.⎥⎤⎢--=03401A 解)⎥⎥⎦⎢⎢⎣201解:前已求得, A 的最小多项式为ψA (x ) =(x -1)2(x -2)xa a x p x a x a a x p m 2122102)(,)(312+='++=⇒=+=⇒满足:'⎧⎪⎨⎧-'+=-=⇒⎪⎨'=+='=++=)2(2)1(3)1(2)1(2)2()1(2)1()1()1(1021210f f f a f f a f a a p f a a a p ⎪⎩'--=⎪⎩=++=)1()1()2()2(42)2(2210f f f a f a a a p=++=2210)(A a A a E a A f(m -1次)sd s )λ1-i d因此:⎤⎡+-+sk k k E A a E a 21)(λ ∑=-⎥⎥⎦⎢⎢⎣-+==k k d k kd A E A a A p A f kk11)()()()(ϕλsk k d s d k d k d k E A E A E A E A A )()()()()(111111λλλλϕ----=+-+- 称以上f (A )的表达式为f (A )的Lagrange-Selvester 内插多项式表示.3:设⎥⎤⎢⎡002例3: , 求矩阵函数f (A )的Lagrange-⎥⎥⎦⎢⎢⎣-=311111A Selvester 内插多项式表示.•与例1得到的多项式表示Af E f f A a E a A f )2()]2(2)2([)(10'+'-=+=相比, 结果是一致的, 只是表示方式不一样.第四节矩阵函数的幂级数表示第五章定义过矩阵幂级数. 设A 的Jordan 标准 -1∑∞=0k kk A c 形J =diag(J 1(λ1),J 2(λ2),,J r (λr )),A =PJP ⇒A k =PJ k P -1=P diag(J 1k (λ1), J 2k (λ2), , J r k (λr ))P -1⇒⎛100220110)(,,)(,)(diag -∞=∞=∞=∞=⎪⎪⎭⎫ ⎝=∑∑∑∑P J c J c J c P A c k r kr k k k k k k k k k k λλλ i i kk d k id k k k k ikk k k ik Cc C c c ∞∞=+--∞=-∞=⎥⎤⎢⎡∑∑∑0110110λλλk k k ik k k ik k i ki k C c c J c ∞=-=∞=⎥⎥⎥⎢⎢⎢=∑∑∑01100)(λλλiidd k ikc ⨯∞=⎥⎦⎢⎣∑0λ与前页结果相同⎥⎤⎢⎡1310041285⎥⎥⎦⎢⎢⎣-511第五节函数矩阵⎛x a x a 定义:设()⎪⎪⎫ ==⨯)()()()(111a x a x A n nm ij 其中: x ∈R , a ij (x )∈R , 称A (x )为函数矩阵——以实函数为⎪⎭⎝)()(1x x a mn m 元素的矩阵•函数行向量、函数列向量、函数矩阵的转置函数矩阵加法纯量函数与函数矩阵乘法函数矩阵与•函数矩阵加法、纯量函数与函数矩阵乘法、函数矩阵与函数矩阵乘法))))定义:设A (x ) =(a ij (x ))为n 阶函数矩阵, 若∃B (x ) =(b ij (x )), 使得∀x ∈[a , b ],A xB x ) =B x A x ) =E ()()()()则称A (x )在[a, b ]上可逆, B (x )是A (x )的逆的逆矩阵矩阵, 记为A -1(x ).x A x B x B x )()()]()+=x d ?)(d )(2)(d 2x A x A x A =d d xx ,可逆时()21)(x A -A x A x A x x A x A x d )()(d )(d )()(211---≠-=))()((1得到可由E x A x A =-。