第6章 均匀平面波的反射和透射
- 格式:pdf
- 大小:729.17 KB
- 文档页数:18


均匀平面波的反射和透射matlab -回复均匀平面波的反射和透射(matlab)引言:均匀平面波的反射和透射是电磁波传播中的基本现象之一。
通过研究波在边界上的反射和透射行为,我们可以更好地理解电磁波的传播规律和性质。
在本文中,我们将使用MATLAB编程来模拟均匀平面波的反射和透射现象,并详细介绍每一步的操作。
第一步:定义均匀平面波首先,我们需要定义一个均匀平面波的初始状态。
假设我们有一个平面波在z轴上传播,其电场分量Ez(x, y, t)可以由下述公式表示:Ez(x, y, t) = E0 * exp(j*(kx*x + ky*y - ωt))其中,E0表示电场强度的振幅,kx和ky分别表示波矢在x和y方向上的分量,ω表示角频率,t表示时间。
我们可以在MATLAB中定义这个函数,并设定合适的参数。
例如:MATLABE0 = 1; 设置电场强度的振幅kx = 2*pi; 设置波矢在x方向上的分量ky = 3*pi; 设置波矢在y方向上的分量omega = 10; 设置角频率t = 0; 设置初始时间定义均匀平面波函数Ez = (x, y) E0 * exp(1j * (kx*x + ky*y - omega*t));第二步:绘制均匀平面波的图像在前面的步骤中,我们定义了一个函数Ez(x, y),用来描述均匀平面波在空间中的电场分布情况。
为了更直观地理解该函数的特性,我们可以使用MATLAB绘制二维图像。
MATLAB[X, Y] = meshgrid(-10:0.1:10); 定义绘制图像所需的坐标点Z = angle(Ez(X, Y)); 计算相位,并将其作为图像的颜色映射绘制二维图像figure;imagesc(X(1,:), Y(:,1), Z);xlabel('x');ylabel('y');colorbar;运行以上代码后,我们将得到一个二维图像,其中不同位置的颜色表示该位置上电场分量的相位。


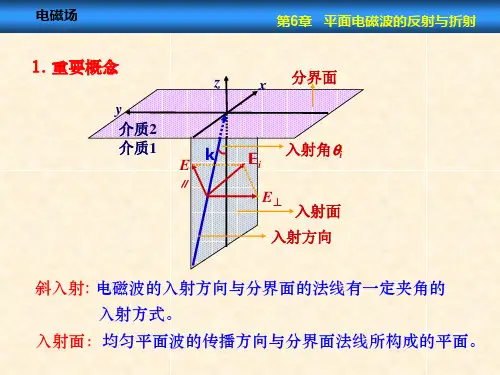
第6章 均匀平面波的反射与透射一、判断题电磁波垂直入射至两种媒质分界面时,反射系数与透射系数之间的关系为ρτ1+=。
( )ρτ【答案】√二、填空题电磁波从理想介质1垂直向理想介质2入射,介质1和2的本征阻抗分别为30Ω和70Ω,则分界面处的反射系数Γ和透射系数τ分别是_______,_______。
【答案】0.4;1.4三、简答题1.简述平面电磁波在媒质分界面处的反射现象和折射现象满足的斯耐尔(Snell )定律;并具体说明什么条件下发生全反射现象,什么是临界角,给出临界角的计算公式。
答:(1)斯耐尔(Snell )定律:①反射线和折射线都在入射面内;②反射角等于入射角,即;r i θθ=③折射角的正弦值与入射角的正弦值之比等于入射波所在的媒质的折射率与折射波所在媒质的折射率之比,即,式中sin sin ii n n ττθθ=n =(2)全反射现象:①理想导体全反射。
在电磁波入射到理想导体表面时,由理想导体表面切向电场为零的条件,反射系数为±1,称为理想导体全反射现象;②理想介质全反射。
当电磁波由光密介质入射到光疏介质时,由于,根据斯耐12n n >尔定律有。
当入射角增加到某一个角度时,折射角就可能等于。
因此,i τθθ>i θπ2c θ<τθπ2在时,就没有向介质2内传播的电磁波存在,即发生全反射现象。
c θθ>能使的入射角称为临界角,有:π2τθ=c θ21sin c n n θ==2.什么是电磁波在媒质分界面的全反射现象和全折射现象?什么是临界角和布儒斯特角?一个任意极化波由空气斜入射到一介质界面,以什么角度入射才能使反射波为线极化波?说明原因。
答:(1)当电磁波由光密介质入射到光疏介质时,由于,根据斯耐尔定律有12n n >。
当入射角增加到某一个角度时,折射角就可能等于。
因此,在i τθθ>i θπ2C θ<τθπ2时,就没有向介质2内传播的电磁波存在,即发生全反射现象。


第6章 均匀平面波的反射与透射(一)思考题6.1 试述反射系数和透射系数的定义,它们之间存在什么关系?答:(1)反射波电场振幅E rm与入射波电场振幅E im的比值为分界上的反射系数;透射波电场振幅E tm与入射波电场振幅E im的比值为分界面上的透射系数。
(2)反射系数Γ和透射系数τ之间的关系为:6.2 什么是驻波?它与行波有何区别?答:频率和振幅均相同,振动方向一致,传播方向相反的两列波叠加后形成的波叫驻波。
行波在介质中传播时,其波等相面随时间前移,而驻波的波形不向前推进。
6.3 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,反射系数大于0?在什么情况下,反射系数小于0?答:均匀平面波垂直入射到两种理想媒质分界时,当时,反射系数Γ>0;当时,反射系数Γ<0。
6.4 均匀平面波向理想导体表面垂直入射时,理想导体外面的合成波具有什么特点?答:均匀平面波向理想导体表面入射时,理想导体外面的合成波具有特点如下:合成波电场和磁场的驻波在时间上有的相移,在空间上也错开了且在导体边界上,电场为零。
驻波的坡印廷矢量的平均值为零,不发生电磁能量的传输过程,仅在两个波节之间进行电场能量和磁场能量的交换。
6.5 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,分界面上的合成波电场为最大值?在什么情况下,分界面上的合成波电场为最小值?答:当均匀平面波垂直入射到两种理想媒质分界面时,的位置时,分界面上的合成波电场为最大值。
的位置时,分界面上的合成波电场为最小值。
6.6 一个右旋圆极化波垂直入射到两种媒质分界面上,其反射波是什么极化波?答:右旋圆极化。
6.7 试述驻波比的定义,它与反射系数之间有什么关系?答:驻波比的定义是合成波的电场强度的最大值与最小值之比,即6.8 什么是波阻抗?在什么情况下波阻抗等于媒质的本征阻抗?答:在空间任意点,均匀平面波的电场与磁场强度的模值之比称为自由空间的波阻抗,在均匀无耗各向同性的无界媒质中,均匀平面波的电场与磁场的模值之比称为媒质中的阻波抗。


第6章习题答案6-1 在1=r μ、4=r ε、0=σ的媒质中,有一个均匀平面波,电场强度是)3sin(),(πω+-=kz t E t z E m若已知MHz 150=f ,波在任意点的平均功率流密度为2μw/m 265.0,试求:(1)该电磁波的波数?=k 相速?=p v 波长?=λ波阻抗?=η (2)0=t ,0=z 的电场?)0,0(=E(3)时间经过μs 1.0之后电场)0,0(E 值在什么地方?(4)时间在0=t 时刻之前μs 1.0,电场)0,0(E 值在什么地方? 解:(1))rad/m (22πεπμεω===r cfk )m/s (105.1/8⨯==r p c v ε)m (12==kπλ )Ω(60120πεμπη=rr=(2)∵ 6200210265.02121-⨯===m rm av E E S εεμη∴ (V/m)1000.12-⨯=m E)V/m (1066.83sin)0,0(3-⨯==πm E E(3) 往右移m 15=∆=∆t v z p(4) 在O 点左边m 15处6-8微波炉利用磁控管输出的2.45GHz 频率的微波加热食品,在该频率上,牛排的等效复介电常数)j 3.01(40~-=rε。
求: (1)微波传入牛排的穿透深度δ,在牛排内8mm 处的微波场强是表面处的百分之几?(2)微波炉中盛牛排的盘子是发泡聚苯乙烯制成的,其等效复介电常数=r ε~ )103.0j 1(03.14-⨯-。
说明为何用微波加热时,牛排被烧熟而盘子并没有被毁。
解:(1)20.8mm m 0208.011211212==⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+==-ωεσμεωαδ%688.20/8/0===--e e E E z δ(2)发泡聚苯乙烯的穿透深度(m)1028.103.1103.01045.22103212213498⨯=⨯⨯⨯⨯⨯⨯⨯=⎪⎭⎫ ⎝⎛===-πμεωεσωμεσαδ可见其穿透深度很大,意味着微波在其中传播的热损耗极小,所以不会被烧毁。
第一章矢量分析①A A Ae =②cos A B A Bθ⋅=⋅③A 在B 上的分量B AB A B A COS BA θ⋅==④e xyz x y z xyzA B e e A A AB B B⨯=⑤A B A B⨯=-⨯ ,()A B C A B A C⨯+=⨯+⨯ ,()()()A B C B C A C A B ⋅⨯=⋅⨯=⋅⨯(标量三重积),()()()A B C B A C C A B ⨯⨯=⋅-⋅⑥ 标量函数的梯度xy z u u u ux y ze e e ∂∂∂∇=++∂∂∂⑦ 求矢量的散度=y x z A xyzA A A ∂∂∂∇⋅++∂∂∂散度定理:矢量场的散度在体积V 上的体积分等于在矢量场在限定该体积的闭合曲面S 上的面积分,即VSFdV F d S ∇⋅=⋅⎰⎰,散度定理是矢量场中的体积分与闭合曲面积分之间的一个变换关系。
⑧ 给定一矢量函数和两个点,求沿某一曲线积分E dl ⋅⎰,x y CCE dl E dx E dy ⋅=+⎰⎰积分与路径无关就是保守场。
⑨ 如何判断一个矢量是否可以由一个标量函数的梯度表示或者由一个矢量函数的旋度表示?如果0A ∇⋅= 0A ∇⨯=,则既可以由一个标量函数的梯度表示,也可以由一个矢量函数的旋度表示;如果0A ∇⋅≠,则该矢量可以由一个标量函数的梯度表示;如果0A ∇⨯≠,则该矢量可以由一个矢量函数的旋度表示。
矢量的源分布为A ∇⋅ A ∇⨯.⑩ 证明()0u ∇⨯∇=和()0A ∇⋅∇⨯=证明:解 (1)对于任意闭合曲线C 为边界的任意曲面S ,由斯托克斯定理有()d d dSCCuu u l l ∂∇⨯∇=∇==∂⎰⎰⎰S l 由于曲面S 是任意的,故有()0u ∇⨯∇=(2)对于任意闭合曲面S 为边界的体积τ,由散度定理有12()d ()d ()d ()d SS S ττ∇∇⨯=∇⨯=∇⨯+∇⨯⎰⎰⎰⎰A A S A S A S 其中1S 和2S 如题1.27图所示。
9.4 垂直入射平面电磁波的反射与透射1. 垂直入射平面电磁波反射和透射的一般规律前面介绍了均匀平面电磁波在单一媒质中传播的一般规律。
在多种媒质中,电磁波传播的情况更加复杂。
在两种媒质分界面处,存在反射和透射现象。
这里只介绍均匀平面电磁波垂直入射媒质分界面的情况。
设0x =是二种媒质的分界面,左侧为第一种媒质,右侧为第二种媒质。
均匀平面电磁波在第一种媒质中沿x 方向传播,到达分界面后,形成透射波和反射波。
对分界面来说,入射波透过分界面形成透射波,透射波在第二种媒质中继续沿x 方向传播;入射波遇到分界面反射回来形成反射波,则在第一种媒质中沿x -方向传播。
假设入射波电场强度只有y 分量,表示为()11e x yx E +-Γ+=E e 则根据均匀平面电磁波中电场和磁场强度关系,可写出入射波磁场强度()111C1e e x x z z E x H Z ++-Γ-Γ+==H e e 将透射波表示为()22t t e x y x E -Γ=E e ()22t tC2e x z E x Z -Γ=H e 将反射波表示为()11e x yx E Γ--=E e ()11C1e x z E x Z -Γ-=-H e 在第一种媒质中,电磁场()()()11111e e x x y yx x x E E +-ΓΓ-+-=+=+E E E e e ()()()11111C1C1e e x x z z E E x x x Z Z ++--ΓΓ-=+=-H H H e e 在第二种媒质中,电磁场()()22t t 2e x y x x E -Γ==E E e ()()22t t2C2e x z E x x Z -Γ==H H e 在均匀平面电磁波垂直入射情况下,相对于分界面电场和磁场都只有切向分量。
根据分界面衔接条件,当0x =时,有()120(0)=E E()120(0)=H H将电场和磁场表达式代入式 列出二个方程t t 211C C C E E E E E E Z Z Z -+-+⎧-=⎪⎨+=⎪⎩ 解此方程组得反射波和透射波分别与入射波的关系2121()()C C C C Z Z E E Z Z -+-=+ , 21121()()C C C C C Z Z H E Z Z Z -+-=-+ t 2122()C C C Z E E Z Z +=+ , t 122()C C H E Z Z +=+ 引入反射系数和透射系数21W 21()()C C C C Z Z R Z Z -=+,2W 122()C C C Z T Z Z =+ 则 W E R E -+= ,W 1C R H E Z -+=- t W E T E += ,t W 2C T H E Z += 反射系数W R 和透射系数W T 的关系W W 1T R -=电磁波传播参数C Z ==j Γ===α=β=j Γ=α+β2. 理想导体表面的反射理想导体就是电导率为无限大的导体。