当前位置：文档之家 › 6-3弹性力学平面问题(极坐标)

6-3弹性力学平面问题(极坐标)

  • 格式：ppt
  • 大小：3.02 MB
  • 文档页数：63

下载文档原格式

  / 63

合集下载

弹性力学第四章平面问题的极坐标解答

弹性力学第四章平面问题的极坐标解答

圆环或圆筒受均布压力（1）
q2 q1
边界条件：
圆环或圆筒受均布压力（2）
q2
q1
两个方程三个未知数，不能求解A，B，
C。因此，需引入位移单值条件：
该项必须为零，否则在环上同一点有两 个不同的位移，故B=0
圆环或圆筒受均布压力（3）
பைடு நூலகம்q2
q1 因此，得到圆筒受均匀压力的拉梅 （ me,1795—1870 ，法国）解答：
小孔口问题的特点：
1.集中性，孔附近的应力远大于较远处的应力。
2.局部性，孔口附近的应力扰动主要发生在距孔 边1.5倍孔口尺寸的范围内。在此区域外，由于开 孔引起的应力扰动一般小于5%，可以忽略不计。
注：圆孔的应力集中程度较低，有凹尖角的孔口 应力集中程度较高，因此，在设计结构时应尽量 避免有凹尖角的孔口。
o
x 在仅有径向位移的情况下，段
P P’ A
PA没有转动，因此：
A’
B
C
y
B’
极坐标中的几何方程（5）
— 纯环向位移下的线应变
o
x
很小，导致P’’A’’与PA
P P’’
的差别可以忽略，因此：
A
B B’’
D
D’
A’’
y
极坐标中的几何方程（6）
— 纯环向位移下的切应变
o
x
P
P’’
A
B B’’
D
D’
A’’
阶，因此假定：
半面体在边界上受集中力（2）
F
ao
c
ρ
代入极坐标中的相容方程：
b
得到：
半面体在边界上受集中力（3）
代入：
F
ao

弹性力学第四章：平面问题的极坐标解答2

弹性力学第四章：平面问题的极坐标解答2
π 2
r
σr +P θ 3σr −σθ 2σcos θ
x3 σx =− π (x2 + y2)2 2P xy2 σy =− π (x2 + y2)2 2P x2 y τxy =− π (x2 + y2)2 2P
2. 位移分量
假定为平面应力情形。 假定为平面应力情形。其极坐标形式的物理方程为
P
O y
由楔形体受集中力的情形， 由楔形体受集中力的情形，可以得到 P
O y
(令 β =0 ,α =π) : 2P cosθ σr = − ( ) π r （4-26） ） σθ =0 —— 极坐标表示的应力分量 极坐标表示的应力分量 τrθ =τθr =0
利用极坐标与直角坐标的应力转换式（ ）， ），可求得 利用极坐标与直角坐标的应力转换式（4-7），可求得
∂r ϕ = f (r)sinθ
θ
ϕ = f (r) (M =常 ) 数
ϕ = f (r)sinθ ϕ = f (r)cosθ (M = P⋅rsinθ) (M =M+P⋅rcosθ)
附1：曲梁应力函数确定的基本方法 ：
思路： 思路： 与直梁确定应力函数的方法类似， 与直梁确定应力函数的方法类似，借且于 梁截面上应力与内力 弯矩、剪力） 应力与内力（ 梁截面上应力与内力（弯矩、剪力）的关 应力与应力函数间微分关系， 系、应力与应力函数间微分关系，来推断 应力函数的分离变量形式。 应力函数的分离变量形式。 梁截面上的应力内力的关系： 梁截面上的应力内力的关系：
θ
M = Py = P⋅rsinθ
由材料力学初等理论，可知截面上正应力 由材料力学初等理论， 由此假定： 由此假定：
σθ ∝M(= P⋅rsinθ)

弹性力学平面问题极坐标

弹性力学平面问题极坐标

r
r
2 2 2 x2 y2
sin cos
r
r
cos2 sin2
r2
sin cos
r2
2
2
2 r 2
1 r
r
1 r2
2 r 2
二. 极坐标系下的平衡微分方程
1. 直角坐标与极坐标系下的应力分量关系
（1）极坐标系下的应力分量和体力分量
O
如图，根据应力状态的定义，过P
点分别以 r 方向和 方向为法线的截面
由半圆上的应力和外力的平衡关系，有
M
O
x
a
r r r
y
Fx 0
Fy 0 Mz 0
0
r
r
a
cos
ad
0
r
r a
sin
ad
0
0
r
ra
cos
r
ra
sin
d
0
0
r
ra
sin
r
ra
cos
d
0
a 0 a 0
0
r
ra
a ad
M
0
0
r
a2d M
ra
a 0
0
r
1 r
2 r
r
Fb
0
三. 极坐标系下的几何方程
1. 直角坐标与极坐标系下的位移分量关系
类似体力分量的投影关系 2. 极坐标系下的应变分量
O
x
r
Pu
u
ur
v
r
y
将P点分别沿 r 和 方向（相互垂直）两线元的线应变 r、 及其切应变 r ， 作为P点的应变分量。
3. 极坐标系下的几何方程

第六章平面问题极坐标解3

第六章平面问题极坐标解3

G
2(1 E
v)
1 E
v
sin [2 A(1 3v) (1 v) 2B (1 v) D ]
E
3
1 E
v
sin
E
[2
A(3
v)
(1
v)
2B
3
(1
v)
D
]
21
E
v
21 v cos
E
2
A
2B
3
D
代入几何方程
u
sin
E
[2
A(1
3v)
(1
v)
2B
3
(1 v) D ]
f At Bte2t Ce2t D
1
df d
A
2
B(1 2ln ) 2C
d 2 f d 2
A
2
B(3 2ln ) 2C
0
(
d2
d 2
1
d
d
)(
d 2 f d 2
1
df ) 0 d
1
d
d
d
d
1
d
d
d f d
0
d
d
1
d
d
d f d
B1
1
d
d
d f d
B1 ln
u
1
u
sin [2 A(3 v)
E
(1
v
)
2B
3
(1 v) D ]
1
u
u
u
2
1
E
v
cos
2
A
2B
3
D
对第一式积分得
u
sin

弹性力学第四章 用极坐标解平面问题

弹性力学第四章 用极坐标解平面问题

第四章 用极坐标解平面问题4.1.极坐标中的平衡微分方程工程上常常可以遇到圆形、环形、楔形或扇形类的结构物。

在这些情况下，用直角坐标描述边界条件会变得相当复杂，由于极坐标使得结构的边界与坐标线一致，因而使边界条件的描述更加简单，使问题更易于求解。

首先我们定义极坐标中的应力分量和体积力分量。

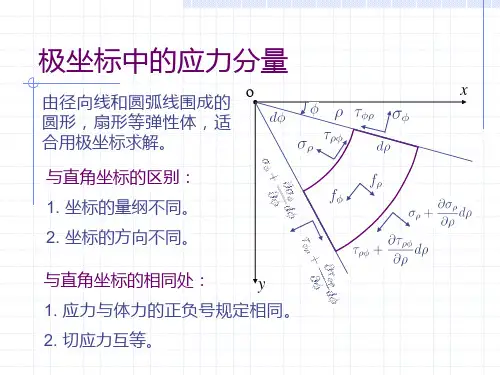
用夹角为ϕd 的两条极径和两条半径相差为ρd 的同心圆弧截取一个微元体（图4.1）。

圆弧截面称为ρ面。

面的法向沿径向而且指向ρ增加方向，这一圆弧面称为正ρ面，反之称为负ρ面。

极径截面称为ϕ面。

面的法向沿环向而且指向ϕ增加方向，这一极径截面称为正ϕ面。

反之称为负ϕ面。

ρ面上的正应力用ρσ表示，剪应力用ρϕτ表示。

ϕ面上的正应力用ϕσ表示，剪应力用ϕρτ表示。

用ρf 表示体积力在径向的分量,用ϕf 表示体积力在环向的分量。

应力的符号规定与直角坐标下的规定完全相同：正面上指向正向（坐标增加的方向）的应力为正值应力，负面上指向负向（坐标减小的方向）的应力亦为正值应力，反之，为负值的应力。

体积力符号规定也与直角坐标下的规定相同，指向坐标轴正向（坐标增加的方向）的体积力为正值，反之，为负值。

直角坐标和极坐标之间具有严格的变换关系。

从理论上说，我们完全可以通过坐标变换的方法由直角坐标的基本方程导出极坐标下的相应方程。

但是，为了加深对极坐标下平衡方程物理意义的理解，我们仍然通过极坐标下的微分单元体的平衡导出极坐标下的平衡微分方程。

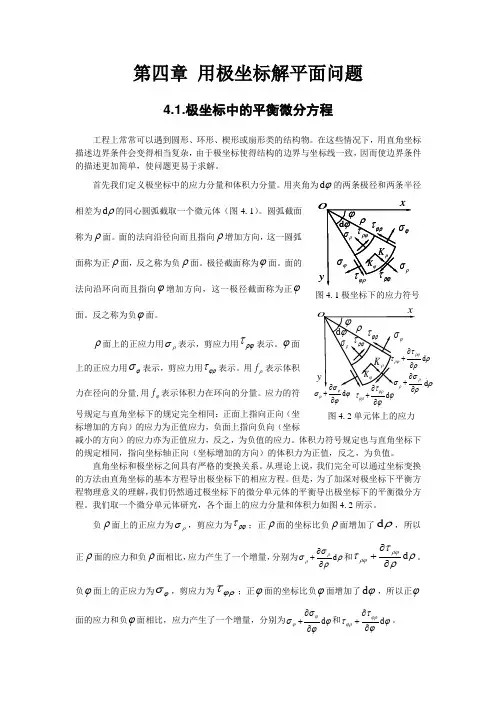
我们取一个微分单元体研究，各个面上的应力分量和体积力如图4.2所示。

负ρ面上的正应力为ρσ，剪应力为ρϕτ；正ρ面的坐标比负ρ面增加了ρd ，所以正ρ面的应力和负ρ面相比，应力产生了一个增量，分别为ρρσσρρd ∂∂+和ρρττρϕρϕd ∂∂+。

负ϕ面上的正应力为ϕσ，剪应力为ϕρτ；正ϕ面的坐标比负ϕ面增加了ϕd ，所以正ϕ面的应力和负ϕ面相比，应力产生了一个增量，分别为ϕϕσσϕϕd ∂∂+和ϕϕττϕρϕρd ∂∂+。

弹性力学平面问题的极坐标解答课件

弹性力学平面问题的极坐标解答课件

b
a
2
ln
a
b2
a
2
0
位移的确定
H, I, K待定
u
1 E
(1 )
A
(1 3 )B
2(1 )B(ln
1)
2(1
)C
I
sin
K
cos
u
4B
E
H
I
cos
K
sin
左端固定：(u )0 0
0,
(u ) 0 0
0,
u
0
0
0
常数的确定：
H
I
0,
K
1 E
极坐标下的双调和方程
代入协调方程，得到应力函数U需满足
的双调和方程
2
2
1
1
2
2
2
2U
2
1
U
1
2
2U
2
0
§7-2 轴对称应力及其位移
应力函数与无关，双调和方程为
d2
d 2
1
d
d
d2 U
d 2
1
dU
d
0
4
d4 U
d 4
23
d3 U
d 3
2
d2 U
d 2
dU
问题描述 任一截面上的弯矩：
M () F cos R tan F R sin
应力函数：
U f () sin
O
m
ba
F
x
n
y
f()的求解及应力表达式
微分方程及其通解
d2
d 2
1
d
d
1
2
d2 f

弹性力学-第八章 平面问题的极坐标解答

弹性力学-第八章 平面问题的极坐标解答
径向线段PA的转角： 径向线段 的转角： 的转角 线段PB的相对伸长： 线段 的相对伸长： 的相对伸长 环向线段PB的转角： 环向线段 的转角： 的转角
ur
∂ur ur + dr ∂r A A′
x
εθ1 =
α1 = 0
P′B′ − PB (r + ur )dθ − rdθ ur （c） ） = = PB rdθ r
σ = σ r er ⊗ er +τ rθ er ⊗ eθ +τθ r eθ ⊗ er + σθ eθ ⊗ eθ 剪应力互等定理 τ rθ = τ θ r 极坐标下的平衡方程
∇ ⋅σ + f = ( ∂ σ r 1 ∂ τ rθ σ r − σ θ + + + f r )e r ∂r r ∂θ r ∂τ 1 ∂σ θ 2τ rθ +( rθ + + + fθ )eθ = 0 ∂r r ∂θ r
θ r dθ
σr τ rθ
B
Pτθr
σθ x
∂r ∂σ r C ∂σθ dθ σr + dr y − σθ + dθ dr ∂r ∂θ ∂τθr 2 ∂σθ dθ σθ + dθ τθr + dθ ∂θ + fr rdrdθ = 0 −σθ dr ∂θ 2 高阶小量，舍去） （高阶小量，舍去）
即
Laplace算子 算子
2
∇ = e r ∂ + eθ 1 ∂ ∂r r ∂θ
(8.1) (8.2)
∂2 1 ∂ 1 ∂2 ∇ = ∇ ⋅∇ = 2 + + 2 2 ∂r r ∂r r ∂θ B.极坐标下的几何方程 极坐标下的几何方程

弹性力学中平面问题的极坐标解答

弹性力学中平面问题的极坐标解答
用 r 表示，沿 方向的正应力称为 切向正应力，用 表示，剪应力用 r
表示，各应力分量的正负号的规定和 直角坐标中一样。径向及环向的体力
分量分别用 Kr 及 K 表示。如图4-1。
o
d r
r P r
x A
B K
Kr
r
r r
dr
y
dr d
r
r
Cr d
r r
dr
图4－1
考虑图示单元体的平衡，有三个平衡方程：
向位移成为多值，这是不可能的，因此，从位移单值条件必须
有B=0。 于是:
A a2
2C
qa
A b2
2C
qb
这样从上面两个方程中可解出A和C，代入应力分量表达式，
得到拉密解答：
r
b2
r2 b2
a2
1 qa
1
1
1
a2
r2 a2
b2
qb
b2
r2 b2
a2
1 qa
1
1 1
a2
r2 a2
b2
qb
下面分别讨论内压力和外压 力单独作用的情况。
两者都属于轴对
o
r
E,
r
E,
r
称应力问题，采用半
逆解法。
设圆筒的应力表达式为：
图4-8
r
A r2
2C,
A r2
2C
设无限大弹性体的应力表达式为：
r
A r2
2C,
A r2
2C
由应力边界条件求待定常数 A 、C 、A 、C。
（1）在圆筒的内表面： ( r )ra q 由此得：
A a2
§4-1 极坐标中的平衡微分方程

弹性力学平面问题极坐标解法

弹性力学平面问题极坐标解法
2
sin θ cosθ ∂ 2 − r2 ∂θ 2
极坐标下的应力函数和相容方程（ 极坐标下的应力函数和相容方程（3）
∂2 ∂2 ∂2 1 ∂ 1 ∂2 + 2 = 2 + + 2 2 r ∂r r ∂θ 2 ∂x ∂y ∂r
应力函数的相容方程
∂2 ∂2 2 ∂2 1 ∂ 1 ∂2 2 ∇ 2ϕ = ( 2 + 2 ) ϕ = ( 2 + + 2 ) ϕ =0 2 ∂x ∂y ∂r r ∂r r ∂θ
极坐标系是正交曲线坐标系 极坐标系是正交曲线坐标系 正交
r坐标曲线：坐标θ为常数的曲线（过原点和空间点的直线） 坐标曲线：坐标 为常数的曲线 过原点和空间点的直线） 为常数的曲线（ 坐标曲线 θ坐标曲线：坐标 为常数的曲线（过空间点的圆弧） 坐标曲线： 为常数的曲线（ 坐标曲线 坐标r为常数的曲线 过空间点的圆弧） 由坐标确定的空间点， 由坐标确定的空间点，既是两条坐标曲线的交点 过一个空间点的两条坐标曲线都是唯一的，且相互正交。 过一个空间点的两条坐标曲线都是唯一的，且相互正交。其 切线构成局部正交坐标标架
极坐标和直角坐标的坐标变换
∂r 2 x = = cos θ ∂x 2r ∂r 2 y = = sin θ ∂y 2r ∂θ 1 −y y sin θ = ⋅ 2 =− 2 =− 2 y x ∂x r r 1+ 2 x 1 1 x cos θ ∂θ = ⋅ 2 = 2 = 2 y x ∂y r r 1+ 2 x
ε
(1) r
P′A′ − PA AA′ − PP′ = = PA PA ∂u (u r + r d r ) − u r ∂ur ∂r = = dr dr ∂r
ε θ(1) =

弹性力学：第四章 平面问题的极坐标解答(1)

弹性力学：第四章 平面问题的极坐标解答(1)

sin cos
r
r
cos 2
r2
sin
2
sin
cos
r2
2 2
r
0
r
1 r
极坐标下应力分量计算公式：
r
1 r
r
1 r2
2 2
2
r 2
（4－5）
r
1 r2
1 r
2 r
r
1 r
可以证明：式（4－5）满足平 衡方程（4－1）。
说明：式（4－5）仅给出体力为零时的 应力分量表达式。
y
r r
x
r yx
xy x
y
r r
（4－8）
(2) 用直角坐标下的应力分量表示极坐标下的应力分量
r
x
2
y
x
2
y
cos 2
xy
sin
2
x
y
2
x
y
2
cos 2
xy
sin
2
r
y
x
2
sin
2
xy
cos 2
（4－9）
O
yx y xy
yxx y
r
x x xy
r
r r
r 2
r r r r
2
sin
cos
r2
cos2
r2
2 2
(b)
2
xy
cos
r
sin
r
sin
r
cos
r
y
x
sin
cos
2
r 2
cos2
sin 2
r
2 r
sin cos

弹性力学 平面问题的极坐标解答2

弹性力学 平面问题的极坐标解答2

r 0
由此可见，应变分量也只是r的 函数，与无关，即应变绕z轴对 称
2、位移分量
u r 1 A r [(1 ) 2 (1 3 ) B r E r 2(1 ) B ln r 2(1 )C ]
积分得：
1 A ur [(1 ) (1 3 ) Br E r 2(1 ) Br (ln r 1) 2(1 )Cr ] 平衡微分方程 4—2 极坐标中的几何方程和物理方程 4—3 极坐标中的应力函数与相容方程 4—4 应力分量的坐标变换式 4—5 轴对称应力和相应的位移
4—6 圆环或圆筒受均布压力 4—8 圆孔的孔边、应力集中
4—9 半平面体在边界上受集中力
4—10 半平面体在边界上受分布力
A r 2 B(1 2 ln r ) 2C r A 2 B(3 2 ln r ) 2C r
r r
由此可以看出，应力分量只是r得函数，不 随而变化，且只有正应力，无剪应力
一、轴对称问题的应变和位移
1、应变分量
1 A r [(1 ) 2 (1 3 ) B E r 2(1 ) B ln r 2(1 )C ] 1 A [(1 ) 2 (3 ) B E r 2(1 ) B ln r 2(1 )C ]
1 sin yx ds sin 1 cos 0
r x cos y sin 2 xy sin cos
2 2
同理，由平衡方程：
F 0
2 2
r ( y x ) sin cos xy (cos sin )
o
x
y yx

第七章_弹性力学平面问题的极坐标系解答

第七章_弹性力学平面问题的极坐标系解答

1 ∂u r ∂uθ uθ + − ∂r r ∂θ r
1.3 变形协调方程
1 ∂ 2ε r 1 ∂ 2 1 ∂2 1 ∂ε r + (rε θ ) − 2 (rγ rθ ) − =0 r ∂r r 2 ∂θ 2 r ∂r 2 r ∂r∂θ
1.4 物理方程 平面应力问题：
εr =
1 1 2(1 + ν ) (σ r − νσ θ ) ， ε θ = (σ θ − νσ r ) ， γ rθ = τ rθ E E E E ν E→ 平面应变问题将上式中 ，ν → 即得。 1 −ν 1 −ν 2
θ
r P y
x
σ σθ ,τrθ=τθ r 应变：εr, εθ ,γrθ=γθ r
应力： r, 位移：u r
, uθ
直角坐标与极坐标之间关系:
y=rsinθ ∂ ∂ ∂r ∂ ∂θ ∂ sin θ ∂ = + = cos − ∂x ∂r ∂x ∂θ ∂x ∂r r ∂θ
x=rcosθ,
∂ ∂ ∂r ∂ ∂θ ∂ cosθ ∂ = + = sin θ − r ∂θ ∂y ∂r ∂y ∂θ ∂y ∂r
2
则
d 2 1 d 1 d dφ 1 d d 1 d dφ ∇ φ =( 2 + ) (r ) = (r ) = 0 r r dr r dr dr r dr dr r dr dr dr
4
逐次积分（四次）可将轴对称问题的φ
(r)基本形式得到：
1 d2 1 dε r ⇒ (rε θ ) − =0 2 r dr r dr
⇒
d (rε θ ) = ε r ——变形协调方程 dr
由几何方程： rε θ

弹性力学简明教程-平面问题的极坐标解答习题详解

弹性力学简明教程-平面问题的极坐标解答习题详解

4第四章年面问軀的級坐标解各典型例题讲解例4T 如图所示，矩形薄板在四边受纯剪切力作用，切应力大小为q 。

如果 离板边较远处有一小圆孔，试求孔边的最大和最小正应力。

例4-1图【解】（1）根据材料力学公式，求极值应力和量大正应力的方位角％其中 = 6 = 0, q = % 得最大正应力。

税“所在截面的方位角为％若在该纯剪切的矩形薄板中，沿与板边成殳方向截取矩形ABCD,则在其边界 4上便承受集度为q的拉力和压力，如图所示。

这样就把受纯剪切作用的板看作与一对边受拉，另一对边受压的板等效。

（2）取极坐标系如图。

由a =t7 cos 2(^(1--^-)(1-3-^5-),P~ P-厂4(4-18)=-^cos2^(l + 3—XP2 2% = -q sin 2卩(1 一二)(i+3 二)・得矩形薄板ABCD内的应力分量为2 2j =gcos2°（l-爲）（1-3牛）（a）=-^ cos 2^（1+ 3^-）（b）p2 2% sin 2卩（1 - $）（1+ 3 爲）（c）其中a为小孔的半径，而孔边最大与最小正应力由式（b）,在p = a处得到兀=-q cos 2^(1 + 3—) = -4cos2©当（P = 0, Tl时，孔边最小正应力为（％）仙=一切，当申=±夕时，孔边最大正应力为（％）*乂= 4q。

分析：矩形板ABCD边界上各点的应力状态与板内无孔时的应力状态相同。

也可以应用叠加法，求解薄板的各种较复杂的平面应力（应变）问题。

习题全解4-1试比较极坐标和直角坐标中的平衡微分方程、几何方程和物理方程，指出哪些项是相似的，哪些项是极坐标中特有的？并说明产生这些项的原因。

【解】（1）极坐标，直角坐标中的平衡微分方程—+——+ ― / =0 dp p d (p p dr 1 Oq-^- + ---------- +—^ + f=0Pdcr dr.K—^ + —+ / =0dx dy ——+ —— + /v =0dy dx将极坐标中的平衡微分方程与直角坐标中的平衡微分方程相比较，第一式中, 前两项与直角坐标相似；而严项是由于正P 面上的面积大于负P 面上的面积而产生 的，-严是由于正负（P 而上的正应力％在通过微分体中心的P 方向有投影而引起的。

平面问题极坐标解答

平面问题极坐标解答

Fx 0
0
a cos
sin ad 0
a
Fy 0
0
a sin
cos ad 0
a
MO 0
0
a ad
a
M
0
a
4.3 stress function and compatibility equation in polar coordinates
τxy=u/y+v/x中的一般规律
• 由τxy=u/y+v/x，总结出一般规律，即设有 两个正交坐标方向，一个坐标方向的位移（如 u）对另一个坐标方向（y）求导为该坐标方向 （y）线段的转角。
1. u/y--x方向的位移 u 对y坐标求导为y方向线 段的转角。
2. v/x--y方向的位移 v 对x坐标求导为x方向线 段的转角。
几何学和物理学三个方面来考虑。
直角坐标不
大方便
弹性力学 第四章
2
Polar coordinates 极坐标
• The position of a point P in polar coordinates is defined
by the radial coordinate ρand the angular coordinate φ.
极坐标中的应力函数及相容方程
1. 极坐标下的应力分量与相容方程
方法1：（步骤）
（1）利用极坐标下的几何方程，求得应变表示的相容方程：
1
2 2
1
2
1
2 ( )
（2）利用极坐标下的物理方程，得应力表示的相容方程：
2
2
1
1
2
2
(
)
0
（常体力情形）

采用极坐标求解弹性力学平面问题基本问题

采用极坐标求解弹性力学平面问题基本问题

采用极坐标求解弹性力学平面问题基本问题一、内容介绍在弹性力学问题的处理时，坐标系的选择从本质上讲并不影响问题的求解，但是坐标的选取直接影响边界条件的描述形式，从而关系到问题求解的难易程度。

对于圆形，楔形，扇形等工程构件，采用极坐标系统求解将比直角坐标系统要方便的多。

本章的任务就是推导极坐标表示的弹性力学平面问题基本方程，并且求解一些典型问题。

二、重点1、基本未知量和基本方程的极坐标形式；2、双调和方程的极坐标形式；3、轴对称应力与厚壁圆筒应力；4、曲梁纯弯曲、楔形体和圆孔等典型问题1 平面问题极坐标解的基本方程学习思路:选取极坐标系处理弹性力学平面问题，首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。

本节的主要工作是介绍基本物理量，包括位移、应力和应变的极坐标形式；并且将基本方程，包括平衡微分方程、几何方程和本构关系转化为极坐标形式。

由于仍然采用应力解法，因此应力函数的极坐标表达是必要的。

应该注意的是坐标系的选取与问题求解性质无关，因此弹性力学直角坐标解的基本概念仍然适用于极坐标。

学习要点：1、极坐标下的应力分量；2、极坐标平衡微分方程；3、极坐标下的应变分量；4、几何方程的极坐标表达；5、本构方程的极坐标表达；6、极坐标系的Laplace算符；7、应力函数。

1、极坐标下的应力分量为了表明极坐标系统中的应力分量，从考察的平面物体中分割出微分单元体ABCD，其由两个相距dρ的圆柱面和互成dϕ的两个径向面构成，如图所示在极坐标系中，用σρ 表示径向正应力，用σϕ 表示环向正应力,τϕρ 和τρϕ 分别表示圆柱面和径向面的切应力，根据切应力互等定理，τϕρ ＝τρϕ 。

首先推导平衡微分方程的极坐标形式。

考虑到应力分量是随位置的变化，如果假设AB面上的应力分量为σρ 和τϕρ,则CD面上的应力分量为如果AD面上的应力分量为σϕ 和τρϕ ，则BC面上的应力分量为。

同时，体力分量在极坐标径向ρ 和环向 ϕ方向的分量分别为F bρϕ 和F bϕ 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可通过微分关系直接由直角坐标系下的几何方程得到。 同前分析，当 0 时，
所以
即
四. 极坐标系下的物理方程
因、方向正交，则物理方程与直角坐标系下具有相同形式。 即 当为平面应变问题时，E1E、1 。
五. 极坐标系下的相容方程
极坐标系下如果用应力函数表示相容方程，体力必须为零 或关于 ( ， ) 有势。
x y
2
f x f y (1 ) x y 0
f f 1 f 1
2
五. 极坐标系下的应力边界条件
设边界S的外法线方向与 、 方向的方向余弦分别为 l1、 l2 ，其上作用的面力沿、方向的分量分别为f、f 。则其 应力边界条件与直角坐标系下具有相同形式。 即
2
2 1 1 2 2 2 2
二. 极坐标系下的平衡微分方程
1. 直角坐标与极坐标系下的应力分量关系
（1）极坐标系下的应力分量和体力分量
O
如图，根据应力状态的定义， 过P 点分别以 方向和 方向为法线的截面 上的应力 、、 ， 作为在极坐 标系下的应力分量。 称为径向应力， y 称为环向向应力。 （2）应力分量的坐标转换
d 1 d 2 0 d d
2 2

f 0
1 u
（不计体力）
f f 1
2
应力分量 边界条件
应力分量 （不计体力）
( ) s l1 ( ) s l2 f ( ) s l1 ( ) s l2 f
应力边界条件
位移边界条件
(u ) s u (u ) s u
§6-6 平面问题在极坐标系下求解
一. 轴对称问题的应力与相应的位移
1.轴对称问题的特征
2 2 cos 2 sin 2 2 sin cos 2 xy sin cos cos 2 sin 2 sin cos 2 2 2 2
2 2 2 2 x y

y
x
当 0 时，O点受集中力偶，但无法使 用圣维南原理进行简化。 可使用截面法建立 外力与内力的关系，即O点的应力边界条件。 由半圆上的应力和外力的平衡关系，有
F
x
0
F
y
0
Mz 0
cos ad sin ad 0 cos sin d 0 a 0 sin cos d 0 a 0 a d M a ad M 0
§6-5 平面问题在极坐标系下的基本方程
在平面问题中，有些物体的截面几何形状（边界）为圆形、扇形，对 于这类形状的物体宜采用极坐标 ( ,) 来解。
一. 直角坐标与极坐标的微分关系
x y
2 2 2
x cos
y sin
y sin 2 x x cos 2 y

x

P


视 P- 为旧坐标，P点的应力状态为 、、 ； 视 O-xy 为新坐标，求P点的应力分量 x、y、xy yx 。
由应力状态的坐标转换公式
代入计算得
（3）体力分量的坐标转换 设极坐标系下的体力分量为 f 、 f 。 将其分别向 x、y 方向投影得
( ) s l1 ( ) s l2 f ( ) s l1 ( ) s l2 f
例6-6
写出图示问题的应力边界条件
O
（1） 上边： 0，l1 0，l2 1
q0
( ) 0 0
( ) 0

l


l


三. 极坐标系下的几何方程
1. 直角坐标与极坐标系下的位移分量关系 类似体力分量的投影关系
O

Байду номын сангаас
x

P u
u u
2. 极坐标系下的应变分量
y

v

将P点分别沿 和 方向（相互垂直）两线元的线应变 、 及其切应变 ， 作为P点的应变分量。
3. 极坐标系下的几何方程
此即一阶微分关系
同理可得各阶微分关系，如
2 sin sin cos cos 2 x sin sin sin sin cos cos cos cos
O
y arctan x x cos x y sin y

x
x y
P y
sin cos x x x cos sin y y y

以此位置的直角坐标系， 建立平衡微分方程。即
同理
x x 0 y 1 2 y 0
xy x 0 xy 1 y 0
物理方程
相容方程
2
1 1 2 , 0 2 2
2 2
2
（无体力）
（计体力）
f f 1 f 或 1
f f f f

x

u u

y
2.轴对称问题的基本方程 平衡微分方程 几何方程 物理方程 相容方程 计体力时
在不计体力的情况下， 可通过微分关系直接由直角坐 标系下的相容方程得到。
1 1 2 , 0 （展开共8项） 2 2 将O-xy坐标系旋转至 x 与 重合，即 0，此时
2 2 2
所以

y


x
当体力不为零或无势时，可用应力表示相容方程
( ) s f
（不计体力）
(u )s u
3.应力函数与应力分量
将相容方程展开得
令
d 4 2 d3 1 d 2 1 d 2 3 0 4 3 2 d d d d
d dt d 1 d d d dt dt
x
q0
y
斜边： ，l1 0，l2 +1
( ) 0
( ) 0
O
P M

x
（2） 内侧： a，l1 1 ，l2 0


( ) a 0
( ) 0 0
a
外侧： b，l1 +1 ，l2 0
b
( ) b 0
2
2 2sin cos 2 sin 2 2sin cos sin 2 2 2 2 cos 2 2 2 2 2 x 2 2 2sin cos 2 cos2 2sin cos cos2 2 2 sin 2 2 2 y 2 2


0 a 0 a
0 a a a 0 a
2
0
a
0
a
a 0
五. 极坐标系下的基本方程总结
1 f 0 1 2 f 0
平衡微分方程

几何方程
x yx fx 0 y x 0 xy y fy 0 y x 0
f x 0
f
f
y 0
f

代入即得
1 f 0 1 2 f 0
( ) b 0
y
上端： 0，l1 0 ，l2 1
O
P M
x
面力向形心简化
a

b
y
或向O简化
（3） 半无限平面
当 0 时，上边
M O a
( ) 0 0 ( ) 0 0
( ) 0 ( ) 0
f O

x

P f
y


2. 极坐标系下的平衡微分方程 由直角坐标系下的平衡微分方程推导
x sin cos cos2 sin 2 2 sin cos x 3 2 2 cos sin cos 2sin cos x sin 2 cos 2 sin cos 当 时 0 y
sin sin 2 2 sin cos 2sin sin cos cos 2

y x
x yx fx 0 x y xy y fy 0 x y
1 2 1 2 cos 2 sin cos 2 sin 2 sin 2 cos sin 2 sin 2 cos
（1）截面的几何形状对称于中心轴，如圆环、圆盘、圆筒。
（2）荷载与约束对称于中心轴。 因此环向体力 f 0 ； 在边界上 ，环向的面力和位移为零；即