光纤光学教学课件-第七讲共25页文档

NA(r) n0 (r)sinimax(r) n2 (r) n22
n2 n n1
2020/4/22
一、倾斜光线
射线方程：
d (n dr) n(r) dS dS
轴向分量方程：
d n dz 0 dS dS
角向分量方程：
n dr d d nr d 0
dS dS dS dS
2020/4/22
约束光线：
条件： n22 n 2 n12 即：
n2 n(r0 )cosz (r0 ) n1
光线存在区域: rg1 r rg2 内散焦面半径： rg1 外散焦面半径： rg 2
n12
ng2
n22
n22
I2 a2
0
2020/4/22 © HUST 2012
n2 r
n2
r
I2 r2
dn dz
0
横向分量：
d dS
ur (rer )
dr dS
ur er
r
ur d er
dS
（矢量关系式
ur d er
d
uur
euur，dde
ur er )
dr dS
ur er
r
d
dS
uur e
d dS
[n
d dS
ur (rer )]
d dS
(n
dr dS
ur er )
d dS
(nr
d
dS
uur e )
r
Const
n ：第一射线不变量,由光线的入射条件所决定！
同一光线：n 值相同；不同光线：n值不同！
轴向运动：广义折射定理
2020/4/22 © HUST 2012

理论——耦合模理论
基本思想：相耦合的两波导中的场, 各自保持了该波导独立 存在时的场分布和传输系数, 耦合的影响表现在场的复数振 幅的沿途变化。设两波导中的复数振幅为A1和A2。由于耦合作 用, 它们沿长度方向变化。
dA1 (z) dz
i(1
C11 ) A1
iC12 A2
dA2
(
Z
)
dz
i(2
•Light of the specified wavelength traveling along the fiber is
reflected from the grating back in the direction from which it came.
•Wavelengths which are not selected are passed through with little
制作工艺：熔锥型、磨抛型
熔锥型器件（强耦合模激励理论），使两光纤芯靠近，使 传播场向外扩展，以便在相当短的锥体颈部区域出现有效 的功率耦合。在耦合器中功率耦合最有效区域（颈部区域） 内的模式基本上是包层模，传播场脱离纤芯，这时场是在 包层和外部媒体（空气或其他适合的填料）所形成的新波 导中传播。
磨抛型器件（弱耦合理论），利用光学冷加工（机械抛磨） 除去光纤的部分包层，使光纤波导能相互靠近，以形成瞬 逝场相互渗透。利用微调装置改变两光纤的相对位置可以 改变耦合器的耦合率。
•the most important aspect is that the effect is asymmetric.
•materials : YIG (YttriumIron-Garnet)
2. Polarisation Independent Isolator

B、光纤检测：
光纤检测的主要目的是保证系统连接的质量，减少故障 因素以及故障时找出光纤的故障点。检测方法很多，主要 分为人工简易测量和精密仪器测量。
a.人工简易测量：
这种方法一般用于快速检测光纤的通断和施工时用来分 辨所做的光纤。它是用一个简易光源从光纤的一端打入可 见光，从另一端观察哪一根发光来实现。这种方法虽然简 便，但它不能定量测量光纤的衰减和光纤的断点。
6.光纤的应用
人类社会现在已发展到了信息社会，声音、图 象和数据等信息的交流量非常大。以前的通讯手 段已经不能满足现在的要求，而光纤通讯以其信 息容量大、保密性好、重量轻体积小、无中继段 距离长等优点得到广泛应用。其应用领域遍及通 讯、交通、工业、医疗、教育、航空航天和计算 机等行业，并正在向更广更深的层次发展。
FC
SC
SC-LC SC-SLCC LC
SC-SC
SC
SC
SC-ST
SC
ST
ST-ST
ST
ST
ST-LC
LC
ST
ST-SC
二、光缆的结构特点、种类 及型号的命名方法
一、光缆结构的特点
光缆的结构与电缆大致相同，但由于 光纤材料的性质和传光特性，所以其结构 与电缆又有不同之处。其特点如下：
膏时，防水效果较好，但连接时防水软膏 （2）它可以用一次涂覆光纤直接放置于骨架槽内，省去二次涂覆过程。
5/125μm，美国标准
的清除比较困难。采用防水带（粉）时， 31μm波长处的衰减值将增大。
活动连接是利用各种光纤连接器件（插头和插座），将站点与站点或站点与光缆连接 起来的一种方法。 因此，在不久的将来实现全球无中继的光纤通信是完全可能的。
1.光纤理论与光纤结构

《 光纤光学》复习提纲
光线理论 模式理论 光纤性能 光纤器件 光纤连接
光线理论
重要概念
– 光波导、光纤分类、子午光线、数值孔径、传输 容量、传光传像特性、散焦面、广义折射率定理、 光线轨迹及特点、光线分类
重要公式
– 射线方程、散焦面半径、折射率分布、数值孔径
模Байду номын сангаас理论
重要概念
– 模式定义及性质、模式分类及场分布特点、模 式简并、线偏振模、主模、分离变量法、传播 常数、导模截止与远离截止、基模场分布函数、 基模偏振特性、色散曲线分析、模式确定及数 目分析、导模光斑分布图、模式输出特性、 WKB近似方法思路
写出SIOF中模式数目与V值的关系式。 弱导光纤中组成线偏振模式的理论依据是什么？
为什么LP0m模式只有两重简并？ 实际光纤中传播的模式是线偏振模式吗？为什么？
画出LP6,8模式场分布示意图。 高阶模式与低阶模式哪个输出角度大？
4
GIOF的数值孔径有何不同? 分别说明内散焦面、外散焦面、辐射散焦 面的物理意义。 为什么GIOF又称为“折射型”光纤？ GIOF中光线角向运动有何特点？ 分别说明约束光线、隧道光线和折射光线 的特点。
2
设计一种光波导结构，其传光波导层为平板形 状，标出折射率结构。 从数学上证明，在均匀折射率介质中，光纤轨 迹为直线传播。 如果已经知道光纤中只允许1个模式存在，能否 通过外界激励获得2个模式传播？ “纵横关系式”有何作用？ 光场分量的哪一个分量总是独立满足波导场方 程？写出该波导场方程式。
大家有疑问的，可以询问和交流
光纤器件
重要概念
– 自聚焦透镜的成像特性、光纤耦合器/WDM器 件的工作原理及设计、光隔离器/环行器的工作 原理及设计、光纤光栅的工作原理及设计、光 纤激光器与放大器的工作原理及设计。

n2
θ2
•
n1
θ1
•
θ
•
θ0
NA n12 n22 n1 2
定义光纤的数值孔径为入射临界角θ0 的正弦,即:
2021/5/18
27
• △ 越大,NA越大，光纤第2聚7页光/共能52页力越强，可得到越高的
2021/5/18
临界光锥 c
非全反射光
全反射光
纤 芯 n( ＞n ) 12 包 层 n( 2)
•
n0
n2
θ2
•
n1
θ1
•
θ
•
θ0
2021/5/18
第二种情况:
光线以大于θ0的角度入射光纤端面,它产生的界 面入射角将小于θc ，光线在包层中的折射角小于 900 ，该光线将射入包层（24 散失掉）。
第24页/共52页
阶跃光纤(step-index fiber)的射线光学分 析(续)
•
n0
n2
θ2
•
n1
θ1
•
θ
•
θ0
2021/5/18
第三种情况:
光线以小于θ0的角度入射光纤端面,它产生的界面 入射角将大于θc ，光线在包层中的折射角大于900 , 该 光 线 将 在 界 面 产 生 全 反25射 ( 从 而 向 前 传 播 ) 。
第25页/共52页
阶跃光纤(step-index fiber)的射线光学分 析(续)
τ= (n1l)/c = (n1Lsecθ1 )/c ≌ (n1L)/c*(1+ θ12/2)
式中C为真空中第的30光页3/0共速52页。
阶跃光纤(step-index fiber)时间延迟
由上式得到最大入射角(θ= θ0)和最小入射角 (θ=0)的光线之间时间延迟差近似为:

62.5/50m
8～10m
1.0m
125m2m
2%
245m10m
15m
2m
•16
光纤：参数
光纤的光学及传输特性参数
• 模场直径 • 衰减系数 • 色散系数 • 截止波长 • 弯曲损耗 • 偏振模色散
•17
光纤：参数
光纤的光学及传输特性参数
模场直径：
高斯分布的单模光纤， 模场直径是光场幅度 分布1/e处各点所围成 圆的直径，也等于光 功率分布1/e2处各点 所围成圆的直径。
一部分入射光将被反射
一部分入射光将进入第二种媒质，并产生折射
1 2
媒质1 折射率n1
媒质2 折射率n2
1=2
媒质1
1
折射率n1
2
媒质2
折射率n2
n1·Sin1=n2·Sin2
•3
折射率 n＝光在真空中的传播速度/光在该媒质中的传播速度
媒质 真空 空气 水 多模光纤 单模光纤 玻璃 钻石
折射率 1.0 1.0003 1.33 1.457 1.471 1.5~1.9 2.42
1
4
4
3
1 非色散位移光纤 2 色散位移光纤 3 色散平坦光纤 4 非零色散位移光纤
2
0 1200
1400 1500 1600 1700 1800 nm
-4
-8
波长(nm)
•22
光纤：参数
光纤的光学及传输特性参数
截止波长：
光纤作为单模光纤工作的最短波长。工作 波长超过此波长时，只能传输基模，此时光纤 为单模光纤；工作波长低于此波长时，除基模 外，高次模也可传输，此时光纤为多模光纤。
如：Corning的Submarine Leaf光纤 Lucent的TrueWave XL光纤

4.常用光纤规格： 单模：8/125μm，9/125μm，10/125μm。多模：50/125μm（欧洲标准） 62.5/125μm（美国标准） 工业，医疗和低速网络：100/140μm，200/230μm 塑料：98/1000μm，用于汽车控制 光缆的种类 1.按敷设方式分有：自承重架空光缆，管道光缆，铠装地埋光缆和海底光缆。 2.按光缆结构分有：束管式光缆，层绞式光缆，紧抱式光缆，带式光缆，非金属光缆和可 分支光缆。 3.按用途分有：长途通讯用光缆、短途室外光缆、混合光缆和建筑物内用光缆。
光纤种类及光纤跳线
3.光纤的种类： A.按光在光纤中的传输模式可分为：单模光纤和多模光纤。 所谓“模”就是指以一定的角度进入光纤的一束光线。多模光纤使用发光二极管（ LED）作为发光设备，而单模光纤使用的则是激光二极管（LD）。 单模光纤芯径小（10m m左右），仅允许一个模式光源传输，色散小，传递数据的 质量更高，传输距离更长。工作在长波长（1310nm和1550nm），与光器件的耦合相对 困难。但其色度色散起主要作用，这样单模光纤对光源的谱宽和稳定性有较高的要求， 即谱宽要窄，稳定性要好。单模光纤通常被用来连接办公楼之间或地理分散更广的网络 。 多模光纤芯径大（62.5m m或50m m），允许上百个模式光源传输，色散大，工作 在850nm或1310nm。与光器件的耦合相对容易。因为不同光线进入光纤的角度不同， 所以到达光纤末端的时间也不同。这就是我们通常所说的模色散。色散从一定程度上限 制了多模光纤所能实现的带宽和传输距离。 这就限制了传输数字信号的频率，而且随距 离的增加会更加严重。 例如：600MB/KM的光纤在2KM时则只有300MB的带宽了。正是 基于这种原因，多模光纤一般被用于同一办公楼或距离相对较近的区域内的网络连接。 而对于光端模块来讲，严格的说并没有单模、多模之分。所谓单模、多模模块，指 的是光端模块采用的光器件与何种光纤配合能获得最佳传输特性。单模收发器可以用于 多模光缆链路，但注意跳线要用多模的。 单模模块一般采用LD或光谱线较窄的LED作为光源，耦合部件尺寸与单模光纤配合 好。多模模块一般采用价格较低的LED作为光源，耦合部件尺寸与多模光纤配合好。

D与B的法向分量连续：
E1t＝E2t; H1t＝H2t; B1n＝B2n; D1n＝D2n
第十四页，共25页。
分离变量：电矢量与磁矢量分离
得到只与电场强度E(x,y,z,t)有关的方程式及只与磁
场强度H(x,y,z,t)有关的方程式：波动方程
第十五页，共25页。
分离变量: 时空坐标分离
前提：光纤传播单色光波，时间函数为简谐函数 令场分量为：
第二十页，共25页。
模式命名
根据场的纵向分量Ez和Hz的存在与否,可将 模式命名为:
(1)横电磁模(TEM): Ez＝Hz＝0;
(2)横电模(TE): Ez＝0, Hz≠0; (3)横磁模(TM): Ez≠0,Hz＝0; (4)混杂模(HE或EH):Ez≠0, Hz≠0。 光纤中存在的模式多数为HE(EH)模,有时 也出现TE(TM)模。
2＝w2emb2＝n2 k02b2横向传播常数
bn(r)k0cosqz 纵向传播常数
第十七页，共25页。
波导场方程的数学物理意义
波导场方程：是波动光学方法的最基本方程。 它是一个典型的本征方程,其本征值为或β。 当给定波导的边界条件时,求解波导场方程可 得本征解及相应的本征值。通常将本征解定 义为“模式”.
分析思路
电磁分离
时空分离 纵横分离
第十三页，共25页。
波动方程 wave equation
亥姆赫兹方程 Helmholtz equation 波导场方程
麦克斯韦方程
H D/t EB/t
D 0 B0
D＝εE B＝μH
e＝e0n2
边界条件：在两种介质交界面上电磁场矢量的E(x,y)和H(x,y)切向分量要连续,
第二十一页，共25页。

光纤课件
目 录
• 光纤基础知识 • 光纤通信系统 • 光纤网络 • 光纤传感技术 • 光纤在医疗领域的应用 • 未来展望
01
光纤基础知识
光的本质与传播
01
02
03
光的波动性
光在传播过程中表现出波 动性质，如干涉、衍射等 。
光的粒子性
光同时具有粒子性质，光 子是光的能量单位，具有 动量和能量。
光的传播速度
低损耗
光纤传输损耗较低，可实现长 距离传输。
带宽大
光纤传输带宽较大，可同时传 输多种信号。
抗干扰能力强
光纤传输不受电磁干扰影响， 具有较高的保密性和稳定性。
温度稳定性好
光纤材料具有较好的温度稳定 性，可在不同环境下稳定传输
。
02
光纤通信系统
光源与光调制
光源
激光器（LD）和发光二极管（ LED）是光纤通信中常用的光源 。它们能够产生单色光，具有较 高的频率和较窄的光谱线宽。
光调制
光调制是将信息转换为光信号的 过程。常见的光调制方式包括开 关键控（OOK）、脉冲位置调制 （PPM）和相位调制（PSK）等 。
光纤的连接与耦合
光纤连接器
光纤连接器是用来连接两根光纤的器 件，常见的光纤连接器有SC、FC、 LC和ST等类型。
光纤耦合器
光纤耦合器是将多根光纤连接在一起 ，实现光信号的分路、合路和传输的 器件。常见的光纤耦合器有1x2、1x4 、1x8等类型。
新工艺
随着纳米技术的发展，光纤制造中的 纳米光刻、化学气相沉积等新工艺逐 渐应用于光纤预制棒的生产，这些新 工艺能够提高光纤的制造精度和降低 生产成本。
光纤通信技术的发展趋势
01
超高速率
随着数据传输需求的增长，光纤通信系统的传输速率不断提高，未来的

侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
光纤光学教学课件-第七讲 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。

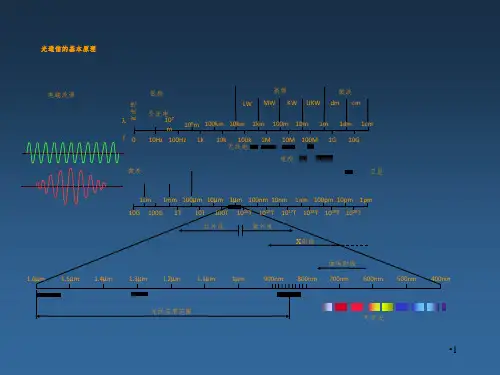
光缆专业基础知识光纤通信是利用光波作载波，以光纤作为传输媒质将信息从一处传至另一处的通信方式，被称之为“有线”光通信。

当今，光纤以其传输频带宽、抗干扰性高和信号衰减小，而远优于电缆、微波通信的传输，已成为世界通信中主要传输方式。

特点：。

采用这样的带宽，20THz（1)通信容量大、传输距离远；一根光纤的潜在带宽可达系统已经投入商400Gbit/s只需一秒钟左右，即可将人类古今中外全部文字资料传送完毕。

，这0.2dB/km1.55μm附近，石英光纤损耗可低于业使用。

光纤的损耗极低，在光波长为比任何传输媒质的损耗都低。

因此，无中继传输距离可达几十、甚至上百公里。

(2)信号干扰小、保密性能好；(3）抗电磁干扰、传输质量佳，电通信不能解决各种电磁干扰问题，唯有光纤通信不受各种电磁干扰。

(4）光纤尺寸小、重量轻，便于铺设和运输；(5）材料来源丰富，环境保护好，有利于节约有色金属铜。

(6）无辐射，难于窃听，因为光纤传输的光波不能跑出光纤以外。

(7)光缆适应性强，寿命长。

(8）质地脆，机械强度差。

(9）光纤的切断和接续需要一定的工具、设备和技术。

(10）分路、耦合不灵活。

(11）光纤光缆的弯曲半径不能过小（>20cm）(12）有供电困难问题。

一、光缆型号光缆型号一般由五个部分组成，第一部分表示分类，第二部分表示加强构件，第三部分派生（形状、特性等），第四部分表示护层，第五部分表示外护层。

1、分类GY 通信用室外光缆，GM 通信用移动式光缆，GJ 通信用室内光缆，GS 通信用设备内光缆，GH 通信用海底光缆，GT 通信用特殊光缆，GR 通信用软光缆、加强构件2．无金属构件，F 非金属加强构件，G 金属重型加强构件，H 非金属重型加强构件3、光缆结构特性无层绞式结构，S 光纤松套被覆结构，J 光纤紧套被覆结构，D 光纤带结构，G 骨架槽结构，X 中心管式结构，T 填充式结构，B 扁平结构，Z 阻燃结构，C 自承式结构，E 护层椭圆截面4、光缆护套Y 聚乙烯，V 聚氯乙烯，F 氟塑料，U 聚氨脂，E 聚脂弹性体A 铝带-聚乙烯粘结护套，S 钢带-聚乙烯粘结护套，W 夹带钢丝的钢带-聚乙烯粘结护套，L 铝，G 钢，Q 铅5、光缆外护套（1）铠装0 无铠装，2 双钢带，3 细圆钢丝，4 粗圆钢丝，5 皱纹钢带6 双层圆钢带（2）外被层或外套1 纤维外护套，2 聚氯乙烯护套，3 聚乙烯护套，4 聚乙烯护套加敷尼龙护套，5 聚乙烯管常用型号列表：下图为实际光缆的外层标示：聚乙-上图所表示的光缆与及意思是：室外通信用、金属加强构件、松套层绞、全填充、钢米。