各种进制的算法(终审稿)

各进制转换方法范文进制转换是指将一个数从一种进制表示转换为另一种进制表示的过程。

常见的进制包括二进制、八进制、十进制和十六进制。

下面将介绍各种进制的转换方法。

一、二进制转换方法：二进制是计算机最基本的进制，它由0和1两个数字组成。

1.十进制到二进制的转换：除2取余法，即将十进制数不断除以2，直到商为0为止。

将每次得到的余数倒序排列，即为二进制数。

例如：将十进制数10转换为二进制数。

10÷2=5余数05÷2=2余数12÷2=1余数01÷2=0余数1所以10的二进制表示为1010。

2.二进制到十进制的转换：将二进制数从右向左依次从0次方开始标记，每个位置上的数与2的次方相乘，然后将结果相加。

例如：将二进制数1010转换为十进制数。

1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=10所以1010的十进制表示为10。

二、八进制转换方法：八进制是以8为基数的进制，用到了0-7这8个数字。

1.十进制到八进制的转换：除8取余法，即将十进制数不断除以8，直到商为0为止。

将每次得到的余数倒序排列，即为八进制数。

例如：将十进制数20转换为八进制数。

20÷8=2余数42÷8=0余数2所以20的八进制表示为242.八进制到十进制的转换：将八进制数从右向左依次从0次方开始标记，每个位置上的数与8的次方相乘，然后将结果相加。

例如：将八进制数24转换为十进制数。

2*8^1+4*8^0=16+4=20所以24的十进制表示为20。

三、十进制转换方法：十进制是我们常用的进制，它由0-9这10个数字组成。

1.二进制到十进制的转换：将二进制数从右向左依次从0次方开始标记，每个位置上的数与2的次方相乘，然后将结果相加。

例如：将二进制数1010转换为十进制数。

1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=10所以1010的十进制表示为10。

2.八进制到十进制的转换：将八进制数从右向左依次从0次方开始标记，每个位置上的数与8的次方相乘，然后将结果相加。

计算机各进制换算现代社会中，计算机几乎遍布各个角落，成为人们工作、学习、娱乐的重要工具。

而作为计算机的基础，进制转换是我们在编程和计算中必不可少的一项技能。

本文将为大家介绍计算机中常见的进制，以及如何进行各进制间的转换。

一．十进制在计算机中，我们最常用的进制是十进制。

十进制采用0-9这十个数字进行计数，每一位的权重是按照10的倍数逐级增加的。

例如数字3876，我们可以将其拆分为千位（3）、百位（8）、十位（7）和个位（6）。

其计算方式为：3876 = 3 * 10^3 + 8 * 10^2 + 7 * 10^1 + 6 * 10^0在计算机中，十进制数常被表示为一串数字，例如3876即表示为3876。

二．二进制二进制由0和1两个数字组成，是计算机内部最基本的进制。

在计算机中，所有数据都是以二进制形式进行存储和运算的。

例如数字1001，我们可以将其拆分为千位（1）、百位（0）、十位（0）和个位（1）。

其计算方式为：1001 = 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0在计算机中，二进制数通常以0b开头表示，例如1001即表示为0b1001。

三．八进制八进制由0-7这八个数字组成，每一位的权重是按照8的倍数逐级增加的。

例如数字235，我们可以将其拆分为百位（2）、十位（3）和个位（5）。

其计算方式为：235 = 2 * 8^2 + 3 * 8^1 + 5 * 8^0在计算机中，八进制数通常以0o开头表示，例如235即表示为0o235。

四．十六进制十六进制由0-9这十个数字和A-F这六个字母组成，每一位的权重是按照16的倍数逐级增加的。

例如数字4AF，我们可以将其拆分为千位（4）、百位（A）和个位（F）。

其中字母A-F分别表示十进制的10-15。

其计算方式为：4AF = 4 * 16^2 + 10 * 16^1 + 15 * 16^0在计算机中，十六进制数通常以0x开头表示，例如4AF即表示为0x4AF。

各种进制的算法范文进制是一种计数系统，用于表示数字和数值。

在计算机科学中，常用的进制有二进制（基数为2）、八进制（基数为8）、十进制（基数为10）、十六进制（基数为16）等。

不同进制对应不同的符号集，以及不同的计数规则。

下面将介绍各种进制的算法。

1.二进制算法：二进制是最基本的进制，仅包含两个数字0和1、二进制的表达方式非常简洁，并且在计算机中被广泛应用。

二进制算法是计算机内部运算的基础，例如加法、减法、乘法、除法等。

-加法算法：对于两个二进制数的相加，从右至左逐位相加，若两个位数相加结果为2，则将其写成0并将进位标记为1；若两个位数相加结果为3，则将其写成1并将进位标记为1、然后继续向左进行相加直至最高位，最后若有进位则写成新的位数。

-减法算法：对于两个二进制数的相减，从右至左逐位相减，若两个位数相减结果为负数，则从较高位借位1，被减位加2、直到最高位。

-乘法算法：对于两个二进制数的相乘，采用类似于十进制乘法的竖式计算。

从被乘数的最低位开始，逐位与乘数进行乘法运算，并将结果相加。

2.八进制算法：八进制是一种基数为8的进制方式，使用8个数字（0-7）。

在计算机科学中，八进制主要用于表示字节和内存地址。

八进制的运算与二进制类似，但每个八进制位代表3个二进制位。

-加法算法：对于两个八进制数的相加，从右至左逐位相加，若两个位数相加结果为8，则将其写成0并将进位标记为1；若两个位数相加结果为9，则将其写成1并将进位标记为1、然后继续向左进行相加直至最高位，最后若有进位则写成新的位数。

-减法算法：对于两个八进制数的相减，从右至左逐位相减，若两个位数相减结果为负数，则从较高位借位1，被减位加8、直到最高位。

3.十进制算法：十进制是最常用的进制方式，基数为10，使用0-9这10个数字。

十进制运算是人类日常生活和大部分计算机系统中最常见的运算方式。

-加法算法：从右至左逐位相加，若两个位数相加结果大于10，则将结果写成个位数并将进位标记为1、然后继续向左进行相加直至最高位，最后若有进位则写成新的位数。

进制的转换与运算进制是数学中的一个重要概念，是指数的计数体系。

常见的进制有十进制、二进制、八进制和十六进制等。

本文将分析进制的转换以及在计算机科学中的运算应用。

一、进制转换进制之间的转换是数学中基本的运算方式之一。

常见的进制转换包括十进制转二进制、二进制转十进制、十进制转八进制、八进制转十进制、十进制转十六进制和十六进制转十进制等。

下面分别进行详细介绍。

1. 十进制转二进制十进制（Decimal）是人们常用的数字表示方法，而计算机中使用二进制（Binary）进行运算。

十进制转二进制的方法是利用除二取余法，不断将十进制数除以二并记录余数，然后将余数倒序排列即可得到对应的二进制数。

2. 二进制转十进制二进制转十进制的方法是根据每一位的权重值进行计算。

对于一个二进制数，从右向左，每一位的权重值是2的n次方（n从0开始，逐位递增），将每一位与对应的权重值相乘后相加即可得到对应的十进制数。

3. 十进制转八进制八进制（Octal）是一种基数为8的计数系统。

十进制转八进制的方法是将十进制数不断除以8并记录余数，然后将余数倒序排列即可得到对应的八进制数。

4. 八进制转十进制八进制转十进制的方法是根据每一位的权重值进行计算。

对于一个八进制数，从右向左，每一位的权重值是8的n次方（n从0开始，逐位递增），将每一位与对应的权重值相乘后相加即可得到对应的十进制数。

5. 十进制转十六进制十六进制（Hexadecimal）是一种基数为16的计数系统，主要用于计算机科学中。

十进制转十六进制的方法是将十进制数不断除以16并记录余数，然后将余数倒序排列并用A~F表示超过9的数字，即可得到对应的十六进制数。

6. 十六进制转十进制十六进制转十进制的方法与八进制和二进制类似，根据每一位的权重值进行计算，将每一位与对应的权重值相乘后相加即可得到对应的十进制数。

二、进制运算在计算机科学中的应用进制运算在计算机科学中具有广泛的应用，特别是二进制运算。

各种进制之间的转换（可编辑修改word版）一：十进制数转换成二进制数。

随便拿出一个十进制数“39”，（假如你今天买书用了39 元）先来把这个39 转换成2 进制数。

商余数步数39/2= 19 1 第一步19/2= 9 1 （这里的19 是第一步运算结果的商）第二步9/2= 4 1 （这里的9 是第二步运算结果的商）第三步4/2= 2 0 （这里的4 是第三步运算结果的商）第四步2/2= 1 0 （这里的2 是第四步运算结果的商）第五步1/2= 0 1 （这里的1 是第五步运算结果的商）第六步那么十进制数39 转换成 2 进制数就是100111. 既39(10)=100111(2)解析一：1. 当要求把一个10 进制数转换成2 进制数的时候，就用那个数一直除以2 得到商和余数。

2. 用上一步运算结果的商在来除以2，再来得到商和余数。

3. 就这样，一直用上一步的商来除以2，得到商和余数！那么什么时候停止呢？4. 请看上述运算图，第六步的运算过程是用1 除以2.得到的商是0，余数是1. 那么请你记住，记好了啊共2 点。

A: 当运算到商为“0”的时候，就不用运算了。

B：1/2 的商为“0”余数为“1”。

这个你要死记住，答案并不是0.5！答案就是商为“0”余数为“1”。

你不用去思考为什么，记好了就行了！5. 在上述图中你会清晰的看到每一步运算结果的余数，你倒着把它们写下来就是“100111”了。

那么这个就是结果了。

6. 在上述图中符号“/”代表“除以”。

二：十进制数转换成八进制数。

随便拿出一个十进制数“358”，（假如你今天买彩票中了358 元）。

358 是我们现实生活中所用10 进制表达出来的一个数值，转换成八进制数十多少？商余数步数358/8= 44 6 第一步44/8= 5 4 （这里的44 是第一步运算结果的商）第二步5/8= 0 5 （这里的5 是第二步运算结果的商）第三步那么十进制数358 转换成8 进制数就是546。

进制数总结1. 什么是进制数进制数是一种用于表示数值的方法，它由一定的基数和一系列的数字符号组成。

常见的进制数有十进制、二进制、八进制和十六进制。

•十进制：使用基数10，由0-9这10个数字组成。

•二进制：使用基数2，由0和1两个数字组成。

•八进制：使用基数8，由0-7这8个数字组成。

•十六进制：使用基数16，由0-9和A-F这16个字符组成。

2. 总结进制间的转换方法2.1. 二进制与十进制的转换将一个二进制数转换为十进制数，可以通过加权求和的方法实现。

首先，从二进制数的最右边（低位）开始，按权重依次将每个二进制位与2的幂次方相乘，再将所有结果相加即可得到十进制数。

例如，二进制数1011转换为十进制数的计算过程如下：1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 0 + 2 + 1 = 11将一个十进制数转换为二进制数，可以使用除2取余法。

将十进制数不断除以2，将余数从低位到高位排列，直到商为0为止。

例如，十进制数25转换为二进制数的计算过程如下：25 / 2 = 商12，余数112 / 2 = 商6，余数06 / 2 = 商3，余数03 / 2 = 商1，余数11 /2 = 商0，余数1所以，十进制数25转换为二进制数10101。

2.2. 十六进制与二进制的转换在计算机领域中，经常使用十六进制表示二进制数，这是因为一位十六进制数可以表示4位二进制数。

通过将每个二进制位组成4位的二进制数，然后将这个4位的二进制数转换为一个十六进制数可以实现十六进制与二进制之间的转换。

例如，二进制数1110可以转换为十六进制数的计算过程如下：1110 = 1110= (1 * 2^3) + (1 * 2^2) + (1 * 2^1) + (0 * 2^0)= 8 + 4 + 2 + 0= E2.3. 八进制与二进制的转换将一个八进制数转换为二进制数，可以将每个八进制数位转换为对应的3位二进制数。

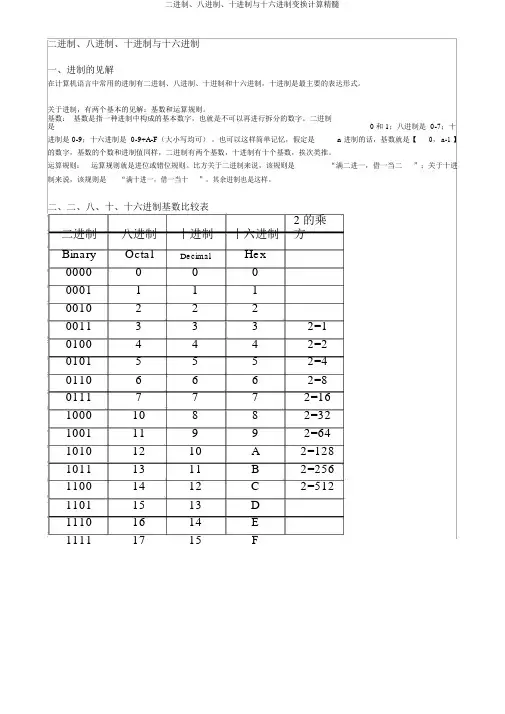
二进制、八进制、十进制与十六进制一、进制的见解在计算机语言中常用的进制有二进制、八进制、十进制和十六进制，十进制是最主要的表达形式。

关于进制，有两个基本的见解：基数和运算规则。

基数：基数是指一种进制中构成的基本数字，也就是不可以再进行拆分的数字。

二进制是0和 1；八进制是 0-7；十进制是 0-9；十六进制是 0-9+A-F（大小写均可）。

也可以这样简单记忆，假定是n 进制的话，基数就是【0， n-1 】的数字，基数的个数和进制值同样，二进制有两个基数，十进制有十个基数，挨次类推。

运算规则：运算规则就是进位或错位规则。

比方关于二进制来说，该规则是“满二进一，借一当二”；关于十进制来说，该规则是“满十进一，借一当十”。

其余进制也是这样。

二、二、八、十、十六进制基数比较表二进制八进制十进制十六进制2的乘方Binary Octal Decimal Hex00000000001111001022200113332=1 01004442=2 01015552=4 01106662=8 01117772=16 100010882=32 100111992=64 10101210A2=128 10111311B2=256 11001412C2=512 11011513D11101614E11111715F三、二进制转变成其余进制1.二制（ Binary ）——>八制（ Octal ）例子 1：将二制数（10010 ） 2化成八制数。

（10010） 2=（ 010 010 ）2= （ 2 2） 8=（ 22） 8例子 2：将二制数（）2化八制数。

（） 2=（ 0. 101 010 ） 2=（ 0. 5 2） 8=（） 8：因每三位二制数一位八制数，所以，以小数点界，整数位将二制数从右向左每开，不足 3位的在左用0填即可；小数位将二制数从左向右每3位一分开，不足3位的在右用可。

3位一隔0填即2.二制（ Binary ）——>十制（ Decimal ）例子 1：将二制数（10010 ） 2化成十制数。

从二进制数的最右数起，最右方的第一个数乘以2的0次方，第二个数乘以2的1次方……依次类推，把各结果累计相加就是转换后的十进制数。

例：1010=0*2^0+1*2^1+0*2^2+1*2^3=0+2+0+8=101、二进制数、八进制数、十六进制数转十进制数有一个公式：二进制数、八进制数、十六进制数的各位数字分别乖以各自的基数的(N-1)次方，其和相加之和便是相应的十进制数。

个位，N=1;十位，N=2...举例：110B=1*2的2次方+1*2的1次方+0*2的0次方=0+4+2+0=6D110Q=1*8的2次方+1*8的1次方+0*8的0次方=64+8+0=72D110H=1*16的2次方+1*16的1次方+0*16的0次方=256+16+0=272D2、十进制数转二进制数、八进制数、十六进制数方法是相同的，即整数部分用除基取余的算法，小数部分用乘基取整的方法，然后将整数与小数部分拼接成一个数作为转换的最后结果。

例：见四级指导16页。

3、二进制数转换成其它数据类型3-1二进制转八进制：从小数点位置开始，整数部分向左，小数部分向右，每三位二进制为一组用一位八进制的数字来表示，不足三位的用0补足，就是一个相应八进制数的表示。

010110.001100B=26.14Q八进制转二进制反之则可。

3-2二进制转十进制：见13-3二进制转十六进制：从小数点位置开始，整数部分向左，小数部分向右，每四位二进制为一组用一位十六进制的数字来表示，不足四位的用0补足，就是一个相应十六进制数的表示。

00100110.00010100B=26.14H十进制转各进制要将十进制转为各进制的方式，只需除以各进制的权值，取得其余数，第一次的余数当个位数，第二次余数当十位数，其余依此类推，直到被除数小于权值，最后的被除数当最高位数。

一、十进制转二进制如：55转为二进制2｜5527――1 个位13――1 第二位6――1 第三位3――0 第四位1――1 第五位最后被除数1为第七位，即得110111 二、十进制转八进制如：5621转为八进制8｜5621702 ―― 5 第一位（个位）87 ―― 6 第二位10 ―― 7 第三位1 ――2 第四位最后得八进制数：127658三、十进制数十六进制如：76521转为十六进制16｜765214726 ――5 第一位（个位）295 ――6 第二位18 ――6 第三位1 ――2 第四位最后得1276516二进制与十六进制的关系2进制0000 0001 0010 0011 0100 0101 0110 011116进制0 1 2 3 4 5 6 72进制1000 1001 1010 1011 1100 1101 1110 111116进制8 9 a(10) b(11) c(12) d(13) e(14) f(15)可以用四位数的二进制数来代表一个16进制，如3A16 转为二进制为：3为0011，A 为1010，合并起来为00111010。

进制的计算知识解析：一、数的进制1.十进制：我们常用的进制为十进制，特点是“逢十进一”。

在实际生活中，除了十进制计数法外，还有其他的大于1的自然数进位制。

比如二进制，八进制，十六进制等。

2.二进制：在计算机中，所采用的计数法是二进制，即“逢二进一”。

因此，二进制中只用两个数字0和1。

二进制的计数单位分别是1、21、22、23、……，二进制数也可以写做展开式的形式，例如100110在二进制中表示为：(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。

二进制的运算法则：“满二进一”、“借一当二”，乘法口诀是：零零得零，一零得零，零一得零，一一得一。

注意：对于任意自然数n ,我们有n 0=1。

3.k 进制：一般地，对于k 进位制，每个数是由0，1，2，，1k -（）共k 个数码组成，且“逢k 进一”．1k k >（）进位制计数单位是0k ，1k ，2k ，．如二进位制的计数单位是02，12，22，，八进位制的计数单位是08，18，28，． 4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+（）十进制表示形式：1010101010n n n n N a a a --=+++； 二进制表示形式：1010222n n n n N a a a --=+++；为了区别各进位制中的数，在给出数的右下方写上k ，表示是k 进位制的数如：8352（），21010（），123145（）,分别表示八进位制，二进位制，十二进位制中的数．5.k 进制的四则混合运算和十进制一样先乘除，后加减；同级运算，先左后右；有括号时先计算括号内的。

二、进制间的转换：一般地，十进制整数化为k 进制数的方法是：除以k 取余数，一直除到被除数小于k 为止，余数由下到上按从左到右顺序排列即为k 进制数．反过来，k 进制数化为十进制数的一般方法是：首先将k 进制数按k 的次幂形式展开，然后按十进制数相加即可得结果．如右图所示:十进制 二进制十六进制八进制例题精讲：模块一、十进制化成多进制【例 1】 把9865转化成二进制、五进制、八进制，看看谁是最细心的。

进制计算是指在不同进制下进行数值计算。

常用的进制包括二进制（base-2）、八进制（base-8）、十进制（base-10）和十六进制（base-16）等。

以下是一些常用的进制计算公式：1. 二进制转十进制：将二进制数按权展开并求和即可，即将每一位上的数乘以对应的权值再相加。

例如，二进制数1011表示的十进制数为：1 x 2³+ 0 x 2²+ 1 x 2¹+ 1 x 2⁰= 8 + 0 + 2 + 1 = 11。

2. 十进制转二进制：除2取余法，将十进制数不断除以2，将余数倒序排列即可得到二进制数。

例如，十进制数13表示的二进制数为：13 ÷2 = 6 余1；6 ÷2 = 3 余0；3 ÷2 = 1 余1；1 ÷2 = 0 余1。

因此，13的二进制表示为1101。

3. 八进制转十进制：将八进制数按权展开并求和即可。

例如，八进制数735表示的十进制数为：7 x 8²+ 3 x 8¹+ 5 x 8⁰= 448 + 24 + 5 = 477。

4. 十进制转八进制：除8取余法，将十进制数不断除以8，将余数倒序排列即可得到八进制数。

例如，十进制数477表示的八进制数为：477 ÷8 = 59 余5；59 ÷8 = 7 余3；7 ÷8 = 0 余7。

因此，477的八进制表示为735。

5. 十六进制转十进制：将十六进制数按权展开并求和即可。

其中，A-F用10-15表示。

例如，十六进制数2AF表示的十进制数为：2 x 16²+ 10 x 16¹+ 15 x 16⁰= 512 + 160 + 15 = 687。

6. 十进制转十六进制：除16取余法，将十进制数不断除以16，将余数倒序排列，其中10-15用A-F表示即可得到十六进制数。

例如，十进制数687表示的十六进制数为：687 ÷16 = 42 余15（F）；42 ÷16 = 2 余10（A）；2 ÷16 = 0 余2。

二进制、十进制、八进制和十六进制是计算机领域中常见的进制表示方法，它们在数据存储、数据传输和编程等方面都有着重要的应用。

本文将对这四种进制进行深入分析和比较，并介绍它们在计算机中的应用。

一、二进制表示方法1. 二进制是计算机中最基本的进制，它由0和1两个数字组成。

在二进制中，每个数字位的权值是2的幂，从右向左依次为1、2、4、8、16等。

二进制在数字存储和逻辑运算中有着重要的作用，如在CPU 中进行逻辑运算和控制信号的传输。

二、十进制表示方法1. 十进制是我们平常生活中最常用的进制，它由0到9共10个数字组成，以10为基数。

在十进制中，每个数字位的权值是10的幂，从右向左依次为1、10、100、1000等。

十进制在日常生活和商业计算中广泛应用，如货币计算和芳龄表示等。

三、八进制表示方法1. 八进制是一种较少使用的进制，它由0到7共8个数字组成，以8为基数。

在八进制中，每个数字位的权值是8的幂，从右向左依次为1、8、64、512等。

八进制在UNIX系统权限设置和程序设计中有时会用到。

四、十六进制表示方法1. 十六进制是一种广泛应用的进制，它由0到9和A到F共16个数字和字母组成，以16为基数。

在十六进制中，每个数字位的权值是16的幂，从右向左依次为1、16、256、4096等。

十六进制在计算机中广泛应用于内存和颜色表示，如网页设计和图形编程等。

五、符号表示方法1. 在计算机中，除了常见的数字表示方法外，还有一些特殊的符号表示方法。

正负号表示正数和负数、小数点表示小数部分、科学计数法表示很大或很小的数值等。

这些符号在计算机中都有着特定的应用，如在数据处理和科学计算中起着重要作用。

六、结论1. 总结来说，二进制、十进制、八进制和十六进制是计算机领域中常见的进制表示方法，它们在不同领域有着不同的应用。

了解和掌握这些进制表示方法对于理解计算机工作原理和提高编程能力都有着重要的意义。

希望通过本文的介绍，读者能对这些进制表示方法有更深入的了解，为日后的学习和工作提供帮助。

各种进制的算法范文在计算机科学中，常见的进制有二进制、八进制、十进制和十六进制。

不同的进制拥有不同的算法和运算规则。

在本文中，将详细介绍各种进制的算法，并讨论它们在计算机科学中的应用。

1.二进制二进制是计算机系统中最基本的数字系统。

它只有两个数字，0和1、二进制数的每一位表示一个权值，权值从右至左依次递增，例如2^0、2^1、2^2等。

二进制数可以进行加法、减法、乘法和除法运算。

二进制数通常用于计算机中的逻辑操作和数据存储。

2.八进制八进制是基数为8的数字系统。

它使用8个数字0-7表示数值。

八进制数和二进制数之间存在一种特殊的转换关系，每一位八进制数可以由三个二进制数位表示。

八进制数可以进行加法、减法、乘法和除法运算。

八进制数在计算机中通常用于代表文件权限和存储器地址。

3.十进制十进制是我们日常生活中最常用的数字系统。

它使用10个数字0-9表示数值。

十进制数的每一位表示一个权值，权值从右至左递增，例如10^0、10^1、10^2等。

十进制数可以进行加法、减法、乘法和除法运算。

十进制数在计算机中常用于表示人类可读的数字。

4.十六进制十六进制是基数为16的数字系统。

它使用0-9和A-F表示数值，其中A-F分别表示10-15、十六进制数和二进制数之间存在一种特殊的转换关系，每一位十六进制数可以由四个二进制数位表示。

十六进制数可以进行加法、减法、乘法和除法运算。

十六进制数在计算机中常用于表示存储器地址、颜色值和编码系统。

在计算机科学中，进制转换是一种重要的操作。

以下是常见的进制转换算法：1.二进制转十进制：将每一位二进制数乘以对应的权值，然后将结果相加即可。

2.二进制转八进制：将二进制数从右至左每三位进行分组，然后将每个分组转换为对应的八进制数即可。

3.二进制转十六进制：将二进制数从右至左每四位进行分组，然后将每个分组转换为对应的十六进制数即可。

4.十进制转二进制：将十进制数依次除以2，并记录每次的余数，直到商为0为止。

1.十进制十进制使用十个数字（0、1、2、3、4、5、6、7、8、9）记数，基数为10，逢十进一。

历史上第一台电子数字计算机ENIAC是一台十进制机器，其数字以十进制表示，并以十进制形式运算。

设计十进制机器比设计二进制机器复杂得多。

而自然界具有两种稳定状态的组件普遍存在，如开关的开和关，电路的通和断，电压的高和低等，非常适合表示计算机中的数。

设计过程简单，可靠性高。

因此，现在改为二进制计算机。

2. 二进制二进制以2为基数，只用0和1两个数字表示数，逢2进一。

二进制与遵循十进制数遵循一样的运算规则，但显得比十进制更简单。

例如：（1）加法：0+0=0 0+1=1 1+0=1 1+1=0（2）减法：0-0=0 1-1=0 1-0=1 0-1=1（3）乘法：0*0=0 0*1=0 1*0=0 1*1=1（4）除法：0/1=0 1/1=1，除数不能为0二、进制转换1．二进制与十进制数间的转换（1）二进制转换为十进制将每个二进制数按权展开后求和即可。

请看例题：把二进制数（）2=1*22+0*21+1*20+1*2-1+0*2-2+1*2-3=（）10二进制数转换为十进制数:二进制数第0位的权值是2的0次方，第1位的权值是2的1次方……所以，设有一个二进制数：0110 0100，转换为10进制为：下面是竖式：0110 0100 换算成十进制第0位 0 * 20= 0第1位 0 * 21= 0第2位 1 * 22= 4第3位 0 * 23= 0第4位 0 * 24= 0第5位 1 * 25= 32第6位 1 * 26= 64第7位 0 * 27= 0＋---------------------------100用横式计算为：0 * 20 + 0 * 21 + 1 * 22 + 1 * 23 + 0 * 24 + 1 * 25 + 1 * 26 + 0 * 27 = 100 0乘以多少都是0，所以我们也可以直接跳过值为0的位：1 * 22 + 1 * 23 + 1 * 25 + 1 * 26 = 100（2）十进制转换为二进制一般需要将十进制数的整数部分与小数部分分开处理。

在我们接触编程知识时，总会接触有关进制转换的知识，最常见的就是10进制与二进制或十六进制之间的转换，很多时候我们总会遗忘，虽然现在也出现了很多可以直接使用的网络在线的进制转换工具，但考试中，我们就要靠自己通过公式进行运算了。

今天就跟大家分享一下有关进制转换的理论知识，大家可以通过对比从里面发现共同点，这样便于我们理解记忆。

在进行讲解之前，我们先在下面放置一个对应表，因为在理解下面转换的时候，你可以随时查看该表。

一、十进制与二进制之间的转换（1）十进制转换为二进制，分为整数部分和小数部分①整数部分方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

下面举例：例：将十进制的168转换为二进制得出结果将十进制的168转换为二进制，（10101000）2分析:第一步，将168除以2商84余数为0。

第二步，将商84除以2，商42余数为0。

第三步，将商42除以2，商21余数为0。

第四步，将商21除以2，商10余数为1。

第五步，将商10除以2，商5余数为0。

第六步，将商5除以2，商2余数为1。

第七步，将商2除以2，商1余数为0。

第八步，将商1除以2，商0余数为1。

第九步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000②小数部分方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。

如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向入一位。

换句话说就是0舍1入。

读数要从前面的整数读到后面的整数，下面举例：例1：将0.125换算为二进制得出结果：将0.125换算为二进制（0.001）2分析：第一步，将0.125乘以2，得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。

进制一位八进制数字可以用三位二进数来表示，一位十六进制数可以用四位二进数来表示，所以二进制和八进制、十六进制间的转换非常简单例1：将(1010111.01101)2转换成八进制数（从小数点方向向左向右算起）1010111.01101=001 010 111. 011 010 （补齐三位，因为一位八进制数字由三位二进制数来表示）↓ ↓↓↓ ↓12 73 2所以(1010111.011.1)2=(127.32)8例2、将(327.5)8转换为二进制3 2 7. 5↓↓↓↓011 010 111. 101所以(327.5)8=(11010111.101)2将(110111101.011101)2转换为十六进制数(110111101.011101)2=0001 1011 1101. 0111 0100 （补齐四位，因为一位十六进制数字由四位二进制数来表示）↓↓↓↓↓1 B D 74所以(110111101.011101)2=(1BD.74)16将(27.FC)16转换成二进制数2 7. F C ↓↓↓↓0010 0111 1111 1100所以(27.FC)16=(100111.111111)2十进制转二进制：用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如302302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110二进制转十进制从最后一位开始算，依次列为第0、1、2...位第n位的数（0或1）乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方＝01乘2的3次方＝80乘2的4次方＝01乘2的5次方＝321乘2的6次方＝640乘2的7次方＝0然后：1＋2＋0＋8＋0＋32＋64＋0＝107．二进制01101011＝十进制107．1．二进制与十进制的转换（1）二进制转十进制<BR>方法："按权展开求和"例：（1011.01）2 ＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10＝（8＋0＋2＋1＋0＋0.25）10＝（11.25）10（2）十进制转二进制· 十进制整数转二进制数："除以2取余，逆序输出"例：（89）10＝（1011001）22 892 44 (1)2 22 02 11 02 5 (1)2 2 (1)2 1 00 (1)· 十进制小数转二进制数："乘以2取整，顺序输出"例：(0．625)10= (0．101)20．625X 21．25X 20．5X 21．0二进制表示原码：每一位表示符号反码：正数同原码，负数除符号外其它位相反补码：正数同原码，负数除符号外，反码+1得到地址总线：地址总线宽度决定了CPU可以访问的物理地址空间，简单地说就是CPU到底能够使用多大容量的内存8位地址总线：一个8位的二进制数最多能表示2的8次方个数据，从00000000到11111111，十进制为0-255，这样，8位地址总线最大能区分的地址是从0到255。

计算机进制算法在我们想深入学习计算机有关知识是，不可避免的会碰到关于各种机制的计算和它们之间的转化，所以我在这里可大家分享一下这方面的知识，希望对大家有帮助。

一、十进制数十进制数是日常生活中使用最广的计数制。

组成十进制数的符号有0，1，2，3，4，5，6，7，8，9等共十个符号，我们称这些符号为数码。

在十进制中，每一位有0～9共十个数码，所以计数的基数为10。

超过9就必须用多位数来表示。

十进制数的运算遵循：加法时：“逢十进一”；减法时：“借一当十”。

十进制数中，数码的位置不同，所表示的值就不相同。

式中，每个对应的数码有一个系数1000,100,10,1与之相对应，这个系数就叫做权或位权。

十进制数的位权一般表示为：10n-1式中，10为十进制的进位基数；10的i次为第i位的权；n表示相对于小数点的位置，取整数；当n位于小数点的左边时，依次取n=1、2、3……n。

位于小数点的右边时，依次取n=-1、-2、-3……因此，634.27可以写为：634.27=6×102+3×101+4×100+2×10-1+7×10-2在正常书写时，各数码的位权隐含在数位之中，即个位、十位、百位等。

二、二进制电子计算机处理的信息，都是仅用“0”与“1”两个简单数字表示的信息，或者是用这种数字进行了编码的信息。

这种数制叫做二进制。

要了解计算机，首先要了解计算机中数的表示方法。

为了区别不同数制表示的数，通常用右括另外下标数字或字母表示数制，十进制数用D表示，二进制用B表示，十六进制数用H表示，八进制用O表示。

二进制计算法的特点：①二进制数只有“0”和“1”两个数码，基数是2，最大的数字是1；②采用逢二进一的原则。

二进制的位权一般表示为：2n-1。

各位的权为以2为底的幂。

例如，(01101010)各位的权自至在依次为27、26、25、24、23、22、21、20。

二进制数的算术四则运算规则，除进、借位外与十进制数相同。