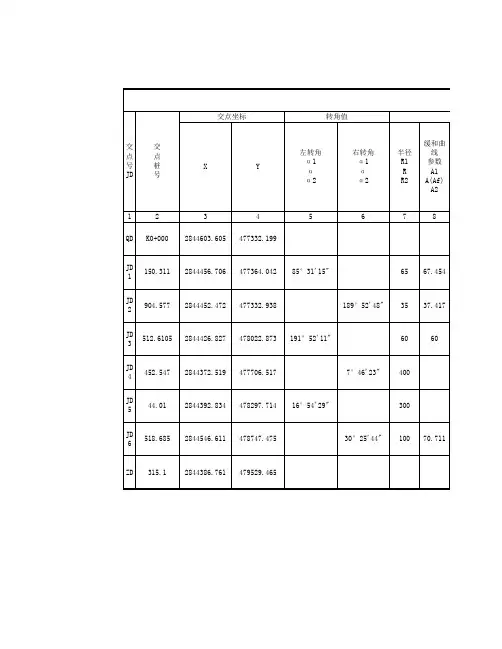
平曲线要素计算表.doc

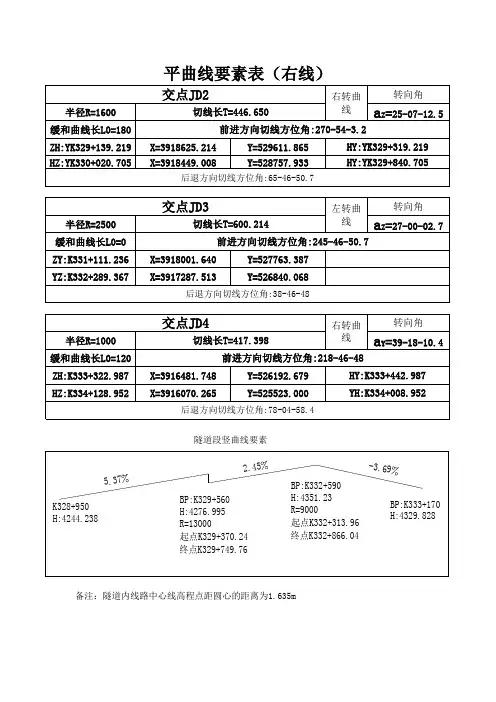
平曲线各要素互相关系间计算及运用
现代金融市场非常发达，市场中经常出现投资机会，投资者要择机有效把握这
些机会，非常需要看清全局，进行系统分析，以期可以取得较大的投资收益。

平曲线（Flat Yield Curve）在金融工程领域有其重要的地位，它的计算及运用可以帮助投资者更加全面的考量投资决策所需的一系列要素。

平曲线是由一系列的收益率（yield）为轴的条形图组成，通过图形即可一目
了然。

一般平曲线由两个位置，一个在短期收益率，另一个在长期收益率。

因此，平曲线可以将短期收益率与长期收益率之间的关系表示出来，进而了解市场收益率水平，从而判断市场中可投资产品。

一般来说，如果短期收益率高于长期收益率，则图中记做正向平曲线;而反之，则称其为反向平曲线。

当平曲线两端的收益率接近时，称为水平曲线。

正向的收益率曲线表明未来的预期收益会比现在的高，这样投资者可以利用短期货币市场把握长期收益机会；反之，反向曲线表明未来收益可能会低于现有状况，这样投资者可以在短期中攫取短期收益。

当投资者看清市场的平曲线，还可以进一步运用其他的要素来权衡投资风险。

例如，日常实战投资者都将注意到波动率，也就是市场中投资品种价格的变动，情况越危险，波动率也会越高。

考虑到这一要素，一般会加重事故损失的可能，实践表明，随着收益率高低，风险会发生变化。

投资者可以通过对相关波动率适当偏移空间来做出投资判断，从而发挥谨慎投资的作用。

总结起来，平曲线是金融投资的重要参照因素，它不仅应用在市场的收益率评估，也可以用于考虑波动率的投资机会的确认，因此投资者应该充分掌握其复杂的计算方法，以便在市场中取得更好的投资收益。

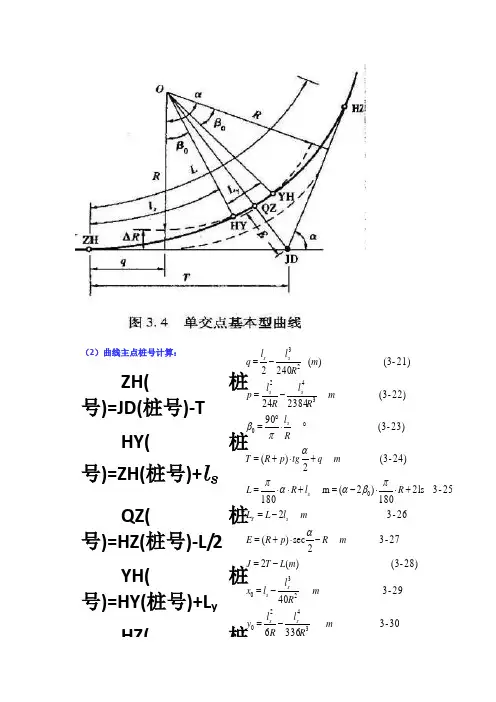
（2）曲线主点桩号计算：ZH(桩号)=JD(桩号)-T HY(桩号)=ZH(桩号)+ls QZ(桩号)=HZ(桩号)-L/2 YH(桩号)=HY(桩号)+L y HZ(桩30-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 24023420230034223m Rl R l y m R l l x m L T J m R p R E m l L L R l R L m q tg p R T Rl m R l R l p m R l l q s s sss Y s s s s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。

可采用抛物线或圆曲线。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：[例1]、某山岭区二级公路，变坡点桩号为K5+030.00，高程为427.68m，i1=+5%，i2=-4%，竖曲线半径R=2000m。

试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程。

解：1.计算竖曲线要素ω= |i2-i1|= |-0.04-0.05| =0.09，为凸型。

曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=（K5+030.00）-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=（K5+030.00）+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处：横距K5x 1=（K5+ 000.00）-（K4+940.00）=60m 竖距h 1=x 12/2R=602/2×2000=0.90m 切线高程=427.68-（90-60）×0.05=426.18m 423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m 桩号K5+100.00处：横距x 2=(K5+120.00)-(K5+100.00)=20m 竖距h 2=x 22/2R=202/2×2000=0.1m切线高程=427.68-（90-20）×0.04=424.88m 设计高程=424.88-0.1=424.78m 横距x 2=(K5+100.00)-(K4+940.00)=160m 竖距h 2=x 22/2R=1602/2×2000=6.4m 切线高程=423.18+160×0.05=431.18m 设计高程=431.18-6.40=424.78m[例2]平原区某二级公路有一弯道，偏角α右=15°28′30″，半径R=600m ，缓和曲线长度Ls=70m ， JD=K2+536.48。

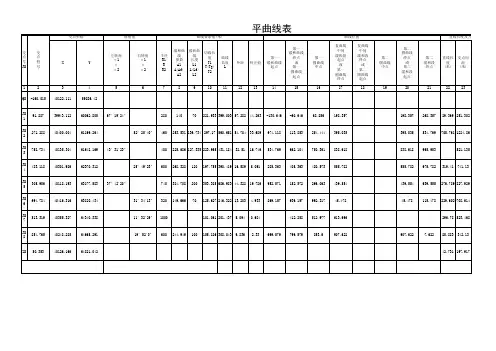
一、路线转角、交点间距的计算（一）在地形图上量出路线起终点及各路线交点的坐标：QD 23810,27180 、JD1 23996，26977 、JD 2 24684，26591 、 JD3 248480，25885 、JD4 25350，25204 、ZD 2606225783，（二）计算公式及方法设起点坐标为 QD X0 ,Y0，第 i 个交点坐标为 JD i X i ,Y i , i 1,2,3,4, 则坐标增量 DX X i X i 1, DY Y i Y i 1交点间距 D (DX )22 DY象限角arctanDYDX方位角 A 是由象限角推算的：象限DX DY A 象限DX DY A Ⅰ+ + A Ⅲ- - A 180o Ⅱ- + A 180o Ⅳ+ - A 360o转角i A i Ai 11.QD与 JD1之间：坐标增量 DX X1 X 0 =23966 23810=186 0DY Y1 Y0 26977 27180 203 0交点间距 D (DX )2 DY 21862 2032275.33m象限角arctan DY arctan 203 47.502 oDX 186方位角 A0 360o 360o 47.502o 312.498o 2.JD1与 JD 2之间：坐标增量 DX X 2 X1 =24684 23966=688 0DY Y2 Y1 26591 26977 386 0交点间距 D 2 222象限角arctanDYarctan 386 29.294 oDX 688 方位角 A 1 360o360o29.294o 330.706o转角 1 =A 1 A 0 330.706o 312.498o 18.208o3. JD 2 与JD 3之间：坐标增量 DXX 3 X 2 =24840 24684=156 0 DYY 3 Y 2 25885 26591706 0交点间距 D(DX )221562 706 2DY 723.03m象限角arctanDYarctan70677.54oDX156方位角 A 2 360o360o 77.54o 282.46o转角 2 =A 2 A 1 282.46o 330.706o 48.246 o4. JD 3与 JD 4 之间：坐标增量 DXX 4 X 3 =25350 24840=510 0DY Y 4 Y 3 25204 25885681 0交点间距 D(DX )225102681 2DY850.8m象限角arctan DYarctan 510 53.171oDX 681方位角 A 3 360o360o 53.171o306.829o转角 3 =A 3 A 2 306.829 282.46 24.369o5. JD 4 与 ZD 之间：坐标增量 DXX X 4 =26062 25350=712 0DYYY 4 2578325204 579 0 交点间距 D (DX )2 27122 5792 917.706mDY 象限角arctanDYarctan57939.118 oDX712方位角 A 039.118o转角o o o二、各平曲线要素的计算( 一) JD 1曲线要素计算取R 800m ,设计速度为 60km/ h ,JD1桩号为K0+275.33，转角1.缓和曲线长度 L S，则：L SV 30.0366030.036 9.72(m)R 800L SV 603 50(m)33.63.6L S R~ R 800 ~ 800 88.89 ~ 800(m) 9 9取整数，采用缓和曲线长120m（《公路工程技术标准》规定：V 最小缓和曲线长度为50m ）.2.圆曲线内移值 RL2S L4S 1202 120 40.75(m)R2688 (R)3 24 800 2688 (800) 324R3.总切线长T hL S L3S 120 120359.989(m)先求 q240R2 2 240 80022所以 T h (R R) tan q (800 18.208 59.989 188.31(m)0.75) tan2 24.曲线总长度 L hL S =0.0752RL h ( 2 ) R 2L S ? R+L S 374.22(m)180 1805.五个基本桩号JD 1 K0+274.33) T h 188.31ZH K 0+087.02 18.208o60 km h 时，) L SHY1) ( L h 2L S )YH1) L SHZ 11L h) 2QZ1120.00K0+207.02134.22 K0+341.24120.00 K0+461.24187.11 K0+274.13E h ( R R)sec R (800 0.75sec 18.208800 10.97(m)2 2超距 D 2T L h 2 188.31 374.22 2.4(m) 。

第三讲公路平面坐标计算1、平曲线认识道路是一个三维空间的工程结构物，它的中线是一个空间曲线，叫路线，其在水平面的投影就是平面线形。

道路平面线形由于受到沿线地形、地质、水文、气候等自然条件和人为条件的制约而改变方向。

在路线平面方向的转折处为满足行车要求，需要用适当的曲线把前、后直线连接起来，这种曲线称为平曲线。

平曲线包括圆曲线和缓和曲线。

①圆曲线要素主点桩号计算：ZY点里程=JD点里程-TQZ点里程=ZY点里程+L/2 YZ点里程=ZY点里程+LJD里程=QZ里程+D/2（校核）②缓和曲线要素切线长： 外距：曲线长：()s s 18022180l aR l a R L h +=+-=πβπ切线加长：q =/2－3/(240R2)圆曲线相对切线内移量：p = 2/(24R)切曲差 Dh = 2T －Lh上式中：α 为线路转向角；β0为缓和曲线角； 其中q 、p 、β0缓和曲线参数。

ZH 桩号 = JD 桩号－T HY 桩号 = ZH 桩号＋QZ 桩号 = HY 桩号＋L/2YH 桩号 = QZ 桩号＋L/2 = HY 桩号＋L = ZH 桩号＋＋LHZ 桩号 = YH 桩号＋= ZH 桩号＋LhJD 桩号 = ZY 桩号－Th ＋Dh （检核）m)2)(（q tgp R T ++=α）（m 2sec)(R p R E -+=αLs Ls Ls Ls Ls Ls注意：上面计算需要大家掌握主点桩号计算，五大主点：ZH、HY、QZ、YH、HZ，还会遇到一些特殊点例如起点QD、终点ZD、公切点GQ。

可以判断下图即可。

重点知识必须掌握（线元法基础）：直线：曲率为0，起终点半径无穷大。

圆曲线：具有一定曲率半径的圆弧，半径为固定值。

缓和曲线：在直线与圆曲线之间或两个不同半径的圆曲线之间设置的曲率连续变化的曲线（指从直线上半径无穷大到圆曲线的定值之间曲率半径逐渐变化的过渡段），我国公路缓和曲线的形式采用回旋线。

（曲率为半径的倒数）A1,A2——缓和曲线参数R——圆曲线半径Ls1,Ls2——缓和曲线长度一段完整缓和曲线满足公式：A²=R x Ls1，A²=R x Ls2入缓和曲线：从ZH点到HY点，A固定不变，随着Ls1的增大，半径从∞减小到R出缓和曲线：从YH点到HZ点，A固定不变，随着Ls2的减小，半径从R增大到∞如果A²≠R x Ls，那么这段缓和曲线是不完整的，叫做不完整缓和曲线。

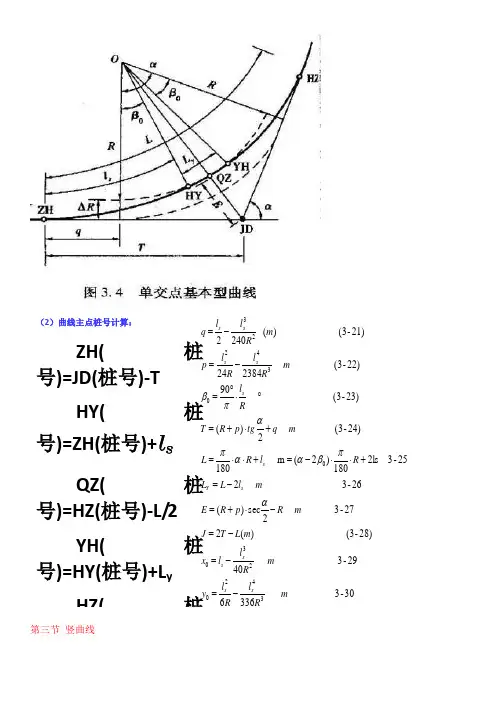
第三节 竖曲线 （2）曲线主点桩号计算： ZH(桩号)=JD(桩号)-T HY(桩号)=ZH(桩号)+l s QZ(桩号)=HZ(桩号)-L/2 YH(桩号)=HY(桩号)+L y HZ(桩30-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-32ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 240234202300034223m R l R l y m R ll x m L T J m R p R E m l L L R l R L m q tg p R T R l m R l R l p m R l l q ss s s s Y s sss ss-=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。

可采用抛物线或圆曲线。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：[例1]、某山岭区二级公路，变坡点桩号为K5+030.00，高程为427.68m，i1=+5%，i2=-4%，竖曲线半径R=2000m。

试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程。

解：1.计算竖曲线要素ω= |i2-i1|= |-0.04-0.05| =0.09，为凸型。

曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=（K5+030.00）-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=（K5+030.00）+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处：横距K5x1=（K5+ 000.00）-（K4+940.00）=60m竖距h1=x12/2R=602/2×2000=0.90m切线高程=427.68-（90-60）×0.05=426.18m423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m桩号K5+100.00处：横距x 2=(K5+120.00)-(K5+100.00)=20m竖距h 2=x 22/2R=202/2×2000=0.1m切线高程=427.68-（90-20）×0.04=424.88m设计高程=424.88-0.1=424.78m横距x 2=(K5+100.00)-(K4+940.00)=160m竖距h 2=x 22/2R=1602/2×2000=6.4m切线高程=423.18+160×0.05=431.18m设计高程=431.18-6.40=424.78m[例2]平原区某二级公路有一弯道，偏角α右=15°28′30″，半径R=600m ，缓和曲线长度Ls=70m ， JD=K2+536.48。