五年级奥数春季班第1讲-勾股定理

勾股定理与弦图课前预习华盛顿的傍晚友爱的小伴侣们：“在那山的那边海那边的美国首都华盛顿，有一位中年人，他聪慧又勤奋，他潜心探讨，他反复思考与演算……”那是1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在闲逛，观赏黄昏的美景，他就是当时美国俄亥俄州共和党议员加菲尔德。

他走着走着，突然发觉四周的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争辩，时而小声探讨。

由于奇异心驱使，加菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。

只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。

于是加菲尔德便问他们在干什么？那个小男孩头也不抬地说：“请问先生，假如直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”加菲尔德答道：“是5呀。

”小男孩又问道：“假如两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”加菲尔德不加思考地回答到：“那斜边的平方确定等于5的平方加上7的平方．”小男孩说：“先生，你能说出其中的道理吗？”加菲尔德一时语塞，无法说明白，心里很不是味道。

加菲尔德不再闲逛，马上回家，潜心探讨小男孩给他出的难题。

他经过反复思考与演算，最终弄清了其中的道理，并给出了简洁的证明方法。

具体方法如下：两个全等的Rt△ABC和Rt△BDE可以拼成直角梯形ACDE，则梯形面积等于三个直角三角形面积之和。

即（AC＋DE）×CD÷2＝AC×BC÷2＋BD×DE÷2＋AB×BE÷2（a＋b）2÷2＝a×b÷2＋a×b÷2＋c×c÷2化简整理得a2＋b2＝c2点评：此种解法主要利用了三角形的面积公式：底×高÷2，和梯形的面积公式：（上底+下底）×高÷2． 而在我国对于勾股定理的证明又做出了那些贡献哪？ 在我国古代，把直角三角形叫做勾股形。

勾股定理【知识要点】1．勾股定理：直角三角形两直角边的平方和等于斜边的平方。

即222a b c +=。

2．勾股定理的逆定理是判别一个三角形为直角三角形常用的方法。

若三角形的三边长a,b,c 满足222a b c +=，则这个三角形是直角三角形。

利用勾股定理的逆定理判别直角三角形的一般步骤： ①先找出最大边（如c ）②计算2c 与22a b +，并验证是否相等。

若2c =22a b +，则△ABC 是直角三角形。

若2c ≠22a b +，则△ABC 不是Rt △。

3． 若a 、b 、c 均为自然数，且无1以外的整数公因式当它们满足关系式222a b c +=时，我们称（a 、b 、c ）为基本勾股数组。

记一记： ()3,4,5，()5,12,13，()7,24,25，()8,15,17，()9,40,41，()11,60,61，…均为基本勾股数组。

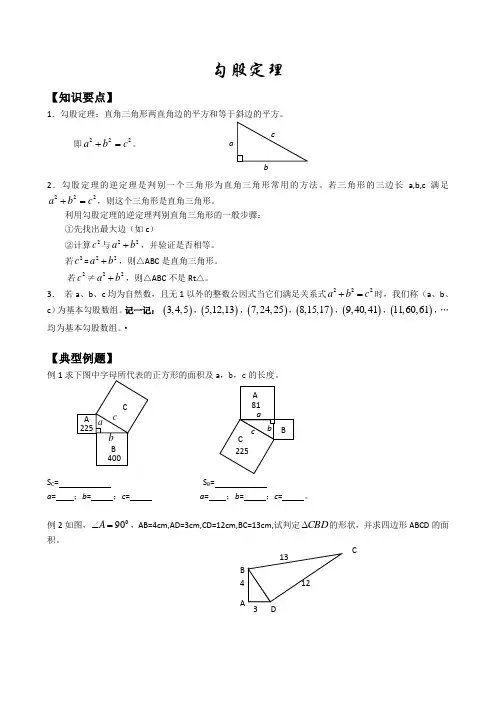
·【典型例题】例1求下图中字母所代表的正方形的面积及a ，b ，c 的长度。

S C = S B =a = ；b = ；c = a = ；b = ；c = 。

例2如图，090=∠A ，AB=4cm,AD=3cm,CD=12cm,BC=13cm,试判定CBD ∆的形状，并求四边形ABCD 的面积。

abcA 81 C 225Ba cb CA BD4 31213A 225CB bc a 400例3如图所示，在△ABC 中，D 是BC 上一点，AB=10，BD=6，AD=8，AC=17。

求△ABC 的面积。

例4直角三角形斜边长为2，两直角边和为6，求此直角三角形面积。

例5写出下表的勾股数3，4，5 5，12，13， 7，24，25 8，15，179，40，416，8，1015，36，3927，120，12328，96，10040，75，85从中发现什么规律思考1：已知6、8、a 是一个三角形的三边长，若该三角形为直角三角形，那么a 是多少？思考2：如图，一架长2.5m 的梯子AB ，斜靠在一竖直的墙AC 上，这时梯足B 到墙底端C 的距离为0.7m ，若梯子的顶端沿墙下滑0.4m 。

勾股定理：直角三角形两直角边（即“勾”，“股”）边长平方和等于斜边（即“弦”）边长的平方。

也就是说，设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2o勾膻定理勾股数★满足关系a2+b2=c2的3个正整数a,b,c称为勾股数。

★常见的勾股数有：①3,4,5；②6,8,10；③8,15,17:④7,24,25；⑤5,12,13；⑥9,12,15…注意：①3,4,5既是勾股数，又是三个连续整数，它们非常特殊，不要认为三个连续整数都是勾股数；②每组勾股数的相同倍数也是勾股数；（如：3,4,5；6,8,10；9,12,15）③勾股数必须都是正整数，（如：0.3,0.4,0.5都是小数，因而不是勾股数）3米例2、一棵大树在离地面3米处折断，树的顶端落在离树的底部4米处，那么这棵树折断之前的高度是多少米？巩固、如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要多少米？巩固、飞机在空中水平飞行，某一时刻刚好飞到一个站着不动的女孩头顶正上方4000m 处,过了20秒，飞机距离这个女孩头顶5000m,则飞机速度是多少？例3、暑假中，小明和同学们到某海岛去探宝旅游，按照如图所示的路线探宝.他们登陆后先往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北走6km处往东一拐，仅走1km就找到了宝藏，则登陆点到埋宝藏点的直线距离为km.丄埋宝藏点632登陆点8巩固、轮船从海中岛A出发，先向北航行9km，又往西航行9km，由于遇到冰山，只好又向南航行4km，再向西航行6km，再折向北航行2km，最后又向西航行9km，到达目的地B,求AB 两地间的距离.例4、一个圆桶，底面直径为24cm，高32cm，则桶内所能容下的最长木棒为多少厘米?如图，是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两相对的端点，A点有一只昆虫想到B点去吃可口的食物，则昆虫沿着台阶爬到B点的最短路程是分米？B例5、下图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A,B，C,D的边长分别是3,5,2,3,则最大正方形E的面积是？巩固、如图所示，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是cm2.巩固、如图所示，阴影部分是一个正方形，则此正方形的面积为?例6、如图，已知直角三角形两直角边BC，AC的长分别为3cm和4cm,那么CD有多长?巩固、三角形的三边长分别为6,&10，它的最短边上的高为，最长边上的高为巩固、若直角三角形的三边长分别为X,6,8,则X2=例7、等腰三角形ABC的腰长为10,底边上的高为6,则底边的长为多少？巩固、如图，一根12米高的电线杆两侧各用15米的铁丝固定，两个固定点之间的距离是。

五年级第一讲勾股定理勾股定理是数学中经典而重要的定理之一，它以古希腊数学家毕达哥拉斯的名字命名。

勾股定理描述了直角三角形中的关系，对于初学者来说会有一定的挑战。

本文将详细介绍勾股定理的概念、证明方法以及一些应用示例。

一、勾股定理的概念勾股定理是指在直角三角形中，直角边的平方和等于斜边的平方。

具体而言，假设直角三角形的两条直角边分别为a和b，斜边长度为c，那么根据勾股定理可以得到以下公式：a² + b² = c²二、勾股定理的证明方法勾股定理的证明有多种方法，这里我们介绍一种基于几何图形的证明方法。

首先，构造一个正方形，边长为a+b，如下图所示：□a b□□c根据正方形的性质，它的对角线长度等于边长的平方根，即(a+b)²的平方根。

接下来，将正方形分割成四个直角三角形，如下图所示：□a b□□ △ □□c可以看出，其中三个直角三角形的直角边分别为a、b和c，斜边长度分别未a+b、a+b和c。

根据三角形的面积公式S = 0.5 ×底 ×高，可以得到以下等式关系：S(△a) + S(△b) + S(△c) = S(□)0.5 × a × a + 0.5 × b × b + 0.5 × c × c = (a+b)²化简上式，可以得到勾股定理的形式：a² + b² = c²因此，我们通过几何图形的分割和面积计算，成功证明了勾股定理。

三、勾股定理的应用示例勾股定理在解决直角三角形问题时起到了重要的作用，我们可以通过一个实际问题来说明其应用。

假设甲地点距离某个高楼的距离为5千米，乙地点距离该高楼的距离为12千米，甲、乙两人正好位于高楼两侧的直角顶点。

现在甲想要测量高楼的高度h，他找到了一个10千米长的测量工具。

根据勾股定理，可以建立以下方程：5² + h² = 10²25 + h² = 100h² = 100 - 25h² = 75h = √75h ≈ 8.66（约等于）因此，高楼的高度约为8.66千米。

第 一 讲 勾 股 定 理【知识链接】（一）勾股定理：如果直角三角形两直角边分别为a 、b,斜边为c ，那么222ab c +=即：直角三角形两直角边的平方和等于斜边的平方。

1．用面积法证明勾股定理：（1）如图，将四个全等的直角三角形拼成正方形。

（Ⅰ）ab c b a S ABCD214)(22⨯+=+=正方形。

a ²+b ²=c ²(Ⅱ) ab b a c S EFGH 214)(22⨯+-==正方形。

c ²=a ²+b ²2.勾股定理各种表达式：在ABC Rt ∆中，︒=∠90C ，∠A 、∠B 、∠C 的对边分别为a 、b 、c.则c ²=a ²+b ²， a ²=c ²-b ²，b ²=c ²-a ²=。

3.勾股定理的面积表示法（如右图） 4．勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）利用勾股定理解决实际问题。

（3）用于证明平方关系的问题。

（二）勾股定理的逆定理：如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形是直角三角形。

勾股定理是直角三角形的性质定理，而勾股定理的逆定理是直角三角形的判定定理。

即：在△ABC 中，若222c b a =+，则△ABC 为Rt △。

1.满足a 2+b 2=c 2的三个正整数，称为勾股数．常用的勾股数组如：3，4,5；6,8,10；···若a ，b ，c 为一组勾股数，那么ka ，kb ，kc （k 为正整数）也是勾股数． 2．如何判定一个三角形是否是直角三角形。

①首先求出最大边（如c ）； ②验证2c 与22b a +是否具有相等关系。

若222b ac +=，则△ABC 是以∠C ＝90°的直角三角形；若222c b a>+，则三角形是锐角三角形； 若222c b a <+，则三角形是钝角三角形。

勾股定理(讲义) -CAL-FENGHAI.-(YICAI)-Company One1勾股定理一、知识归纳1．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a，b，斜边为c，那么222+=a b c2．勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形3．勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC∠=︒，则c=b=，a=∆中，90C②知道直角三角形一边，可得另外两边之间的数量关系二、题型题型一：直接考查勾股定理例１. 在ABC∠=︒∆中，90C⑴已知6BC=．求AB的长AC=，8⑵已知17AC=，求BC的长AB=，15解：题型二：应用勾股定理建立方程例２.⑴在ABCBC=cm，CD AB⊥于D，CD＝AB=cm，3∠=︒，5∆中，90ACB⑵已知直角三角形的两直角边长之比为3:4，斜边长为15，则这个三角形的面积为⑶已知直角三角形的周长为30cm，斜边长为13cm，则这个三角形的面积为21DCB AAB CD E例３.如图ABC ∆中，90C ∠=︒，12∠=∠， 1.5CD =， 2.5BD =，求AC 的长例4.如图Rt ABC ∆，90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆，求阴影部分面积题型三：实际问题中应用勾股定理例5.如图有两棵树，一棵高8cm ，另一棵高2cm ，两树相距8cm ，一只小鸟从一棵树的树梢飞到另一棵数的树梢，至少飞了 m三、勾股定理的逆定理知识归纳 1. 勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a 2＋b 2＝c 2，那么这个三角形是直角三角形，其中c 为斜边。

2. 常用的平方数112＝_______，122＝_______，132＝_______，142＝_______，152＝_______，162＝_______，172＝_______，182＝_______，192＝_______，202＝_______，252＝_______．注意.如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边。

华盛顿的傍晚亲爱的小朋友们：“在那山的那边海的那边的美国首都华盛顿，有一位中年人，他聪明又勤奋，他潜心探讨，他反复思考与演算……”，那是1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员加菲尔德。

他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。

由于好奇心驱使，加菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。

只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。

于是加菲尔德便问他们在干什么？那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”加菲尔德答道：“是5呀。

”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”加菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方．”小男孩说：“先生，你能说出其中的道理吗？”加菲尔德一时语塞，无法解释了，心里很不是滋味。

加菲尔德不再散步，立即回家，潜心探讨小男孩给他出的难题。

他经过反复思考与演算，终于弄清了其中的道理，并给出了简洁的证明方法。

具体方法如下： 两个全等的Rt △ABC 和Rt △BDE 可以拼成直角梯形ACDE ， 则梯形面积等于三个直角三角形面积之和。

即 （AC ＋DE ）×CD÷2＝AC×BC÷2＋BD×DE÷2＋AB×BE÷2 （a ＋b ）2÷2＝a×b÷2＋a×b÷2＋c×c÷2 化简整理得a 2＋b 2＝c 2点评：此种解法主要利用了三角形的面积公式：底×高÷2，和梯形的面积公式：（上底+下底）×高÷2．课前预习勾股定理与弦图而在我国对于勾股定理的证明又做出了那些贡献哪？在我国古代，把直角三角形叫做勾股形。

第一讲勾股定理勾股定理是一个基本几何定理，是用代数思想解决几何问题的最重要的工具之一，之一，也是数形结合的纽带之一。

勾股定理约有也是数形结合的纽带之一。

勾股定理约有400种证明方法，是数学定理中证明方法最多的定理之一。

“勾三股四弦五”是勾股定理最基本的公式。

“勾三股四弦五”是勾股定理最基本的公式。

一．勾股定理1.勾股定理：求长度：构造直角三角形，已知两边求第三边2.用途：证明直角：若三边关系满足a2+b2=c2，则该三角形为直角三角形则该三角形为直角三角形 3.勾股数：满足a2+b2=c2的三个数（a、b、c）称为勾股数常用的勾股数有以下两组：常用的勾股数有以下两组：常用的勾股数有以下两组：①（①（3n，4n，5n）：例如常用的（例如常用的（3,4,5,3,4,5,3,4,5,）和（）和（）和（6,8,106,8,106,8,10）等；）等；）等；②（5,12,13）、（7,24,25）、（9,40,41），……——由平方差公式——由平方差公式a2−b2=（a+b)(a−b)推导得来。

推导得来。

4.4.勾股定理的两个常用模型：勾股定理的两个常用模型：勾股定理的两个常用模型：①毕达哥拉斯树①毕达哥拉斯树①毕达哥拉斯树: A+B=C: A+B=C: A+B=C ②米奇模型②米奇模型②米奇模型: A+B=C: A+B=C5.图形的对折问题：——找全等图形（相等的边、相等的角）若直角三角形的两条直角边长度分别为a和b，斜边长度为c，那么a2+b2=c2C 二．常用公式复习1.平方差公式：a 2−b 2=（a +b)(a −b)推导过程： 如图：大正方形边长为a ，小正方形边长为b ；那么：S 阴影=a 2−b 2；将阴影部分重新剪拼将阴影部分重新剪拼又可得：S 阴影=（a +b)(a −b)2.完全平方公式：(a ±b)2=a 2±2ab +b 2 以以(a +b)2=a 2+2ab +b 2为例，推导过程如下：为例，推导过程如下：如图：小、中正方形边长分别为如图：小、中正方形边长分别为a ，b整体：整体：S 大正方形=(a +b)2 分解：分解：S 大正方形=a 2+2ab +b 2三．练习题【练习1】根据下图所给数据，求出AB 长度。

勾股定理例 1. 2002 年在北京召开了国际数学家大会，大会会标如图下所示，它由四个相同的直角三角形拼成的，直角边的长分别为 2 和3。

问大正方形的面积为多少？例2. 已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积。

例3. 已知一个梯形的上底为5，下底为10，两边的腰分别为 3 和4，求这个梯形的面积是多少？例4. 如图，正方形的边长为10cm，AB=2cm，CD=3cm，求阴影部分的面积。

例5. 已知，如图，在直角三角形ABC中，∠C=90°，∠1=∠2，求AC的CD=1.5,BD=2.5,长.例6. 如图，在三角形AB C中，A B=A C，P为B C上任意一点，请用学过的知识说明：AB×A B－A P×A P=PB×P C。

练习题（1）如图，铁路上A，B 两点相距25km，C，D 为两村庄，DA⊥AB 于A ，C B⊥AB于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E 站的距离相等则站应建在离 A 站多少km处E（2）已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B 与点D重合，折痕为EF，则三角形ABE的面积为多少？（3）小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多 1 米，当他把绳子的下端拉开 5 米后，发现下端刚好接触地面，求旗杆的高度。

（4）如下图所示，四边形的面积为多少？CD，又BD=4，AC=3，且（5）如图所示，梯形ABCD中，AB平行于AB+CD=5 ，试求梯形ABCD的面积。