面面垂直→线面垂直几个条件

线面、面面平行和垂直的八大定理一、线面平行。

1、判定定理：平面外一条直线与平面内一条直线平行，那么这条直线与这个平面平行。

符合表示：βββ////ababa⇒⎪⎭⎪⎬⎫⊂⊄2、性质定理：如果一条直线与平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

符号表示：babaaa////⇒⎪⎪⎭⎪⎪⎬⎫=⊂⊄βαβαα二、面面平行。

1、判定定理：如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。

符号表示：βα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==NnmMbaambn2、性质定理：如果两个平面平行同时与第三个平面相交，那它们的交线平行。

符号表示：dldl////⇒⎪⎭⎪⎬⎫==γβγαβα（更加实用的性质：一个平面内的任一直线平行另一平面）三、线面垂直。

1、判定定理：如果一条直线与一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面。

符号表示： α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a ＄：三垂线定理：（经常考到这种逻辑）在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

符号表示：PA a A oA a po oA a ⊥⇒⎪⎪⎭⎪⎪⎬⎫=⊥⊥⊂⊂ααα2、性质定理：垂直同一平面的两条直线互相平行。

（更加实用的性质是：一个平面的垂线垂直于该平面内任一直线。

）四、面面垂直。

1、判定定理：经过一个平面的垂线的平面与该平面垂直。

βααβ⊥⇒⊂⊥a a ,2、性质定理：已知两个平面垂直，在一个平面内垂直于交线的直线垂直于另一个平面。

βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,，。

面面垂直的判定、面面垂直的性质1.在证明线面垂直、面面垂直时，一定要注意判定定理成立的条件．同时抓住线线、线面、面面垂直的转化关系，即：2．在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决，如有平面垂直时，一般要用性质定理．3．几个常用的结论：(1)过空间任一点有且只有一条直线与已知平面垂直．(2)过空间任一点有且只有一个平面与已知直线垂直．4．判定面面垂直的方法：(1)面面垂直的定义．(2)面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．5．在已知平面垂直时，一般要用性质定理进行转化，转化为线面垂直或线线垂直．转化方法：在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．6.证明直线和平面垂直的常用方法有：(1)利用判定定理．(2)利用判定定理的推论(a∥b，a⊥α⇒b⊥α)．(3)利用面面平行的性质(a⊥α，α∥β⇒a⊥β)．(4)利用面面垂直的性质．当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面．2．设α，β，γ是三个不重合的平面，l是直线，给出下列命题①若α⊥β，β⊥γ，则α⊥γ；②若l上两点到α的距离相等，则l∥α；③若l⊥α，l ∥β，则α⊥β；④若α∥β，l⊄β，且l∥α，则l∥β.其中正确的命题是()A．①②B．②③C．②④D．③④解析：选D对于①：若α⊥β，β⊥γ，则α⊥γ，前者不是后者的充分条件，比如当α∥γ时，也有α⊥β，β⊥γ.对于②：显然错误，当l⊥α，l∩α＝A时，l上到A距离相等的两点到α的距离相等．③④显然正确．4.(2013·济南模拟)如图，在斜三棱柱ABC－AB1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部解析：选A由AC⊥AB，AC⊥BC1，∴AC⊥平面ABC1.又∵AC⊂面ABC，∴平面ABC1⊥平面ABC.∴C1在面ABC上的射影H必在两平面交线AB上．5.(2012·曲阜师大附中质检)如图所示，直线P A垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面P AC的距离等于线段BC的长．其中正确的是()A．①②B．①②③C．①D．②③解析：选B对于①，∵P A⊥平面ABC，∴P A⊥BC.∵AB为⊙O的直径，∴BC⊥AC.∴BC⊥平面P AC.又PC⊂平面P AC，∴BC⊥PC；对于②，∵点M为线段PB的中点，∴OM ∥P A.∵P A⊂平面P AC，∴OM∥平面P AC；对于③，由①知BC⊥平面P AC，∴线段BC的长即是点B到平面P AC的距离，故①②③都正确．6.(2012·济南名校模拟)如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下面命题正确的是()A．平面ABD⊥平面ABC B．平面ADC⊥平面BDCC．平面ABC⊥平面BDC D．平面ADC⊥平面ABC解析：选D在平面图形中CD⊥BD，折起后仍有CD⊥BD，由于平面ABD⊥平面BCD，故CD⊥平面ABD，CD⊥AB，又AB⊥AD，故AB⊥平面ADC，所以平面ABC⊥平面ADC.10. 如图所示，已知三棱锥A－BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．(1)求证：DM∥平面APC；(2)求证：平面ABC⊥平面APC.证明：(1)由已知，得MD是△ABP的中位线，所以MD∥AP.又MD⊄平面APC，AP⊂平面APC，故MD∥平面APC.(2)因为△PMB为正三角形，D为PB的中点，所以MD⊥PB.所以AP⊥PB.又AP⊥PC，PB∩PC＝P，所以AP⊥平面PBC.因为BC⊂平面PBC，所以AP⊥BC.又BC⊥AC，AC∩AP＝A，所以BC⊥平面APC.因为BC⊂平面ABC，所以平面ABC⊥平面APC.3.(2012·莆田模拟)如图，在三棱锥P－ABC中，△P AC，△ABC分别是以A，B为直角顶点的等腰直角三角形，AB＝1.(1)现给出三个条件：①PB＝3；②PB⊥BC；③平面P AB⊥平面ABC.试从中任意选取一个作为已知条件，并证明：P A⊥平面ABC；(2)在(1)的条件下，求三棱锥P－ABC的体积．解：法一：(1)选取条件①在等腰直角三角形ABC中，∵AB＝1，∴BC＝1，AC＝ 2.又∵P A＝AC，∴P A＝ 2.∴在△P AB中，AB＝1，P A＝ 2.又∵PB＝3，∴AB2＋P A2＝PB2.∴∠P AB＝90°，即P A⊥AB.又∵P A⊥AC，AB∩AC＝A，∴P A⊥平面ABC.(2)依题意得，由(1)可知P A⊥平面ABC，V三棱锥P－ABC＝13P A·S△ABC＝13×2×12×12＝26.法二：(1)选取条件②∵PB⊥BC，又AB⊥BC，且PB∩AB＝B，∴BC⊥平面P AB.∵P A⊂平面P AB，∴BC⊥P A.又∵P A⊥AC，且BC∩AC＝C，∴P A⊥平面ABC.(2)依题意得，由(1)可知P A⊥平面ABC. ∵AB＝BC＝1，AB⊥BC，∴AC＝2，∴P A＝2，∴V三棱锥P－ABC＝13P A·S△ABC＝13×12AB·BC·P A＝13×12×1×1×2＝26.法三：(1)选取条件③若平面P AB⊥平面ABC，∵平面P AB∩平面ABC＝AB，BC⊂平面ABC，BC⊥AB，∴BC⊥平面P AB.∵P A⊂平面P AB，∴BC⊥P A.∵P A⊥AC，且BC∩AC＝C，∴P A⊥平面ABC.(2)同法二．。

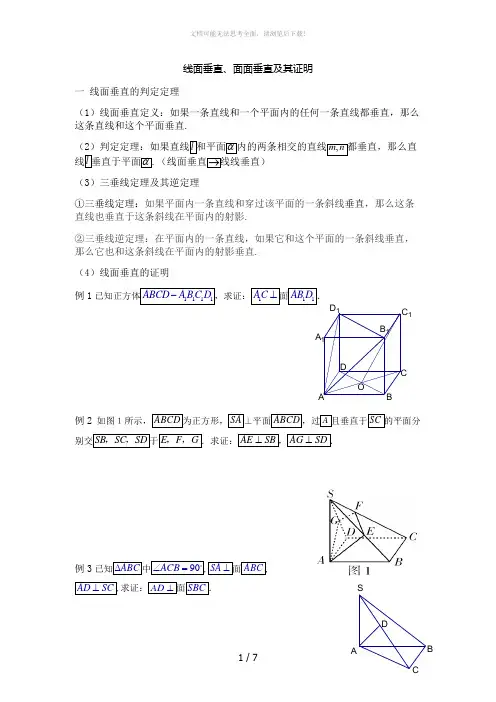
线面垂直、面面垂直及其证明一 线面垂直的判定定理（1）线面垂直定义：如果一条直线和一个平面内的任何一条直线都垂直，那么这条直线和这个平面垂直.（2（3）三垂线定理及其逆定理①三垂线定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影.②三垂线逆定理：在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直. （4）线面垂直的证明例1例2例3SDD 1ODBA C 1B 1A 1C例4在正方体1111ABCD A BC D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD .练习1 在正方体1111ABCD A BC D -中. （1）求证：AC ⊥平面11B D BD .（2）求证：1BD ⊥平面1ACB .练习2在三棱锥A BCD -中，BC AC =，AD BD =，作BE CD ⊥，E 为垂足，作AH BE ⊥于H .求证：AH ⊥平面BCD .在四棱锥P ABCD -中，PA ⊥底面ABCD ，AB AD ⊥，AC CD ⊥，60ABC ︒∠=，PA AB BC ==，E 是PC 的中点.（1）求证：CD AE ⊥. （2）求证：PD ⊥面ABE .二 面面垂直（1条直线叫做二面角的棱，每个半平面叫做二面角的面，若棱为l ，两个面分别为，,αβ二面角记作为l αβ--.（2）二面角的平面角定义：在二面角l αβ--棱l 上取一点O ，在半平面α和β内，从点O 分别作垂直于棱l 的射线,OA OB ，射线组成AOB ∠.则AOB ∠叫做二面角的平面角.二面角的取值范围为[0,180]︒︒.（3）面面垂直定义：若两个平面的二面角为直二面角(平面角是直角的二面角)，则这两个平面互相垂直.（4）面面判定定理：一个平面过另一个平面，则这两个面相互垂直. （5）面面垂直的正面即：面面垂直→线面垂直→线线垂直. 例1如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点.（1）求证：1//AC 平面BDE ； （2）求证：平面1A AC ⊥平面BDE . .例2如图，直三棱柱111C B A ABC -中，侧棱垂直于底面，90ACB ︒∠=121AA BC AC ==，D 是棱1AA 的中点，求证：平面1BDC 平面BDC ．AC B1B 1A D1C练习 如图，过S 引三条长度相等但不共面的线段,,SA SB SC ，且60ASB ASC ︒∠=∠=，90BSC ︒∠=，求证：平面ABC ⊥平面BSC ．三 立体几何高考证明例1（2013江苏）如图，在三棱锥中，平面平面，，，过作，垂足为，点分别是棱的中点．求证：（1）平面平面； （2）．例2（2012江苏）如图，在直三棱柱111ABC A B C -中，1111A B A C =，D E，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F⊥，为11B C 的中点．求证：（1） 平面ADE ⊥平面11BCC B ； （2） 直线1//A F 平面ADE ．ABC S -⊥SAB SBC BC AB ⊥AB AS =A SB AF ⊥F G E ，SC SA ，//EFG ABC SA BC ⊥ABCSGFE例3如图，四棱锥P ABCD -中，底面ABCD 为平行四四边形，60DAB ︒∠=，2AB AD =，PD ⊥底面ABCD .（1）证明：PA BD ⊥（2）设1PD AD ==，求棱锥D PBC -的高.练习1如图，几何体E ABCD -是四棱锥，ABD 为正三角形，,CB CD EC BD =⊥.(Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =︒，M 为线段AE 的中点，求证：DM ∥平面BEC .练习2（2011天津）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，45ADC ∠=︒，1AD AC ==，O 为AC 的中点，PO ABCD ⊥平面，2PO =，M为PD 的中点．(Ⅰ) 证明：//PB ACM 平面；MP(Ⅱ)(Ⅲ)。

空间中的垂直关系1.线面垂直直线与平面垂直的判定定理:如果 ,那么这条直线垂直于这个平面。

推理模式:直线与平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线 。

2.面面垂直两个平面垂直的定义:相交成 的两个平面叫做互相垂直的平面。

两平面垂直的判定定理:(线面垂直⇒面面垂直)如果 ,那么这两个平面互相垂直。

推理模式:两平面垂直的性质定理:(面面垂直⇒线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的 的直线垂直于另一个平面。

一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面就是判定定理,而从后面推出前面就是性质定理.同学们应当学会灵活应用这些定理证明问题.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,下面举例说明.例题:1.如图,AB 就是圆O 的直径,C 就是圆周上一点,PA ⊥平面ABC.(1)求证:平面PAC ⊥平面PBC;(2)若D 也就是圆周上一点,且与C 分居直径AB 的两侧,试写出图中所有互相垂直的各对平面.2、如图,棱柱111ABC A B C -的侧面11BCC B 就是菱形,11B C A B ⊥证明:平面1AB C ⊥平面11A BC3、如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 就是棱CC 1的中点 (Ⅰ)求异面直线A 1M 与C 1D 1所成的角的正切值;(Ⅱ)证明:平面ABM ⊥平面A 1B 1M 14、如图,AB 就是圆Ｏ的直径,Ｃ就是圆周上一点,PA ⊥平面ABC .若AE ⊥PC ,Ｅ为垂足,Ｆ就是PB 上任意一点,求证:平面AEF ⊥平面PBC .5、如图,直三棱柱ABC —A 1B 1C 1 中,AC ＝BC ＝1,∠ACB ＝90°,AA 1 ＝2,D 就是A 1B 1 中点.(1)求证C 1D ⊥平面A 1B ;(2)当点F 在BB 1 上什么位置时,会使得AB 1 ⊥平面C 1DF ？并证明您的结论6、S 就是△ABC 所在平面外一点,SA ⊥平面ABC,平面SAB⊥平面SBC,求证AB ⊥BC 、7、在四棱锥中,底面ABCD 就是正方形,侧面VAD 就是正三角形,平面VAD ⊥底面ABCD证明:AB ⊥平面VAD8、如图,平行四边形ABCD 中,60DAB ︒∠=,2,4AB AD ==,将CBD ∆沿BD 折起到EBD ∆的位置,使平面EDB ⊥平面ABD 、求证:AB DE ⊥VDC B A SAB9、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD,AB=AD,∠BAD=60°,E 、F 分别就是AP 、AD 的中点求证:(1)直线EF ‖平面PCD;(2)平面BEF ⊥平面PAD10、如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,AB AS BC AB =⊥,、过A 作SB AF ⊥,垂足为F ,点G E ,分别就是棱SC SA ,的中点。

两平面垂直的充要条件的证明
如果一个平面内有一条直线与另一个平面垂直，那么这两个平面垂直。
如果两个平面的垂线互相垂直，那么这两个平面垂直。
特殊情况下的判定条件
如果两个平面都垂直于第三个平面，那么这两个平面互相垂直。
如果两个平面分别与另外两个互相垂直的平面平行，那么这两个平面互相垂直。
Part
03
解析法判定面面垂直
01
建立坐标系
02
判定条件
ቤተ መጻሕፍቲ ባይዱ
在空间中建立合适的坐标系，将两个 平面的方程表示为Ax+By+Cz+D=0 的形式。
如果两个平面的法向量（即方程中x 、y、z的系数）互相垂直，则这两个 平面垂直。可以通过计算两个法向量 的数量积是否为0来判断它们是否垂 直。
03
应用
解析法适用于已知平面方程的情况下 ，通过计算判断两个平面是否垂直。
面面垂直的性质定理及其证明
面面垂直的性质定理
如果两个平面都垂直于第三个平面，那么这两个平面互相垂直。
证明
假设有两个平面α和β，它们都垂直于平面γ。在平面α内任取一点A，并作直线 AB垂直于平面β，垂足为B。由于AB垂直于平面β，因此AB所在的平面与平面β 垂直。又因为AB在平面α内，所以平面α与平面β垂直。
在实际问题中的应用
建筑学
地理学
在建筑设计中，经常需要判断两面墙 是否垂直，以确保建筑物的稳定性和 美观性。
在地质勘探和地形测量中，需要判断 地层或地形的走向和倾斜角度，以确 定是否存在垂直构造或地形特征。
工程学
在机械设计和制造中，需要确保某些 部件的表面与其他部件的表面垂直， 以确保机械的正常运转和精度。
Part

如果一个平面经过另一个平面的一 条垂线，那么这两个平面互相垂直
l α 符号表 αβ l β 示：
线线 垂直 线面 垂直
C A
l
B D
面面 垂直
（2）若 PDA 45，求证：MN 面PCD
P E N A M B D
例3 如图，已知 PA 矩形ABCD所在平面，M、 N分别是AB、PC的中点求证： （1）MN CD;
β B பைடு நூலகம் l A a
C
练1. 四边形ABCD中，AD∥BC， AD=AB，∠BCD=450， ∠BAD=900，将△ABD沿BD折起，使平面ABD⊥平面 BCD，构成四面体ABCD. 求证:平面ADC⊥平面ABC A
A
D
D
B
C
B
C
练2.平面四边形ABCD中，AB=BC=CD=a， ∠B=90°，∠DCB=135°，沿对角线AC将 四边形折成直二面角. (1)证明：AB⊥面BCD； (2)求面ABD与面ACD所成的角.
2.已知两个平面垂直,下列命题为真命题的是____ ①一个平面内已知直线必垂直于另一个平面内的任意 一条直线. ②一个平面内的已知直线必垂直于另一个平面的无数 条直线. ③一个平面内的任一条直线必垂直于另一个平面 ④过一个平面 内任意一点作交线的垂线,则此垂线必 垂直于另一个平面.

例1 a
如图已知平面α、β,α⊥β,α∩β = l , 直线a⊥β, α，试判断直线a与平面α的位置关系.
a b
α
直线与平面垂直的性质定理.
垂直于同一个平面的两条直线平行 线面垂直的性质定理： 反证法 已知:a⊥α, b⊥α, 求证:a // b
证明： 假设 a与b不平行. 记直线b和α的交点为o, 则可过o作 b’∥a. ∵a⊥α , ∴b’⊥α. ∴过点o的两条直线 b和 b’都垂直平面α , 这不可能! ∴ a∥ b

立体几何之垂直关系【知识要点】空间中的垂直关系如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直．如果一个平面过另一个平面的一条垂线，则两个平面互相垂直． 如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．解决空间问题的重要思想方法：等价转化——化空间问题为平面问题．空间平行、垂直关系证明的基本思想方法——转化与联系，如图所示．题型1 平移证明线线垂直 例1 如图，在四棱锥ABCD P -中，N M AD BC AB AD BC BC AB ,.2,1,,===⊥分别为DC PD ,的中点，求证：AC MN ⊥例2 底面ABCD 是正方形，Q G BE PD PD BE ,,2,=‖分别为AP AB ,的中点，求证：CG QE ⊥例3 如图，在正方形1111D C B A ABCD -中，M 为1CC 的中点，F E ,分别为11,D A CD 的中点，AC 交BD 于点O ，求证：OM EF ⊥题型2 线面垂直判定例1 如图，在三棱锥ABC P -中，PAB ∆是等边三角形。

①若ABC ∆是等边三角形，证明：PC AB ⊥②若 90=∠=∠PBC PAC ，证明：PC AB ⊥例 2 已知四棱台1111D C B A ABCD -的上下底面边长分别是2和4的正方形，41=AA 且ABCD AA 底面⊥1，点P 为1DD 的中点，求证：PBC AB 面⊥1例3 如图，在三棱柱111C B A ABC -中，AC AB BAC ==∠,90，1A 在底面ABC 的射影为BC 的中点，D 为11C B 的中点。

证明：⊥D A 1平面BC A 1题型3 线面垂直性质证明线线垂直例1 如图，在三棱柱111C B A ABC -中，侧棱垂直于底面，D AA AC ACB ,21,901==∠ 是棱1AA 的中点，求证：BD DC ⊥1例2 已知正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直，M 为AC 上一点，N 为BF 上一点，且FN AM =。

面面垂直线面垂直的判定定理一、引言在几何学中，面面垂直是一个基本的概念。

当两个平面垂直时，我们称它们是面面垂直的。

本文将介绍面面垂直线面垂直的判定定理。

二、定义1. 面：在三维空间中，由无数条线段组成的平坦曲面。

2. 平行：两条线或两个平面在同一平面内，且不相交。

3. 垂直：两条线或两个平面相交于一个角度为90度的交点。

4. 面面垂直：当两个平面相互垂直时，它们被称为“面面垂直”。

三、定理如果一条直线同时与两个不同的平面相交，并且这条直线与其中一个平面的交线是另一个平面上的一条直线，则这两个平面是“面面垂直”的。

四、证明假设有两个不同的平面A和B，并且这两个平面相互垂直。

我们需要证明如果一条直线同时与这两个不同的平面相交，并且这条直线与其中一个平面A的交线是另一个平面B上的一条直线，则这两个平面是“ 面面垂直”的。

首先，我们需要证明这条直线存在。

假设这两个平面A和B相交于一条直线L。

因为这两个平面相互垂直，所以它们的交角为90度，因此直线L与平面A和平面B的交线都是垂直的。

接下来，我们需要证明这条直线与平面A和平面B的交线是垂直的。

假设这条直线与平面A的交点为P，与平面B的交点为Q，并且PQ 在平面B上。

我们需要证明AP和BQ是垂直的。

由于PQ在平面B上，所以PQ与平面A的交线PA也在平面B上。

因此，我们可以得到三角形APQ和三角形BPQ共享一个角度PQB，并且它们有一个共同边界PQ。

根据余弦定理：cos(APQ) = (AQ² + PQ² - AP²) / (2 * AQ * PQ)cos(BPQ) = (BQ² + PQ² - BP²) / (2 * BQ * PQ)由于AP = BQ（因为它们都等于L），所以AP² = BQ²。

将其代入上式中可得：cos(APQ) = cos(BPQ)因此，APQ = BPQ因此，AP和BP是垂直的。

已知正方形ABCD和矩形 和矩形ACEF所在的平面互相垂 练 已知正方形 和矩形 所在的平面互相垂 直，AB= 2 ，AF=1，M是线段 的中点。 ， 是线段EF的中点。 是线段 的中点 平面BDE； （1）求证 ）求证AM//平面 平面 ； 的大小； （2）求二面角 −DF−B的大小； ）求二面角A− − 的大小 上确定一点P，使得PF与 所成的 （3）试在线段 上确定一点 ，使得 与BC所成的 ）试在线段AC上确定一点 E 角是60° 角是 °。
注1：① α ：
⊥ β ,α I β = l, a ⊂ α , a ⊥ b ⇒ a ⊥ β
证明： 在平面 内过B点作 ⊥ l， 证明： 在平面β内过 点作 内过 点作BE⊥ ， 又∵AB⊥ l， ⊥ ， ∴∠ABE就是二面角 -l -β的平面角 就是二面角α∴∠ 就是二面角 的平面角 ∴∠ABE=90 ，即AB⊥BE ∴∠ ⊥ 又∵l∩BE=B， ， ∴AB⊥β ⊥
如图， 于点A， 于点B， 例 如图，已知 α I β = l, CA ⊥ α于点 ，CB ⊥ β于点 ， 求证： a ⊂ α, a ⊥ AB, 求证：a // l .
注意：空间内，垂直于同一条直线的两直线平行的结论不成立 注意：空间内，垂直于同一条直线的两直线平行的结论不成立.
C β B α l A a
。
α
a
A
l
B E
β
面面垂直⇒ 面垂直” ②该定理作用：“面面垂直⇒线面垂直”，是判定线面垂 该定理作用： 面面垂直 直的依据，可以帮助我们快速找到面的垂线——平面内垂 直的依据，可以帮助我们快速找到面的垂线 平面内垂 直于两平面的交线的直线. 直于两平面的交线的直线
例 判断下列命题的真假 1.若α⊥β，那么 内的所有直线都垂直于 内的所有直线都垂直于β. 若 ⊥ ，那么α内的所有直线都垂直于

误区警示
1．不要将
ab⊥⊥αα⇒a∥b 及
aa⊥⊥αβ⇒α∥β，及
a∥b
a∥c
⇒b∥c，及 αα∥∥βγ⇒β∥γ，错误迁移到 αα⊥⊥γβ⇒β∥γ、
ab∥∥αα⇒a∥b、
aa⊥⊥bc⇒b⊥c、
aa⊥⊥bc⇒b∥c 及
α⊥β
α⊥γ
⇒β⊥γ 致误．.
2．不要将“经过一点有且仅有一条直线与平面垂 直”；“经过一点有且仅有一个平面与已知直线垂直”； “经过平面外一点有无数条直线与已知平面平行，这无 数条直线在同一个平面内，即经过平面外一点有且仅有 一个平面与已知平面平行”；“经过直线外一点有且仅 有一条直线 l 与已知直线平行，有无数个平面与已知直线 平行，这无数个平面的交线为 l”弄混错用．
面 A1BC1 与平面 AB1D 相交于经过 D 点的一条交线，又 A1B⊂平面 A1BC1，AB1⊂平面 AB1D，设 AB1 与 A1B 相 交于 O，∴平面 A1BC1∩平面 AB1D＝OD，故只须证明
BC1∥OD.
解析：(1)D 为 A1C1 的中点，证明如下：
∵BC1∥平面 AB1D，BC1⊂平面 A1BC1，
D．a⊥α，b⊥β
[答案] D
[解析]
bα⊥⊥ββ⇒b∥α 或 b⊂α，又 a∥α，此时 a 与
b 位置关系不确定，排除 A；设 α∩β＝l，当 a∥b∥l 时，
排除 B；同 A 的讨论一样可排除 C；
aα⊥⊥αβ⇒a∥β或a⊂β⇒a⊥b，故 D 正确.
b⊥β
线面垂直的判定与性质
[例 2] 已知长方体 AC1 中，棱 AB＝BC＝1，棱 BB1 ＝2，连结 B1C，过 B 点作 B1C 的垂线交 CC1 于 E，交 B1C 于 F.

面面垂直在解析几何中的应用
判定定理的应用
在解析几何中，利用面面垂直的判定定理可以确定两个平面是否垂直，进而解决与垂直相关的问题。
空间角的计算
通过面面垂直的关系，可以计算两个平面之间的夹角，即二面角的大小。
面面垂直的推广与应用前景
推广至一般曲面
在机械工程中的应用
将面面垂直的概念推广至一般曲面， 研究曲面间的垂直关系及其性质。
判定条件的证明
条件一的证明
假设有两个平面α和β，且α∩β=l ，如果直线m⊥α且m⊂β，那么 根据面面垂直的定义，我们可以 得出α⊥β。
条件二的证明
假设有两个平面α和β，且直线 m⊥α，如果m∥β，那么我们可 以过直线m作一个平面γ，使得γ 与β相交于一条直线n。由于m∥n 且m⊥α，根据线面垂直的性质定 理，我们可以得出n⊥α。又因为 n⊂β，所以根据面面垂直的判定 定理，我们可以得出α⊥β。
条件三的证明
假设有两个平面α和β，它们的法 向量分别是n1和n2。如果 n1·n2=0（即n1和n2互相垂直） ，那么根据面面垂直的定义，我 们可以得出α⊥β。
03
面面垂直的性质
面面垂直与线面垂直的关系
01
如果两个平面互相垂直，那么在 一个平面内垂直于它们交线的直 线垂直于另一个平面。
02
如果两个平面互相垂直，那么经 过第一个平面内的一点并垂直于 第二个平面的直线在第一个平面 内。
机械制造
在机械制造中，许多零部件需要保持 严格的垂直关系以确保设备的正常运 行。例如，机床的主轴与工作台需要 保持垂直，以确保加工的精度和效率 。
06
面面垂直的拓展与延伸
面面垂直与空间向量的关系
空间向量法
利用空间向量的数量积判断两个平面的法向量是否垂直，从而确定两个平面是否垂直。

线面、面面垂直的判定与性质知识回顾1．直线与平面垂直的判定（1）定义：如果直线l 与平面α内的任意一条直线都垂直，就说直线l 与平面α垂直，记作l ⊥α．（2）判定定理文字表述：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．符号表述：⎭⎪⎬⎪⎫l ⊥a l ⊥b⇒l ⊥α． 2．直线与平面垂直的性质文字表述：垂直于同一个平面的两条直线平行。

符号表述：⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒ a ∥b 3. 直线与平面所成的角定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．4．平面与平面的垂直的判定（1）定义：如果两个平面相交，且它们所成的二面角是直角，就说这两个平面互相垂直．（2）面面垂直的判定定理文字语言：一个平面过另一个平面的垂线，则这两个平面垂直．符号表示：⎭⎪⎬⎪⎫a ⊥β⇒α⊥β． 5．平面与平面垂直的性质两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直． 用符号表示为：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ⇒a ⊥β． 6．二面角二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．二面角的平面角：如图，在二面角α－l－β的棱l上任取一点O，在半平面α和β内分别作垂直于棱l的射线OA和OB，则∠AOB叫做二面角的平面角．题型讲解题型一例1、空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是()A．垂直且相交 B．相交但不一定垂直C．垂直但不相交 D．不垂直也不相交答案：C例2、如图所示，PA⊥平面ABC，△ABC中BC⊥AC，则图中直角三角形的个数为()A．4 B．3 C．2 D．1答案：A例3、如图所示，在正方体ABCD—A1B1C1D1中，E、F分别是棱B1C1、B1B的中点．求证：CF⊥平面EAB．证明在平面B1BCC1中，∵E、F分别是B1C1、B1B的中点，∴△BB1E≌△CBF，∴∠B1BE＝∠BCF，∴∠BCF＋∠EBC＝90°，∴CF⊥BE，又AB⊥平面B1BCC1，CF⊂平面B1BCC1，∴AB⊥CF，AB∩BE＝B，∴CF⊥平面EAB．题型二例4、若m 、n 表示直线，α表示平面，则下列命题中，正确命题的个数为( ) ①⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α； ② ⎭⎪⎬⎪⎫m ⊥αn ⊥α⇒m ∥n ； ③⎭⎪⎬⎪⎫m ⊥αn ∥α⇒M ⊥n; ④⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥α．A ．1B ．2C ．3D ．4答案：C例5、如图所示，在正方体ABCD —A 1B 1C 1D 1中，M 是AB 上一点，N 是A 1C 的中点，MN ⊥平面A 1DC ．求证：(1)MN ∥AD 1； (2)M 是AB 的中点．证明 (1)∵ADD 1A 1为正方形， ∴AD 1⊥A 1D ．又∵CD ⊥平面ADD 1A 1，∴CD ⊥AD 1． ∵A 1D∩CD ＝D ，∴AD 1⊥平面A 1DC ． 又∵MN ⊥平面A 1DC ， ∴MN ∥AD 1．(2)连接ON ，在△A 1DC 中， A 1O ＝OD ，A 1N ＝NC ． ∴ON12CD 12AB ， ∴ON ∥AM ． 又∵MN ∥OA ，∴四边形AMNO 为平行四边形，∴ON ＝AM ．∵ON ＝12AB ，∴AM ＝12AB ，∴M 是AB 的中点．题型三例6、直线a 与平面α所成的角为50°，直线b ∥a ，则直线b 与平面α所成的角等于( )A ．40°B ．50°C ．90°D ．150°答案：B例7、在正方体ABCD －A 1B 1C 1D 1中，(1)直线A 1B 与平面ABCD 所成的角是________； (2)直线A 1B 与平面ABC 1D 1所成的角是________； (3)直线A 1B 与平面AB 1C 1D 所成的角是________． 答案：(1)45° (2)30° (3)90° 题型四例6、在边长为1的菱形ABCD 中，∠ABC ＝60°，把菱形沿对角线AC 折起，使折起后BD ＝32，则二面角B －AC －D 的余弦值为( ) A ．13 B ．12 C ．223 D ．32答案：B [如图所示，由二面角的定义知∠BOD 即为二面角的平面角． ∵DO ＝OB ＝BD ＝32， ∴∠BOD ＝60°．]例7、过正方形ABCD 的顶点A 作线段AP ⊥平面ABCD ，且AP ＝AB ，则平面ABP 与平面CDP 所成的二面角的度数是________．答案：45° 题型五例8、下列命题中正确的是()A．平面α和β分别过两条互相垂直的直线，则α⊥βB．若平面α内的一条直线垂直于平面β内两条平行线，则α⊥βC．若平面α内的一条直线垂直于平面β内两条相交直线，则α⊥βD．若平面α内的一条直线垂直于平面β内无数条直线，则α⊥β答案：C例9、如图所示，四棱锥P—ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝3．(1)证明：平面PBE⊥平面PAB；(2)求二面角A—BE—P的大小．9．(1)证明如图所示，连接BD，由ABCD是菱形且∠BCD＝60°知，△BCD是等边三角形．因为E是CD的中点，所以BE⊥CD．又AB∥CD，所以BE⊥AB．又因为PA⊥平面ABCD，BE⊂平面ABCD，所以PA⊥BE．而PA∩AB＝A，因此BE⊥平面PAB．又BE⊂平面PBE，所以平面PBE⊥平面PAB．(2)解由(1)知，BE⊥平面PAB，PB⊂平面PAB，所以PB⊥BE．又AB⊥BE，所以∠PBA是二面角A—BE—P的平面角．在Rt△PAB中，tan∠PBA＝PAAB＝3，则∠PBA＝60°．故二面角A—BE—P的大小是60°．题型六例10、平面α⊥平面β，直线a∥α，则()A．a⊥β B．a∥βC．a与β相交 D．以上都有可能答案：D例11、如图所示，在多面体P—ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD 是等边三角形，已知BD＝2AD＝8，AB＝2DC＝45．(1)设M是PC上的一点，求证：平面MBD⊥平面PAD；(2)求四棱锥P—ABCD的体积．11．(1)证明在△ABD中，∵AD＝4，BD＝8，AB＝45，∴AD2＋BD2＝AB2．∴AD⊥BD．又∵面PAD⊥面ABCD，面PAD∩面ABCD＝AD，BD⊂面ABCD，∴BD⊥面PAD，又BD⊂面BDM，∴面MBD⊥面PAD．(2)解过P作PO⊥AD，∵面PAD⊥面ABCD，∴PO⊥面ABCD，即PO为四棱锥P—ABCD的高．又△PAD是边长为4的等边三角形，∴PO＝23．在底面四边形ABCD中，AB∥DC，AB＝2DC，∴四边形ABCD为梯形．在Rt△ADB中，斜边AB边上的高为4×845＝855，此即为梯形的高． ∴S 四边形ABCD ＝25＋452×855＝24． ∴V P —ABCD ＝13×24×23＝163．跟踪训练1．正方体A 1B 1C 1D 1－ABCD 中，截面A 1BD 与底面ABCD 所成二面角A 1－BD －A 的正切值等于( )A ．33B ．22C ． 2D ． 3答案：C[解析] 设AC 、BD 交于O ，连A 1O ，∵BD ⊥AC ，BD ⊥AA 1，∴BD ⊥平面AA 1O ，∴BD ⊥A 1O ，∴∠A 1OA 为二面角的平面角． tan ∠A 1OA ＝A 1AAO＝2，∴选C.2．过两点与一个已知平面垂直的平面( ) A ．有且只有一个 B ．有无数个 C ．有且只有一个或无数个 D ．可能不存在答案：C [当两点连线与平面垂直时，有无数个平面与已知平面垂直，当两点连线与平面不垂直时，有且只有一个平面与已知平面垂直．]3．如图，正方体ABCD －A 1B 1C 1D 1中，点P 在侧面BCC 1B 1及其边界上运动，并且总是保持AP ⊥BD 1，则动点P 的轨迹是( )A ．线段B 1C B ．线段BC 1C ．BB 1中点与CC 1中点连成的线段D ．BC 中点与B 1C 1中点连成的线段 答案：A[解析] ∵DD 1⊥平面ABCD ， ∴D 1D ⊥AC ，又AC ⊥BD ，∴AC ⊥平面BDD 1， ∴AC ⊥BD 1.同理BD 1⊥B 1C. 又∵B 1C ∩AC ＝C ， ∴BD 1⊥平面AB 1C.而AP ⊥BD 1，∴AP ⊂平面AB 1C.又P ∈平面BB 1C 1C ，∴P 点轨迹为平面AB 1C 与平面BB 1C 1C 的交线B 1C.故选A. 4．如图所示，在正方体ABCD －A 1B 1C 1D 1中，M 、N 分别是棱AA 1和AB 上的点，若∠B 1MN 是直角，则∠C 1MN ＝________．答案：90°解析 ∵B 1C 1⊥面ABB 1A 1， ∴B 1C 1⊥MN ． 又∵MN ⊥B 1M ， ∴MN ⊥面C 1B 1M ， ∴MN ⊥C 1M ．∴∠C 1MN ＝90°．5．如图所示，平面α⊥平面β，A ∈α，B ∈β，AA′⊥A′B′，BB′⊥A′B′，且AA′＝3，BB′＝4，A′B′＝2，则三棱锥A －A′BB′的体积V ＝________.答案： 4[解析] ∵α⊥β，α∩β＝A′B′，AA′⊂α，AA′⊥A′B′， ∴AA′⊥β，∴V ＝13S △A′BB′·AA′＝13×(12A′B′×BB′)×AA′＝13×12×2×4×3＝4.6. 如图所示，已知PA 垂直于⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上任意一点，过点A 作AE ⊥PC 于点E .求证：AE ⊥平面PBC .证明 ∵PA ⊥平面ABC ，∴PA ⊥BC . 又∵AB 是⊙O 的直径，∴BC ⊥AC . 而PA ∩AC ＝A ，∴BC ⊥平面PAC . 又∵AE ⊂平面PAC ，∴BC ⊥AE .又∵PC ⊥AE ，且PC ∩BC ＝C ，∴AE ⊥平面PBC .7．如图，已知AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ，F 为CD 的中点．求证：平面BCE ⊥平面CDE.证明 取CE 的中点G ，连接FG ，BG ，AF. ∵F 为CD 的中点， ∴GF ∥DE ，且GF ＝12DE.∵AB ⊥平面ACD ，DE ⊥平面ACD ， ∴AB ∥DE.则GF ∥AB. 又∵AB ＝12DE ，∴GF ＝AB.则四边形GFAB 为平行四边形．于是AF ∥BG. ∵△ACD 为等边三角形，F 为CD 的中点， ∴AF ⊥CD.∵DE ⊥平面ACD ，AF ⊂平面ACD ，∴DE ⊥AF. 又∵CD ∩DE ＝D ，CD ，DE ⊂平面CDE ， ∴AF ⊥平面CDE.∵BG ∥AF ，∴BG ⊥平面CDE.∵BG ⊂平面BCE ，∴平面BCE ⊥平面CDE.8．如图，在四棱锥P－ABCD中，底面是边长为a的正方形，侧棱PD＝a，PA＝PC＝2a，求证：(1)PD⊥平面ABCD；(2)平面PAC⊥平面PBD；(3)二面角P－BC－D是45°的二面角．证明(1)∵PD＝a，DC＝a，PC＝2a，∴PC2＝PD2＋DC2.∴PD⊥DC.同理可证PD⊥AD，又AD∩DC＝D，∴PD⊥平面ABCD.(2)由(1)知PD⊥平面ABCD，∴PD⊥AC.而四边形ABCD是正方形，∴AC⊥BD.又BD∩PD＝D，∴AC⊥平面PBD.又AC⊂平面PAC，∴平面PAC⊥平面PBD.(3)由(1)知PD⊥BC，又BC⊥DC，∴BC⊥平面PDC.∴BC⊥PC.∴∠PCD为二面角P－BC－D的平面角．在Rt△PDC中，PD＝DC＝a，∴∠PCD＝45°.∴二面角P－BC－D是45°的二面角．6．如图，在直三棱柱ABC—A1B1C1中，AA1＝AC，且BC1⊥A1C．(1)求证：平面ABC1⊥平面A1ACC1；(2)若D、E分别是A1C1和BB1的中点，求证：DE∥平面ABC1.11解析： (1)∵直三棱柱ABC －A 1B 1C 1中，AA 1＝AC ， ∴ACC 1A 1为正方形， ∴A 1C ⊥AC 1.又∵BC 1⊥A 1C ，AC 1∩BC 1＝C 1，∴A 1C ⊥平面ABC 1， 又∵A 1C ⊂平面A 1ACC 1， ∴平面A 1ACC 1⊥平面ABC 1.(2)如图，取AA 1的中点F ，连接DF 、EF.∵D 、E 、F 分别为A 1C 1、BB 1、AA 1的中点， ∴DF ∥AC 1，EF ∥AB ，DF∩EF ＝F ， ∴平面DEF ∥平面ABC 1， ∴DE ∥平面ABC 1.。

β
a
l
α
A
问题4：面面垂直性质定理用途? 面面垂直线面垂直 问题5：什么情况下用?
符号语言：
a
l
a
a l
已知面面垂直时.
平面与平面垂直的性质定理： 问题6：体现了什么数学思想? 转化
三、例题讲解 例1：PA⊥平面ABC，面PAB⊥面PBC，求证：BC⊥AB
P 问题7：要证BC垂直于AB，要会选择，选择BC垂直于AB，还是AB垂直于
已知：
, A ,C B D ,C A D .求B 证： CD
发展条件 α
转化结论
C
B
D
E
β
A
证明：
在平面β内过D作直线 DE ⊥AB
则 CD 是 E二面 -A B 角 的平面角
由 ⊥β 得CD ⊥ DE
又CD ⊥ AB, 且DE ∩ AB =D 所以直线CD⊥平面β
平面与平面垂直的性质定理： 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
线面垂直的性质定理：
垂直于同一个平面的两条直线平行
符号语言?
a ,b a//b
简述： 如何证明？
线面垂直
线线平行
知识探究： 问题2:面α与面β垂直，线L在面α内，线L与面β的关系有哪几种？（讨论一下）
α L
β 平行
问题3：怎样才能垂直？
α L
β 相交
α
L β
线在面内
思考3: 如何找地面的垂线？
注:若l ,b
则l b.
l
A
αb
2.直线与平面垂直的判定定理？ 直线与面内的两条相交直线都垂直，则该线与面垂直
图形表示
a
m

C
例3 , a , a , 判断a与 位置关系
证明：设

l
b
α
a //
a
在α内作直线b⊥l
β l b b 又a a // b
l
线面垂直 性质
bl

面面垂直性质
b a // a
相交
线在面内
知识探究：
思考2:黑板所在平面与地面所在平面垂 直，在黑板上是否存在直线与地面垂直？ 若存在，怎样画线？
α
β
平面与平面垂直的性质定理：
两个平面垂直，则一个平面内垂直于交线 的直线与另一个平面垂直。
β a
符号语言：
l
α A
al 作用： 面面垂直线面垂直
l a a
D'
' '
C'
B'
A'
D A
C B
(2)如图, a , b , 那么直线a, b一定 平行吗?
a b
α
线面垂直的性质定理： 垂直于同一个平面的两条直线平行 符号语言： a
, b a / /b
线线平行
简述： 线面垂直
1.已知:a⊥α,b⊥α 求证:a//b ’ 证明：假设 a与b不平行. 记直线 b b b a
(2)又∵ BC P
C
O
B
平面PBC ，∴平面PBC⊥平面PAC
例2：如图，已知PA⊥平面ABC， 平面PAB⊥平面PBC，求证：BC⊥平面PAB
证明：过点A作AE⊥PB，垂足 P 为E， ∵平面PAB⊥平面PBC， 平面PAB∩平面PBC=PB， A ∴AE⊥平面PBC ∵BC 平面PBC ∴AE⊥BC ∵PA⊥平面ABC，BC 平面ABC ∴PA⊥BC ∵PA∩AE=A，∴BC⊥平面PAB B