【必备】2019年北京中考数学习题精选：圆的基本性质

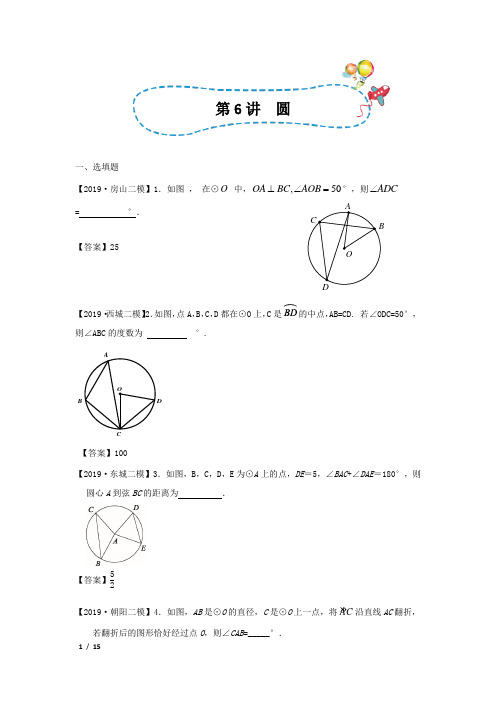
一、选填题【2019·房山二模】1．如图，在⊙O中，,50OA BC AOB⊥∠=°，则ADC∠= °．【答案】25【2019·西城二模】2．如图，点A，B，C，D都在⊙O上，C是的中点，AB=CD. 若∠ODC=50°，则∠ABC的度数为°.【答案】100【2019·东城二模】3．如图，B，C，D，E为⊙A上的点，DE＝5，∠BAC+∠DAE＝180°，则圆心A到弦BC的距离为．【答案】52【2019·朝阳二模】4．如图，AB是⊙O的直径，C是⊙O上一点，将»AC沿直线AC翻折，若翻折后的图形恰好经过点O，则∠CAB=_____°．ABOD第6讲圆COBDDCABO OABCD【答案】 30【2019·怀柔二模】5．如图，在O e 中，直径AB ⊥GH 于点M ，N 为直径上一点， 且OM=ON ，过N 作弦CD ，EF.则弦AB ，CD ，EF ，GH 中最短的是 . 【答案】GH【2019·丰台二模】6．如图，⊙O 的直径AB 垂直于弦CD ，垂足是E ，OE=CE ，则∠CAD=°【答案】45【2019·海淀二模】7．如图，在⊙O 中，弦BC 与半径OA 相交于点D ，连接AB ，OC ．若∠A =60°，∠ABC =20°，则∠C 的度数为 .【答案】40【2019·门头沟二模】8．如图，线段AB 是⊙O 的直径，弦CD 丄AB ，∠CAB = 30°，OD = 2，那么DC 的长等于A ．2B ．4C 3D ．23【答案】D【2019·平谷二模】9．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ．若AB =10，AE =1，则弦CD 的长是 ．【答案】6N M F E A O DC H GDCAOBCE OBA【2019·石景山二模】10．如图，AB 是⊙O 的弦，直径CD 交AB 于点E ，若AE =EB =3，∠C =15°，则OE 的长为（A 3 （B ）4 （C ） 6 （D ）33【答案】D 二、解答题【2019·房山二模】1．如图，△ABC 是⊙O 的内接三角形，∠ACB ＝45°，∠AOC =150°，过点C 作⊙O 的切线交AB 的延长线于点D. （1）求证：CD =CB ；（2）如果⊙O 2，求AC 的长. 【答案】（1）证明：连结OB .∵»»AB AB =，∠ACB ＝45°， ∴290AOB ACB ∠=∠=︒，∵OA=OB ，∴45OAB OBA ∠=∠=︒ ∵∠AOC =150°，∴60COB ∠=︒ ∵OC=OB ，∴△OCB 是等边三角形， ∴60OCB OBC ∠=∠=︒， ∴75CBD ∠=︒， ∵CD 是⊙O 的切线，∴90OCD OCB BCD ∠=∠+∠=︒， ∴30BCD ∠=︒， ∴75D CBD ∠=∠=︒， ∴CD =CB .（2）解：过点B 作BE ⊥AC 于点E ，BCP∵△OCB是等边三角形，∴BC OC==∵∠ACB＝45°，∴1CE BE==，∵»»BC BC=，∠BOC＝60°，∴1302EAB BOC∠=∠=︒，∴tanBEEABAE∠=，∴13AE=，∴AE=∴1AC AE CE=+=，【2019·昌平二模】2．如图，在Rt△ABC中,∠C=90°，以AC为直径的⊙O交AB于点D，点Q为CA延长线上一点，延长QD交BC于点P，连接OD，∠ADQ=12∠DOQ.（1）求证：PD是⊙O的切线；（2）若AQ=AC，AD= 2时，求BP的长.【答案】（1）连接DC，∵»»AD AD=∴∠DCA=12∠DOA∵∠ADQ=12∠DOQ ∴∠DCA=∠ADQ∵直径AC ∴∠ADC=90°∴∠DCA+∠DAC=90°∵∠ADQ+∠DAC=90°，∠ADO=∠DAO.∴∠ADQ+∠ADO=90°∴DP是⊙O切线.（2）∵∠C=90°，OC为半径.∴PC是⊙O切线.∴PD=PC.连接OP∴∠DPO=∠CPO.∴OP⊥CD.∴OP∥AD. ∵AQ=AC=2OA.∴23 QA AD QO OP==∵AD=2∴OP=3∵OP是△ACB的中位线. ∴AB=6.∵CD⊥AB，∠C=90°.∴BC2=BD·BA=24.∴：BC=26∴BP6【2019·西城二模】3．如图，AB是⊙O的直径，CA与⊙O相切于点A，且CA=BA．连接OC，过点A作AD⊥OC于点E，交⊙O于点D，连接DB．（1）求证：△ACE≌△BAD；（2）连接CB交⊙O于点M，交AD于点N．若AD=4，求MN的长．【答案】（1）证明：∵AB是⊙O的直径，∴∠ADB=90°∵AD⊥OC于点E，∴∠AEC=90°，∴∠AEC=∠ADB.∵CA与⊙O相切于点A，∴CA⊥BA∴∠CAB=90°即∠CAE+∠DAB=90°.∵∠CAE+∠ACE=90°， ∴∠DAB=∠ACE. ∵CA=BA ∴△ACE≌△BAD（2）解：连接AM ，如图∵AD⊥OC 于点E ，AD=4， ∴AE=ED=12AD=2.∵△ACE≌△BAD， ∴BD=AE=2,CE=AD=4.在Rt △ABD 中，AB=AD 2+DB 2=2 5 在Rt △ABC 中，BC=AB 2+AC 2=210. ∵∠CEN =∠BDN=90°，∠CNE=∠BND, ∴△CEN∽△BDN . ∴CN BN =CEBD =2.∴BN=13BC=2103∵AB 是⊙O 的直径， ∴∠AMB=90°，即AM ⊥CB. ∵CA=BA,∠CAB=90° ∴BM=12BC=10∴MN=BM -BN=103【2019·东城二模】4．如图，⊙O 是△ABC 的外接圆，连接OC ，过点A 作AD ∥OC 交BC 的延长线于点D ，∠ABC ＝45°． （1）求证：AD 是⊙O 的切线；（2）若sin ∠CAB ＝35，⊙O 52，求AB 的长．EDBACO【答案】（1）证明：如图，连接OA∵∠AOC ＝2∠ABC ，∠ABC ＝45° ∴∠AOC ＝90° ∵OC ∥AD∴∠AOC ＋∠OAD=180° ∴∠OAD ＝90°. ∴OA ⊥AD∵OA 是⊙O 的半径，∴AD 是⊙O 的切线 （2）解：如图，作CE ⊥AB 于点E 由（1）可知，∠AOC ＝90° ∵OA ＝OC ＝52∴AC ＝5在Rt △ACE 中，∠AEC ＝90° sin ∠CAE ＝CE AC ＝35∴CE ＝3，AE ＝4在Rt △BCE 中，∠CEB ＝90°，∠ABC ＝45° ∴∠BCE ＝45° ∴CE ＝BE ＝3 ∴AB ＝AE ＋BE ＝7【2019·朝阳二模】5．如图，△ABC 内接于以AB 为直径的⊙O ，过点A 作⊙O 的切线，与BC 的延长线相交于点D ，在CB 上截取CE =CD ，连接AE 并延长，交⊙O 于点F ，连接CF ．（1）求证：AC =CF ； （2）若AB =4，3sin 5B，求EF 的长．【答案】（1）证明：∵AD 是⊙O 的切线，∴∠DAB =90°． ∴∠CAD +∠CAB =90°． ∵AB 是⊙O 的直径， ∴∠ACB =90°． ∴∠CAB ＋∠B =90°． ∴∠CAD =∠B ． ∵CE =CD ， ∴AE =AD ．∴∠CAE =∠CAD =∠B ． ∵∠B =∠F ， ∴∠CAE =∠F ． ∴AC =CF ．（2）解：由（1）可知，sin ∠CAE =sin ∠CAD =sin B=35． ∵AB =4，∴在Rt △ABD 中，AD =3，BD =5． ∴在Rt △ACD 中，CD =95． ∴DE =185，BE =75． ∵∠CEF =∠AEB ，∠B =∠F ， ∴CEF AEB ∆∆:． ∴35EF CE EB AE ==． ∴EF =2521． 【2019·怀柔二模】6．如图，AB 是O e 的直径，弦EF ⊥AB 于点C ，点D 是AB 延长线上一点，30A ∠=︒，30D ∠=︒. （1）求证：FD 是O e 的切线；OFEDCBAM OFE DC BA（2）取BE 的中点M ，连接MF ，若7，求O e 的半径. 【答案】解：（1）连接OE ，OF ．∵EF AB ⊥，AB 是O e 的直径，∴DOF DOE =∠∠∵2DOE A =∠∠，30A ∠=︒， ∴60DOF ∠=︒ ．∵30D ∠=︒.∴90OFD ︒=∠.∴OF FD ⊥. ∴FD 为O e 的切线， （2）图形如图所示.连接OM .∵AB 为O e 的直径，∴O 为AB 中点， 90AEB ∠=︒． ∵M 为BE 的中点，∴OM AE ∥，1=2OM AE . ∵30A ∠=︒，∴30MOB A ∠=∠=︒．∵260DOF A ∠=∠=︒ ， ∴90MOF ∠=︒. ∴222+OM OF MF =．设O e 的半径为r ．∵90AEB ∠=︒，30A ∠=︒，∴cos303AE AB r ︒=⋅=.∴132OM r ．∵7FM 22213)+7)2r r =. 解得=2r ．（舍去负根）∴O e 的半径为2．【2019·丰台二模】7．如图，AB 是⊙O 的直径，P 是BA 延长线上一点，过点P 作⊙O 的切线，切点为D ，连接BD ，过点B 作射线PD 的垂线，垂足为C 。

2019年中考数学试题分类汇编28：圆的基本性质(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019年中考数学试题分类汇编28：圆的基本性质(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019年中考数学试题分类汇编28：圆的基本性质(word版可编辑修改)的全部内容。

一、选择题1. （2019山东滨州，6，3分）如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BCD＝40°，则∠ABD的大小为( ）A．60°B．50°C．40°D．20°【答案】B【解析】如图，连接AD，∵AB为⊙O的直径，∴∠ADB=90°．∵∠A和∠BCD都是弧BD所对的圆周角,∴∠A=∠BCD=40°，∴∠ABD=90°－40°=50°．故选B．【知识点】圆周角定理及其推论2。

（2019山东聊城,8，3分）如图,BC是半圆O的直径,D,E是BC上两点,连接BD,CE并延长交于点A，连接OD，OE，如果∠A＝70°，那么∠DOE的度数为A。

35° B.38°C。

40°D。

42°第8题图【答案】C【解析】∵∠A＝70°,∴∠B+∠C＝110°，∴∠BOE+∠COD＝220°,∴∠DOE＝∠BOE+∠COD－180°＝40°,故选C.【知识点】三角形内角和定理，圆周角定理3。

（2019山东省潍坊市,11，3分)如图，四边形ABCD内接于⊙O，AB为直径，AD=CD．过点D作DE⊥AB于点E．连接AC交DE于点F．若sin∠CAB=35，DF=5，则BC的长为( ）A．8 B．10 C．12 D．16【答案】C【思路分析】连接BD，先证明∠DAC=∠ACD=∠ABD=∠ADE，从而可得AF=DF=5，根据sin∠CAB=3 5 ,求得EF和AE的长度，再利用射影定理求出BE的长度从而得到直径AB，根据sin∠CAB=35求得BC的长度．【解题过程】连接BD．∵AD=CD,∴∠DAC=∠ACD．∵AB为直径，∴∠ADB=∠ACB=90°．∴∠DAB+∠ABD=90°．∵DE⊥AB，∴∠DAB+∠ADE=90°．∴∠ADE=∠ABD．∵∠ABD=∠ACD，∴∠DAC=∠ADE．∴AF=DF=5．在Rt△AEF中，sin∠CAB=35 EFAF=∴EF=3,AE=4．∴DE=3+5=8．由DE2=AE▪EB，得228164DEBEAE===．∴AB=16+4=20．在R t△ABC中，sin∠CAB=35 BC AB=∴BC=12．【知识点】圆周角，锐角三角比4。

圆专题【2019东城二模】24．如图，⊙O是△ABC的外接圆，连接OC，过点A作AD∥OC交BC的延长线于点D，∠ABC＝45°．（1）求证：AD是⊙O的切线；（2）若sin∠CAB＝35，⊙O，求AB的长．24.（1）证明：如图，连接OA∵∠AOC＝2∠ABC，∠ABC＝45°∴∠AOC＝90°………………………………………………………………1分∵OC∥AD∴∠AOC＋∠OAD=180°…………………………………………………2分∴∠OAD＝90°.∴OA⊥AD∵OA是⊙O的半径，∴AD是⊙O的切线 (3)分（2）解：如图，作CE⊥AB于点E由（1）可知，∠AOC＝90°∵OA＝OC∴AC＝5………………………………………………………………4分在Rt△ACE中，∠AEC＝90°sin∠CAE＝CEAC ＝35∴CE＝3，AE＝4………………………………………………………………5分在Rt△BCE中，∠CEB＝90°，∠ABC＝45°∴∠BCE＝45°∴CE＝BE＝3∴AB＝AE＋BE＝7………………………………………………………………6分【2019西城二模】23. 如图，AB是⊙O的直径，CA与⊙O相切于点A，且CA=BA．连接OC，过点A 作AD⊥OC于点E，交⊙O于点D，连接DB．（1）求证：△ACE≌△BAD；（2）连接CB交⊙O于点M，交AD于点N．若AD=4，求MN的长．2【2019海淀二模】22．如图，AB 是⊙O 的直径，PA ，PC 与⊙O 分别相切于点A ，C ，连接AC ，BC ，OP ，AC 与OP 相交于点D ．（1）求证：90B CPO ∠+∠=︒；（2）连结BP ，若AC ＝125，sin ∠CPO ＝35，求BP 的长．22．（本小题满分5分） （1）证明：连接OC ，如图.∵ P A ，PC 与⊙O 分别相切于点A ，C ，∴ OC ⊥PC ，OA ⊥P A ，∠APC =2∠CPO ． ∴ ∠OCP =∠OAP =90°．∵ ∠AOC +∠APC +∠OCP +∠OAP =360°，∴ ∠AOC +∠APC =180°． ∵ ∠AOC =2∠B ， ∴ 90B CPO ∠+∠=︒．4（2）解： 连接BP ，如图． ∵ AB 是⊙O 的直径，∴∠ACB =90°．∴∠ABC+∠BAC =90°．∵90ABC CPO ∠+∠=︒，∴ ∠BAC =∠CPO =∠APO .∵AC ＝125，sin ∠BAC ＝35,∴ 3AB =,32OA =． ∵32OA =，sin ∠APO ＝35, ∴ 2AP =.∴PB【2019朝阳二模】22．如图，△ABC 内接于以AB 为直径的⊙O ，过点A 作⊙O 的切线，与BC 的延长线相交于点D ，在CB 上截取CE =CD ，连接AE 并延长，交⊙O 于点F ，连接CF ．（1）求证：AC =CF ； （2）若AB =4，3sin 5B =，求EF 的长．22．（1）证明：∵AD 是⊙O 的切线，∴∠DAB =90°．∴∠CAD +∠CAB =90°． ∵AB 是⊙O 的直径， ∴∠ACB =90°． ∴∠CAB ＋∠B =90°． ∴∠CAD =∠B ．∵CE =CD ， ∴AE =AD ．∴∠CAE =∠CAD =∠B ． ∵∠B =∠F ， ∴∠CAE =∠F ． ∴AC =CF ．（2）解：由（1）可知，sin ∠CAE =sin ∠CAD =sin B=35． ∵AB =4，∴在Rt △ABD 中，AD =3，BD =5 ∴在Rt △ACD 中，CD =95． ∴DE =185，BE =75． ∵∠CEF =∠AEB ，∠B =∠F ， ∴CEFAEB ∆∆． ∴35EF CE EB AE ==． ∴EF =2521．【2019丰台二模】22. 如图，AB 是⊙O 的直径，P 是BA 延长线上一点，过点P 作⊙O 的切线，切点为D ，连接BD ，过点B 作射线PD 的垂线 ，垂足为C ． （1）求证： BD 平分∠ABC ； （2）如果AB =6，sin ∠CBD =，求PD 的长．22.（1）证明：连接OD.6∵PC 切⊙O 的于D ， ∴OD ⊥PC . ∴∠ODP =90°. ∵BC ⊥PC ， ∴∠BCP =90°. ∴∠ODP =∠BCP . ∴OD ∥BC . ∴∠ODB =∠DBC . ∵OD=OB ， ∴∠ODB =∠OBD . ∴∠OBD =∠DBC . ∴BD 平分∠ABC . 2分（2）解：连接AD.∵AB 是⊙O 的直径， ∴∠ADB =90°.在Rt △ADB 中，∵1sin sin 3AD ABD CBD AB ∠=∠==， AB=6，∴AD=2.∴BD =在Rt △CBD 中， ∵1sin 3CD CBD DB ∠==，∴CD =.∴163BC =.∵OD ∥BC ， ∴△PDO ∽△PCB . ∴PD OD PC BC =. ∴34163PD PD =.∴PD =【2019石景山二模】22．如图，在Rt △ABC 中，∠C =90º，点O 在边AC 上，⊙O 与边AC 相交于点D 、与 边AB 相切于点E ，过点D 作DP ∥BC 交AB 于点P ． （1）求证：PD=PE ；（2）连接CP ，若点E 是AP 的中点，OD : DC =2:1，CP =13，求⊙O 的半径．B8【2019门头沟二模】23．如图，点C 在⊙O 上，AB 为直径，BD 与过点C 的切线垂直于D ，BD 与⊙O 交于点E ．（1）求证：BC 平分∠DBA ； （2）如果1cos 2ABD ∠=，OA = 2，求DE 的长．【2019房山二模】22. 如图，△ABC 是⊙O 的内接三角形，∠ACB ＝45°，∠AOC =150°，过点C 作⊙O 的切线交AB 的延长线于点D. （1）求证：CD =CB ；B（2）如果⊙O，求AC的长.【2019顺义二模】22. 已知：如图，在△ABC中，∠ACB=90°，以BC为直径的⊙O交AB于点D，E为BD的中点.（1）求证：∠ACD=∠DEC；（2）延长DE、CB交于点P，若PB=BO ，DE=2，求PE的长10【2019平谷二模】22．如图，AB 是⊙O 直径，BC ⊥AB 于点B ，点C 是射线BC 上任意一点，过点C 作CD 切⊙O 于点D ，连接AD . （1）求证：BC=CD ；（2）若∠C =60°，BC =3，求AD 的长.BCA12【2019怀柔二模】23. 如图，AB 是的直径，弦EF ⊥AB 于点C ，点D 是AB 延长线上一点，30A ∠=︒，30D ∠=︒.（1）求证：FD 是的切线；（2）取BE 的中点M ，连接MF ，若，求的半径.O O ODA【2019昌平二模】23．如图，在Rt△ABC中,∠C=90°，以AC为直径的⊙O交AB于点D，点Q为CA延长线上一点，延长QD交BC于点P，连接OD，∠ADQ=12∠DOQ.（1）求证：PD是⊙O的切线；（2）若AQ=AC，AD= 2时，求BP的长.14。

第一讲：圆的基本概念、性质及其关系知识精解一、概念、性质的要点回顾1. 圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆．平面内到定点O的距离等于定长R的点所组成的图形叫做圆,记作⊙O.2. 等弧:在同圆或等圆中，能够互相________的弧叫做等弧．问题：长度相等的两条弧是等弧吗？为什么？3. 圆周角定义的两个基本特征：(1)顶点在_______上；(2)两边都和圆相交。

二、关于确定圆的条件剖析定理：过____________________上的三个点确定一个圆．1）“确定”的含义：过不在一直线上的三点能作圆，并且只能作一个圆（存在性唯一性）.2）由于任意一个三角形的三个顶点都不在同一直线上，所以由定理可知，经过三角形三个顶点可以作且只能作一个圆．(1)三角形的外接圆和圆的内接三角形：经过一个三角形三个顶点的圆叫做这个三角形的____________，这个三角形叫做圆的内接三角形．(2)三角形的外心：三角形_________圆的圆心叫做这个三角形的外心.三角形的外心是三角形三边中垂线的交点．(3)如图：⊙O称为△ABC的外接圆，△ABC称为⊙O的内接三角形，O为三角形A BC的外心。

三、重要的等量关系在同圆或等圆中，弦，弧，圆心角，弦心距等几何量之间是相互关联的，即它们中间只要有一组量相等，(例如圆心角相等)，那么其它各组量也分别相等(即相对应的弦、弦心距以及弦所对的弧也分别相等)。

*如果它们中间有一组量不相等，那么其它各组量也分别不等。

四、圆周角定理(1)圆周角的度数等于它所对的弧（或圆心角）的度数的_______．(2)半圆(或直径)所对的圆周角是_______，90°的圆周角所对的弦是_____．(3)如果三角形一边上的中线等于这边的一半，那么这边所对的内角等于_______°．自主学习例1、 现有一块打碎的圆形玻璃镜子残片，想重新去玻璃店配一块同样大 小的圆形玻璃镜子，请问这块残片还有用吗？怎样去配制？例2、AB 是⊙O 的弦，∠AOB ＝80°则弦AB 所对的圆周角是 .例3、有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三 角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧． 其中正确的有（ ）A ．4个B ．3个C ．2个D ． 1个例4、如图，AB 是⊙O 的直径，C D E ，，是⊙O 上的点，则12∠+∠= ．例5、如图，已知⊙O 的弦AB 、CD 相交于点E ，的度数为60°，的度数为100°，则∠AEC 等于（ ）A. 60°B. 100°C. 80°D. 130°例6、如图，△ABC内接于⊙O，∠C＝45°，AB＝4，则⊙O的半径为（）．A． B．4 C．．5例7、如图，AB为⊙O直径，动点P在⊙O的下半圆，定点Q在⊙O的上半圆，设∠POA=x°，∠PQB=y°，当P点在下半圆移动时，求y与x之间的函数关系式。

北京中考圆的证明与计算1．（2018•北京）如图，A B是⊙O的直径，过⊙O外一点P作⊙O的两条切线P C，P D，切点分别为C，D，连接O P，C D．（1）求证：O P⊥C D；（2）连接A D，B C，若∠D A B＝50°，∠C B A＝70°，O A＝2，求O P的长．2．（2017•北京）如图，A B是⊙O的一条弦，E是A B的中点，过点E作E C⊥O A于点C，过点B作⊙O的切线交C E的延长线于点D．（1）求证：D B＝D E；（2）若A B＝12，B D＝5，求⊙O的半径．3．（2016•北京）如图，A B为⊙O的直径，F为弦A C的中点，连接O F并延长交̂A C于点D，过点D作⊙O的切线，交B A的延长线于点E．（1）求证：A C∥D E；（2）连接C D，若O A＝A E＝a，写出求四边形A C D E面积的思路．4．（2015•北京）如图，A B是⊙O的直径，过点B作⊙O的切线B M，弦C D∥B M，交A B于点F，且̂D A=̂D C，连接A C，A D，延长A D交B M于点E．（1）求证：△A C D是等边三角形；（2）连接O E，若D E＝2，求O E的长．5．（2014•北京）如图，A B是⊙O的直径，C是̂A B的中点，⊙O的切线B D交A C的延长线于点D，E是O B的中点，C E的延长线交切线B D于点F，A F交⊙O于点H，连接B H．（1）求证：A C＝C D；（2）若O B＝2，求B H的长．6．（2018•海淀区一模）如图，A B是⊙O的直径，弦E F⊥A B于点C，过点F作⊙O的切线交A B的延长线于点D．（1）已知∠A＝α，求∠D的大小（用含α的式子表示）；（2）取B E的中点M，连接M F，请补全图形；若∠A＝30°，M F=7，求⊙O的半径．7．（2018•昌平区二模）如图，A B是⊙O的直径，弦C D⊥A B于点E，过点C的切线交A B的延长线于点F，连接D F．（1）求证：D F是⊙O的切线；（2）连接B C，若∠B C F＝30°，B F＝2，求C D的长．8．（2019•淮阴区一模）如图，A B为⊙O的直径，点C，D在⊙O上，且点C是̂B D的中点，过点C作A D的垂线E F交直线A D于点E．（1）求证：E F是⊙O的切线；（2）连接B C，若A B＝5，B C＝3，求线段A E的长．9．（2018•海淀区二模）如图，A B是⊙O的直径，M是O A的中点，弦C D⊥A B于点M，过点D作D E⊥C A交C A的延长线于点E．（1）连接A D，则∠O A D＝°；（2）求证：D E与⊙O相切；（3）点F在̂B C上，∠CD F＝45°，D F交A B于点N．若D E＝3，求F N的长．10．（2018•朝阳区二模）A B为⊙O直径，C为⊙O上的一点，过点C的切线与A B的延长线相交于点D，C A＝C D．（1）连接B C，求证：B C＝O B；（2）E是̂A B中点，连接C E，B E，若B E＝2，求C E的长．11．（2018•西城区一模）如图，⊙O的半径为r，△A B C内接于⊙O，∠B A C＝15°，∠A C B ＝30°，D为C B延长线上一点，A D与⊙O相切，切点为A．（1）求点B到半径O C的距离（用含r的式子表示）．（2）作D H⊥O C于点H，求∠A D H的度数及C BC D的值．12．（2017•西城区二模）如图，A B是⊙O的直径，C是⊙O是一点，过点B作⊙O的切线，与A C延长线交于点D，连接B C，O E∥B C交⊙O于点E，连接B E交A C于点H．（1）求证：B E平分∠A B C；（2）连接O D，若B H＝B D＝2，求O D的长．13．（2017•仙游县模拟）如图，A B为⊙O的直径，C为⊙O上一点，过点C作⊙O的切线，交B A的延长线交于点D，过点B作B E⊥B A，交D C延长线于点E，连接O E，交⊙O于点F，交B C于点H，连接A C．（1）求证：∠E C B＝∠E B C；（2）连接B F ，C F ，若C F ＝6，s i n ∠F C B =35，求A C 的长．北京中考圆的证明与计算参考答案与试题解析一．解答题（共15小题）1．（2018•北京）如图，A B是⊙O的直径，过⊙O外一点P作⊙O的两条切线P C，P D，切点分别为C，D，连接O P，C D．（1）求证：O P⊥C D；（2）连接A D，B C，若∠D A B＝50°，∠C B A＝70°，O A＝2，求O P的长．【解答】解：（1）方法1、连接O C，O D，∴O C＝O D，∵P D，P C是⊙O的切线，∵∠O D P＝∠O C P＝90°，，在R t△O D P和R t△O C P中，{O D=O CO P=O P∴R t△O D P≌R t△O C P，∴∠D O P＝∠C O P，∵O D＝O C，∴O P⊥C D；方法2、∵P D，P C是⊙O的切线，∴P D＝P C，∵O D＝O C，∴P，O在C D的中垂线上，∴O P⊥C D（2）如图，连接O D，O C，∴O A＝O D＝O C＝O B＝2，∴∠A D O ＝∠D A O ＝50°，∠B C O ＝∠C B O ＝70°，∴∠A O D ＝80°，∠B O C ＝40°，∴∠C O D ＝60°，∵O D ＝O C ，∴△C O D 是等边三角形，由（1）知，∠D O P ＝∠C O P ＝30°，在R t △O D P 中，O P =O D c o s 30°=433．2．（2017•北京）如图，A B 是⊙O 的一条弦，E 是A B 的中点，过点E 作E C ⊥O A 于点C ，过点B 作⊙O 的切线交C E 的延长线于点D ．（1）求证：D B ＝D E ；（2）若A B ＝12，B D ＝5，求⊙O 的半径．【解答】（1）证明：∵A O ＝O B ，∴∠O A B ＝∠O B A ，∵B D 是切线，∴O B ⊥B D ，∴∠O B D ＝90°，∴∠O B E +∠E B D ＝90°，∵E C ⊥O A ，∴∠C A E +∠C E A ＝90°，∵∠C E A ＝∠D E B ，∴∠E B D ＝∠B E D ，∴D B ＝D E ．（2）作D F ⊥A B 于F ，连接O E ．∵D B ＝D E ，A E ＝E B ＝6，∴E F =12B E ＝3，O E ⊥A B ，在R t △E D F 中，D E ＝B D ＝5，E F ＝3，∴D F =52-32=4，∵∠A O E +∠A ＝90°，∠D E F +∠A ＝90°，∴∠A O E ＝∠D E F ，∴s i n ∠D E F ＝s i n ∠A O E =A E A O =45，∵A E ＝6，∴A O =152．∴⊙O 的半径为152．3．（2016•北京）如图，A B 为⊙O 的直径，F 为弦A C 的中点，连接O F 并延长交̂A C于点D ，过点D 作⊙O 的切线，交B A 的延长线于点E ．（1）求证：A C ∥D E ；（2）连接C D，若O A＝A E＝a，写出求四边形A C D E面积的思路．【解答】（1）证明：∵E D与⊙O相切于D，∴O D⊥D E，∵F为弦A C中点，∴O D⊥A C，∴A C∥D E．（2）解：作D M⊥O A于M，连接C D，C O，A D．首先证明四边形A C D E是平行四边形，根据S平行四边形A C D E＝A E•D M，只要求出D M即可．（方法二：证明△A D E的面积等于四边形A C D E的面积的一半）∵A C∥D E，A E＝A O，∴O F＝D F，∵A F⊥D O，∴A D＝A O，∴A D＝A O＝O D，∴△A D O是等边三角形，同理△C D O也是等边三角形，∴∠C D O＝∠D O A＝60°，A E＝C D＝A D＝A O＝D O＝a，∴A O∥C D，又A E＝C D，∴四边形A C D E是平行四边形，易知D M=3 2a，∴平行四边形A C D E面积=3 2a2．4．（2015•北京）如图，A B是⊙O的直径，过点B作⊙O的切线B M，弦C D∥B M，交A B于点F ，且̂D A=̂D C，连接A C ，A D ，延长A D 交B M 于点E ．（1）求证：△A C D 是等边三角形；（2）连接O E ，若D E ＝2，求O E 的长．【解答】（1）证明：∵A B 是⊙O 的直径，B M 是⊙O 的切线，∴A B ⊥B E ，∵C D ∥B E ，∴C D ⊥A B ，∴̂A D=̂A C，∵̂D A=̂D C，∴̂A D=̂A C =̂C D，∴A D ＝A C ＝C D ，∴△A C D 是等边三角形；（2）解：连接O E ，过O 作O N ⊥A D 于N ，由（1）知，△A C D 是等边三角形，∴∠D A C ＝60°∵A D ＝A C ，C D ⊥A B ，∴∠D A B ＝30°，∴B E =12A E ，O N =12A O ，设⊙O 的半径为：r ，∴O N =12r ，A N ＝D N =32r ，∴E N ＝2+32r ，B E =12A E =3r +22，在R t △N E O 与R t △B E O 中，O E 2＝O N 2+N E 2＝O B 2+B E 2，即（r 2）2+（2+3r 2）2＝r 2+(3r +22)2，∴r ＝23，∴O E 2=(3)2+25＝28，∴O E ＝27．5．（2014•北京）如图，A B 是⊙O 的直径，C 是̂A B的中点，⊙O 的切线B D 交A C 的延长线于点D ，E 是O B 的中点，C E 的延长线交切线B D 于点F ，A F 交⊙O 于点H ，连接B H ．（1）求证：A C ＝C D ；（2）若O B ＝2，求B H 的长．【解答】（1）证明：连接O C ，∵C 是̂A B的中点，A B 是⊙O 的直径，∴C O ⊥A B ，∵B D 是⊙O 的切线，∴B D ⊥A B ，∴O C ∥B D ，∵O A ＝O B ，∴A C ＝C D ；（2）解：∵E 是O B 的中点，∴O E ＝B E ，在△C O E 和△F B E 中，{∠C E O =∠F E B O E =B E ∠C O E =∠F B E，∴△C O E ≌△F B E （A S A ），∴B F ＝C O ，∵O B ＝2，∴B F ＝2，∴A F =A B 2+B F 2=25，∵A B 是直径，∴B H ⊥A F ，∴△A B F ∽△B H F ，∴A B B H =A F B F，∴A B •B F ＝A F •B H ，∴B H =A B ⋅B F A F =4×225=455．6．（2018•海淀区一模）如图，A B是⊙O的直径，弦E F⊥A B于点C，过点F作⊙O的切线交A B的延长线于点D．（1）已知∠A＝α，求∠D的大小（用含α的式子表示）；（2）取B E的中点M，连接M F，请补全图形；若∠A＝30°，M F=7，求⊙O的半径．【解答】解：（1）连接O E，O F，如图，∵E F⊥A B，A B是⊙O的直径，∴∠D O F＝∠D O E．∵∠D O E＝2∠A，∠A＝α，∴∠D O F＝2α，∵F D为⊙O的切线，∴O F⊥F D．∴∠O F D＝90°．∴∠D+∠D O F＝90°，∴∠D＝90°﹣2α；（2）连接O M，如图，∵A B为⊙O的直径，∴O为A B中点，∠A E B＝90°．∵M为B E的中点，∴O M ∥A E ，∵∠A ＝30°，∴∠M O B ＝∠A ＝30°．∵∠D O F ＝2∠A ＝60°，∴∠M O F ＝90°，设⊙O 的半径为r ，在R t △O M B 中，B M =12O B =12r ，O M =3B M =32r ，在R t △O M F 中，O M 2+O F 2＝M F 2．即（32r ）2+r 2＝（7）2，解得r ＝2，即⊙O 的半径为2．7．（2018•昌平区二模）如图，A B 是⊙O 的直径，弦C D ⊥A B 于点E ，过点C 的切线交A B 的延长线于点F ，连接D F ．（1）求证：D F 是⊙O 的切线；（2）连接B C ，若∠B C F ＝30°，B F ＝2，求C D 的长．【解答】（1）证明：连接O D ，如图，∵C F 是⊙O 的切线∴∠O C F ＝90°，∴∠O C D +∠D C F ＝90°∵直径A B ⊥弦C D ，∴C E ＝E D ，即O F 为C D 的垂直平分线∴C F ＝D F ，∴∠C D F ＝∠D C F ，∵O C ＝O D ，∴∠C D O ＝∠O C D∴∠C D O +∠C D B ＝∠O C D +∠D C F ＝90°，∴O D ⊥D F ，∴D F 是⊙O 的切线；（2）解：∵∠O C F ＝90°，∠B C F ＝30°，∴∠O C B ＝60°，∵O C ＝O B ，∴△O C B 为等边三角形，∴∠C O B ＝60°，∴∠C F O ＝30°∴F O ＝2O C ＝2O B ，∴F B ＝O B ＝O C ＝2，在R t △O C E 中，∵∠C O E ＝60°，∴O E =12O C ＝1，∴C E =3O E =3，∴C D ＝2C E =23．8．（2019•淮阴区一模）如图，A B 为⊙O 的直径，点C ，D 在⊙O 上，且点C 是̂B D的中点，过点C 作A D 的垂线E F 交直线A D 于点E ．（1）求证：E F 是⊙O 的切线；（2）连接B C ，若A B ＝5，B C ＝3，求线段A E 的长．【解答】（1）证明：连接O C ，∵O A ＝O C ，∴∠O C A ＝∠B A C ，∵点C 是̂B D的中点，∴∠E A C ＝∠B A C ，∴∠E A C ＝∠O C A ，∴O C ∥A E ，∵A E ⊥E F ，∴O C ⊥E F ，即E F 是⊙O 的切线；（2）解：∵A B 为⊙O 的直径，∴∠B C A ＝90°，∴A C =A B 2-B C 2=4，∵∠E A C ＝∠B A C ，∠A E C ＝∠A C B ＝90°，∴△A E C ∽△A C B ，∴A E A C =A C A B，∴A E =A C 2A B =165．9．（2018•海淀区二模）如图，A B 是⊙O 的直径，M 是O A 的中点，弦C D ⊥A B 于点M ，过点D 作D E ⊥C A 交C A 的延长线于点E ．（1）连接A D ，则∠O A D ＝60°；（2）求证：D E 与⊙O 相切；（3）点F 在̂B C 上，∠C D F ＝45°，D F 交A B 于点N ．若D E ＝3，求F N 的长．【解答】解：（1）如图1，连接O D ，A D∵A B 是⊙O 的直径，C D ⊥A B∴A B 垂直平分C D∵M 是O A 的中点，∴O M =12O A =12O D ∴c o s ∠D O M =O M O D =12∴∠D O M ＝60°又：O A ＝O D∴△O A D 是等边三角形∴∠O A D ＝60°故答案为：60°（2）∵C D⊥A B，A B是⊙O的直径，∴C M＝M D．∵M是O A的中点，∴A M＝M O．又∵∠A M C＝∠D M O，∴△A M C≌△O M D．∴∠A C M＝∠O D M．∴C A∥O D．∵D E⊥C A，∴∠E＝90°．∴∠O D E＝180°﹣∠E＝90°．∴D E⊥O D．∴D E与⊙O相切．（3）如图2，连接C F，C N，∵O A⊥C D于M，∴M是C D中点．∴N C＝N D．∵∠C D F＝45°，∴∠N C D＝∠N D C＝45°．∴∠C N D＝90°．∴∠C N F＝90°．由（1）可知∠A O D＝60°．∴∠A C D=12∠A O D=30°．在R t △C D E 中，∠E ＝90°，∠E C D ＝30°，D E ＝3，∴C D=D E s i n 30°=6．在R t △C N D 中，∠C N D ＝90°，∠C D N ＝45°，C D ＝6，∴C N=C D ⋅s i n 45°=32．由（1）知∠C A D ＝2∠O A D ＝120°，∴∠C F D ＝180°﹣∠C A D ＝60°．在R t △C N F 中，∠C N F ＝90°，∠C F N ＝60°，C N=32，∴F N=C N t a n 60°=6．10．（2018•朝阳区二模）A B 为⊙O 直径，C 为⊙O 上的一点，过点C 的切线与A B 的延长线相交于点D ，C A ＝C D ．（1）连接B C ，求证：B C ＝O B ；（2）E 是̂A B中点，连接C E ，B E ，若B E ＝2，求C E 的长．【解答】（1）证明：连接O C ．∵A B 为⊙O 直径，∴∠A C B ＝90°，∵C D 为⊙O 切线∴∠O C D ＝90°，∴∠A C O ＝∠D C B ＝90°﹣∠O C B ，∵C A ＝C D ，∴∠C A D ＝∠D ．∴∠C O B ＝∠C B O ．∴O C ＝B C ．∴O B ＝B C ；（2）解：连接A E ，过点B 作B F ⊥C E 于点F ．∵E 是A B 中点，∴̂A E =̂B E，∴A E ＝B E ＝2．∵A B 为⊙O 直径，∴∠A E B ＝90°．∴∠E C B ＝∠B A E ＝45°，A B=22．∴C B=12A B=2．∴C F ＝B F ＝1．∴E F =3．∴C E =1+3．11．（2018•西城区一模）如图，⊙O 的半径为r ，△A B C 内接于⊙O ，∠B A C ＝15°，∠A C B ＝30°，D 为C B 延长线上一点，A D 与⊙O 相切，切点为A ．（1）求点B 到半径O C 的距离（用含r 的式子表示）．（2）作D H ⊥O C 于点H ，求∠A D H 的度数及C B C D的值．【解答】解：（1）如图，作B E ⊥O C 于点E ．∵在⊙O 的内接△A B C 中，∠B A C ＝15°，∴∠B O C ＝2∠B A C ＝30°．在R t △B O E 中，∠O E B ＝90°，∠B O E ＝30°，O B ＝r ，∴B E =O B 2=r 2，∴点B 到半径O C 的距离为r 2．（2）连接O A ．由B E ⊥O C ，D H ⊥O C ，可得B E ∥D H ．∵A D 于⊙O 相切，切点为A ，∴A D ⊥O A ，∴∠O A D ＝90°．∵D H ⊥O C 于点H ，∴∠O H D ＝90°．∵在△O B C 中，O B ＝O C ，∠B O C ＝30°，∴∠O C B=180°-∠B O C 2=75°．∵∠A C B ＝30°，∴∠O C A ＝∠O C B ﹣∠A C B ＝45°．∵O A ＝O C ，∴∠O A C ＝∠O C A ＝45°，∴∠A O C ＝180°﹣2∠O C A ＝90°，∴四边形A O H D 为矩形，∠A D H ＝90°，∴D H ＝A O ＝r ．∵B E =r 2，∴B E =D H 2．∵B E ∥D H ，∴△C B E ∽△C D H ，∴C BC D=B ED H=12．12．（2017•西城区二模）如图，A B是⊙O的直径，C是⊙O是一点，过点B作⊙O的切线，与A C延长线交于点D，连接B C，O E∥B C交⊙O于点E，连接B E交A C于点H．（1）求证：B E平分∠A B C；（2）连接O D，若B H＝B D＝2，求O D的长．【解答】（1）证明：∵A B为⊙O的直径，∴∠A C B＝90°，∵O E∥B C，∴O E⊥A C，∴̂A E=̂C E，∴∠1＝∠2，∴B E平分∠A B C；（2）解：∵B D是⊙O的切线，∴∠A B D＝90°，∵∠A C B＝90°，B H＝B D＝2，∴∠C B D＝∠2，∴∠1＝∠2＝∠C B D，∴∠C B D ＝30°，∠A D B ＝60°，∵∠A B D ＝90°，∴A B ＝23，O B =3，∵O D 2＝O B 2+B D 2，∴O D =7．13．（2017•仙游县模拟）如图，A B 为⊙O 的直径，C 为⊙O 上一点，过点C 作⊙O 的切线，交B A 的延长线交于点D ，过点B 作B E ⊥B A ，交D C 延长线于点E ，连接O E ，交⊙O 于点F ，交B C 于点H ，连接A C ．（1）求证：∠E C B ＝∠E B C ；（2）连接B F ，C F ，若C F ＝6，s i n ∠F C B =35，求A C 的长．【解答】（1）证明：∵B E ⊥O B ，∴B E 是⊙O 的切线，∵E C 是⊙O 的切线，∴E C ＝E B ，∴∠E C B ＝∠E B C ．（2）解：连接C F 、C O 、A C ．∵E B ＝E C ，O C ＝O B ，∴E O ⊥B C ，∴∠C H F ＝∠C H O ＝90°，在R t △C F H 中，∵C F ＝6，s i n ∠F C H =35，∴F H ＝C F •s i n ∠F C H =185，C H =C F 2-F H 2=245，设O C ＝O F ＝x ，在R t △C O H 中，∵O C 2＝C H 2+O H 2，∴x 2＝（245）2+（x -185）2，∴x ＝5，∴O H =75，∵O H ⊥B C ，∴C H ＝H B ，∵O A ＝O B ，∴A C ＝2O H =145．。

专题19 圆的有关计算及圆的综合学校：___________姓名：___________班级：___________一、选择题：（共4个小题）1．【2015成都】如图，正六边形A BCDEF 内接于⊙O ，半径为4，则这个正六边形的边心距OM 和BC 弧线的长分别为（ ）A ．2，3πB ．πC 23πD ．43π【答案】D ．【解析】【考点定位】1．正多边形和圆；2．弧长的计算．2．【2015攀枝花】如图，已知⊙O 的一条直径AB 与弦CD 相交于点E ，且AC =2，AE CE =1，则图中阴影部分的面积为（ ）A ．9B ．9C ．29πD ．49π【答案】D．【解析】【考点定位】1．扇形面积的计算；2．勾股定理的逆定理；3．圆周角定理；4．解直角三角形．3．【2015凉山州】将圆心角为90°，面积为4πcm2的扇形围成一个圆锥的侧面，则所围成的圆锥的底面半径为（）A．1cm B．2cm C．3cm D．4cm【答案】A．【解析】试题分析：设扇形的半径为R，根据题意得2904360rππ=，解得R=4，设圆锥的底面圆的半径为r，则12•2π•r•4=4π，解得r=1，即所围成的圆锥的底面半径为1cm．故选A．【考点定位】圆锥的计算．4．【2015河池】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y kx=+与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（）A．6 B．8 C．10 D．12【答案】A．【解析】【考点定位】1．切线的性质；2．一次函数图象上点的坐标特征；3．新定义；4．动点型；5．综合题．二、填空题：（共4个小题）5．【2015贵阳】小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上，此时，光盘与AB ，CD 分别相切于点N ，M ．现从如图所示的位置开始，将光盘在直尺边上沿着CD 向右滚动到再次与AB 相切时，光盘的圆心经过的距离是 ．【解析】试题分析：如图，当圆心O 移动到点P 的位置时，光盘在直尺边上沿着CD 向右滚动到再次与AB 相切，切点为Q ，∵ON ⊥AB ，PQ ⊥AB ，∴ON ∥PQ ，∵ON =PQ ，∴OH =PH ，在Rt △PHQ 中，∠P =∠B =60°，PQ =1，∴PH则OP =3，故答案为：3．【考点定位】1．切线的性质；2．轨迹；3．应用题；4．综合题．6．【2015自贡】如图，已知AB 是⊙O 的一条直径，延长AB 至C 点，使AC =3BC ，CD 与⊙O 相切于D 点．若CD ＝3，则劣弧AD 的长为 ．【答案】 32． 【解析】【考点定位】1．切线的性质；2．弧长的计算．7．【2015莱芜】如图，在扇形OAB 中，∠AOB =60°，扇形半径为r ，点C 在AB 上，CD ⊥OA ，垂足为D ，当△OCD 的面积最大时，AC 的长为 ．【答案】14r π．【解析】【考点定位】1．垂径定理；2．弧长的计算；3．解直角三角形；4．最值问题；5．二次函数的最值；6．圆的综合题．8．【2015成都】如图，在半径为5的⊙O 中，弦AB =8，P 是弦AB 所对的优弧上的动点，连接AP ，过点A 作AP 的垂线交射线PB 于点C ．当△PAB 是等腰三角形时，线段BC 的长为________．【答案】8BC =或5615． 【解析】试题分析：（1）当AB =AP 时，如图（1），作OH ⊥AB 于点H ，延长AO 交PB 于点G ；∵AB =AP ，∴AP AB =，∵AO 过圆心，∴AG ⊥PB ，∴PG =BG ，∠OAH =∠PAG ，∵OH ⊥AB ，∴∠AOH =∠BOH ，AH =BH =4，∵∠AOB =2∠P ，∴∠AOH =∠P ，∵OA =5，AH =4，∴OH =3，∵∠OAH =∠PAG ，∴sin ∠OAH =sin ∠PAG ，∴358PG =，∴PG =245，∵∠AOH =∠P ，∴cos ∠AOH =cos ∠P ，AP OH PC AO =，∴54033PC AP ==，∴BC =PC －2PG =4048563515-=；（3）当BA =BP 时，如图（3），∵BA =BP ，∴∠P =∠BAP ，∵∠P +∠C =90°，∠CAB +∠BAP =90°，∴∠C =∠CAB ，∴BC =AB =8．故答案为：8BC =或5615．【考点定位】1．等腰三角形的性质；2．解直角三角形；3．分类讨论；4．综合题．三、解答题：（共2个小题）9．【2015广安】如图，PB 为⊙O 的切线，B 为切点，过B 作OP 的垂线BA ，垂足为C ，交⊙O 于点A ，连接PA 、AO ，并延长AO 交⊙O 于点E ，与PB 的延长线交于点D ．（1）求证：PA 是⊙O 的切线；（2）若23OC AC =，且OC =4，求PA 的长和tanD 的值．【答案】（1）证明见试题解析；（2）512．【解析】（2）连接BE，根据已知23OCAC=，且OC=4，可求AC，OA的值，然后由射影定理可求PC的值，从而可求OP的值，然后由勾股定理可求AP的值；由AC=BC，AO=OE，得到OC是△ABE的中位线，进而可得BE∥OP，BE=2OC=8，进而可证△DBE∽△DPO，进而可得：BD BEPD OP=，从而求出BD的值，进而即可求出tanD的值．试题解析：（1）连接OB，则OA=OB，∵OP⊥AB，∴AC=BC，∴OP是AB的垂直平分线，∴PA=PB，在△PAO 和△PBO中，∵PA=PB，PO=PO，OA=OB，∴△PAO≌△PBO（SSS），∴∠PBO=∠PAO，PB=PA，∵PB为⊙O的切线，B为切点，∴∠PBO=90°，∴∠PAO=90°，即PA⊥OA，∴PA是⊙O的切线；（2）连接BE，∵23OCAC=，且OC=4，∴AC=6，∴AB=12，在Rt△ACO中，由勾股定理得：AO∴AE=2OA=OB=OA=在Rt△APO中，∵AC⊥OP，∴2AC OC PC=⋅，解得：PC=9，∴OP=PC+OC=13，在Rt△APO中，由勾股定理得：APPB=PA=∵AC=BC，OA=OE，∴OC=12BE，OC∥BE，∴BE=2OC=8，BE∥OP，∴△DBE∽△DPO，∴BD BEPD OP=，即813=，解得：BDRt△OBD中，tanD=OBBD==512．【考点定位】1．切线的判定与性质；2．相似三角形的判定与性质；3．解直角三角形．10．【2015南宁】如图，AB 是⊙O 的直径，C ，G 是⊙O 上两点，且AC =CG ，过点C 的直线CD ⊥BG 于点D ，交BA 的延长线于点E ，连接BC ，交OD 于点F ．（1）求证：CD 是⊙O 的切线．（2）若32=FD OF ，求∠E 的度数． （3）连接AD ，在（2）的条件下，若CD =3，求AD 的长．【答案】（1）证明见试题解析；（2）30°；（3【解析】（2）由OC ∥BD ，得到△OCF ∽△BDF ，△EOC ∽△EBD ，得到23OC OF BD DF ==，23OC OE BD BE ==，根据直角三角形的性质即可得到结论； （3）如图2，过A 作AH ⊥DE 于H ，解直角三角形得到BD ，DE ，BE ，在R t △DAH 中，用勾股定理即可得到AD 的长．（3）如图2，过A 作AH ⊥DE 于H ，∵∠E =30°，∴∠EBD =60°，∴∠CBD =12∠EBD =30°，∵CD ∴BD =3，DE =，BE =6，∴AE =13BE =2，∴AH =1，∴EH =，∴DH =，在R t △DAH 中，AD【考点定位】1．圆的综合题；2．切线的判定与性质；3．相似三角形的判定与性质；4．压轴题．。

一、选择题1.（2018北京朝阳区二模）5.⊙O 是一个正n 边形的外接圆，若⊙O 的半径与这个正n 边形的边长相等，则n 的值为（A ）3 （B ）4 （C ）5 （D ）6 答案:D2．（2018北京市朝阳区一模）如图，四边形ABCD 内接于⊙O ，E 为CD 延长线上一点，若∠ADE =110°，则∠AOC 的度数是（A ）70° （B ）110° （C ）140° （D ）160° 答案C3．（2018北京顺义区初三练习）如图所示圆规，点A 是铁尖的端点，点B 是铅笔芯尖的端点，已知点A 与点B 的距离是2cm ，若铁尖的端点A 固定，铅笔芯尖的端点B 绕点A 旋转一周，则作出的圆的直径．．是 A ．1 cm B ．2 cm C ．4 cm D ． cm 答案：C4.（2018北京海淀区二模）如图，圆O 的弦GH ，EF ，CD ，AB 中最短的是A . GH B. EF C. CDD. AB答案：A5.（2018北京房山区一模）如图，在⊙O 中，AC 为⊙O 直径，B 为圆上一点，若∠OBC =26°，则∠AOB 的度数为A ．26°B ．52°C ．54°D ．56° 答案B6．（2018北京市大兴区检测）如图，⊙O 的直径AB 垂直于弦CD ，垂足是E ， ∠A=22.5°，OC=6，则CD 的长为 Ａ．3Ｂ．Ｃ．6Ｄ．答案D7.（2018年北京昌平区第一学期期末质量抽测）如图，⊙O 是△ABC 的外接圆，∠A =50︒，则∠BOC 的大小为 A ．40° B ．30° C ．80° D ．100°答案：D8.（2018北京朝阳区第一学期期末检测）如图，AB 为⊙O 的直径，C ，D 为⊙O 上的两点，若AB =14，BC =7.则∠BDC 的度数是 (A) 15° (B) 30° (C) 45°(D) 60°答案：B9.（2018北京大兴第一学期期末）如图，点A ，B ，P 是⊙O 上的三点，若︒=∠40AOB ， 则APB ∠的度数为A. ︒80B. ︒140C. ︒20D. ︒50 答案：C10.（2018北京东城第一学期期末）边长为2的正方形内接于M ，则M 的半径是AA．1B．2CD．答案：C11.（2018北京房山区第一学期检测）7．如图，在⊙O中，AB AC=，∠AOB=50°，则∠ADC的度数是A．50°B．45°C．30°D．25°答案：D12.（2018北京丰台区第一学期期末）如图，A，B是⊙O上的两点，C是⊙O上不与A，B重合的任意一点. 如果∠AOB=140°，那么∠ACB的度数为A．70°B．110°C．140°D．70°或110°答案：D13.（2018北京怀柔区第一学期期末）如图，⊙O是△ABC的外接圆，∠BOC=100°，则∠A的大小为（）A．40︒B．50︒C．80︒D．100︒答案：B14.（2018北京怀柔区第一学期期末）某校科技实践社团制作实践设备，小明的操作过程如下：①小明取出老师提供的圆形细铁环，先通过在圆一章中学到的知识找到圆心O，再任意找出圆O的一条直径标记为AB（如图1），测量出AB=4分米；②将圆环进行翻折使点B落在圆心O的位置，翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D（如图2）；③用一细橡胶棒连接C、D两点（如图3）；④计算出橡胶棒CD的长度.小明计算橡胶棒CD 的长度为 A ．22 分米 B ． 23分米 C ．32 分米 D ．33分米答案：B15.（2018北京门头沟区第一学期期末调研试卷） 如图，DCE ∠是圆内接四边形ABCD 的一个外角，如果75DCE ∠=︒，那么BAD ∠的度数是A ．65︒B ．75︒C ．85︒D ．105︒ 答案：B16.（2018北京密云区初三（上）期末）如图，ABC ∆内接于O ，80AOB ∠=︒，则ACB ∠的大小为 A. 20︒ B. 40︒ C. 80︒ D. 90︒答案：B 17.（2018北京平谷区第一学期期末）如图，△ABC 内接于⊙O ，连结OA ，OB ，∠ABO =40°，则∠C 的度数是（A ）100° （B ）80° （C ）50° （D ）40°答案：C18.（2018北京石景山区第一学期期末）如图，AB 是⊙O 的直径，点C 、D 在⊙O 上．若︒=∠25ACD ，则B O D ∠的度数为（A ）︒100（B ）︒120（C ）︒130（D ）︒150答案：C19.（2018北京石景山区第一学期期末）如图，在⊙O 中，弦AB 垂直平分半径OC ．若⊙O 的半径为4，则弦AB 的长为（A ）32 （B ）34（C ）52（D ）54答案：B20.（2018北京顺义区初三上学期期末）如图，已知⊙O 的半径为6，弦AB 的长为8，则圆心O 到AB 的距离为AB． C． D ．10答案：B21.（2018北京通州区第一学期期末）如图，AB 是⊙O 的直径，点C ，D 在⊙O 上.若︒=∠55ABD ，则BC D ∠的度数为（ ）ABA ．︒25B ．︒30C ．︒35D ．︒40 答案：C22.（2018北京通州区第一学期期末）如图，⊙O 的半径为4.将⊙O 的一部分沿着弦AB 翻折，劣弧恰好经过圆心O .则折痕AB 的长为（ ）O ABC DEA. 3B. 32C. 6D. 34答案：D23.（2018北京西城区第一学期期末）如图，AB 是⊙O 的直径，CD 是⊙O 的弦，如果∠ACD =34°，那么∠BAD 等于（ ）． A ．34° B ．46° C ．56° D ．66°答案：C24.（2018北京燕山地区第一学期初四年级期末）如图，圆心角 ∠ AOB=25°，将 AB 旋转 n °得到 CD ，则∠ COD 等于A ． 25°B ． 25°+ n °C ． 50°D ． 50°+ n °答案： A.二、填空题25.（2018北京房山区二模）如图，AB 为⊙O 的直径，弦CD AB ，垂足为点E ，连结OC ，若OC =5，CD =8，则AE = .答案： 226.（2018北京东城区二模）如图，在△ABC 中，AB =AC ，BC =8. O e 是△ABC 的外接圆，其半径为5.若点A 在优弧BC 上，则tan ABC ∠的值为_____________.答案： 227.. （2018北京西城区二模）如图，AB 为⊙O 的直径，AC 与⊙O 相切于点A ，弦BD ∥OC .若36C ∠=︒，则∠DOC= ︒． 答案：5428.（2018北京朝阳区二模）如图，△ABC 内接于⊙O ，AB 是⊙O的直径，点D 在圆O 上，弧BD =弧CD ，AB=10，AC =6，连接OD 交BC 于点E ，DE = ．答案：229.（2018北京昌平区二模）如图，在圆O 的内接四边形ABCD 中，AB =3，AD =5，∠BAD =60°，点C 为弧BD 的中点，则AC 的长是 ．答案：330.．（2018北京延庆区初三统一练习）如图，AB 是⊙O 的弦，∠AOC =42°，那么∠CDB 的度数为____________．答案：21°C31.．（2018北京西城区九年级统一测试）如图，AB 为⊙O 的直径，C 为AB 上一点，50BOC ∠=︒，AD OC ∥，AD 交⊙O 于点D ，连接AC ，CD ，那么ACD ∠=__________．答案：4032.（2018北京市朝阳区综合练习（一）） 如图，点A ，B ，C 在⊙O 上，四边形OABC 是平行四边形，OD ⊥AB 于点E ，交⊙O 于点D ，则∠BAD = 度.答案15第13题图33. （2018北京门头沟区初三综合练习）如图，PC 是⊙O 的直径，PA 切⊙O 于点P ，AO 交⊙O 于点B ；连接BC ，若∠C =32°，则∠A =_____________ °． 答案26°34．（2018北京平谷区中考统一练习）如图，AB 是⊙O 的直径，AB ⊥弦CD 于点E ，若AB =10，CD =8，则BE = ． 答案235．（2018北京石景山区初三毕业考试）如图，AB 是⊙O 的直径，CD是弦，CD AB ⊥于点E ，若⊙O 的半径是5，8CD =，则AE = ．ODCBA答案：236．（2018北京丰台区一模）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ．如果∠A = 15°，弦CD = 4，那么AB 的长是 ．答案837.（2018北京朝阳区第一学期期末检测）如图，正六边形ABCDEF 内接于⊙O ，⊙O 的半径为3，则正六边形ABCDEF 的边长为 .答案：338.（2018北京大兴第一学期期末）如图，在半径为5cm 的⊙O 中，如果弦AB 的长为8cm ，OC ⊥AB ，垂足为C ，那么OC 的长为 cm ．A B答案： 3.39.（2018北京东城第一学期期末）如图，AB 是O 的弦，C 是AB 的中点，连接OC 并延长交O 于点D .若CD =1，AB =4,则O 的半径是 .答案： 2.540.（2018北京东城第一学期期末）O 是四边形ABCD 的外接圆,AC 平分∠BAD ，则正确结论的序号是 .①AB =AD ; ②BC =CD ; ③AB AD =; ④∠BCA =∠DCA ; ⑤BC CD =答案：②⑤41.（2018北京房山区第一学期检测）如图，⊙O 的半径为5， AB 为弦，OC ⊥AB ，垂足为E ，如果CE=2，那么AB 的长是 ．答案：842.（2018北京丰台区第一学期期末）如图，等边三角形ABC 的外接圆⊙O 的半径OA 的长为2，则其内切圆半径的长为 .答案：143.（2018北京丰台区第一学期期末）在平面直角坐标系中，过三点A （0，0），B （2，2），C （4，0）的圆的圆心坐标为 . 答案：（2，0）44.（2018北京门头沟区第一学期期末调研试卷）如图，在△ABC 中，∠A =60°，⊙O 为△ABC 的外接圆．如果BC=,那么⊙O 的半径为________.答案：245.（2018北京平谷区第一学期期末）13．“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣.”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法，即“割圆术”．“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆．刘徽从圆内接正六边形出发，将边数逐次加倍，并逐次得到正多边形的周长和面积．如图，AB 是圆内接正六边形的一条边，半径OB =1，OC ⊥AB 于点D ，则圆内接正十二边形的边BC 的长是（结果不取近似值）．=46.（2018北京石景山区第一学期期末）如图，在Rt △ABC 中，︒=∠90C ，AB =10．若以点C 为圆心，CB 为半径的圆恰好经过AB 的中点D ，则AC =________．答案：3547.（2018北京通州区第一学期期末）⊙O 的半径为1，其内接ABC △的边2=AB ，则C ∠的度数为______________.答案：45°或135°48.（2018北京西城区第一学期期末）如图，⊙O 的半径等于4，如果弦AB 所对的圆心角等于120︒，那么圆心O 到弦AB 的距离等于.答案：249.（2018北京西城区第一学期期末）如图，⊙O 的半径为3，A ，P 两点在⊙O 上，点B 在⊙O 内，4tan 3APB ∠=，AB AP ⊥.如果OB ⊥OP ，那么OB 的长为.答案：150.（2018北京燕山地区第一学期初四年级期末）如图，AB 、AC 是⊙O 的弦，OM ⊥ AB ，ON ⊥ AC ，垂足分别为 M 、N ．如果 MN=2.5，那么 BC=答案： 551.（2018北京丰台区二模）数学课上，老师提出如下问题：△ABC 是⊙O 的内接三角形，OD ⊥BC 于点D .请借助直尺，画出△ABC中∠BAC 的平分线. 晓龙同学的画图步骤如下：（1）延长OD 交»BC于点M ； （2）连接AM 交BC 于点N.所以线段AN 为所求△ABC 中∠BAC 的平分线.请回答：晓龙同学画图的依据是 .答案：垂径定理，等弧所对的圆周角相等52.（2018北京燕山地区第一学期初四年级期末）如图，量角器的直径与直角三角尺 ABC 的斜边 AB 重合，其中量角器 0 刻度线的端点 N 与点 A 重合，射线 CP 从 CA 处出发沿顺时针方向以每秒 3°的速度旋转，CP 与量角器的半圆弧交于 点 E ，则第 20 秒点 E 在量角器上对应的读数是 °答案 ：120° 三、解答题53．（2018北京海淀区第二学期练习）如图，AB 是⊙O 的直径，弦EF AB ⊥于点C ，过点F 作⊙O 的切线交AB 的延长线于点D .（1）已知A α∠=，求D ∠的大小（用含α的式子表示）； （2）取BE 的中点M ，连接MF ，请补全图形；若30A ∠=︒，MF =，求⊙O 的半径.解：（1）连接OE ，OF ．∵EF AB ⊥，AB 是O 的直径， ∴DOF DOE =∠∠．∵2DOE A =∠∠，A α=∠，∴2DOF α=∠． ………………1分 ∵FD 为O 的切线， ∴OF FD ⊥.∴90OFD ︒=∠.∴+90D DOF ︒=∠∠. 902D α∴∠=︒-． ………………2分（2）图形如图所示.连接OM .∵AB 为O 的直径，∴O 为AB 中点， 90AEB ∠=︒． ∵M 为BE 的中点， ∴OM AE ∥，1=2OM AE . ………………3分DADAC A ∵30A ∠=︒，∴30MOB A ∠=∠=︒． ∵260DOF A ∠=∠=︒ ，∴90MOF ∠=︒. ………………4分∴222+OM OF MF =． 设O 的半径为r ． ∵90AEB ∠=︒，30A ∠=︒，∴cos30AE AB ︒=⋅=.∴OM ． ………………5分∵FM∴222)+r =. 解得=2r ．（舍去负根） ∴O 的半径为2．54.（2018年北京昌平区第一学期期末质量抽测）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，连接AC ，BC ． （1）求证：A BCD ∠=∠； （2）若AB =10，CD =8，求BE 的长．答案：（1）证明：∵ 直径AB ⊥弦CD ，∴弧BC =弧BD . …………………… 1分 ∴A BCD ∠=∠.…………………… 2分（2）解：连接OC∵ 直径AB ⊥弦CD ，CD =8， ∴CE =ED =4. …………………… 3分∵ 直径AB =10，∴CO =OB =5.在Rt △COE 中3OE …………………… 4分∴2BE =.…………………… 5分55.（2018北京朝阳区第一学期期末检测）如图，四边形ABCD 是⊙O 的内接四边形，对角线AC 是⊙O 的直径，AB=2，∠ADB ＝45°. 求⊙O 半径的长. 答案：18．解：∵AC 是⊙O 的直径，∴∠ABC =90°. ………………分A∵∠ADB ＝45°，∴∠ACB =∠ADB ＝45°. …………………………………………………………2分 ∵AB=2，∴B C =A B =2. ……………………………………………………………………3分 ∴2222=+=BC AB AC .…………………………………………………………4分 ∴⊙O 半径的长为2. ………………………………………………………………5分56.（2018北京大兴第一学期期末）已知： 如图，⊙O 的直径AB 的长为5cm ，C 为⊙O 上的一个点，∠ACB 的平分线交⊙O 于点D ，求BD 的长． 答案：21. 解：∵ AB 为直径，∴ ∠ADB =90°， ……………………………… 1分 ∵ CD 平分∠ACB ， ∴ ∠ACD =∠BCD ，∴ AD⌒ =BD ⌒ ．………………………………… 2分 ∴ AD =BD ……………………………………… 3分 在等腰直角三角形ADB 中， BD =AB sin45°=5× 2 2 =52 2 ……………… 5分∴ BD =522 .57.（2018北京大兴第一学期期末）已知：如图，AB 为半圆O 的直径，C 是半圆O 上一点，过点C 作AB 的平行线交⊙O 于点E ，连接AC 、BC 、AE ，EB . 过点C 作CG ⊥AB 于点G ，交EB 于点H. （1）求证：∠BCG=∠E BG ； （2）若55sin =∠CAB ，求GB EC的值.答案： 证明：（1）∵AB 是直径，∴∠ACB =90°.………………………………………………..1分 ∵CG ⊥AB 于点G ， ∴∠ACB=∠ CGB =90°.∴∠CAB =∠BCG . .………………………………………………..2分DB∵CE ∥AB ， ∴∠CAB =∠ACE . ∴∠BCG =∠ACE 又∵∠ACE =∠EBG∴∠BCG =∠EBG . .………………………………………………..3分（2）解：∵sin 5CAB ∠=∴1tan 2CAB ∠=，………………………………………………..4分 由（1）知，∠HBG =∠EBG =∠ACE =∠CAB ∴在Rt △HGB 中，1tan 2GH HBG GB ∠==. 由（1）知，∠BCG =∠CAB 在Rt △BCG 中，1tan 2GB BCG CG ∠==. 设GH=a ，则GB=2a ，CG=4a .CH =CG －HG =3a . ……………..6分 ∵EC ∥AB ，∴∠ECH =∠BGH ，∠CEH =∠GBH∴△ECH ∽△BGH ．……………………………………………..7分 ∴33EC CH aGB GH a ===．…………………………………………8分58.（2018北京东城第一学期期末） 已知等腰△ABC 内接于O , AB =AC ，∠BOC =100°，求△ABC 的顶角和底角的度数.解：如图1，当点A 在优弧上时， ∠A =50°，∠ABC =∠ACB =65°；--------------------3分 如图2，当点A 在劣弧上时， ∠A =130°，∠ABC =∠ACB =25°. -------------------5分图1 图259.（2018北京密云区初三（上）期末）21. 如图，AB 是O 的弦，O 的半径OD AB ⊥ 垂足为C.若AB =，CD=1 ，求O 的半径长.答案：21.解：AB 是O 的弦，O 的半径OD AB ⊥ 垂足为C，AB =∴…………………………………………………..2分连接OA.设O 半径为r ，则 222OA AC OC =+即222(r 1)r =+- …………………………………..4分解得：2r = …………………………………………………………………5分60.（2018北京平谷区第一学期期末）如图，AB 是⊙O 的直径，弦CD ⊥AB 于E ，∠A =15°，AB =4．求弦CD 的长．答案：解：∵∠A =15°，∴∠COB =30°． ........................................................................................................... 1 ∵AB =4，∴OC =2． ..................................................................................................................... 2 ∵弦CD ⊥AB 于E ，∴CE =12CD ． ............................................................................................................. 3 在Rt △OCE 中，∠CEO =90°，∠COB =30°，OC =2，∴CE =1． ..................................................................................................................... 4 ∴CD =2． (5)61.（2018北京顺义区初三上学期期末）已知：如图， AB 为⊙O 的直径，CE ⊥AB 于E ，BF ∥OC ，连接BC ，CF ．求证：∠OCF =∠ECB ．答案：证明： 延长CE 交⊙O 于点G ．∵AB 为⊙O 的直径，CE ⊥AB 于E ，∴BC =BG ，∴∠ G =∠2，……………………………………………..2分 ∵BF ∥OC ，∴∠1=∠F ，………………………………………………3分 又∵∠G =∠F ，………………………………………..….5分 ∴∠1=∠2．…………………………………………….…6分（其它方法对应给分）62.（2018北京通州区第一学期期末）如图，ABC △内接于⊙O .若⊙O 的半径为6，︒=∠60B ，求AC 的长．答案：63.（2018北京燕山地区第一学期初四年级期末）如图，A B 为⊙O 的直径，弦CD ⊥A B 于点E，连接BC．若A B ＝6，∠B ＝30°，求：弦CD 的长。

2019 备战中考数学（北师大版）专题练习-圆（含答案）2019 备战中考数学（北师大版）专题练习-圆（含答案）一、单选题1.如图， AB 是圆 O 的直径， BC、CD、DA 是圆 O 的弦，且 BC=CD=DA，则∠ BCD等于（）A. 100 °B. 110 °C. 120 °D. 135 °2.如图，P 是∠O外一点，PA是∠O的切线，PO=26cm， PA=24cm，则∠O的周长为（）A. 18πcmB. 16πcmC. 20πcmD. 24πcm3.如图，∠ ABC内接于∠O，OD∠ BC于 D，∠ A=50，°则∠ OCD的度数是（A. 40°B. 45°C. 50°）D. 60°4.如图，在∠O中，直径AB∠弦CD，垂足为M ，则下列结论一定正确的是（）A. AC=CDB. OM=BMC. ∠ A=∠ ACDD. ∠ A=∠ BOD5.在∠O中， AB、 CD是两条相等的弦，则下列说法中错误的是（）A. AB、 CD所对的弧一定相等B. AB、 CD 所对的圆心角一定相等C. ∠ AOB和∠ COD能完全重合D. 点 O 到 AB、 CD的距离一定相等6.过圆内一点 A 可以作出圆的最长弦有（）A. 1条B. 2 条C. 3条D. 1条或无数条7.一个扇形的圆心角为60°，它所对的弧长为2π cm，则这个扇形的半径为（）A. 6cmB. 12cmC.cmD.cm2019 备战中考数学（北师大版）专题练习-圆（含答案）8.如图，是半圆，O为AB中点，C、D两点在上，且AD∠ OC，连接BC、BD．若=62 °，则的度数为何？（）A. B. C. D.二、填空题9.如图，在5×5正方形网格中，一条圆弧经过A， B， C 三点，已知点 A 的坐标是（ -2， 3），点 C 的坐标是（ 1， 2），那么这条圆弧所在圆的圆心坐标是________.10.制作一个圆锥模型，要求圆锥母线长9cm，底面圆直径为10cm，那么要制作的这个圆锥模型的侧面展开扇形的纸片圆心角度数是________度．11.如图， PA、PB 是∠0的切线， A、B 为切点， AC是∠O的直径，∠ P=40，°则∠ BAC=．12.如图，PA、PB切∠O于 A、B，，点C是∠O上异于A、B的任意一点，则＝________．13.如图， MN 是∠O的直径， MN=4，∠ AMN=40°，点 B 为弧 AN 的中点，点 P 是直径 MN 上的一个动点，则 PA+PB的最小值为 ________．14.若一个扇形的圆心角为60°，面积为6π，则这个扇形的半径为________15.如图所示， PA 切∠O于 A，PB 切∠O于 B，OP交∠O于 C，下列说法：① PA=PB，②∠ 1=∠2，③ OP 垂直平分AB，其中正确说法的序号是________16.如图， PA、PB 分别切圆O 于 A、B，并与圆 O 的切线，分别相交于C、D，已知 PA=7cm，则∠PCD的周长等于 ________ cm．17.已知：扇形 OAB 的半径为 12 厘米，∠ AOB=150，°若由此扇形围成一个圆锥的侧面，则这个圆锥底面圆的半径是 ________ 厘米．18.已知扇形的半径是 3 厘米，如果弧长是 6.28 厘米，这个扇形的面积是________平方厘米．三、解答题19.如图，在∠O中， C﹑ D 为∠O上两点， AB 是∠O的直径，已知∠ AOC=130，°AB=2．求：（ 1）的长；（2）∠D的度数．20.如图所示，在平面直角坐标系 xOy 中，半径为 2 的∠P的圆心 P 的坐标为（ -3， 0），将∠P沿 x 轴正方向平移，使∠P与 y 轴相切，求平移的距离 .21.如图所示，已知甲、乙、丙三种图案的地砖，它们都是边长为 4 的正方形．① 甲地砖以正方形的边长为半径作弧得到甲图所示的阴影部分；② 乙地砖以正方形的边长为直径作弧得到乙图所示的阴影部分；③ 丙地砖以正方形边长的一半为直径作弧得到丙图所示的阴影部分；设三种地砖的阴影部分面积分别为S 甲、 S 乙和 S 丙．（1）求 S甲．（结果保留π）（2）请你直接将 S 甲和 S 乙的数量关系填在横线上： ________．（3）由题（ 2）中面积的数量关系，可直接求得S 丙＝ ________．（结果保留π）四、综合题22.如图， D 是∠O直径 CA延长线上一点，点 B 在∠O上，且 AB=AD=AO．（1）求证： BD 是∠O的切线．（2）若 E是劣弧上一点，AE与BC相交于点F，∠BEF的面积为9，且 cos∠BFA=，求2019 备战中考数学（北师大版）专题练习-圆（含答案）∠ ACF的面积．23.如图，在∠ ABC中，点 O 在边 AC 上，∠O与∠ ABC的边 BC， AB 分别相切于C，D 两点，与边AC 交于 E 点，弦 CF 与 AB 平行，与 DO 的延长线交于 M 点．（1）求证：点 M 是 CF的中点；（2）若 E是的中点，BC=a，写出求AE 长的思路．24.如图，已知AB 是∠O的直径，点C、 D 在∠O上，点 E 在∠O外，∠EAC=∠ D=60．°（1）求∠ABC的度数；（2）求证： AE 是∠O的切线；（3）当 BC=4时，求劣弧 AC 的长．2019 备战中考数学（北师大版）专题练习-圆（含答案）答案解析部分一、单选题1.【答案】 C【考点】圆心角、弧、弦的关系【解析】【解答】解：连接OC、OD，∠BC=CD=DA，∠∠COB=∠ COD=∠，DOA∠∠COB+∠ COD+∠ DOA=180，°∠∠COB=∠ COD=∠ DOA=60，°∠∠BCD=×2（180 °﹣60°）=120 °．故选 C．【分析】由已知可得，弦BC、 CD、DA 三等分半圆，从而不难求得∠BCD的度数．2.【答案】 C【考点】切线的性质【解析】【分析】如图，连接 OA，根据切线的性质证得∠AOP是直角三角形，由勾股定理求得OA 的长度，然后利用圆的周长公式来求∠O 的周长。