西安交通大学数学实验报告(用MATLAB绘制二维、三维图形)(MATLAB循环结构、选择结构)

数字图像处理第二次作业摘要本次报告主要记录第二次作业中的各项任务完成情况。

本次作业以Matlab 2013为平台，结合matlab函数编程实现对lena.bmp,elain1.bmp图像文件的相关处理：1.分别得到了lena.bmp 512*512图像灰度级逐级递减8-1显示，2.计算得到lena.bmp图像的均值和方差，3.通过近邻、双线性和双三次插值法将lena.bmp zoom到2048*2048，4. 把lena和elain 图像分别进行水平shear（参数可设置为1.5，或者自行选择）和旋转30度，并采用用近邻、双线性和双三次插值法zoom到2048*2048。

以上任务完成后均得到了预期的结果。

1.把lena 512*512图像灰度级逐级递减8-1显示（1）实验原理：给定的lena.bmp是一幅8位灰阶的图像，即有256个灰度色。

则K位灰阶图像中某像素的灰度值k(x,y)(以阶色为基准)与原图同像素的灰度值v(x,y)(以256阶色为基准)的对应关系为：式中floor函数为向下取整操作。

取一确定k值，对原图进行上式运算即得降阶后的k位灰阶图像矩阵。

（2）实验方法首先通过imread()函数读入lena.bmp得到图像的灰度矩阵I，上式对I矩阵进行灰度降阶运算，最后利用imshow()函数输出显示图像。

对应源程序为img1.m。

（3）处理结果8灰度级7灰度级6灰度级5灰度级4灰度级3灰度级2灰度级1灰度级（4）结果讨论：由上图可以看出，在灰度级下降到5之前，肉眼几乎感觉不出降阶后图像发生的变化。

但从灰度级4开始，肉眼明显能感觉到图像有稍许的不连续，在灰度缓变区常会出现一些几乎看不出来的非常细的山脊状结构。

随着灰度阶数的继续下降，图像开始出现大片的伪轮廓，灰度级数越低，越不能将图像的细节刻画出来，最终的极端情况是退化为只有黑白两色的二值化图像。

由此可以得出，图像采样的灰度阶数越高，灰度围越大，细节越丰富，肉眼看去更接近实际情况。

MATLAB绘图实验报告三MATLAB绘图实验报告三**大学实验报告学院：计信学院专业：网络工程班级：网络092姓名实验时间实验项目名称实1.掌握绘制二维图形及三维图形的方法。

验2.掌握图形控制与修饰处理的方法。

目3.了解图像处理及动画制作的基本方法。

的实验要求实验PC 机、MATLAB7.0仪器在MATLAB7.0下认真独立完成各个实验，并了解和掌握绘制二维、三围图形的方法，学会图形制作的基本方法。

学号指导教师实验组成绩实验3.MATLAB绘图实验MATLAB程序设计教程第四章课后实验习题1、2、4内容1.（1）（2）实验数据2.4.（1）（2）1.在MATLAB中，绘制直角坐标系下的二维曲线可以利用plot函数。

实验总2.在绘制图形的同时，可对图形添加图形标注，以使图形意义更加明确，可读性强。

3.Mesh函数用于绘制三维网格图，在不需要绘制特别精细的三维曲面图时，可通过三维网格图来表示三维曲面。

结4.MATLAB有功能极强的图形处理工具箱，可对图像进行更专业的处理---图形处理；描绘质点运动轨迹的动画轨迹动画。

指导教师意见签名：年月日注：各学院可根据教学需要对以上栏木进行增减。

表格内容可根据内容扩充。

扩展阅读：MATLAB绘图实验报告实验项目：MATLAB作图实验目的：1）了解MATLAB平面绘图的命令，如MATLAB常用的二维及三维绘图命令。

2）了解MATLAB立体图形的绘制，其中包括常用的立体绘图函数的理解。

实验原理：一、平面绘图命令1）plot：线性二维图。

plot函数常用的格式：plot(x,y)或者plot(x,y,s)或plot(x1,y1,x2,y2,...)或plot(x1,y1,s1,x2,y2,s2,...)其中x,x1,x2,…为横坐标，y,y1,y2,…为纵坐标，s,s1,s2,…为绘图方式参数。

绘图方式参数及含义：颜色：bblue；ggreen；rred；ccyan；mmagenta；yyellow；kblack。

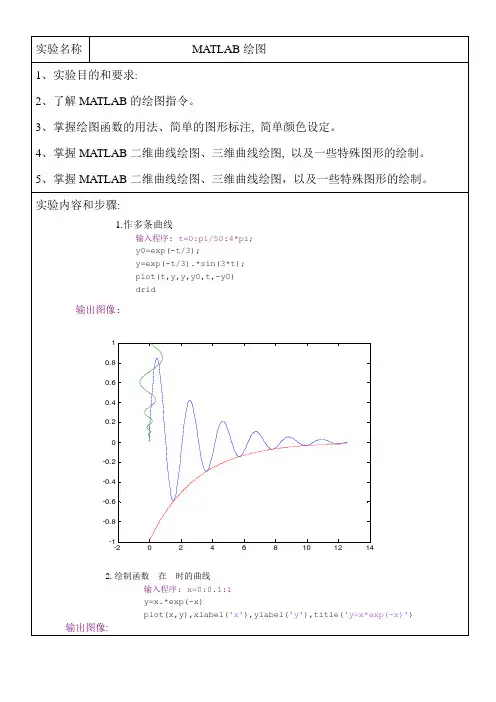
四、实验内容与步骤:1.绘制下列曲线.(1) y=x-(x^3)/6程序输入如下:fplot('x-(x^3)/6',[-5,5],'r.');程序输出:(2) x^2+2*y^2=64程序输入如下:ezplot(' x^2+2*y^2-64',[-8,8]) 程序输出:2.设y=1/(1+exp(-t)) –pi<=t<=pi在同一图形窗口采用子图的形式绘制条形图阶梯图杆图和对数坐标图等不同图形,并对不同图形加标注说明.程序输入如下:t=-pi:pi/10:pi;y=1./(1+exp(-t));subplot(2,2,1);bar(t,y,'r');title('条形图');axis([-4,4,0,1]);subplot(2,2,2);stairs(t,y,'b');title('阶梯图');axis([-4,4,0,1]);subplot(2,2,3);stem(t,y,'g');title('杆图');axis([-4,4,0,1]);subplot(2,2,4);semilogx(t,y,'k');title('对数坐标图');axis([-4,4,0,1]);程序输出:3.绘制下列极坐标图.(1) y=5*cos(x)+4(2) y=(5*sin(x)*sin(x))/cos(x) (1)程序输入:x=0:pi/50:2*pi;y=5*cos(x)+4;polar(x,y,'-*');程序输出:(2)程序输入:x=-pi/3:pi/50:pi/3;y=(5.*sin(x).*sin(x))./cos(x);polar(x,y,'-*');程序输出:4.绘制下列三维图形(1)x=exp(-t/20).*cos(t)y=exp(-t/20).*sin(t)z=t0<=t<=2*pi(2)z=5abs(x)<=5abs(y)<=5要求应用插值着色处理(1)程序输入:t=0:pi/10:2*pi;x=exp(-t/20).*cos(t);y=exp(-t/20).*sin(t);z=t;plot3(x,y,z);title('三维图形4-1');xlabel('x');ylabel('y');zlabel('z'); grid on;程序输出:(2)程序输入:[x,y]=meshgrid(-5:0.5:5); z=0*(x-y)+5;surf(x,y,z);shading interp;title('三维图形4-2');程序输出:五、实验总结:2.绘制下列曲线,(1) y=exp(-x*x/2)/(2*pi)程序输入:fplot('exp(-x*x/2)/(2*pi)',[0,5],'r.')程序输出:(2) x=t*sin(t)y=t*cos(t)程序输入:t=0:0.1:2*pi;x=t.*sin(t);y=t.*cos(t);plot(x,y);程序输出:3.在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点(1) y=2*x-0.5(2) x=sin(3*t).*cos(t)y= sin(3*t).*sin(t)0<=t<=pi程序输入:t=0:pi/100:pi;x=sin(3*t).*cos(t);y2=sin(3*t).*sin(t);y1=2*x-0.5;plot(x,y1,'m',x,y2,'g');hold onk=find(abs(y2-y1)<1e-4);x1=x(k);y3=2*x1-0.5;plot(x1,y3,'bp');程序输出:4.分别用plot和fplot函数绘制函数y=sin(1/x)的曲线,分析两曲线的差别程序输入:x=-1:pi/100:1;y=sin(1./x);subplot(2,1,1);plot(x,y,'g');subplot(2,1,2);fplot('sin(1./x)',[-1,1],'m');程序输出:两曲线的差别plot函数在取数据点时一般都是等间隔采样,fplot函数可自适应地对函数进行采样,能更好的反应函数的变化规律6.绘制曲面图形(1)x=3*u*sin(v)y=2*u*cos(v)z=4*u*u程序输入:[u,v]=meshgrid(0:pi/100:2*pi);x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.*u;mesh(x,y,z);程序输出:严重觉得对细节方面很重要,,差一个点就能导致整个程序的不能运行。

实验四
专业：电子信息工程2班姓名：李书杰学号：3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。

2.掌握图形控制与修饰处理的方法。

3.了解图像处理及动画制作的基本方法。

二、实验内容
1.绘制下列图形曲线。

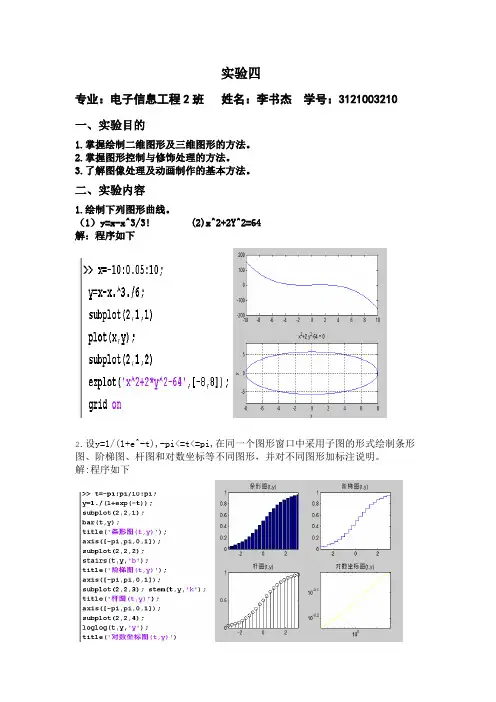
（1）y=x-x^3/3! (2)x^2+2Y^2=64
解：程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形，并对不同图形加标注说明。

解:程序如下
3.绘制下列极坐标图。

（1）ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解：程序如下
思考练习：
2.绘制下列曲线
（1）y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解：程序如下
（1）
结果如下：
（2）
结果如下：
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。

（1）y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解：程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线，分析两曲线的差别。

解：程序如下
结果如下：
5.绘制下列极坐标图：
(1）p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解：程序如下
结果如下：。

实验五数据可视化一、实验目的掌握MATLAB 二维、三维图形绘制，掌握图形属性的设置和图形修饰。

二、实验内容(1)二维图形绘制。

(2)三维曲线和三维曲面绘制。

三、实验步骤1．二维图形绘制(1) 二维图形绘制主要使用函数plot。

(2)函数plot 的参数也可以是矩阵。

(3) 选用绘图线形和颜色(4) 添加文字标注。

(5) 修改坐标轴范围。

6) 子图和特殊图形绘制。

2. 三维曲线和三维曲面绘制(1) 三维曲线绘制使用plot3 函数。

绘制一条空间螺旋线：z=0:0.1:6*pi;x=cos(z);y=sin(z);plot3(x,y,z);(2) 三维曲面图的绘制：MATLAB 绘制网线图和曲面图的函数分别是mesh( )和surf( )，其具体操作步骤是：①用函数meshgrid( )生成平面网格点矩阵[X,Y]；②由[X,Y]计算函数数值矩阵Z；③用mesh( )绘制网格图，用surf( )绘制曲面图。

绘制椭圆抛物面：clear all,close all;x=-4:0.2:4;y=x;[X,Y]=meshgrid(x,y);Z=X.^2/9+Y.^2/9;mesh(X,Y,Z);title('椭圆抛物面网格图')figure(2)surf(X,Y,Z);title('椭圆抛物面曲面图')绘制阔边帽面：clear all,close all;x=-7.5:0.5:7.5;y=x;[X,Y]=meshgrid(x,y);R=sqrt(X.^2+Y.^2)+eps; %避开零点，以免零做除数Z=sin(R)./R;mesh(X,Y ,Z);title('阔边帽面网格图')figure(2)surf(X,Y ,Z);title('阔边帽面曲面图')四、练习：1、写出图 A2 的绘制方法。

提示：按照以下的步骤进行(1)产生曲线的数据(共有 3组数据)；(2)选择合适的线形、标记、颜色(正弦曲线为红色，余弦曲线为青色)；(3)添加图例及文字说明信息；(4)添加坐标轴说明与图标题。

实验报告（二）完成人：L.W.Yohann注：本次实验主要学习了用MATLAB绘制二维、三维图形的基本命令、图形的标识与修饰以及用符号函数绘图，在学习完成后小组对52页的上机练习题进行了程序编辑和运行。

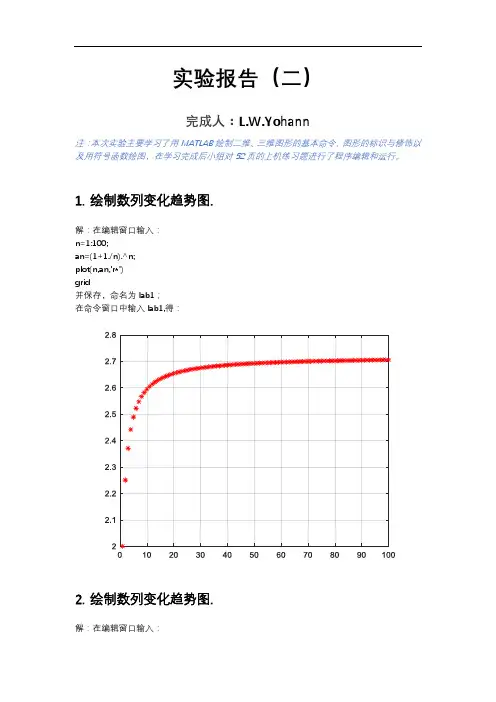
1.绘制数列变化趋势图.解：在编辑窗口输入：n=1:100;an=(1+1./n).^n;plot(n,an,'r*')grid并保存，命名为lab1；在命令窗口中输入lab1,得：2.绘制数列变化趋势图.解：在编辑窗口输入：n=1:0.1:50;an=n.^(1./n);plot(n,an,'r*')grid并保存，命名为lab2；在命令窗口中输入lab2,得：3.绘制函数在无定义点处的变化趋势.解：在编辑窗口输入：x=-10:0.05:10;y=sin(x)./x;plot(x,y,'r*')grid并保存，命名为lab3；在命令窗口中输入lab3,得：4.在同一坐标系中画出函数及其Taylor多项式的图像解：y=sinx在编辑窗口输入：syms xf=sin(x);T6=taylor(f,x);T8=taylor(f,x,'Order',8);T10=taylor(f,x,'Order',10);T12=taylor(f,x,'Order',12);fplot([T6 T8 T10 T12 f])xlim([-8 8])grid onlegend('approximation of sin(x) up to O(x^6)',...'approximation of sin(x) up to O(x^8)',...'approximation of sin(x) up to O(x^{10})',...'approximation of sin(x) up to O(x^{12})',...'sin(x)','Location','Best')title('Taylor Series Expansion')并保存，命名为lab4sin；在命令窗口中输入lab4sin,得：y=exp(x)在编辑窗口输入：syms xf=exp(x);T6=taylor(f,x);T8=taylor(f,x,'Order',8);T10=taylor(f,x,'Order',10);T12=taylor(f,x,'Order',12);fplot([T6 T8 T10 T12 f])xlim([-8 8])grid onlegend('approximation of exp(x) up to o(x^6)',...'approximation of exp(x) up to o(x^8)',...'approximation of exp(x) up to o(x^{10})',...'approximation of exp(x) up to o(x^{12})',...'exp(x)','Location','Best')title('Taylor Series Expansion')并保存，命名为lab4exp；在命令窗口中输入lab4exp,得：5.符号函数绘图.注：在matlab r2010b 和matlab r2019b中对绘制函数图像的输入方法有不同的要求，故此类题分两个版本来求解。

matlab实验报告《matlab 实验报告》一、实验目的通过本次实验，熟悉 MATLAB 软件的基本操作和功能，掌握使用MATLAB 进行数学计算、数据处理、图形绘制等方面的方法和技巧，提高运用 MATLAB 解决实际问题的能力。

二、实验环境1、计算机：＿____2、操作系统：＿____3、 MATLAB 版本：＿____三、实验内容及步骤（一）矩阵运算1、创建矩阵在 MATLAB 中，可以通过直接输入元素的方式创建矩阵，例如：｀A ＝ 1 2 3; 4 5 6; 7 8 9`，创建了一个 3 行 3 列的矩阵 A。

还可以使用函数来创建特定类型的矩阵，如全零矩阵`zeros(m,n)｀、全 1 矩阵`ones(m,n)｀、单位矩阵`eye(n)｀等。

2、矩阵的基本运算加法和减法：两个矩阵相加或相减，要求它们的维度相同，对应元素进行运算。

乘法：矩阵乘法需要满足前一个矩阵的列数等于后一个矩阵的行数。

转置：使用`A'｀来获取矩阵 A 的转置。

（二）函数的使用1、自定义函数可以在 MATLAB 中自定义函数，例如定义一个计算两个数之和的函数：｀｀｀matlabfunction s ＝ add_numbers(a,b)s ＝ a ＋ b;end｀｀｀2、调用函数在命令窗口中输入`add_numbers(3,5)｀即可得到结果 8。

（三）数据的读取和写入1、读取数据使用`load`函数可以读取数据文件，例如`load(＇datatxt'）｀。

2、写入数据使用`save`函数可以将数据保存到文件中，例如`save(＇resulttxt'，A)｀，将矩阵 A 保存到`resulttxt`文件中。

（四）图形绘制1、二维图形绘制折线图：使用`plot(x,y)｀函数，其中 x 和 y 分别是横坐标和纵坐标的数据。

绘制柱状图：使用`bar(x,y)｀函数。

2、三维图形绘制三维曲线：使用`plot3(x,y,z)｀函数。

实验四MATLAB绘图01070801 寇琪一、实验目的1、学习MATLAB的各种2维绘图；2、学习MATLAB的3维绘图；3、MATLAB的绘图修饰。

（多种绘图，图形注释，绘图颜色，色图矩阵）二、实验内容在下面的实验操作中，认真记录每项操作的作用和目的。

（一）基本二维绘图1、向量绘图函数：plot(x,y,'s')输入：x=0:2*pi/100:2*pi;y1=sin(2*x);y2=cos(2*x);plot(x,y1)plot(x,y2)plot(x,y1,x,y2)输出：保持作图输入：plot(x,y1);hold on;plot(x,y2);hold off; 输出：矩阵作图输入：plot(x',[y1' y2']) 输出：设定颜色与线型输入：plot(x,y1,'c:',x,y2,'wo') 输出：多窗口绘图输入：figure(1);plot(x,y1);figure(2);plot(x,y2); 输出：子图绘图输入：subplot(221);plot(x,y1);subplot(222);plot(x,y2);subplot(223);plot(x,y1,x,y1+y2);subplot(224);plot(x,y2,x,y1-y2);输出：复变函数绘图输入：w=0.01:0.01:10;G=1./(1+2*w*i);subplot(121);plot(G);subplot(122);plot(real(G),imag(G)); 输出：插值绘图输入：x = 0:2*pi/8:2*pi; y = sin(x);plot(x,y,'o');hold on;xi = 0:2*pi/100:2*pi;yi = spline(x,y,xi);plot(xi,yi,'m');输出：反白绘图与绘图背景色设定输入：whitebg('k')输出：2、函数绘图函数：fplot('function',[XMIN XMAX YMIN YMAX],'s') 输入：fplot('sin',[0 4*pi])f='sin(x)';fplot(f,[0 4*pi])fplot('sin(1/ x)', [0.01 0.1],1e-3)fplot('[tan(x),sin(x),cos(x)]',[-2*pi 2*pi -2*pi 2*pi])输出：3、符号函数快捷绘图f='exp(-0.5*x)*sin(x)';ezplot(f,[0,10])（二）多种二维绘图1、半对数绘图（频率特性绘图）输入：w=logspace(-1,1); %横坐标对数分度g=20*log10(1./(1+2*w*i)); %模纵坐标取分贝(dB)p=angle(1./(1+2*w*i))*180/pi; %角纵坐标取度( )subplot(211);semilogx(w,g);grid; %幅频特性子图，半对数绘图，加网线subplot(212);semilogx(w,p);grid; %相频特性子图，半对数绘图，加网线输出：2、极坐标绘图输入：t=0:2*pi/180:2*pi;mo=cos(2*t);polar(t,mo);输出：3、直方图输入：t=0:2*pi/8:2*pi; y=sin(t);bar(t,y)输出：4、离散棒图输入：t=0:2*pi/8:2*pi;y=sin(t);stem(t,y)输出：5、阶梯图输入：t=0:2*pi/8:2*pi;y=sin(t);stairs(t,y)输出：6、彗星绘图输入：t = -pi:pi/200:pi;comet(t,tan(sin(t))-sin(tan(t))); 输出：（三）图形注释y1=dsolve('D2u+2*Du+10*u=0','Du(0)=1,u(0)=0','x');y2=dsolve('D2u+2*Du+10*u=10','Du(0)=0,u(0)=0','x');y=sym('[0 0]');y=sym(y,1,1,y1);y=sym(y,1,2,y2);fplot(y,[0,5])title('二阶系统时间响应'); %图题标注xlabel('时间t');ylabel('响应幅值y'); %坐标标注gtext('零输入响应'); %用鼠标作曲线标注gtext('零状态响应'); %用鼠标作曲线标注grid %加网格线（四）三维绘图1、三维线图输入：t = 0:pi/50:10*pi;plot3(sin(t),cos(t),t);comet3(sin(t),cos(t),t);输出：2、单变量高度网线图输入：Z2=[1 1;1 -1];Z4=[Z2 Z2;Z2 -Z2];Z8=[Z4 Z4;Z4 -Z4];mesh(Z8)输出：3、三维变量马鞍面网线图输入：x=-4:0.5:4;y=x;[X,Y]=meshgrid(x,y);Z=X.^2-Y.^2;mesh(X,Y,Z);输出：4、圆锥面网线图输入：t1=0:0.1:0.9;t2=1:0.1:2;r=[t1 -t2+2];[X,Y,Z]=cylinder(r,40); 输出：5、视角修饰输入：t1=0:0.1:0.9;t2=1:0.1:2;r=[t1 -t2+2];[X,Y,Z]=c ylinder(r,30);mesh(X,Y,Z);subplot(2,2,1);mesh(X,Y,Z);view(0,0);subplot(2,2,2);mesh(X,Y,Z);view(-20,20);subplot(2,2,3);mesh(X,Y,Z);view(-30,30);subplot(2,2,4);mesh(X,Y,Z);view(-40,40); 输出：6、MATLAB暖色(hot)函数色图输入：peaks(20);axis('off')c olormap(hot);c olorbar('horiz');输出：7、光照修饰输入：surfl(peaks(20));c olormap(gray);shading interp; 输出：8、表面修饰输入：subplot(131);peaks(20);shading flat;subplot(132);peaks(20);shading interp;subplot(133);peaks(20);shading fac eted; 输出：9、透视与消隐输入；P=peaks(30);subplot(121);mesh(P);hidden off;subplot(122);mesh(P);hidden on;输出：10、裁剪修饰输入：P=peaks(30);subplot(121);meshz(P);P(20:23,9:15)=NaN*ones(4,7);subplot(122);meshc(P);输出：11、水线修饰输入：w aterfall(peaks(20))c olormap([1 0 0])输出：12、等高线修饰输入：c ontour(peaks(20),6)c ontour3(peaks(20),10)c label(c ontour(peaks(20),4))c label(c ontour3(peaks(20),3))输出：。

实验目的1．掌握MATLAB的基本绘图命令。

2．掌握运用MATLAB绘制一维、二维、三维图形的方法.3．给图形加以修饰。

一、预备知识1．基本绘图命令plotplot绘图命令一共有三种形式：⑴plot（y)是plot命令中最为简单的形式，当y为向量时,以y的元素为纵坐标，元素相应的序列号为横坐标,绘制出连线；若y为实矩阵，则按照列绘出每列元素和其序列号的对应关系，曲线数等于矩阵的列数;当y为复矩阵时，则按列以每列元素的实部为横坐标，以虚部为纵坐标，绘出曲线，曲线数等于列数。

⑵ plot（x,y,［linspec］）其中linspec是可选的，用它来说明线型。

当x和y为同维向量时，以x为横坐标，y为纵坐标绘制曲线;当x是向量，y是每行元素数目和x维数相同的矩阵时,将绘出以x为横坐标，以y中每行元素为纵坐标的多条曲线，曲线数等于矩阵行数；当x为矩阵，y为相应向量时，使用该命令也能绘出相应图形。

⑶ plot（x1,y1,x2,y2，x3,y3……）能够绘制多条曲线,每条曲线分别以x和y为横纵坐标，各条曲线互不影响。

线型和颜色MATLAB可以对线型和颜色进行设定，线型和颜色种类如下：线：—实线：点线 -.虚点线——折线点：.圆点 +加号 *星号 x x型 o 空心小圆颜色：y 黄 r 红 g 绿 b 蓝 w 白 k 黑 m 紫 c 青特殊的二维图形函数表5 特殊2维绘图函数[1］ 直方图在实际中,常会遇到离散数据,当需要比较数据、分析数据在总量中的比例时，直方图就是一种理想的选择，但要注意该方法适用于数据较少的情况。

直方图的绘图函数有以下两种基本形式。

·bar(x,y) 绘制m*n 矩阵的直方图.其中y 为m ＊n 矩阵或向量,x 必须单向递增。

·bar(y） 绘制y 向量的直方图，x 向量默认为x=1：m close all; ％关闭所有的图形视窗。

x=1:10；y=rand （size(x ）); bar(x,y ）; ％绘制直方图.123456789100.51Bar(）函数还有barh （）和errorbar （）两种形式，barh()用来绘制水平方向的直方图，其参数与bar()相同，当知道资料的误差值时，可用errorbar （)绘制出误差范围,其一般语法形式为：errorbar （x,y,l,u)其中x,y 是其绘制曲线的坐标,l ，u 是曲线误差的最小值和最大值，制图时，l 向量在曲线下方,u 向量在曲线上方。

.实验报告（201 /201 学年第学期）课程名称实验名称二维图形与三维图形的绘制实验时间年月日实验室指导教师学生姓名学号班级专业实验报告三、实验内容及原理（包括硬件原理图、算法、逻辑框图，关键代码等，可续页）（一）二维图形的绘制1、绘制二维曲线的基本函数：○1plot函数plot函数的基本调用格式为：plot(x,y);其中x和y为长度相同的向量，分别用于存储x坐标和y坐标数据。

例，绘制参数方程曲线。

程序如下：含多个输入参数的plot函数调用格式为：p lot(x1,y1,x2,y2,…,xn,yn);含选项的plot函数调用格式为：plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n);例，用不同线型和颜色在同一坐标内绘制曲线y=2e-0.5x sin(2πx)及其包络线。

程序如下：○2双纵坐标函数plotyyplotyy函数是MATLAB 5.X新增的函数。

它能把函数值具有不同量纲、不同数量级的两个函数绘制在同一坐标中。

调用格式为：plotyy(x1,y1,x2,y2);其中x1-y1对应一条直线，x2-y2对应另一条曲线。

横坐标的标度相同，纵坐标有两个，左纵坐标用于x1-y1数据对，右纵坐标用于x2-y2数据对。

2、绘制二维图形的其他函数在线性直角坐标系中，其他形式的图形有条形图、阶梯图、杆图和填充图等，所采用的函数分别是：bar(x,y,选项);stairs(x,y,选项);stem(x,y,选项);fill(x1,y1,选项1,x2,y2,选项2,…);例，分别以条形图、填充图、阶梯图和杆图形式绘制曲线y=2e-0.5x。

程序如下：（二）三维图形的绘制1、绘制三维曲线的基本函数plot3函数与plot函数用法十分相似，其调用格式为：plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n); 例，绘制空间曲线。

程序如下：2、绘制三维曲面的函数surf函数和mesh函数的调用格式为：surf(x,y,z,e);mesh(x,y,z,e);例，绘制两个直径相等的圆管的相交图形。

实验报告2课程 数学实验与数学软件 实验名称 matlab 的二维绘图 第 1 页专业 数学与应用数学 班级_08级数学3班__ ______ 学号_182__ 姓名 郑贞贞 实验日期：2010 年 03 月18 日 评分一、实验目的1. 了解plot 函数的用法和matlab 绘图的基本原理。

2. 了解图形属性的设置。

二、实验内容1．用 plot 函数在一个坐标系下绘制以下函数的图形：y 1 用黑色间断线点标记为星号 y 2 用红色实线点标记为小方格 y 3 用蓝色虚线点标记为小圆圈2.在不同的图形子窗口中绘制如下曲线：Y=sin(x)的线型为虚线，点为菱形，点标记表面色为红； Y=cos(x)的线型为－.，点为左三角形，点标记表面色为黑； Y=1.2^x 的线型为实线，点为o 形，点标记表面色为黄; 字体大小为15； 线粗细为2；123sin(),cos(),sin(2), 02y x y x y x x π===≤≤3．使用text, title, xlabel和plot绘制下面图形：4、如何使用subplot命令创建下面的图形窗口：5、在同一个窗口中画出三条曲线，并给出图例和栅格线三、实验环境（1）硬件：PC机（2）软件：Windows 操作系统、matlab7.0四、实验步骤1、x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);y3=sin(2*x);plot(x,y1,'k-.*',x,y2,'r-s',x,y3,'b:o')2、x=-2*pi:pi/10:2*pi;subplot(2,2,1)y=sin(x);plot(x,y,'d:','linewidth',2, 'markerfacecolor','r') title('y=sin(x)函数图像','fontsize',15);xlabel('x\in[-2*pi,2*pi]')legend('sin(x)')subplot(2,2,3)x=0:pi/10:2*pi;y=cos(x);plot(x,y,'<-','linewidth',2, 'markerfacecolor','k') title('y=cos(x)函数图像','fontsize',15)xlabel('x\in[0,2*pi]')legend('cos(x)')subplot(2,2,[2 4])x=-10:1:100;y=1.2.^x;plot(x,y,'o-','linewidth',2, 'markerfacecolor','y') title('y=1.2^x函数图像','fontsize',15)xlabel('x\in[-10,100]')ylabel('y=1.2^x','fontsize',15)3、x=0:pi/10:2*pi;y=sin(2*x-1);plot(x,y,'ro-','markerfacecolor','b')xlabel('x\in[0,2*pi]')title('{\omega}=2,{\beta}=-1')text(5,0.4,'\leftarrowy=sin({\omega}x+{\beta})') 4、x=-4:0.5:4;y=x.*x;figuresubplot(2,2,1);plot(x,y)y=2.^x;subplot(2,2,2);plot(x,y)y=-x.*x;subplot(2,2,[3,4]);subplot('position',[0.29,0.1,0.5,0.38]);plot(x,y)5x=0:3:60;y=2*x-1;figure;plot(x,y,'color','b')hold ony=-2*x;plot(x,y,'color','r');hold ony=x;plot(x,y,'color','g');legend('y=2*x-1','y=-2*x','y=x') grid on五、实验结果与讨论实验结果如下：x∈[-2*pi,2*pi] x∈[0,2*pi]7y=1.2x函数图像x∈[-10,100]y=1.2xx ∈[0,2*pi]-4-2024-4-20240102030405060-150-100100150六、总结（说明实验过程中遇到的问题及解决办法；新发现或个人的收获；未解决/需进一步研讨的问题或建议新实验方法等）问题：没有注意到点乘，出现了一些差错，后来通过翻书了解了，偶尔用中文输入法忘了改标点符号收获：学会在同一个窗口显示几个图像，及安排各个子窗口位置不足：需要对各种函数多加了解，对各种线型点型符号需要了解。

MATLAB绘画实验报告MATLAB绘画实验报告引言：MATLAB是一种强大的科学计算软件，它不仅可以进行数值计算、数据分析和模拟仿真等工作，还可以用于绘制各种图形。

在本次实验中，我将通过使用MATLAB进行绘画，探索其绘图功能的强大之处。

一、绘制基本图形首先，我使用MATLAB绘制了一些基本图形，如直线、曲线和点等。

通过设置不同的参数，我可以控制图形的形状、颜色和线条样式等。

这为我后续的绘图工作奠定了基础。

二、绘制二维图形接下来，我使用MATLAB绘制了一些二维图形，如折线图、散点图和柱状图等。

通过输入数据并选择合适的绘图函数，我可以将数据以直观的方式展示出来。

例如，我可以使用折线图来展示某个变量随时间的变化趋势，或者使用散点图来展示两个变量之间的关系。

三、绘制三维图形除了二维图形，MATLAB还可以绘制各种各样的三维图形。

我使用MATLAB绘制了一些三维曲面图和三维散点图。

通过设置坐标轴和数据，我可以将复杂的数据以立体的方式展示出来。

这对于研究三维数据的分布和趋势非常有帮助。

四、绘制动画除了静态图形，MATLAB还可以绘制动画。

我使用MATLAB编写了一些简单的动画程序，如小球的运动轨迹和图形的变换等。

通过控制时间和参数，我可以实现图形的动态变化，使得观察者可以更好地理解图形背后的规律和特点。

五、图形处理与分析MATLAB不仅可以绘制图形，还可以对图形进行处理和分析。

我使用MATLAB 对一些图形进行了平滑处理、噪声去除和边缘检测等操作。

这些图形处理技术可以帮助我们更好地理解图像中的信息，并提取出我们感兴趣的特征。

六、应用实例最后，我将MATLAB的绘图功能应用到了实际问题中。

我使用MATLAB绘制了一幅地形图，并通过设置不同的参数，展示了地形在不同条件下的变化。

这对于地质学家和地理学家来说非常有用，可以帮助他们更好地理解地球表面的形态和特征。

结论：通过本次实验，我深刻体会到了MATLAB绘图功能的强大之处。

实验三ＭＡTLAＢ绘图一、实验目得1。

掌握二维图形得绘制.２．掌握图形得标注３.了解三维曲线与曲面图形得绘制.二、实验得设备及条件计算机一台(带有MＡTLAB7、0以上得软件环境）。

设计提示１。

Matｌab 允许在一个图形中画多条曲线:plot（x1,y1，ｘ2,y2，……）指令绘制y1 = f1(x１）, y2 = f2 (ｘ2 )等多条曲线。

Matlａｂ自动给这些曲线以不同颜色。

标注可用ｔeｘt 函数。

2。

绘图时可以考虑极坐标与直角坐标得转换。

３.三维曲线绘图函数为ｐｌot3,注意参考帮助中得示例.三、实验内容1．生成1×１0 维得随机数向量a，分别用红、黄、蓝、绿色绘出其连线图、杆图、阶梯图与条形图,并分别标出标题“连线图"、“杆图”、“阶梯图”、“条形图"。

2、绘制函数曲线，要求写出程序代码。

（１）在区间[０:２π]均匀得取50个点,构成向量t（2) 在同一窗口绘制曲线y1=ｓin(2＊t-0、3）；ｙ2＝３ｃos（t＋0、5)；要求y1曲线为红色点划线，标记点为圆圈;ｙ２为蓝色虚线，标记点为星号.(３）分别在靠近相应得曲线处标注其函数表达式.３、将图形窗口分成两个绘图区域,分别绘制出函数:在[0，３］区间上得曲线,并利用axis调整轴刻度纵坐标刻度,使在［0，1２］区间上,在[—2，１、5］区间上。

4。

用meｓｈ或suｒf函数,绘制下面方程所表示得三维空间曲面，x与ｙ得取值范围设为[-3，3］。

思考题：1.编写一个mcircle(r）函数，调用该函数时，根据给定得半径ｒ，以原点为圆心，画一个如图所示得红色空心圆.(图例半径ｒ=5);左图参考polａr函数得用法,右图绘制圆形得参数方程为x=ｓiｎ（t），ｙ=cos（t)。

其中，t得区间为0～2*pｉ，步长为0、1.2.(１)绘一个圆柱螺旋线（形似弹簧）图.圆柱截面直径为10，高度为５,每圈上升高度为1。

如左图所示。