实验一达西定律验证实验

一、实验目的1. 理解和掌握液体流动的基本原理；2. 观察液体在不同条件下的流动现象；3. 分析液体流动速度与液体性质、管道结构等因素的关系。

二、实验原理液体流动是指液体在重力、压力、粘度等作用下，在管道内流动的过程。

液体流动的基本原理包括：1. 牛顿粘性定律：液体的流动速度与剪切应力成正比，与剪切率成反比；2. 达西定律：液体在管道内流动时，其流量与管道长度、管道截面积、液体粘度和压力差成正比；3. 伯努利方程：在液体流动过程中，流速增加，压力降低。

三、实验材料与仪器1. 实验材料：水、酒精、肥皂水、色拉油等；2. 实验仪器：管道、阀门、流量计、计时器、压力计、温度计等。

四、实验步骤1. 实验一：观察液体在管道中的流动现象（1）将管道安装好，连接好阀门和流量计；（2）打开阀门，观察水在管道中的流动现象，记录流量计的读数；（3）分别将肥皂水、酒精、色拉油等液体加入管道中，观察其流动现象，记录流量计的读数；（4）分析不同液体在管道中的流动速度、压力、粘度等参数。

2. 实验二：观察液体流动速度与管道结构的关系（1）将管道连接好，安装好阀门和流量计；（2）调整管道的弯曲程度、管道直径、管道长度等参数；（3）观察液体在管道中的流动现象，记录流量计的读数；（4）分析不同管道结构对液体流动速度的影响。

3. 实验三：观察液体流动速度与液体性质的关系（1）将管道连接好，安装好阀门和流量计；（2）调整液体的粘度、密度等参数；（3）观察液体在管道中的流动现象，记录流量计的读数；（4）分析不同液体性质对流动速度的影响。

五、实验结果与分析1. 实验一：观察液体在管道中的流动现象实验结果显示，不同液体在管道中的流动速度、压力、粘度等参数存在差异。

肥皂水在管道中的流动速度较快，压力较低；酒精的流动速度较慢，压力较高；色拉油的流动速度最慢，压力最高。

2. 实验二：观察液体流动速度与管道结构的关系实验结果显示，管道的弯曲程度、管道直径、管道长度等参数对液体流动速度有显著影响。

达西定律实验引言：达西定律是描述流体流动的经验定律之一，由法国科学家达西于1799年提出。

该定律表明，当流体通过管道流动时，流速增大、压力降低。

为了验证达西定律的准确性，并进一步了解流体在管道中的流动规律，科学家们进行了一系列的实验。

实验一：流体通过水平管道实验目的：通过实验验证达西定律在水平管道中的适用性，并观察不同流速下的压力变化。

实验装置和步骤：1. 准备一根水平透明管道，长度为1米，管径为2厘米，并在管道两端安装好压力计和流量计。

2. 将流体（如水）注入管道中，并控制不同的流速。

3. 测量不同流速下管道入口和出口处的压力，并记录数据。

实验结果和讨论：经过实验观察和数据分析，我们发现达西定律在水平管道中得到了有效验证。

随着流速的增大，管道入口处的压力降低，出口处的压力也较低。

这与达西定律的预期结果相符。

实验二：流体通过斜管道实验目的：通过实验验证达西定律在斜管道中的适用性，并研究不同斜度对流体流动的影响。

实验装置和步骤：1. 准备一根倾斜的透明管道，长度为1米，管径为2厘米，并在管道两端安装好压力计。

2. 将流体注入管道中，并控制不同斜度下的流速。

3. 测量不同斜度下管道入口和出口处的压力，并记录数据。

实验结果和讨论：根据实验结果和数据分析，我们可以得出结论：在斜管道中，流体流动时同样符合达西定律。

不同斜度下流速的增大，导致入口处和出口处的压力下降情况类似于水平管道中的观察结果。

实验三：流体通过不同直径的管道实验目的：通过实验验证达西定律在不同直径管道中的适用性，并研究不同管道直径对流体流动的影响。

实验装置和步骤：1. 准备两根透明管道，长度均为1米，其中一根管径为2厘米，另一根管径为4厘米。

2. 将流体注入这两根管道中，并控制相同的流速。

3. 测量两根管道入口和出口处的压力，并记录数据。

实验结果和讨论：实验结果表明，不同直径的管道中达西定律同样成立。

尽管管径变大，但流速增加，从而导致管道入口和出口处的压力均有所降低。

一、实验目的1. 理解渗透定律试验的基本原理。

2. 掌握渗透定律试验的操作方法。

3. 学习如何通过实验数据计算渗透系数。

4. 分析不同条件下渗透系数的变化规律。

二、实验原理渗透定律，又称达西定律，描述了在层流条件下，土体中水渗流速度与水力梯度之间的关系。

其表达式为：\[ V = k \cdot i \]其中，\( V \) 为水渗流速度，\( k \) 为渗透系数，\( i \) 为水力梯度。

渗透系数 \( k \) 是土体渗透性能的重要指标，其数值的大小取决于土体的颗粒组成、孔隙结构、孔隙水性质等因素。

三、实验仪器与材料1. 达西实验装置：包括直立圆筒、滤板、土样、测压管等。

2. 天然土样：采集不同类型的土样，如砂土、粘土等。

3. 量筒、天平、计时器等。

四、实验步骤1. 准备实验装置，包括直立圆筒、滤板、土样等。

2. 将土样放入圆筒中，使其密实。

3. 在土样上下两端分别安装测压管，并用橡皮塞封闭。

4. 向圆筒中加入水，使水位高于土样顶部。

5. 记录初始水头差 \( h_1 \)。

6. 打开橡皮塞，让水自由渗流，同时开始计时。

7. 每隔一定时间 \( t \) 记录测压管中的水头差 \( h_2 \)。

8. 当水头差基本稳定时，记录最终水头差 \( h_3 \)。

9. 重复上述步骤，进行多次实验。

五、实验数据与结果处理1. 计算水力梯度 \( i \)：\[ i = \frac{h_2 - h_1}{L} \]其中，\( L \) 为土样长度。

2. 计算渗透速度 \( V \)：\[ V = \frac{h_2 - h_1}{t} \]3. 计算渗透系数 \( k \)：\[ k = \frac{V}{i} \]六、实验结果与分析1. 通过实验数据计算不同土样的渗透系数 \( k \)。

2. 分析不同压实方式和配合比对渗透系数的影响。

3. 比较不同土样的渗透系数，探讨其渗透性能差异。

七、实验结论1. 渗透定律适用于层流条件下土体中水的渗流。

不同填料的渗透系数测定实验——达西定律一、实验意义通过描绘流速与水头差的函数关系图，来确定渗透流量与水头损失的关系，从而来验证达西定律。

以及通过平行实验和对比实验，对数据进行比较处理，从而可知那些数据受到粒径的影响。

二、实验目的1.了解达西实验装置，通过稳定流条件下的渗流实验，测定不同粒径填料的渗透系数k 值。

2.加深理解渗流速度、水力梯度、渗透系数之间的关系，并验证达西定律。

二、实验仪器1.达西实验装置（自行设计），分别装有不同粒径的均质试样：①砂体（粒径＜0.5mm ，0.7~1mm ）；②煤块（粒径5~10mm ）；③砖块（粒径5~10mm ）。

2.秒表、量筒、直尺、温度计、电子称等。

三、实验原理室内渗透系数测定是根据达西关于多孔介质中地下水的线性渗透定律而设计的。

由达西定律，在常水头条件下，水流在单位时间内透过岩石空隙的流量（Q ）与岩石的断面面积（ω）、水力坡度（I ）成正比：测定不同试样的渗透系数。

H Q K K I Lωω∆==式中：Q ——渗透流量（cm 3）； ω——过水断面面积（cm 2）；∆H ——上下游过水断面的水头差（cm ）；L ——渗透途径（cm ）；I ——水力梯度。

由上式可推知，QV KIIω==，亦即，渗透系数在数值上等于水力坡度为1时，透过某单位过水断面的渗流量（亦即渗流速度）。

达西实验装置示意图1—试样；2—进水管；3—出水管；4—测压管；5—溢流口；6—仪器架四、实验步骤1234651．测量仪器的几何参数。

分别测量过水断面面积（ ω ）、测压管a 、b 的间距或渗透途径（L ）；记入（表1）。

2．调试仪器。

打开进水管，将水引入实验筒内，底部控制阀T 打开，此时要保持溢水管有少量水溢出，这时可以进行第一次实验。

3．测定水头待a 、b 两个测压管的水位稳定后，读出各测压管的水头值，记入（表1）中。

4．测定流量在进行步骤3的同时，利用秒表和量筒测量t 时间内水管流出的水体积，及时计算流量Q 。

建立实验装置
根据实验需求，设计并建立渗流装置，包括渗流管、压力源、流量 计等。
设定实验条件
设定恒定的水头压力、流量等实验条件，确保实验数据的准确性和 可靠性。
实验结果分析
01
02
03
数据记录
详细记录实验过程中的水 头压力、流量等数据，并 确保数据的准确性和完整 性。
数据处理
对实验数据进行整理、分 析和处理，绘制水头压力 与流量之间的关系曲线。
达西定律的发现可以追溯到19世纪初，由法国工程师达西通 过实验观察到流体在砂质土壤中的流动规律，并提出了该定 律。
达西定律的概述
达西定律描述了流体在多孔介质中的流动速度与压力梯度 之间的关系。具体来说，当流体在多孔介质中流动时，流 速与作用在流体上的压力梯度成正比，同时与介质的渗透 系数有关。
达西定律的数学表达式为：v = -K * grad(p)，其中v是流速， K是介质的渗透系数，grad(p)是压力梯度。该公式表明流速 与压力梯度成正比，与渗透系数成反比。
达西定律与实际渗流过程的联系
01
达西定律是描述均匀、定常、不可压缩流体在多孔介质中稳态 流动的基本定律。
02
它指出，在一定条件下，流体的流量与压力梯度成正比，与介
质孔隙的阻力成反比。
达西定律适用于小孔径、低流速、高孔隙度、均质的多孔介质。
03
达西定律的局限性
1
达西定律不适用于非均匀、非定常、非线性流动， 以及大孔径、高流速、低孔隙度、非均质的多孔 介质。
渗流的基本定律（达西定律）
目录
• 引言 • 达西定律的数学表达 • 达西定律的物理意义 • 达西定律的实验验证 • 达西定律的应用实例 • 达西定律的发展与展望
01 引言

达西实验报告
《达西实验报告》
在科学研究领域，达西实验是一种经典的实验方法，它被广泛应用于物理学、
化学、生物学等领域。

达西实验的原理是通过控制变量的方法，观察不同条件
下的实验结果，从而得出科学结论。

本文将介绍达西实验的基本原理和应用。

首先，达西实验的基本原理是设计实验条件，控制变量，观察实验结果，从而
得出科学结论。

在达西实验中，研究者需要设计实验条件，例如温度、压力、
光照等，然后控制其他变量不变，观察实验结果的变化。

通过比较不同条件下
的实验结果，研究者可以得出科学结论，指导后续的科学研究和实践应用。

其次，达西实验在物理学、化学、生物学等领域都有广泛的应用。

在物理学中，达西实验可以用于研究光学、热力学等问题；在化学中，可以用于研究化学反应、物质变化等问题；在生物学中，可以用于研究生物体对环境因素的适应能
力等问题。

通过达西实验，科学家们可以深入研究各种自然现象，为人类社会
的发展提供科学依据。

最后，达西实验的结果对科学研究和实践应用都具有重要意义。

通过达西实验，科学家们可以得出结论，指导后续的科学研究和实践应用。

例如，在医学领域，通过达西实验可以研究药物的疗效和副作用，为临床治疗提供科学依据；在环
境保护领域，通过达西实验可以研究污染物的分布和迁移规律，为环境保护提
供科学依据。

总之，达西实验是一种重要的科学研究方法，它通过控制变量的方法，观察实
验结果，得出科学结论，指导后续的科学研究和实践应用。

在未来的科学研究中，达西实验将继续发挥重要作用，为人类社会的发展做出更大的贡献。

达西定律实验水力学及流体力学实验仪系列产品DXY型达西定律实验仪仪器编号：北京新华教仪科贸有限公司华同丰(北京)科技有限公司达西定律实验一、实验目的1.测定渗透砂体的渗透量与水头损失的关系，验证渗流的达西定律。

2.测定均质砂的渗透系数K值;二、实验设备设备由水泵、供水箱、存水箱及升降装置构成供水系统。

实验箱内装均质砂，底部及砂体的上表面各装一块滤板，中部设二个多孔测压管测定渗流水头损失。

用体积法测流量。

1—水泵2—升降定位手柄3—供水箱4—供水箱溢流槽5—供水调节阀6—排气软管7—测压管8—实验箱溢流槽9—实验箱10—多孔测压管11—转向阀12—计量箱13—存水箱14—泄流槽15—泄水阀16—供水阀*实验前请用地脚螺丝调平实验台三、实验原理及计算式液体在孔隙介质中流动时，由于粘滞性作用将会产生能量损失。

达西（Henri Darcy）在1852-1855年间通过实验，总结出渗流能量损失与渗流速度成一次方的线性规律，后人称为达西定律。

由于渗流速度很小，故速度水头可以忽略不计。

因此总水头H可用测管水头h来表示，水头损失h w可用测管水头差来表示，即于是，水力坡度J可用测管水头坡度来表示：式中，L为两个测压管孔之间的距离，h1与h2为两个测压孔的测管水头。

达西通过实验，得到实验圆筒内渗流量Ｑ与圆筒断面积A和水力坡度J成正比，并和土壤的透水性有关，所建立基本关系式如下：Q＝KAJ v=Q/A=KJ式中，v为渗流简化模型的断面平均流速，系数K为反映孔隙介质透水性能的综合系数，称为参透系数。

实验中的渗流区为一圆柱形的均质砂体，属于均匀渗流，可以认为各点的流动状态是相同的，任意点的渗流流速u等于断面平均渗流流速，因此达西定律也可以表示为：u= v= KJ上式表明，渗流的水力坡度，即单位距离上的水头损失与渗流流速的一次方成正比，因此称为渗流线性定律。

Darcy’s Law 是描述以粘滞力为主、雷诺数Re< 1~10的层流状态下的地下水渗流基本定律，指出渗流速度V与水力坡度J成线性关系，V=KJ，或Q=KAJ，又称线性渗透定律。

系数有关，因此在计算温热矿水或预测不同水温的渗透系数时，应考虑水
温的影响，现以校正成水温为10℃时为例对渗透系数校正计算，其计算公
式为：
；
K10

KT
10 T
K10
KT
mT m1
T

m0 mT
式中： K0，K10, KT―分别为水温在10℃；T℃的渗透系数。
t0，t10, tT ―分别为水温在10℃；T℃的温度校正系数。
渗 透
速 度
V＝ Q/F (cm 3/s)
测 压 管 水 位 (cm )
h1 h2 h3 h1-h2
水 位 差 (cm )
h2-h3 平 均 h
水 渗 透 力 系 数 坡 度 Kt I (cm /s)
水 温 t oC
平 均 渗 透 系 数Kcp
(cm /s)
I II III
实验一 达西定律--4．作业要求
表1-1 普阿杰里表
m
T℃
m
0.0139
16 0.0111
0.0135 17
0.0108
0.0131 18
0.0105
0.0127 19
0.0103
0.0124 20
0.0101
0.0120 21
0.0117
22
0.0114
23
0.0099 0.0097 0.0095
T℃ m
24 0.0093 25 0.0091 26 0.0089 27 0.0087 28 0.0085 29 0.0083 30 0.0081
(1) 掌握实验室测定岩石渗透系数的方法，加深对岩石渗透系数 的认识。 (2) 验证达西定律，从而提高对直线渗透定律的理解。

实验一达西定律实验【实验目的】1．观察单向不可压缩液体流过均质、等厚地层压力分布规律；2．验证达西定律，测定多孔介质渗透率K 。

【实验原理】单相不可压缩液体在水平等厚均质地层中的单向渗流，其压力变化是随距离成线性关系变化的。

即X Lp p p we ⋅-=而液体在等直径的管路中流动的情况也是一样，压头线为一条沿流向倾斜下降的直线，而其渗流阻力也都是随距离的增加成线性关系增加。

所以可以以水平等直径的管路流动来模拟均质等厚水平地层的单向渗流，以此观察研究此种情况下的压力变化规律及渗流阻力的变化规律，以便近似确定介质的平均渗透率。

【实验装置】实验流程如图1所示图1-1．多孔介质渗透率测定仪1~10.测压刻度管11.供液阀12.供液筒13.溢流管14.供液控制夹15.填砂模型a 16.支架17.填砂模型b 18.出液控制夹19.量筒【实验方法与步骤】1．准备好秒表和量筒；2．检查测压刻度管的液面是否一致；3．打开出液控制夹，调整适当的流量；4．当流量稳定后，记录测压刻度管液面高度；5．用秒表和量筒测量出液口的流量，重复三次取平均值；6．从小到大改变出口流量三次，并记录测压管液面高度和流量；7．关闭出液口开关，使液面恢复水平。

【数据处理】不可压缩液体在多孔介质中作稳定渗流时，是遵循达西定律的，即流量与压降成正比，压降分布曲线呈一直线。

知道已知数据，测出流量和压差，由达西定律即可求出多孔介质的渗透率。

pA LQ k ∆∆=μ式中：Δp=ΔHρg，g=9.81m/s2；ΔH为压差（H1～H5）或（H6～H10），（m）；Q为液体流量（m/s）；μ为液体的粘度（mPa·s）；ΔL为测压管(H1～H5）或（H6～H10）间的距离（m）；A为填砂模型的横截面积（m2）１．将实验基础数据填入以下空格，其它实验数据记录在数据表；填砂模型15的内径D1=0.0787m，其截面积A1=m2；填砂模型17的内径D2=0.0391m，其截面积A2=m2；液体温度T=℃，液体粘度μ=mPa·sH1～H5距离ΔL1=m，H６～H１０距离ΔL2=m２．用达西定律求出两种不同直径模型在不同流量下的平均渗透率3．以液柱高H为纵坐标、长度L为横坐标，绘出三个流量下的压力分布曲线（两种渗透面积）。

达西定律实验流程一、实验前的准备。

咱做这个达西定律实验呀，那得先把东西都准备好呢。

实验器材可不能少，就像士兵上战场得带齐武器一样。

得有装砂的容器，这砂可是实验的关键角色哦。

还有测压管，它就像小眼睛一样，能帮我们看到压力的变化呢。

再有就是供水装置啦，要是没有水，这实验可就没法做啦，水就像是这个实验的活力源泉。

另外呀，流量测量装置也得准备好，这样我们才能知道水流动的速度呢。

在准备砂的时候呀，要选择合适的砂哦。

不能太粗，也不能太细，就像我们选衣服一样，得大小合适。

太粗了可能实验结果就不准确啦，太细的话可能又会有其他的小麻烦。

把砂小心地装进容器里，要装得均匀一点，可不能这边高那边低的，就像我们铺床一样，得铺得平平整整的。

二、开始实验。

好啦，准备工作做好了，咱们就可以开始做实验喽。

先打开供水装置，这时候就能听到水流动的声音啦，就像小溪在唱歌一样呢。

水慢慢流进装砂的容器里，我们要仔细观察测压管哦。

看着测压管里水面的高度在变化，是不是很有趣呀。

这时候就像在看一场小小的魔术表演呢。

随着水的流动，我们要开始测量流量啦。

这流量测量可不能马虎，就像我们数钱的时候得一张一张数清楚一样。

记录下不同时刻的流量数值，这些数值可都是宝贝呢，以后分析实验结果全靠它们啦。

在实验过程中，要是发现有什么不对劲的地方，比如说水流得太急或者测压管的读数有点奇怪，不要慌哦。

就像我们走路不小心摔了一跤，爬起来看看是哪里出问题就好啦。

可能是砂在容器里有点松动了，或者是供水装置出了小故障。

这时候就停下来检查检查，把问题解决了再继续实验。

三、实验后的整理。

好啦，实验做完了，可还没完事儿呢。

咱们得把实验器材都整理好呀。

就像玩完玩具要把玩具收起来一样。

把砂从容器里清理出来，可不能让它留在里面搞得乱七八糟的。

测压管也要擦干净，供水装置检查一下有没有损坏的地方，如果有就赶紧报告老师或者实验室的管理员哦。

流量测量装置也要好好收起来，放在它该放的地方。

做完这些整理工作呀，我们就可以坐下来分析实验结果啦。

达西实验定律达西实验定律，又称达西-勒傅氏定律，是描述液体通过多孔介质渗透的规律。

它是由法国物理学家亨利·达西和法国工程师亚历山大·勒傅氏在19世纪上半叶发现并提出的。

这个定律在流体力学和渗流理论的研究中具有重要的地位。

达西实验定律的基本内容是：液体在渗透过程中的流速与压力之间存在着一种函数关系。

具体地说，当液体通过多孔介质渗透时，渗透速度正比于液体的粘度和渗透面积，反比于多孔介质的长度和黏度。

达西实验定律的实验证明，液体在渗透过程中，流速与压力呈线性关系。

这意味着当压力增加时，液体的渗透速度也随之增加，反之亦然。

这个定律的发现对于理解液体渗流现象以及工程设计和科学研究中的相关问题具有重要意义。

为了验证达西实验定律，达西和勒傅氏进行了一系列实验。

他们使用了不同的多孔介质，如过滤纸、细砂和活性炭等，将液体通过这些介质进行渗透。

通过测量液体的流速和压力，他们得出了渗透速度与压力的线性关系。

这一发现为达西实验定律的提出提供了实验证据。

在工程和科学领域中，达西实验定律有着广泛的应用。

例如，在地下水资源管理和开采方面，达西实验定律可以帮助工程师和研究人员预测地下水的流动速度和压力分布，从而指导地下水资源的合理利用和管理。

在石油工程中，达西实验定律可以用来预测油井中的渗流速度和压力分布，为油田开发和生产提供技术支持。

达西实验定律还可以应用于过滤和分离技术。

通过控制渗透压，可以实现对溶液中溶质的选择性分离和浓缩。

这种技术在化学工业和生物医学工程中有着广泛的应用，例如海水淡化、药物分离和蛋白质纯化等。

达西实验定律是描述液体通过多孔介质渗透的基本规律。

它的发现和应用对于理解和解决液体渗透和渗流相关的问题具有重要意义。

达西实验定律的提出不仅推动了流体力学和渗流理论的发展，还为工程和科学领域的应用提供了理论基础。

达西定律实验流程一、实验准备阶段。

达西定律实验呀，就像一场有趣的探索之旅，在开始之前呢，我们得把各种东西都准备好。

那要准备啥呢？首先得有实验装置啦，这个装置就像是我们的魔法道具一样。

一般会有一个装满砂或者土壤的圆筒，这个圆筒可是很重要的哦，它就像一个小小的世界，砂或者土壤在里面就是我们要研究的对象。

还有呢，我们需要水，水就像这个小世界里的精灵，在实验中起着关键的作用。

要有进水口和出水口的装置，这样水才能乖乖地流进流出。

再有就是测量水压的设备啦，没有这个，我们怎么知道水在这个小世界里的压力变化呢？这就像我们想要知道精灵的力量大小一样，必须得有测量的工具呀。

另外，还得准备好量筒，用来量水的体积，就像给精灵们数数一样，知道有多少精灵流过去了。

二、开始实验。

好啦，东西都准备好了，那我们就可以开始这个超有趣的实验啦。

我们先把水从进水口放进圆筒里，这个时候就像打开了通往魔法世界的大门，水精灵们开始欢快地往砂或者土壤的世界里跑啦。

看着水慢慢流进去，感觉就像是一场神奇的表演开始了呢。

在水流动的过程中，我们就要开始用测量水压的设备去记录不同位置的水压啦。

这个过程可得仔细点哦，就像在观察小精灵们的秘密一样。

每个数据都很重要，它能告诉我们水在这个小世界里的压力到底是怎么变化的。

同时呢，我们还得盯着量筒，看看有多少水从出水口流出来了。

这就像是在数从魔法世界跑出来的精灵有多少一样。

三、数据记录与分析。

把水压的数据和水流量的数据都收集好了之后呢，就到了我们像小侦探一样分析数据的时候啦。

我们要把这些数据按照一定的规则记录下来，就像把小精灵们的特点都写下来一样。

比如说，在这个位置水压是多少，对应的水流量又是多少。

然后呢，我们就要根据达西定律的公式来分析这些数据啦。

达西定律就像是这个魔法世界的一个神秘规则一样，我们要看看我们收集的数据是不是符合这个规则。

如果符合呢，那就说明我们的实验很成功，就像我们成功解开了小精灵们的秘密一样。

化工原理达西定律我在化工的世界里遨游了这么久，发现有一个定律就像一颗璀璨的明珠，那就是达西定律。

嘿，你可别小瞧这个定律，它在化工原理里的地位，那可是相当重要的呢！记得我刚接触化工原理的时候，对那些流体在管道里流来流去的现象简直是一头雾水。

就像一群调皮的小虫子，它们到底是怎么动的呢？为啥有的流得快，有的流得慢呢？当时我就在想，要是有个魔法规则能让我一下子搞清楚就好了。

嘿，这时候达西定律就像一个智慧的长者站了出来。

达西定律说的是啥呢？简单来讲，它就像是流体流动的交通规则。

想象一下，你在一个超级大的迷宫里，这个迷宫就是那些管道啥的。

流体就像一群小蚂蚁，它们想要从迷宫的这头走到那头。

达西定律就告诉我们，这些小蚂蚁走得快慢呀，和好多因素有关呢。

我有个朋友，他是个急性子。

他当时就问我：“这达西定律到底有啥用啊？感觉就像那些枯燥的数学公式，离我们的生活远着呢！”我就跟他说：“你可错喽！你看咱们家里的水管子，水为啥能流到水龙头里？这背后就有达西定律在悄悄起作用呢。

要是没有这个定律，那水管子的设计就乱套了，可能水都流不到你想要的地方去。

”从科学的角度来说，达西定律主要描述了不可压缩流体在多孔介质中的线性渗流规律。

这是什么意思呢？就好比是沙子堆成的城堡，里面有很多小空隙。

如果有液体想要穿过这个沙子城堡，那它的流动速度就和这个沙子城堡的一些特性，比如空隙的大小啊，形状啊，还有液体本身的粘性之类的有关。

这就和达西定律描述的差不多。

我曾经参加过一个化工小组的讨论。

小组里有个学霸，他对达西定律那是相当精通。

他说：“达西定律就像是一把钥匙，能打开理解流体在复杂介质中流动的大门。

”大家都纷纷点头。

然后有个同学就问：“那这个定律在化工实际生产中有啥具体的体现呢？”学霸就开始滔滔不绝了。

他说在石油开采中，石油在地下岩石的缝隙里流动，就像那些小蚂蚁在迷宫里找路一样。

达西定律就可以帮助工程师们预测石油的流速，这样就能更好地设计开采方案了。

水力学及流体力学实验仪系列产品DXY型达西定律实验仪仪器编号：北京新华教仪科贸有限公司华同丰(北京)科技有限公司达西定律实验一、实验目的1.测定渗透砂体的渗透量与水头损失的关系，验证渗流的达西定律。

2.测定均质砂的渗透系数K值;二、实验设备设备由水泵、供水箱、存水箱及升降装置构成供水系统。

实验箱内装均质砂，底部及砂体的上表面各装一块滤板，中部设二个多孔测压管测定渗流水头损失。

用体积法测流量。

1—水泵2—升降定位手柄3—供水箱4—供水箱溢流槽5—供水调节阀6—排气软管7—测压管8—实验箱溢流槽9—实验箱10—多孔测压管11—转向阀12—计量箱13—存水箱14—泄流槽15—泄水阀16—供水阀*实验前请用地脚螺丝调平实验台三、实验原理及计算式液体在孔隙介质中流动时，由于粘滞性作用将会产生能量损失。

达西（Henri Darcy）在1852-1855年间通过实验，总结出渗流能量损失与渗流速度成一次方的线性规律，后人称为达西定律。

由于渗流速度很小，故速度水头可以忽略不计。

因此总水头H可用测管水头h来表示，水头损失h w可用测管水头差来表示，即于是，水力坡度J可用测管水头坡度来表示：式中，L为两个测压管孔之间的距离，h1与h2为两个测压孔的测管水头。

达西通过实验，得到实验圆筒内渗流量Ｑ与圆筒断面积A和水力坡度J成正比，并和土壤的透水性有关，所建立基本关系式如下：Q＝KAJ v=Q/A=KJ 式中，v为渗流简化模型的断面平均流速，系数K为反映孔隙介质透水性能的综合系数，称为参透系数。

实验中的渗流区为一圆柱形的均质砂体，属于均匀渗流，可以认为各点的流动状态是相同的，任意点的渗流流速u等于断面平均渗流流速，因此达西定律也可以表示为：u= v= KJ上式表明，渗流的水力坡度，即单位距离上的水头损失与渗流流速的一次方成正比，因此称为渗流线性定律。

Darcy’s Law 是描述以粘滞力为主、雷诺数Re< 1~10的层流状态下的地下水渗流基本定律，指出渗流速度V与水力坡度J成线性关系，V=KJ，或Q=KAJ，又称线性渗透定律。

不同填料的渗透系数测定实验——达西定律一、实验意义通过描绘流速与水头差的函数关系图，来确定渗透流量与水头损失的关系，从而来验证达西定律。

以及通过平行实验和对比实验，对数据进行比较处理，从而可知那些数据受到粒径的影响。

二、实验目的1.了解达西实验装置，通过稳定流条件下的渗流实验，测定不同粒径填料的渗透系数k 值。

2.加深理解渗流速度、水力梯度、渗透系数之间的关系，并验证达西定律。

二、实验仪器1.达西实验装置（自行设计），分别装有不同粒径的均质试样：①砂体（粒径＜0.5mm ，0.7~1mm ）；②煤块（粒径5~10mm ）；③砖块（粒径5~10mm ）。

2.秒表、量筒、直尺、温度计、电子称等。

三、实验原理室内渗透系数测定是根据达西关于多孔介质中地下水的线性渗透定律而设计的。

由达西定律，在常水头条件下，水流在单位时间内透过岩石空隙的流量（Q ）与岩石的断面面积（ω）、水力坡度（I ）成正比：测定不同试样的渗透系数。

H Q K K I Lωω∆==式中：Q ——渗透流量（cm 3）； ω——过水断面面积（cm 2）；∆H ——上下游过水断面的水头差（cm ）；L ——渗透途径（cm ）；I ——水力梯度。

由上式可推知，QV KIIω==，亦即，渗透系数在数值上等于水力坡度为1时，透过某单位过水断面的渗流量（亦即渗流速度）。

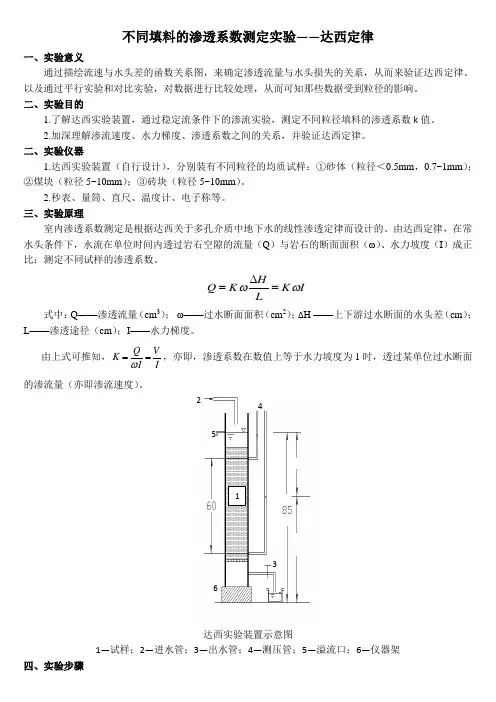
达西实验装置示意图1—试样；2—进水管；3—出水管；4—测压管；5—溢流口；6—仪器架四、实验步骤1234651．测量仪器的几何参数。

分别测量过水断面面积（ ω ）、测压管a 、b 的间距或渗透途径（L ）；记入（表1）。

2．调试仪器。

打开进水管，将水引入实验筒内，底部控制阀T 打开，此时要保持溢水管有少量水溢出，这时可以进行第一次实验。

3．测定水头待a 、b 两个测压管的水位稳定后，读出各测压管的水头值，记入（表1）中。

4．测定流量在进行步骤3的同时，利用秒表和量筒测量t 时间内水管流出的水体积，及时计算流量Q 。

3.达西（Dracy）渗透定律(1)达西渗透实验与达西定律地下水在土体孔隙中渗透时，由于渗透阻力的作用，沿程必然伴随着能量的损失。

为了揭示水在土体中的渗透规律，法国工程师达西(H.darcy)经过大量的试验研究，1856年总结得出渗透能量损失与渗流速度之间的相互关系即为达西定律。

达西（Henri Philibert Gaspard Darcy,1803～1858）,法国著名工程师，1855年提出了达西定律，1857年提出了紊流沿程水头损失计算的著名经验公式。

图2-3 达西渗透实验装置图达西实验的装置如图2-3所示。

装置中的①是横截面积为A的直立圆筒，其上端开口，在圆筒侧壁装有两支相距为l 的侧压管。

筒底以上一定距离处装一滤板②，滤板上填放颗粒均匀的砂土。

水由上端注入圆筒，多余的水从溢水管③溢出，使筒内的水位维持一个恒定值。

渗透过砂层的水从短水管④流入量杯⑤中，并以此来计算渗流量q。

设△t时间内流入量杯的水体体积为△V, 则渗流量为q=△V /△t。

同时读取断面1-1和段面2-2处的侧压管水头值h1，h2，Δh为两断面之间的水头损失。

达西分析了大量实验资料，发现土中渗透的渗流量q与圆筒断面积A及水头损失△h 成正比，与断面间距l成反比，即（2-1）或（2-2）式中i=△h/l，称为水力梯度，也称水力坡降；k为渗透系数，其值等于水力梯度为1时水的渗透速度，cm/s 。

式（2-1）和（2-2）所表示的关系称为达西定律，它是渗透的基本定律。

（2）达西定律的适用范围达西定律是由砂质土体实验得到的，后来推广应用于其他土体如粘土和具有细裂隙的岩石等。

进一步的研究表明，在某些条件下，渗透并不一定符合达西定律，因此在实际工作中我们还要注意达西定律的适用范围。

大量试验表明，当渗透速度较小时，渗透的沿程水头损失与流速的一次方成正比。

在一般情况下，砂土、粘土中的渗透速度很小，其渗流可以看作是一种水流流线互相平行的流动——层流，渗流运动规律符合达西定律，渗透速度v与水力梯度i的关系可在v-i坐标系中表示成一条直线，如图2-4(a)所示。

《水文地质学基础》实验报告实验名称：达西定律实验实验人：实验日期：一、实验目的1、测定渗透砂体的渗透量与水头损失的关系，验证渗流的达西定律。

2、测定均质砂的渗透系数K值;二、实验设备：1.供水器装置（马氏瓶）：以法国物理学家Mariotte的马利奥特瓶装置，是一种能控制水位又能自动连续补给水的量测装置。

2.渗透装置（试样筒）：有机玻璃圆筒，上部设有进水孔，底部装有过滤板，下端有出水孔，供测量渗流量用。

侧面有三个测压孔。

3.测压装置（测压板和测压管）：在测压板上装有三根5－8mm带刻度的玻璃管，分别与试样筒上的三个测压孔连接，用于测定三个断面上的测压水位。

三个测压管用胶管分别与试样筒相应的管孔连结。

4.排水装置：在测压板上均匀分布有一系列的圆孔，用于调节排水水位。

其它设备有：100m1的量筒、水槽、漏斗、捣捧、装样杯、秒表、温度计、管夹、胶皮管及吸气球等。

三、实验原理：达西通过大量实验，得到圆筒过水断面的渗流量Q与圆筒断面F和水力坡度I成正比，并和土壤的透水性能有关，所建立基本关系式如下：式中：v---为渗流简化模型的断面平均流速；K---为岩石的渗透系数，反映了孔隙介质透水性能。

四、实验步骤：1.检查仪器设备是否齐全、完好。

胶管与仪器连结处是否漏气漏水或堵塞。

2.装样：岩样有两种，即原状样和扰动样。

原状样就是在野外取来土柱直接装到渗透装置（有机玻璃圆筒）内；扰动样则要按天然容重分层捣实，尽量接近天然状态，否则就没有实验意义了。

装样前，在过滤筛板上放二层铜丝网，然后装样，每装3—5cm厚时，用捣捧轻击数次，并测定试样的孔隙度或容重，使其结构尽量符合实际状态。

重复上述过程，直至试样超过最上一个测压孔以上5cm为止。

3.饱和试样（因达西定律是饱水带重力水运动的基本定律）：先将排水水位调节高于试样水面，饱和试样时要自上而下进行注水（便于排气），打开供水管夹，待试样表面出现水膜时（即饱和了），立即关闭供水夹，观察试样筒及三个侧压管水位是否在同一水平面上（因此时试样筒与测压管是U型连通器），如果测压管水位不在同一水平面上，则说明有气泡存在或测压管被堵塞，这时需要排气，排气的方法有两种，即将测压板倾斜或用吸耳气球从偏高或偏低水位的管中吸出气泡，达到水平，各测压管水位差<1mm为准。