当前位置：文档之家 › 第三章 运输问题-转运问题20101029

第三章 运输问题-转运问题20101029

  • 格式：ppt
  • 大小：523.00 KB
  • 文档页数：32

下载文档原格式

  / 32

合集下载

运筹学胡运权第三版第三章运输问题

运筹学胡运权第三版第三章运输问题
产销平衡运输问题的数学模型可表示如下：
§1运 输 问 题 及 其 数 学 模 型
二、运输问题数学模型的特点： 运输问题一定有最优解；基变量的个数=m+n-1 运输问题约束条件的系数矩阵：
x1m
x2m
xm1
xmm
x11
x12
…
x21
x22
…
xm2
…
…
m行
n行
§1运 输 问 题 及 其 数 学 模 型
解 的 最 优 性 检 验
运输问题及其数学模型
用表上作业法求解运输问题
运输问题的进一步讨论
应用问题举例
本章内容
3运输问题进一步讨论
01.
产销不平衡的运输问题 有转运的运输问题
02.
1.当产大于销时，即 产销不平衡问题 平衡后的数学模型为： 加入假想销地（假想仓库），销量为 ，由于实际并不运 送，它们的运费为 = 0；
解 的 最 优 性 检 验
解 的 最 优 性 检 验
销地产地
B1
B2
B3
B4
产量
ui
A1
16
u1(1)
A2
10
u2(0)
A3
22
u3(-4)
销量
8
14
12
14
48
vj
v1(2)
v2(9)
v3(3)
v4(10)
4
2
8
12
5
4
10
11
3
9
6
11
表3-9
1.增加一位势列和位势行并计算位势
其中
8
10
2
6
8
产量
A1

第3章运输问题

第3章运输问题
13
§2 表上作业法
一、表上作业法迭代步骤 1. 按某种规则找出一个初始基可行解； 2. 对现行解作最优性判断，即求各非基变量的检 验数，判别是否达到最优解，如已是最优解，则 停止计算，如不是最优解，则进行下一步骤； 3. 在表上对初始方案进行改进，找出新的基可行 解，再按第2步进行判别，直至找出最优解。
21
用最小元素法确定例2初始调运方案
调 运 量 产地 销地
A
100
B
90
X12
C
70 100 100
X13
产量
200 100
250 100
甲
X11
80 150 65 100 75
乙
销 量
X21
X22
X23
100
150
200 100
450
22
得到初始调运方案为：
x11=100，x13=100，x22=150，x23=100
B
90
C
产量
甲
X11
70 100 100 -20
X12 X13
200
250
乙
销 量
15
80 150 65 100 75
X22 X23
X21
100
150
200
450
32
用沃格尔法确定的初始调运方案的检验数
调 运 量 产地 销地
A
50
B
90 150
X12
C
70 65 15 100
产量
200
甲 乙
销 量
为运输问题的一个基可行解。由于基变量 的检验数等于零，故有：
ui1 v j1 ci1 j1 u v c i2 j2 i2 j 2 uis v js cis js

第三章--运输问题--运筹学

第三章--运输问题--运筹学

地运往B 设：诸如这类有多个不同的生产、消费者，如何合理不同的生产者和消费者之 xij—— 从Ai地运往Bj地的货物数量 诸如这类有多个不同的生产、消费者，
间的分配关系， 3x + 4x + 2x + 3x + 5x + 3x 间的分配关系，达到最小费用的问题也运筹学最重要的问题之一。 运价 min z= 达到最小费用的问题也运筹学最重要的问题之一。我们把这种 11 13 21 22 23 分派问题称为运输问题 运输问题。 分派问题称为运输问题。 12 x11 + x12 + x13 广义的 运输” = 10 在运筹学中，运输问题是一个广义 在运筹学中，运输问题是一个广义的 “运输”，即许多其它问题也可以通 x21 + x22 + x23 过适当的手段，把它们转化为运输问题加以解决。 = 4 过适当的手段，把它们转化为运输问题加以解决。这部分也是我们这学期主要 约束 st. + x21 = 3 学习内容之一。 学习内容之一。 x11 条件 x12 + x22 = 5 x13 + x23 = 6 xij ≥ 0
运输问题的数学模型（假定产销平衡）
若由以上方程组解得的某组解满足对偶问题约束条件， 若由以上方程组解得的某组解满足对偶问题约束条件，这 时可以证明： 时可以证明：
X = (X B, X
N
) = ( x x 1 j 1 , x i 2 j 2 , L x isjs , 0 , 0 , L , 0 ) T
2）运输问题系数矩阵非常特殊 ） 4）一般运输问题约束有一个多余的约束 ）
5）一般运输问题都是产销平衡的（不平衡问题要化为平衡问题） ）一般运输问题都是产销平衡的（不平衡问题要化为平衡问题） 6）一般产 、销n有（m*n）个变量和（m+n）个约束（没有去掉多余） ）一般产m、 有 ）个变量和（ ）个约束（没有去掉多余） 7）产m、销n运输问题最多有（m+n-1）个值为非零的变量 ） 运输问题最多有（ 、 运输问题最多有 ） 因为有一个约束多余， 因为有一个约束多余，既R（A）= m+n-1 （ ）

广工管理运筹学第三章运输问题

广工管理运筹学第三章运输问题

闭合回路法的优点是能够找到全局最 优解，适用于大型复杂运输问题。但 该方法的计算复杂度较高，需要较长 的计算时间。
商位法
01
商位法是一种基于商位划分的优化算法，用于解决运输问题。该方法通过将供 应点和需求点划分为不同的商位，并最小化总运输成本。
02
商位法的计算步骤包括：根据地理位置和货物需求量，将供应点和需求点划分 为不同的商位；根据商位的地理位置和货物需求量，计算总运输成本；通过比 较不同商位的总运输成本，确定最优的配送路线。
80%
线性规划法
通过建立线性规划模型，利用数 学软件求解最优解，得到最小化 总成本的运输方案。
100%
启发式算法
采用启发式规则逐步逼近最优解 ，常用的算法包括节约算法、扫 描算法等。
80%
遗传算法
基于生物进化原理的优化算法， 通过模拟自然选择和遗传机制来 寻找最优解。
02
运输问题的数学模型
变量与参数
约束条件
供需平衡
每个供应点的供应量等于对应 需求点的需求量，这是运输问 题的基本约束条件。
非负约束
运输量不能为负数，即每个供 应点对每个需求点的运输量都 应大于等于零。
其他约束条件
根据实际情况，可能还有其他 约束条件，如运输能力的限制 、运输路线的限制等。
03
运输问题的求解算法
表上作业法
总结词
直到达到最优解。这两种方法都可以通过构建线性规划模型来求解最优解。
04
运输问题的优化策略
节约法
节约法是一种基于节约里程的优化算法，用于解决 运输问题。该方法通过比较不同配送路线的距离和 货物需求量，以最小化总运输距离为目标，确定最 优的配送路线。
节约法的计算步骤包括：计算各供应点到需求点的 距离，找出最短路径；根据最短路径和货物需求量 ，计算节约里程；按照节约里程排序，确定最优配 送路线。

运筹学第3章：运输问题

运筹学第3章：运输问题
收点 发点 B1 10 B2 5 7 10 12 7 15 15 3 5 8
5
B3
B4
产量
B1
B2
B3
B4
A1
A2 A3 销量
15 5
25 18 3 5 45
20
22 12
11
17 24
30
19 16
21
30 28
对应的目标函数值为： z＝10×20＋5×11+7×17+15×19＋30×3+5×28＝889(元) 3、伏格尔法 ⑴在运价表中分别增加一行(列差额)和一列(行差额)，并分 别计算出各行和各列次最小运价和最小运价的差额。 ⑵从行差额或列差额中选出最大者，选择它所在的行或列中 的最小运价优先安排运量。
第三章 运输问题
(Transportation Problem)
运输问题及其数学模型 表上作业法 运输问题的进一步讨论
WinQSB软件应用
第一节 运输问题及其数学模型
一、运输问题的数学模型
【例1】已知某产品有A1、A2、A3三个生产地，其可供应的产量分别为15、 25、5吨；有B1、B2、B3、B4四个销售地可以销售该产品，其对该产品的需求 量分别为10、12、15、8吨。从Ai运往Bj单位产品的运价如下表所示。
⑴在运价表中找到最小运价cLk； ⑵将AL的产品给B k；
①若aL>b k，则将aL改写为aL-bk，划掉bk，同时将运价表中 K列的运价划掉； ②若aL<b k，则将bk改写为bk-aL，划掉aL，同时将运价表中 L行的运价划掉。
如此重复⑴、⑵，直到分配完毕。
【例3-2】以例3-1为例进行说明。
二、运输问题的特点
1、平衡运输问题必有可行解，也必有最优解； 2、运输问题的基本可行解中应包括 m+n-1个基变量。

运筹学 第三版 清华大学出版社 第3章运输问题

运筹学 第三版 清华大学出版社 第3章运输问题

运输问题应用—建模
1
1.运输问题的数学模型.
问题的提出 一般的运输问题就是要解决把 某种产品从若干个产地调运到若干个 销地，在每个产地的供应量与每个销 地的需求量已知，并知道各地之间的 运输单价的前提下，如何确定一个使 得总的运输费用最小的方案。
2
例3.1:某公司从两个产地A1、A2将物 品运往三个销地B1、B2、B3，各产地的 产量、各销地的销量和各产地运往各销 地每件物品的运费如下表所示，问：应 如何调运可使总运输费用最小？
32
2.运输问题求解 —表上作业法
1、初始基本可行解的确定 （1）西北角法：从西北角（左上 角）格开始，在格内的右下角标上允 许取得的最大数。然后按行（列）标 下一格的数。若某行（列）的产量 （销量）已满足，则把该行（列）的 其他格划去。如此进行下去，直至得 到一个基本可行解。
33
2.运输问题求解 —表上作业法
表3-3 运输问题数据表
销地 产地
B1 c11 c21
B2 … Bn c12 … c1n c22 … c2n
产量
┇
A1 A2
┇
┇
Am
销量
cm1 b1
cm2 b2
┇ ┇ … cmn
┇
a1 a2
am
… bn
设 xij 为从产地 Ai 运往销地 Bj 的运 输量，根据这个运输问题的要求，可以建立 9 运输变量表（表 3-4）。
2.运输问题求解 —表上作业法
一、初始基本可行解的确定
根据上面的讨论，要求得运输 问题的初始基本可行解，必须保证 找到 m + n – 1 个不构成闭回路的 基变量。 一般的方法步骤如下：
26
2.运输问题求解 —表上作业法

《运筹学》第三章 运输问题

《运筹学》第三章 运输问题

一、典例
某食品公司经营糖果业务，公司下设三个工厂A1、A2、 A3，四个销售门市部B1、B2、B3、B4。已知每天各自的生产 量、销售量及调运时的单位运输费用情况。问：如何调运可 使总费用最小？
生产量：A1——7吨， A2 —— 4吨， A3 —— 9吨
销售量：B1 —— 3吨，B2 —— 6吨，B3 —— 5吨，B4 —— 6吨
销地
产地
B1
B2
A1
3
11
A2
1
9
A3
7
4
B3
B4
3
10
2
8
10
5
精品课件
4
7吨 A1
产 4吨 A2 地
调运示意图
x11
B1 3吨
B2 6吨
销
B3 5吨
地
9吨 A3
x34
B4 6吨
精品课件
5
二、建立模型
设 xij——第i产地到第j销地之间的调运量，则有
34
Min z =
cij· xij i=1 j=1
销量 3 6 5 6
单位运价表
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
△z=c11-c13+c23-c21=1=11 △z=c12-c14+c34-c32=2=12
ห้องสมุดไป่ตู้
B1 B2 B3 B4 产量
A1 (0) (2) 5 2 7 A2 3 (2) (1) 1 4 A3 (9) 6 (12) 3 9 销量 3 6 5 6
j=1 0 ······ 0
·· ·· ···· ·· ··
·· ·· ··

运筹学课件第三章运输问题

运筹学课件第三章运输问题

运筹学课件第三章运输问题第三章运输问题一、学习目的与要求1、掌握表上作业法及其在产销平衡运输问题求解中的应用2、掌握产销不平衡运输问题求解方法二、课时 6学时第一节运输问题及其数学模型一、运输问题的数学模型单一品种运输问题的典型情况：设某种物品有m 个产地A 1,A 2,…,A m ，各产地的产量分别是a 1,a 2,…,a m ；有N 个销地B 1,B 2,…,B n ，各销地地销量分别为b 1,b 2,…,b n 。

假定从产地A i (i =1,2, …,m )向销地B j (j =1,2,…,n )运输单位物品的运价是c ij ，问怎样调运这些物品才能使总运费最小？表中x ij i j ij i j如果运输问题的总产量等于其总销量，即有∑∑===nj jm i i ba 11则称该运输问题为产销平衡运输问题；反之，称为产销不平衡运输问题。

产销平衡运输问题的数学模型如下：≥=====∑∑∑∑===+=0,...,2,1,...,2,1..min 11111ij m i jij nj iij m i n j ijij x nj b x mi a x t s x c z这就是运输问题的数学模型，它包含m ×n 个变量，(n 十m)个约束方程．其系数矩阵的结构比较松散，且特殊。

二、运输问题数学模型的特点1、运输问题有有限最优解，即必有最优基本可行解2、运输问题约束条件的系数矩阵A 的秩为(m+n-1)该系数矩陈中对应于变量x ij 的系数向量p ij ，其分量中除第i 个和第m 十j 个为1以外，其余的都为零．即 A ij ＝(0…1…1…0)’=e i +e m+j对产销平衡的运输问题具有以下特点：(1)约束条件系数矩阵的元素等于0或1(2)约束条件系数矩阵的每一列有两个非零元素，对应于每一个变量在前m 个约束方程中出现一次，在后n 个约束方程中也出现一次。

此外，对于产销平衡问题，还有以下特点(3)所有结构约束条件都是等式约束 (4)各产地产量之和等于各销地销量之和第二节用表上作业法求解运输问题解题步骤第1步：确定初始基本可行解。

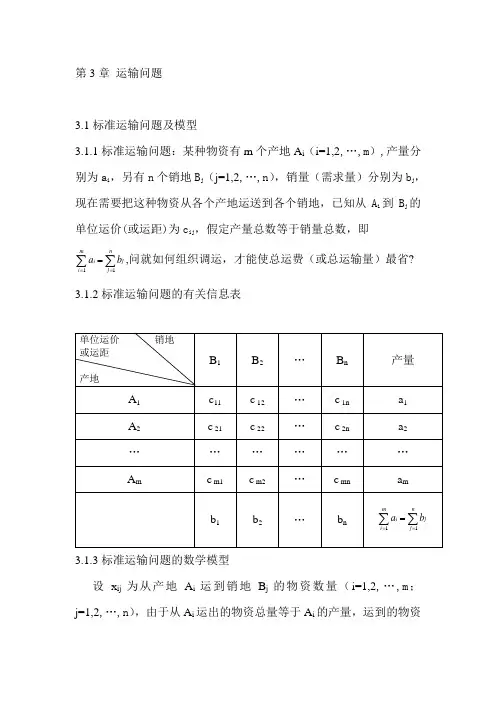
运筹学学习(自制笔记)第3章 运输问题

运筹学学习(自制笔记)第3章 运输问题

第3章 运输问题3.1标准运输问题及模型3.1.1标准运输问题：某种物资有m 个产地A i （i=1,2,…,m ）,产量分别为a i ，另有n 个销地B j （j=1,2,…,n ），销量（需求量）分别为b j ，现在需要把这种物资从各个产地运送到各个销地，已知从A i 到B j 的单位运价(或运距)为c ij ，假定产量总数等于销量总数，即11m niji j a b ===∑∑,问就如何组织调运，才能使总运费（或总运输量）最省?3.1.2标准运输问题的有关信息表3.1.3标准运输问题的数学模型设x ij 为从产地A i 运到销地B j 的物资数量（i=1,2,…,m ；j=1,2,…,n ），由于从A i 运出的物资总量等于A i 的产量，运到的物资总量等于的销量，得模型如下： mi Z=11mnij iji j c x==∑∑s.t.1nijij xa ==∑1mijj i xb ==∑0ij x ≥且有11m niji j a b Q ====∑∑即满足产销平衡条件，故此模型描述的是产销平衡运输问题。

3.1.4标准运输问题的特点⑴平衡条件下的运输问题必有最优解此问题是一个有m ×n 个变量，m+n 个等型约束条件的线性规划最小化问题，由于目标函数不可能为负，故有下界存在，而/ij i j x a b Q =是问题的一组可行解，因此一定有最优解。

既是线性规划问题，无疑可用单纯形法求解，但其数学模型自身结构有其特殊性，可以利用更简便的表上作业法求解。

⑵标准运输问题约束方程组的系数矩阵运输问题是一个具有m ×n 个变量，m+n 个等型约束条件的线性规划问题，问题的约束方程组的系数矩阵A 是一个只有0和1两个数值的稀疏矩阵，ij x 对应的列ij P 只有第i 行和第m+j 行为1，其余各行皆为0。

⑶标准运输问题的基变量总数为m+n-1。

可以证明系数矩阵A 和增广矩阵A ′的秩为m+n-1。

管理运筹学 第3章 运输问题

管理运筹学 第3章 运输问题
j 1
m
s.t.
xij bj ( j 1, 2,L , n)
i 1
xij 0
2.产量小于销量（
m

ai
n
＜
bj ）
i 1
j 1
mn
min z
cij xij
i 1 j 1
n
xij ai (i 1, 2,L , m)
j 1
m
s.t.
xij bj ( j 1, 2,L , n)
方法:最小元素法,即对单位运价最小的变量先分 配运输量.
例、食品公司有三个生产面包的分厂A1，A2，A3，有四个销 售公司B1，B2，B3，B4，其各分厂每日的产量、各销售公司 每日的销量以及各分厂到各销售公司的单位运价如表所示， 在表中产量与销量的单位为吨，运价的单位为百元/吨。问 该公司应如何调运产品在满足各销点的需求量的前提下总运 费最少？
季度 生产能力(台) 单位成本(万元)
1
25
10.8
2
35
11.1
3
30
11.0
4
10
11.3
解: 设xij为第i季度生产的第j季度交货的柴油机的数目 Cij为第i季度生产的第j季度交货的每台柴油机的 实际成本.
j
i
1
2
3
4
1
10.8 10.95 11.10 11.25
2
11.10 11.25 11.40
25
销量
60 40 20 15
销地 产地
A B C 销量
甲
4 2 8
8
乙
12 10 5
14
丙
4 3 11

第三章--运输问题课件

第三章--运输问题课件
第三章 运输问题
PPT学习交流
1
第一节 运输问题及模型
• 一、产销平衡的运输问题
• （一）数学模型
• 例：某公司有三个加工厂A1、 A2、A3 生产某种产品，每日 的产量分别为7吨、4吨、9吨， 该公司把这些产品分别运往四 个销地B1、B2、B3、B4，各 销售点每日销量分别为3吨、6 吨、5吨、6吨，从各工厂到各
12
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
PPT学习交流
13
PPT学习交流
7
• 例题：已知某物资的产量和销量及运价，另外还 假定这些物资在三个产地之间可以互相调运，在 四个销地之间可以互相调运，运价如表所示，另 外再假定还有四个纯中转站，他们到各产地、销 地及中转站之间的运价如表所示，问在考虑到产 销地之间直接运输和非直接转运的各种可能方案 的情况下，怎样将三个产地的物资运往销地总运 费最省。
出ui和 vj • 3）计算空格的检验数
• 3.方案调整
PPT学习交流
4
第三节 产销不平衡运输问题
• 1、直达运输问题
• 求解思路：通过增加虚拟点，使产销不平衡问题变为产 销平衡问题，再进行求解。
PPT学习交流
5
2、可中转的运输问题
• 1）问题的提出：
• 产地和销地之间没有直达路线，货物从产地到销地必须 通过某中转站转运
• 步骤：
• 1.确定初始调运方案——最小元素法 • 原则：根据运价最低的原则安排运量 • 方法：选择最小运价进行调运，同时划掉被满足的行或列，
但只能划一次，同时标注剩余运量。 • 检验：有数字格的数量=行数+列数-1=划线数量
PPT学习交流
3
• 2.判断方案是否最优——乘数法

管理运筹学讲义 第3章 运输问题

管理运筹学讲义 第3章 运输问题

21
石家庄经济学院
管理科学与工程学院
§3.2.1 初始基本可行解的确定
与一般线性规划问题不同，产销平衡运输问题总是存在 可行解。不难验证
xij ai b j d
≥
0 (i 1,2,, m; j 1,2,, n; d ai b j )
i 1 j 1
m
n
就是模型（3-1）的可行解。又因，目标函数值有下界， 故产销平衡的运输问题必有最优解。
A1、 A2、 A3 ，有四个销售点 B1、 B2、B3、 B4 销售
这种化工产品。各产地的产量、各销地的销量和各
产地运往各销地每吨产品的运费（百元）如下表所
示。
30 石家庄经济学院 管理科学与工程学院
产销平衡表
运价表
销 产
A1 A2
B1
B2
B3
B4
产量 75 40
B1 3 2
B2 8 9
B3 5 4
27
石家庄经济学院
管理科学与工程学院
销地 产地 A1 A2 A3 销量
B1 3 1 7 3
B2 11 9 4 6
B3 3 2 10 5
B4 10 8 5 6
产量 7 4 9 20 （产销平衡）
问应如何调运，可使得总运输费最小?
28
石家庄经济学院
管理科学与工程学院
产销平衡表
运价表
销 产 A1 A2 A3 需求
B4 9 8
A3
需求 35 40 55 65
80
195
6
3
7
5
问应如何调运，可使得总运输费最小?
31 石家庄经济学院 管理科学与工程学院
解：用西北角法求初始基本可行解

管理学第三章运输问题

管理学第三章运输问题
点.各销售点每日销量为:B1为3吨,B2为6 吨,B3为5吨,B4为6吨.已知从各工厂到各 销售点的单位产品的运价见表3-5所示.问
该公司应如何调运产品,在满足各销售点
的需要量的前提下,使总运费最少.
表3-5信息表
第三章 运输问题
B 1 B 2 B 3 B 4 产量
A1
3 11
3 10 7
A2
19
基于此，采用伏格尔法确定初始基本可行解，仍以例２为例 第一步：在运价表中计算出各行最小运费和次最小运费的差额， 行差额记为ui，i=1,2,…,m；同时求出每列次小运价与最小运价 之差，记为vj，j=1,2,…,n；填入表中的最右列和最下行
第三章 运输问题
第二步：从行或列差额中选出最大者，选择它所在行或列中 的最小运价．即L=max{ui，vi}，差额L对应行或列的最小运
……
m
cm1 cm2 … cmn
第三章 运输问题
【解】设xij为从产地Ai运往销地Bj的物资数 量（i=1，…m；j=1，…n），由于从Ai 运出的物资总量应等于Ai的产量ai，因此 xij应满足：
n
xij ai
j 1
i 1,2, , m
第三章 运输问题
同理，运到Bj的物资总量应该等于Bj的销量bj，所以xij还 应满足：
（4）粮食的运量应大于或等于零（非负要求），即
有些问题表面上与运输问题没有多大关系，其模型的数学 结构与例1运输问题模型形式相同，我们把这类模型都称为 运输模型。
不失一般性.
第三章 运输问题
设有m个产点Ai, i=1,2,…,m. 可供应某种物资, 其供应量(产量)分别为ai , i=1,2,…,m. 有n个 销地Bj , j=1,2,…,n. 其需要量分别为bj, j=1,2,…,n. 从Ai到Bj运输单位物资的运价为

运筹学课件：第三章 运输问题[1]

运筹学课件：第三章 运输问题[1]
实例
某公司下属两个工厂，生产同一种产品。产品均可运往三个中心 仓库去销售。已知每个工厂的产量，各仓库的销量及各工厂到每 个仓库的运输单价如下表所示。问如何组织调运可使生产与运输 的总费用最少?
Operation Research
运输问题的数学模型（2）
建立模型
第七讲
Operation Research
运输问题检验数的计算公式
第七讲
求解检验数的关键在于如何确定ui和vj
Operation Research 求解ui和vj
第七讲
Operation Research
表上作业法（8）
第七讲
运输问题解的讨论
有无穷多最优解
空格（非基变量）的检验数全部大于等于0，并且某个空格（非基变量） 的检验数为0。
Operation Research
运输问题的数学模型（4）
建立模型
第七讲
Operation Research
第七讲
运输问题的数学模型（5）
Operation Research
运输问题的特征（1）
产销平衡的运输问题必有可行解也必有最优解 运输问题的约束条件矩阵属于大型稀疏矩阵
第七讲
Operation Research
Operation Research
表上作业法（4）
第七讲
确定初始基可行解——伏格尔（Vogel)法
基本思路：元素差额法，在一行（或一列）中，算出最小元素和 次小元素的差额，如果差额很大，则优先用最小元素所对应的供 应关系供应。
方法：
（1）分别计算各行和各列的最小运费和次小运费差额，并填入表中；
在整个运输系统内部，各类点之间的运输关系为：
Q

第三章 运输问题101029

第三章 运输问题101029

100
1.8
0.8
1.5
200
2.2
1.2
1.2
1.4
1.6
300
A2
0
1.5
50
1.4
100
1.2
150
1.5
200 100
1.0
400
A3
0.3
100
0.5
50
-0.4 100
300
0.9
150
0 100
200
100
Z=100*1.2+50*1.5+200*1.6+100*1.2+150*1.2+100*1.6 =1135

二、解的改进方法
第四步：调整已知解 为了使目标函数值减小得最快， 一般应取检验数绝对值最大者所对应的空格为候选调整格。 （最负的检验数） max c ij | c ij 0


调整方法：在调整空格处首先调入运输量 值。
[空格 ] A 2 [ 50
+ + A 4 [ 300 ] 250
A33[[100 ]] A 150
T
其列向量结构 p ij ( 0 , 0 ,1, 0 , 0 , , 0 ,1, 0 , 0 ) 矩阵的秩： r A m n 1
因满足 a
i 1
第i个 m
i
第(m+j) 个

b
j 1
n
j
二、运输问题的数学模型（一般形式）
运输问题有两类问题 ：
1、平衡运输问题，产销平衡
取为在此空格中对应的闭回路上， 减项（负项）顶点的运输量的最小值。
则该数字格成为空格， 原空格为新的数字格。

运筹学 第3章运输问题

运筹学 第3章运输问题

3
运输问题的数学模型
设xij代表为从第i个产地调运给第j个销地的物资
m
n
的数量.在产销平衡的条件下，即
ai bj
i 1
j 1
使总的运费支出最小，可以表为以下数学形式：
mn
min z
cij xij
i 1 j 1
n

xij ai
i 1,, m
j 1
32
⑵ 退化解： ※ 表格中一般要有(m+n-1)个数字格。但有时在分配运量时则需要同时划去一
行和一列，这时需要补一个0，以保证有(m+n-1)个数字格作为基变量。一般可在 划去的行和列的任意空格处加一个0即可。
※ 利用进基变量的闭回路对解进行调整时，标有负号的最小运量（超过2个最 小值）作为调整量θ，选择任意一个最小运量对应的基变量作为换出变量，而经 调整后，得到退化解。这时另一个数字格必须填入一个“0”以示它为基变量。
z
cij xij
i 1 j1
n
xij ai (i 1, 2, ......m)
j1
s.t .
m
xij bj
( j 1,
2, ......n)
i1

xij

0,
i 1,
2, ......m, j 1,

2, ......n
如下），求总运费最少的调运方案。
销地 产地
A1 A2 A3 收量（T）
表3-3
B1
B2
B3
B4 发量（T）
3
11
3
10
7
1
9
2
8
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

转运 3
销地 4 5 接收量 40 40
30
10
40 40
40
40 40 60
40
60
运输问题的悖论
在运输问题中，有一种在若干 个产、销地的运价不变的情况下， 当调运量增加，总运费反而会下降 的奇怪现象。这就是运输问题的悖 论
有一位调度员上月做了一个最优调度如 下（检验数全为非正）
B1 A2 A3 bj vj 164 8 -2 4 16 B2 96 5 -6 45 11 9 B3 67 2 2 -1 115 1 8 -2 12 21 B4 138 4 -1 9 -1 8 13 B5 1 6 -1 51 11 15 ai ui 7 18 6 46 -1 5 0 -1 0 -5
1
040
41-M 2-1 1 M
3
2
15-M 040 4 411-M
4
110
M10 40 040 58-M
5
M
320 4 5 040
发送 量
500
70M-1 403 40-1
5
接收量
40M-4
400
401-M 40-3 601
604-M
最优方案
接收 产地 发送 产地 1 2 1 40 40 10 2 转运 销地 3 4 10 20 5 发送 量 50 70
5-10+4=
B4 138 56 105 8 13 11 15 B5
-1
ai 18 6 15 46 ui 0 -1 0 -5
最小调整运量=5，u3+V2=-10+9=-1
7 + 5 -1 5
总运量=56千吨，总运费=409千元
B1 A 1 A 2 A 3 A 4 bj 4 415 11+10 12 8 164 96 B2 B3 612 138 511 10 11 B4 B5 ai 7+5 18 6+5 15 56
A 1 0 5
A 2 5 0
运 价 B1 B2 B3
B1 0 4 5
B2 4 0 6
B3 5 6 0
运 价 A1
B1 16
B2 10
B3 8
供 应 量 80 40 120
解：由于产地的总产量=120，可以令Q=150 A2 12 8 13
需 要 量 30 35 55
运 价 A1 A2 B1 B2 B3 需 要 量
B1 A1 A2 A3 A4 bj vj 4 16 164
B2 96 410 11+5 9
B3 612
B4 138
B5
ai 18
ui 0 -1 0 -5
7 + 5 -1 5 56 105 6 15 46
12 21
8 13
11 15
负费用C35-C45+C42=
B1 A1 A2 A3 A4 bj vj 4 16 410 11+5 9 12 21 164 96 B2 B3 612
0150 12 4 5 180
0150 4 6 185
0150 6
最小元素法
运 价 A1 A2 B1 B2 B3 需 要 量 A1 5 16 10 8 150 A2 B1 16 B2 10 835 B3 855 13 5 0150 205 0150 5 12 8 13 150 供 应 量 230 190 150 150 150 870
得到新的运输方案
运 价 A1 A2 B1 B2 B3 需 要 量 150 150 25 180 185 A1 150 150 5 150 150 125 205 35 A2 B1 B2 B3 80 供 应 量 230 190 150 150 150 870
计算检验数，全为非正，得到最优化方案
运 价 A1 A2 B1 B2 B3 vj
A 1 1 4 -1 3 1 5 -2 1
1 3 -1 5 1 4 -1 4
A 4 1 2 -1
1010 15
空格（A1，B2）存在闭回路（A1，B2） -（A1，B3）-（A3，B3）-（A3，B5） -（A4，B2）有如下特征： （1）空格处的行列位势和为负数，即
u1+v2=
-15+9=
-6
（2）这条路有奇数个数字格（7，5， 1，10，5）被偶数条横线和竖线（三 横三竖共6条）依次交错的连接着。
转运的运输问题
例 已知从产地A1、A2到销地B1、B2、 B3、B4的直接运价表，生产地之间的运 价表，销地之间的运价表如下，要制定 运费最小的转运方案。 B1 B2 B3 运 价 供 应 量
A1 A235
8 13 55
80 40 120
运 价 A 1 A 2
10
1
3
2
4 4
20
3
5
4
2
20
提示：不能直接到达则 用M表示运费。
如图1运输系 统，包括产地 1、2,销地4、 5和转运站3,箭 头数字表示产 地产量或销地 销量，联线数 字表示运费， 节点旁红数字 表示转运单价。
接收 产地
转运 销地 2
4
040 1 M 3
发送 产地 1
2 转运 3 销地 4
（3）第奇数位数字格的运价减去偶数位 数字格运价之代数和为负，即： C13-C33+C35-C45+C42 = 6-11+5-10+4 = -6 （4）第偶数位数字格最小运输量为正。
最小运输量=Min（X33，X45）= 5
满足上述条件的回路称为负费用路。
调整运量5千吨，减小运费30千元。
总运量=51千吨，总运费=414千元
0 1 5 0 6 -7
1 3 -2 0 5 2 5
得到最优化方案
运 价 A1 A2 B1 B2 B3 需 要 量
A1 150
A2 150
B1 5 150
B2 35 150
B3 80
供 应 量 230 190 150 150
25 150 150 180 185
125 205
150 870
最优调运方案：
总运费=6*12+16*4+9*6+13*8+5*11+4*15 =409（千元）（比上月减少35千元） 总运量=56（千吨）（比上月增加10千吨）
B1 A1 A2 A3 A4 bj 4 164
B2 96
B3 612
B4 138
B5
ai 12 18
11 415 21 12 8
511 10 11
11 15 56
调整运量，寻找闭回路。
运价 A1 A2 A1 0150 5-1 A2 B1 B2 B3 vj 5-9
B1
B2 835 0150 12
B3 13-9 5-13 6-10 0150 8
ui 0 -4 -16 -12 -8
1625 10(-2) 855
0150 125
16-32 12-24 0150 4-8 10-22 8-16 40 0 4 16 8-16 13-17 5(-3) 6-2
生产地 销地 发货量
A1------------A2-------------
B3
B1
80
5
A2-------------
B2
35
25
B3--------------- B1 总运费=1105（元）
如果不考虑转运方式，直接调运最优方案总 费用=1130（元）
转运练习
1
30
2
3 4 1 2 1 4 5
0150 125
0150 6
得到初始方案
运 价 A1 A2 B1 B2 B3 需 要 量 150 150 180 185 A1 150 150 A2 B1 25 5 150 150 150 205 35 B2 B3 55 供 应 量 230 190 150 150 150 870
计算检验数，（B3，B1）为正且最大
调整运量=25。
运价 A1 A2 A1 0150 5-1 A2 B1 B2 B3 vj 5-9 B1 16 B2 835 0150 6-2 12 B3 13-9 5-13 6-10 0125 8 ui 0 -4 -16 -12 -8 10(-2) 880
0150 125
16-32 12-24 0150 4-8 10-22 8-16 40 8-16 13-17 525 0 4 16
A2 运价 A1 A1 0150 5-1 A2 B1 B2 B3 vj 5-9 B1 B2 835 0150 12 B3 13-9 5-13 6-10 0150 8 ui 0 -4 -16 -12 -8
1625 10(-2) 855
0150 125
16-32 12-24 0150 4-8 10-22 8-16 40 0 4 16 8-16 13-17 5(-3) 6-2
0150 12 4 5 180
0150 4 6 185
0150 6
最小元素法
运 价 A1 A2 B1 B2 B3 需 要 量 A1 5 16 10 8 150 A2 B1 16 B2 10 835 B3 855 13 5 0150 205 0150 5 12 8 13 150 供 应 量 230 190 150 150 150 870
A1 0 5 16 10 8
A2 5 0 12 8 13
B1 16 12 0 4 5
B2 10 8 4 0 6
B3 8 13 5 6 0
供 应 量 230 190 150 150 150
150 150 180 185 205 870
最小元素法
运 价 A1 A2 B1 B2 B3 需 要 量 A1 5 16 10 8 150 A2 B1 16 B2 10 8 B3 8 13 5 0150 205 0150 5 12 8 13 150 供 应 量 230 190 150 150 150 870