利用全等三角形证明线段的和差关系

备考2021年九年级数学中考复习专题：全等三角形性质与判定（五）1．“截长补短法”证明线段的和差问题：先阅读背景材料，猜想结论并填空，然后做问题探究．背景材料：（1）如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系．探究的方法是，延长FD到点G．使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出的结论是．探索问题：（2）如图2，若四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD 上的点，且∠EAF＝∠BAD，上述结论是否仍然成立？成立的话，请写出推理过程．2．已知：如图，∠BAC的角平分线与BC的垂直平分线DG交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F．（1）求证：BE＝CF；（2）若AF＝6，△ABC的周长为20，求BC的长．3．如图，已知AB＝DC，AB∥CD，E、F是AC上两点，且AF＝CE．（1）求证：△ABE≌△CDF；（2）若∠BCE＝30°，∠CBE＝70°，求∠CFD的度数．4．如图，在△ABC中，∠ACB＝90°，CD是AB边上的中线，点E为CD的中点，过C 作CF∥AB交AE的延长线于点F，连接BF．（1）求证：△ADE≌△FCE；（2）四边形BDCF是怎样的特殊四边形？请加以证明．5．如图，△ABC是等边三角形，点D是边BC边上的任意一点（除B、C外），以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．求证：EF＝CD．6．如图所示，在四边形ABCD中，AC与BD交于O，AB＝AD，CB＝CD．BE⊥CD于E，BE与AC交于F．CF＝2BO．（1）求证：△BEC是等腰直角三角形；（2）求tan∠ACD的值．7．如图，四边形ABCD是正方形，点E在直线BC上，连接AE．将△ABE沿AE所在直线折叠，点B的对应点是点B′，连接AB′并延长交直线DC于点F．（1）当点F与点C重合时如图（1），易证：DF+BE＝AF（不需证明）；（2）当点F在DC的延长线上时如图（2），当点F在CD的延长线上时如图（3），线段DF、BE、AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．8．如图，四边形ABCD为正方形，E为对角线AC上的点，连接BE并作BE⊥EF，交边CD于点F，过点F作FG⊥AC交对角线AC于点G．（1）请在图中找出与BE长度相等的边并加以证明：（2）求的值．9．如图，在△ABC中，AB＝AC，∠BAC＝90°，AE是过点A的一条直线，且B、C在AE 的两侧，BD⊥AE于D，CE⊥AE于E．（1）求证：△ABD≌△CAE；（2）若DE＝3，CE＝2，求BD．10．如图，在△ABC中，AB＝BC，CD⊥AB于点D，CD＝BD，BE平分∠ABC，交AC于E．交CD于F．点H是BC边的中点，连接DH，交BE于点G，连接CG．（1）求证：CE＝BF；（2）判断△ECG的形状，并证明你的结论．°．参考答案1．证明：（1）在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△AGF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF；故答案为：EF＝BE+DF．（2）解：结论EF＝BE+DF仍然成立；理由：延长FD到点G．使DG＝BE．连结AG，在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△AGF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF．2．（1）证明：连接DB、DC．∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE＝DF，∵DG垂直平分BC，∴DB＝DC，在Rt△BED和Rt△CFD中，，∴Rt△BED≌Rt△CFD（HL），∴BE＝CF；（2）解：∵∠DAE＝∠DAF，∠AED＝∠AFD＝90°，AD＝AD，∴△AED≌△AFD（AAS），∴AF＝AE＝6，由（1）得：BE＝CF，∵△ABC的周长＝AB+AC+BC，＝AE+EB+AF﹣CF+BC，＝AE+AF+BC＝20，∴BC＝20﹣12＝8．3．（1）证明：∵AB∥CD，∴∠BAE＝∠FCD，∵AF＝CE，∴AE＝CF，又∵AB＝CD，∴△ABE≌△CDF（SAS）．（2）解：∵∠BCE＝30°，∠CBE＝70°，∴∠AEB＝∠BCE+∠CBE＝30°+70°＝100°，∵△ABE≌△CDF，∴∠CFD＝∠AEB＝100°．4．证明：（1）∵CF∥AB，∴∠CF A＝∠BAF，∠ADC＝∠FCD，∵点E为CD的中点，∴DE＝CE，∴△ADE≌△FCE（AAS）；（2）解：四边形BDCF是菱形．证明如下：∵△ADE≌△FCE，∴AD＝CF，∵CD是Rt△ABC的中线，∴CD＝AD＝BD，∴CF＝BD，且CF∥AB，∴四边形BDCF是平行四边形，且CD＝BD，∴四边形BDCF是菱形．5．证明：∵△AED是等边三角形，△ABC是等边三角形，∴AD＝AE＝ED，AB＝CA＝BC，∠ADE＝60°，∠B＝∠F AC＝60°，∵ED∥FC，∴∠EDB＝∠FCB，∵∠BDA＝∠ADE+∠EDB＝60°+∠EDB，∠AFC＝∠B+∠FCB＝60°+∠FCB，∴∠BDA＝∠AFC，在△ABD和△CAF中，，∴△ABD≌△CAF（AAS），∴AD＝FC，∵AD＝ED，∴ED＝CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF＝CD．6．证明：（1）∵AB＝AD，CB＝CD，∴AC垂直平分BD，∴BD＝2BO，∵CF＝2BO，∴CF＝BD，∵∠DBE+∠BDE＝90°，∠BDE+∠DCO＝90°，∴∠DBE＝∠FCE，又∵∠BED＝∠CEF，∴△BDE≌△CFE（AAS），∴BE＝CE，又∵BE⊥CD，∴△BEC是等腰直角三角形；（2）如图，连接DF，∵△BDE≌△CFE，∴DE＝EF，∴DF＝EF，∵AC垂直平分BD，∴BF＝DF＝EF，∴BE＝BF+EF＝（+1）EF，∴CE＝（+1）EF，∴tan∠ACD＝＝﹣1．7．解：（1）由折叠可得AB＝AB′，BE＝B′E，∵四边形ABCD是正方形，∴AB＝DC＝DF，∠B′CE＝45°，∴B′E＝B′F，∴AF＝AB′+B′F，即DF+BE＝AF；（2）图（2）的结论：DF+BE＝AF；图（3）的结论：BE﹣DF＝AF；图（2）的证明：延长CD到点G，使DG＝BE，连接AG，需证△ABE≌△ADG，∵CB∥AD，∴∠AEB＝∠EAD，∵∠BAE＝∠B′AE，∴∠B′AE＝∠DAG，∴∠GAF＝∠DAE，∴∠AGD＝∠GAF，∴GF＝AF，∴BE+DF＝AF；图（3）的证明：在BC上取点M，使BM＝DF，连接AM，需证△ABM≌△ADF，∵∠BAM＝∠F AD，AF＝AM∵△ABE≌AB′E∴∠BAE＝∠EAB′，∴∠MAE＝∠DAE，∵AD∥BE，∴∠AEM＝∠DAB，∴∠MAE＝∠AEM，∴ME＝MA＝AF，∴BE﹣DF＝AF．8．解：（1）BE＝EF，证明如下：如图1，过P作MN∥AD，交AB于M，交CD于N，∵BE⊥EF，∴∠BEF＝90°，∴∠MEB+∠NEF＝90°，∵四边形ABCD是正方形，∴∠BAD＝∠D＝90°，∵AD∥MN，∴∠BME＝∠BAD＝∠ENF＝∠D＝90°，∴∠MEB+∠MBE＝90°，∴∠NEF＝∠MBE，Rt△ENC中，∠ECN＝45°，∴△ENC是等腰直角三角形，∴EN＝CN，∵∠BME＝∠ENC＝∠ABC＝90°，∴四边形MBCN是矩形，∴BM＝CN，∴BM＝EN，∴△BME≌△ENF（ASA），∴BE＝EF；（2）如图2，设正方形ABCD的中心为点O，连接OB，∵点O是正方形ABCD对角线AC的中点，∴OB⊥AC，∴∠AOB＝90°，∴∠AOB＝∠EGF＝90°，∴∠OBE+∠BEO＝90°，∵∠BEF＝90°，∴∠BEO+∠GEF＝90°，∴∠OBE＝∠GEF，由（1）得：BE＝EF，∴△OBE≌△GEF（AAS），∴OB＝EG，∵∠BAO＝45°，∴，∴．9．（1）证明：∵BD⊥AE于D，CE⊥AE于E，∠BAC＝90°，∴∠BDA＝∠AEC＝90°，∠DBA+∠BAD＝90°，∠BAD+∠EAC＝90°，∴∠DBA＝∠EAC，在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）；（2）解：由（1）知，△ABD≌△CAE，则BD＝AE，AD＝CE．∵DE＝3，CE＝2∴AE＝AD+DE＝CE+DE＝5．∴BD＝AE＝5．10．证明：（1）∵AB＝BC，BE平分∠ABC，∴BE⊥AC，CE＝AE，∴∠A+∠ACD＝90°，∵CD⊥AB，∴∠A+∠DBF＝90°∴∠ACD＝∠DBF，在△ADC和△FDB中，∠ACD＝∠DFB，CD＝BD，∠ADC＝∠BDF，∴△ADC≌△FDB（ASA）；∴AC＝BF，又∵CE＝AE，∴CE＝BF；（2）△ECG为等腰直角三角形．∵点H是BC边的中点，∴GH垂直平分BC，∴GC＝GB，∵∠DBF＝∠GBC＝∠GCB＝∠ECF，得∠ECG＝45°，又∵BE⊥AC，∴△ECG为等腰直角三角形；。

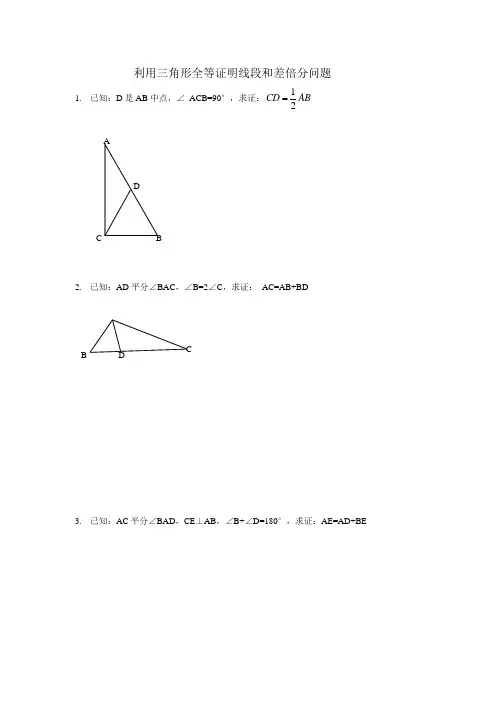
利用三角形全等证明线段和差倍分问题1. 已知：D 是AB 中点，∠ ACB=90°，求证：12CD AB2. 已知：AD 平分∠BAC ，∠B=2∠C ，求证： AC=AB+BD3. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BECDB4·如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD 上。

求证：BC=AB+DC。

5·已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证：AC-AB=2BE6．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．7．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ． 求证：BD =2CE ．8·在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.PEDCB A F E DCBA9·如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD 相等吗？请说明理由10·如图，已知在△ABC中，∠BAC为直角，AB=AC，D为AC上一点，CE⊥BD于E．（1）若BD平分∠ABC，求证CE=12 BD；（2）若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，求出它的度数，并说明理由。

EDCB。

全等三角形中线段的和、差问题证明线段的和、差问题，通常采用的方法就是截长补短法，这也是初中数学几何题中一种常用辅助线的添加方法，截长就是在一条线上截取成两段，补短就是在一条边上延长，使其等于一条所求边。

例题1：已知：在△ABC中，∠BAC＝90°，AB＝AC，AE是过点A的一条直线，且BD⊥AE，垂足为点D，CE⊥AE，垂足为点E．（1）当直线AE处于如图①的位置时，有BD＝DE+CE，请说明理由；（2）当直线AE处于如图②的位置时，则BD、DE、CE的关系如何？请说明理由．证明：（1）∵∠BAC＝90°，∴∠2+∠3＝90°，∵BD⊥AE，∴∠1+∠3＝90°，∴∠1＝∠2，在△ABD和△CAE中，，∴△ABD≌△CAE，∴BD＝AE，AD＝CE，∵AE＝AD+DE，∴BD＝DE+CE；（2）BD＝DE﹣CE，理由如下：∵∠BAC＝90°，∴∠2+∠3＝90°，∵BD⊥AE，∴∠1+∠3＝90°，∴∠1＝∠2，在△ABD和△CAE中，，∴△ABD≌△CAE，∴BD＝AE，AD＝CE，∵AE＝DE﹣AD，∴BD＝DE﹣CE．例题2：阅读下面材料：小明遇到这样一个问题：如图1，在四边形ABCD中，E是BC的中点，AE是∠BAD的平分线，AB∥DC，求证：AD＝AB+DC．小明发现以下两种方法：方法1：如图2，延长AE、DC交于点F；方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．（1）根据阅读材料，任选一种方法，证明：AD＝AB+DC；用学过的知识或参考小明的方法，解决下面的问题：（2）如图4，在四边形ABCD中，AE是∠BAD的平分线，E是BC的中点，∠BAD＝60°，∠ABC＝180°﹣∠BCD，求证：CD＝CE．解：（1）方法1：如图2，延长AE、DC交于点F；∵AB∥DF，∴∠B＝∠ECF，∵BE＝EC，∠BEA＝∠CEF，∴△ABE≌△FCE（ASA），∴AB＝CF，∵EA平分∠BAD，∴∠BAE＝∠DAF＝∠F，∴AD＝DF，∴AD＝CD+AB．方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．∵AB＝AG，∠BAE＝∠GAE，AE＝AE，∴△BAE≌△GAE（SAS），∴BE＝EG＝EC，∠AEB＝∠AEG，∴∠EGC＝∠ECG，∵∠BEG＝∠EGC+∠ECG，∴∠BEA＝∠ECG，∴AE∥CG，∴∠EAG＝∠CGD，∵AB∥CD，AE∥CG，∴∠BAE＝∠DCG，∴∠DCG＝∠DGC，∴CD＝DG，∴AD＝AB+CD．（2）证明：如图4中，作CM∥AB交AE的延长线于M，CM交AD于N，连接EN．由（1）可知：AN＝NM，AE＝EM，∴EN平分∠ANM，∵∠BAD＝60°，MN∥AB，∴∠MND＝∠BAD＝60°，∴∠ENM＝∠ENA＝60°，∴∠CND＝∠CNE，∵∠B+∠ECN＝180°，∠ABC＝180°﹣∠BCD，∴∠NCE＝∠NCD，∵CN＝CN，∴△CNE≌△CND（ASA），∴CE＝CD．习题1．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，延长AE交BC 的延长线于点F．（1）求证：△DAE≌△CFE；（2）若AB＝BC+AD，求证：BE⊥AF；（3）在（2）的条件下，若∠D＝90°，AD＝，AF＝10，则点E到AB的距离是．（直接写出结果即可，不用写出演推过程）2．如图，△ACB和△DCE均为等腰三角形，点A、D、E在同一直线上，连接BE．（1）如图1，若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°①求证：AD＝BE；②求∠AEB的度数．（2）如图2，若∠ACB＝∠DCE＝120°，CM为△DCE中DE边上的高，BN为△ABE 中AE边上的高，试证明：AE＝2CM+BN．3．（1）已知，如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE＝BD+CE．（2）如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意钝角，请问结论DE＝BD+CE 是否成立？若成立，请你给出证明：若不成立，请说明理由．4．如图：在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥MN 于M，BN⊥MN于N．（1）求证：MN＝AM+BN．（2）若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之间有什么关系？请说明理由．5．如图，△ABC的两条高AD，BE交于点F，∠ABC＝45°，∠BAC＝60°．（1）求证：DF＝DC；（2）连接CF，求证：AB＝AC+CF．6．如图，在△ABC中，∠ABC＝45°，CD⊥AB，垂足为D，DH⊥BC，垂足为H．点E在边AC上，BE分别与CD、DH相交于点F、G．（1）求证：BG＝CG；（2）若AB＝BC，且BE⊥AC．①求证：BF＝CA；②求证：BG＝CE+EF7．在△BCF中，点D是边CF上的一点，过点D作AD∥BC，过点B作BA∥CD交AD于点A，点G是BC的中点，点E是线段AD上一点，且∠CDG＝∠ABE＝∠EBF．（1）若∠F＝60°，∠C＝45°，BC＝2，请求出AB的长；（2）求证：CD＝BF+DF．8．如图，E是BC的中点，DE平分∠ADC．（1）如图1，若∠B＝∠C＝90°，求证：AE平分∠DAB；（2）如图2，若DE⊥AE，求证：AD＝AB+CD．9．四边形ABCD中，∠ABC+∠D＝180°，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F．求证：（1）△CBE≌△CDF；（2）AB+DF＝AF．10．（1）如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，求证：AD＝DC+AB，（2）如图②，在四边形ABCD中，AB∥DC，F是DC延长线上一点，连接AF，E是BC的中点，若AE是∠BAF的平分线，求证：AB＝AF+CF．11．如图所示，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，延长AE交BC的延长线于点F．（1）判断FC与AD的数量关系，并说明理由；（2）若AB＝BC+AD，则BE⊥AF吗？为什么？12．探究：如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥m于点D，CE⊥m于点E，求证：△ABD≌△CAE．应用：如图②，在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC，求证：DE＝BD+CE．13．如图，已知∠MAN＝120°，AC平分∠MAN，∠ABC+∠ADC＝180°，求证：①DC＝BC；②AD+AB＝AC．14．（1）如图①，已知：△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥m 于D，CE⊥m于E，求证：DE＝BD+CE；（2）拓展：如图②，将（1）中的条件改为：△ABC中，AB＝AC，D、A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，α为任意锐角或钝角，请问结论DE＝BD+CE 是否成立？如成立，请证明；若不成立，请说明理由；（3）应用：如图③，在△ABC中，∠BAC是钝角，AB＝AC，∠BAD＞∠CAE，∠BDA ＝∠AEC＝∠BAC，直线m与BC的延长线交于点F，若BC＝2CF，△ABC的面积是12，求△ABD与△CEF的面积之和．全等三角形中线段的和、差问题参考答案与试题解析一．解答题（共16小题）1．【解答】（1）证明：∵AD∥BC，∴∠ADC＝∠ECF，∵E是CD的中点，∴DE＝EC，∵在△ADE与△FCE中，，∴△ADE≌△FCE（ASA）；（2）证明：由（1）知△ADE≌△FCE，∴AE＝EF，AD＝CF，∵AB＝BC+AD，∴AB＝BC+CF，即AB＝BF，在△ABE与△FBE中，，∴△ABE≌△FBE（SSS），∴∠AEB＝∠FEB＝90°，∴BE⊥AE；（3）解：在（2）的条件下有△ABE≌△FBE，∴∠ABE＝∠FBE，∴E到BF的距离等于E到AB的距离，由（1）知△ADE≌△FCE，∴AE＝EF＝AF＝5，∵∠D＝90°，∴DE＝＝＝，∴CE＝DE＝，∵CE⊥BF，∴点E到AB的距离为．2．【解答】（1）①证明：∵∠CAB＝∠CBA＝∠CDE＝∠CED＝50°，∴∠ACB＝∠DCE＝180°﹣2×50°＝80°，∵∠ACB＝∠ACD+∠DCB，∠DCE＝∠DCB+∠BCE，∴∠ACD＝∠BCE，∵△ACB，△DCE都是等腰三角形，∴AC＝BC，DC＝EC，在△ACD和△BCE中，∴△ACD≌△BCE（SAS），∴AD＝BE．②解：∵△ACD≌△BCE，∴∠ADC＝∠BEC，∵点A、D、E在同一直线上，且∠CDE＝50°，∴∠ADC＝180°﹣∠CDE＝130°，∴∠BEC＝130°，∵∠BEC＝∠CED+∠AEB，∠CED＝50°，∴∠AEB＝∠BEC﹣∠CED＝80°．（2）证明：∵△ACD≌△BCE，∴∠DAC＝∠EBC，∵△ACB，△DCE都是等腰三角形，∠ACB＝∠DCE＝120°∴∠CAB＝∠CBA＝∠CDE＝∠CED＝30°，∵CM⊥DE，∴∠CMD＝90°，DM＝EM，∴ME＝CM，∴DE＝2CM，∵∠BEN＝∠BAE+∠ABE＝∠BAE+∠EBC+∠CBA＝∠BAE+∠DAC+∠CBA＝30°+30°＝60°，∴∠NBE＝30°，∴BE＝2EN，EN＝BN，∴BE＝BN，∵AD＝BE，∴AE＝AD+DE，∴AE＝2CM+BN．3．【解答】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．4．【解答】证明：（1）∵AM⊥MN，BN⊥MN，∴∠AMC＝∠CNB＝90°，∵∠ACB＝90°，∴∠MAC+∠ACM＝90°，∠NCB+∠ACM＝90°，∴∠MAC＝∠NCB，在△AMC和△CNB中，∠AMC＝∠CNB，∠MAC＝∠NCB，AC＝CB，△AMC≌△CNB（AAS），AM＝CN，MC＝NB，∵MN＝NC+CM，∴MN＝AM+BN；（2）结论：MN＝BN﹣AM．∵AM⊥MN，BN⊥MN，∴∠AMC＝∠CNB＝90°，∵∠ACB＝90°，∴∠MAC+∠ACM＝90°，∠NCB+∠ACM＝90°，∴∠MAC＝∠NCB，在△AMC和△CNB中，∠AMC＝∠CNB，∠MAC＝∠NCB，AC＝CB，△AMC≌△CNB（AAS），AM＝CN，MC＝NB，∵MN＝CM﹣CN，∴MN＝BN﹣AM．5．【解答】（1）证明：∵AD⊥BC，∴∠ADB＝∠ADC＝90°，∵∠ABC＝45°，∴∠DBA＝∠DAB＝45°，∴BD＝DA，∵BE⊥AC，∴∠BEC＝90°，∴∠DAC+∠C＝90°，∠CBE+∠C＝90°，∴∠DAC＝∠DBF，在△BDF和△ADC中，，∴△BDF≌△ADC（ASA），∴DF＝DC．（2）证明：延长FE到K，使得EK＝EF，连接CF．∵∠BAC＝60°，∠ABC＝45°，∴∠ACB＝180°﹣60°﹣45°＝75°，∵DF＝DC，∠FDC＝90°，∴∠FCD＝∠DFC＝45°，∴∠ECF＝30°，∵∠CEF＝90°，∴CF＝2EF，∵FK＝2EF，∴CF＝FK，∵AE⊥FK，EF＝EK，∴AF＝AK，∴∠K＝∠AFE，∠EAF＝∠EAF，∵∠ADC＝90°，∠ACD＝75°，∴∠DAC＝15°，∴∠EAF＝∠EAK＝15°，∴∠K＝90°﹣15°＝75°，∴∠BAK＝∠BAD+∠DAK＝75°，∴∠BAK＝∠K，∴BA＝BK，∴AB＝BF+FK＝BF+CF．6．【解答】证明：（1）∵CD⊥AB，∴∠CDB＝90°，∵∠ABC＝45°，∴∠DBC＝∠DCB＝45°，∴DB＝DC，∵DH⊥BC，∴BH＝CH，∴GB＝GC．（2）①∵BA＝BC，BE⊥AC，∠ABC＝45°，∴∠ABE＝∠CBE＝22.5°，∴∠A＝∠ACB＝67.5°，∵∠ADC＝90°，∴∠ACD＝∠DBF＝22.5°，∵∠BDF＝∠ADC＝90°，BD＝DC，∴△BDF≌△CDA（SAS），∴BF＝AC．②作DN∥BC交AC于点N，连接FN．∵△BDF≌△CDA，∴DF＝AD，∵DN∥BC，∴∠NDC＝∠DCB＝45°，∵DN＝DB，∴△NDA≌△NDF（SAS），∴∠A＝∠DFN＝67.5°∵∠DFN＝∠FCN+∠CNF，∠FCN＝22.5°，∴∠CNF＝45°，∴NE＝EF，∵∠NDC＝∠GDB＝45°，BD＝DC，∠DBG＝∠DCN，∴△BDG≌△CDN（ASA），∴BG＝CN，∵CN＝EN+EC＝EF+CE，∴BG＝EC+EF．7．【解答】解：（1）过点E作EH⊥AB交AB于点H．∵AD∥BC，AB∥CD，∴四边形ABCD为平行四边形．∴AB＝DC，∠DAB＝∠DBC，在△CGD和△AEB中，，∴△CGD≌△AEB，∴∠DGC＝∠BEA，∴∠DGB＝∠BED，∵AD∥BC，∴∠EDG+∠DGB＝180°，∴∠EDG+∠BED＝180°∴EB∥DG，∴四边形BGDE为平行四边形，∴BG＝ED，∵G是BD的中点，∴BG＝BC，∴BC＝AD，ED＝BG＝AD，∵BC＝2，∴AE＝AD＝，在Rt△AEH中，∵∠EAB＝45°，sin∠EAB＝sin 45°＝＝，∴EH＝，∵∠EHA＝90°，∴△AHE为等腰直角三角形，∴AH＝EH＝，∵∠F＝60°，∴∠FBA＝60°，∵∠EBA＝∠EBF，∴∠EBA＝30°，在Rt△EHB中，tan∠EBH＝tan 30°＝＝，∴HB＝3，∴AB＝3+（2）连接EF，延长FE交AB与点M．∵∠A＝∠EDF，AE＝DE，∠AEM＝∠DEF，∴△AEM≌△DEF（ASA），∴DF＝AM，ME＝EF，又∵∠EBA＝∠EBF，∴△MBF是等腰三角形∴BF＝BM，又∵AB＝AM+BM，∴CD＝BF+DF．8．【解答】解：（1）如图1，延长DE交AB的延长线于F，∵∠ABC＝∠C＝90°，∴AB∥CD，∴∠CDE＝∠F，又∵E是BC的中点，∴CE＝BE，∴△CDE≌△BFE（AAS），∴DE＝FE，即E为DF的中点，∵DE平分∠ADC，∴∠CDE＝∠ADE，∴∠ADE＝∠F，∴AD＝AF，∴AE平分∠DAB；（2）如图2，在DA上截取DF＝DC，连接EF，∵DE平分∠ADC，∴∠CDE＝∠FDE，又∵DE＝DE，∴△CDE≌△FDE（SAS），∴CE＝FE，∠CED＝∠FED，又∵E是BC的中点，∴CE＝BE，∴FE＝BE，∵∠AED＝90°，∴∠AEF+∠DEF＝90°，∠AEB+∠DEC＝90°，∴∠AEF＝∠AEB，又∵AE＝AE，∴△AEF≌△AEB（SAS），∴AF＝AB，∴AD＝AF+DF＝AB+CD．9．【解答】证明：（1）∵AC平分∠BAD，CE⊥AB，CF⊥AD∴CE＝CF∵∠ABC+∠D＝180°，∠ABC+∠EBC＝180°∴∠EBC＝∠D．在△CBE与△CDF中，，∴△CBE≌△CDF（AAS）；（2）在Rt△ACE与Rt△ACF中，，∴Rt△ACE≌Rt△ACF（HL），∴AE＝AF，∴AB+DF＝AB+BE＝AE＝AF．10．【解答】（1）证明：如图①中，延长AE交DC的延长线于点F，∵E是BC的中点，∴CE＝BE，∵AB∥DC，∴∠BAE＝∠F，在△AEB和△FEC中，，∴△AEB≌△FEC（AAS），∴AB＝FC，∵AE是∠BAD的平分线，∴∠BAE＝∠EAD，∵AB∥CD，∴∠BAE＝∠F，∴∠EAD＝∠F，∴AD＝DF，∴AD＝DF＝DC+CF＝DC+AB．（2）如图②，延长AE交DF的延长线于点G，∵E是BC的中点，∴CE＝BE，∵AB∥DC，∴∠BAE＝∠G，在△AEB和△GEC中，，∴△AEB≌△GEC（AAS），∴AB＝GC，∵AE是∠BAF的平分线，∴∠BAG＝∠F AG，∵AB∥CD，∴∠BAG＝∠G，∴∠F AG＝∠G，∴F A＝FG，∴AB＝CG＝AF+CF．11．【解答】（1）解：结论：CF＝AD．理由：∵AD∥BC，∴∠ADC＝∠ECF，∵E是CD的中点，∴DE＝EC，∵在△ADE与△FCE中，，∴△ADE≌△FCE（ASA），∴FC＝AD；（2）结论：BE⊥AF．理由：由（1）知△ADE≌△FCE，∴AE＝EF，AD＝CF，∵AB＝BC+AD，∴AB＝BC+CF，即AB＝BF，∵△ADE≌△FCE，∴AE＝EF，∴BE⊥AE；12．【解答】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS）；（2）设∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．13．【解答】证明：①在AN上截取AE＝AC，连接CE，如图所示：∵AC平分∠MAN，∠MAN＝120°，∴∠CAB＝∠CAD＝60°，∴△ACE是等边三角形，∴∠AEC＝60°，AC＝EC＝AE，又∵∠ABC+∠ADC＝180°，∠ABC+∠EBC＝180°，∴∠ADC＝∠EBC，在△ADC和△EBC中，，∴△ADC≌△EBC（AAS），∴DC＝BC，AD＝BE；②由①得：AD＝BE，∴AB+AD＝AB+BE＝AE，∴AB+AD＝AC．14．【解答】（1）证明：∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）解：结论DE＝BD+CE成立；理由如下：∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（3）解：∵∠BAD＞∠CAE，∠BDA＝∠AEC＝∠BAC，∴∠CAE＝∠ABD，在△ABD和△CEA中，，∴△ABD≌△CEA（AAS），∴S△ABD＝S△CEA，设△ABC的底边BC上的高为h，则△ACF的底边CF上的高为h，∴S△ABC＝BC•h＝12，S△ACF＝CF•h，∵BC＝2CF，∴S△ACF＝6，∵S△ACF＝S△CEF+S△CEA＝S△CEF+S△ABD＝6，∴△ABD与△CEF的面积之和为6．。

全等三角形中线段和差处理技巧
1. 嘿，看到全等三角形里那些线段和差，是不是有时候觉得有点头疼啊？就像一团乱麻！那来试试延长线段法呀。

比如在那个三角形 ABC 和三角形DEF 全等中，把线段 AB 延长一点，你会发现新天地哦，问题一下子就清晰多啦！
2. 哇塞，利用等量代换处理线段和差那可太妙啦！想象一下，就像在拼图中找到了关键的那块。

比如在三角形 MNO 和三角形 PQR 全等时，一条边等于另一条边，通过等量代换，线段的和差关系就明明白白啦！
3. 嘿呀，将线段和差转化为其他已知条件，这招简直绝了！就如同给你指出了一条明路。

在三角形 XYZ 和三角形 UVW 全等的那个题里，把那些线段
巧妙转换一下，问题不就迎刃而解了嘛！
4. 哦哟，利用三角形的中线来处理线段和差可别小瞧哦！这就像手里有个秘密武器。

就像在三角形 ABC 中，AD 是中线，那处理起线段和差来，可轻
松多啦！
5. 哈哈，辅助线这个妙招可不能忘啊！它就像是给你开了个外挂。

在三角形GHI 和三角形 JKL 全等那道难住很多人的题里，加上条辅助线，哇，一切
都豁然开朗啦！
6. 小伙伴们，构造全等三角形来处理线段和差也很棒呀！就像是搭建起了一座桥梁。

在那道复杂的图形里，构造出全等三角形后，原本纠结的线段和差变得简单明了！
7. 哇哦，直接计算线段长度来找线段和差关系也是个好办法呢！这就像是拿着一把钥匙去开锁。

比如在那个具体的三角形中，算出每条边的长度，线段和差自然就搞清楚啦！
结论：处理全等三角形中线段和差的技巧有很多，每一种都有着独特的作用，关键在于我们要灵活运用，找到最适合的那个方法呀！。

四、利用全等三角形证线段之间的和差倍分问题证一条线段等于其它两条线段的和或差，常将其转化成证明线段的相等问题，常用的方法如下：(1)利用图形中已有的线段和差关系进行证明。

(2)延长一条线段，作出两条线段的和，然后证明这条线段等于第三条线段。

(3)在第三条线段上截取一段等于第一条线段，然后证余下的线段等于第二条线段。

后两种方法，就是通常所说的截长补短。

例1.已知：如图在△ABC中，∠ABC的平分线与∠ACB相邻外角∠ACG的平分线相交于D，DE∥BC交AB于E，交AC于F，求证：EF=BE-CF分析：要证EF=BE-CF，而图中EF=ED-FD，若证出BE=ED，CF=FD，则此题可证出。

（证明略）例2.已知：如图，四边形ABCD中，AC平分∠BAD，CE⊥AB 于E，且∠B+∠D=180°，求证：AE=AD+BE分析：要证AE=AD+BE，则可转化为证AE-BE=AD，则需找到一条线段使它等于AE-BE，再证其与AD相等，在EA上截取EF=BE，连结CF，问题转化为证AF=AD，即要证出△AFC≌△ADC证明：在EA上截取EF=BE，连结CF∵CE⊥AB于E（已知）∴CF=CB（在线段垂直平分线上的点，到线段两个端点的距离相等）∴∠1=∠B（等边对等角）∵∠1+∠2=180°（平角定义）∠B+∠D=180°（已知）∴∠2=∠D（等角的补角相等）（再往下证明略）3.如图，△ABC是等边三角形，∠BDC=120°，且BD=CD,∠MDN=60°，AB=12cm. (1)证明MN=BM＋NC.（2）求△AMN的周长。

（3）若点M、N分别是AB、CA延长线上的点，，请说明BM、MN、NC之间的关系。

分析：（1）证明MN=BM＋NC.是典型的三条线段之间的关系的题型，这种题型一般是采用“截长补短法”来证明。

“截长法”是在最长的线段MN上找一点F，将MN截为两部分(如图4)，比如截为MN=MF＋NF,且使MF=BM（或NF=NC）.再求证剩余的线段NF=NC，从而得到MN=BM＋NC。

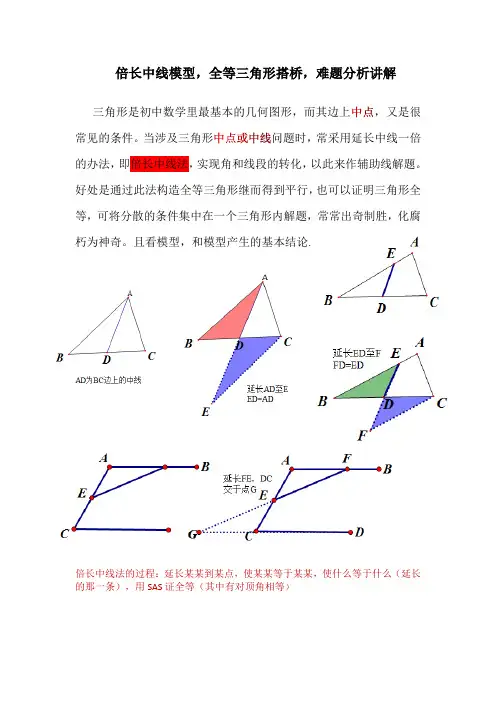
倍长中线模型，全等三角形搭桥，难题分析讲解三角形是初中数学里最基本的几何图形，而其边上，又是很常见的条件。

当涉及三角形问题时，常采用延长中线一倍的办法，即倍长中线法，实现角和线段的转化，以此来作辅助线解题。

好处是通过此法构造全等三角形继而得到平行，也可以证明三角形全等，可将分散的条件集中在一个三角形内解题，常常出奇制胜，化腐朽为神奇。

且看模型，和模型产生的基本结论.倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（其中有对顶角相等）例1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围。

分析：延长AD 至E ，使ED=AD ，连接BE ，见模型1，可证△ABD 与△ECD 全等，把AB 边转移到EC 上了，再看△AEC ，用第三边大于两边之差小于两边之和可解。

【归纳总结】1. 三角形的三边关系是求线段范围的常用方法．2. 出现中线时，常考虑倍长中线构造全等三角形，实现线段的转化．例 2：已知在△ABC 中，AD 是 BC 边上的中线， E 是AD 上的一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF延长ED 至G ，使GD=ED ，利用SAS 可证△BED与△CGD 全等，把BE 转移到GC 上，∠G=∠1，由已知BE=AC ，得到GC=AC ，由等腰三角形性质可知∠G=∠3，通过∠G 传递，得到∠2=∠3，得证AF=EF例3：已知：如图，在△ABC 中，AB ≠AC ，D 、E 在BC 上，且DE=EC ，过D 作DF//BA 交AE 于点F ，DE=AC ，求证：AE 平分∠BAC证明：如图，延长FE 到G ，使EG=EF ，连接CG ．在△DEF 和△CEG 中，∵ ，∴△DEF ≌△CEG ． ∴DF=GC ，∠DFE=∠G ．∵DF ∥AB ，∴∠DFE=∠BAE ．∵DF=AC ，∴GC=AC ．∴∠G=∠CAE ．∴∠BAE=∠CAE ．即AE 平分∠BAC⎪⎩⎪⎨⎧==FG FE CEG ＝∠DEF ∠EC ED例4：如图；在△ABC中，AB=AC，延长AB到D，使得BD=AB，取AB的中点E，连结CD和CE，求证：CD=2CE证明：延长CE至F，使EF＝CE，则CF＝2CE易证△ACE≌△BFE，∴AC＝BF＝AB＝BD，∠ABF＝∠BAC∴∠DBC＝∠ACB+∠BAC＝∠ABC+∠ABF＝∠FBC∴△BCF≌△BCD（SAS）∴CD＝CF＝2CE【融会贯通】1、在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F。

《三角形全等的断定》教学反思《三角形全等的断定》教学反思《三角形全等的断定》教学反思1 本节课探究三角形全等的断定方法一，是后面几种断定方法的根底，也是本章的重点也是难点。

教材看似简单，仔细研究后才发现对学生来说有些困难，处理不好可能难以成功。

备课时发现本节课的难点就是处理从确定一个三角形到得到三角形全等的断定方法这个环节，让学生动手操作和学生互相交流验证很好地解决了问题，圆满地完本钱节课的教学任务。

反思整个过程，我觉得做得较为成功的有以下几个方面：1、教学设计整体化，内容生活化。

在课题的引入方面，让学生动手做、裁剪三角形。

既提问复习了全等三角形的定义，又很好的过渡到确定一个三角形需要哪些条件的问题上来。

把知识不知不觉地表达出来，学得自然新颖。

数学学习来于生活实际，学生学得轻松有趣。

2、把课堂充分地让给了学生。

我和学生做了些课前交流，临上课前我先对他们提了四个要求：认真听讲，积极考虑，大胆尝试，踊跃发言。

其实，这是一个调动学生积极性，同时也是鼓励彼此的过程。

在上课过程中，我尽量不做过多的讲解，通过引导让学生发现问题并通过动手操作、交流讨论来解决问题。

3、在难点的打破上获得了成功。

上这堂课前，我一直担忧学生在得出三角形全等的断定方法上出现理解困难。

课堂上我通过让学生动手制作一个两边长分别为6cm和8cm，并要求互相之间互相比拟发现制作的三角形形状和大小完全一样，即三角形都全等，最后同学们都不约而同地得出了三角形全等的断定方法。

但也有几处是值得考虑和在以后教学中应该改良的地方：〔1〕、在课堂上优等生急着演示、发言，后进生却成了观众和听众。

如何做到面向全体，人人学有所得，也值得我们数学老师来讨论。

〔2〕、课堂学生的操作应努力做到学生自发生成的，而不是老师说"你们比拟下三角形的形状和大小"，应换为自发地比拟更好。

〔3〕、教学细节需进一步改良，教学时应多关注学生，在学习新知后，虽然大局部的学生都掌握了，但有少数后进生仍然是不理解。

全等三角形中的探索两线段关系问题全等三角形是八年级数学中的重点内容，对于初学几何的初二学生来说学起来相对困难，但是也是培养学生数学素养和学习数学兴趣的必修知识，更是区分智商高低两级分化的知识点.尤其是全等三角形中探索问题对于学生来说更是难上加难.但是全等三角形是中考中的重点内容，也是热点，每年必考并且多于探究有关，下面就全等三角形的探索问题解答技巧进行分析.探索两线段的关系. 两线段的关系一般情况下从两个方面考虑，一是数量关系也是大小或倍数关系，二是位置关系，位置关系一般情况下是平行和垂直两种关系，对于刚接触几何内容的同学来说总是思考不周.例1.如图，在△ABC中，BE，CF分别是AC,AB两边上的高，在BE 上截取BD=AC，在CF的延长线上截取CG=AB，连接AD,AG，探索AD、AG 的关系。

【解析】探索两线段关系时，需要从数量关系和位置关系两个方面考虑.数量关系大多是相等关系或者是倍数关系，位置关系有平行或垂直关系.答：AD、AG的关系是：AD=AG;AD⊥AG理由如下：∵BE，CF分别是AC,AB两边上的高∴∠AFC=∠AEB=90°HGEFDC BA在Rt △ACF 中，∠AFC=90° ∠ACD+∠CAB=90° 在R t △ABE 中，∠AEB=90° ∠ABE+∠BAC=90° ∴∠ACD=∠ABE 在△ABD 与△GCA 中⎪⎩⎪⎨⎧=∠=∠=CA BD ACG ABD GC AB ∴△ABD ≌△GCA(SAS) ∴AD=AG ∠G=∠BAD∵∠AFC=90°，∴∠AFG=180°- ∠AFC=90° 在R t △AGF 中，∠AFG=90° ∴∠G+∠GAF=90°∴∠BAD+∠GAF=90°，即AD ⊥AG . ∴AD=AG AD ⊥AG小结：本题图形相对来说比较复杂，对于初二学生来说找到全等三角形比较困难，还有探索两线段关系时，学生很容易想到的是数量关系，位置关系容易忽略.在书写过程时有的同学会运用对顶角相等证明∠ACD=∠ABE.这样写也是正确的..例2.如图，点B 在线段AC 上，点E 在线段BD 上，∠ABD=∠DBC ，AB=DB ，EB=CB ，M,N 分别是AE,CD 的中点，试探索BM 和BN 的关系，并证明你的结论.【分析】规范书写过程：∵∠ABD=∠DBC ，且∠ABD+∠DBC=180° ∴∠ABD=∠DBC=90°在△ABE 与△DBC 中⎪⎩⎪⎨⎧=∠=∠=BC BE DBC ABE DB AB ∴△ABE ≌△DBC （SAS ） ∴AE=DC ∠BAE=∠BDC ∵M,N 分别是AE,CD 的中点 ∴AM=21AE ; DN=21DC ∴AM=DN在△ABM 与△DBN 中⎪⎩⎪⎨⎧=∠=∠=DN AM BDN BAM DB AB ∴△ABM ≌△DBN （SAS ） ∴BM=BN ∠ABM=∠DBN ∴∠ABM+∠MBD=∠DBN+∠MBD ∴∠MBN=∠ABD=90°，∴BM ⊥BN 小结：通过测试发现容易失分的地方有两处：（1） 证明∠ABD=∠BDC=90°时，不写∠ABD+∠DBC=180°，而直接由全等三角形对应角相等得出90°（2） 在书写M,N 分别是AE,CD 的中点时，没有写出中点的定义MNE DCBAAM=21AE ; DN=21DC ：而是由中点直接得出AM=DN ，思维不严谨.练习1.如图，OE 平分∠AOB ，在OA,OB 上取OC=OD ，PM ⊥CE 于M ，PN ⊥DE 于N ，探索PM,PN 的关系。

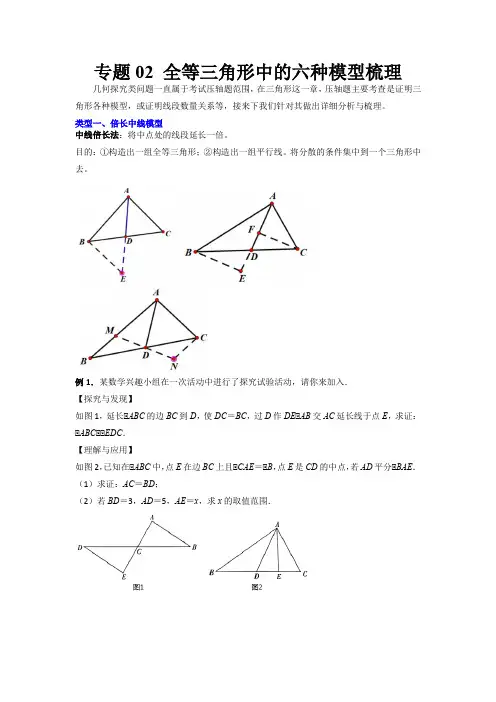
专题02 全等三角形中的六种模型梳理几何探究类问题一直属于考试压轴题范围，在三角形这一章，压轴题主要考查是证明三角形各种模型，或证明线段数量关系等，接来下我们针对其做出详细分析与梳理。

类型一、倍长中线模型中线倍长法：将中点处的线段延长一倍。

目的：①构造出一组全等三角形；②构造出一组平行线。

将分散的条件集中到一个三角形中去。

例1．某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．【探究与发现】如图1，延长△ABC的边BC到D，使DC＝BC，过D作DE△AB交AC延长线于点E，求证：△ABC△△EDC．【理解与应用】如图2，已知在△ABC中，点E在边BC上且△CAE＝△B，点E是CD的中点，若AD平分△BAE．（1）求证：AC＝BD；（2）若BD＝3，AD＝5，AE＝x，求x的取值范围．【变式训练1】如图1，在ABC 中，CM 是AB 边的中线，BCN BCM ∠=∠交AB 延长线于点N ，2CM CN =．（1）求证AC BN =；（2）如图2，NP 平分ANC ∠交CM 于点P ，交BC 于点O ，若120AMC ∠=︒，CP kAC =，求CPCM的值．【变式训练2】（1）如图1，已知ABC 中，AD 是中线，求证：2AB AC AD +>； （2）如图2，在ABC 中，D ，E 是BC 的三等分点，求证：AB AC AD AE +>+； （3）如图3，在ABC 中，D ，E 在边BC 上，且BD CE =．求证：AB AC AD AE +>+．【变式训练3】在ABC 中，点P 为BC 边中点，直线a 绕顶点A 旋转，BM ⊥直线a 于点M ．CN ⊥直线a 于点N ，连接PM ，PN ．（1）如图1，若点B ，P 在直线a 的异侧，延长MP 交CN 于点E ．求证：PM PE =．（2）若直线a 绕点A 旋转到图2的位置时，点B ，P 在直线a 的同侧，其它条件不变，此时7BMP CNP S S +=△△，1BM =，3CN =，求MN 的长度．（3）若过P 点作PG ⊥直线a 于点G ．试探究线段PG 、BM 和CN 的关系．类型二、截长补短模型截长补短法使用范围：线段和差的证明（往往需证2次全等）例．在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ，P 为△ABC 外一点，且△MPN ＝60°，△BPC ＝120°，BP ＝CP ．探究：当点M 、N 分别在直线AB 、AC 上移动时，BM ，NC ，MN 之间的数量关系．(1)如图①，当点M 、N 在边AB 、AC 上，且PM ＝PN 时，试说明MN ＝BM +CN ． (2)如图②，当点M 、N 在边AB 、AC 上，且PM ≠PN 时，MN ＝BM +CN 还成立吗？ 答： ．（请在空格内填“一定成立”“不一定成立”或“一定不成立”）．(3)如图③，当点M 、N 分别在边AB 、CA 的延长线上时，请直接写出BM ，NC ，MN 之间的数量关系．【变式训练1】如图，在四边形ABCD 中，,180AB AD B ADC =∠+∠=︒，点E 、F 分别在直线BC 、CD 上，且12EAF BAD ∠=∠．(1)当点E 、F 分别在边BC 、CD 上时（如图1），请说明EF BE FD =+的理由．(2)当点E 、F 分别在边BC 、CD 延长线上时（如图2），（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出EF 、BE 、FD 之间的数量关系，并说明理由．【变式训练2】（1）阅读理解：问题：如图1，在四边形ABCD 中，对角线BD 平分ABC ∠，180A C ∠+∠=︒．求证：DA DC =．思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题．方法1：在BC 上截取BM BA =，连接DM ，得到全等三角形，进而解决问题； 方法2：延长BA 到点N ，使得BN BC =，连接DN ，得到全等三角形，进而解决问题． 结合图1，在方法1和方法2中任选一种．．．．，添加辅助线并完成证明． （2）问题解决：如图2，在（1）的条件下，连接AC ，当60DAC ∠=︒时，探究线段AB ，BC ，BD 之间的数量关系，并说明理由；（3）问题拓展：如图3，在四边形ABCD 中，180A C ∠+∠=︒，DA DC =，过点D 作DE BC ⊥，垂足为点E ，请直接写出线段AB 、CE 、BC 之间的数量关系．【变式训练3】在ABC 中，BE ，CD 为ABC 的角平分线，BE ，CD 交于点F ． （1）求证：1902BFC A ∠=︒+∠；（2）已知60A ∠=︒．①如图1，若4BD =， 6.5BC =，求CE 的长； ②如图2，若BF AC =，求AEB ∠的大小．类型三、做平行线证明全等 例1．如图所示：ABC 是等边三角形，D 、E 分别是AB 及AC 延长线上的一点，且BD CE =，连接DE 交BC 于点M ． 求让：MD ME =【变式训练1】 P 为等边△ABC 的边AB 上一点，Q 为BC 延长线上一点，且P A ＝CQ ，连PQ 交AC 边于D ． （1）证明：PD ＝DQ ．（2）如图2，过P 作PE △AC 于E ，若AB ＝6，求DE 的长．【变式训练2】已知在等腰△ABC 中，AB =AC ，在射线CA 上截取线段CE ，在射线AB 上截取线段BD ，连接DE ，DE 所在直线交直线BC 与点M ．请探究：(1)如图（1），当点E 在线段AC 上，点D 在AB 延长线上时，若BD =CE ，请判断线段MD 和线段ME 的数量关系，并证明你的结论．(2)如图（2），当点E 在CA 的延长线上，点D 在AB 的延长线上时，若BD =CE ，则（1）中的结论还成立吗？如果成立，请证明；如果不成立，说明理由；类型四、旋转模型 例．如图1，AC BC =，CD CE =，ACB DCE α∠=∠=，AD 、BE 相交于点M ，连接CM ．（1）求证：BE AD =，并用含α的式子表示AMB ∠的度数；（2）当90α=︒时，取AD ，BE 的中点分别为点P 、Q ，连接CP ，CQ ，PQ ，如图2，判断CPQ 的形状，并加以证明．【变式训练1】四边形ABCD 是由等边ABC ∆和顶角为120︒的等腰ABD ∆排成，将一个60︒角顶点放在D 处，将60︒角绕D 点旋转，该60︒交两边分别交直线BC 、AC 于M 、N ，交直线AB 于E 、F 两点．（1）当E 、F 都在线段AB 上时（如图1），请证明：BM AN MN +=；（2）当点E 在边BA 的延长线上时（如图2），请你写出线段MB ，AN 和MN 之间的数量关系，并证明你的结论；（3）在（1）的条件下，若7AC =， 2.1AE =，请直接写出MB 的长为 ．【变式训练2】（1）问题发现：如图1，△ACB 和△DCE 均为等边三角形，当△DCE 旋转至点A ，D ，E 在同一直线上，连接BE ．则：①△AEB 的度数为 °；②线段AD 、BE 之间的数量关系是 ． （2）拓展研究：如图2，△ACB 和△DCE 均为等腰三角形，且△ACB ＝△DCE ＝90°，点 A 、D 、E 在同一直线上，若AD ＝a ，AE ＝b ，AB ＝c ，求a 、b 、c 之间的数量关系． （3）探究发现：图1中的△ACB 和△DCE ，在△DCE 旋转过程中，当点A ，D ，E 不在同一直线上时，设直线AD 与BE 相交于点O ，试在备用图中探索△AOE 的度数，直接写出结果，不必说明理由．【变式训练3】如图1，在Rt ABC 中，90A ∠=︒，AB AC =，点D ，E 分别在边AB ，AC 上，AD AE =，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是______，位置关系是______． （2）探究证明：把ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断PMN 的形状，并说明理由；（3）拓展延伸：把ADE 绕点A 在平面内自由旋转，若4=AD ，10AB =，请直接写出PMN 面积的最大值．类型五、手拉手模型例．在等边ABC 中，点D 在AB 上，点E 在BC 上，将线段DE 绕点D 逆时针旋转60°得到线段DF ，连接CF ．(1)如图（1），点D 是AB 的中点，点E 与点C 重合，连接AF ．若6AB =，求AF 的长； (2)如图（2），点G 在AC 上且60AGD FCB ∠=︒+∠，求证：CF DG =；(3)如图（3），6AB =，2BD CE =，连接AF ．过点F 作AF 的垂线交AC 于点P ，连接BP 、DP ．将BDP △沿着BP 翻折得到BQP ，连接QC ．当ADP △的周长最小时，直接写出CPQ 的面积．【变式训练1】△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形．(1)问题发现：如图1，若点A ，D ，E 在同一直线上，连接AE ，BE ． ①求证：△ACD △△BCE ；②求△AEB 的度数．(2)类比探究：如图2，点B 、D 、E 在同一直线上，连接AE ，AD ，BE ，CM 为△DCE 中DE 边上的高，请求△ADB 的度数及线段DB ，AD ，DM 之间的数量关系，并说明理由． (3)拓展延伸：如图3，若设AD （或其延长线）与BE 的所夹锐角为α，则你认为α为多少度，并证明．【变式训练2】（1）如图1，锐角△ABC 中，分别以AB 、AC 为边向外作等腰直角△ABE 和等腰直角△ACD ，使AE ＝AB ，AD ＝AC ，∠BAE ＝∠CAD ＝90°，连接BD ，CE ，试猜想BD 与CE 的大小关系，不需要证明．【深入探究】（2）如图2，四边形ABCD 中，AB ＝5，BC ＝2，∠ABC ＝∠ACD ＝∠ADC ＝45°，求BD 2的值；甲同学受到第一问的启发构造了如图所示的一个和△ABD 全等的三角形，将BD 进行转化再计算，请你准确的叙述辅助线的作法，再计算；【变式思考】（3）如图3，四边形ABCD 中，AB ＝BC ，∠ABC ＝60°，∠ADC ＝30°，AD ＝6，BD ＝10，则CD ＝ ．【变式训练3】（1）问题发现：如图1，ACB △和DCE 均为等腰直角三角形，90ACB DCE ∠=∠=︒，连接AD ，BE ，点A 、D 、E 在同一条直线上，则AEB ∠的度数为__________，线段AD 、BE 之间的数量关系__________；（2）拓展探究：如图2，ACB △和DCE 均为等腰直角三角形，90ACB DCE ∠=∠=︒，连接AD ，BE ，点A 、D 、E 不在一条直线上，请判断线段AD 、BE 之间的数量关系和位置关系，并说明理由． （3）解决问题：如图3，ACB △和DCE 均为等腰三角形，ACB DCE α∠=∠=，则直线AD 和BE 的夹角为__________．（请用含α的式子表示）类型六、一线三角模型例.在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C 且AD MN ⊥于D ，BE MN ⊥于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：①ADC △CEB △；②DE AD BE =+；(2)当直线MN 烧点C 旋转到图2的位置时，求证：DE AD BE =-；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．【变式训练1】【问题解决】（1）已知△ABC 中，AB =AC ，D ，A ，E 三点都在直线l 上，且有△BDA =△AEC =△BAC ．如图①，当△BAC =90°时，线段DE ，BD ，CE 的数量关系为：______________；【类比探究】（2）如图②，在（1）的条件下，当0°<△BAC<180°时，线段DE，BD，CE的数量关系是否变化，若不变，请证明：若变化，写出它们的关系式；【拓展应用】（3）如图③，AC=BC，△ACB=90°，点C的坐标为（-2，0），点B的坐标为（1，2），请求出点A的坐标．【变式训练2】（1）如图1，在△ABC中，△BAC＝90°，AB＝AC，直线m经过点A，BD△直线m，CE△直线m，垂足分别为点D、E．求证：△ABD△△CAE；（2）如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有△BDA＝△AEC＝△BAC＝α，其中α为任意锐角或钝角．请问结论△ABD△△CAE是否成立？如成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图3，D，E是D，A，E三点所在直线m上的两动点（D，A，E三点互不重合），点F为△BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若△BDA＝△AEC＝△BAC，求证：△DEF是等边三角形．【变式训练3】探究：（1）如图（1），已知：在△ABC中，△BAC=90°，AB=AC，直线m经过点A，BD△直线m，CE△直线m，垂足分别为点D、E．请直接写出线段BD，DE，CE之间的数量关系是．拓展：（2）如图（2），将探究中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有△BDA=△AEC=△BAC=α，其中α为任意锐角或钝角．请问探究中的结论是否成立？如成立，请你给出证明；若不成立，请说明理由．应用：（3）如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为△BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若△BDA=△AEC=△BAC，请直接写出△DEF的形状是．。

江夏区第一初级中学“三为主，N环节”教学模式数学学科导学案序号：20 设计者：洪彩虹班级：姓名：时间：课题利用截长补短法构造全等三角形教学目标利用截长补短法构造全等三角形，从而证明线线段之间的和差关系教学重难点：利用截长补短法构造全等三角形。

一、目标导学，引入新课证明一条线段等于两条线段和差时，通常采用截长法或补短法。

截长法就是在较长线段上截取一段，使之等于其中一段短线段，再设法证明剩下的线段等于另一短线段；补短法就是延长短线段中的一条，使延长来的线段等于另一短线段，再证明两线段之和等于较长线段，或直接将某短线段延长至等于较长的线段。

二、典型例题如图：已知AC∥BD，E是CD上一点，且EA、EB分别平分∠CAB和∠DBA，求证：AB=AC+BD 证明：方法一（截长法）在AB上截取AF=AC，连接EF。

（自已完成下面的证明）方法二：（补短法）延长AC至F，使AF=AB，连接EF。

三、巩固应用1、如图，在ΔABC中，∠B=60º，两条角平分线AD、CE交于点O求证：AC=AE+CD2、如图：E是正方形ABCD的BC边上的中点，EF⊥AE于E交∠DCM的角平分线于F，（1）试探究线段AE与EF的数量关系。

（2）若点E是BC边上不同于B、C的任意一点，其他条件不变，上述结论仍然成立吗？画出图形并证明。

（3）若点E是BC延长线上一点，其他条件不变，结果又如何？请直接写出结论。

3、如图：正方形ABCD中，E、F分别在BC、CD边上，且∠EAF=45º，求证：BE+DF=EF4、如图：在ΔABC中AB>AC，∠1=∠2，P为AD上任意一点，求证：AB-AC>PB-PC5、如图：平面直角坐标系中，P（1，1）A为y负半轴上一点，B为X正半轴上一点，PA=PB，（1）求∠P的度数，（2）若A（0，-2）求B点坐标。

（3）当点A在y负半轴上运动时，OB-OA的值是否发生变化？为什么？四、布置作业：完成《新观察》P32。